Quantifying ecosystem metabolism in the middle reaches of Murrumbidgee River during irrigation flow releases
S. Vink A B , M. Bormans A , P. W. Ford A and N. J. Grigg AA CSIRO Land and Water, GPO Box 1666, Canberra, ACT 2601, Australia.
B Corresponding author. Email: sue.vink@csiro.au
Marine and Freshwater Research 56(2) 227-241 https://doi.org/10.1071/MF04187
Submitted: 14 July 2004 Accepted: 31 January 2005 Published: 12 April 2005
Abstract
The relative importance of floodplain carbon inputs and in-stream metabolic processes have not been well quantified in major Australian rivers. We quantified seasonal phytoplankton primary production and net ecosystem production during irrigation flow regimes at four sites each located ~100 km apart in the middle Murrumbidgee River. During flow periods dominated by storage release, ecosystem gross primary productivity, system respiration and phytoplankton chlorophyll concentrations all increased downstream so that overall net ecosystem metabolism was strongly net heterotrophic upstream and closer to balanced downstream. Phytoplankton production dominated ecosystem production throughout the entire reach and was likely to have been phosphorus limited throughout the study. Additionally, phytoplankton biomass was limited by short residence times at the upstream sites and nitrogen limited downstream in summer, despite an increase in turbidity. Both production and respiration rates were generally lower in winter, as expected, owing to lower temperatures.
Extra keywords: carbon cycling, heterotrophic, phytoplankton production, respiration, river metabolism.
Acknowledgments
We thank the following individuals and organisations for help with routine sampling: Peter Pollock and Terry Dowel from Gundagai Shire; Nicole Vonax, Gemma Urquart and the plant operators at Riverina County Water; Richard and Nicholas Hart from Kooba Station; Stephen Thurstan and Matt McLellan from Narrandera Inland Fisheries Research Centre; Roy Zandona, Stuart Paterson and Wendy Minato from CLW Griffith; and Brendan Ebner from Environment-ACT. Thanks also to Rob Cawley (DIPNR) for rating curves, river cross-sections and other data as well as many fruitful discussions. The manuscript was greatly improved by comments from Barbara Robson, Richard Davis and two anonymous reviewers.
Baldwin, D. S. , Whittington, J. , and Oliver, R. (2003). Temporal variability of dissolved P speciation in a eutrophic reservoir-implications for predicting algal growth. Water Research 37, 4595–4598.
| Crossref | GoogleScholarGoogle Scholar | PubMed |
Caraco, N. F. , Cole, J. J. , Raymond, P. A. , Strayer, D. L. , Pace, M. L. , Findlay, S. E. , and Fischer, D. T. (1997). Zebra Mussel invasion in a large, turbid river: phytoplankton response to increased grazing. Ecology 78, 588–602.
Chapra, S. C. , and Di Toro, D. M. (1991). The delta method for estimating community production, respiration and reaeration in streams. Journal of Environonmental Engineering 117, 640–655.
Froelich, P. N. (1988). Kinetic control of dissolved phosphate in natural rivers: a primer on the phosphate buffer mechanism. Limnology and Oceanography 33, 649–668.
Holm-Hansen, O. , and Reimann, B. (1978). Chlorophyll a determination: improvements in methodology. Oikos 30, 438–457.
Kelly, M. G. , Hornberger, G. H. , and Cosby, B. J. (1974). Continuous automated measurement of rates of photosynthesis and respiration in an undisturbed river community. Limnology and Oceanography 19, 305–312.
Leuning, R. , Cleugh, H. A. , Zegelin, S. J. , and Hughes, D. (2005). Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry Savanna in Australia: Measurements and comparison with MODros. Inf. Serv. remote sensing estimates. Agricultural and Forest Meteorology ,in press.
Lorenzen, C. (1967). Determination of chlorophyll and phaeopigments: Spectrophotometric equations. Limnology and Oceanography 12, 343–346.
Pace, M. L. , Findlay, S. E. G. , and Lints, D. (1992). Zooplankton in advective environments: the Hudson River community and a comparative analysis. Canadian Journal of Fisheries and Aquatic Sciences 49, 1060–1069.
Richey, J. E. , Hedges, J. I. , Devol, A. H. , Quay, P. D. , Victoria, R. , Martinelli, L. , and Forsberg, B. R. (1990). Biogeochemistry of carbon in the Amazon River. Limnology and Oceanography 35, 352–371.
Webster, I. T. , Ford, P. W. , and Hancock, G. (2001). Phosphorus dynamics in Australian lowland rivers. Marine and Freshwater Research 52, 127–137.
| Crossref | GoogleScholarGoogle Scholar |
Wilcock, R. J. , McBride, G. B. , Nagels, J. W. , and Northcott, G. L. (1995). Water quality in a polluted lowland sream with chronically depressed dissolved oxygen: causes and effects. New Zealand Journal of Marine and Freshwater Research 29, 277–288.
with those computed simultaneously with k20 by curve fitting showed generally good agreement. However for a few (~7% in total) 24 h periods, curve fitting yielded kex values that were close to zero. These kex values were also extremely low relative to values calculated for the previous and following days. Since flow and other general conditions had not changed appreciably between the days in question we concluded that the kex estimated by curve fitting was in error on these days. The exact reason for this discrepancy is not readily apparent at this time and is being investigated further. Consequently, in order to attain the most reliable estimates of GPP and R24, we computed an average daily value for kex using hourly flow and water depth records at each site in Eqn (A1) above. Thus in our analysis, Eqn (1) was solved for only 2 parameters k20 and Pmax.
Optimisation procedure and computation of confidence limits on GPP and R24
Typically, a least-squares method is used to evaluate the optimum parameter values of k20 and Pmax in Eqn (1) (e.g. Kelly et al. 1974); however, we used a maximum-likelihood analysis (Hilborn and Mangel 1997). This method is equivalent to performing a least-squares fit but provides an error estimate to be calculated for each parameter that encompasses the uncertainty associated with the estimated values of the other parameters in addition to measurement/sampling errors.
Initial values for k20 and Pmax were chosen from the literature (Wilcock et al. 1998), we then used Matlab’s ‘ode45’ function to numerically integrate Eqn (1) over each 24 h period to produce a modelled dissolved O2 time series. The goodness of fit between the modelled dissolved O2 time series and the in-situ measured times series was determined by calculating the negative log-likelihood (L):
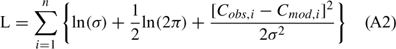
where Cobs,i and Cmod,i are the measured and modelled CO2 values for the ith data point. This method assumes that the CO2 measurement errors are normally distributed with zero mean and known standard deviation, σ. The standard deviation of the dissolved O2 data was determined by placing the multiprobe instruments into water equilibrated with the air for ~1 h. The standard deviation of these measurements for each instrument was averaged and used in the log-likelihood analysis. Note that in this particular case the measurement error is assumed to be normally distributed, and so minimising Eqn (A2) is equivalent to minimising the sum of the squared deviation between measured and modelled values.
Matlab’s ‘fminsearch’ function was used to repeat the integration iteratively and find parameter values that minimise Eqn (5) for each 24 h period. Once optimum values of Pmax and k20 had been estimated for each 24 h period, we quantified the uncertainty in each parameter value using a likelihood ratio test. One parameter was fixed at a given value and the remaining parameter was estimated using the optimisation routine. The fixed parameter was then changed to another value and the process repeated. The negative log-likelihood (L) values calculated from this procedure were used to calculate confidence bounds on GPP, R24 using a likelihood ratio test (Hilborn and Mangel 1997).


