Comparison of two methods for attributing length of hospital stay to healthcare-acquired infection
Nicholas Graves A B D , Edward Tong A , Malcolm Faddy C and Michael Whitby AA The Centre for Healthcare Related Infection Surveillance and Prevention, Princess Alexandra Hospital, Brisbane, Qld 4102, Australia.
B Institute for Health and Biomedical Innovation, Queensland University of Technology, Brisbane, Qld 4059, Australia.
C School of Mathematics, Queensland University of Technology, Brisbane, Qld 4059, Australia.
D Corresponding author. Email: n.graves@qut.edu.au
Healthcare Infection 13(4) 111-119 https://doi.org/10.1071/HI08027
Published: 5 December 2008
Abstract
The development of models of the cost-effectiveness of infection control programs must be informed by valid estimates of the extra length of hospital stay due to healthcare-acquired infection (HAI). The aim of this study was to compare two competing methods for attributing extra hospital stay to healthcare-acquired infection. Data were collected prospectively from two Australian hospitals. The two competing methods used to attribute extra hospital days to HAI were: (i) a matched cohort design; and (ii) a procedure for selecting predictors associated with length of stay and their subsequent inclusion in a statistical model of length of stay. There were 40 patients exposed to multiple HAIs among 4488 patients recruited over 95 days of data collection (incidence rate 0.89%). The estimates from five separate matching procedures were between 23.38 and 31.78 extra days in hospital, and the results of the statistical model suggested an exposed patient independently increased length of hospital stay by a mean of 21.0 days (95% confidence interval 17.3, 25.1). Matching studies may suffer from two potential sources of bias: the selection of exposed patients from over-matching may underestimate the true cost of HAI, and the omission of important predictors may overstate the cost of HAI. Statistical regression techniques can be used to mitigate both potential problems.
Acknowledgements
This work was supported by the Queensland Health Quality Improvement and Enhancement Program. The authors have no conflict of interest.
[1] Graves N. Economics and preventing hospital-acquired infection. Emerg Infect Dis 2004; 10 561–6.
| PubMed | [accessed 4 April 2007].
[17] Beyersmann J, Dettenkofer M, Bertz H, Schumacher M. A competing risks analysis of bloodstream infection after stem-cell transplantation using subdistribution hazards and cause-specific hazards. Stat Med 2007; 26 5360–9.
| Crossref | GoogleScholarGoogle Scholar | PubMed | was
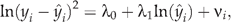
where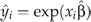 
from the generalised linear model specification. The estimate of the coefficient λ1 on the log of the raw scale prediction indicated the family distribution to be employed. If λ1 was 0, the Gaussian family was employed, where the variance was constant. If λ1 was 1, the Poisson family was indicated, where the variance was proportional to the mean. If λ1 was 2, the gamma family was selected, where the variance was proportional to the mean squared. If λ1 was 3, the inverse Gaussian family was employed, where the variance was proportional to the cube of the mean. The modified Park test suggested coefficient λ1 = 1.91, which supported the gamma family since λ1 was not significantly different from 2, F(1, 4363) = 3.01, P = 0.08, where the variance was proportional to the square of the mean. The gamma family was then employed in the GEE model.