Determining the height of deep volcanic eruptions over the tropical western Pacific with Himawari-8
Chris Lucas A *
A *
A The Bureau of Meteorology, GPO Box 1289, Melbourne, Vic. 3001, Australia.
Journal of Southern Hemisphere Earth Systems Science 73(2) 102-115 https://doi.org/10.1071/ES22033
Submitted: 26 September 2022 Accepted: 13 April 2023 Published: 10 May 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of the Bureau of Meteorology. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Volcanic eruptions are significant aviation hazards due to the formation of airborne volcanic ash clouds. Further, deep eruptions that reach the upper troposphere and lower stratosphere may have significant weather and climate impacts. A key variable for both dispersion model forecasting for aviation hazards and understanding climate impacts is the volcanic plume height. This work presents a method to quickly and reliably estimate the maximum plume heights of volcanic eruptions that interact with the tropical tropopause layer in the tropical western Pacific region. The method uses infrared (11.2 μm) data from Himawari-8 to identify ‘stratospheric warm spots’ in optically thick portions of the eruption cloud top by searching for reversals in the local-brightness temperature gradient. The brightness temperature of these warm spots is converted to height using seasonal stratospheric reference temperature profiles derived from 20 years of radiosonde data from 17 stations spread throughout the western Pacific. An approach for estimating the height of cold ‘overshooting tops’ is also adopted. Based on the radiosonde data, estimates of the uncertainty in the plume height depend on the height and range within 0.5–5.0 km. A case study of the 19 December 2021 eruption of Hunga Tonga-Hunga Ha’apai demonstrates the technique. The heights are robustly determined with this simple technique and compare well with height estimates of eruptions in the literature that use more complex satellite techniques.
Keywords: aviation, climate, cloud top height, dispersion modelling, radiosonde, satellite, stratosphere, temperature, tropopause, volcanic ash, volcanic cloud, volcano.
1.Introduction
Deep volcanic plumes in the tropics – here considered those that interact with the tropical tropopause layer (TTL) between 14 and 18 km (Fueglistaler et al. 2009) – can have significant effects on both weather and climate around the globe. Over the tropical western Pacific, observations for 2015–2022 indicate that there are typically 1–3 such eruptions every year (Lucas 2022). Further, these observations show that the volcanic plumes in these eruptions regularly extend above the TTL and into the stratosphere. Herein, the ‘plume’ represents the vertical extent of the eruption column and is the highest part of the eruption cloud, whereas the ‘umbrella’ is cloud spread radially outward at the level of neutral buoyancy, analogous to the anvil of a cumulonimbus cloud (e.g. Mastin et al. 2009; Mastin and Van Eaton 2020).
A primary user of volcanic related information is the aviation industry. Volcanic ash in the atmosphere can severely damage jet aircraft and inhibit their ability to operate safely (Guffanti et al. 2010; Lechner et al. 2018). An integral component for operationally managing the risks from volcanic ash in real time are numerical simulations made with atmospheric dispersion models. The key parameter needed for accurate operational dispersion modelling is the height of the volcanic plume, which serves as the basis for many parameterisations of the source term characteristics (e.g. Mastin et al. 2009; Witham et al. 2012; Zidikheri and Lucas 2020). Specifying the height correctly in dispersion models also ensures that the simulated ash is being transported at the appropriate levels of the atmosphere, leading to a more skilful forecast (e.g. Zidikheri et al. 2018). Generally, this requires the maximum plume height observed in the initial phases of the eruption.
Volcanic eruptions, particularly those in the tropics, can also have a climatic impact. Very large eruptions, such as the eruption events of Mount Pinatubo in 1991 or El Chichón in 1982, can inject large amounts of aerosol into the stratosphere resulting in the cooling of the global surface temperature (e.g. Robock 2000), alteration of precipitation patterns (e.g. Zuo et al. 2019), a contraction of the tropics (Lucas et al. 2021) and possibly the triggering of an El Niño or La Niña event (e.g. Swingedouw et al. 2017; Pausata et al. 2020). The cumulative effect of multiple smaller eruptions may also affect the climate, changing the temperature (Stocker et al. 2019) and aerosol loading (Vernier et al. 2011; Andersson et al. 2015) in the upper troposphere–lower stratosphere (UTLS), potentially leading to decadal-scale changes in climate (Ridley et al. 2014; Santer et al. 2014). Full understanding of these effects requires knowing the eruption height of these events.
Estimating the height of volcanic plumes from satellite data can be challenging, particularly in an operational setting; see the discussion regarding the June 2011 eruption height of the Eritrean volcano Nabro for an example (Bourassa et al. 2012; Fromm et al. 2013; Vernier et al. 2013). The standard, simplest and most common approach to determine cloud height is to use a vertical profile of temperature, say from a nearby radiosonde or operational numerical weather prediction (NWP) data, and identify the height level in the profile that matches the observed brightness temperature (BT) of the pixel representative of the top of the cloud (e.g. Woods and Self 1992; Oppenheimer 1998; McKee et al. 2021). Difficulties arise because the temperature profile of the stratosphere is inverted (i.e. increases with height) and so cloud top height estimates considering the UTLS together can yield multiple solutions; the complex structure of the TTL can also add ambiguity. Further, this approach requires that the emissivity (ε) of the volcanic cloud is ~1, a reasonable assumption in the early stages of an eruption near the source, but generally not as reliable at later times or greater spatial distances from the eruption because the cloud becomes optically thin.
An analogous approach using the wind profile is also used in operations, particularly in situations with strong directional shear. Here, observed changes in the direction of the cloud motion are related to the heights of the vertical wind shear layers in a profile, yielding the height of the cloud, or at least particular portions of it. This approach does not require particular emissivity characteristics of the cloud but is more appropriate some time after the initial eruption has passed and the differential motion of the clouds is clearer in imagery.
Satellite-based retrieval methodologies using optimal estimation (e.g. Francis et al. 2012; Pavolonis et al. 2013; Prata et al. 2022) return quantitative estimates of cloud top height, mass loading and particle size information. These retrievals require volcanic clouds to be semi-transparent (ε < 1); retrievals in ‘optically thick’ clouds are not possible and height estimates in that circumstance are generally equivalent to the temperature profile methodology described above. In optically thick volcanic clouds from eruptions of Manam, Papua New Guinea, during 2005, Tupper et al. (2007) used a CO2-slicing retrieval methodology with multiple channels of wavelengths >13 μm. The technique is not readily available in real time and has difficulty with cloud tops at and above the tropopause.
Other satellite-based techniques for estimating the height of volcanic plumes have been reported. Satellite stereo spectroscopy with near-simultaneous observations from two geostationary satellites has been successfully used to photogrammetrically estimate the height (Merucci et al. 2016; Carr et al. 2022; Proud et al. 2022). A conceptually similar technique using the Multi-Angle SpectroRadiometer has been applied for volcanoes in Kamchatka and other regions (Flower and Kahn 2017). A methodology for the use of ‘near-limb’ satellite observations has been developed (Horváth et al. 2021a, 2021b), in which imagery from the edge of a full disc is used to get a side-on view of a volcanic plume, from which heights may be directly estimated through a geometrical approach. In most cases, these techniques require the eruption to occur in particular locales (i.e. within the view of two geostationary satellites or on the limb), which is not always possible. In the Kelud eruption of 2014, a fortunate satellite overpass allowed for the determination of plume height directly from the space-borne Cloud-Aerosol Lidar with Orthogonal Projection instrument (Kristiansen et al. 2015; Vernier et al. 2016). Finally, the length of shadows cast by volcanic plumes can be exploited with consideration of the satellite viewing angles and solar geometry (e.g. Shettigara and Sumerling 1998; Prata and Grant 2001). This technique is only available in the daytime and performs best near sunrise and sunset when shadow lengths are extended. In general, these approaches work well for research applications, but are not available operationally.
In this work, the focus is on using a refined version of the brightness temperature methodology to determine the maximum eruption plume height of clouds that reach the UTLS over the tropical western Pacific and eastern Indian Ocean. The BT methodology is straightforward, simple to apply and readily available in an operational environment. A complication in the approach is the selection of an appropriate UTLS temperature profile. Typically, the nearest radiosonde station is identified, with that temperature profile assumed to be representative of the atmosphere at the eruption site. However, the sparseness of available radiosonde sites and the low vertical resolution of the reported data can present challenges. As an alternative, a temperature profile from an NWP model or reanalysis (in post event analysis) can eliminate the issue of distance from the eruption, but the vertical resolution of the data in the stratosphere is often poor. Further, stratospheric data from NWP systems are often not routinely available on the operational forecast software platforms, with little data available above 100 hPa. Additionally, models and forecast systems often fail to accurately resolve important stratospheric processes, which results in biases and degrades skill of the system (Lawrence et al. 2022).
The temperature variability of tropical UTLS also presents challenges to identifying a representative profile. In general, the underlying tropical UTLS temperature structure is largely spatially homogeneous, with only small regional variability in temperatures (Scherllin-Pirscher et al. 2021). This temperature structure results from a balance of radiative, chemical and large-scale dynamical processes. Randel and Wu (2015) show that the seasonal cycle is the primary source of variability in much of the stratosphere. The Quasi-Biennial Oscillation (QBO) and El Niño–Southern Oscillation (ENSO) can play significant roles on interannual time scales. Other factors, including poorly understood forcing from polar sudden stratospheric warmings and changes in chemical composition from aerosol and ozone (e.g. from volcanic eruptions or bushfires) can affect temperatures on seasonal (or longer) time scales.
This slow variability is overwhelmed by that associated with ubiquitous gravity wave activity, which dominates the stratosphere (Kim and Alexander 2015). In the tropics, these waves occur across a range of scales, with typical horizontal scales of 10–1000 km, vertical wavelengths of 2–10 km and time scales of ~1 day (e.g. Scherllin-Pirscher et al. 2021). These waves can be readily apparent when looking at stratospheric temperature profiles from radiosonde data in the tropics (Vincent and Alexander 2000). This strong spatial and temporal variability on short time-scales raises questions about the representativeness of any individual profile in estimating the height of a stratosphere volcanic eruption, adding a significant and largely unknown uncertainty.
The key contributions of this paper are to address distinguishing between stratospheric–tropospheric eruptions and the choice of an appropriate temperature profile. With this information, the results can be as accurate as other techniques with considerably less overhead. In this paper, a methodology to formalise the detection of stratospheric plumes utilising the horizontal gradients of BT on the volcanic cloud top is introduced. To facilitate the conversion of BT to heights, a new high-resolution ‘reference profile’ for the tropical UTLS is created using historical radiosonde data. Examples from the 19 December 2021 eruption of Hunga Tonga-Hunga Ha’apai (HTHH) are presented to illustrate the techniques. The argument for the use of the climatology-based reference temperature profile is supported, particularly in an operational setting. Brief comparisons of the height estimates made with the technique defined here with independent estimates for the 26 June 2019 eruption of Ulawun and the 15 January 2022 eruption of HTHH reported in the literature using different techniques further illustrate the validity of this approach.
2.Data and method
2.1. Satellite
Satellite data used in this study come from the Japanese Meteorological Agency’s Himawari-8 satellite in geostationary orbit (Bessho et al. 2016). The primary instrument on Himawari is the Advanced Himawari Imager, a 16-channel instrument measuring radiance from the visible to the thermal infrared (IR). In the IR channels, the pixel resolution at the sub-satellite point is 2 km. For this work, channel 14 centred at 11.2 μm is the primary channel. Data are processed and archived by the Australian Bureau of Meteorology and accessed using Australia’s National Computing Infrastructure supercomputer (Australian Bureau of Meteorology 2021).
Because the stratosphere is isothermal or warms with height, identifying the height of volcanic plumes that extend into the stratosphere is difficult. When plumes are confined to the troposphere, the minimum BT can be identified with reasonable assurance that this temperature represents the coldest (and therefore highest) cloud top. When plumes are stratospheric, an examination of the horizontal structure of the volcanic cloud top is necessary to ascertain the height of the plume. Generally speaking, volcanic plumes that ascend into the stratosphere appear either as (1) persistent clouds (~1–12 h) that have a distinctive ‘stratospheric warm spot’ (SWS) signature or as (2) short-lived overshooting tops (OTs) that are notably colder than the surrounding cloud top. Conceptually, plumes that appear as an SWS are assumed to have stopped their rapid ascent, produced or transported enough ash, ice and cloud to produce a radiometric signal, and are in thermodynamic equilibrium with the ambient environment. Clouds that manifest as OTs are presumably regions of recent strong ascent, with largely undilute central updrafts. A parcel in this circumstance is negatively buoyant and is decelerating and beginning to mix with the ambient environment. As a result of these processes, OTs can evolve into SWSs on short time scales.
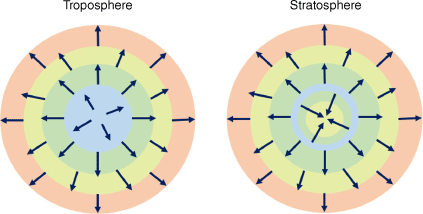
The first concept is illustrated in schematic form (Fig. 1), with colours representing BT contours as they might be visualised in satellite imagery. In the idealised tropospheric cloud (left), the coldest cloud portion of the cloud top is in the interior, and the gradient of the brightness temperature (∇BT) is axisymmetric about the coldest, highest portion of the cloud, with vectors directed outward towards the edges of the cloud feature. With the idealised stratospheric cloud (right), the contours in the centre of the cloud ‘reverse’ with warmer temperatures observed inside the coldest contour, creating a distinct signature, the SWS noted earlier. In many cases, only the SWS corresponds to the stratospheric cloud; most of the cloud remains in the troposphere as part of the umbrella. Corresponding to the SWS, ∇BT changes direction and locally points inwards towards the warmer cloud, creating divergence of the vectors in the ∇BT field.
Schematic diagram illustrating behaviour of brightness temperature in tropospheric and stratospheric cloud tops. Colours represent infra-red brightness temperature contours, with red > yellow > green > blue, arrows depict the direction of the local gradient of the brightness temperature.
In many SWS cases, a stratospheric cloud can be readily identified via visual inspection of satellite imagery. The ability to do so depends on factors like the choice of enhancement used to visualise the imagery and the relative strength of the SWS, i.e. the BT contrast. In other events, the SWS is more subtle and difficult to identify. Following the discussion above, one useful metric is to evaluate the Laplacian of BT:
The calculation is performed at the scale of individual pixels using a standard centred finite difference approach. From a practical viewpoint, the pixel level calculations are noisy and can pick up on small fluctuations in BT; to alleviate this issue the results are smoothed over a 3 × 3 pixel area, putting the focus on larger-scale structures in the cloud top. Negative values indicate a reversal of the temperature gradient and possible SWSs as depicted Fig. 1. This calculation provides a useful guide to assist in the analysis; it does not exclusively and objectively identify SWSs without human intervention.
For the OT scenario, we adopt the approach described by Griffin et al. (2016). This approach calculates overshooting top height ZOT:
where ZU is the height of the umbrella (estimated from the umbrella BT, BTU), BTOT is the BT of the OT, and LR is the lapse rate, describing how the cloud cools above the umbrella/anvil. From a purely parcel theory perspective, this rate would be equivalent to the adiabatic LR; given the minute amounts of water vapour at the altitudes under consideration here, this is essentially the dry adiabatic LR = 9.8 K km−1, modified by the physical process of entrainment. Owing to issues of sensor spatial resolution creating warm biases in the satellite imagery, Griffin et al. (2016) set LR = 7.3 K km−1 for 1-km pixels from the Aqua satellite; lower spatial resolution onboard geostationary creates even larger biases; linear regression identified the magnitudes of these biases for 3- and 4-km resolution sensors (SEVIRI and GOES-13 respectively). Bedka et al. (2018) adopted this approach for the Australian region using the 4-km JMA MTSAT series of satellites, suggesting LR = 3.4–4.9 K km−1. Using typical BTs for umbrella and OT observed here, the SEVIRI regression suggests a LR bias of ~1 K km−1. The resolution of AHI is higher than SEVIRI, and the modelled bias may be an overestimate. For this work we assume LR = 6.5 K km−1, equivalent to a bias of 0.8 K km−1.
2.2. Radiosondes
To create of standardised reference profile for the UTLS in the region of interest, radiosonde data from Version 2 of Integrated Global Radiosonde Archive (IGRA2; Durre et al. 2018) are used. Radiosondes are widely spaced, but frequently launched (sub-daily in many cases) with an extensive historical record. Profiles of pressure, temperature, humidity and wind are reported on pre-defined ‘mandatory levels’ at fixed pressures and on sporadic ‘significant levels’, points where the wind, temperature or humidity observations deviate from the prevailing tendencies of the profile in question. Radiosondes reliably reach altitudes of 30–35 km, well into the stratosphere. Radiosondes may be subject to homogenisation issues related to instrumentation changes and reporting techniques (e.g. Jovanovic et al. 2017). These are not accounted for in this work.
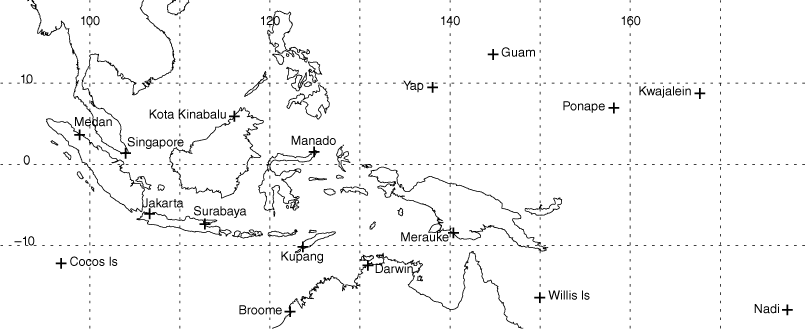
Given the limitations of radiosondes, data from multiple stations over an extended time period are required to construct an adequate reference profile. A further constraint is that the area from which the stations are drawn should show a high degree of spatial homogeneity. This study focuses on a large area of the tropical western Pacific, approximately 95–180°E to 15°N–20°S (Fig. 2) with 17 long-term stations chosen for analysis (Table 1). This area broadly covers tropical portions of the VAAC Darwin, VAAC Tokyo and portions of VAAC Wellington and VAAC Washington. Data are analysed over the period of 2000–2021 to ensure that the reference profile reflects observed stratospheric temperature changes of 1–3 K since 1979 (Steiner et al. 2020; Scherllin-Pirscher et al. 2021). At a minimum, all selected stations have records that extend back to the early 1970s.
| Station number | Station name | Longitude | Latitude | Number of sounds used |
|---|---|---|---|---|
| 48698 | Singapore, Republic of Singapore | 103.98 | 1.37 | 15 606 |
| 91212 | Guam | 144.79 | 13.47 | 15 792 |
| 91348 | Pohnpei, Federated States of Micronesia | 158.20 | 6.95 | 15 188 |
| 91366 | Kwajalein, Republic of the Marshall Islands | 167.73 | 8.73 | 7177 |
| 91413 | Yap, Federated States of Micronesia | 138.07 | 9.48 | 15 561 |
| 91680 | Nadi, Fiji | 177.45 | −17.75 | 10 185 |
| 94120 | Darwin, Northern Territory, Australia | 130.89 | −12.42 | 15 719 |
| 94203 | Broome, Western Australia, Australia | 122.24 | −17.95 | 8658 |
| 94299 | Willis Island, Queensland, Australia | 149.97 | −16.28 | 8605 |
| 96035 | Medan, Sumatra, Indonesia | 98.88 | 3.64 | 10 288 |
| 96471 | Kota Kinabalu, Borneo, Malaysia | 116.05 | 5.93 | 12 962 |
| 96749 | Jakarta, Java, Indonesia | 106.65 | −6.12 | 11 827 |
| 96935 | Surabaya, Java, Indonesia | 112.79 | −7.38 | 10 302 |
| 96996 | Cocos Islands | 96.83 | −12.19 | 8605 |
| 97014 | Manado, Sulawesi, Indonesia | 124.92 | 1.53 | 11 379 |
| 97372 | Kupang, Timor, Indonesia | 123.67 | −10.17 | 9556 |
| 97980 | Merauke, Irian Jaya, Indonesia | 140.38 | −8.47 | 8681 |
Listed are the World Meteorological Organization station number, the name and location of the station and the total number of soundings used from the station in constructing the reference profile. Total number of radiosondes used is 196 091.
The aim of the analysis is to create a high-resolution (0.5 km) reference profile that can be used to convert satellite-based IR BTs into reliable, consistent estimates for the height of volcanic plumes that reach the UTLS. We confine the analysis here to pressures below 200 hPa, ~12.5-km altitude, using ‘mandatory’ and ‘significant’ level data for temperature (T), pressure (P) and geopotential height (Z). The Z is generally only reported on mandatory levels in IGRA2 data and so it is calculated using the hypsometric equation, neglecting water vapour (virtual temperature TV ≈ T at these levels) and the Eötvös effect (Ong and Roundy 2020). The reported 200-hPa value of Z is used as the baseline for the calculation. The values of Z, P and T for both the ‘lapse-rate tropopause’ (LRT), based on the standard World Meteorological Organization (1957) definition, and the ‘cold point tropopause’, the coldest point in the sounding, are also estimated for each sounding; the reported LRT ‘flags’ in the data are often not reliable or missing.
The processed sounding data are placed into two joint frequency distributions (JFDs), one each for Z–T and Z–P. These JFDs have bin sizes of ΔZ = 0.5 km, ΔT = 1.0 K and ΔP = 1 hPa and cover the ranges Z = 12–42 km, T = 178–278 K and P = 1–200 hPa. The JFDs are tabulated over months, with all years in the analysis period included in the appropriate month. Seasonal and annual means are determined by combining JFDs for individual months. Each of the 17 stations has its own set of JFDs. To generate the profiles, means are computed along height levels of the JFD to get the pressure and temperature profile at a given station; uncertainty is estimated by determining the range from the 16th to the 84th percentile at a height level, equivalent to a 1 standard deviation (s.d.) span where the data are normally distributed. All-station means for the larger area are estimated by averaging profiles generated at the individual stations.
2.3. Supplemental data
Additional data from several sources are used in the discussion of the environments of the 19 December 2021 eruption of HTHH. First, profiles of European Centre for Medium-range Weather Forecasts ERA5 reanalysis (Hersbach et al. 2020) T and Z interpolated to pressure levels with the standard 0.25° horizontal resolution within a 6 × 6° box centred on the volcano are used. Second, Global Navigation Satellite System Radio Occultation measurements made from the University Corporation for Atmospheric Research (UCAR) Constellation Observing System for Meteorology Ionosphere and Climate (COSMIC-2) are used (UCAR COSMIC Program 2019). Specifically, the COSMIC-2 ‘wetPrF’ 1D-var retrieval data within 1000 km and ±6 h of the eruption time are used.
3.Climatological temperature profile
3.1. Joint frequency distributions
The range of data quality and sampling is seen by comparing the Z–T JFDs for the radiosonde stations at Yap and Medan (Fig. 3). Yap is an excellent sample, whereas that at Medan is weaker, but still adequate for the task. From the number of observations in each height bin it is obvious that the height bins that contain mandatory levels are better sampled, with 2–3 times more observations than the others. The better sample at Yap has a larger number of observations extending up to 35-km altitude and beyond, well above the 10-hPa mandatory level, whereas at Medan the total number of observations drops off above ~25-km altitude.
Annual geopotential height–temperature (Z–T) joint frequency distributions (JFDs) at Yap (left) and Medan (right). Shaded contours represent the frequency observed in each bin, with contours at [1e−5, 1e−3, 1e−2, 3e−2, 5e−2, 7e−2, 1e−1, 2e−1]. Thick yellow line represents the mean profile, with horizontal bars being the approximate 1-s.d. spread. Thick black contours represent the JFD for LRT height, with contours at [1e−4, 1e−3, 1e−2, 3e−2, 5e−2]. Red plot to right of each panel is the total number of samples in each height bin.
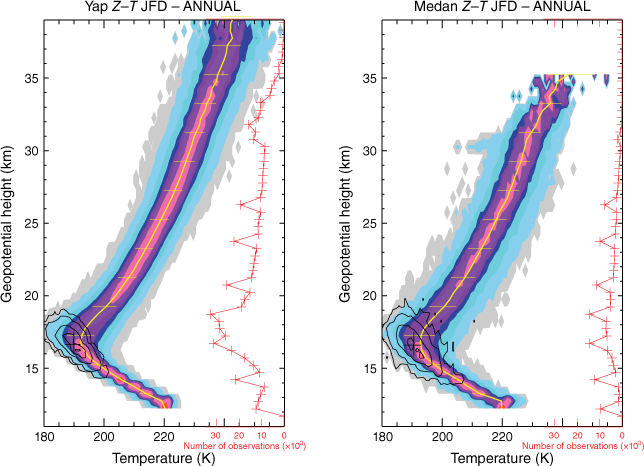
In both examples, the data are well clustered around the mean, with the middle two-thirds of the data confined to within 3–4 K of the mean, but with large tails. The distributions are narrower in the troposphere, but wider in the stratosphere where the gravity waves dominate. The largest variability is near the tropopause at 16–18 km, where temperature range is 180–205 K. Tropopause heights and temperatures vary similarly; at the more poorly sampled stations, the tropopause is more erratic with more frequent outliers, but still generally consistent. Overall, although there is variability in the sampling of the JFDs, the number of observations are generally adequate below heights of 30–35 km and the reliability and spread of the data are adequate for the task.
3.2. Annual and seasonal means
Station profiles from each of the 17 stations are computed and all are averaged to all-station mean pressure and temperature profiles representative of the entire region. The annual all-station mean Z–P profile (Fig. 4a) shows remarkable consistency with height across stations. The logarithmic variation of pressure with height is evident. Plausible, consistent pressure estimates are available up to 38-km altitude. The annual all-station mean Z–T profile (Fig. 4b) also shows strong consistency across stations, with a reliable temperature profile available up to ~35 km. The largest temperature spread is identified near the 17 km, with a second spread in the data between 20 and 25 km. Although there is more variability between stations compared to the pressure profile, there is a remarkable spatial consistency in the data. The consistency of the results between stations across the network builds confidence that a suitable reference profile is being captured in the analysis.
Annual all-station mean (a) Z–P and (b) Z–T profiles (black and yellow dashed line) with annual means from individual stations (thin coloured lines).
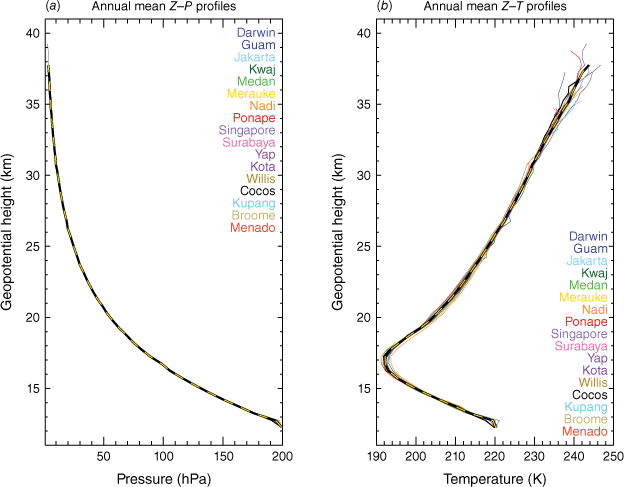
The complex structure of the TTL is well-captured by this analysis. The main portion of the TTL here is identified within ~16–18 km, a region where vertical temperature variation is minimal as the LR transitions from cooling-with-height to warming-with-height. The analysis also captures the ‘tropopause inversion layer’ in the lower stratosphere (e.g. Bell and Geller 2008), a region of enhanced static stability above the TTL, despite not being in ‘tropopause-relative coordinates’. Overall, the general temperature structure approximately matches in absolute value with the profile (up to 25 km) presented in fig. 1 of Scherllin-Pirscher et al. (2021).
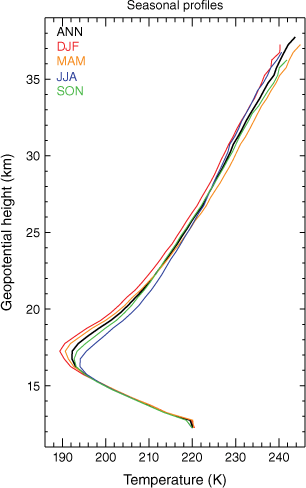
Profiles based on the traditional meteorological seasons (e.g. December–January–February, DJF; March–April–May, MAM) reveal the magnitude and direction of the annual cycle (Fig. 5), with the upper and lower stratosphere behaving differently across the year. The TTL (and the stratosphere below ~22 km) is at its highest and coldest during DJF, and at its warmest and lowest during JJA. Conditions are close to the annual average during the equinoctial seasons. Above 26 km, the temperature profile is warmest during MAM and coldest during JJA and DJF. There is little seasonal variation in the upper troposphere below 16 km.
Both the direction and magnitude of these seasonal variations agrees well with the monthly variations of stratospheric temperature from ERA-40 reanalysis of Fueglistaler et al. (2009). That study identified a peak-to-peak change in temperature of ~8 K at the 80-hPa level; in this work, the maximum T difference is ~7 K at 17.75 km, ~81 hPa. In the upper stratosphere, anomalies in T from the annual mean are ~1.5 K in MAM and cooler in other seasons, again in good agreement with Fueglistaler et al. (2009). The seasonal variation in the Brünt–Vaisala frequency and associated structure of the tropopause inversion layer (not shown) agrees well with Scherllin-Pirscher et al. (2021).
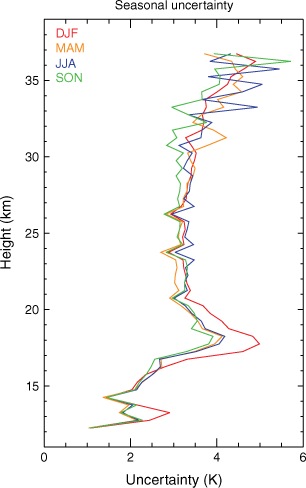
The seasonal uncertainty profile estimates for the means are useful for understanding the vertical structure of the uncertainty (Fig. 6). The numbers represent the station averaged 16–84th percentile range divided by 2 to approximate the s.d. In the upper troposphere, below 16.5 km, uncertainty is typically 2–3 K. The TTL, ~16.5–20 km, is where the largest uncertainty is found. Here it ranges within 3–5 K, with the largest uncertainty noticeably occurring in DJF. In the stratosphere (20–35 km), the uncertainty is 3–3.5 K at most heights.
3.3. Seasonal reference profiles
The consistency of the results and the strong agreement with previous studies indicate that the technique to construct the profiles is appropriate. The structure and variability of the UTLS annual cycle over the tropical western Pacific is adequately captured in this analysis; other sources of the multi-year variability driven by the QBO and ENSO and the short-term gravity wave fluctuations are inherent in the uncertainty estimates of Fig. 6. With that in mind, Table 2 presents standard reference profiles for the region. The left column is the height, with the numbers under the middle columns being the reference temperature at that height. The right column is an estimate of the uncertainty of the height estimate, derived from the horizontal uncertainty (Fig. 6) and the vertical structure of the profile by considering the change in height resulting by adding or subtracting the uncertainty value to or from the reference temperature in that layer. For all seasons, the profiles are extrapolated to a nominal stratopause by assuming a constant LR of +2 K km−1. This is equal to the mean LR for 25–35-km altitude in the profiles, approximately equal to the LR in the US Standard Atmosphere (Minzner 1977), but with different starting values.
| Height (km) | DJF | MAM | JJA | SON | ANN | Ht Uncert (km) |
|---|---|---|---|---|---|---|
| 13 | 217 | 217 | 216 | 216 | 217 | ±0.5 |
| 14 | 208 | 208 | 207 | 207 | 208 | |
| 15 | 200 | 200 | 200 | 200 | 200 | |
| 16 | 193 | 194 | 195 | 194 | 194 | |
| 17 | 190 | 191 | 194 | 193 | 192 | ±1.5 |
| 18 | 192 | 193 | 199 | 197 | 195 | |
| 19 | 197 | 198 | 203 | 201 | 200 | |
| 20 | 202 | 203 | 207 | 205 | 204 | |
| 22 | 209 | 211 | 212 | 210 | 211 | ±2.0 |
| 24 | 215 | 216 | 217 | 216 | 216 | |
| 26 | 219 | 221 | 221 | 220 | 220 | |
| 28 | 224 | 226 | 225 | 225 | 225 | |
| 30 | 227 | 230 | 228 | 229 | 228 | |
| 35 | 236 | 240 | 237 | 239 | 238 | |
| 40 | 246 | 250 | 247 | 249 | 248 | ±5.0 |
| 45 | 256 | 260 | 257 | 259 | 258 | |
| 50 | 266 | 270 | 267 | 269 | 268 | |
| 55 | 276 | 280 | 277 | 279 | 278 |
Valid for 20°N–20°S and 90–180°E. Ht Uncert, estimated uncertainty in height.
4.Example: the 19 December 2021 eruption of Hunga Tonga-Hunga Ha’apai
On 19 December 2021, a large eruption of HTHH (175.382°W, 20.536°S) was noted (Global Volcanism Program 2021). The cited report suggests that the volcano began erupting at 20:35 hours UTC, reaching a height of 6 km by 20:40 hours UTC, and later attaining an altitude of 16 km above sea level. Based on pilot observations, the VAAC Wellington noted that the cloud rose 6.1–12.2 km (~20 000–40 000 ft) above sea level. Data from the World Wide Lightning Location Network (WWLLN): Global Volcanic Lightning Monitor (http://wwlln.net/volcanoMonitor.html) indicated a strong lightning signature beginning at 20:42 hours UTC on 19 December 2021. Nearly half (412) of the 843 flashes reported by WWLLN within 20 km radius of HTHH were observed before 21:30 hours UTC on 19 December 2021.
4.1. 20:40 hours UTC image
Fig. 7 shows an image of the eruption from the Himawari-8 scan beginning at 20:40 hours UTC on 19 December 2021, the first satellite scene where the eruption is visible. The actual sampling time at the latitude of the volcano is ~7.5 min after the nominal image start time. The image combines a Rayleigh-corrected ‘True Colour’ RGB (e.g. Broomhall et al. 2019) with selected contours of AHI channel 14 (11.2 μm) IR brightness temperature and negative ∇2BT, indicating a reversal of the gradient. The scene is very complex and tells a significantly different story to the official account.
Rayleigh corrected 1000-m ‘True Colour’ imagery of the Hunga Tonga-Hunga Ha’apai eruption from the Himawari-8 scan beginning on 20:40 hours UTC on 19 December 2021. Black contours show 2000-m channel 14 (11.2 μm) BT between 200 and 215 K at 5 K intervals. Green contours are ∇2BT at values of −0.1 (solid) and −1.5 (dashed) indicating a reversal of the cloud top temperature gradient. Latitude–longitude grid lines are spaced every 0.1°. The nominal location of the volcano is noted with the (red) triangle. Annotations are discussed in the text.
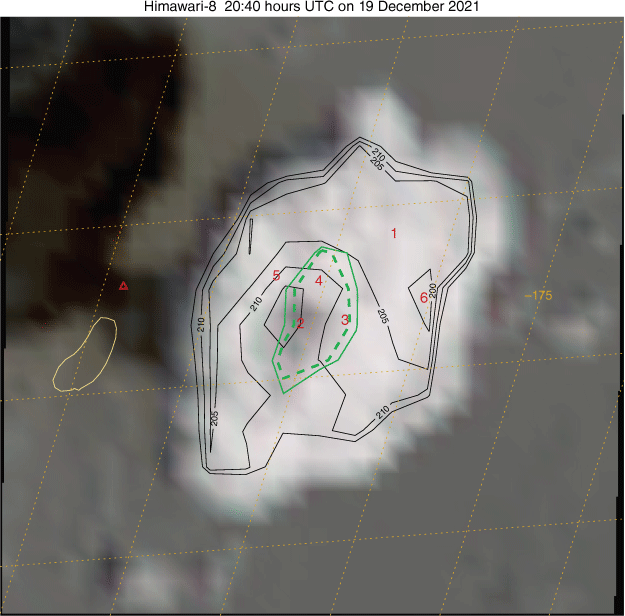
The cloud top portion annotated with a ‘1’ is most reminiscent of a traditional anvil or umbrella. The coldest BTs here are 201–202 K; the reference profiles (Table 2) indicate that this region lies below the tropopause, 15 ± 0.5-km altitude. This value agrees with the analysis of the umbrella height for this event by Gupta et al. (2022). Near ‘2’, a significant SWS is noted by the negative ∇2BT and is quite obvious in the IR contours. Note that the smoothed ∇2BT does not fully capture the extent of the SWS; this is a function of the smoothing as the strong outward pointing gradient to the west nearer the cloud edge ‘corrupts’ the score. Maximum IR temperatures in the SWS are 218.8 K. Also note the dark spot near ‘2’, which is at least partially due to a shadow cast by the ‘brighter spot’ at ‘3’. The BT at this cloud feature is 208–209 K, with Table 2 suggesting a height of 22 km. Bright cloud tops noted at ‘4’ and ‘5’ vary in BT between 206 and 214 K, indicating that the plume top height is 21–24 km. Also note the weak OT near ‘6’; its minimum BT is 197.9 K, with the OT equation indicating that it is ~500 m higher than the umbrella top at ‘1’, ~15.5 km, in general agreement with what would be predicted using Table 2.
In this scene, there is strong evidence that the eruption cloud top height reached at least 24 km in the first 10 min of this eruption. The warmest cloud top feature is at ‘2’ and suggests the height at least briefly reached 26 km from Table 2. Uncertainty in these heights estimates is ±2 km. The shadow or dark cloud does not indicate an active, growing plume at that location. Careful examination of the image does suggest a subtle shift in colour to the surrounding background. One hypothesis is that the eruption grew to that height, but collapsed quickly due to a loss of buoyancy, leaving only a transient cloud that has detrained from the plume. A second possibility is this is a pileus cloud generated above the rapidly rising plume. Given the dryness of the stratosphere in general, the first possibility is more probable. In either case, these clouds must be optically thick enough to generate the warm temperatures observed by the satellite.
4.2. 20:50 hours UTC image
Fig. 8 is an image in the same format as Fig. 7, but at 20:50 hours UTC; as before, the scan time of the volcanic cloud is 7.5 min past the nominal image time. The volcanic cloud has increased in area by a factor of ~2.5 from the previous image; the area covered by the SWS has similarly grown, and now contains three areas of stronger ∇2BT. As before, the identification of the obvious warm spot is not perfect as the smoothing of regions near the cloud edge dilutes the signal. The umbrella (‘1’) remains at ~201–202 K as it moves off to the north and north-east. Table 2 suggests that this is near 15-km altitude. The regions marked ‘2’ are the locations of the high cloud tops annotated as ‘4’, ‘5’ and ‘6’ in Fig. 7. The rightmost one aligns with the incipient OT noted previously at 15.5-km altitude (‘6’); it now has an IR BT of 206 K and ~21-km altitude based on Table 2. This illustrates the transition of an OT into an SWS over a 10-min period. The other regions marked ‘2’ (previously ‘4’ and ‘5’) have BTs that are slightly cooler than in the previous image, suggesting the previously identified clouds are not growing vertically or have begun to collapse.
As in Fig. 7, except at 20:50 hours UTC 19 December 2021. Note that area covered by the image is approximately twice that of Fig. 7.
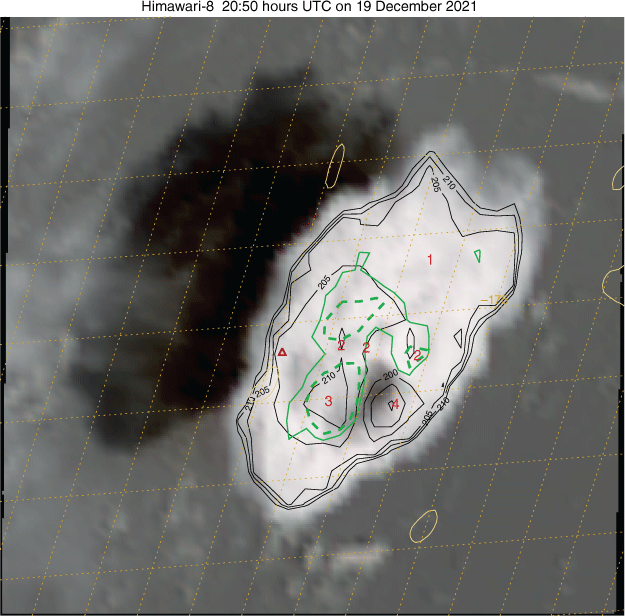
The region marked ‘3’ is the warmest part of the cloud top with several pixels with IR ~213 K, ~23 km based on Table 2. Close examination of the True Colour image indicates a different colour and texture of the cloud here. To the east of this feature, a significant OT cloud is apparent; a significant shadow is visible but is blocked by the higher cloud of the main plume. The minimum BT of 189.4 K indicates this extends 1.8 km over a 201 K anvil, ~16.8 km in height.
4.3. Later imagery
Summarising later imagery (not shown), an SWS continues to be maintained and replenished until at least 21:50 hours UTC in the vicinity of the volcano. Several further OTs are identified, and a maximum warm spot temperature of 219.8 K is observed at 21:30 hours UTC, placing the top above the 26 km level. After 21:50 hours UTC, an SWS is detectable, but decaying and drifting toward the south–south-east until 22:30 hours UTC. This analysis suggests that the eruption was well into the stratosphere for 1–2 h. After that time, cloud top BTs gradually increase and the cloud becomes optically thin. Simultaneously, the umbrella in the troposphere continues to spread to the north and north-east and reaches widespread minimum BTs of 195–198 K, placing it within ~15.5–16.5 km. The eruption continues although reaching much lower altitudes; BTs in the active plume do not go below 200 K from 01:00 hours UTC on 20 December 2021. The apparent eruption on IR ceases at 05:20 hours UTC, although the remnants of the volcanic cloud remain detectable beyond 10:00 hours UTC.
4.4. Choice of temperature profile
Fig. 9 shows temperature profiles from a variety of sources on 19 and 20 December. Aside from the climatological profile, the only information on this plot that was operationally available are the three radiosonde profiles from Nadi, Pago Pago and Funafuti, 800–1400 km distant from the eruption at the nominal time of 00:00 hours UTC on 19 December, nearly 1 day before the eruption (solid, coloured lines). Considerable differences are seen in the profiles, illustrating the difficulty in choosing a representative profile. Individual profiles, including those from ERA5 at the nominal eruption time, are noisy and show large variations both spatially and temporally; the influence of gravity waves is apparent in the vertical structure. The largest differences between data sources are within the TTL. Overall, the DJF climatological profile provides the best match to the detailed radiosonde observations at those heights. Some individual COSMIC-2 profiles capture the extremely cold temperatures, whereas the ERA5 pressure-level data poorly resolves the complex structure. Above the TTL, between 18 and 26 km, the ERA5 and COSMIC-2 mean profiles are up to ~4 K warmer than the climatological profile; individual profiles, including the radiosondes, vary considerably, being both warmer and cooler than the climatological profile. On average, height estimates are 1–2 km lower using data from the day, although those estimates both above and below that of the climatological profile all lie within the estimated uncertainty of the climatological profile.
UTLS temperature profiles from different sources on 19 and 20 December 2021. Shown are the DJF climatological profile (red dash), the three closest radiosonde sites (green, orange and pink) on 19 (solid) and 20 December (dash–dot) at 00:00 hours UTC. Also shown are 16 COSMIC-2 profiles (cyan) and their mean (blue dash) and 625 profiles from the ERA5 reanalysis (grey ‘shading’) and their mean (black dash). The map inset shows the locations of Hunga Tonga-Hunga Ha’apai (red diamond), the radiosonde sites (squares), COSMIC-2 profiles (blue crosses) and the ERA5 box (grey).
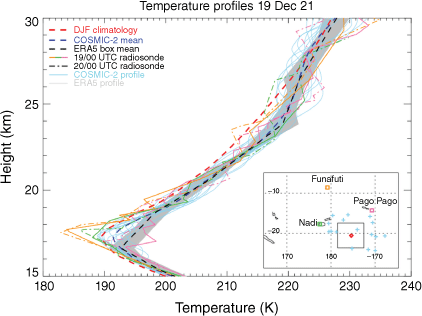
This analysis shows that the climatological profiles are accurate enough for operational usage, particularly accounting for the largely unknown uncertainties associated with individual observations. For post-event analysis, heights of volcanic plumes may require refinement using data not available in real time; appropriate averaging should be used in these cases to remove the short-term effects of gravity waves in individual profiles, particularly in the stratosphere.
5.Further verification
Maximum plume heights of other recent eruptions in the tropical western Pacific that can be used to independently verify the results calculated using the technique described here are provided in Table 3. Horváth et al. (2021b) report the maximum height of the 26 June 2019 climactic eruption of Ulawun, Papua New Guinea, at 22.3 km using a geometric estimate from limb-based profiles from the NOAA GOES-17. Error estimates for fixed targets (e.g. mountain peaks) with this technique were reported as ±500 m (Horváth et al. 2021a), with additional unspecified errors for volcanic clouds. The warmest SWS observed with this approach was 216.1 K in the 06:20 hours UTC Himawari-8 image, equivalent to 24 ± 2 km. During 06:10–07:00 hours UTC, multiple SWSs were observed with temperatures of 206–215 K, placing the heights at 20–23 km.
| Volcano | Date | Time (hours UTC) | SWS temp (K) | Height (km) | Reported height (km) | Reference |
|---|---|---|---|---|---|---|
| Ulawun | 26 Jun 19 | 06:20 | 216.1 | 24 | 22.3 | Horváth et al. (2021b) |
| Hunga Tonga-Hunga Ha’apai | 15 Jan 22 | 04:40 | 270.5 | 53 | 55–58 | Carr et al. (2022), Proud et al. (2022) |
Carr et al. (2022) used a stereoscopic approach with GOES-17 and Himawari-8 to estimate the heights at the peak of the paroxysmal eruption of HTHH on 15 January 2022. Peak heights in the 04:30 hours UTC images analysed were 54–56 km, reported as 55 km. Proud et al. (2022) used similar techniques and estimated a height of 57 km. Millán et al. (2022) also reported a water vapour signature at 53 km on the day of the eruption using the Microwave Limb Sounding instrument onboard the NASA Aura Satellite. The warmest SWS observed here had a peak BT of 270.5 K at 20:50 hours UTC on 15 January 2022, for an estimated height of 53 km following Table 2. Other SWSs of 255–260 K were observed during 04:40–05:20 hours UTC, suggesting heights of 45–50 km over an extended period. Note that these heights are in the extrapolated portion of the reference profiles in Table 2, well above the altitudes that radiosondes reach. Further, these heights are above the nominal stratopause height of 45 km (Minzner 1977). To obtain the values reported here, the stratospheric LR has been extrapolated upwards, suggesting that the stratopause on this day was elevated above its assumed climatological altitude.
In both of these independent events, the technique described in this work compares favourably with the more complex satellite approaches, providing further confidence that technique and the stratospheric reference profile derived here are robust and suitable for use in the fast-paced operational environment.
6.Concluding remarks
This work presents a method to estimate the top heights of volcanic plumes quickly and reliably in the tropical western Pacific region. The method involves identifying SWSs in optically thick (ε ≈ 1) portions of the umbrella with a lightly smoothed Laplacian operator to identify reversals in the cloud top temperature gradient indicative of stratospheric penetration. The temperature of these warm spots is converted to height using seasonal stratospheric reference temperature profiles derived from 20 years of radiosonde data from 17 stations spread throughout the western Pacific. An approach for estimating the height of cold OTs is also adopted. Estimates of the uncertainty in the height are provided.
This technique is designed specifically for the tropical western Pacific (90–180°E) within ~20°N–20°S. In this region the background temperature of the UTLS has a reliable increase in height, is spatially homogeneous and varies over a limited range. Temperature variability occurs on long time scales from the annual cycle, ENSO and QBO. Short-term variability (<1000 km, 1 day) from ubiquitous gravity waves is also significant and makes it difficult to interpret the representativeness of any given observation. The technique could likely be extended to other tropical regions and more poleward (perhaps by 5–10° latitude) in the summer hemisphere as stratospheric spatial variability is typically low in these regions; this needs further verification.
A case study of the 19 December 2021 eruption of HTHH demonstrates the technique and shows how the height can be quickly and robustly determined. The analysis of this event here indicated a considerably more intense eruption than that presented in the official account. An examination of temperature profiles from non-real time sources suggests that the height determined here may be too high in this event, but the most probable estimate lies within the specified uncertainty range of the climatological profile. Favourable comparison of the heights determined using this approach with independent height estimates of eruptions in the literature using more complex satellite techniques provides confidence in the robustness of the results. However, the climatological profile derived here is best suited for operational purposes. It provides broadly accurate results, although additional data that are suitably averaged to remove the effects of gravity waves can refine the heights in post-event analysis. Further work is needed to refine these techniques. Getting the height correct is crucial to producing an accurate dispersion model forecast for aviation operations and to understanding any possible climate impacts. Although the technique as applied in this study is manual, the approaches here are straightforward and could be automated for even quicker use. Regardless of the approach, better use and operational analysis of satellite data is needed to fully understand the impact of deep volcanic eruptions.
Data availability
The data used to generate the results of this work are broadly available. The IGRA2 and COSMIC-2 data are available on the World Wide Web from https://doi.org/10.7289/V5X63K0Q and https://doi.org/10.5065/t353-c093 respectively. Himawari-8 satellite data are processed by the Bureau of Meteorology and are available at on the NCI from https://doi.org/10.25914/61A609F9E7FFA. The ERA5 data come from the collection replicated on the NCI at https://dx.doi.org/10.25914/5f48874388857. Individual profiles of radiosonde data were obtained from the Atmospheric Sounding website at the University of Wyoming (http://weather.uwyo.edu/upperair/sounding.html).
Conflicts of interest
Chris Lucas is an Associate Editor for the Journal of Southern Hemisphere Earth Systems Science but did not at any stage have editor-level access to this manuscript while in peer review, as is the standard practice when handling manuscripts submitted by an editor to this journal. JSHESS encourages its editors to publish in the journal and they are kept totally separate from the decision-making processes for their manuscripts. The authors have no further conflicts of interest to declare.
Acknowledgements
The author thanks Caroline Poulsen and Meelis Zidikheri for helpful comments on the manuscript. Andy Prata and an anonymous reviewer also provided comments that improved the manuscript. VAAC Darwin Manager Jarrad Denman helped to clarify the procedures and operational availability of NWP in the Darwin VAAC.
References
Andersson SM, Martinsson BG, Vernier J-P, Friberg J, Brenninkmeijer CAM, Hermann M, van Velthoven PFJ, Zahn A (2015) Significant radiative impact of volcanic aerosol in the lowermost stratosphere. Nature Communications 6(1),.
| Crossref | Google Scholar |
Australian Bureau of Meteorology (2021) ‘Bureau of Meteorology Satellite Observations (Collection).’ (NCI Australia) 10.25914/61A609F9E7FFA
Bedka KM, Allen JT, Punge HJ, et al. (2018) A long-term overshooting convective cloud-top detection database over Australia derived from MTSAT Japanese advanced meteorological imager observations. Journal of Applied Meteorology and Climatology 57(4), 937-951.
| Crossref | Google Scholar |
Bell SW, Geller MA (2008) Tropopause inversion layer: seasonal and latitudinal variations and representation in standard radiosonde data and global models. Journal of Geophysical Research: Atmospheres 113(5), D05109.
| Crossref | Google Scholar |
Bessho K, Date K, Hayashi M, et al. (2016) An introduction to Himawari-8/9 — Japan’s new-generation geostationary meteorological satellites. Journal of the Meteorological Society of Japan (Series II) 94(2), 151-183.
| Crossref | Google Scholar |
Bourassa AE, Robock A, Randel WJ, et al. (2012) Large volcanic aerosol load in the stratosphere linked to Asian monsoon transport. Science 337(6090), 78-81.
| Crossref | Google Scholar |
Broomhall MA, Majewski LJ, Villani VO, et al. (2019) Correcting Himawari-8 advanced Himawari imager data for the production of vivid true-color imagery. Journal of Atmospheric and Oceanic Technology 36(3), 427-442.
| Crossref | Google Scholar |
Carr JL, Horváth Á, Wu DL, et al. (2022) Stereo plume height and motion retrievals for the record-setting Hunga Tonga-Hunga Ha’apai eruption of 15 January 2022. Geophysical Research Letters 49(9), e2022GL098131.
| Crossref | Google Scholar |
Durre I, Yin X, Vose RS, et al. (2018) Enhancing the data coverage in the Integrated Global Radiosonde Archive. Journal of Atmospheric and Oceanic Technology 35(9), 1753-1770.
| Crossref | Google Scholar |
Flower VJB, Kahn RA (2017) Assessing the altitude and dispersion of volcanic plumes using MISR multi-angle imaging from space: sixteen years of volcanic activity in the Kamchatka Peninsula, Russia. Journal of Volcanology and Geothermal Research 337, 1-15.
| Crossref | Google Scholar |
Francis PN, Cooke MC, Saunders RW (2012) Retrieval of physical properties of volcanic ash using Meteosat: a case study from the 2010 Eyjafjallajökull eruption. Journal of Geophysical Research: Atmospheres 117(2), D00U09.
| Crossref | Google Scholar |
Fromm M, Nedoluha G, Charvát Z (2013) Comment on “Large volcanic aerosol load in the stratosphere linked to Asian monsoon transport”. Science 339(6120), 647.
| Crossref | Google Scholar |
Fueglistaler S, Dessler AE, Dunkerton TJ, et al. (2009) Tropical tropopause layer. Reviews of Geophysics 47(1), RG1004.
| Crossref | Google Scholar |
Global Volcanism Program (2021) Report on Hunga Tonga-Hunga Ha’apai (Tonga). In ‘Weekly Volcanic Activity Report’, 15–21 December 2021. (Ed. SK Sennett) (Smithsonian Institution and US Geological Survey) Available at https://volcano.si.edu/showreport.cfm?wvar=GVP.WVAR20211215-243040
Griffin SM, Bedka KM, Velden CS (2016) A method for calculating the height of overshooting convective cloud tops using satellite-based IR imager and CloudSat cloud profiling radar observations. Journal of Applied Meteorology and Climatology 55(2), 479-491.
| Crossref | Google Scholar |
Guffanti M, Casadevall TJ, Budding K (2010) Encounters of aircraft with volcanic ash clouds: a compilation of known incidents, 1953–2009. US Geological Survey Data Series, 545(1.0). Available at http://pubs.usgs.gov/ds/545/
Gupta AK, Bennartz R, Fauria KE, Mittal T (2022) Eruption chronology of the December 2021 to January 2022 Hunga Tonga-Hunga Ha’apai eruption sequence. Communications Earth & Environment 3(1),.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, et al. (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146(730), 1999-2049.
| Crossref | Google Scholar |
Horváth Á, Carr JL, Girina OA, et al. (2021a) Geometric estimation of volcanic eruption column height from GOES-R near-limb imagery – part 1: methodology. Atmospheric Chemistry and Physics 21(16), 12189-12206.
| Crossref | Google Scholar |
Horváth Á, Girina OA, Carr JL, et al. (2021b) Geometric estimation of volcanic eruption column height from GOES-R near-limb imagery – part 2: case studies. Atmospheric Chemistry and Physics 21(16), 12207-12226.
| Crossref | Google Scholar |
Jovanovic B, Smalley R, Timbal B, et al. (2017) Homogenized monthly upper-air temperature data set for Australia. International Journal of Climatology 37(7), 3209-3222.
| Crossref | Google Scholar |
Kim J-E, Alexander MJ (2015) Direct impacts of waves on tropical cold point tropopause temperature. Geophysical Research Letters 42(5), 1584-1592.
| Crossref | Google Scholar |
Kristiansen NI, Prata AJ, Stohl A, et al. (2015) Stratospheric volcanic ash emissions from the 13 February 2014 Kelut eruption. Geophysical Research Letters 42, 588-596.
| Crossref | Google Scholar |
Lawrence ZD, Abalos M, Ayarzagüena B, et al. (2022) Quantifying stratospheric biases and identifying their potential sources in subseasonal forecast systems. Weather and Climate Dynamics 3(3), 977-1001.
| Crossref | Google Scholar |
Lechner P, Tupper A, Guffanti M, et al. (2018) Volcanic ash and aviation—the challenges of real-time, global communication of a natural hazard. In ‘Advances in Volcanology’. (Eds CJ Fearnley, DK Bird, K Haynes, WJ McGuire, G Jolly) pp. 51–64. (Springer: Cham, Switzerland) 10.1007/11157_2016_49
Lucas C (2022) A census of deep volcanic eruptions in the tropics as observed by Himawari-8. In ‘12th Asia-Oceania Meteorological Satellite Users’ Conference’, 11–18 November 2022, held virtually. p. S42-08. (Japan Meteorological Agency) Available at https://www.data.jma.go.jp/mscweb/en/aomsuc12/index.html
Lucas C, Rudeva I, Nguyen H, et al. (2021) Variability and changes to the mean meridional circulation in isentropic coordinates. Climate Dynamics 58, 257-276.
| Crossref | Google Scholar |
Mastin LG, Van Eaton AR (2020) Comparing simulations of umbrella-cloud growth and ash transport with observations from pinatubo, kelud, and calbuco volcanoes. Atmosphere 11(10), 1038.
| Crossref | Google Scholar |
Mastin LG, Guffanti M, Servranckx R, et al. (2009) A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. Journal of Volcanology and Geothermal Research 186(1), 10-21.
| Crossref | Google Scholar |
McKee K, Smith CM, Reath K, et al. (2021) Evaluating the state-of-the-art in remote volcanic eruption characterization. Part I: Raikoke volcano, Kuril Islands. Journal of Volcanology and Geothermal Research 419, 107354.
| Crossref | Google Scholar |
Merucci L, Zakšek K, Carboni E, et al. (2016) Stereoscopic estimation of volcanic ash cloud-top height from two geostationary satellites. Remote Sensing 8(3), 206.
| Crossref | Google Scholar |
Millán L, Santee ML, Lambert A, et al. (2022) The Hunga Tonga‐Hunga Ha’apai hydration of the stratosphere. Geophysical Research Letters 49(13), e2022GL099381.
| Crossref | Google Scholar |
Minzner RA (1977) The 1976 Standard Atmosphere and its relationship to earlier standards. Reviews of Geophysics 15(3), 375-384.
| Crossref | Google Scholar |
Ong H, Roundy PE (2020) Nontraditional hypsometric equation. Quarterly Journal of the Royal Meteorological Society 146(727), 700-706.
| Crossref | Google Scholar |
Oppenheimer C (1998) Volcanological applications of meteorological satellites. International Journal of Remote Sensing 19(15), 2829-2864.
| Crossref | Google Scholar |
Pausata FSR, Zanchettin D, Karamperidou C, et al. (2020) ITCZ shift and extratropical teleconnections drive ENSO response to volcanic eruptions. Science Advances 6(23), eaaz5006.
| Crossref | Google Scholar |
Pavolonis MJ, Heidinger AK, Sieglaff J (2013) Automated retrievals of volcanic ash and dust cloud properties from upwelling infrared measurements. Journal of Geophysical Research: Atmospheres 118(3), 1436-1458.
| Crossref | Google Scholar |
Prata AJ, Grant IF (2001) Retrieval of microphysical and morphological properties of volcanic ash plumes from satellite data: application to Mt Ruapehu, New Zealand. Quarterly Journal of the Royal Meteorological Society 127(576), 2153-2179.
| Crossref | Google Scholar |
Prata AT, Grainger RG, Taylor IA, et al. (2022) Uncertainty-bounded estimates of ash cloud properties using the ORAC algorithm: application to the 2019 Raikoke eruption. Atmospheric Measurement Techniques 15(20), 5985-6010.
| Crossref | Google Scholar |
Proud SR, Prata AT, Schmauß S (2022) The January 2022 eruption of Hunga Tonga-Hunga Ha’apai volcano reached the mesosphere. Science 378(6619), 554-557.
| Crossref | Google Scholar |
Randel WJ, Wu F (2015) Variability of zonal mean tropical temperatures derived from a decade of GPS radio occultation data. Journal of the Atmospheric Sciences 72(3), 1261-1275.
| Crossref | Google Scholar |
Ridley DA, Solomon S, Barnes JE, et al. (2014) Total volcanic stratospheric aerosol optical depths and implications for global climate change. Geophysical Research Letters 41(22), 7763-7769.
| Crossref | Google Scholar |
Robock A (2000) Volcanic eruptions and climate. Reviews of Geophysics 38(2), 191-219.
| Crossref | Google Scholar |
Santer BD, Bonfils C, Painter JF, et al. (2014) Volcanic contribution to decadal changes in tropospheric temperature. Nature Geoscience 7(3), 185-189.
| Crossref | Google Scholar |
Scherllin-Pirscher B, Steiner AK, Anthes RA, et al. (2021) Tropical temperature variability in the UTLS: new insights from GPS radio occultation observations. Journal of Climate 34(8), 2813-2838.
| Crossref | Google Scholar |
Shettigara V, Sumerling G (1998) Height determination of extended objects using shadows in SPOT images. Photogrammetric Engineering and Remote Sensing 64(1), 35-43.
| Google Scholar |
Steiner AK, Ladstädter F, Randel WJ, et al. (2020) Observed temperature changes in the troposphere and stratosphere from 1979 to 2018. Journal of Climate 33(19), 8165-8194.
| Crossref | Google Scholar |
Stocker M, Ladstädter F, Wilhelmsen H, et al. (2019) Quantifying stratospheric temperature signals and climate imprints from post-2000 volcanic eruptions. Geophysical Research Letters 46(21), 12486-12494.
| Crossref | Google Scholar |
Swingedouw D, Mignot J, Ortega P, et al. (2017) Impact of explosive volcanic eruptions on the main climate variability modes. Global and Planetary Change 150, 24-45.
| Crossref | Google Scholar |
Tupper A, Itikarai I, Richards M, et al. (2007) Facing the challenges of the International Airways Volcano Watch: the 2004/05 eruptions of Manam, Papua New Guinea. Weather and Forecasting 22(1), 175-191.
| Crossref | Google Scholar |
UCAR COSMIC Program (2019) COSMIC-2 Data Products [Data Set]. 10.5065/t353-c093
Vernier J-P, Thomason LW, Pommereau J-P, et al. (2011) Major influence of tropical volcanic eruptions on the stratospheric aerosol layer during the last decade. Geophysical Research Letters 38(12), L12807.
| Crossref | Google Scholar |
Vernier J-P, Thomason LW, Fairlie TD, Minnis P, Palikonda R, Bedka KM (2013) Comment on “Large volcanic aerosol load in the stratosphere linked to Asian monsoon transport”. Science 339(6120), 647.
| Crossref | Google Scholar |
Vernier J-P, Fairlie TD, Deshler T, et al. (2016) In situ and space‐based observations of the Kelud volcanic plume: the persistence of ash in the lower stratosphere. Journal of Geophysical Research: Atmospheres 121(18), 11,104-11,118.
| Crossref | Google Scholar |
Vincent RA, Alexander MJ (2000) Gravity waves in the tropical lower stratosphere: an observational study of seasonal and interannual variability. Journal of Geophysical Research: Atmospheres 105(D14), 17971-17982.
| Crossref | Google Scholar |
Witham C, Webster H, Hort M, Jones A, Thomson D (2012) Modelling concentrations of volcanic ash encountered by aircraft in past eruptions. Atmospheric Environment 48, 219-229.
| Crossref | Google Scholar |
Woods AW, Self S (1992) Thermal disequilibrium at the top of volcanic clouds and its effect on estimates of the column height. Nature 355(6361), 628-630.
| Crossref | Google Scholar |
World Meteorological Organization (1957) Meteorology – a three dimensional science: Second session of the Comission of Aerology. WMO Bulletin VI(4), 134-138.
| Google Scholar |
Zidikheri MJ, Lucas C (2020) Using satellite data to determine empirical relationships between volcanic ash source parameters. Atmosphere 11(4), 342.
| Crossref | Google Scholar |
Zidikheri MJ, Lucas C, Potts RJ (2018) Quantitative verification and calibration of volcanic ash ensemble forecasts using satellite data. Journal of Geophysical Research: Atmospheres 123(8), 4135-4156.
| Crossref | Google Scholar |
Zuo M, Zhou T, Man W (2019) Wetter global arid regions driven by volcanic eruptions. Journal of Geophysical Research: Atmospheres 124(24), 13648-13662.
| Crossref | Google Scholar |