Critical phosphorus values from the Better Fertiliser Decisions for Pastures project: early insights from validation trials
David Rogers A H , David Weaver
A H , David Weaver  A , Robert Summers
A , Robert Summers  B , Eric Dobbe A , Ronald Master A , Robert McFerran C , Graham Mussell D , Luke Dawson E , Justin Mercy E , Peta Richards F and Deborah Holtham G
B , Eric Dobbe A , Ronald Master A , Robert McFerran C , Graham Mussell D , Luke Dawson E , Justin Mercy E , Peta Richards F and Deborah Holtham G
A Department of Primary Industries and Regional Development, 444 Albany Highway, Albany, WA 6330, Australia.
B Department of Primary Industries and Regional Development, 45 Mandurah Terrace, Mandurah, WA 6210, Australia.
C Department of Water and Environmental Regulation, 72 Duchess Street, Busselton, WA, Australia.
D Graham Mussell Consulting, 52 Whitemoss Drive, Vasse, WA 6280, Australia.
E CSBP Limited, Kwinana Beach Road, Kwinana, WA 6966, Australia.
F Department of Primary Industries and Regional Development, 28527 South West Highway, Manjimup, WA 6258, Australia.
G Department of Water and Environmental Regulation, Prime House, 8 Davidson Terrace, Joondalup, WA 6027, Australia.
H Corresponding author. Email: david.rogers@dpird.wa.gov.au
Crop and Pasture Science - https://doi.org/10.1071/CP20236
Submitted: 6 July 2020 Accepted: 1 February 2021 Published online: 27 May 2021
Journal Compilation © CSIRO 2021 Open Access CC BY
Abstract
Phosphatic fertilisers have made grazing in the south-west of Western Australia (WA) viable. However, there is evidence that a large proportion of pasture paddocks exceed soil test critical values at which 95% of maximum yield is achieved as identified in the national Better Fertiliser Decisions for Pasture (BFDP) project. Of 22 000 soil samples collected between 2009 and 2020, 56% exceeded the critical value for phosphorus (P), although there were constraints to potassium (K) and sulfur (S) and from soil acidity. Soils with available P exceeding the critical value are expected to lead to excessive losses of P to waterways, resulting in eutrophication. A trial program was established to validate the critical P values from BFDP so that concerns can be addressed about the relevance of these critical P values to WA conditions and to contemporary pasture varieties. Measured relative yields for 19 trials in the first year were mostly within 10% of that predicted from BFDP for soils with a P buffering index (PBI) >10. Soils with PBI <10 had measured relative yields up to 25% greater than predicted by BFDP, suggesting response calibrations for low PBI soils may require adjustment in the BFDP dataset. Some pasture yield gaps occurred when soil pH and P were low. Application of nitrogen (N), K and S almost doubled the yield when P was limiting or sufficient. Agronomic advice and practice should seek to optimise these multiple inputs, thereby optimising P use rather than applying P to levels above the critical value.
Keywords: Colwell P, critical values, pasture, phosphorus, phosphorus buffering index, soil testing.
Introduction
Nutrient and fertiliser management on pasture soils is important from economic and environmental perspectives. Fertilisers can account for a significant proportion of farm input costs, and the egress of nutrients from agriculture and impacts on riverine and estuarine water quality are of increasing public concern (Melland et al. 2008; Gourley and Weaver 2012). These factors highlight the importance of using an evidence-based approach to fertiliser decision making, contingent on soil test critical values derived from nutrient response trials. An evidence-based approach will lead to improvement of on-farm nutrient use efficiency, minimised offsite nutrient loss risk, and optimised return on fertiliser investment.
The projects Better Fertiliser Decisions for Pastures (BFDP; Gourley et al. 2019) and Better Fertiliser Decisions for Crops (BFDC; Speirs et al. (2013) focused on collation, filtering and packaging of existing trial data rather than collection of new data. In both BFDP and BFDC, significant historical trial data were contributed from government agencies and fertiliser companies around Australia. For example, the BFDP database consists of data from 3000 experimental years, 250 experiments, 1600 field sites, and 48 000 pasture yield measures. BFDC has been developed into a web-based system that allows authorised users to supplement the dataset with more results as they become available, whereas BFDP does not have this facility. This may contribute to a perception of a lack of currency of the BFDP data. The outcome of BFDP was a suite of critical soil test values for phosphorus (P), potassium (K) and sulfur (S) for grazed pastures in Australia.
Nutrient and fertiliser recommendations for crops and pastures are based on the predictive functions and critical soil test values of decision support systems (DSS) derived from nutrient response trials. Some landholders and industry stakeholders are reluctant to base fertiliser decisions on the evidence provided in studies such as BFDP. This is despite many years of trials, meta-analysis of nationally aggregated trial information (Speirs et al. 2013; Gourley et al. 2019), peer-reviewed scientific publications, and the utilisation of critical values in DSS and extension programs. Instead, there is a preference to adhere to traditional fertiliser practice of ‘one bag of superphosphate per acre per year’ (i.e. 200 kg superphosphate/ha.year) because of strong memories of responses of pasture to P applications on infertile agricultural land in south-west Western Australia (WA) in the 1960s. Other factors cited for this reluctance also include the lack of contemporary pasture varieties used in the trials that contributed to BFDP, with concerns that the newer cultivars may have higher P requirements than earlier cultivars, and that the trials were conducted from 1955 to 2006 and are therefore not contemporary from a scientific and extension perspective, and therefore the derived critical values are not relevant to conditions in south-west WA.
When assessed against critical values determined from studies such as BFDP, records of soil tests reinforce the notion that there is a tendency for landholders to follow traditional fertiliser practice rather than use an evidence-based approach (Weaver and Reed 1998; Weaver and Wong 2011; Gourley et al. 2019). For example, Weaver and Reed (1998) showed that of 7950 soils sampled (0–10 cm) on the south coast of WA in 1988 and 1989, 49% had high P status when assessed against critical Colwell P (Colwell 1965) values determined from pasture trials (Yeates 1993). Weaver and Wong (2011) demonstrated that of 109 000 soil sample records (0–10 cm) collected in south-west WA during 2008–10, 57–69% exceeded the critical Colwell P value to achieve 90% of relative yield (RY) for pastures, and 39–93% exceeded the critical Colwell P value to achieve 90% of RY for crops, depending on soil P buffering index (PBI; Burkitt et al. (2002). Weaver and Wong (2011) also showed that of 2160 soil samples (0–10 cm) from Australian dairy farms collected in 2007 and 2008, 80–95% exceeded the critical Colwell P value to achieve 95% of RY for pastures.
These findings from an assessment of soil test records belie the notion that an evidence-based approach to fertiliser decision making is ubiquitous. It is clear that approaches beyond the collection and publication of data from nutrient response trials are required to persuade landholder and industry stakeholders that production or cost effectiveness of fertiliser use does not increase when soils are fertilised to levels above critical values (Simpson et al. 2009; Gourley et al. 2019). With this background, a project called ‘uPtake’, supported by a technical reference group with representatives from government departments, catchment groups, grazing and fertiliser industry groups, research scientists and farmers, is conducting pasture trials to derive PBI-specific soil test P response calibrations and critical values for pastures grown at >600 mm rainfall in south-west WA. Results from 19 trials conducted in the first year are presented and compared with data from BFDP (Gourley et al. 2019). The primary objective of the trials was to validate the critical P values in BFDP. Secondary objectives were to deliver behavioural change outcomes including: (i) landholders and industry stakeholders accepting and using critical soil test P values to support evidence-based fertiliser recommendations; (ii) increased profitability for landholders; and (iii) improved water quality by reducing excessive P levels in the soil. A scientific framework to allow comparison with BFDP was central to achieving the primary objective, and to add credibility to the secondary objectives.
Materials and methods
Background
The present study has limited resources, time and trials for achieving outcomes similar to and outputs as extensive as BFDP. Hence, the current understanding of the science behind the responsiveness of soils with different PBI and levels of soil P fertility (Gourley et al. 2019) was applied to the selection of trial locations so that P response calibrations could be developed and comparisons with BFDP drawn. Gourley et al. (2019) notes the importance of soil PBI to the determination of critical Colwell P values for pastures. A similar meta-analysis for crop nutrient response relationships in Australia could find no PBI-dependent critical P values (Bell et al. 2013), which the authors attributed to insufficient data and a range of knowledge gaps relating to current cropping practices, including minimum tillage and soil characterisation. In addition, BFDC lists the minimum requirements for a trial to qualify for inclusion in its national dataset. Some essential requirements include records of: (i) site location; (ii) crop type; (iii) experimental design; (iv) soil sampling depth; (v) soil test method and the units reported; (vi) mean yield (t/ha) for each treatment; (vii) Y0, Ymax and the equation fitted treatment yields, where Y0 is the mean yield from the control and Ymax is the maximum yield from a fitted response equation or from the maximum nutrient rate depending on the trial design.
Site selection framework
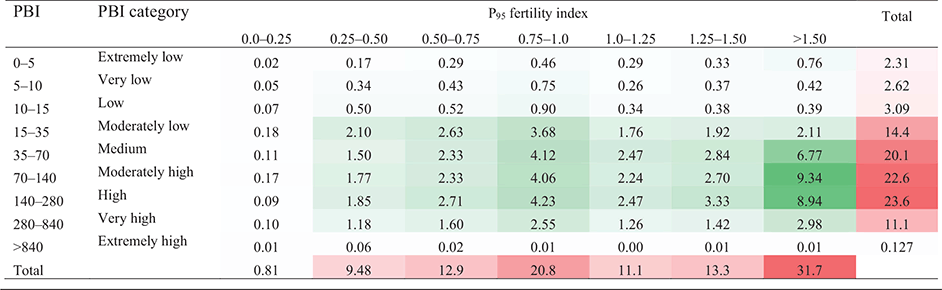
Soil test data from an annual soil-sampling program guided the selection of potential trial sites. A framework (Fig. 1) based on PBI and P fertility groups enabled the selection of sites for development of nutrient response calibrations for each PBI group. Historical soil-sampling programs provided information on the likelihood that sites with the required PBI and P fertility characteristics could be identified (Table 1). These data were skewed towards high P fertility and towards medium–high PBI, with 56% of soils showing a P95 fertility index >1 (see below for explanation of index). The lowest and highest PBI groups were not well represented (Table 1). The 19 field sites chosen for the first year of the 4-year program partially represented the range of P fertility and PBI (Fig. 1a) required to develop response calibrations.

|
Prior to trial establishment, soil samples (0–10 cm) were collected to determine initial site conditions such as PBI, Colwell P and K (Colwell 1965), pH (in CaCl2, pHCa), and KCl-40S (Blair et al. 1991). A soil P fertility index was calculated (Cope and Rouse 1973; Simpson et al. 2011). This index simplifies soil P fertility interpretation and removes the need to use a complex array of PBI-specific critical Colwell P values which increase with increasing soil PBI (Gourley et al. 2019). The index was calculated as the ratio of pre-trial Colwell P to critical Colwell P (Gourley et al. 2019) to achieve 95% RY and is referred to here as P95 fertility index. Soils with a P95 fertility index of 1 should achieve 95% RY assuming no other constraints, whereas soils with a P95 fertility index <1 should show response to applications of P depending on the degree of deficiency, and those with a P95 fertility index >1 should be non-responsive to P applications. The P95 fertility index (Eqn 1) can be applied at any target RY, but in most studies a target of 90% or 95% RY is used:
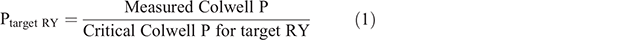
Within the framework, narrowed ranges of P95 fertility index and PBI were defined (Fig. 1) to limit the likelihood that analytical variability could place a trial site in a different PBI group at the boundaries of each PBI range. Equally, the P fertility ranges recommended in the framework span the region where a P response calibration is likely to be well defined, and are an attempt to follow the BFDC criteria that at least three points must fall in the 80–95% RY range.
At each site, a P response curve was developed, with a higher intercept expected for sites with higher starting P fertility (Fig. 1b). Within each PBI category, the relative response to P was compared with the BFDP relationship and data (Fig. 1c). Each trial contributes a single point consisting of an initial Colwell P and PBI value from soil testing, and a RY measurement from the trial to the response calibration. The current dataset represents the first of 4 years of trials. After 4 years, the response calibrations will be compared with the series of BFDP curves where the curvature varies with PBI (Fig. 1d).
Trial treatments and management
Sites were seeded with pasture varieties in consultation with the individual farmers about which varieties they wished to plant that were appropriate for their soil type and rainfall zone. Pastures were sown with grower equipment in mixes that included ryegrass and legume clover. Where necessary, the existing pasture was supplemented with pasture varieties that included mixes of oats; Winterhawk, Vortex, Ascend and Arnie annual ryegrass; Gosse, Narrikup, Dalkeith and Denmark subterranean clover; Lightning Persian clover; Zulu II arrowleaf clover; and Vista balansa clover. Knockdown herbicides were used before sowing, and selective herbicides were applied if required during the season to control weeds. Sites were sown from mid-April through to mid-June as rainfall permitted. Stock exclusion was achieved with fencing, the timing of which was dependent on trial type (Table 2). Trial design 1a was fenced as soon as it was established. Trial designs 1b and 2 allowed stock access to the trial until late August or early September (depending on pasture development), when fencing was erected and stock were excluded (Table 2).

|
Trial designs 1a and 1b were a randomised block design with three replicates of each treatment, whereas trial design 2 was randomised split plot (Table 2). Designs 1a and 1b included five rates of P from 0 to 40 kg/ha with basal nutrients (nitrogen (N), K, S, copper (Cu), zinc (Zn)) and two rates of P (0 and 40 kg/ha) without the basal nutrients. Plots were 2.2 m by 20 m with a buffer of 0.55 m between treatments. There were 12 trials with design 1a or 1b: seven trials were fenced for the entire season and mown every 5–6 weeks for biomass determination (1a), and five trials were grazed until spring then locked up for biomass measurements (1b). Seven trials used design 2 and included three rates of P (0, 5 and 40 kg/ha); the plots were split and basal nutrients (N, K, S, Cu, Zn) were applied to one half. Design 2 plots were narrower than design 1a and 1b plots, and were managed by allowing stock access until spring lockup before biomass measurements.
All P treatments were achieved with the application of All Phos fertiliser (CSBP), selected for its low S content (20.3% P, 1.0% S). Design 1 trials had a basal fertiliser (N, K, S, Cu, Zn) applied at establishment, and pasture was cut to 5 cm with a mower at intervals of ~6 weeks from June to September, depending on growth rates. After every cut, in-season applications of N, K and S basal fertiliser were applied (Table 2). Trials using designs 1b and 2 had a basal fertiliser (N, K, S, Cu, Zn) applied at establishment of trial. Two further in-season applications of N, K and S basal fertiliser were applied, one at lockup and one in late September (Table 2).
For design 1a trials, the entire site was mown following each biomass assessment and the pasture removed to simulate grazing, whereas trials using designs 1b and 2 retained stock access until spring, when the site was locked up to enable a flush of growth during spring for subsequent biomass assessment.
Pasture measurements
Pasture growth was determined by weighing strips of mown pasture of known length and width within the plots. Wet pasture was weighed, the weight recorded, and a subsample of known weight retained and dried to determine dry matter.
Percentages of clover, grass and weeds were assessed using the BOTANAL method as described by Cayley and Bird (1996). Sites of type 1a design were assessed twice in the season (once at the first biomass assessment and then again in October). Trials with designs 1b and 2 were assessed once only, in October.
Species-specific tissue testing was conducted for all sites at or just before 10% flowering (mid–late September, depending on site growth). If composition of the pasture sward was >30% legume, the legume component was sampled. If the legume composition of the sward was <30%, ryegrass was sampled. Species-specific tissue testing was chosen owing to budget constraints, and although plant tissue results are of value in assisting with interpretation, they were secondary to the primary objective of validating critical P values from BFDP. Plant tissue samples were analysed for P, K, S, calcium, magnesium, sodium, iron and boron, using the methods described by McQuaker et al. (1979). In brief, a mixture of hydrogen peroxide and nitric acid is added to a dry plant sample and heated until completely digested. Digests are then read by inductively coupled plasma spectroscopy, which determines total elements present within the plant. Plant tissue was analysed for N by method 9G2 of Rayment and Lyons (2011). In this method, plant samples are analysed for total N via the Dumas high-temperature combustion method in a LECO analyser. Samples are loaded into a combustion tube at 950°C and flushed with oxygen. Gases generated from this process are measured for N by using a thermal conductivity cell.
Data analyses
Several non-linear statistical relationships have been used to describe yield response. The most successful of these is the Mitscherlich equation (Eqn 2), which was applied to the trial data when there were five rates of P in the trial design (Table 2):
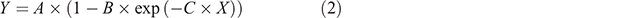
where Y is plant yield, absolute (t/ha) or relative (%); A is Ymax (nutrient non-limiting); B is site responsiveness, (A – Y0)/A, where Y0 is yield when X = 0 and ranges from 0 to 1; C is curvature coefficient; and X is amount of nutrient measured in the soil test (mg/kg) or applied (kg/ha).
When there were at least three P rates in the trial design (Table 2), RY was estimated using Y0 (yield from the control) and Ymax (yield from maximum P rate).
Analysis of variance (ANOVA) including interactions was undertaken with Genstat 20th Edn (VSN International) to detect differences (P < 0.05) in dry matter produced for the treatments for each trial. Blocking was included as a factor for the trials with randomised block designs (1a and 1b) to account for spatial variation, but not for trials with design 2 because of trial layout constraints. A post hoc analysis determined least significant differences (l.s.d.) (Gramm et al. 2007).
Relative yield was then determined from Eqn 3:

where Y0 is pasture yield with no nutrient applied, and Ymax is maximum pasture yield when non-limiting nutrient is applied.
Collated Colwell P, PBI, P95, RY and ANOVA information was used to classify the trials as responsive or non-responsive, and RY was compared with the predicted RY from BFDP (eqns 6 and 7 from Gourley et al. 2019; referred to here as Eqns 4 and 5):
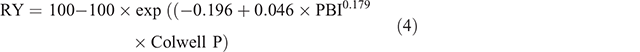
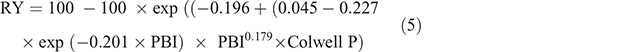
Equation 4 modified the Mitscherlich equation (Eqn 2) to include a c coefficient that varied according to PBI, and Eqn 5 made further adjustments to the c coefficient to account for other published work suggesting lower critical Colwell P values and greater responsiveness for sites that had low PBI (Yeates 1993; Moody 2007). A trial was deemed non-responsive if ANOVA determined no significant response to P application. In these cases where a Mitscherlich fit was used, RY was assigned 100% for trials that showed no response to P application.
The trial results (Colwell P and RY pairs) were also compared with the BFDP data by plotting 95% prediction intervals (Helsel and Hirsch 1992) associated with Colwell P and RY pairs from the BFDP data for PBI ranges in which the trial results were situated (Fig. 1a, c). This allows an assessment of whether a new observation (i.e. these trials) is likely to have come from the same distribution as previous data (BFDP) or from a different distribution.
Estimates of P removal in harvested biomass were made by multiplying median dry matter yield by the median P concentration of sampled plant tissue for trial treatments. For trial designs 1b and 2, which maintained stock access until spring lockup, it was assumed that only 20% of the P in harvested biomass was removed in stock (Weaver and Wong 2011), whereas for trial design 1, 100% of the P was assumed to have been removed in harvested dry matter.
Results
The PBI of the selected sites corresponded with the PBI categories most represented by soil types in the study area (Table 1): moderately low, medium and high PBI categories. The other PBI categories are yet to be well represented in this study. The medium and high PBI categories included a wide range of P95 fertility index soils, whereas the extremely low PBI category included only one site and both the moderately high and very high PBI categories none (Fig. 1).
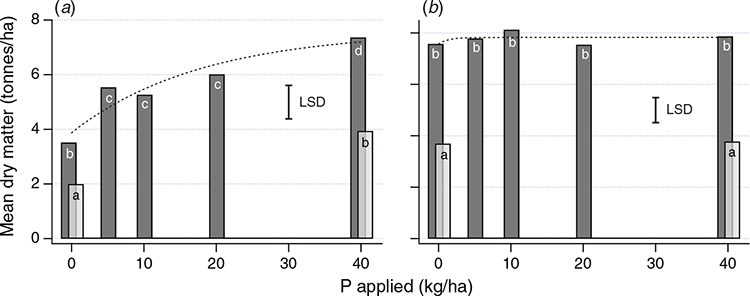
Table 3 presents initial soil characteristics and whether a P response was predicted at each trial site. Response of mean annual cumulative dry matter to P applied is shown for typical trials with a P response (Fig. 2a) and without a response (Fig. 2b). The responsive trial (Fig. 2a) showed a significant (P < 0.05) increase in dry matter at rates of applied P from 5 to 40 kg/ha. The RY of the control (0 kg P/ha) was almost identical with basal nutrients applied (47.8%), without basal nutrients applied (50.8%), and determined from a Mitscherlich curve fit (51.1%). The dry matter yield increase from the addition of basal nutrients was significant (P < 0.05), and similar for applied P rates of 0 kg P/ha (76%) and 40 kg P/ha (87%) (Fig. 2a).

|
The median P concentration of subterranean clover sampled from the typical responsive trial at 0 kg P/ha with and without basal nutrients was 0.13% and 0.14%, respectively, resulting in P removal in dry matter of 4.04 and 2.41 kg/ha. For the same trial when 40 kg P/ha was applied, the median P concentration with and without basal nutrients was 0.23% and 0.26%, respectively, resulting in P removal in dry matter of 17.29 and 10.34 kg P/ha.
The median P concentration of ryegrass sampled from the typical non-responsive trial at 0 kg P/ha with and without basal nutrients was 0.26% and 0.31%, respectively, resulting in P removal in dry matter of 19.95 and 11.19 kg P/ha. For the same trial when 40 kg P/ha was applied, the median P concentration with and without basal nutrients was 0.32% and 0.38%, respectively, resulting in P removal in dry matter of 26.22 and 13.33 kg P/ha.
The non-responsive trial showed no significant (P > 0.05) increase in dry matter at any P application rate (Fig. 2b). The RY of the control (0 kg P/ha) was almost identical with basal nutrients applied (96.2%), without basal nutrients applied (97.7%), and determined from a Mitscherlich curve fit (100%). The dry matter yield increase from the addition of basal nutrients was significant (P < 0.05), and similar for applied P rates of 0 kg P/ha (104%) and 40 kg P/ha (108%) (Fig. 2b).
Of the 19 trial sites, 14 sites did not respond to P applications, and five sites did. Of the 11 trial sites predicted to respond, five sites were responsive to P application (e.g. Fig. 2a), and six sites were not (e.g. Fig. 2b). All five trials that did respond were predicted to respond based on the models in BFDP (Gourley et al. 2019). Of the eight trial sites predicted not to respond to P, none responded. Fifteen trials were responsive to the addition of basal nutrients with or without the addition of P, and 12 trials were responsive to basal nutrients alone without the addition of P. None of the trials showed a significant interaction between basal nutrients and P rate.
For the same P supply, whether that be from the soil alone (0 kg P/ha), or from soil with applied P at 40 kg/ha, the addition of basal nutrients increased dry matter and P removal in biomass, and therefore P demand by >100% (Fig. 2a, b). Omitting basal nutrients caused a yield gap of almost 50% in both 0 kg P/ha and 40 kg P/ha treatments (Fig. 2a, b). This significant effect of basal nutrients was seen to varying degrees in 15 of the 19 trials. The dry matter increase ranged from 141% to 267% for 0 kg P/ha, and from 137% to 244% for 40 kg P/ha.
Most sites did not respond to applications of P even when they were predicted to be responsive on the basis of soil test results (Fig. 3a, Table 3). The P95 fertility index ranged from 0.33 to 0.73 at responsive sites, and from 0.62 to 2.06 at non-responsive sites. The RY measured in the trials, compared with Eqn 5, was within 10% of the predicted response based on soil test results in most cases (Table 3, Fig. 3b). Non-responsive trials always had a positive RY difference, whereas responsive trials always showed a negative RY difference. Non-responsive trials had RY differences of up to +15%. Similar patterns were observed when RY differences were estimated by using Eqn 4; however, as PBI decreased to <15, the RY differences increased by as much as 20%.

|
Three responsive trials had a difference in RY of –20%, and at two of these sites, pHCa was 4.7 (site 9) and 4.1 (site 11) (Table 3). The mean pH of responsive sites was 4.7, and non-responsive sites 5.1, but this difference when the data was grouped was not significant (P > 0.05).
The BFDP data and 95% prediction intervals for the same overlapping PBI ranges specified by Gourley et al. (2019) are shown in Fig. 4 with Colwell P and RY pairs from this study. All 19 trials fall within the 95% prediction interval boundaries from BFDP.

|
Discussion
Results from the 19 trials to date are consistent with the national BFDP data and within the 95% prediction interval bands (Fig. 4), suggesting that the trials are in the same population (Helsel and Hirsch 1992). The trials are consistent with the expected P response (Fig. 3), and critical soil test values derived using Eqn 5. Although only five of 11 trials expected to respond to P showed a P response, the range of 95% prediction intervals (Fig. 4) from a large number of trials suggests that it would not be unusual in a small dataset of 19 trials to identify such an anomaly. This also highlights the importance of deriving critical soil test values from large datasets such as those in BFDP (Gourley et al. 2019), and emphasises that although small datasets such as these 19 trials add value to BFDP, their primary value is to validate.
Differences in RY became systematically wider and more positive when Eqn 4 was used (Fig. 3b), implying that RY would be underestimated by using this equation when PBI is <15. The RY differences assessed by using the equations from Gourley et al. (2019) indicate that Eqn 5 better estimates the trial results from this study.
The trial results are consistent with the notion that if soil tests for Colwell P indicate adequate P for pasture production, adding more P does not increase productivity and may increase fertiliser costs and add to the risk of nutrient loss offsite (Weaver and Wong 2011; Gourley et al. 2019). Equally, the results indicate that applying P according to soil test should result in the predicted RY. The results also indicate that correcting nutrient deficiencies consistent with the Sprengel–Liebig law of the minimum (van der Ploeg et al. 1999) can dramatically increase production (Fig. 2). In the examples of responsive and non-responsive sites shown here, production increases of 137–267% were observed when N, K and S were applied to non-limiting levels. For the responsive site (Fig. 2a), an almost 4-fold increase in dry matter was observed when all nutrient constraints (N, P, K, S) were corrected, again consistent with the Sprengel–Liebig law of the minimum.
The Sprengel–Liebig law of the minimum is clearly shown when the application of basal nutrients led to large increases in dry matter for the same P supply, whether that be from the soil alone (0 kg P/ha), or from the soil and applied P (40 kg P/ha) (Fig. 2). The law of diminishing returns is also demonstrated in Fig. 2a where increases in dry matter decreased with increasing P application rate, and in Fig. 2b where no further increases in dry matter resulted from P application because there was already sufficient P in the soil. In the case of these trials where P was at or above optimum, large increases in dry matter were related to removal of other nutrient constraints (N, K, S); however, increases or decreases in absolute dry matter yield can also occur through fluctuations in rainfall, highlighting the importance of RY in the determination of soil test critical values. Critical soil test values are unlikely to be related to absolute yield, but are clearly influenced by soil PBI and are related to RY (Gourley et al. 2019).
The median P concentration of subterranean clover sampled from the typical responsive trial at 0 kg P/ha with and without basal nutrients was low (0.13 and 0.14%), and would be classified as deficient compared with reported critical values of 0.25–0.5% (Weir and Cresswell 1994), 0.16–0.32% (Sandral et al. 2019), and 0.23% (McCaskill et al. 2019). For subterranean clover from the same trial when 40 kg P/ha was applied with and without basal nutrients, the P concentration (0.23% and 0.26%) in most cases would be classified as adequate, except when the critical ranges of Reuter and Robinson (1997) are used (0.32–0.70%). The P concentration of ryegrass from the non-responsive trial at 0 kg P/ha with and without basal nutrients (0.26% and 0.31%) was below the critical range described as adequate (0.35–0.70%) by Reuter and Robinson (1997), and would therefore be classified as deficient. Using these same critical ranges, the P concentration of ryegrass from the non-responsive trial for all treatments except when 40 kg P/ha was applied without basal nutrients would be classified as deficient. Compared with the critical range of 0.25–0.55% cited by Weir and Cresswell (1994), the P concentrations of ryegrass in all treatments from the non-responsive trial would be classified as adequate, consistent with the lack of response shown in Fig. 2b. The critical ranges used to determine deficiency or adequacy in plant tissues require further investigation given that some non-responsive sites showed P concentrations in the plant tissue that could be lower than, or within, critical ranges suggested for adequacy, depending on the range used.
Among these general findings, there were some larger, negative deviations in RY that require further exploration. Although all of the trials fall within the 95% prediction intervals (Fig. 4), some larger RY deviations of ~20% were found for trials 5, 9 and 11 (Fig. 3b). These three sites have soil pH lower than desired (pHCa 5.5); however, 16 of the 19 trial sites have low pH. The target value of pHCa 5.5 is chosen because the region has almost entirely continuous pasture with minimal soil disturbance when lime is surface-applied (lime was not applied as part of these trials). Aiming for pH 5.5 in the 0–10 cm layer encourages increases in pH beyond a depth of 10 cm under these conditions, meeting the pH requirements of most pasture species and for nodulation of clover. However, sites 5, 9 and 11 also had low P fertility (Table 3). Observations of the effects of soil pH on the P concentration of subterranean clover provide a possible explanation for the RY deviations (Weaver et al. 2020). Those authors observed that the P concentration of clover was significantly depressed under conditions of low P fertility (P90 fertility index <0.6) and low pH (pHCa <5) compared with conditions of similar P fertility but higher pH. Weaver et al. (2020) compared critical P ranges for subterranean clover (from Reuter and Robinson 1997) with the P concentrations in subterranean clover sampled from soils with varying P fertility and pH. The authors identified that clover at sites with low P fertility was deficient in P (0.15–0.25% interquartile range) at pHCa <5 and contained 0.25–0.30% P (interquartile range) at pHCa >5. Low soil pH is therefore likely to contribute to lower than expected dry matter and RY at some sites. Weaver et al. (2020) also observed that the negative effect of soil pH on P concentration in subterranean clover was overcome if the soil had higher P fertility than required as determined by published critical Colwell P values (Gourley et al. 2019). Acidic conditions can reduce root growth through aluminium toxicity, limiting the volume of soil from which plants can access P. Increasing soil P fertility could reduce this limitation, because, as indicated by Barrow et al. (2020), P availability may not be as limited by low pH as previously thought. Ideally application of lime could ameliorate this issue, reducing downstream consequences of P loss from these paddocks. However, where lime is not applied, Weaver et al. (2020) suggested using a P90 fertility index of 1.2 for soils with pHCa <5, above which there was sufficient P in the soil to overcome effects of soil acidity on reduced P uptake. In practice the environmental impact of acidic and low-P sites is limited by the small proportion of such sites; Table 1 indicates that a high proportion of sites in the study area have high P fertility (56% with a P95 fertility index >1) and low pH (80% with pH <5.5) and are therefore unlikely to have pasture productivity reduced because of low pH affecting P uptake.
Pasture composition is another factor that may influence RY, pasture responsiveness and the deviations shown in Fig. 3b. Many of the trials conducted here were sown with mixed, contemporary pasture species, and these will not necessarily have the same responsiveness as those used in pasture trials collated by BFDP from 1955 to 2006. For example, it is widely accepted that clover has a higher P requirement than ryegrass (Ozanne et al. 1969; Helyar and Anderson 1971; Jackman and Mouat 1972; Barrow 1975; Ozanne et al. 1976; Hill et al. 2010; Sandral et al. 2019). Hence, pasture composition in particular trials and in treatments within trials can also influence responsiveness and, potentially, RY measurements. For example, for the responsive trial (Fig. 2a) where P supply was sufficient (40 kg P/ha) without basal nutrient applied, plots were dominated by 70% clover because the grasses did not have ready access to available N, whereas for the same 40 kg P/ha treatment with basal nutrients applied, plots were dominated by 90% ryegrass (Goodman and Collison 1981). Notwithstanding these factors, the results here are consistent with the values and variability of data from BFDP.
A simple observation from these trials is the importance of soil testing to providing evidence-based fertiliser decision making. Weaver and Wong (2011), Barrow (2015) and Crawford et al. (2020) note the requirement in many situations in Australia for P management to move into a maintenance phase, based around soil testing to guide any capital or maintenance P requirements. This approach needs to replace the traditional approach to P management, which in many cases is to apply P annually irrespective of need, and which has led to legacy P stores that now contribute unnecessarily to offsite water quality problems (Gourley and Weaver 2012). This provides significant opportunity for landholders to redirect current P expenditure to other aspects of the Sprengel–Liebig law of the minimum (van der Ploeg et al. 1999), concurrently increasing production and minimising offsite impacts.
Further research is required to establish the economic requirement of targets for RY. Current agronomic guidance is dominated by the dairy industry, which has been at the forefront of soil testing but has a greater yield requirement targeting predominantly 95% of RY for most paddocks. This target is unlikely to be economic or environmentally desirable for the majority of the grazing areas of WA, which are dominated by beef production. This deserves detailed consideration considering the large improvements in yield from non-P inputs shown here.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
This work is jointly funded through Royalties for Region’s Healthy Estuaries WA and the Australian Government’s National Landcare Program. The project team thanks the farmers who contributed by offering access to paddocks for this work, as well as technical field staff including Ian Rose, John Grant and Paul Matson. In addition, we thank the uPtake team and Technical Reference Group who contributed to the trial design and site selection, including Brad Degens, Cameron Gourley, Daniel Kidd, Garan Peirce, Gary Haddon, Harley Royce, Jeff Kraak, Jeisane Accioly, Joel Hall, Kath Lynch, Malcolm Robb, Mark Gheradi, Mick Taylor, Peta Richards, Ralph Papalia, Richard Bell, Ross Milne, Sam Taylor and Tim Prosser.
References
Barrow N (1975) The response to phosphate of two annual pasture species. I. Effect of the soil’s ability to adsorb phosphate on comparative phosphate requirement. Australian Journal of Agricultural Research 26, 137–143.| The response to phosphate of two annual pasture species. I. Effect of the soil’s ability to adsorb phosphate on comparative phosphate requirement.Crossref | GoogleScholarGoogle Scholar |
Barrow N (2015) Soil phosphate chemistry and the P-sparing effect of previous phosphate applications. Plant and Soil 397, 401–409.
| Soil phosphate chemistry and the P-sparing effect of previous phosphate applications.Crossref | GoogleScholarGoogle Scholar |
Barrow N, Debnath A, Sen A (2020) Measurement of the effects of pH on phosphate availability. Plant and Soil 454, 217–224.
| Measurement of the effects of pH on phosphate availability.Crossref | GoogleScholarGoogle Scholar |
Bell R, Reuter D, Scott B, Sparrow L, Strong W, Chen W (2013) Soil phosphorus crop response calibration relationships and criteria for winter cereal crops grown in Australia. Crop & Pasture Science 64, 480–498.
| Soil phosphorus crop response calibration relationships and criteria for winter cereal crops grown in Australia.Crossref | GoogleScholarGoogle Scholar |
Blair G, Chinoim N, Lefroy R, Anderson G, Crocker G (1991) A soil sulfur test for pastures and crops. Australian Journal of Soil Research 29, 619–626.
| A soil sulfur test for pastures and crops.Crossref | GoogleScholarGoogle Scholar |
Burkitt L, Moody P, Gourley C, Hannah M (2002) A simple phosphorus buffering index for Australian soils. Australian Journal of Soil Research 40, 497–513.
| A simple phosphorus buffering index for Australian soils.Crossref | GoogleScholarGoogle Scholar |
Cayley J, Bird P (1996) ‘Techniques for measuring pastures.’ (Agriculture Victoria: Hamilton, Vic.)
Colwell J (1965) An automatic procedure for the determination of phosphorus in sodium hydrogen carbonate extracts of soils. Chemistry & Industry 22, 893–895.
Cope J, Rouse R (1973) Interpretation of soil test results. In ‘Soil testing and plant analysis’. (Eds L Walsh, J Beaton) pp. 35–54. (Soil Science Society of America: Madison, WI, USA)
Crawford D, Mitchard B, Burton W (2020) Recent trends in soil fertility across the farms of East Gippsland. Soil Research 58, 561–575.
| Recent trends in soil fertility across the farms of East Gippsland.Crossref | GoogleScholarGoogle Scholar |
Goodman PJ, Collison M (1981) Uptake of 32P labelled phosphate by clover and ryegrass growing in mixed swards with different nitrogen treatments. Annals of Applied Biology 98, 499–506.
| Uptake of 32P labelled phosphate by clover and ryegrass growing in mixed swards with different nitrogen treatments.Crossref | GoogleScholarGoogle Scholar |
Gourley C, Weaver D (2012) Nutrient surpluses in Australian grazing systems management practices, policy approaches, and difficult choices to improve water quality. Crop & Pasture Science 63, 805–818.
| Nutrient surpluses in Australian grazing systems management practices, policy approaches, and difficult choices to improve water quality.Crossref | GoogleScholarGoogle Scholar |
Gourley C, Weaver D, Simpson R, Aarons S, Hannah M, Peverill K (2019) The development and application of functions describing pasture yield responses to phosphorus, potassium and sulfur in Australia using meta-data analysis and derived soil-test calibration relationships. Crop & Pasture Science 70, 1065–1079.
| The development and application of functions describing pasture yield responses to phosphorus, potassium and sulfur in Australia using meta-data analysis and derived soil-test calibration relationships.Crossref | GoogleScholarGoogle Scholar |
Gramm J, Guo J, Hüffner F, Niedermeier R, Piepho H-P, Schmid R (2007) Algorithms for compact letter displays: comparison and evaluation. Computational Statistics & Data Analysis 52, 725–736.
| Algorithms for compact letter displays: comparison and evaluation.Crossref | GoogleScholarGoogle Scholar |
Helsel D, Hirsch R (1992) ‘Statistical methods in water resources.’ (Elsevier Science Publishers)
Helyar K, Anderson A (1971) Effects of lime on the growth of five species, on aluminium toxicity, and on phosphorus availability. Australian Journal of Agricultural Research 22, 707–720.
| Effects of lime on the growth of five species, on aluminium toxicity, and on phosphorus availability.Crossref | GoogleScholarGoogle Scholar |
Hill JO, Simpson RJ, Ryan MH, Chapman DF (2010) Root hair morphology and mycorrhizal colonisation of pasture species in response to phosphorus and nitrogen nutrition. Crop & Pasture Science 61, 122–131.
| Root hair morphology and mycorrhizal colonisation of pasture species in response to phosphorus and nitrogen nutrition.Crossref | GoogleScholarGoogle Scholar |
Hintze JL, Nelson RD (1998) Violin plots: a box plot–density trace synergism. The American Statistician 52, 181–184.
Jackman RH, Mouat MCH (1972) Competition between grass and clover for phosphate. New Zealand Journal of Agricultural Research 15, 653–666.
| Competition between grass and clover for phosphate.Crossref | GoogleScholarGoogle Scholar |
McCaskill M, Mitchell M, Zollinger R, Armstrong R, Partington D (2019) Dry matter and nutritive value responses of native, naturalised and sown pasture species to soil Olsen P. Crop & Pasture Science 70, 1097–1109.
| Dry matter and nutritive value responses of native, naturalised and sown pasture species to soil Olsen P.Crossref | GoogleScholarGoogle Scholar |
McQuaker N, Brown D, Kluckner P (1979) 975.03. Analytical chemistry 51. ‘AOAC official methods of analysis.’ 15th edn. (AOAC International: Rockville, MD, USA)
Melland A, Mc Caskill M, White R, Chapman D (2008) Loss of phosphorus and nitrogen in runoff and subsurface drainage from high and low input pastures grazed by sheep in southern Australia. Australian Journal of Soil Research 46, 161–172.
| Loss of phosphorus and nitrogen in runoff and subsurface drainage from high and low input pastures grazed by sheep in southern Australia.Crossref | GoogleScholarGoogle Scholar |
Moody P (2007) Interpretation of a single-point P buffering index for adjusting critical levels of the Colwell soil P test. Australian Journal of Soil Research 45, 55–62.
| Interpretation of a single-point P buffering index for adjusting critical levels of the Colwell soil P test.Crossref | GoogleScholarGoogle Scholar |
Ozanne P, Keay J, Biddiscombe E (1969) The comparative applied phosphate requirements of eight annual pasture species. Australian Journal of Agricultural Research 20, 809–818.
| The comparative applied phosphate requirements of eight annual pasture species.Crossref | GoogleScholarGoogle Scholar |
Ozanne P, Howes K, Petch A (1976) The comparative phosphate requirements of four annual pastures and two crops. Australian Journal of Agricultural Research 27, 479–488.
| The comparative phosphate requirements of four annual pastures and two crops.Crossref | GoogleScholarGoogle Scholar |
Rayment G, Lyons D (2011) ‘Soil chemical methods: Australasia.’ (CSIRO Publishing: Melbourne, Vic.)
Reuter D, Robinson J (1997) ‘Plant analysis, an interpretation manual.’ (CSIRO Publishing: Melbourne, Vic.)
Sandral GA, Price A, Hildebrand SM, Fuller CG, Haling RE, Stefanski A, Yang Z, Culvenor RA, Ryan MH, Kidd DR, Diffey S, Lambers H, Simpson RJ (2019) Field benchmarking of the critical external phosphorus requirements of pasture legumes for southern Australia. Crop & Pasture Science 70, 1080–1096.
| Field benchmarking of the critical external phosphorus requirements of pasture legumes for southern Australia.Crossref | GoogleScholarGoogle Scholar |
Simpson R, Graham P, Davies LEZ (2009) ‘Five easy steps to ensure you are making money from superphosphate. Decision support tool.’ (CSIRO & Industry and Investment NSW: Sydney)
Simpson R, Oberson A, Culvenor R, Ryan M, Veneklaas E, Lambers H, Lynch J, Ryan P, Delhaize E, Smith F, Smith S, Harvey P, Richardson A (2011) Strategies and agronomic interventions to improve the phosphorus-use efficiency of farming systems. Plant and Soil 349, 89–120.
| Strategies and agronomic interventions to improve the phosphorus-use efficiency of farming systems.Crossref | GoogleScholarGoogle Scholar |
Speirs S, Reuter D, Peverill K, Brennan R (2013) Making better fertiliser decisions for cropping systems in Australia: an overview. Crop & Pasture Science 64, 417–423.
| Making better fertiliser decisions for cropping systems in Australia: an overview.Crossref | GoogleScholarGoogle Scholar |
van der Ploeg RR, Böhm W, Kirkham MB (1999) On the origin of the theory of mineral nutrition of plants and the law of the minimum. Soil Science Society of America Journal 63, 1055–1062.
| On the origin of the theory of mineral nutrition of plants and the law of the minimum.Crossref | GoogleScholarGoogle Scholar |
Weaver D, Reed A (1998) Patterns of nutrient status and fertiliser practice on soils of the south coast of Western Australia. Agriculture, Ecosystems and Environment 67, 37–53.
| Patterns of nutrient status and fertiliser practice on soils of the south coast of Western Australia.Crossref | GoogleScholarGoogle Scholar |
Weaver DM, Wong MTF (2011) Scope to improve phosphorus (P) management and balance efficiency of crop and pasture soils with contrasting P status and buffering indices. Plant and Soil 349, 37–54.
| Scope to improve phosphorus (P) management and balance efficiency of crop and pasture soils with contrasting P status and buffering indices.Crossref | GoogleScholarGoogle Scholar |
Weaver D, Summers R, Rogers D, Richards P (2020) The effect of soil pH on phosphorus content of clover pasture. Resource Management Technical Report 417. Department of Primary Industries and Regional Development, Perth, W. Aust.
Weir RG, Cresswell GC (1994) ‘Plant nutrient disorders 4: pastures and field crops.’ (Butterworth-Heinemann: Oxford, UK)
Yeates J (1993) Changing fertiliser practices. Fertilizer Research 36, 135–140.
| Changing fertiliser practices.Crossref | GoogleScholarGoogle Scholar |


 ) for the ‘high’ PBI category with fitted response calibration for BFDP data. (d) Conceptual P response calibrations for soils within different PBI categories (
) for the ‘high’ PBI category with fitted response calibration for BFDP data. (d) Conceptual P response calibrations for soils within different PBI categories (