A Computational Comparative Study for the Spectroscopic Evaluation of Triazine Derivative Dyes in Implicit Solvation Model Systems Using Semi-Empirical and Time-Dependent Density Functional Theory Approaches

Keywords: spectroscopic evaluation, PM3, ZINDO, TDDFT, computational chemistry, implicit solvation, rational chemical design, computational chemical design, computational cost.

Computational methods utilised in the chemical sciences present versatile modelling tools for predicting the properties and performance of molecules under vacuum, in the solution state, and even in simulated biological systems. The spectroscopic properties of fluorescent dyes, namely cyclopenta-[d][1,2,3]-triazine derivatives have been investigated by other researchers.^[1–3] Here, we evaluate several computational methods for predicting the spectroscopic properties of this class of triazine dye.

The computational methods used to evaluate the spectroscopic transitions in implicit solvation systems include the wavelengths of electronic transitions for ground-state absorption, excited-state emission, and the oscillator strength (f). The f-value is a dimensionless quantity that measures the probability of electronic excitations occurring between molecular orbitals.^[4] This value can be correlated with the experimental absorption and emission intensity. In addition, electronic transitions between molecular orbitals, such as the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy gap, can be modelled.

The semi-empirical methods for ground state structure optimisation based on the Neglect of Diatomic Differential Overlap (NDDO) approach^[5] were selected based on their relatively low computational cost, including the Austin Model 1 (AM1),^[6] parametric method 3 (PM3),^[7,8] and parametric method 6 (PM6)^[9] approaches. These optimisation models were paired with Zerner’s Intermediate Neglect of Differential Overlap (ZINDO)^[10] to model absorption data through single-point energy (SPE) calculations in the first excited state, notably, without optimisation of the excited state geometry (i.e. vertical excitation energy). Thus, the SPE calculations are expected to provide reasonably accurate spectroscopic data for the third-row element heteroatoms with 3d orbitals attached to the triazine skeleton.

The semi-empirical approaches reported for other fluorescent dyes have been reported to yield acceptably accurate spectroscopic data.^[11–17] Nevertheless, the presence of the sulfur atom in proximity with a N-heterocyclic ring structure was considered to significantly destabilise the ring due to the inductive effect, which may provide a difficult system to model computationally, especially if the sulfur atom causes geometric perturbation^[16] and inaccurate spectroscopic data estimation as reported in Tubert-Brohman et al.^[18] As a result of these complexities, the lower computational cost of the semi-empirical methods compared with ab initio methods had to be weighed against the accuracy of the spectroscopic data acquired. Nevertheless, absorbance data of a satisfactory accuracy has been obtained for conjugated ring structures containing sulfur substituents using semi-empirical optimisation methods combined with the ZINDO/S model.^[12,13]

Despite the higher computational cost involved in using time-dependent density functional theory (TDDFT) methods, it is increasingly becoming the preferred computational approach for spectroscopic evaluation,^[19] including for studies of triazine derivative dyes.^[20] It has been established that the TDDFT approach has rendered semi-empirical methods such as ZINDO/1 almost obsolete for predicting the emission data of fluorescent dye molecules, involving optimisation of the excited-state structure (i.e. adiabatic excitation energy).^[19]

Therefore, this study investigates semi-empirical methods for evaluating the absorbance data of triazine derivative fluorescent dyes both under vacuum and in solution, using the linear response method^[21] combined with the polarisation continuum model (PCM) to model solvation. In addition, we compare the accuracy of TDDFT for predicting both absorption and emission data for this class of triazine dye. Also, we compare the basic linear response model and the more accurate state-specific solvation approach^[22] – accounting for the non-equilibrium solvation of the excited-state structure. It is expected that the application of computational cost across different synthetic designs could assist chemists to predict spectroscopic properties of dyes with geometric perturbation defects before synthesis.

The synthesis and characterisation of compounds 1 to 7 have previously been reported.^[1–3] The absorption and emission measurements of compounds 1 to 3 of the original sample were measured directly without further purification, and compounds 4 to 7 were obtained from the literature.^[3] RCI Labscan supplied all the HPLC grade solvents used for the absorption and emission measurements for compounds 1 to 3, except for dimethyl formamide (DMF) and acetonitrile (MeCN) which were dried over molecular sieves (4 Å pellets, with 1.6 mm diameter). The steady-state absorption and emission measurements of compounds 1–3 were recorded at room temperature using Cary 50 BIO UV/Vis and Fluorolog 22 (Jobin Yvon Horiba) spectrophotometers.

The structures were produced and visualised using Avogadro (software version 1.90.0).^[23] Calculations were completed using Gaussian 16 software (Wallingford, Connecticut, USA) (full reference provided in the Supplementary Material) for all methods utilised. The triazine derivative dyes 1 to 7 were initially subject to geometry optimisation through the Berny analytical gradient method^[24] incorporated into Gaussian 16 followed by vibrational frequency analysis. All structures were confirmed to be stable intermediates (minima on the potential energy surface) and ensured no imaginary frequencies present during simulation. Solvation of dyes 1 to 7 was modelled through the self-consistent reaction field (SCRF) approach^[25] with the PCM.^[26] The following solvents: dimethyl sulfoxide (DMSO), MeCN, tetrahydrofuran (THF), toluene, and DMF were implemented by specifying them from the built-in solvent list contained in Gaussian 16 software. The 2-methyltetrahydrofuran (2-MeTHF) was implemented by specifying the specific solvent characteristics from the literature values (see Supplementary Material).

For the semi-empirical approaches, the structures were optimised using either the AM1, PM3, or PM6 method followed by SPE calculations at the ZINDO/S semi-empirical level, specified by 10 singlet excited states. For the TDDFT analysis, the ωB97X-D long-range corrected hybrid exchange-correlation functional^[27] was selected mainly for its ability to model long range interactions and proven performance in TDDFT studies.^[28] In addition, when combined with the 6–31G(d) basis set,^[29,30] it provided suitably accurate data for a reasonable computational cost. Therefore, for this study, six singlet excited states were specified for TDDFT analysis. The linear response and state-specific solvation approaches were utilised for calculating absorption data using TDDFT while the state-specific approach was utilised for excited state emission data.

The wavelength of the maximum absorption () and the corresponding f values for triazine derivative dyes 1 to 7 determined using the semi-empirical methods trialled in this investigation are provided in Table 1. Ten excited states were specified to gain a solid understanding of the electronic transitions occurring. The vertical excitation energies are provided in Table 2. In all cases, the absorption wavelength () recorded in Table 1 corresponded to the first strongly allowed electronic transition – that is, the first electronic transition to possess an oscillator strength (f) value greater than 0.08.^[28,31] The maximum absorption wavelengths obtained experimentally are also provided.

Table 1.  Spectroscopic data obtained from semi-empirical methods and experimental values
Ground state absorption maxima () and oscillator strength (f) of triazine dyes 1 to 7 calculated using ZINDO/S for vertical excitation energies. Experimental data were either obtained from ref. [3] or measured directly. ND, not determined

Table 2.  Vertical excitation energies (ΔE) for triazine dyes 1 to 7 calculated using ZINDO/S with the AM1, PM3, and PM6 semi-empirical optimisation methods

The AM1 semi-empirical method combined with ZINDO/S consistently predicted values greater than the values recorded experimentally for triazine dyes 1 to 7 in each solvent (obtained either from Zhu et al.^[3] or measured directly). As previously reported by other investigators, the AM1 method is less parameterised than either the PM3 or PM6 semi-empirical methods.^[7–9,32] This may explain some of the issues observed in accurately modelling the relatively complex triazine dye structures investigated in this study. Moreover, the sulfur atom bonded to the heterocyclic nitrogen ring present in each triazine derivative dye 1 to 7 may inhibit the ability of the AM1 method to accurately optimise the structures.

The combined PM3 semi-empirical method with ZINDO/S provided data with relatively close agreement to experimentally observed absorption data. This combination of methods provided an impressive correlation between the experimental and calculated absorption maxima. Triazine derivative dye 4 (MOT) was modelled accurately for the combined PM3 with ZINDO/S. Several studies have also reported the increased tendency of the PM3 geometry optimisation method to provide more accurate starting structures for calculation of absorption data compared with the AM1 method.^[7,8,32]

The implicit solvation of dyes through the linear response method proved relatively effective for PM3 combined with ZINDO/S, proving capable of reproducing the experimental solvatochromic trends. Solvents recording higher bathochromic shifts (i.e. DMSO) generally recorded the longer wavelengths in the ground state, , while shorter wavelengths were recoded for THF and 2-MeTHF (which recorded close values). MeCN demonstrated variable changes in absorption maxima for both the experimentally recorded and computationally observed data. One plausible explanation could have been that the MeCN formed a complex triad group, making it difficult to model the triazine dye structures accurately for implicit solvent that involved MeCN for 1 to 7. The PM3 method predicted relatively accurate absorption maxima for triazine derivative dyes 1 to 4 and reflected greater absorbance values for 5 (AMT) and 6 (BMT) (although less accurate for these dyes). However, the PM3 method was unsuccessful at reproducing the high absorption values for dye 7 (EOT) in the various solvents, indicating that this method is not universally accurate. Apparently, the combined methods of PM3 with ZINDO/S provides a valuable tool for synthetic chemists aiming to rapidly predict the spectroscopic properties of newly functionalised triazine derivative dyes before synthesis.

The combined PM6 semi-empirical method with ZINDO/S calculated absorption data did not agree with the experimentally observed data. Each calculation predicted relatively higher values than the experimentally observed absorption maxima. While the PM6 semi-empirical method is relatively new and more parameterised than the PM3 method,^[9] the extra parameterisation was not successful at predicting the complex structure of the triazine dyes 1 to 7, making PM3 the most accurate semi-empirical method for geometry optimisation trialled in this study.

It was also observed that the AM1, PM3, and PM6 methods required almost the same computational costs to complete calculations. Triazine derivative dye 1 (BPT) consistently required the greatest computational costs in each solvent trialled at the AM1, PM3, and PM6 levels. This is potentially due to the structural positioning of the benzyl group attached to a sulfide bond and the pyrrolidine group (Fig. 1). In comparison, triazine derivative dyes 5 (AMT) and 7 (EOT) recorded the lowest computational costs, which may likely be due to the simplicity of their structures (Fig. 1). For triazine derivative dyes 1 (BPT), 2 (BDT), and 3 (MPT), the greatest computational costs were recorded for calculations specifying 2-MeTHF as the solvent, as the 2-MeTHF is not included in the list of built-in solvents within Gaussian 16 software. Therefore, it had to be manually specified for each computation study.

Fig. 1.  The structure, IUPAC nomenclature, and abbreviated names of the triazine dyes 1 to 7 studied here.

The presence of a sulfur atom on the triazine dye was replaced with an oxygen atom to form dye 8 (ETC) (see Fig. 2). Absorbance data for dye 8 (ETC) was obtained using the ZINDO/S method applied to structures optimised with the AM1, PM3, and PM6 methods indicated in Table 3. The vertical excitation energies (ΔE) are recorded in Table 4. Interestingly, the semi-empirical methods trialled for dye 8 (ETC) gave values close to the recorded values for dye 7 (EOT). Thus, the PM3 optimisation method provided structures for ZINDO/S calculations that predicted considerably lower values than the AM1 or PM6 optimisation method; regardless of the substitution of the sulfur atom. Therefore, it is probable that the lower accuracy recorded for the semi-empirical methods was not solely due to the presence of the sulfur atom but influenced by additional structural factors, for instance, the triazine ring.

Fig. 2.  The structure, IUPAC nomenclature, and abbreviated name of the model triazine dye, 3-ethyl-5-methoxy-4-oxo-4,6-dihydro-3H-cyclopenta[d][1,2,3]triazine-7-carboxamide (8, ETC).

Table 3.  Spectroscopic data obtained by semi-empirical methods for a model triazine dye, ETC (8)
Ground state absorption maxima () and oscillator strength (f) calculated using ZINDO/S for vertical excitation energies with the AM1, PM3, and PM6 semi-empirical optimisation methods

Table 4.  Vertical excitation energies (ΔE) calculated for ETC (8) calculated using ZINDO/S with the AM1, PM3, and PM6 semi-empirical optimisation methods

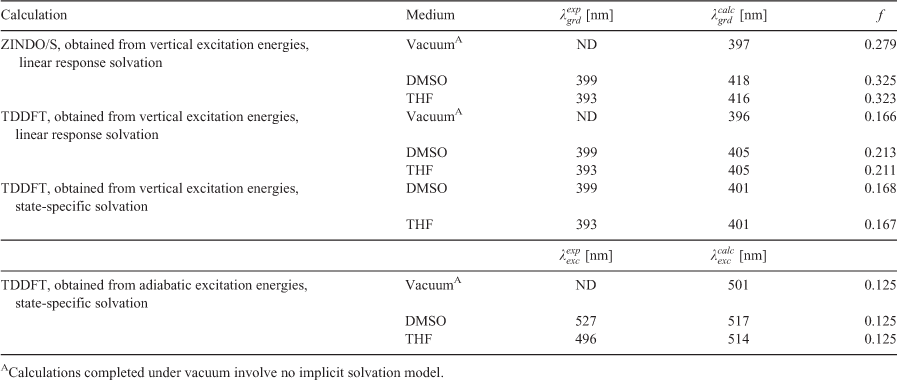
While the semi-empirical methods are sufficient at calculating vertical excitation energies for providing ground-state absorption data, improved emission data was obtained using the TDDFT method. TDDFT allowed for adiabatic excitation energy calculation through excited-state geometry optimisation. Furthermore, TDDFT offers a higher accuracy for the spectroscopic prediction of the triazine dyes 1 to 7 compared with the semi-empirical methods but with a greater computational cost.^[33] Accordingly, utilising TDDFT accurately predicted the ground state absorption (), the excited state emission (), and the f-value of triazine derivative dye 7 (EOT) at the ωB97X-D/6–31G(d) level, as indicated in Table 5. The vertical and adiabatic excitation energies are recorded in Table 6. These values corresponded to the experimental absorption and emission data ( and , respectively). The data was calculated under vacuum and solvated in DMSO and THF using the PCM model. The absorption data was calculated using the linear response and state-specific solvation models while emission data was calculated using only the state-specific approach.

Table 5.  Comparative electronic ground state absorption () and excited state emission () data with the corresponding oscillator strengths (f) for EOT (7)
Calculated using ZINDO/S applied to geometry optimised at the ωB97X-D/6–31G(d) level or using TDDFT analysis. Experimental data were either obtained from ref. [3] or measured directly. and are the experimental absorption and emission maxima respectively. Computational absorptions were calculated using (i) the linear response or (ii) state-specific solvation models. The emission data were calculated only through the state-specific approach. ND, not determined

Table 6.  Vertical and adiabatic excitation energies for triazine dye, EOT (7)
ΔE calculated using ZINDO/S applied to geometry optimised at the ωB97X-D/6–31G(d) level and using TDDFT analysis. Experimental data were either obtained from ref. [3] or measured directly. Absorption data was calculated using both the linear response and the state-specific solvation models. The emission data was calculated using only the state-specific approach

The effect of solvation was calculated to decrease the HOMO–LUMO energy gap, indicated by the increase in both the maximum absorption and emission wavelengths for solvation in DMSO and THF relative to the calculation completed under vacuum. An analogous bathochromic shift was observed for each of the semi-empirical calculations in each solvent relative to the value recorded under vacuum. Analysis of the electronic transition data for dye 7 (EOT) calculated through TDDFT also demonstrated that both the absorbance and emission maxima were due to the same electronic transition involving the HOMO and LUMO molecular orbitals (with a relative contribution > 97 % in all cases). Fig. 3 demonstrates the shapes of the HOMO – 1, HOMO, LUMO, and LUMO + 1 molecular orbitals for dye 7 (EOT) calculated through TDDFT. It can be observed that each of the molecular orbitals possess a considerable electron density on the conjugated ring structures, contributing to the absorption and emission properties observed. The effect of altering the electron withdrawing substituents attached to the rings will decrease the electron density present on the ring structures, thus altering the energy levels of molecular orbitals and changing the spectroscopic properties observed.

Fig. 3.  Visualisation of the HOMO – 1, HOMO, LUMO, and LUMO + 1 molecular orbitals for dye 7 (EOT) in DMSO calculated at the ωB97X-D/6–31G(d) level (structures visualised using Avogadro software version 1.2.0).

Both the linear response solvation model and the state-specific approach provided absorption data (via directly computed vertical excitation energies) that corresponded relatively closely to the experimental data. Furthermore, the emission data calculated through the state-specific approach produced data that corresponded to the experimental data. Thus, the computational data in this study demonstrates that TDDFT analysis may be suited for the accurate predictions of emission data of this class of fluorescent dyes as well. Nonetheless, TDDFT analysis required by far the greatest computational cost techniques investigated in this work. This computational cost is expected to increase even more for more complex structures, such as triazine dye 1 (BPT). Nevertheless, the increased computational cost is necessary for estimating accurate emission data that can satisfactorily model experimental spectra.

An additional set of vertical excitation energy calculations were conducted for dye 7 (EOT) using the ZINDO/S semi-empirical method on structures optimised at the ωB97X-D/6–31G(d) level. Calculations were carried out using the linear response solvation model in an analogous method to that applied to structures optimised using the AM1, PM3, and PM6 semi-empirical methods (see Tables 5 and 6). Interestingly, absorbance data predicted by ZINDO/S for structures optimised at the ωB97X-D/6–31G(d) level were considerably higher than the experimental absorbance maxima and relatively close to the data yielded for ZINDO/S calculations applied to structures optimised at the AM1 and PM6 levels. Therefore, the experimental data of the ZINDO/S method combined with the PM3 optimisation method may be due to a cancellation of errors between the optimised structures and the subsequent ZINDO/S vertical excitation calculations. Nevertheless, the combination of the PM3 optimisation method with ZINDO/S may prove useful, especially for providing a rapid method for predicting the spectroscopic properties for this class of dyes.

Computational approaches were used to model the spectroscopic data of a class of triazine derivative dye through the implicit solvation model. From the three semi-empirical methods (AM1, PM3, and PM6) utilised for geometry optimisation in conjunction with the ZINDO/S for calculating vertical excitation energies, the PM3 model produced the most promising method. For PM3 combined with ZINDO/S, absorbance data with a reasonably low computational cost was obtained. However, it should be considered that the closer agreement of the combination of PM3 with ZINDO/S may be due to a cancellation of errors between the two methods. In addition, TDDFT analysis completed at the ωB97X-D/6–31G(d) level was used to predict absorption and emission data through both the linear response and the state-specific approach. The calculated data corresponded to the experimental data but the considerable computational cost limits the accessibility of this investigation to 7 (EOT) only in this study. We expect this method to be applicable to other classes of dyes as well.

The full reference details for Gaussian 16 software and the solvent parameters utilised to model 2-methyltetrahydrofuran (2-MeTHF) are available on the Journal’s website.

All data are either presented in this manuscript or are available from the corresponding author on request.

The authors declare no conflicts of interest.

V. A. acknowledges Griffith University for an Australian Research Training Scholarship, a Postgraduate Research Scholarship, and an International Postgraduate Scholarship.