Introducing Pseudoramps and Mixed Ramp-Gaussian Jensen Basis Sets for Better Nuclear Densities
Claudia S. Cox A and Laura K. McKemmish
A and Laura K. McKemmish  A B
A B
A School of Chemistry, University of New South Wales, Kensington, NSW 2052, Australia.
B Corresponding author. Email: l.mckemmish@unsw.edu.au

Dr Laura McKemmish is an emerging leader in computational molecular spectroscopy. As both a quantum chemist and molecular physicist, she uses cutting-edge computational techniques to enable discoveries in astrochemistry. After completing her undergraduate studies at the University of Sydney, Ph.D. degree at the Australian National University, and post-doctoral research under a Marie Skłodowska-Curie research fellowship at University College London, Laura has been building her research team in the School of Chemistry at University of New South Wales since 2018, where she continues to be amazed by the quality and enthusiasm of her students. |
Australian Journal of Chemistry 75(2) 126-134 https://doi.org/10.1071/CH21092
Submitted: 16 April 2021 Accepted: 28 June 2021 Published: 22 July 2021
Journal Compilation © CSIRO 2022 Open Access CC BY-NC
Abstract
Gaussian basis sets dominate quantum chemistry but struggle to model near-core electron densities and thus nuclear magnetic resonance (NMR) spectral properties. Mixed ramp-Gaussian (RG) basis sets show significant promise for these core properties due to the inclusion of a ramp-function with a non-zero nuclear-electron cusp. To enable quicker testing of the potential of RG basis sets for core chemistry, here we approximate ramps as a large linear combination of Gaussians called pseudoramps, thus enabling standard quantum chemistry packages to be used to approximate RG basis set results. We produce and test rampified general-purpose segmented Jensen basis sets. These basis sets retain the valence chemistry of their parent all-Gaussian basis sets, as desired, but unfortunately fail to show significantly improved performance in core chemistry. Crucially, for NMR spin-spin couplings (the most promising potential application of RG basis sets), general-purpose basis sets are so poorly performing that results cannot be interpreted. For chemical shifts, P-ramps are likely required for improved performance. We conclude that the use of pseudoramps to test the performance of ramp-Gaussian basis sets is extremely helpful, decoupling methodology development and evaluation from implementation, but that more sophisticated basis set optimisation will be required to identify potential advantages of ramp-Gaussian basis sets over all-Gaussian basis sets.
Keywords: basis sets, ramp-Gaussian basis sets, quantum chemistry, computational chemistry, core chemistry, NMR spectroscopy, basis set construction, molecular quantum chemistry.
Introduction
Basis Sets and Core Chemistry
The rise of computational molecular quantum chemistry over recent decades relied on the strength of Gaussian basis sets[1–3] in describing valence electrons while possessing a low computational cost.[4,5] However, due to their lack of an electron-nuclear cusp, Gaussian basis functions are fundamentally ill-suited to model the core-electron region[6] meaning large specialised basis sets are required for properties such as nuclear magnetic resonance chemical shifts,[7,8] spin-spin couplings[9,10] and X-ray spectroscopy.[11]
Mathematically, Gaussian basis function, denoted herein by 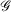 , with exponent α and angular momentum quantum numbers ℓ and m is given by
, with exponent α and angular momentum quantum numbers ℓ and m is given by 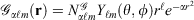 , where
, where 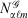 is the normalisation factor and Yℓm(θ,φ) are spherical harmonics. Gaussian functions’ inherent flaws in modelling core regions of the nuclei can be partially overcome by using a large number of Gaussian primitive functions with large exponents in the contracted basis function.[3] Thus, it is usual even for general-purpose chemistry to use 6-10 primitive Gaussians to be used to construct core basis functions (e.g. 6 in 6-31G(d)). For specialised core-dependent properties, even larger numbers of primitive functions must be used. However, this is not a ideal solution, as does not address the underlying flaws of Gaussian basis functions.
is the normalisation factor and Yℓm(θ,φ) are spherical harmonics. Gaussian functions’ inherent flaws in modelling core regions of the nuclei can be partially overcome by using a large number of Gaussian primitive functions with large exponents in the contracted basis function.[3] Thus, it is usual even for general-purpose chemistry to use 6-10 primitive Gaussians to be used to construct core basis functions (e.g. 6 in 6-31G(d)). For specialised core-dependent properties, even larger numbers of primitive functions must be used. However, this is not a ideal solution, as does not address the underlying flaws of Gaussian basis functions.
Mixed ramp-Gaussian basis sets[12] aim to address this issue at a more fundamental level. Mixed ramp-Gaussian basis sets take advantage of the strengths of Gaussian functions in describing valence electrons whilst introducing a new ramp basis function (denoted by 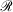 ),[13,14] which has an electron-nuclear cusp, to describe core electrons. A ramp function with degree n and angular momentum quantum numbers ℓ and m is defined by
),[13,14] which has an electron-nuclear cusp, to describe core electrons. A ramp function with degree n and angular momentum quantum numbers ℓ and m is defined by 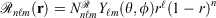 for r ≤ 1 and 0 otherwise, where
for r ≤ 1 and 0 otherwise, where 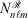 is the normalisation factor and n is the degree of the ramp (not the principal quantum number). The finite extent of the ramp function enables the elimination of two-centre ramp-ramp shell-pairs and thus dramatically reduces the complexity of two-electron integrals.[15] In combination with modelling ramp-Gaussian shell pairs as a linear combination of ramps, it has been demonstrated that calculation times of ramp-Gaussian basis sets can be competitive with or slightly faster than similar all-Gaussian basis sets[15] for low-angular momentum basis sets.
is the normalisation factor and n is the degree of the ramp (not the principal quantum number). The finite extent of the ramp function enables the elimination of two-centre ramp-ramp shell-pairs and thus dramatically reduces the complexity of two-electron integrals.[15] In combination with modelling ramp-Gaussian shell pairs as a linear combination of ramps, it has been demonstrated that calculation times of ramp-Gaussian basis sets can be competitive with or slightly faster than similar all-Gaussian basis sets[15] for low-angular momentum basis sets.
Preliminary investigations find that mixed ramp-Gaussian basis sets have comparable valence chemistry properties to their parent basis sets.[12] In addition, mixed ramp-Gaussian basis sets can model electron densities at the nucleus much more effectively than all-Gaussian basis sets.[16] These results indicate that mixed ramp-Gaussian basis sets offer a promising alternative in modelling core electrons.
History of Mixed Ramp-Gaussian Basis Sets
Mixed ramp-Gaussian basis sets have a long history, originally being known as cusped-Gaussian basis sets. Ramps were first proposed by Bishop[17,18] in the 1960s, while Steiner and coauthors[19–26] performed extensive explorations with these basis functions in the 1970s and 1980s, before the idea was abandoned until 2014. These original papers found significant promise in RG basis sets in reproducing electron[24] and spin density[25] at the nucleus in small molecules far more easily than all-Gaussian basis sets. However, this was not translated to widespread uptake of these basis sets – instead Gaussian basis sets became dominant in a world with rapidly increasing computer power.
We argue the abandonment of the mixed ramp-Gaussian basis set concept between 1988 and 2013 occurred because there was insufficient evidence of the usefulness of the ramp-Gaussian basis sets over Gaussian basis sets to justify the extensive integral evaluation research, basis set development and implementation effort that is required to translate a new type of basis set into a widely used program. Furthermore, computational quantum chemistry method, basis set and program development was focused largely on valence chemistry such as molecular geometries, reaction energies and infrared spectroscopy, where ramp-Gaussian basis sets do not offer significant advantages over all-Gaussian basis sets. However, if we instead consider NMR spectroscopy predictions, an area where computational quantum chemistry has been so far underutilised, their improved core properties should mean ramp-Gaussian basis sets will be far superior to all-Gaussian basis sets. This hypothesis needs testing.
Evaluating Ramp-Gaussian Basis Sets Quickly
There are two major barriers to widespread use of mixed ramp-Gaussian basis sets: (1) full optimisation of mixed ramp-Gaussian basis sets will take significant time (as for all-Gaussian basis sets), (2) implementation of a full mixed ramp-Gaussian basis set integral package that can treat basis functions with high angular momentum within a mainstream quantum chemistry program is a significant task. It is wise, therefore, to conduct further preliminary research into the properties of mixed ramp-Gaussian basis sets to assess their suitability for large scale implementation, as is done in this paper.
To address the first barrier, basis set optimisation, early ramp-Gaussian basis sets have been and will continue to be designed based on existing successful all-Gaussian basis sets to take advantage of this significant body of research expertise. In a process we call ‘rampification’, the core basis function(s) of the all-Gaussian basis set is replaced by a mixed ramp-Gaussian basis set while the valence basis functions are retained. Rampification has been performed for the 6-31G family of basis sets to produce the R-31G family,[12] and for STO-nG to produce the STO-RG and STO-R2G basis sets.[27] This rampification process is most straightforward when the parent all-Gaussian basis set is segmented and is single-core-zeta (i.e. only one basis function contributes significantly to each core molecular orbital). Recent investigations[27] demonstrated that the 6-311G will be challenging to rampify as the basis set is double-core-zeta while the Dunning basis sets, cc-pVnZ, are challenging to rampify as they are generally contracted. In contrast, the small to medium pcseg-n (n = 0, 1, 2) Jensen basis sets, optimised for DFT calculations, are straightforward to rampify; see the section Jensen-Style Ramp-Gaussian Basis Sets, R-pcseg-n and STOR2G-pcseg-n. These basis sets will be the focus of this paper.
The fastest way to produce meaningful results for mixed ramp-Gaussian basis sets (and address the second barrier) is to effectively leverage existing software integral packages, rather than extending the initial RampItUp code[15] to higher angular momentum functions and integrating into a mainstream package. To achieve this goal and shortcut the first barrier outlined above, in the section Pseudoramps, we introduce pseudoramps, large linear combinations of Gaussian functions that very closely approximates a ramp basis function, with quantifiable errors. A ramp-Gaussian basis set can therefore be easily transformed into a pseudoramp-Gaussian basis set whose properties can be evaluated using standard integral packages and quantum chemistry programs. Pseudoramp-Gaussian calculations will of course be significantly slower than both all-Gaussian and fully implemented ramp-Gaussian basis sets.
To fulfil their intended purpose, derived ramp-Gaussian basis sets should retain the valence chemistry of their parent basis set (e.g. very similar reaction energies and geometries), but substantially improve in some or all core property predictions. Using accurate pseudoramps, we can easily evaluate the valence chemistry of our derived mixed ramp-Gaussian basis sets over a large selection of properties and molecules. In the subsection Valence Chemistry of the section Molecular Comparisons, we work with a subset of the diet-GMTKN55 database[28] (based on the larger GMTKN55 database[29] and shown to produce similar results) containing only elements H-Ne, using the ACCDB[30] suite of programs to aid our benchmarking. Systematic benchmark databases are less well established for core-dependent properties. Instead, in the subsection Core Chemistry, we consider the behaviour of our mixed ramp-Gaussian basis sets compared to their all-Gaussian parent basis sets in five small organic molecules for three core-dependent properties, electron density at the nucleus, spin-spin coupling parameters and NMR chemical shieldings.
Jensen-Style Ramp-Gaussian Basis Sets, R-pcseg-n and STOR2G-pcseg-n
Approach
Here, we consider two approaches to rampify all Gaussian pcseg-n basis sets:
Basis-set-specific direct Gaussian-fitted core replacement: Fitting a new RG basis set to the core all-Gaussian 1s basis function; for pcseg-n, this creates the R-pcseg-n basis sets.
Basis-set-independent Slater-fitted core replacement: Replacing the core 1s basis function with the core 1s basis function of the STO-R2G basis set; for pcseg-n, this creates the STOR2G-pcseg-n basis sets. Note the same core basis function is used across all zeta quality basis sets.
To implement the Gaussian-fitted approach to produce R-pc-{0,1,2} from pc-{0,1,2}, we follow the procedure recommended in Cox, Zapata, and McKemmish,[27] fitting a new core basis function with 1 S-ramp and 1 s-Gaussian basis function, A, to the parent core s-Gaussian basis function, B through minimising 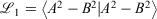 using Mathematica.[31] For the triple-zeta pc-2 basis set, a grid search on initial guesses was employed to obtain the optimal parameters due to the sensitivity of the fit to the initial guess. The quality of our fit was: 1000
using Mathematica.[31] For the triple-zeta pc-2 basis set, a grid search on initial guesses was employed to obtain the optimal parameters due to the sensitivity of the fit to the initial guess. The quality of our fit was: 1000 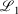 = 0.503, 0.158, 0.112 for pcseg-0,1,2 respectively; by comparison R-31G fit to 6-31G has 1000
= 0.503, 0.158, 0.112 for pcseg-0,1,2 respectively; by comparison R-31G fit to 6-31G has 1000 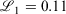 . A second Gaussian primitive in the ramp-Gaussian core basis function was tested but did not provide significant advantages, as was found for R2-31G compared to R-31G.[27]
. A second Gaussian primitive in the ramp-Gaussian core basis function was tested but did not provide significant advantages, as was found for R2-31G compared to R-31G.[27]
In the Slater-fitted approach (which has not been previously tested), the 1s basis function of pcseg-n is simply removed and the basis function from STO-R2G is used with no adjustments; see Cox, Zapata, and McKemmish[27] for full details of the derivation of these Slater-fitted RG core basis functions. The Slater-fitted RG functions are less similar to the parent basis function than those derived in the first approach: specifically, 1000 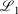 = 1.730, 2.672 and 2.487 for pcseg-0,1,2 compared to STOR2G core basis functions. However, Slater functions are a superior description of the core orbitals so we hypothesise that generic Slater-fitted RG core function may outperform basis-set-specific Gaussian-fitted RG core function.
= 1.730, 2.672 and 2.487 for pcseg-0,1,2 compared to STOR2G core basis functions. However, Slater functions are a superior description of the core orbitals so we hypothesise that generic Slater-fitted RG core function may outperform basis-set-specific Gaussian-fitted RG core function.
Specifications of the basis set parameters for carbon are provided in Table 1; results for other atoms, discussion of R2-pcseg-n and further details are provided in the Supplementary Material.
Evaluation
In this section, we evaluate the properties of the new core basis functions, focusing on the question of how closely each derived core basis function matches its parent basis function. This paper is the first time ramp-Gaussian basis sets have been derived for single or triple-zeta Gaussian basis sets, and the first time Approach 2 (use of core basis function designed to match the 1s atomic orbital itself rather than the Gaussian core basis function approximation) has been tried; our analysis will focus on this effect. Evaluation of their valence and core chemistry properties is deferred to the section Molecular Comparisons as it requires the development of pseudoramps in the section Pseudoramps. This section contains only results for carbon as this is the most important element for most applications and broadly representative of the results for other atoms.
Fig. 1 shows a visual comparison of the different basis functions and their radial probability distributions for carbon.
It is clear that the R-pcseg-n derived basis functions are all very similar to their parent pcseg-n core basis functions overall. Fig. 1a, b shows that very close to the nuclei the core all-Gaussian basis function (especially the smaller pcseg-0 and pcseg-1) significantly undershoot the other basis functions as they lack the very large Gaussian exponents required to accurately represent the electron-nuclear cusp; the ramp-Gaussian basis functions all have better performance than their all-Gaussian parent functions as the ramps naturally have the electron-nuclear cusp. When considering the probability distribution (Fig. 1c, d) rather than the basis function itself (Fig. 1a, b), the differences between the derived and parent basis set is more evenly distributed across radial distance from the nuclei.
Fig. 1 shows little difference in the ramp-Gaussian core functions fitted through direct rampification of the core basis functions in the Jensen single, double or triple zeta basis sets, despite significant differences in the parent core basis function. This result is confirmed quantiatively in Table 1 which shows the parameters of these three basis function are very similar (and indeed similar to the R-31G parameters).
The Slater-fitted and Gaussian-fitted RG core basis functions, however, are different in their parameters (Table 1) and visually (Fig. 1). These differences justify the consideration of the two fitting methods, but do not yet provide information about the best approach.
As an initial evaluation of the differences between the Slater-fitted and Gaussian-fitted RG core functions across the Jensen single, double and triple zeta basis sets, we examine three properties of the core basis functions in Table 2 and compute the rampdev, Δ, of property P by the equation
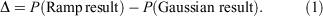
The first property is the electron density at the nucleus, quantifying the visual differences shown in Fig. 1 as 1.5–8 % and discussed earlier.
The second property is the one-electron energy with Zeff = 5.67. We find the rampdev modifies this energy by 5–28 mEH or 13–74 kJ mol−1; this is an undesirably large effect. However, we expect chemical reaction energies rampdevs to be significantly less than this value through cancellation of core electron errors as is standard in quantum chemistry. As expected, the Slater-fitted core functions have lower one-electron energies – and thus according to the variational principle a better one-electron wavefunction – than the Gaussian-fitted core functions because Slater core functions are optimised for this problem.
The third property is the electron-nuclear cusp, which is compared against the Slater type orbital as it is 0 for all-Gaussian basis functions; the Slater-fitted function performs 50 times better than the Gaussian-fitted function but even the Gaussian-fitted function has relative errors of less that 5 % (far better than the 100 % error of all-Gaussian functions).
Pseudoramps
With the exception of the RampItUp exploratory software,[15] current computational software does not yet support the usage of ramp-Gaussian basis sets. To provide meaningful results for mixed ramp-Gaussian basis sets quickly for initial analysis, we approximate ramp functions using pseudoramps.
Definition
Pseudoramps are a linear combination of N even-tempered Gaussian primitives, fitted to the ramp function. Mathematically, pseudoramps are defined by
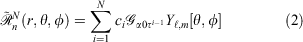
where ci, α0 and τ are the coefficients, smallest exponent and geometric series ratio respectively. In this paper, we focus on pseudoramps with zero angular momentum, denoted as 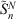 .
.
Construction
The easiest and fastest way to find our pseudoramps is to find the pseudoramp parameters that minimise the 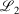 metric defined[27] as
metric defined[27] as 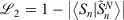 . The fits were complicated and numerically very sensitive, especially for large N, and it is likely we did not find the global minimum in many cases. Nevertheless, it was only necessary to get a good approximation to the ramp function, not the best approximation.
. The fits were complicated and numerically very sensitive, especially for large N, and it is likely we did not find the global minimum in many cases. Nevertheless, it was only necessary to get a good approximation to the ramp function, not the best approximation.
We provide data for all integer ramps with n = 4 – 11 in the Supplementary Material. Different contraction lengths are provided to help assess errors and because different quantum chemistry packages differ in the number of Gaussian primitives allowed in a single contracted function.
The smallest and largest Gaussian exponent (α0 and αmax) of the n = 7 pseudoramps are listed on the left-side of Table 3 for different contraction lengths N along with the geometric progression ratio, τ. α0 is relatively constant as a function of N. The αmax usually increases for larger N as the pseudoramp cusp is better represented, though a double minimum around N = 12 causes a slight deviation in this trend. τ decreases as N increases, indicating the Gaussian exponents in the pseudoramp become closer.

|
Lower fit quality metrics, 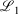 and
and 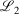 , correspond to higher accuracy pseudoramp approximations. The quality metric being optimised,
, correspond to higher accuracy pseudoramp approximations. The quality metric being optimised, 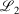 , always decreases with larger N as required, while the other fit quality also usually decreases. Note that the quality of the fit between large pseudoramps and the ramp is far superior (i.e. lower
, always decreases with larger N as required, while the other fit quality also usually decreases. Note that the quality of the fit between large pseudoramps and the ramp is far superior (i.e. lower 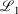 ,
, 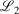 ) to the fit quality between the ramp-Gausssian basis function and its parent all-Gaussian basis function (e.g. see previous section). For example, for N = 20, L1 for S7 and
) to the fit quality between the ramp-Gausssian basis function and its parent all-Gaussian basis function (e.g. see previous section). For example, for N = 20, L1 for S7 and 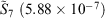 is two orders of magnitude better than the fit between 1s basis functions in R-pcseg-0 and pc-seg-0 (5.03 × 10−5, obtained in previous section), despite the fact that the former pseudoramp fit optimises to minimise
is two orders of magnitude better than the fit between 1s basis functions in R-pcseg-0 and pc-seg-0 (5.03 × 10−5, obtained in previous section), despite the fact that the former pseudoramp fit optimises to minimise 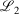 not
not 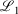 while the latter fit optimises to minimise
while the latter fit optimises to minimise 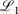 . This result provides confidence that large pseudoramps with N > 20 should approximate ramps sufficiently well for meaningful conclusions to be made on the properties of mixed ramp-Gaussian basis sets compared to all-Gaussian basis sets. (Note small pseudoramp results are of course not useful, as this would be equivalent to a reparameterisation of commonly used all-Gaussian basis sets; they are included to demonstrate convergence.)
. This result provides confidence that large pseudoramps with N > 20 should approximate ramps sufficiently well for meaningful conclusions to be made on the properties of mixed ramp-Gaussian basis sets compared to all-Gaussian basis sets. (Note small pseudoramp results are of course not useful, as this would be equivalent to a reparameterisation of commonly used all-Gaussian basis sets; they are included to demonstrate convergence.)
Appropriate Use
Pseudoramps can be used to approximate the value of ramp-including one- and two-electron integrals within a standard molecular quantum chemistry program by replacing the ramp function with the N-fold contracted Gaussian pseudoramp.
The pseudoramp error, δ, of property P is defined by
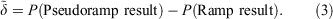
Pseudoramps can be used to approximate ramp results for evaluation purposes as long as the pseudoramp error is less than the effect under consideration.
Often the effect being investigated is the difference between a parent all-Gaussian basis set and a derived mixed ramp-Gaussian basis set, i.e. the rampdev. The pseudorampdev 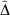 of property P defined by
of property P defined by
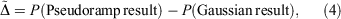
analogous to the rampdev, Δ, definition in Eqn 2. Mathematically, if 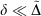 , then
, then 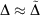 ; in other words, if pseudoramp error is much less than pseudorampdev, then pseudorampdev very well approximates rampdev for the purposes of evaluation of the mixed ramp-Gaussian basis set.
; in other words, if pseudoramp error is much less than pseudorampdev, then pseudorampdev very well approximates rampdev for the purposes of evaluation of the mixed ramp-Gaussian basis set.
Table 4 compares a variety of energetic properties between all-Gaussian, ramp-Gaussian and pseudoramp-Gaussian basis sets. In all cases, 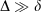 , with δ < 0.01 kJ mol−1 for all chemical energies even with a small ramp. Larger pseudoramps have smaller δ, indicating convergence towards the true ramp value.
, with δ < 0.01 kJ mol−1 for all chemical energies even with a small ramp. Larger pseudoramps have smaller δ, indicating convergence towards the true ramp value.
When interpreting data, it is worth noting that though the pseudorampdev or rampdev are useful properties to consider, it may be more relevant to compare the basis set incompleteness error (BSIE) of the parent and derived basis set; the relative BSIE provides context on whether the effect of rampification is important in the particular context. For example, a rampdev of 10 kJ mol−1 would be extremely concerning in a context where the BSIE of the parent basis set is 1 kJ mol−1 and very high accuracy is desired but is essentially negligible when the BSIE is, say, 200 kJ mol−1.
Molecular Comparisons
In this section, we compare the valence and core chemistry of ramp-Gaussian and all-Gaussian segmented Jensen basis sets, using pseudoramps to approximate the ramp results. For ramp-Gaussian basis sets to be useful, we desire very similar valence chemistry (e.g. relative energies) to the parent all-Gaussian basis set, with significant improvements to properties relating to core electrons, i.e. core chemistry.
We create PR-pcseg-n and STOPR2G-pcseg-n by replacing the S ramps in R-pcseg-n and STOR2G-pcseg-n by N = 30 pseudoramps.
Valence Chemistry
It is important that the newly-developed rampified and pseudorampified basis sets faithfully replicate the valence chemistry of their parents to a reasonable degree. This was tested by calculating the relative energies for a variety of reactions and comparing the errors. The reactions were sourced from the diet150 dataset[28] of the GTMKN55 database,[29] excluding reactions with non-first-row elements in the molecules as well as the C60ISO set of reactions (due to its high computational cost). Out of the initial 150 reactions, 93 reactions across 37 datasets remained after screening. We retained the original weightings from Gloud.[28] Calculations were done using the ωB97X-D3[32] density functional approximation. All calculations were done in ORCA,[33] and were carried out using the snakemake workflow using ACCDB.[30]
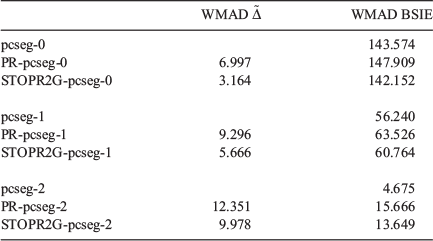
Table 5 shows the weighted mean absolute deviations (WMAD) of the basis set incompleteness error (BSIE) for all considered basis sets, a measure of the completeness of each basis set for valence chemistry problems.
|
The BSIE for the single and double-zeta pseudoramp and all-Gaussian basis sets led to a slight but contextually negligible decrease in the quality of the valence chemistry predictions. However, while pcseg-2 has BSIE of 4.7 kJ mol−1, about chemical accuracy, the rampified basis set errors are about three times worse. The context of very small basis set incompleteness errors in large basis sets make the rampification errors (here predicted by pseudorampification errors) too large to be acceptable. To construct triple and quadrupole-zeta quality ramp-Gaussian basis sets, a full optimisation of basis set exponents is probably required rather than a simple replacement of core basis function. Alternatively, perhaps an additional Gaussian primitive is required.
Considering the two different ways to produce a ramp-Gaussian core basis function, PR-pcseg-n has a higher BSIE than STOPR2G-pcseg-n for all basis sets, with the differences between the two basis sets being comparable to the differences between the pseudoramp-Gaussian and all-Gaussian basis sets.
Table 5 also includes for comparison the WMAD of the pseudorampdev, (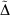 ); this value quantifies the difference in the valence chemistry predicted by the two basis sets. This WMAD
); this value quantifies the difference in the valence chemistry predicted by the two basis sets. This WMAD  is between 3.2 and 12.4 kJ mol−1, increasing slightly with basis set size. The WMAD
is between 3.2 and 12.4 kJ mol−1, increasing slightly with basis set size. The WMAD  are slightly higher than the difference in WMAD BSIE, but produce the same trends. BSIE is easier to interpret and will be used in the further analysis, though we note that it may be harder to compute in some cases as it requires knowledge of the complete basis set limit.
are slightly higher than the difference in WMAD BSIE, but produce the same trends. BSIE is easier to interpret and will be used in the further analysis, though we note that it may be harder to compute in some cases as it requires knowledge of the complete basis set limit.
Core Chemistry
The central aim of the rampified basis sets is not to replicate valence chemistry (although this is necessary), but to improve calculations of core properties. We considered three core properties – electron density at the nucleus, absolute NMR shieldings (from which chemical shifts can be calculated with reference data), spin-spin coupling parameters. Here, we have tested pcseg-n, PR-pcseg-n and STOPR2G-pcseg-n, comparing against the DFT/CBS limit. Five small organic molecules were considered (C2H6, NH3, H2O, CO2 and HCN). The electron density at the nucleus and absolute NMR shielding calculations were done with the ωB97X-D3[32] functional using ORCA,[33] while the spin-spin coupling calculations were done using QChem[34] with the B3LYP[35,36] functional as range-separated functionals were not available.
This is not intended to be a thorough investigation, but instead a brief exploration of the potential of ramp-Gaussian basis sets to direct future studies.
Electron Density at the Nucleus
The electron density at the nucleus, ρ, is an important property that can be used to determine several spectroscopic parameters, such as the Fermi contact term of the NMR spin-spin coupling constant (eqn 4 in ref. [9]), the Darwin term of relativistic calculations (eqn 87 in ref. [37]) and the Mössbauer isomer shift (eqn 1 in ref. [38]).
Fig. 2 shows the deviation of pcseg-n, PR-pcseg-n and STOPR2G-pcseg-n from the DFT/CBS limit (calculated with the ωB97X-D3 functional and extrapolated from pcJ-3 and pcJ-4). The results show that the PR-pcseg-n basis sets all outperforms the parent basis set, though larger basis sets offer little improvement over the PR-pcseg-0 basis set. The STOPR2G-pcseg-n basis set has poorer performance that the PR-pcseg-n but is better than the all-Gaussian pcseg-n except for n = 2.
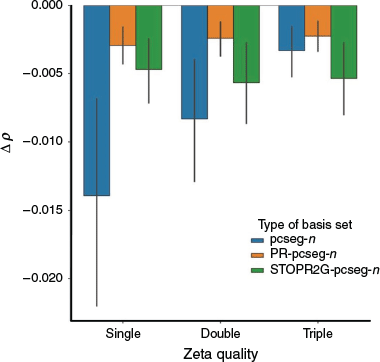
|
These results are consistent with McKemmish and Gilbert,[16] where R-31G was found to predict electron densities at the nucleus with the accuracy of cc-pVQZ.
NMR Shieldings (Key Contribution to Chemical Shifts)
Fig. 3 presents the average deviation of absolute chemical shielding for pcseg-n, PR-pcseg-n and STOPR2G-pcseg-n from the CBS limit (calculated with the ωB97X-D3 functional and extrapolated from pcSseg-3 and pcSseg-4). All results are very similar, with the pseudoramp-Gaussian basis sets not providing reliably improved results over the all-Gaussian basis sets.
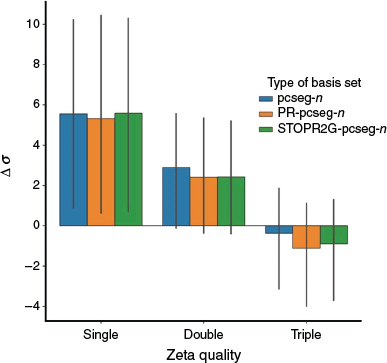
|
These results are consistent with the results of Jensen[7] which optimised all-Gaussian basis sets for NMR shielding by adding a single tight p function. This function enabled better description of the paramagnetic spin-orbit component; the other components of the shielding were well represented within the existing basis set.
To achieve superior chemical shifts using ramp-Gaussian basis sets, it is likely that P-ramps must be incorporated into even first-row (i.e. Li-Ne) basis sets.
Spin-Spin Coupling Parameters
Table 6 shows our results for the spin-spin coupling parameters of CO2 using B3LYP with pcseg-n and PR-pcseg-n (n = 0, 1, 2) compared to pcJ-3, divided into the component contributions. It is clear from this table that the pcseg-n does such a poor job of representing the spin-spin coupling in CO2 that pseudorampifying the core does little but produce new numbers; no chemical insight on this property can be gained from any of the general-purpose basis sets.
Decontracting the smallest Gaussian primitive from the pcseg-2 and PR-pcseg-2 core 1s basis functions for Li-Ne to produce the d-pcseg-2 and d-PR-pcseg-2 basis sets yields much better results that are chemically reasonable and can be interpreted at least partially. d-PR-pcseg-2 produces the basis set limit for the Fermi contact term in the C-O spin-spin coupling clearly better than the d-pcseg-2 basis set (and this improves the total result), but is slightly poorer in the O-O case. There is essentially no impact on any other component of the spin-spin coupling constant. This is weak evidence in favour of the expectation that ramps will improve the Fermi contact term over an all-Gaussian core basis function, but hardly compelling.
To produce the compelling evidence would unfortunately require a specialised ramp-Gaussian basis set optimised for spin-spin coupling. The specialised all-Gaussian basis sets are so highly decontracted in the core that a straightforward rampification of the core basis function in isolation (e.g. replacing 6 Gaussians with 1 ramp and 1 Gaussian that overlap strongly) like we have pursued previously is impossible. Instead, a full reoptimisation is necessary; this is beyond the scope of this paper.
Discussion and Conclusion
The ubiquitous Gaussian basis sets cannot represent the nuclear-electron cusp and thus struggle to describe core electron-dependent properties, such as nuclear magnetic resonance spectral parameters. Specialised all-Gaussian basis sets with decontracted core basis functions and primitives with very high Gaussian exponents can address the issue, but a more natural approach is to use a better core basis function type such as the ramp. However, the obstacles for new basis function types to be widely utilised are substantial, specifically: (1) integral evaluation must be sufficiently fast to be competitive with all-Gaussian basis functions, (2) new integral packages need to be designed and implemented within a mainstream quantum chemistry package, (3) new basis sets need to be optimised, and (4) the new basis sets must display superior performance to all-Gaussian basis sets for at least some important properties. Obstacle (1) has previously been overcome for ramp-Gaussian basis sets,[15] showing the algorithmic pathway towards addressing barrier (2). This paper focuses on taking shortcuts to overcome obstacles (2) and (3) to enable evaluation of (4), the performance of these ramp-Gaussian basis sets.
Specifically, to address obstacle (2), this paper introduces pseudoramps, large linear combinations of Gaussian functions that closely approximate a ramp function. These pseudoramps can be used to reliably predict the performance of mixed ramp-Gaussian basis sets for valence and core chemistry using existing all-Gaussian integral evaluation packages in modern quantum chemistry programs.
To address obstacle (3), we continue our recent approach of simply replacing the highly contracted all-Gaussian core basis function with a ramp-Gaussian core function.[12,27] In the section Jensen-Style Ramp-Gaussian Basis Sets, R-pcseg-n and STOR2G-pcseg-n, this paper introduced and analysed rampified segmented Jensen basis sets, the first time that ramp-Gaussian basis sets of differing zeta-quality have been computed. We further innovate by considering two different approaches to constructing the ramp-Gaussian core s basis function, matching the new core basis function to either the all-Gaussian core basis function (Gaussian-fitting producing in this case R-pcseg-n) or the Slater core basis function which more accurately represents the true wavefunction (Slater-fitting, producing STOR2G-pcseg-n).
Though superior performance is the primary goal (obstacle 4), this needs to be accomplished without negatively impacting the existing areas of strong performance. In the section Molecular Comparisons, we used pseudoramps to demonstrate that single and double-zeta Jensen ramp-Gaussian basis sets had good performance in valence chemistry (i.e. very little change between the derived and parent basis set) but the triple-zeta Jensen ramp-Gaussian basis sets had unacceptably large changes in the valence chemistry (due largely to the higher accuracy of the triple-zeta basis set).
Using pseudoramps and rampified basis sets, we investigated the hypothesis that ramp-Gaussian basis sets produce superior core chemistry (addressing obstacle 4) in the second part of the section Molecular Comparisons. Our results are mixed and inconclusive. Electron densities at the nucleus did improve for single and double-zeta ramp-Gaussian basis sets results compared to their all-Gaussian parents (confirming our previous results[16]), but not for triple-zeta basis sets. Absolute NMR shielding constants (i.e. input to chemical shifts) did not improve because the dominant paramagnetic term requires flexible and accurate description of the p and higher angular momentum functions that were not impacted by simple rampification of the core function. Finally, for spin-spin coupling the general-purpose basis sets were so poorly performing that comparisons of the all-Gaussian and ramp-Gaussian results were essentially meaningless; partially decontracted large basis sets show some weak indication of improved Fermi contact term but are insufficient evidence.
Our core chemistry results mostly serve to illustrate that the current approach to addressing obstacle (3) is insufficient for core chemistry. General-purpose basis sets – whether all-Gaussian or ramp-Gaussian – do not have the correct properties to describe core chemistry general-purpose basis sets; instead, specialised basis sets are required. Constructing specialised ramp-Gaussian basis sets is far more complicated as there is usually not an identifiable ‘core’ all-Gaussian basis function to replace. Instead a full optimisation of at least the core basis functions is required; the best decomposition of these core basis functions in terms of ramp and Gaussian primitives is an open question. This optimisation is beyond the scope of this paper, but is probably the salient future research direction in ramp-Gaussian basis sets.
With the optimisation, it is not yet clear whether the valence basis functions could be adopted from existing all-Gaussian basis sets or would need to be reoptimised; the former would of course be preferable for initial evaluation purposes if sufficiently accurate. The results in this paper comparing the Gaussian and Slater-fitting approaches for the core basis functions give confidence that the valence and core basis functions can be considered separately to some extent. Specifically, we found overall that these different core basis functions produce similar atomic results (using ramps, section Jensen-Style Ramp-Gaussian Basis Sets, R-pcseg-n and STOR2G-pcseg-n) and valence and core chemistry molecular results (using pseudoramps, section Molecular Comparisons). The most clear distinction is the quality of the predictions of electron density at the nucleus where the Gaussian-fitted R-pcseg-n was clearly superior.
With respect to obstacle (1), integral evaluation, for completeness we note that algorithms have been developed and implemented[15] to compute integrals involving S-ramps and s and p-Gaussians, with calculation times of 6-31G and R-31G similar for modest size molecules. Expansion to higher angular momentum ramps and Gaussians should be achievable with similar approaches without the need for substantial algorithmic changes or innovations. In particular, we note that modelling the new types of ramp-Gaussian shell pairs as a linear combination of ramp functions with different angular momentum is the central step of the integral evaluation procedure, after which existing approaches can calculate most two-electron integrals.
Supplementary Material
Full basis set specification for R-pcseg-n, R2-pcseg-n, and STOR2G-pcseg-n; pseudoramp parameter specifications; template pseudoramp-Gaussian Jensen basis set input files for ORCA; and csv files with core and valence chemistry results for all basis sets and molecules investigated are available on the Journal’s website.
Data Availability Statement
The data that support this study are available in the article and accompanying online supplementary material.
Conflicts of Interest
The authors declare no conflicts of interest.
Declaration of Funding
This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI Australia), an NCRIS enabled capability supported by the Australian Government.
Acknowledgements
We thank Frank Jensen, Anna-Maree Syme and Juan Camilo Zapata Trujilo for their helpful feedback.
References
[1] F. Jensen, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 273.| Crossref | GoogleScholarGoogle Scholar |
[2] J. G. Hill, Int. J. Quantum Chem. 2013, 113, 21.
| Crossref | GoogleScholarGoogle Scholar |
[3] B. Nagy, F. Jensen, Rev. Comput. Chem. 2017, 30, 93.
| Crossref | GoogleScholarGoogle Scholar |
[4] P. M. W. Gill, Adv. Quantum Chem. 1994, 25, 141.
| Crossref | GoogleScholarGoogle Scholar |
[5] S. Reine, T. Helgaker, R. Lindh, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 290.
| Crossref | GoogleScholarGoogle Scholar |
[6] L. K. McKemmish, P. M. Gill, J. Chem. Theory Comput. 2012, 8, 4891.
| Crossref | GoogleScholarGoogle Scholar | 26593182PubMed |
[7] F. Jensen, J. Chem. Theory Comput. 2008, 4, 719.
| Crossref | GoogleScholarGoogle Scholar | 26621087PubMed |
[8] F. Jensen, J. Chem. Theory Comput. 2015, 11, 132.
| Crossref | GoogleScholarGoogle Scholar | 26574211PubMed |
[9] F. Jensen, Theor. Chem. Acc. 2010, 126, 371.
| Crossref | GoogleScholarGoogle Scholar |
[10] U. Benedikt, A. A. Auer, F. Jensen, J. Chem. Phys. 2008, 129, 064111.
| Crossref | GoogleScholarGoogle Scholar | 18715055PubMed |
[11] M. A. Ambroise, F. Jensen, J. Chem. Theory Comput. 2019, 15, 325.
| Crossref | GoogleScholarGoogle Scholar | 30495950PubMed |
[12] L. K. McKemmish, A. T. Gilbert, P. M. Gill, J. Chem. Theory Comput. 2014, 10, 4369.
| Crossref | GoogleScholarGoogle Scholar | 26588134PubMed |
[13] D. M. Bishop, J. Chem. Phys. 1964, 40, 1322.
| Crossref | GoogleScholarGoogle Scholar |
[14] D. M. Bishop, J. Chem. Phys. 1968, 48, 291.
| Crossref | GoogleScholarGoogle Scholar |
[15] L. K. McKemmish, J. Chem. Phys. 2015, 142, 134104.
| Crossref | GoogleScholarGoogle Scholar | 25854225PubMed |
[16] L. K. McKemmish, A. T. Gilbert, J. Chem. Theory Comput. 2015, 11, 3679.
| Crossref | GoogleScholarGoogle Scholar | 26574451PubMed |
[17] D. M. Bishop, J. Chem. Phys. 1964, 40, 1322.
| Crossref | GoogleScholarGoogle Scholar |
[18] D. M. Bishop, J. Chem. Phys. 1968, 48, 291.
| Crossref | GoogleScholarGoogle Scholar |
[19] E. Steiner, S. Sykes, Mol. Phys. 1972, 23, 643.
| Crossref | GoogleScholarGoogle Scholar |
[20] E. Steiner, Mol. Phys. 1972, 23, 657.
| Crossref | GoogleScholarGoogle Scholar |
[21] E. Steiner, Mol. Phys. 1972, 23, 669.
| Crossref | GoogleScholarGoogle Scholar |
[22] E. Steiner, B. C. Walsh, J. Chem. Soc., Faraday Trans. II 1975, 71, 921.
| Crossref | GoogleScholarGoogle Scholar |
[23] E. Steiner, B. C. Walsh, J. Chem. Soc., Faraday Trans. II 1975, 71, 926.
| Crossref | GoogleScholarGoogle Scholar |
[24] E. Steiner, J. Chem. Soc., Faraday Trans. II 1980, 76, 391.
| Crossref | GoogleScholarGoogle Scholar |
[25] E. Steiner, J. Chem. Soc., Faraday Trans. II 1985, 81, 1101.
| Crossref | GoogleScholarGoogle Scholar |
[26] E. Steiner, J. Chem. Soc., Faraday Trans. II 1987, 83, 783.
| Crossref | GoogleScholarGoogle Scholar |
[27] C. Cox, J. C. Zapata, L. McKemmish, Aust. J. Chem. 2020, 73, 911.
| Crossref | GoogleScholarGoogle Scholar |
[28] T. Gould, Phys. Chem. Chem. Phys. 2018, 20, 27735.
| Crossref | GoogleScholarGoogle Scholar | 30387792PubMed |
[29] L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi, S. Grimme, Phys. Chem. Chem. Phys. 2017, 19, 32184.
| Crossref | GoogleScholarGoogle Scholar | 29110012PubMed |
[30] P. Morgante, R. Peverati, J. Comput. Chem. 2019, 40, 839.
| Crossref | GoogleScholarGoogle Scholar | 30582189PubMed |
[31] Wolfram Inc., Mathematica, Version 12.2 2020 (Wolfram: Champaign, IL).
[32] Y.-S. Lin, G.-D. Li, S.-P. Mao, J.-D. Chai, J. Chem. Theory Comput. 2013, 9, 263.
| Crossref | GoogleScholarGoogle Scholar | 26589028PubMed |
[33] F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327.
| Crossref | GoogleScholarGoogle Scholar |
[34] Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, et al. Mol. Phys. 2015, 113, 184.
| Crossref | GoogleScholarGoogle Scholar |
[35] C. Lee, W. Yang, R. G. Parr, Phys. Rev. B 1988, 37, 785.
| Crossref | GoogleScholarGoogle Scholar |
[36] A. D. Becke, J. Chem. Phys. 1993, 98, 5648.
| Crossref | GoogleScholarGoogle Scholar |
[37] T. Helgaker, W. Klopper, D. P. Tew, Mol. Phys. 2008, 106, 2107.
| Crossref | GoogleScholarGoogle Scholar |
[38] F. Neese, Inorg. Chim. Acta 2002, 337, 181.
| Crossref | GoogleScholarGoogle Scholar |




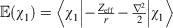 – of the core χ1s basis function of the pcseg-n up to triple zeta quality, and the errors obtained using R-pcseg-n and STOR2G-pcseg-n approximations to these core χ1 basis functions
– of the core χ1s basis function of the pcseg-n up to triple zeta quality, and the errors obtained using R-pcseg-n and STOR2G-pcseg-n approximations to these core χ1 basis functions

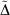 , and the basis set incompleteness error (BSIE) (all values are in kJ mol−1)
, and the basis set incompleteness error (BSIE) (all values are in kJ mol−1)
