Understanding the Mechanism of Activation/Deactivation of GLP-1R via Accelerated Molecular Dynamics Simulation
Xiuchan Xiao A B E , Miao Qin A B , Fuhui Zhang C , Yan Su C , Bo Zhou B D E and Zheng Zhou A B
A B E , Miao Qin A B , Fuhui Zhang C , Yan Su C , Bo Zhou B D E and Zheng Zhou A B
A School of Material Science and Environmental Engineering, Chengdu Technological University, Chengdu 611730, China.
B Center of Big Data for Smart Environmental Protection, Chengdu Technological University, Chengdu 611730, China.
C School of Chemistry, Sichuan University, Chengdu 610064, China.
D School of Electronic Engineering, Chengdu Technological University, Chengdu 611730, China.
E Corresponding authors. Email: xxchan@edtu.edu.cn; bozhou@zju.edu.cn
Australian Journal of Chemistry 74(3) 211-218 https://doi.org/10.1071/CH20127
Submitted: 22 April 2020 Accepted: 18 August 2020 Published: 17 September 2020
Journal Compilation © CSIRO 2021 Open Access CC BY-NC-ND
Abstract
Glucagon-like peptide-1 receptor (GLP-1R), as a member of the class B G protein-coupled receptors (GPCRs), plays a crucial role in regulating blood glucose level signal recognition through its activation. The conformation changes during the activation pathway are of particular importance for its function. To investigate the activation mechanism of GLP-1R, the crystal structures of active and inactive forms are chosen to perform a total of 2 μs of accelerated molecular dynamics (aMD) simulations and 400 ns of conventional molecular dynamics (cMD) simulations. With the aid of structural analysis and potential of mean force (PMF) calculations, we reveal the role of different helices in the activation and deactivation process and obtain the intermediate states during activation and deactivation that are difficult to capture in experiments. Protein structure network (PSN) was utilised to clarify the allosteric communication pathways of activation and deactivation and reveal the mechanisms of its activation and deactivation. The results could advance our understanding of the activation mechanism of GLP-1R and the related drug design.
Introduction
G protein-coupled receptors (GPCRs), as the largest class of membrane proteins, are crucial for cell signalling in the human genome.[1] Glucagon-like peptide-1 (GLP-1) is an important hormone that regulates insulin secretion, carbohydrate metabolism, and appetite, and it exerts physiological regulation by binding to the glucagon receptor (GLP-1R).[2] GLP-1R belongs to B class GPCRs, as a validated drug target for the treatment of type 2 diabetes and obesity.[3] It can transmit signals from extracellular molecules to G proteins, and then increases pancreatic β cell expression, biosynthesis, and insulin secretion.[4] It is reported that peripheral administration of GLP-1 receptor agonists attenuates drug-associated behavioural responses including cocaine-induced conditioned place preference (CPP) and the locomotor-activating effects of cocaine.[5–7] Therefore, there is a requirement for a detailed understanding of how agonists bind to cause inhibition of cocaine seeking and the analysis of the activation mechanism of GLP-1R.
Recently the first three-dimensional structures of GLP-1R were resolved, e.g. an X-ray crystal structure of GLP-1R in its inactive state bound to different allosteric modulators at 2.7 Å resolution,[8] an X-ray crystal structure of GLP-1R in its active state bound to a truncated peptide agonist at 3.7 Å resolution,[3] and the fully active cryogenic electron microscopy (cryo-EM) structure of GLP-1R coupled with a Gs protein at 4.1 Å resolution.[9] This is helpful for scientists to reveal how GLP-1R interacts with ligands and participates in the cellular signal transduction pathways by computational techniques, especially molecular dynamics simulation, which has increased our understanding significantly as it allows us to model functions that cannot currently be experimentally resolved.[10] In 2018, Carla et al.[11] analysed the interaction between GLP-1R and a ligand by 430 ns molecular dynamics simulation, revealing the important role of TM6 in the activation process. Although this work studied some of the activation characteristics of GLP-1R, due to the limitations of the simulation method, it was difficult to obtain sufficient spatial sampling and the intermediate state of the activation process of GLP-1R. It was known that GPCR activation induces changes of intracellular and extracellular domains and rearrangement of the transmembrane helix. Zhang et al.[12] revealed the conformational transition mechanism of the extracellular domain (ECD) during GLP-1R activation induced by agonist through molecular dynamics simulation and Markov model. However, the rearrangement of transmembrane helices which is the prominent feature of activation relative to an inactive or active structure, particularly conformational changes of the intercellular parts of helices, has not been revealed.
To our knowledge, the computational research on GLP-1R rarely involves its deactivation mechanism and its activation process generally occurs on the millisecond time scale of simulation. In order to break through the time limitation and get more GLP-1R conformational change related to biological functions, accelerated dynamics simulation (aMD) was applied to increase the conformation sampling and achieve a better effect on a longer time scale.[13–15] This method is different from the general enhanced sampling method and does not require preset reaction coordinates. It reduces the energy barrier of transition between different state conformations by adding a non-negative potential energy, and then the frequency of the conformational transformation increases, thereby sampling more conformation in a limited time. It has been successfully applied to multiple GPCR systems like CCR5 and M2 receptor.[16,17]
Studies have shown that inactive GPCRs in the apo state can undergo some degree of self-activation, while GPCRs that are fully activated will be deactivated when removing agonists and G proteins.[18,19] Based on the obtained completely inactive and the active structure of GLP-1R,[3,8,9] 1 μs aMD simulation was performed for the GLP-1R/inactive state and GLP-1R/active state systems, respectively. Potential of mean force (PMF) calculation was utilised to capture the intermediate states (which are relatively stable in energy during activation or inactivation process) and observe the activation of GLP-1R from the inactive crystal structure and the stable states in the process of conformation changes. Meanwhile, the correlations analysis and protein structure network further reveal the allosteric pathways and mechanisms of the activation and deactivation processes. These observations could provide more structure information at the atomic level for better understanding of the activation and deactivation mechanisms and are beneficial to drug design targeting GLP-1R.
Results and Discussion
Activation of GLP-1R from the Inactive Crystal Structure (PDBID: 5vew)
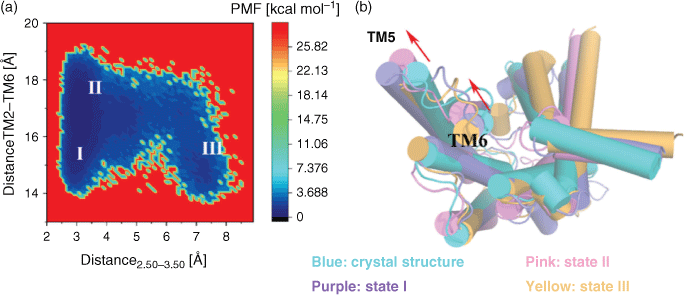
In order to observe the activation mechanism of GLP-1R from the inactive crystal structure, the stable states in the process of conformation changes were captured in free energy landscape by PMF calculation. As is known, the most significant rearrangement of helices during GPCR activation is the outward movement of the intercellular part in TM6.[20,21] Therefore, the outward movement of TM6 was characterised by monitoring the centre of mass distance of 10 residues in the intracellular end of the TM2 and TM6.[6,22] The highly conserved HETx motif in class B GPCR plays the same functional role as the E/DRY conserved motif of class A GPCR,[23] whose interactions have also been shown to stabilise the inactive state.[21] Accordingly, mutation of HETx motif residues results in activation of many family B GPCRs.[24–25] The important polar interaction between H1802.50 and E2473.50 only exists in the inactive structure of GLP-1R, but it disappears in the active crystal structure,[8] so the distance between H1802.50 and E2473.50 was also chosen to identify the activation of GLP-1R. Therefore, the distance between the intracellular end of TM2 and TM6 as well as the distance between H1802.50 and E2473.50 were selected as the reaction coordinates to calculate the PMF profiles for the two systems.
At the beginning, a file contained the two reaction coordinates were built, so that the information of energy and reaction coordinates were obtained and the corresponding frame was found after PMF calculation. According to the PMF calculation results, we selected the point with the lowest energy corresponding to PMF in a specific state, found the corresponding frame according to the corresponding reaction coordinates corresponding to the lowest energy point, and then extracted the structure of the corresponding frame. For each state we considered an ensemble of structures to analyse information. The PMF of GLP-1R/inactive state system (see Fig. 1a), which was simulated from the inactive structure, exhibits three stable states. In state I, the TM2–TM6 distance is ~15 Å, which is close to the distance of 14.79 Å found in the inactive crystal structure. In state II, the TM2–TM6 distance is 18 Å (close to 22 Å in the active crystal structure). The H1802.50 and E2473.50 distance is ~3 Å in state I and state II. State III shows a TM2–TM6 distance of 15.0 Å versus the distance between H1802.50 and E2473.50 of 7.5 Å. The PMF could determine the free energy difference of states, state I (~0.478 kcal mol−1) represented the conformation close to the inactive state, the conformation of GLP-1R overcame an energetic barrier of ~0.32 kcal mol−1 (state II: ~0.794 kcal mol−1) corresponded to the intermediate state and continued to cross an energy barrier of ~0.7 kcal mol−1 to change the conformation of GLP-1R into state III (~1.506 kcal mol−1), which mainly represented the active state (as mentioned in the Experimental, the aMD trajectory has not been reweighed, the free energy values of the conformational states are not quantitatively accurate).
Using Amber tools, PDB files were dumped for the representative structure from the ensemble of structures for each state. Fig. 1b shows the overlap of the representative conformations from the three states and the crystal structure in the inactive state. The conformational analysis indicates that state I is close to the inactive state, but still exhibits a tendency towards an active state, such as the outward movement of TM5 found in the state I (see Fig. 1b). This outward movement of TM5 is also observed in the activation of other class B GPCRs.[26] State II and state III are both active-like states. Compared with the inactive crystal structure, TM5 and TM6 in state II move outward obviously, and the TM2–TM3 distance in state III increases. Therefore, we speculate that although the outward movement of TM6 and the distance increase of TM2–TM3 are important features for the activation of class B GPCRs, the outward movement of TM5 may be a beginning of GLP-1R activation.
Deactivation of GLP-1R from the Active Crystal Structure (PDB ID: 5vai)
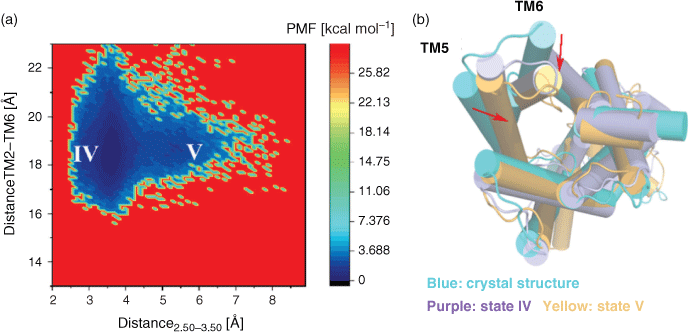
Studies have shown that the presence of agonists and G proteins are beneficial for stabilising the receptor in a fully activated state, and with the removal of agonist and G protein the receptor will gradually deactivate.[21,22] To observe the deactivation process of the active GLP-1R (5vai), the PMF profiles are calculated similar to the GLP-1R/inactive state system mentioned above, based on the same reaction coordinates: the distance between the intracellular ends of TM2 and TM6 and distance of H1802.50 and E2473.50.
As shown in Fig. 2, the GLP-1R/active state system starting from the active structure exhibits two low energy states, in state IV, the distance between H1802.50 and E2473.50 is ~3.5 Å, and the distance between the intracellular end of TM2 and TM6 is between 17–21 Å, while state V is centred on the 5.3 Å H1802.50–E2473.50 distance and the 18.5 Å TM2–TM6 distance, and state IV is close to the active state while they are 22 and 3.3Å, respectively. The intermediate states that we capture through PMF are only intermediate states that are relatively stable in energy during the activation or inactivation process. The free energy of state IV (~0.249 kcal mol−1) and state V (~1.688 kcal mol−1) represented the conformation of GLP-1R and overcame an energy barrier of ~0.1.44 kcal mol−1 during the deactivation process. Although the activation process and the deactivation process are two contrary processes, since there are many intermediate states, the intermediate states that occur in these two processes are not exactly the same.
Two representative conformations were extracted from these two stable states, and overlapped with the active crystal structure (see Fig. 2b). It is shown in Fig. 2b that TM6 of state V and state IV moves inward, and TM5 also moves towards the centre of the helices, showing a certain deactivation characteristic.[26] It is clear that state V is more close to the active state than state V, so we speculate that in the process of GLP-1R deactivation, TM6 undergoes significant inward movement followed by TM5 moving inward and the distance reducing between TM2 and TM3. This is completely different from the previous activation process of an GLP-1R/inactive state system. For the activation of GLP-1R, it begins with the outward movement of TM5, and then TM6 moves outward and the polar interaction between TM2 and TM3 is destroyed. It indicates that although the overall characteristics of the receptor during activation and deactivation are identical, the steps of the receptor in completing the activation and deactivation processes are not completely consistent.
Analysis of Correlated Motions and Structural Changes
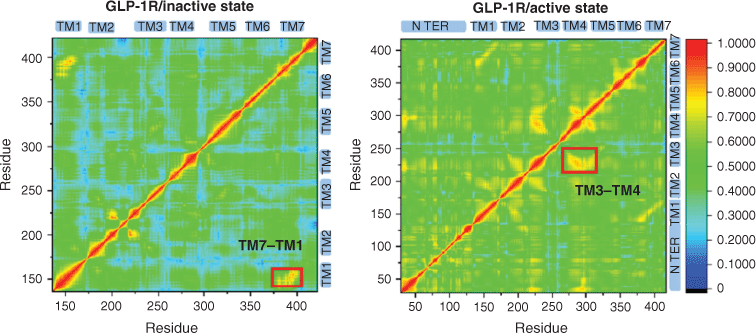
The movement of each region is not independent when the receptor undergoes a conformational change. In order to explore the correlation between the regions during the change of receptor activity, we calculated the residue cross-correlations for the two systems of GLP-1R (see Fig. 3).
|
Obviously, the overall correlation of the GLP-1R/active state system is higher than the GLP-1R/inactive state system for there are many higher related regions with cross-correlation values larger than 0.6 in the GLP-1R/active state system. An activation study on M2 receptors by Miao et al. indicates the apo receptor is more likely to transform between inactive, intermediate, and active states,[16] so a receptor in the apo state shows higher correlations than the receptor bound by the antagonist QNB. Although the two systems for GLP-1R are all in the apo state, the overall correlation of the GLP-1R/active state system is higher, indicating that GLP-1R/active state system has more possibilities to transform between different conformation states, and the deactivation and activation process may have different energy barriers. Meanwhile, a higher correlation is observed between TM1 and TM7 in the GLP-1R/inactive state system, and the GLP-1R/active state system shows a higher correlation between TM3 and TM4, which further indicates the difference between the activation and deactivation process.
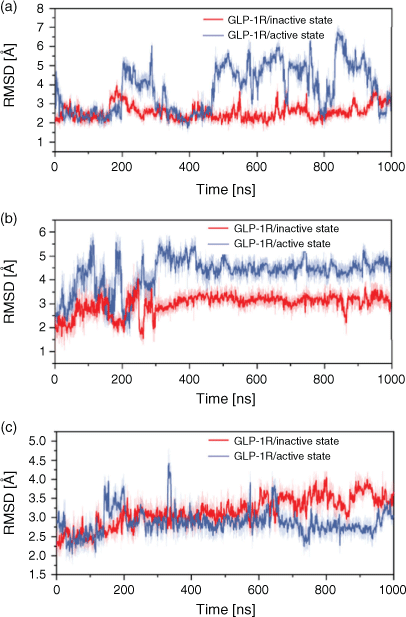
To further explore the difference in some functional regions during the activation and deactivation process, we calculated the root-mean-square deviation (RMSD) of these regions of GLP-1R. The G-protein binding site located in the cytoplasmic end served as the opening of the cytoplasmic part in TM6 and the movement of TM5 from a cavity with TM2, TM3, and TM7, and it interacts directly with H8 and ICL1. Meanwhile, the highly conserved HETx region is also adjacent to H8 and ICL1. Thus, we have analysed the dynamic changes of H8 and ICL1 during the activation and deactivation process through monitoring its RMSD change (see Fig. 4). H8 in the GLP-1R/active state system presents a larger RMSD fluctuation than in the GLP-1R/inactive state system, which may indicate that H8 changes in the process of deactivation before the activation process. At the same time, the RMSD values of ICL1 in the GLP-1R/active state system are larger and fluctuate more greatly than in the GLP-1R/inactive state system, indicating that the deactivation of GPCR after omitting the G-protein has an obvious effect on ICL1 of G-protein binding site. Moreover, the RMSD of ECL2 which performs the function of a ‘lock’ and occupies the binding site of GLP-1 was calculated. The RMSD values of ECL2 in the GLP-1R/inactive state system are higher than that in the GLP-1R/active state system, which is beneficial to the ligand binding, indicating that the first step for the activation process is the obvious change of ligand-binding site. Our observations further show that the first significant change in the deactivation process is the region associated with G-protein binding, while for the activation process, the ligand-binding site changes significantly. It is further confirmed that the signal of activation is transmitted from the extracellular side to intracellular part.
|
Protein Structure Network (PSN)
In order to further explore how signals are transmitted from the extracellular to intracellular part, how ligand-binding regions and G protein binding regions are co-regulated, and the similarities and differences of signal transduction pathways between activation and deactivation processes, a protein structure network (PSN) analysis tool was used to analyse the allosteric signal transduction pathways of these two systems of GLP-1R. We selected the residues of the ligand-binding region and the residues of the G-protein binding region as the starting and end nodes of the PSN search, respectively.[3,9,10] Fig. 5 shows the pathway with the highest frequency in the two systems. In the GLP-1R/inactive state system, the residue N2403.43 in the ligand-binding pocket is used as the starting point, and the signal is transmitted to the residue S3526.41 in the G protein binding region via the residues F1872.57, L1832.53, and Y4027.57. These residues are located in TM2, TM3, TM6, and TM7. It is further confirmed that these helices play important roles in the activation process, and these helices involved in activation signal transduction have been confirmed in many class A GPCR.[17,21,22,27] For the GLP-1R/active state system, the allosteric pathway is composed of N2403.43–S1862.56–W2433.46–I1792.49–Y2503.53. These residues only involve TM2 and TM3, and not TM6, which may be related to the inward movement of TM6 in the deactivation process. Although the signal transduction pathways in the process of activation and deactivation are different, the signal transduction of both systems start with N2403.43, which is the key residue of the ligand-binding region.[3] Its appearance in these two pathways confirms its importance of maintaining the function of GLP-1R.
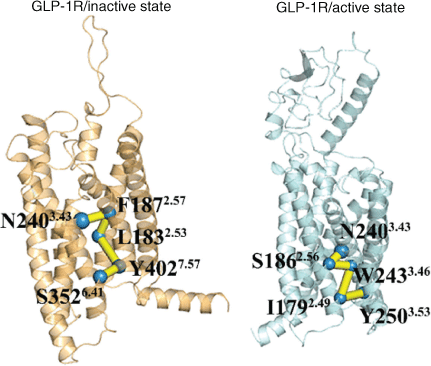
|
In order to clarify whether the difference of communication pathways (Fig. 5) was influenced by the presence of the N-terminal in the active structure, we constructed a third system of active GLP-1R from 5vai but without an N-terminal (denoted as GLP-1R/active state-without N-terminal) (see Supplementary Material). The PSN was analysed on the 1 μs aMD simulation of the GLP-1R active state-without N-terminal system. As shown in Table S1 (Supplementary Material), the allosteric pathways between the ligand-binding site and the G-protein pocket is similar to the GLP-1R active state system (just one more amino acid L2543.49 which locates in the G protein pocket compared with the GLP-1R active sate), but the frequency value decreased from 84 to 30 %. Although the N-terminal may play an important role in the receptor conformational transition process (Fig. S2 and Fig. S3, Supplementary Material), the presence or removal of the N-terminal in the active structure has a weak effect on the residues’ composition of signal transduction pathways in the activation process.
Through the exploration of the allosteric pathways above, it was found that the signal transduction pathways of activation and deactivation processes are not mutually reversible. It is also consistent with our previous results that the steps of activation and deactivation are not the same.
Experimental
System Preparation
The cryo-EM structure of GLP-1R in active (PDB ID: 5vai) and X-ray crystal structure of GLP-1R in inactive (PDB ID: 5vew) states were obtained from the PDB bank. In order to obtain the activation and deactivation processes of GLP-1R, we constructed two models: a) GLP-1R/inactive state – the negative allosteric modulator and one monomer in the crystal structure (PDB ID: 5vew) were removed; b) GLP-1R/active state – the G-protein, ligand, and nanobody in the crystal structure (PDB ID: 5vai) were removed and the missing residues were also repaired. The missing residues were repaired using Modeller 9.16.[28] All operations of system preparations were carried out via CHARMM-GUI,[29] the N-termini and C-termini of the receptors were capped by neutral groups (acetylamide and methylamide), and then the CHARMM force field was used to set the protonation state according to the physiological pH conditions. The prepared protein structures were then inserted into an equilibrated POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) bilayer phospholipid as depicted by Dickson et al.[30] with lipids located within 1 Å of the complexes removed, and then solvated in a rectangular water box with the TIP3P water model. The entire system was electrically neutralised with 0.15 M NaCl. Each system contains ~80000 atoms with a box size of 81 Å × 81 Å × 134 Å.
Molecular Dynamics Simulations
Using AMBER 16 software,[31] we carried out accelerated MD (aMD) and conventional MD (cMD) simulations. In the cMD simulation process, four steps were performed to reach the equilibrium. First, the POPC lipids were energy minimised within 100 ps with all other atoms fixed. Then, 100 ps energy minimisation was done for the waters, followed by 100-ps minimisation for the receptor. Finally, all the atoms were released in 1 ns minimisation. After that, the systems were heated gradually from 0 to 310 K followed by 5 ns NVT simulation using Berendsen temperature coupling[32] and periodic boundary conditions. Finally, a 200 ns NPT simulation was performed under the conditions of 1 atm and 310 K. The ff14SB force-field[33] was used for the receptor and the POPC lipids utilised the lipid.[34] All bonds associated with a hydrogen atom are limited by the SHAKE algorithm,[32] and the electrostatic interaction was handled with a 10 Å non-bonded cutoff by the particle mesh Ewald algorithm.[35] The time step was set to 2 fs and the trajectories were stored every 10 ps for further analysis. In addition, the final structure from the cMD simulation served as the initial structure for the aMD simulation.
In order to simultaneously improve the sampling of spatial and diffused degrees of freedom, aMD adopts a ‘dual-boost’ method based on torsion potential and total potential energy.[15] The aMD modification of the potential is defined by Eqns 1 and 2:
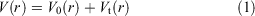
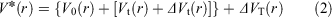
where V0(r) is the initial potential and Vt(r) is the torsion potential. ΔVt(r) and ΔVT(r) are the increasing potential energies applied to the torsional potential energy Vt(r) and the total potential energy VT(r), respectively. In terms of Eqns 3 and 4, the acceleration parameters for the dihedral potential and total potential energy were calculated:
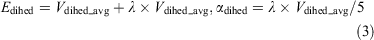
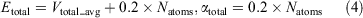
where Natoms represents the total numbers of atoms, and Vdihed_avg and Vtotal_avg are the average dihedral and total potential energies, which were calculated from the 200 ns cMD simulations. λ is an adjustable acceleration parameter. Herein, λ = 0.3 was chosen to calculate the dihedral potential energy since the value was reported to be appropriate for enhanced sampling of GPCRs.[16,36] The starting structure of the aMD simulation was selected from the final structure of the cMD simulation. Finally, a 1 μs aMD simulation was performed for each system.
Potential of Mean Force (PMF)
PMF, also known as the free energy landscape, can examine the changes in free energy with specific reaction coordinates. Thus, the PMF profiles of two systems were calculated in terms of two reaction coordinates selected: the distance between the cytoplasmic ends of TM6 and TM2, and the distance between H1802.50 and E2473.50. Along the two reaction coordinates, the energy landscape could be calculated according to the Python scripts ‘PyReweighting’ supported at http://mccammon.ucsd.edu/computing/amdReweighting/,[37] which is based on Eqn 5:
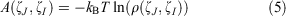
where kB represents the Boltzmann constant, T denotes the temperature, ζJ and ζI are reaction coordinates, and ρ denotes the probability of distribution. Due to the large size of the system, the free energy landscape of the aMD simulations can be reweighted but overflow errors may arise in calculating the weights, and it was found that the unweighted PMF profiles from the aMD simulations match well the PMF profiles of cMD simulations,[16] so the unweighted free energy landscapes were used in the work. Here, the PMF method was used to capture the stable state and distinguish the difference between the states by examining the changes in free energy.
Cross-Correlation Analysis
Correlation analysis can reveal the coupling relationship between atoms, which facilitates an in-depth understanding of the dynamics of a receptor during activation and deactivation. Therefore, we used the DCC algorithm[38] to calculate the correlation between residues (see Eqn 6).
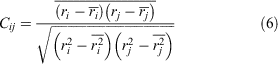
where i and j represent atoms or residue, and Cij is the covariance matrix of i and j.
Protein Structure Network (PSN)
Protein Structure Network (PSN)[39] is a structure-based network approach, which can provide integral network characteristics, such as nodes, hubs, and edges for proteins. It can be used to gain insight into the overall properties of protein dynamics, topological rearrangements, and important residues, and to provide information about intramolecular and intermolecular communication, which is important for proteins to perform their biological functions. In PSN, the residue acts as a node of the network, and when the percentage of interaction between the two nodes is greater than or equal to a given threshold, the two nodes are connected by one edge (see Eqn 7):
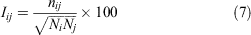
where Iij presents the interaction percentage for the nodes i and j, nij represents the number of side chain atoms in a given distance cutoff range, and Ni and Nj are the normalisation factors for residues i and j, respectively.
Wordom software[40] was used for correlation analysis and protein structure analysis, and the cpptraj module of AMBER 16[32] for other MD analyses.
Conclusions
Despite intense interest in the GLP-1R, knowledge about the activation and deactivation mechanism is very limited. Thus, many questions remain partially or completely unanswered on experiments. To gain insight into the difference of conformational changes during activation and deactivation and obtain the intermediate states that are difficult to capture for experiments, we combined aMD and cMD to simulate the active and inactive GLP-1R and coupled this with PMF calculations, structure analysis, correlation analysis, and PSN analysis to study the mechanism of activation and deactivation.
As evidenced by PMF results, there are five intermediate states during the activation and deactivation processes. The conformational analysis of these states revealed that the activation of GLP-1R was first by the outward movement of TM5, followed by TM6 off-shoring, and the increasing of distance between TM2 and TM3, while the deactivation of GLP-1R was the obvious inward movement of TM6, and then the inward shift of TM5. Although both processes involve the movement of TM5 and TM6, the order of them is different, which may be the difference between activation and deactivation.
It was shown by structural analysis that during the activation process, the ECL2 associated with ligand binding first changed greatly, which is beneficial to the binding of peptide ligands. But on the contrary, in the process of deactivation, the H8 and ICL1 regions related to the G-protein binding site change first. The correlation of overall residues in the GLP-1R/inactive state system is weaker than that in the GLP-1R/active state system. Moreover, TM1–TM7 maintains a high correlation during activation process, while TM3–TM4 exhibits a high correlation in the process of deactivation.
The protein structure network (PSN) further reveals the allosteric pathways between the ligand-binding site and the G-protein pocket during activation and deactivation processes. Although TM5 and TM6 have obvious conformational changes in these two processes, the allosteric communication pathways in these two processes are different, and signal transduction of activation and deactivation is not reversible. At the same time, it also confirms the important role of N2403.43 in maintaining the function of GLP-1R. The N-terminal may play a part in the activation/deactivation conformational transition process, and the importance of the N-terminal will be further studied.
In summary, the observations from this work could provide molecular information for elucidating the mechanisms of activation and deactivation, and reveal the allosteric regulation of the ligand-binding and G-protein binding site in these two processes. It promotes our understanding of the structure and function of GPCR and is beneficial to drug design targeting GLP-1R.
Supplementary Material
The simulation results of the third system of active GLP-1R from 5vai but without N-terminal (denoted as GLP-1R/active state-without N-terminal) are available on the Journal’s website.
Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgements
The authors thank the National Youth Foundation of China (Grant No. 21705011) for financial support.
References
[1] D. M. Rosenbaum, S. G. F. Rasmussen, B. K. Kobilka, Nature 2009, 459, 356.| Crossref | GoogleScholarGoogle Scholar | 19458711PubMed |
[2] J. Todd, S. Bloom, Diabet. Med. 2007, 24, 223.
| Crossref | GoogleScholarGoogle Scholar | 17263764PubMed |
[3] A. Jazayeri, M. Rappas, A. J. H. Brown, J. Kean, J. C. Errey, N. J. Robertson, C. Fiez-Vandal, S. P. Andrews, M. Congreve, A. Bortolato, J. S. Mason, A. H. Baig, I. Teobald, A. S. Doré, M. Weir, R. M. Cooke, F. H. Marshall, Nature 2017, 546, 254.
| Crossref | GoogleScholarGoogle Scholar | 28562585PubMed |
[4] D. J. Drucker, J. Philippe, S. Mojsov, W. L. Chick, J. F. Habener, Proc. Natl. Acad. Sci. USA 1987, 84, 3434.
| Crossref | GoogleScholarGoogle Scholar | 3033647PubMed |
[5] J. A. Engel, E. Jerlhag, CNS Drugs 2014, 28, 875.
| Crossref | GoogleScholarGoogle Scholar | 24958205PubMed |
[6] M. R. Hayes, H. D. Schmidt, Curr. Opin. Behav. Sci. 2016, 9, 66.
| Crossref | GoogleScholarGoogle Scholar | 27066524PubMed |
[7] K. P. Skibicka, Front. Neurosci. 2013, 7, 181.
| Crossref | GoogleScholarGoogle Scholar | 24133407PubMed |
[8] G. Song, D. Yang, Y. Wang, C. de Graaf, Q. Zhou, S. Jiang, K. Liu, X. Cai, A. Dai, G. Lin, D. Liu, F. Wu, Y. Wu, S. Zhao, L. Ye, G. W. Han, J. Lau, B. Wu, M. A. Hanson, Z.-J. Liu, M.-W. Wang, R. C. Stevens, Nature 2017, 546, 312.
| Crossref | GoogleScholarGoogle Scholar | 28514449PubMed |
[9] Y. Zhang, B. Sun, D. Feng, H. Hu, M. Chu, Q. Qu, J. T. Tarrasch, S. Li, T. S Kobilka, B. K. Kobilka, G. Skiniotis, Nature 2017, 546, 248.
| Crossref | GoogleScholarGoogle Scholar | 28538729PubMed |
[10] S. Durdagi, B. Dogan, I. Erol, G. Kayık, B. Aksoydan, Curr. Opin. Struct. Biol. 2019, 55, 93.
| Crossref | GoogleScholarGoogle Scholar | 31082696PubMed |
[11] C. Gomez Santiago, E. Paci, D. Donnelly, Biochem. Biophys. Res. Commun. 2018, 498, 359.
| Crossref | GoogleScholarGoogle Scholar | 29397068PubMed |
[12] J. Zhang, Q. Bai, H. Pérez-Sánchez, S. Shang, X. Yao, Phys. Chem. Chem. Phys. 2019, 21, 8470.
| Crossref | GoogleScholarGoogle Scholar | 30957116PubMed |
[13] D. Hamelberg, J. Mongan, J. A. McCammon, J. Chem. Phys. 2004, 120, 11919.
| Crossref | GoogleScholarGoogle Scholar | 15268227PubMed |
[14] P. R. Markwick, J. A. McCammon, Phys. Chem. Chem. Phys. 2011, 13, 20053.
| Crossref | GoogleScholarGoogle Scholar | 22015376PubMed |
[15] D. Hamelberg, C. A. F. de Oliveira, J. A. McCammon, J. Chem. Phys. 2007, 127, 155102.
| Crossref | GoogleScholarGoogle Scholar | 17994855PubMed |
[16] Y. Miao, S. E. Nichols, P. M. Gasper, V. T. Metzger, J. A. McCammon, Proc. Natl. Acad. Sci. USA 2013, 110, 10982.
| Crossref | GoogleScholarGoogle Scholar | 23781107PubMed |
[17] F. Zhang, Y. Yuan, H. Li, L. Shen, Y. Guo, Z. Wen, X. Pu, RSC Adv. 2018, 8, 37855.
| Crossref | GoogleScholarGoogle Scholar |
[18] J. Li, A. L. Jonsson, T. Beuming, J. C. Shelley, G. A. Voth, J. Am. Chem. Soc. 2013, 135, 8749.
| Crossref | GoogleScholarGoogle Scholar | 23678995PubMed |
[19] A. Benians, J. L. Leaney, A. Tinker, Proc. Natl. Acad. Sci. USA 2003, 100, 6239.
| Crossref | GoogleScholarGoogle Scholar | 12719528PubMed |
[20] S. G. F. Rasmussen, B. T. DeVree, Y. Zou, A. C. Kruse, K. Y. Chung, T. S. Kobilka, F. S. Thian, P. S. Chae, E. Pardon, D. Calinski, J. M. Mathiesen, S. T. A. Shah, J. A. Lyons, M. Caffrey, S. H. Gellman, J. Steyaert, G. Skiniotis, W. I. Weis, R. K. Sunahara, B. K. Kobilka, Nature 2011, 477, 549.
| Crossref | GoogleScholarGoogle Scholar |
[21] N. R. Latorraca, A. Venkatakrishnan, R. O. Dror, Chem. Rev. 2016, 117, 139.
| Crossref | GoogleScholarGoogle Scholar | 27622975PubMed |
[22] A. S. Rose, M. Elgeti, U. Zachariae, H. Grubmüller, K. P. Hofmann, P. Scheerer, P. W. Hildebrand, J. Am. Chem. Soc. 2014, 136, 11244.
| Crossref | GoogleScholarGoogle Scholar | 25046433PubMed |
[23] S. G. F. Rasmussen, H. J. Choi, D. M. Rosenbaum, T. S. Kobilka, F. S. Thian, P. C. Edwards, M. Burghammer, V. R. P. Ratnala, R. Sanishvili, R. F. Fischetti, G. F. X. Schertler, W. I. Weis, B. K. Kobilka, Nature 2007, 450, 383.
| Crossref | GoogleScholarGoogle Scholar |
[24] S. A. Hjorth, C. Ørskov, T. W. Schwartz, Mol. Endocrinol. 1998, 12, 78.
| Crossref | GoogleScholarGoogle Scholar | 9440812PubMed |
[25] E. Schipani, K. Kruse, H. Juppner, Science 1995, 268, 98.
| Crossref | GoogleScholarGoogle Scholar | 7701349PubMed |
[26] R. Singh, N. Ahalawat, R. K. Murarka, J. Phys. Chem. B 2015, 119, 2806.
| Crossref | GoogleScholarGoogle Scholar | 25607803PubMed |
[27] X. Xiao, X. Zeng, Y. Yuan, N. Gao, Y. Guo, X. Pu, M. Li, Phys. Chem. Chem. Phys. 2015, 17, 2512.
| Crossref | GoogleScholarGoogle Scholar | 25494239PubMed |
[28] B. Webb, A. Sali, Curr. Protoc. Bioinf. 2014, 47, 5.6.1.
| Crossref | GoogleScholarGoogle Scholar |
[29] J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda, W. Im, J. Chem. Theory Comput. 2016, 12, 405.
| Crossref | GoogleScholarGoogle Scholar | 26631602PubMed |
[30] C. J. Dickson, L. Rosso, R. M. Betz, R. C. Walker, I. R. Gould, Soft Matter 2012, 8, 9617.
| Crossref | GoogleScholarGoogle Scholar |
[31] D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao, P. A. Kollman, AMBER 2016 2016 (University of California: San Francisco, CA).
[32] H. J. C. Berendsen, J. P. M. Postma, W. F. V. Gunsteren, A. Dinola, J. R. Haak, J. Chem. Phys. 1984, 81, 3684.
| Crossref | GoogleScholarGoogle Scholar |
[33] J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser, C. Simmerling, J. Chem. Theory Comput. 2015, 11, 3696.
| Crossref | GoogleScholarGoogle Scholar | 26574453PubMed |
[34] C. J. Dickson, D. M. Benjamin, A. A. Skjevik, R. M. Betz, K. Teigen, R. C. Walker, J. Chem. Theory Comput. 2014, 10, 865.
| Crossref | GoogleScholarGoogle Scholar | 24803855PubMed |
[35] T. Darden, L. Perera, L. Li, L. Pedersen, Structure 1999, 7, R55.
| Crossref | GoogleScholarGoogle Scholar | 10368306PubMed |
[36] K. W. Kastner, J. A. Izaguirre, Proteins: Struct. Funct. Bioinf. 2016, 84, 1480.
| Crossref | GoogleScholarGoogle Scholar |
[37] Y. Miao, W. Sinko, L. Pierce, D. Bucher, R. C. Walker, J. A. McCammon, J. Chem. Theory Comput. 2014, 10, 2677.
| Crossref | GoogleScholarGoogle Scholar | 25061441PubMed |
[38] J. A. McCammon, S. C. Harvey, Dynamics of Proteins and Nucleic Acids 1988 (Cambridge University Press: Cambridge).
[39] N. Kannan, S. Vishveshwara, J. Mol. Biol. 1999, 292, 441.
| Crossref | GoogleScholarGoogle Scholar | 10493887PubMed |
[40] M. Seeber, A. Felline, F. Raimondi, S. Muff, R. Friedman, F. Rao, A. Caflisch, F. Fanelli, J. Comput. Chem. 2011, 32, 1183.
| Crossref | GoogleScholarGoogle Scholar | 21387345PubMed |