Reaction-norm analysis of neonatal lamb mortality suggests heritability varies with cold-stress: an example in the Elsenburg Merino selection lines
C. L. Nel A B * , Y. Steyn C , A. R. Gilmour D , D. Waters
A B * , Y. Steyn C , A. R. Gilmour D , D. Waters  E , S. A. Clark E , J. H. J. van der Werf E , A. A. Swan
E , S. A. Clark E , J. H. J. van der Werf E , A. A. Swan  F , K. Dzama B and S. W. P. Cloete
F , K. Dzama B and S. W. P. Cloete  B
B
A Directorate: Animal Sciences, Western Cape Department of Agriculture, Elsenburg 7607, South Africa.
B Department of Animal Sciences, Stellenbosch University, Stellenbosch 7602, South Africa.
C Department of Animal and Dairy Science, University of Georgia, Athens, GA 30605, USA.
D 11 Holman Way, Orange, NSW 2800, Australia.
E School of Environmental and Rural Science, University of New England, Armidale, NSW 2351, Australia.
F Animal Genetics & Breeding Unit, University of New England, Armidale, NSW 2350, Australia.
Animal Production Science 63(11) 1017-1030 https://doi.org/10.1071/AN22464
Submitted: 14 December 2022 Accepted: 16 March 2023 Published: 13 April 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Coping with high levels of cold stress should be beneficial to survival of lambs, given the high mortality rate associated with severe winter storms. The Elsenburg Merino selection experiment involved divergent selection for reproduction. Phenotypic results comparing the positively selected H-Lines and negatively selected L-Lines suggested that cold-stress adaption could have contributed to the favourable genetic trends for survival of H-Line lambs. However, observing the genetic merit of better adapted animals depends on the presence of cold stress at the time of recording. A genotype by environment component (G × E) could, thus, be important when assessing survival/mortality phenotypes.
Aim: This study proposed the genetic analysis of this possible G × E component and compared the H- and L-Lines in this regard.
Methods: The sire model allowed the use of progeny phenotypes for neonatal mortality recorded during different levels of cold stress, and the possible G × E could be investigated through the reaction-norm approach. Genetic parameters were evaluated as random regression components by implementing a Gibbs sampling approach. A data set of 5723 individual lamb records was analysed as the progeny of 213 sires.
Results: A modelled G × E component played an important role in mortality outcomes, with the mean estimate (and 95% confidence interval) for the slope (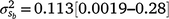 ) only marginally smaller than the corresponding estimate for the intercept (
) only marginally smaller than the corresponding estimate for the intercept (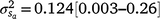 ). The reaction-norm model showed a higher heritability (h2 ± posterior standard deviation) for mortality at 3 days of age during high cold-stress (0.22 ± 0.16 at ~1100 KJm−2h−1) than during mild (0.13 ± 0.10 at ~960 KJm−2h−1) conditions, suggesting a greater ability to discriminate between sires at increasing stress levels.
). The reaction-norm model showed a higher heritability (h2 ± posterior standard deviation) for mortality at 3 days of age during high cold-stress (0.22 ± 0.16 at ~1100 KJm−2h−1) than during mild (0.13 ± 0.10 at ~960 KJm−2h−1) conditions, suggesting a greater ability to discriminate between sires at increasing stress levels.
Conclusions: Failure to account for this G × E component putatively contributes to the low h2 commonly reported for survival traits. The higher h2 at increased levels of cold stress could have played an important part in the higher survival of the H-Line progeny, who were better at coping with cold, wet and windy conditions.
Implications: Larger studies representing a wider environmental trajectory are recommended. This should be very feasible since cold stress can be derived from commonly available weather-station data.
Keywords: chill index, early mortality, genotype by environment interaction, Gibbs sampling, lamb survival, random regression, sheep, welfare.
Introduction
The incidence of lamb mortality is of great importance from both an economical and welfare point of view (Brien et al. 2014; Hinch and Brien 2014). There has thus been considerable interest in improving lamb survival by targeting additive genetic effects. However, this approach has been discouraged by the low heritability (h2) for survival traits reported for Merinos (Brien et al. 2009a; Hatcher et al. 2010) and other breeds (Lopez-villalobos and Garrick 1999; Morris et al. 2000; Riggio et al. 2008; Vanderick et al. 2015). The first days after birth have been identified as particularly critical having the highest mortality rates (Hatcher et al. 2009), and a possibly higher level of genetic variation (Sawalha et al. 2007; Riggio et al. 2008; Hatcher et al. 2010). The neonatal period delivers a stringent test to the adaptive capacity of lambs, including a dramatic change in temperature on leaving the uterine environment. The ability of the lamb to quickly respond with its own mechanisms of thermoregulation has been emphasised as a key factor contributing to lamb viability (Plush et al. 2016). In extensive production systems, this period can be particularly challenging when lambs are born into cold, wet and windy conditions, which interact to exacerbate the level of cold stress. Exposure to a high rate of heat loss slows lamb progress by a group of inter-related factors, such as poor feeding, behaviour and thermoregulation. Lambs who succumb to cold stress are typically identified by aetiology named the ‘starvation–mismothering–exposure’ complex at autopsy (Haughey 1991; Cloete and Scholtz 1998). The expected rate of heat loss has been quantified as a function of ambient temperature, rainfall and windspeed as an environmental stress variable termed the ‘chill index’ (Nixon-Smith 1972; Donnelly 1984). Cold stress represented by increasing values of the chill index has been linked to high mortality rates in new-born lambs (Donnelly 1984; Gudex et al. 2005; Oldham et al. 2011; Geenty et al. 2014), extending on earlier reports of ‘bad weather’ (Alexander et al. 1980) or the interaction among cold, wet and windy conditions (Obst and Day 1968).
An opportunity to mitigate these effects is presented by the fact that individuals vary in their ability to tolerate high rates of heat loss. Differences in the ability to resist cold stress have been reported across breeds (Dwyer and Morgan 2006), selection lines (Slee and Stott 1986), sire lines (Gudex et al. 2005), and individuals (Slee et al. 1991). It could be expected that genotypes better adapted to high levels of cold stress should incur lower incidences of mortality under conditions of severe cold exposure. However, the favourable merit of these genotypes would not be observed in environments where cold stress is absent or limited. A genotype by environment interaction (G × E) could thus be an important component of neonatal lamb survival, particularly in extensive conditions where there is often little protection against environmental elements.
The presence of a significant G × E effect means that the observed merit of genotypes depends on the environment they are evaluated in (Falconer and Mackay 1996), and implies that the estimated breeding value (EBV) varies according to environmental factors. This variation has often been described as the ‘environmental sensitivity’ (ES) or ‘phenotypic plasticity’ of the genotype. A high ES is generally not desirable, since a breeding objective would target ‘robust’ genotypes capable of expressing their potential despite varying environments (Knap 2005). If the environment at recording can be reliably quantified, the presence of G × E can be investigated by the ‘reaction-norm’ (RN) approach (de Jong 1995; de Jong and Bijma 2002). Reaction-norm models define breeding values as continuous functions of an environmental descriptor by random regression of genetic effects across the environmental trajectory, such as the gradient of cold stress. Random regression models has been proposed for survival analysis (Veerkamp et al. 1998) and could contribute to better understanding of the role of G × E in neonatal lamb mortality, but this has not been investigated.
The Elsenburg Merino selection lines have been divergently selected for reproductive fitness (lambs weaned per ewe joined) from 1986 to 2020. Despite the low h2, worthwhile and divergent genetic trends for lamb survival were reported for the H-Lines (positive selection) and L-Lines (negative selection; Cloete et al. 2009; Nel et al. 2021a). In a phenotypic comparison between H- and L-Line lambs, H-Line lambs coped better with stressful levels of cold exposure (Nel et al. 2021b), suggesting that the relative fitness of H-Line lambs could be linked with better cold-stress adaption. Since the start of the experiment, the incidence of lamb mortality has been recorded in close proximity to weather stations, providing data to quantify cold stress on a daily basis. The influence of G × E can thus be investigated by linking phenotypes of mortality to the variable gradients of cold stress during the neonatal period. The first aim of this study was thus to use the RN approach to investigate the potential contribution of G × E to genetic parameters of neonatal mortality across an environmental trajectory defined by cold stress. Second, the study aimed to determine whether the favourable fitness of the H-Line (Cloete and Scholtz 1998; Cloete et al. 2009; Nel et al. 2021b) can be linked to cold-stress resistance on the genetic level by comparing RN components of H- and L-Line sires during selected periods of the selection experiment. The within-flock analysis was constrained by the fact that the edited data set was small, but was aided by the historic divergence of the flock, as discussed by the above references.
Materials and methods
The Elsenburg Merino flock
The history of the selection lines is divided into two periods defined by the location of the flock. From 1986 to 1992, the flock was maintained at the Tygerhoek research farm near to the town of Riviersonderend (34°8′S, 21°11′E), in the Western Cape, South Africa. In 1992, the flock was moved to Elsenburg research farm near the town of Stellenbosch (33°51′S, 18°50′E) in the same province. Weather data were available for both sites used during the selection experiment but lambing at the Tygerhoek site generally commenced during the autumn season. The warmer climate thus confounded year or site effects, and data collected during the Tygerhoek period of this experiment were discarded to avoid a biased presentation of the effects of the environmental descriptor (described below).
Except at joining, the two lines were maintained as a single flock of ~200–260 ewes for most of the year. Pregnant ewes were randomly allocated to 10–20 kikuyu lambing paddocks of approximately 0.3–0.4 ha each, prior to the commencement of lambing. Ewes remained in their lambing paddocks for 3–14 days (depending on year and the research conducted), before being drifted from their lambing paddocks onto larger (1–2 ha) Lucerne paddocks in larger groups of 30–40 (Cloete et al. 1998). Other details pertaining to management and nutrition are available elsewhere (Cloete et al. 2004).
The H- and L-Lines were formed from the same base population at the commencement of the selection experiment in 1986. After the flocks were generated by random sampling within age groups, selection proceeded by screening subsequent cohorts of ram and ewe replacements according to their rankings for number of lambs weaned per joining (Cloete et al. 2004). Except for misadventure and severe health issues, replacement ewes remained in the flock for at least five joinings. At the beginning of the experiment, roughly 120 ewes were assigned into each selection line. The H-line has since grown to 130–200 ewes, while numbers in the L-Line decreased to about 40–80 breeding ewes. Selection of rams was predominantly based on the progeny of dams on the basis of at least three joinings. Five rams were initially used for each line and a ram was used only for a single year until 1992, after which two to three rams per line were used across years to provide sire links. Following the results by Cloete et al. (2004), selection from 2003 was also guided by the use of best linear unbiased prediction (BLUP) breeding values derived from a single-trait repeatability model fitted to ewe reproduction records. During this period, the original ranking values were still considered in tandem to BLUP-derived breeding values, but BLUP values have been the only selection criterion since 2010. From 2008 to 2019, 349 H-Line lambs and 151 L-Line lambs were born as the progeny of external sires, selected from other flocks on the same criteria as used in the Elsenburg flock (i.e. national or within-flock breeding values for number of lambs weaned per joining/lambing). These animals were also considered for selection and 740 H-Line, and 118 L-Line lambs were subsequently born as grand-progeny of external sires between 2010 and 2019.
Data and recording
The recording of incidences of mortality (0 = lamb survived, 1 = lamb did not survive) and birth weight (BW) took place during daily lambing rounds from 08:00 am that identified all lambs born within the previous 24-h period with their dams, thus enabling linkage back to the selection line and sire (Cloete et al. 2004, 2009). Data for lamb survival were recorded as lambs having succumbed at disjoined intervals starting with mortality at birth (MB) and, subsequently, before 3 days of age (M3), tail-docking (MT) and weaning (MW), which sum to total mortality (TM) at weaning. Birth weight was also recorded to the nearest 0.1 kg. The pedigree file identified the sires (n = 282) and dams (n = 2141) for the vast majority of animals.
Environmental descriptor
Climatic data were available from a weather station near the lambing paddocks. During the entire history (1986–2020) of the selection experiment, 8446 records of BW and mortality were originally recorded. Owing to discarding the data linked to the Tygerhoek site (n = 1521) and random technical errors at the Elsenburg weather station (n = 1202) where climate data were missing in a few seasons, a reduced data set of 5723 mortality records of 213 sires could be linked to the environmental descriptor. The weather station (33°51′S, 18°50′E, alt: 171 m) was within an 1800 m radius to the furthest boundary of the lambing paddocks used after 1992. The weather station recorded daily data that included windspeed, rainfall and ambient temperature. These data allowed for the quantification of an environmental-stress variable defined as the chill-index (Nixon-Smith 1972; Donnelly 1984). This index estimates heat loss per unit surface area per hour such that
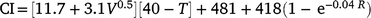
where CI is the chill index that depicts colds stress as the estimated heat loss (KJ m−2 h−1), V is the mean daily wind velocity (m s−1), T is the mean daily temperature (°C) and R is the total daily rainfall (mm). To define CI as a single measure of cold stress, daily data were used to define the mean values for the first 3 days of age, including the date of birth. This definition of CI has been observed as an important predictor to M3, but with little to no relationship for other periods of mortality (Nel et al. 2021b). Consequently, only M3 was subject to extended analysis in this study and only summary statistics of MB, MT, and MW are reported.
Statistical analyses
Given the discrete expression of the mortality phenotype as either alive (0) or dead (1), it could be beneficial to analyse M3 as a threshold character (Falconer 1989) that considers a hypothetical normal distribution on the underlying liability scale. This issue justifies some comment. Theoretically, linear models are not ideal for the analysis of threshold or binary phenotypes, and the same restrictions would apply to random regression models. However, examples of analysis of survival data on both underlying and observed scale (Matos et al. 2000; Everett-Hincks et al. 2014; Vanderick et al. 2015) have shown that linear models have very similar predictive properties to those of transformed or threshold models. Following this reasoning and leading on from previous examples for survival and/or other binary traits such as fertility (Haile-Mariam et al. 2008; Dominik and McWilliams 2014), preliminary analysis evaluated survival data by random regression on the observed scale. However, linear analysis delivered unreasonably high correlation estimates (>0.95) between intercept and slope components of the sire reaction norms (defined below), suggesting that breeding values at a particular point of the environmental trajectory could also have been a function of the mean at that point rather than a true discrimination between sires. Consequently, it was deduced that random regression on a linear scale was unreliable if the incidence (and thus the mean) of the binary variable is very low (e.g. the ~6% incidence observed for M3), likely because the large proportional change in variance across the environmental trajectory is too great a violation of the assumptions of linear models.
Subsequently, analysis commenced on the transformed/underlying scale in two phases. First, fixed effects and the phenotypic relationship between CI and M3 were tested by fitting generalised linear models by using a logit transformation so as to obtain a ‘fixed effects’ model for downstream analysis. Second, following previous analysis of binary variables by random regressions across time (Tsuruta et al. 2009) or across a heat stress index (Brügemann et al. 2013), random variance components of M3 were estimated through a threshold model by implementing a Gibbs sampling approach within the Bayesian framework, as outlined below.
Fixed effects
Estimation of fixed effects commenced using the ASREML® program (Gilmour et al. 2015). The factors that were considered as fixed included selection line (H-Line or L-Line), sex (male or female), age of dam (2–7+ years), and birth type (singles vs pooled multiples), and BW was also considered as a linear and quadratic covariate. In a preliminary analysis on the phenotypic level, CI was treated as a standard covariate to test for significance and predict mortality rates overall and for comparing selection lines across the cold-stress trajectory. For these phenotypic predictions of selection lines as fixed effects, pedigree information was not included in the model. The least-square means for selection line predictions were estimated on the logit scale and back-transformed to the observed scale by the inverse link function 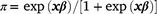 where x represents the matrix of fixed effects and β the vector of solutions for fixed effects. Generally, factors and covariates observed as significant (P < 0.05) in this first phase of the analysis were retained in the ‘fixed effects model’ that provided the basis for estimating random variance components. However, there were some notes pertaining to the ‘fixed effects model’ applied in estimating genetic parameters, and subsequently used to compare breeding values of the H- and L-Lines. First, since the H- and L-Lines displayed divergent genetic trends for early survival (Nel et al. 2021a), the effect of selection line was retained as a fixed term to report genetic parameters better aligning to what could be expected from a traditional flock. Subsequently, the selection line term was removed from analysis for comparing H- and L-Line breeding values, and these results are reported separately and retaining ‘selection line’ as a fixed effect would adjust breeding values accordingly (Cloete et al. 2004). Furthermore, to represent the ‘population norm’ that defines the mean relationship in RN analysis, the relationship between CI and M3 was included only as first-order Legendre coefficients as fixed terms.
where x represents the matrix of fixed effects and β the vector of solutions for fixed effects. Generally, factors and covariates observed as significant (P < 0.05) in this first phase of the analysis were retained in the ‘fixed effects model’ that provided the basis for estimating random variance components. However, there were some notes pertaining to the ‘fixed effects model’ applied in estimating genetic parameters, and subsequently used to compare breeding values of the H- and L-Lines. First, since the H- and L-Lines displayed divergent genetic trends for early survival (Nel et al. 2021a), the effect of selection line was retained as a fixed term to report genetic parameters better aligning to what could be expected from a traditional flock. Subsequently, the selection line term was removed from analysis for comparing H- and L-Line breeding values, and these results are reported separately and retaining ‘selection line’ as a fixed effect would adjust breeding values accordingly (Cloete et al. 2004). Furthermore, to represent the ‘population norm’ that defines the mean relationship in RN analysis, the relationship between CI and M3 was included only as first-order Legendre coefficients as fixed terms.
The reaction-norm model
For M3 data, RNs were derived by building the genetic relationship matrix according to a sire model. Of the 213 sires with records in the data file, the average sire had ~26–27 progeny and, with variable climatic conditions, sire genotypes could be evaluated by progeny performance at varying levels of the environmental trajectory described by the CI. Subsequently, the RN model was structured as a random regression by fitting a first degree Legendre polynomial nesting-sire genetic effects within the trajectory of the cold-stress gradient, CI. In Legendre polynomials, the values observed for the environmental trajectory (CI) were first standardised to an interval between −1 and 1, aligning with the minimum and maximum values of CI respectively. The standardised value, m, at the ith environmental level was obtained as: 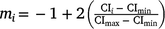 . The elements mi are presented in matrix M, with dimensions (t × n) dependent on the t environmental levels and n the order of the polynomial. The elements of M are then scaled to the appropriate Legendre coefficients by matrix Λ. For a first-order polynomial, the resulting Legendre coefficients for three environmental levels (min, intercept, max) can be defined in matrix ϕ as follows:
. The elements mi are presented in matrix M, with dimensions (t × n) dependent on the t environmental levels and n the order of the polynomial. The elements of M are then scaled to the appropriate Legendre coefficients by matrix Λ. For a first-order polynomial, the resulting Legendre coefficients for three environmental levels (min, intercept, max) can be defined in matrix ϕ as follows:
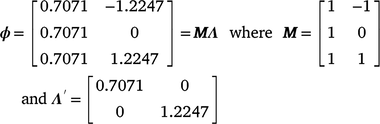
Genetic parameters of the RN model are thus represented as sire variances at the intercept (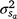 ), the slope (
), the slope (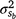 ), and their covariance (
), and their covariance (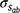 ). The single-trait threshold model with a random regression on CI was defined as follows (in matrix notation):
). The single-trait threshold model with a random regression on CI was defined as follows (in matrix notation):
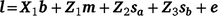
where l is the vector of unobserved liabilities for observations, b is a vector of fixed effects including the fixed coefficients of the population norm, m the vector of maternal effects, sa and sb the sire genetic effects for the intercept and slope respectively, and e is the vector of residual effects. X1 is a design matrix relating l to the appropriate coefficients for fixed effects. Z1 related l to the appropriate random solutions for maternal genetic effects, Z2 and Z3 were design matrices relating l to the sire EBVs for the intercept (sa) and slope (sb), with Z2 containing the Legendre regression coefficients for the intercept on the diagonal (i.e. 0.7071) and Z3 containing the Legendre regression coefficients for the slope corresponding to each record in l on the diagonal.
The variance–covariance structure of random variance components was assumed as
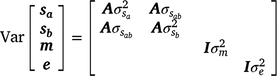
where 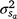 and
and 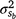 are sire genetic variances for the intercept and slope respectively,
are sire genetic variances for the intercept and slope respectively, 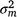 is the maternal effect, and
is the maternal effect, and 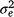 is the residual variance. A is the numerator relationship matrix containing sire relationships, and I an identity matrix of the appropriate order. The permanent maternal environmental component (
is the residual variance. A is the numerator relationship matrix containing sire relationships, and I an identity matrix of the appropriate order. The permanent maternal environmental component (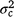 ) was determined by subtracting
) was determined by subtracting 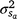 from the total maternal variance (
from the total maternal variance (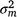 ).
).
The estimation of random variance components was performed within the Bayesian framework, using the THRGIBBS1F90 software package (Misztal et al. 2014). In total, 200 000 samples were generated in a single cycle, of which the first 50 000 were discarded as the burn-in period, and the remaining samples were plotted against iterations for visual inspection. A stable convergence of all random variance components was observed within this chain length, and longer cycles were not investigated. Following the burn-in period, every 10th sample was stored, which delivered 15 000 samples for the calculation of posterior statistics such as the posterior means, standard deviation (PSD) and 95% highest posterior density (HPD) confidence intervals. Point estimates reported were based on the posterior mean of the respective variance components.
Covariance functions (CF)
To estimate sire genetic variance at t levels of the environmental descriptor, the matrix 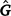 of dimensions t × t was derived as
of dimensions t × t was derived as
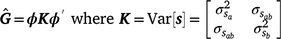
where ϕ is a t × n matrix that contains the n Legendre polynomial coefficients for each of t environmental levels. The ith diagonals of 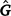 were the estimates of sire genetic variances when t = i. In the case of first-degree polynomials, a diagonal element of
were the estimates of sire genetic variances when t = i. In the case of first-degree polynomials, a diagonal element of 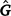 can be defined as
can be defined as
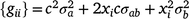
where c is the constant coefficient for the intercept, and x is the appropriate coefficient for the slope at the ith environmental level. The phenotypic (co)variance matrix 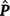 was determined by summing the variance components where the permanent maternal environmental and residual variances were homogenously added to all elements of
was determined by summing the variance components where the permanent maternal environmental and residual variances were homogenously added to all elements of 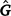 , as follows:
, as follows:
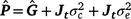
The heritability (h2) across t environments are then
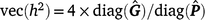
For threshold models, the mean residual variance is ±1 for a convergent chain of samples. All estimates of h2 in this study are reported on the underlying scale.
Sire EBVs and selection-line comparisons
The RN of sires with five or more progeny were represented by plotting ϕS′ where the first to nth column of S contained the sire genetic solutions and ϕ contained the appropriate Legendre coefficients corresponding to the environmental levels for which a particular sire had progeny. This was first reported for sire solutions from the first analysis where selection line was maintained in fixed-model terms. Subsequently, for the RNs of H- and L-Line sires to be compared, sire solutions were derived from the second analysis where selection line was excluded from the fixed terms. The RNs of H- and L-Line sires with progeny in the latter period (born after 2003) of the selection experiment were plotted as previously described but identified by selection line of origin. The timeframe was chosen since genetic trends for perinatal survival reported elsewhere (Nel et al. 2021a) reported differences between the lines to be more or less manifested by the mid-2010s (following 18–22 years of selection). So as to represent the general trend of H- and L-Line RNs over the duration of the experiment, the intercept and slope solutions of ‘pure’ H- or L-Line (>75% of line-specific genetic background) sires were plotted for all sires with progeny in the dataset. Simple linear regression lines were fitted to within-line intercept and slope solutions and tested for significant coefficients and divergence using individual standard errors and pooled standard errors respectively. These regression lines were forced through the origin according to the initial start of the experiment in 1985 (year zero).
Results
Summary statistics
In total, 22% of lambs succumbed before weaning. According to partitioned time periods, 4% were recorded dead at birth, 6% died before 3 days of age (M3), 6% before tail-docking and the remaining 7% before weaning. Lambs were thus particularly susceptible in the 3-day period defined by M3, since this narrow timeframe contributed a large proportion (27%) of the total incidence of mortality within only the first three days of age. The mean rate of heat loss (CI) of the three days following birth across all observations of M3 was 963.5 KJ m−2 h−1. The dataset was adjusted for 40 erratic records by deleting values of CI outside of the interval between 800 and 1250 KJ m−2 h−1 to better fit a normal distribution (Fig. 1). However, the dataset remained skewed slightly right with a longer tail of higher CI values. This was considered acceptable for downstream analysis, but had implications for the interpretation of the ‘intercept’ component of regression equations. According to Legendre polynomials, the intercept (as the midpoint between tmax and tmin) was represented by 1025 KJ m−2 h−1, which was higher than the aforementioned arithmetic mean.
|
|
Fixed effects
The outcome of M3 was affected by birth type (P < 0.01) but not sex (P > 0.05), with multiples being more likely to succumb. However, the inclusion of BW as a linear covariate eliminated these effects, indicating that BW was the primary driver of these differences between singles and multiples. According to the retransformed values from the logit scale, selection lines differed (P < 0.01) substantially in their incidence of neonatal mortality, with M3 for the L-Line (0.051 ± 0.007) about 46% higher than the predicted rate for H-Line lambs (0.035 ± 0.004).
On the phenotypic level, the CI was an important (P < 0.01) predictor for M3, and Fig. 2 shows the predicted M3 with an increasing cold stress for the whole population, as well as for individual selection lines. When cold stress was absent, M3 was below 2%, but could increase to nearly 15% when levels of cold stress were extreme (~1200 KJ m−2 h−1). The L-Line lambs appeared particularly susceptible when subjected to these conditions (Fig. 2), but the wide standard errors surrounding these predictions point to limited statistical power at the extreme upper levels of the environmental trajectory.
Posterior distributions
The posterior distributions for the random variance components can be seen in Fig. 3. Skewed distributions of the intercept (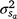 ) and slope components (
) and slope components (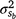 ) attributable to sires were visible, but this could be expected given that the low estimates of M3 were approaching the lower theoretical boundary. A modelled G × E component played an important role in mortality outcomes, with the mean estimate (and 95% confidence interval) for the slope (
) attributable to sires were visible, but this could be expected given that the low estimates of M3 were approaching the lower theoretical boundary. A modelled G × E component played an important role in mortality outcomes, with the mean estimate (and 95% confidence interval) for the slope (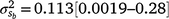 ) only marginally smaller than the corresponding estimate for the intercept (
) only marginally smaller than the corresponding estimate for the intercept (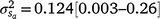 ), suggesting a strong influence of the environmental trajectory on sire breeding values. The mean estimate of the covariance between the intercept and slope components was positive in absolute direction (
), suggesting a strong influence of the environmental trajectory on sire breeding values. The mean estimate of the covariance between the intercept and slope components was positive in absolute direction (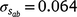 ), but included some negative values, with a 95% HPD confidence interval between −0.074 and 0.22 (Fig. 3). The correlation was positive and moderately high (rab = 0.541), suggesting that sires favoured at the intercept tended to retain their ranking as the CI increased. The posterior distribution for the total maternal component was normal (Fig. 3) and with a comparatively large mean estimate (
), but included some negative values, with a 95% HPD confidence interval between −0.074 and 0.22 (Fig. 3). The correlation was positive and moderately high (rab = 0.541), suggesting that sires favoured at the intercept tended to retain their ranking as the CI increased. The posterior distribution for the total maternal component was normal (Fig. 3) and with a comparatively large mean estimate (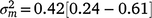 ). An estimate of the dam permanent environmental variance ratio (
). An estimate of the dam permanent environmental variance ratio (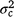 ) was derived (
) was derived (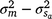 ) as 0.30, which was thus the largest random variance component affecting M3 after excluding the residual variance (
) as 0.30, which was thus the largest random variance component affecting M3 after excluding the residual variance (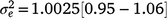 ).
).
|
|
Heritability of M3 across the cold-stress trajectory
The magnitude of the h2 of M3 varied considerably according to the intensity of cold stress during the neonatal period (Fig. 4). Surrounding the environment of the mean (~960 KJ m−2 h−1) or that of the intercept (1025 KJ m−2 h−1), h2 (mean ±PSD) was moderately low (h2 = 0.13 ± 0.10 to 0.15 ± 0.11). Following an increasing gradient of CI, absolute h2 accordingly increased markedly with the intensity of cold stress. At ~1100 KJ m−2 h−1, absolute h2 was moderate (0.22 ± 0.16), but tended towards values as high as 0.40 at levels of extreme cold stress where the CI was 1150 KJ m−2 h−1 or larger. Along with the marked changes in absolute h2, it was clear that the reliability of h2 estimates also continuously decreased for estimates extending further away from the mean, with the largest PSD being observed at either end of the environmental trajectory. Following the curvilinear trend of the resulting parabola, a slight increase in absolute h2 was also observed for lower values of the CI gradient, an estimate of 0.22 ± 0.17 when CI was ~850 KJ m−2 h−1. The wide PSD margins are arguably a function of the small data set and complicate comparisons among h2 estimates.
Individual-sire reaction norms
Sire RNs suggested a highly variable ES across sire genotypes (Fig. 5). With an increasing cold stress, there was more discrimination across sire breeding values, especially when the CI exceeded ~1000 KJ m−2 h−1. Some evidence of re-ranking was also visible at CI gradients between 850 and 900 KJ m−2 h−1, but in these cases sire RNs tended to intersect below the environment of the intercept of ~1025 KJ m−2 h−1. This is also expected from the positive correlation (0.54) between the intercept and slope components, which suggested that sires tended to maintain their ranking at the intercept across increasing values of the CI trajectory.
From a separate analysis where selection line was excluded as fixed effect, the patterns of RN generally resembled the same patterns as for Fig. 5, but the RNs of H-Line sires were generally associated with favourable rankings predicting a greater resistance to mortality as cold stress progressively increased (Fig. 6). It was also clear that the scale separating the RNs was influenced by the removal of the selection line fixed effect, with considerably larger differences between sire RNs in Fig. 6 than in Fig. 5. Similar to Fig. 5, sire reaction norms tended to intersect below ~900 KJ m−2 h−1, but any evidence of re-ranking would apply only to very low values of CI not rigorously tested in this dataset.
Individual intercept and slope components of H- and L-Line sires can be seen in Fig. 7, which shows that the selection line solutions trend in favour of the H-Line sires from the year 1994 onward. The coefficients of the linear regressions fit within line for both intercept and slope components of sire RNs were significant (P < 0.01) as the H-Line trended downward for the intercept (−0.0046 ± 0.0008) and slope (−0.0024 ± 0.0005) components. These trends were divergent (P < 0.01) from L-Line trends that were upward for the corresponding intercept (0.0047 ± 0.0008) and slope (0.0028 ± 0.0006) components (Fig. 7).
|
|
Discussion
Genetic parameters for neonatal lamb mortality according to the RN model
This study has shown that a G × E component could play an important role in the genetic basis for neonatal mortality. The magnitude of the 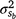 component and the variable h2 (Fig. 4) suggested that genetic merit of M3 depended considerably on the environment during the first days after birth. To our knowledge, this is the first study to model the genetic merit of neonatal mortality (or survival) as a function of cold exposure, and no directly comparable results were found in the literature. The influence of fixed effects in the Elsenburg Merino dataset has been discussed elsewhere (Nel et al. 2021a, 2021b; Nel 2022) and are not repeated here. Instead, only genetic parameters will be highlighted, with the additional treatment of the H- and L-Lines.
component and the variable h2 (Fig. 4) suggested that genetic merit of M3 depended considerably on the environment during the first days after birth. To our knowledge, this is the first study to model the genetic merit of neonatal mortality (or survival) as a function of cold exposure, and no directly comparable results were found in the literature. The influence of fixed effects in the Elsenburg Merino dataset has been discussed elsewhere (Nel et al. 2021a, 2021b; Nel 2022) and are not repeated here. Instead, only genetic parameters will be highlighted, with the additional treatment of the H- and L-Lines.
Estimates of h2 at the intercept (h2 ~ 0.13–0.15) could be considered high compared with the very low values common for lamb survival/mortality traits (see review Brien et al. 2014), but the differences in data and approach of analysis complicate direct comparisons. First of all, the intercept point on the environmental trajectory (~1025 KJ m−2 h−1 in the current study) is sensitive to the distribution of CI in a particular dataset. Currently, it was also slightly higher than the arithmetic mean (~960 KJ m−2 h−1) and arguably represents a significant level of cold stress. An interpretation of the intercept component (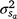 ) as an estimate directly comparable to the ‘average environment’ assumed by standard genetic analysis is thus not entirely appropriate.
) as an estimate directly comparable to the ‘average environment’ assumed by standard genetic analysis is thus not entirely appropriate.
Furthermore, the magnitude of variance components also tends to vary according to the framework used for the analysis of binary survival/mortality phenotypes. A very low h2 of 0.03 ± 0.01 (±standard error, or s.e.) for perinatal survival (up to 3 days of age, but also including survival at birth) was derived from the animal model from the same flock, but reported on the observed scale from linear model analyses (Nel et al. 2021a). Other estimates derived for Merinos by linear models yielded similarly low h2-values of 0.04 (Brien et al. 2009b) for survival up to 3 days of age and 0.02 (Hatcher et al. 2010) for survival up to 7 days of age. However, on the underlying scale, Cloete et al. (2009) reported a h2 (±s.e.) of 0.12 ± 0.06 for lamb survival from birth to tail docking (~3–4 weeks), and 0.39 ± 0.23 for tail docking to weaning from the same dataset (only including records up to 2007). A h2 estimate of 0.11 was also reported for total survival (to weaning) from a threshold analysis by Welsh et al. (2006). Accordingly, Matos et al. (2000) reported that the threshold model h2 of total survival was about three-fold the magnitude of that derived by linear models in the same study. In other species, Weller et al. (1988) reported h2 estimates for calf mortality from sire threshold models (0.084) also between three- and four-fold of that derived by linear analysis (0.027). A pattern of differences in h2 is thus visible across analyses, but is expected given the loss of information when treating binary traits on the observed scale.
Regardless of the approach in analysing survival/mortality datasets, the low h2 of survival traits have led to the suggestion that genetic selection for improved outcomes would not be worth-while (Everett-Hincks et al. 2005; Everett-Hincks and Cullen 2009). However, it stands to reason that a variable h2 as observed in Fig. 4 is plausible when a phenotype is directly linked to an environmental covariate such as mortality and cold stress. In addition to the current results (Fig. 2), the moderate to severe impact of cold exposure on early lamb mortality has been well documented (Alexander 1962; Obst and Day 1968; Alexander et al. 1980; Mccutcheon et al. 1981), including studies that quantified cold stress by the same or a similar chill index (Donnelly 1984; Gudex et al. 2005; Oldham et al. 2011; Geenty et al. 2014). A base level of mortality can always be expected (Alexander 1984). In some cases, the genetic make-up of the lamb will have little to no influence (e.g. misadventure) on mortality outcome, and the phenotypes will be of little value as indicators of stress resilience. In turn, if M3 is recorded during events characterised by significant levels of cold stress (e.g. 950–1000 KJ m−2 h−1 or higher), these phenotypes arguably reflect an ability to cope with the stress variable. Assuming that this resilience is significantly influenced by genetic variation, it is plausible to expect an increase in h2 (Fig. 4), as well as an increased scope to discriminate between sires (Fig. 5) in higher cold-stress conditions. The contention for such genetic components is supported by considering that cold-stress resistance is affected by sire lines (Gudex et al. 2005) as well as short-term (4 year) selection experiments (Slee and Stott 1986). The few estimates of the h2 of cold-stress resistance were estimated with a suboptimal accuracy and from outdated parent–offspring regression methods, but has been reported as moderate (0.44 ± 0.18; Wolff et al. 1987) to high (0.52 ± 0.23; Slee et al. 1991) after also adjusting for BW.
A high dependence of genetic parameters on the environmental trajectory has important implications for traditional selection programs where the weighted merit of performance in mild and stressful environments is considered equal. This describes the general issue of G × E, which reduces the response to selection when breeding programs do not account for such effects (Mulder and Bijma 2005).
The increase in h2 estimates suggested that greater genetic gains are possible if selection is focused on cases of survival/mortality known to be recorded in stressful environments. Fig. 4 delivers the first formal presentation of the much earlier suggestion by Haughey (1991) that selection targets genotypes ‘born during, and surviving severe weather conditions’. However, the h2 estimates at the ends of the trajectory could be judged unrealistic also from the perspective of the underlying scale. The limitation of only few data points outside of ~850–1200 KJ m−2 h−1 (Fig. 1) is also clearly reflected by the higher PSD of h2 (Fig. 4). Even in large or uniformly distributed datasets, the reliability of Legendre polynomials has been a concern when approaching the extremes of the trajectory in random regression analysis (Van Der Werf et al. 1998; Meyer 2001; Fischer et al. 2004), and should be treated with caution beyond the bulk of the data.
The evidence for re-ranking of genotypes (Figs 5, 6) and the apparent increase in h2 at low levels of CI (Fig. 4) also deserves some comment. This was an interesting observation, but most likely a mathematical consequence of considering only first-order Legendre polynomials. With only limited flexibility to model breeding values over the entire range of the cold-stress trajectory, the resulting parabola would inevitably be symmetrical around the vertex (~950 KJ m−2 h−1), which would explain the slight increase in h2 below 900 KJ m−2 h−1 (Fig. 4). Since there were few records with CI < 850 KJ m−2 h−1, this is thus likely to be an artefact of the model reflecting the increase in h2 at high CI, rather than a genuine result when CI is low. Higher-order models could improve on these results, but we maintain that the restriction to linear RNs was a worth-while trade-off for the benefit of simplicity when analysing a binary trait of low incidence.
It would be of interest to revisit this issue on a larger dataset recorded across a wider range of climatic variables. At values of CI of <850 KJ m−2 h−1, the environment could be approaching a temperature gradient that is too low for animals to dissipate heat at a favourable rate, i.e. resulting in heat stress. If the merit of cold-stress resistance can be supported from future studies, a critical question would be whether the same ‘cold-resistant’ animals are able to cope well with hot and humid weather. Different breeding programs would be needed if the genetic correlation among points along the environmental descriptor is low, and especially when it is negative (Mulder et al. 2006). From this perspective, it is essential to consider that the genetic improvement of M3 depends not only on where the h2 is highest (e.g. 1000–1100 KJ m−2 h−1), but also on the environment where the progeny will be tested (Kolmodin and Bijma 2004), and it is certain that a much wider CI range is possible if a dataset were to include different areas and seasons. For example, at the Tygerhoek site that made use of an autumn lambing season, lambs were sometimes born when CI was ~780 KJ m−2 h−1 or lower (data not shown). At this level, the mean temperature over 24 h reached 22°C and the maximum temperatures regularly reached 28°C or higher. Excluding the effect of wind or rainfall, this range of CI could putatively have represented a degree of heat stress, since the upper critical range for adult sheep is roughly between 25°C and 32°C (Hahn 1985). However, the effects of high cold exposure are likely to be the biggest constraint to lamb production in an extensive winter lambing season in the H- and L-Lines, suggesting that G × E components could be exploited to improve fitness in a winter-lambing season when CI-values are within the cold-stress range.
Genetic gains in the Elsenburg selection lines
Cold-stress adaption was likely a key mechanism contributing to the favourable outcome of the Elsenburg selection experiment. Theoretically, the RN approach delivers an opportunity to improve ‘overall’ performance by selecting for an increased performance in the average environment (i.e. the intercept), instead of selecting for genes that are beneficial only in selected environments (i.e. the slope; de Jong and Bijma 2002). However, in the current dataset, the average environment presented at least some level of cold-stress challenge, and it is thus reasonable to assume that adaption to these circumstances would have played a role in the divergent selection responses separating the H- and L-Lines (Fig. 7).
The resulting differences in H- and L-Line RN slopes (Fig. 7) supported previous contentions that a positive correlation between the intercept and slope can lead to favourably exploiting ES when selecting for performance at the intercept (Kolmodin et al. 2003; Knap and Su 2008). G × E scenarios where genotypes intersect or cross to the left of the intercept (Figs 5, 6), are beneficial if exploiting G × E is the objective, since favourable changes in the slope are reflected in the same direction at the intercept (see figs 3, 4 of Falconer (1990)). This was supported by the positive and moderately high correlation (rab = 0.54) between intercept and slope components, although this estimate did not differ from zero with this specific dataset. A more reliable estimate of genetic correlation is needed from larger datasets, but the argument is well supported on the phenotypic level, showing H-Line lambs to be better at maintaining homeothermy under cold-stress conditions (Nel et al. 2021b). Also, a selection history that successfully exploited G × E components offers at least a partial explanation for the rate of genetic gain (Cloete et al. 2009; Nel et al. 2021a) exceeding expectation for survival traits (Fogarty et al. 2006; Brien et al. 2009a). The mean performance of H-Line lambs, also clear on the phenotypic level (Nel et al. 2021a, 2021b), could thus have benefited from the higher h2 observed for the upper levels of the CI (Fig. 4). However, considering the RNs of H-Line genotypes as favourable to robustness depends on the assumption that the next generation will be tested within generally similar environmental conditions present during selection of previous generations. More elaborate studies are thus needed, and some suggestions are outlined below.
Future perspectives
The understanding of the G × E components of neonatal mortality would benefit from studies across environments with a larger window of climatic variation. Highly variable environments are a realistic concern in South Africa where sheep production is spatially dispersed over regions with vastly variable climates and marked differences in available resources (Cloete and Olivier 2010; Cloete et al. 2014). More comprehensive studies are important, since the results reported here are relevant to the growing interest in selecting animals more resilient to the extreme environments anticipated from climate change (Hayes et al. 2013; Misztal 2017; Berghof et al. 2019).
Linking cold stress to mortality up to 3 days of age, but excluding birth, has also recently been supported by Horton et al. (2019). Since climate data are commonly available, large-scale studies linking climatic stress to neonatal lamb performance (e.g. M3) is possible wherever time of death was recorded reasonably close to weather stations. This approach is also attractive because a reliable and independent covariable circumvents some of the issues of environmental trajectories based on contemporary group means (Strandberg 2006). Good examples of the large-scale implementation of such a system were evident in genetic analyses of heat-stress sensitivity in dairy cattle (e.g. Ravagnolo and Misztal 2000, 2002; Bohmanova et al. 2008; Cheruiyot et al. 2020).
Improvements on the recording program are also possible. A better phenotyping protocol was proposed by Gudex et al. (2005) that eliminates obvious causes of death not typified by an aetiology indicative of starvation–mismothering-exposure. A variation of the survival phenotyping protocol outlined by Vanderick et al. (2015) could also be useful. Also, if records from an autumn or early summer lambing season were to be included, the use of the current equation for CI (Nixon-Smith 1972) is not the ideal descriptor of heat stress. In contrast, the temperature–humidity index (Ravagnolo and Misztal 2000) commonly used to model heat stress does not account for the cooling influence of wind or rainfall. An appropriate bilateral stress index is needed to investigate the hypothesised antagonism between climatic extremes. Last, additional recording of phenotypes indicating animal wellbeing (see review Brito et al. 2020) will be more expensive than are survival records, but could deliver multiple benefits, including the following: they will be more articulate in indicating resilience; will be simpler to analyse than is M3 (which is binary and of low incidence); and could benefit from the gains in accuracy of including genomic information (Mulder 2016). For example, rectal temperature has been used in field studies of cold-stress resistance (Sykes et al. 1976; Nel et al. 2021b), and can be easily adopted into the lambing rounds, which is standard protocol for breeding flocks that maintain a pedigree (Brien et al. 2010).
Conclusions
This study was the first to show that a G × E interaction with cold exposure plays an important role in determining genetic merit for neonatal mortality. The findings support previous notions that G × E is generally largest in fitness traits, which partially explains the low h2 of such traits recorded across variable environments. Comparing the RNs of selection lines showed that divergent selection for a correlated trait (number of lambs weaned per ewe mated) resulted in worth-while gains in fitness as described by the G × E model fitted. However, this positive result is likely to be linked to perpetual selection of the same population within a relatively stable environmental descriptor. Better gains could be possible if the environment at recording could be quantified and accounted for in genetic evaluation. Re-ranking of genotypes suggests that genetic adaption to cold stress could be detrimental to animal resilience in hot environments, but research across a wider environmental trajectory is needed to confirm or refute this notion.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
The authors have no conflicts of interest to declare.
Declaration of funding
Financial support for this study hinged on contributions by various external funders, including the South African Wool Industry (Cape Wools SA), the Western Cape Agricultural Research Trust (WCART) and the Technology and Human Resources for Industry Program (THRIP) of the South African National Research Foundation (NRF).
References
Alexander G (1962) Temperature regulation in the new-born lamb. IV. The effect of wind and evaporation of water from the coat on metabolic rate and body temperature. Australian Journal of Agricultural Research 13, 82–99.| Temperature regulation in the new-born lamb. IV. The effect of wind and evaporation of water from the coat on metabolic rate and body temperature.Crossref | GoogleScholarGoogle Scholar |
Alexander G (1984) Constraints to lamb survival. In ‘Reproduction in sheep’. (Eds D Lindsay, D Pearce) pp. 199–209. (Australian Academy of Science and the Australian Wool Corportation: Melbourne, Vic., Australia)
Alexander G, Lynch JJ, Mottershead BE, Donnelly JB (1980) Reduction in lamb mortality by means of grass wind-breaks: results of a five-year study. Proceedings of the Australian Society of Animal Production 13, 329–331.
Berghof TVL, Poppe M, Mulder HA (2019) Opportunities to improve resilience in animal breeding programs. Frontiers in Genetics 9, 692
| Opportunities to improve resilience in animal breeding programs.Crossref | GoogleScholarGoogle Scholar |
Bohmanova J, Misztal I, Tsuruta S, Norman HD, Lawlor TJ (2008) Short Communication: Genotype by environment interaction due to heat stress. Journal of Dairy Science 91, 840–846.
| Short Communication: Genotype by environment interaction due to heat stress.Crossref | GoogleScholarGoogle Scholar |
Brien FD, Hebart ML, Hocking Edwards JE, Greeff JC, Hart KW, Refshauge G, Gaunt G, Behrendt R, Thomson K, Hinch G, Geenty KG, Van Der Werf JHJ (2009a) Genetics of lamb survival: preliminary studies of the information nucleus flock. Proceedings of the Association for the Advancement in Animal Breeding and Genetics 18, 108–111.
Brien FD, Hebart ML, Jaensch KS, Smith DH, Grimson RJ (2009b) Genetics of lamb survival: a study of Merino resource flocks in Australia. Proceedings of the Association for the Advancement in Animal Breeding and Genetics 18, 492–495.
Brien FD, Hebart ML, Smith DH, Edwards JEH, Greeff JC, Hart KW, Refshauge G, Bird-Gardiner TL, Gaunt G, Behrendt R, Robertson MW, Hinch GN, Geenty KG, Van Der Werf JHJ (2010) Opportunities for genetic improvement of lamb survival. Animal Production Science 50, 1017–1025.
| Opportunities for genetic improvement of lamb survival.Crossref | GoogleScholarGoogle Scholar |
Brien FD, Cloete SWP, Fogarty NM, Greeff JC, Hebart ML, Hiendleder S, Edwards JEH, Kelly JM, Kind KL, Kleemann DO, Plush KL, Miller DR (2014) A review of the genetic and epigenetic factors affecting lamb survival. Animal Production Science 54, 667–693.
| A review of the genetic and epigenetic factors affecting lamb survival.Crossref | GoogleScholarGoogle Scholar |
Brito LF, Oliveira HR, McConn BR, Schinckel AP, Arrazola A, Marchant-Forde JN, Johnson JS (2020) Large-scale phenotyping of livestock welfare in commercial production systems: a new frontier in animal breeding. Frontiers in Genetics 11, 793
| Large-scale phenotyping of livestock welfare in commercial production systems: a new frontier in animal breeding.Crossref | GoogleScholarGoogle Scholar |
Brügemann K, Gernand E, von Borstel UU, König S (2013) Application of random regression models to infer the genetic background and phenotypic trajectory of binary conception rate by alterations of temperature × humidity indices. Livestock Science 157, 389–396.
| Application of random regression models to infer the genetic background and phenotypic trajectory of binary conception rate by alterations of temperature × humidity indices.Crossref | GoogleScholarGoogle Scholar |
Cheruiyot EK, Nguyen TTT, Haile-Mariam M, Cocks BG, Abdelsayed M, Pryce JE (2020) Genotype-by-environment (temperature-humidity) interaction of milk production traits in Australian Holstein cattle. Journal of Dairy Science 103, 2460–2476.
| Genotype-by-environment (temperature-humidity) interaction of milk production traits in Australian Holstein cattle.Crossref | GoogleScholarGoogle Scholar |
Cloete SWP, Olivier JJ (2010) South African sheep and wool industries. In ‘The International sheep and wool handbook’. (Ed. DJ Cottle) pp. 95–112. (Nottingham University Press: Manor Farm, Thrumpton, Nottingham, UK)
Cloete SWP, Scholtz AJ (1998) Lamb survival in relation to lambing and neonatal behaviour in medium wool Merino lines divergently selected for multiple rearing ability. Australian Journal of Experimental Agriculture 38, 801–811.
| Lamb survival in relation to lambing and neonatal behaviour in medium wool Merino lines divergently selected for multiple rearing ability.Crossref | GoogleScholarGoogle Scholar |
Cloete SWP, Scholtz AJ, Aucamp BB (1998) Environmental effects, heritability estimates and genetic trends in a Western Cape Dohne Merino nucleus flock. South African Journal of Animal Science 28, 185–195.
Cloete SWP, Gilmour AR, Olivier JJ, van Wyk JB (2004) Genetic and phenotypic trends and parameters in reproduction, greasy fleece weight and liveweight in Merino lines divergently selected for multiple rearing ability. Australian Journal of Experimental Agriculture 44, 745–754.
| Genetic and phenotypic trends and parameters in reproduction, greasy fleece weight and liveweight in Merino lines divergently selected for multiple rearing ability.Crossref | GoogleScholarGoogle Scholar |
Cloete SWP, Misztal I, Olivier JJ (2009) Genetic parameters and trends for lamb survival and birth weight in a Merino flock divergently selected for multiple rearing ability. Journal of Animal Science 87, 2196–2208.
| Genetic parameters and trends for lamb survival and birth weight in a Merino flock divergently selected for multiple rearing ability.Crossref | GoogleScholarGoogle Scholar |
Cloete SWP, Olivier JJ, Sandenbergh L, Snyman MA (2014) The adaption of the South Africa sheep industry to new trends in animal breeding and genetics: a review. South African Journal of Animal Science 44, 307–321.
| The adaption of the South Africa sheep industry to new trends in animal breeding and genetics: a review.Crossref | GoogleScholarGoogle Scholar |
de Jong G (1995) Phenotypic plasticity as a product of selection in a variable environment. The American Naturalist 145, 493–512.
| Phenotypic plasticity as a product of selection in a variable environment.Crossref | GoogleScholarGoogle Scholar |
de Jong G, Bijma P (2002) Selection and phenotypic plasticity in evolutionary biology and animal breeding. Livestock Production Science 78, 195–214.
| Selection and phenotypic plasticity in evolutionary biology and animal breeding.Crossref | GoogleScholarGoogle Scholar |
Dominik S, McWilliams S (2014) Gene by environment interaction for reproduction traits in Australian sheep. Final Report. Meat & Livestock Australia, Sydney, NSW, Australia.
Donnelly JR (1984) The productivity of breeding ewes grazing on lucerne or grass and clover pastures on the tablelands of southern Australia. III. Lamb mortality and weaning percentage. Australian Journal of Agricultural Research 35, 709–721.
| The productivity of breeding ewes grazing on lucerne or grass and clover pastures on the tablelands of southern Australia. III. Lamb mortality and weaning percentage.Crossref | GoogleScholarGoogle Scholar |
Dwyer CM, Morgan CA (2006) Maintenance of body temperature in the neonatal lamb: effects of breed, birth weight, and litter size. Journal of Animal Science 84, 1093–1101.
| Maintenance of body temperature in the neonatal lamb: effects of breed, birth weight, and litter size.Crossref | GoogleScholarGoogle Scholar |
Everett-Hincks JM, Cullen NG (2009) Genetic parameters for ewe rearing performance. Journal of Animal Science 87, 2753–2758.
| Genetic parameters for ewe rearing performance.Crossref | GoogleScholarGoogle Scholar |
Everett-Hincks JM, Lopez-Villalobos N, Blair HT, Stafford KJ (2005) The effect of ewe maternal behaviour score on lamb and litter survival. Livestock Production Science 93, 51–61.
| The effect of ewe maternal behaviour score on lamb and litter survival.Crossref | GoogleScholarGoogle Scholar |
Everett-Hincks JM, Mathias-Davis HC, Greer GJ, Auvray BA, Dodds KG (2014) Genetic parameters for lamb birth weight, survival and death risk traits. Journal of Animal Science 92, 2885–2895.
| Genetic parameters for lamb birth weight, survival and death risk traits.Crossref | GoogleScholarGoogle Scholar |
Falconer DS (1989) ‘Introduction to quantitative genetics.’ (Longmans Green: Harlow, Essex, UK/John Wiley & Sons: New York, NY, USA)
Falconer DS (1990) Selection in different environments: effects on environmental sensitivity (reaction norm) and on mean performance. Genetical Research 56, 57–70.
| Selection in different environments: effects on environmental sensitivity (reaction norm) and on mean performance.Crossref | GoogleScholarGoogle Scholar |
Falconer DS, Mackay TFC (1996) ‘Introduction to quantitative genetics.’ (Longman Group: Harlow, Essex, UK)
Fischer TM, Van der Werf JHJ, Banks RG, Ball AJ (2004) Description of lamb growth using random regression on field data. Livestock Production Science 89, 175–185.
| Description of lamb growth using random regression on field data.Crossref | GoogleScholarGoogle Scholar |
Fogarty NM, Safari E, Gilmour AR, Ingham VM, Atkins KD, Mortimer SI, Swan AA, Brien FD, Greeff JC, van der Werf JHJ (2006) Wool and meat genetics – the joint possibilities. International Journal of Sheep and Wool Science 54, 22–27.
Geenty KG, Brien FD, Hinch GN, Dobos RC, Refshauge G, McCaskill M, Ball AJ, Behrendt R, Gore KP, Savage DB, Harden S, Hocking-Edwards JE, Hart K, van der Werf JHJ (2014) Reproductive performance in the Sheep CRC Information Nucleus using artificial insemination across different sheep-production environments in southern Australia. Animal Production Science 54, 715–726.
| Reproductive performance in the Sheep CRC Information Nucleus using artificial insemination across different sheep-production environments in southern Australia.Crossref | GoogleScholarGoogle Scholar |
Gilmour AR, Gogel BJ, Welham SJ (2015) ASReml user guide release 4.1 structural specification. Available at www.vsni.co.uk
Gudex BW, Hickford JGH, Frampton CM (2005) Sire-line differences in lamb losses from starvation-exposure. Proceedings of the New Zealand Society of Animal Production 65, 186–190.
Hahn GL (1985) Management and housing of farm animals in hot environments. In ‘Stress physiology in livestock. Vol. II. Ungulates’. (Ed. MK Yousef) pp. 151–174. (CRC Press, Inc.: Boca Raton, FL, USA)
Haile-Mariam M, Carrick MJ, Goddard ME (2008) Genotype by environment interaction for fertility, survival, and milk production traits in Australian dairy cattle. Journal of Dairy Science 91, 4840–4853.
| Genotype by environment interaction for fertility, survival, and milk production traits in Australian dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Hatcher S, Atkins KD, Safari E (2009) Phenotypic aspects of lamb survival in Australian Merino sheep. Journal of Animal Science 87, 2781–2790.
| Phenotypic aspects of lamb survival in Australian Merino sheep.Crossref | GoogleScholarGoogle Scholar |
Hatcher S, Atkins KD, Safari E (2010) Lamb survival in Australian Merino sheep: a genetic analysis. Journal of Animal Science 88, 3198–3205.
| Lamb survival in Australian Merino sheep: a genetic analysis.Crossref | GoogleScholarGoogle Scholar |
Haughey KG (1991) Perinatal lamb mortality – its investigation, causes and control. Journal of the South African Veterinary Association 62, 78–91.
| Perinatal lamb mortality – its investigation, causes and control.Crossref | GoogleScholarGoogle Scholar |
Hayes BJ, Lewin HA, Goddard ME (2013) The future of livestock breeding: genomic selection for efficiency, reduced emissions intensity, and adaptation. Trends in Genetics 29, 206–214.
| The future of livestock breeding: genomic selection for efficiency, reduced emissions intensity, and adaptation.Crossref | GoogleScholarGoogle Scholar |
Hinch GN, Brien F (2014) Lamb survival in Australian flocks: a review. Animal Production Science 54, 656–666.
| Lamb survival in Australian flocks: a review.Crossref | GoogleScholarGoogle Scholar |
Horton BJ, Corkrey R, Doughty AK, Hinch GN (2019) Estimation of lamb deaths within 5 days of birth associated with cold weather. Animal Production Science 59, 1720–1726.
| Estimation of lamb deaths within 5 days of birth associated with cold weather.Crossref | GoogleScholarGoogle Scholar |
Knap PW (2005) Breeding robust pigs. Australian Journal of Experimental Agriculture 45, 763–773.
| Breeding robust pigs.Crossref | GoogleScholarGoogle Scholar |
Knap PW, Su G (2008) Genotype by environment interaction for litter size in pigs as quantified by reaction norms analysis. Animal 2, 1742–1747.
| Genotype by environment interaction for litter size in pigs as quantified by reaction norms analysis.Crossref | GoogleScholarGoogle Scholar |
Kolmodin R, Bijma P (2004) Response to mass selection when the genotype by environment interaction is modelled as a linear reaction norm. Genetics Selection Evolution 36, 435–454.
| Response to mass selection when the genotype by environment interaction is modelled as a linear reaction norm.Crossref | GoogleScholarGoogle Scholar |
Kolmodin R, Strandberg E, Jorjani H, Danell B (2003) Selection in the presence of a genotype by environment interaction: response in environmental sensitivity. Animal Science 76, 375–385.
| Selection in the presence of a genotype by environment interaction: response in environmental sensitivity.Crossref | GoogleScholarGoogle Scholar |
Lopez-villalobos N, Garrick DJ (1999) Genetic parameter estimates for lamb survival in Romney sheep. Proceedings of the New Zealand Society of Animal Production 59, 121–124.
Matos CAP, Thomas DL, Young LD, Gianola D (2000) Genetic analyses of lamb survival in Rambouillet and Finnsheep flocks by linear and threshold models. Animal Science 71, 227–234.
| Genetic analyses of lamb survival in Rambouillet and Finnsheep flocks by linear and threshold models.Crossref | GoogleScholarGoogle Scholar |
Mccutcheon SN, Holmes CW, Mcdonald MF (1981) The starvation-exposure syndrome and neonatal lamb mortality. A review. Proceedings of the New Zealand Society of Animal Production 41, 209–217.
Meyer K (2001) Estimating genetic covariance functions assuming a parametric correlation structure for environmental effects. Genetics Selection Evolution 33, 557–585.
| Estimating genetic covariance functions assuming a parametric correlation structure for environmental effects.Crossref | GoogleScholarGoogle Scholar |
Misztal I (2017) Breeding and Genetics Symposium: resilience and lessons from studies in genetics of heat stress. Journal of Animal Science 95, 1780–1787.
| Breeding and Genetics Symposium: resilience and lessons from studies in genetics of heat stress.Crossref | GoogleScholarGoogle Scholar |
Misztal I, Tsuruta S, Lourenco D, Masuda Y, Aguilar I, Legarra A, Vitezica Z (2014) Manual for BLUPF90 family of programs. Available at http://nce.ads.uga.edu/wiki/lib/exe/fetch.php?media=blupf90_all7.pdf
Morris CA, Hickey SM, Clarke JN (2000) Genetic and environmental factors affecting lamb survival at birth and through to weaning. New Zealand Journal of Agricultural Research 43, 515–524.
| Genetic and environmental factors affecting lamb survival at birth and through to weaning.Crossref | GoogleScholarGoogle Scholar |
Mulder HA (2016) Genomic selection improves response to selection in resilience by exploiting genotype by environment interactions. Frontiers in Genetics 7, 178
| Genomic selection improves response to selection in resilience by exploiting genotype by environment interactions.Crossref | GoogleScholarGoogle Scholar |
Mulder HA, Bijma P (2005) Effects of genotype x environment interaction on genetic gain in breeding programs. Journal of Animal Science 83, 49–61.
| Effects of genotype x environment interaction on genetic gain in breeding programs.Crossref | GoogleScholarGoogle Scholar |
Mulder HA, Veerkamp RF, Ducro BJ, van Arendonk JAM, Bijma P (2006) Optimization of dairy cattle breeding programs for different environments with genotype by environment interaction. Journal of Dairy Science 89, 1740–1752.
| Optimization of dairy cattle breeding programs for different environments with genotype by environment interaction.Crossref | GoogleScholarGoogle Scholar |
Nel CL (2022) Studies on genetic responses and genomic characterisation in South African and Australian sheep. PhD thesis, University of Stellenbosch, Stellenbosch, South Africa.
Nel CL, Swan AA, Dzama K, Scholtz AJ, Cloete SWP (2021a) Genetic parameters and trends for lamb survival following long-term divergent selection for number of lambs weaned in the Elsenburg Merino flock. Animal Production Science 61, 1965–1981.
| Genetic parameters and trends for lamb survival following long-term divergent selection for number of lambs weaned in the Elsenburg Merino flock.Crossref | GoogleScholarGoogle Scholar |
Nel CL, Cloete SWP, Kruger ACM, Dzama K (2021b) Long term genetic selection for reproductive success affects neonatal lamb vitality across cold stress conditions. Journal of Thermal Biology 98, 102908
| Long term genetic selection for reproductive success affects neonatal lamb vitality across cold stress conditions.Crossref | GoogleScholarGoogle Scholar |
Nixon-Smith WF (1972) ‘The forecasting of chill risk ratings for new born lambs and off-shears sheep by the use of a cooling factor derived from synoptic data.’ Working Paper No. 150. (Bureau of Meteorology: Canberra, ACT, Australia)
Obst JM, Day HR (1968) The effect of inclement weather on mortality of Merino and Corriedale lambs on kangaroo island. Proceedings of the Australian Society of Animal Production 7, 239–242.
Oldham CM, Thompson AN, Ferguson MB, Gordon DJ, Kearney GA, Paganoni BL (2011) The birthweight and survival of Merino lambs can be predicted from the profile of liveweight change of their mothers during pregnancy. Animal Production Science 51, 776–783.
| The birthweight and survival of Merino lambs can be predicted from the profile of liveweight change of their mothers during pregnancy.Crossref | GoogleScholarGoogle Scholar |
Plush KJ, Brien FD, Hebart ML, Hynd PI (2016) Thermogenesis and physiological maturity in neonatal lambs: a unifying concept in lamb survival. Animal Production Science 56, 736–745.
| Thermogenesis and physiological maturity in neonatal lambs: a unifying concept in lamb survival.Crossref | GoogleScholarGoogle Scholar |
Ravagnolo O, Misztal I (2000) Genetic component of heat stress in dairy cattle, parameter estimation. Journal of Dairy Science 83, 2126–2130.
| Genetic component of heat stress in dairy cattle, parameter estimation.Crossref | GoogleScholarGoogle Scholar |
Ravagnolo O, Misztal I (2002) Effect of heat stress on nonreturn rate in holstein cows: genetic analyses. Journal of Dairy Science 85, 3092–3100.
| Effect of heat stress on nonreturn rate in holstein cows: genetic analyses.Crossref | GoogleScholarGoogle Scholar |
Riggio V, Finocchiaro R, Bishop SC (2008) Genetic parameters for early lamb survival and growth in Scottish Blackface sheep. Journal of Animal Science 86, 1758–1764.
| Genetic parameters for early lamb survival and growth in Scottish Blackface sheep.Crossref | GoogleScholarGoogle Scholar |
Sawalha RM, Conington J, Brotherstone S, Villanueva B (2007) Analyses of lamb survival of Scottish Blackface sheep. Animal 1, 151–157.
| Analyses of lamb survival of Scottish Blackface sheep.Crossref | GoogleScholarGoogle Scholar |
Slee J, Stott AW (1986) Genetic selection for cold resistance in Scottish Blackface lambs. Animal Production 43, 397–404.
| Genetic selection for cold resistance in Scottish Blackface lambs.Crossref | GoogleScholarGoogle Scholar |
Slee J, Alexander G, Bradley LR, Jackson N, Stevens D (1991) Genetic aspects of cold resistance and related characters in newborn Merino lambs. Australian Journal of Experimental Agriculture 31, 175–182.
| Genetic aspects of cold resistance and related characters in newborn Merino lambs.Crossref | GoogleScholarGoogle Scholar |
Strandberg E (2006) Analysis of genotype by environment interaction using random regression models. In ‘Proceedings of the 8th world congress on genetics applied to livestock production’. pp. 5–25.
Sykes AR, Griffiths RG, Slee J (1976) Influence of breed, birth weight and weather on the body temperature of newborn lambs. Animal Science 22, 395–402.
| Influence of breed, birth weight and weather on the body temperature of newborn lambs.Crossref | GoogleScholarGoogle Scholar |
Tsuruta S, Misztal I, Huang C, Lawlor TJ (2009) Bivariate analysis of conception rates and test-day milk yields in Holsteins using a threshold-linear model with random regressions. Journal of Dairy Science 92, 2922–2930.
| Bivariate analysis of conception rates and test-day milk yields in Holsteins using a threshold-linear model with random regressions.Crossref | GoogleScholarGoogle Scholar |
Vanderick S, Auvray B, Newman S-A, Dodds KG, Gengler N, Everett-Hincks JM (2015) Derivation of a new lamb survival trait for the New Zealand sheep industry. Journal of Animal Science 93, 3765–3772.
| Derivation of a new lamb survival trait for the New Zealand sheep industry.Crossref | GoogleScholarGoogle Scholar |
Veerkamp RF, Brotherstone S, Meuwissen THE (1998) Survival analysis using random regression models. Interbull Bulletin 21, 36–40.
Weller JI, Misztal I, Gianola D (1988) Genetic analysis of dystocia and calf mortality in Israeli-Holsteins by threshold and linear models. Journal of Dairy Science 71, 2491–2501.
| Genetic analysis of dystocia and calf mortality in Israeli-Holsteins by threshold and linear models.Crossref | GoogleScholarGoogle Scholar |
Welsh CS, Garrick DJ, Enns RM, Nicoll GB (2006) Threshold model analysis of lamb survivability in Romney sheep. New Zealand Journal of Agricultural Research 49, 411–418.
| Threshold model analysis of lamb survivability in Romney sheep.Crossref | GoogleScholarGoogle Scholar |
Wolff JE, Baker RL, Dobbie PM, Ford AJ, Jordan RB (1987) Genetic aspects of cold resistance in newborn lambs. Proceedings of the New Zealand Society of Animal Production 47, 93–98.
Van Der Werf JHJ, Goddard ME, Meyer K (1998) The use of covariance functions and random regressions for genetic evaluation of milk production based on test day records. Journal of Dairy Science 81, 3300–3308.
| The use of covariance functions and random regressions for genetic evaluation of milk production based on test day records.Crossref | GoogleScholarGoogle Scholar |


