On the value of adding commercial data into the reference population of the Angus SteerSELECT genomic tool
Antonio Reverter A * , Laercio Porto-Neto A , Brad C. Hine
A * , Laercio Porto-Neto A , Brad C. Hine  B , Pamela A. Alexandre A , Malshani Samaraweera C , Andrew I. Byrne C , Aaron B. Ingham A and Christian J. Duff
B , Pamela A. Alexandre A , Malshani Samaraweera C , Andrew I. Byrne C , Aaron B. Ingham A and Christian J. Duff  C
C
A CSIRO Agriculture and Food, Queensland Bioscience Precinct, 306 Carmody Road, St Lucia, Brisbane, Qld 4067, Australia.
B CSIRO Agriculture and Food, F.D. McMaster Laboratory, Chiswick, New England Highway, Armidale, NSW 2350, Australia.
C Angus Australia, 86 Glen Innes Road, Armidale, NSW 2350, Australia.
Animal Production Science 63(11) 947-956 https://doi.org/10.1071/AN22452
Submitted: 13 December 2022 Accepted: 20 February 2023 Published: 14 March 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Angus SteerSELECT is a genomic tool designed to provide genomic estimated breeding values (GEBV) for nine traits related to growth, feedlot performance, carcase characteristics and immune competence. At present, GEBV for carcase characteristics are based on a reference population of 3766 Australian Angus steers.
Aims: We aimed to investigate the potential benefit of incorporating commercial data into the existing reference population of the Angus SteerSELECT. To this aim, we employ a population of 2124 genotyped commercial Angus steers with carcase performance data from four commercial feedlot operators.
Methods: The benefit of incorporating the commercial data (COMM) into the reference (REFE) population was assessed in terms of quality and integrity of the COMM data and meta-data to model the phenotypes adequately. We computed bias, dispersion, and accuracy of GEBV for carcase weight (CWT) and marbling (MARB) before and after including the COMM data, in whole or in partial, into the REFE population.
Key results: The genomic estimate of the Angus content in the COMM population averaged 96.9% and ranged from 32.87% to 100%. For CWT, the estimates of heritability were 0.419 ± 0.026 and 0.368 ± 0.038 for the REFE and COMM populations respectively, and with a genetic correlation of 0.756 ± 0.068. For MARB, the same three parameter estimates were 0.357 ± 0.027, 0.340 ± 0.038 and 0.879 ± 0.073 respectively. The ACC of CWT GEBV increased significantly (P < 0.0001) from 0.475 when the COMM population was not part of the REFE to 0.546 (or 15%) when a random 50% of the COMM population was included in the REFE. Similarly significant increases in ACC were observed for MARB GEBV (0.470–0.521 or 11%).
Conclusions: The strong genomic relationship between the REFE and the COMM populations, coupled with the significant increases in GEBV accuracies, demonstrated the potential benefits of including the COMM population into the reference population of a future improved version of the Angus SteerSELECT genomic tool.
Implications: Commercial feedlot operators finishing animals with a strong Angus breed component will benefit from having their data represented in the reference population of the Angus SteerSELECT genomic tool.
Keywords: accuracy, beef cattle, bias, carcase, feedlot, genomic predictions, heritability, marbling.
Introduction
Genomic-based technologies are allowing commercial beef producers to predict the genetic merit of individual animals in their herds of unknown pedigree for the first time (Reverter et al. 2016; Hine et al. 2021; Alexandre et al. 2022). Angus SteerSELECT is a genomic-based tool that aims to predict the performance of Australian Angus steers during feedlot finishing, especifically in commercial Australian feedlots. It provides genomic predictions for a range of traits including growth, feed intake, carcase and immune competence. The ability of Angus SteerSELECT to predict differences in performance, in terms of carcase weight, marbling score, ossification score and carcase value, has been previously validated by Hine et al. (2021) by using a population of 522 short-fed (100 days) or long-fed (270 days) Angus steers finished in commercial feedlots.
Over the past decade, a great deal of effort has been devoted towards finding and understanding the factors influencing genomic prediction accuracy. These include the size of the reference population (Daetwyler et al. 2008; Goddard 2009; Habier et al. 2010), heritability of the trait (Goddard 2009; Daetwyler et al. 2010), relatedness between reference and validation population (de Roos et al. 2009; Wientjes et al. 2013), linkage disequilibrium (LD) between single-nucleotide polymorphism (SNP) markers and quantitative train loci (QTL; Habier et al. 2007; Wientjes et al. 2013), marker density (Meuwissen and Goddard 2010; Clark et al. 2011), number of QTL (Daetwyler et al. 2010; Clark et al. 2011), and minor allele frequencies of causative mutations and the SNP markers used in the predictions (Druet et al. 2014; Wientjes et al. 2015).
De los Campos et al. (2013) argued that the critical factor driving accuracy is the extent to which marker-based relationships properly describe the unobserved genetic relationships at trait loci. Hence, if the training and test data sets have related individuals, the markers can be good predictors even if the LD between markers and trait genes is weak (see also Wray et al. 2013).
From these findings, here we have focussed primarily on improving our understanding of the effect of the size of the reference population and its genomic relationship with the validation population, specifically as it relates to the Angus SteerSELECT genomic tool. These factors are of interest as they are operational (as opposed to biological) and can be manipulated during the development and application of a genomic selection program.
A recent study by Takeda et al. (2021) with Japanese Black cattle population showed that for carcase traits, a total of 7000–11 000 animals is a sufficient reference population size for genomic prediction. In this sense, previous studies have explored the benefits of expanding the reference population, such as, for instance, incorporating multiple breeds in the context of crossbreeding programs and for the selection of purebreds for optimal crossbred performance (Porto-Neto et al. 2015; van Grevenhof and van der Werf 2015; Karaman et al. 2021).
In the present study, we explore the potential benefits of incorporating data from commercial un-pedigreed and un-registered cattle into the existing reference population of the Angus SteerSELECT genomic tool.
Materials and methods
Reference and commercial population details
For carcase traits, the reference (REFE) population underpinning the Angus SteerSELECT tools currently comprises phenotypes and genotypes for 3766 Angus steers that were progeny of the Australian Angus Sire Benchmarking Program (ASBP), representing Years 1–8 of the program (described as Cohorts 1–8 with 360, 514, 570, 273, 547, 559, 520 and 423 steers respectively). The ASBP is a major initiative of Angus Australia, with support from Meat & Livestock Australia (MLA) and industry partners, that aims to generate progeny test data on contemporary Angus bulls, particularly for hard-to-measure traits such as feed efficiency, carcase measurements, meat-quality attributes and female reproduction (https://www.angusaustralia.com.au/sire-benchmarking).
The contemporary group (CG) for steers in the REFE population (CGR) was defined as a combination of cohort, property of origin, month of birth, management group and date of phenotype measurement. Management group accounted for some steers being short-fed (~100 days) and others long-fed (~270 days) during the feedlot period. In total, there were 105 CGR with an average of 35.9 steers per CG and ranging from 5 to 213 steers per CG.
After initial edits aimed at removing steers without genotypes or from CG with fewer than five individuals, the commercial (COMM) population comprised 2124 Angus-based steers from four commercial feedlots identified herein as Flot_1 (N = 453), Flot_2 (N = 720), Flot_3 (N = 495 steers) and Flot_4 (N = 456). The CG for the COMM population (CGC) was defined as a combination of feedlot, supplier (N = 19), abattoir and kill date. Steers were slaughtered in 23 kill groups from 18 January 2021 to 2 June 2022. There were 46 CGC, with an average of 46.2 steers per CG and ranging from 5 to 271 steers per CG.
For the present study, phenotypes for the REFE population included hot carcase weight (CWT) and Meat Standards Australia marbling score (MSA-MARB) measured in scores ranging from 100 to 1100 in increments of 10, with higher scores indicating greater marbling (McGilchrist et al. 2019). For the COMM population, phenotypes included CWT and AUSMEAT marbling score using the AUSMEAT scoring system, which ranges from 0 (nil) to 9 (abundant) in increments of 1 (AUS-MEAT 2005).
Genotypes for 45 364 autosomal SNPs were available for all the animals included in this study (i.e. 3766 REFE + 2124 COMM = 5890 total) and were used to compute the genomic relationship matrix (G) following Method 1 of VanRaden (2008), with the modification of Karoui et al. (2012) to make it invertible, as follows:
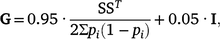
where S is the centred matrix relating SNP genotypes (recoded as 0, 1 or 2) in columns with animals in rows, and pi is the frequency of the second allele of the ith SNP, and I is an identity matrix included to make the genomic relationship matrix (GRM) invertible by enlarging the diagonal elements.
To obtain a measure of the genomic similarity between the two populations, we explored the SNP allele frequencies, the values of the GRM and performed a principal-component analysis (PCA) on the basis of a singular value decomposition of the GRM (Misztal and Legarra 2017).
Genomic predictions and cross-validation models
Variance components, heritability (h2), genetic (rg) and residual (re) correlations were estimated on the basis of GBLUP methodology using the Qxpak5 software (Pérez-Enciso and Misztal 2011). For the genomic prediction models, we performed GBLUP analyses by using a series of uni- and bi-variate analyses and three cross-validation schemes. In all cases, for the REFE population, the GBLUP models for the analysis of CWT and MSA-MARB contained the fixed effects of CGR and age of dam in years (AOD, six levels, 2–7+ years) and the linear regression covariates of age at measurement (AGE) in days, and the first three principal components of the GRM. Similarly, for the COMM population, the GBLUP models for the analysis of CWT and AUS-MARB contained the fixed effect of CGC and the linear regression covariates of days on feed (DOF), and the first three principal components of the GRM.
Additionally, the random additive polygenic and residual effects were fitted in the GBLUP models with assumed distributions N(0, 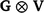 ) and N(0,
) and N(0, 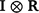 ) respectively, where G represents the genomic relationship matrix described earlier, V is the genetic co-variance matrix, I is an identity matrix, R is the residual variance–covariance matrix and
) respectively, where G represents the genomic relationship matrix described earlier, V is the genetic co-variance matrix, I is an identity matrix, R is the residual variance–covariance matrix and 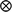 represents the Kronecker product.
represents the Kronecker product.
First, to obtain a measure of the genetic similarity, based on h2 and rg for a given trait in the two populations, we fitted two bi-variate GBLUP models. The first bi-variate model treated CWT as a different trait in the two populations. The second bi-variate model contained MSA-MARB and AUS-MARB for REFE and COMM respectively. The intent was to confirm that each trait had similar h2 in both populations and, equally importantly, a strong positive rg.
Second, the genotypes and phenotypes from both populations were merged into a single dataset and, for each trait CWT and MARB, the resulting genomic estimated breeding values (GEBV) from the analysis using this merged dataset are termed 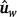 to indicate that they are based on the whole dataset. Before merging them, phenotypes were adjusted for fixed effects and covariates, and, within population, standardised using the z-score transformation (i.e. dividing by the within-population standard deviation). This was particularly important for marbling traits as they were measured on different scales in the two populations.
to indicate that they are based on the whole dataset. Before merging them, phenotypes were adjusted for fixed effects and covariates, and, within population, standardised using the z-score transformation (i.e. dividing by the within-population standard deviation). This was particularly important for marbling traits as they were measured on different scales in the two populations.
Third, for the cross-validation of genomic predictions, we employed three validation scenarios (VAL1, VAL2 and VAL3) depending on how many COMM phenotypes were included in the reference population, as follows:
-
VAL1 – all-out: no commercial phenotypes were included in the reference population. So, the reference population comprised the original REFE of 3766 steers with genotypes and phenotypes.
-
VAL2 – leave-one-feedlot-out: phenotypes from a given feedlot were excluded from the reference, while those from the remaining three feedlots were included. This approach was repeated four times, excluding phenotypes from one of the four feedlots each time.
-
VAL3 – leave-half-out: a random 50% of the COMM phenotypes across all feedlots were included in the reference, with the remainder being excluded from the reference but included in the validation.
In each cross-validation schema, the resulting GEBV from the analyses that treated as missing values records from a given commercial feedlot are termed 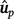 to indicate that they are based on partial data.
to indicate that they are based on partial data.
Finally, traditional (Bolormaa et al. 2013) and linear regression (LR) method (Legarra and Reverter 2018) approaches were used to estimate accuracy, bias and dispersion of GEBV. The following four metrics were employed:
-
Traditional accuracy (ACCT): in the context of cross-validation, the accuracy of a GEBV is traditionally computed from the Pearson correlation between a GEBV and the adjusted phenotype (y*: phenotype y adjusted for fixed effects) for individuals in the validation population, and divided by the square root of heritability, as follows:
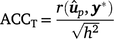
-
Method LR accuracy (ACCLR): for individuals in the validation population, Method LR accuracy was computed as follows:
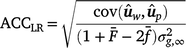 where
where 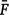 is the average inbreeding coefficient,
is the average inbreeding coefficient, 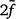 is the average relationship between individuals, and
is the average relationship between individuals, and 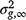 is the genetic variance at equilibrium in a population under selection. Assuming the individuals in the validation population are not under selection,
is the genetic variance at equilibrium in a population under selection. Assuming the individuals in the validation population are not under selection, 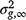 can be approximated by the additive genetic variance estimated from the partial dataset.
can be approximated by the additive genetic variance estimated from the partial dataset. -
Method LR bias (BiasLR): difference among the average GEBVs of individuals in the validation population by using the partial data minus that using the whole data, as follows:
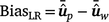 In the absence of bias, the expected value of BiasLR is zero, while positive and negative values indicate respectively, over-estimation and under-estimation of GEBV for validation animals when their own observation was not included.
In the absence of bias, the expected value of BiasLR is zero, while positive and negative values indicate respectively, over-estimation and under-estimation of GEBV for validation animals when their own observation was not included. -
Method LR dispersion (
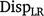 ): for individuals in the validation population, dispersion was measured from the slope of the regression of
): for individuals in the validation population, dispersion was measured from the slope of the regression of 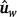 on
on 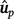 , as follows:
, as follows: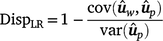
In the absence of bias, the expected value of DispLR is 0. Values less than 0 indicate under-dispersion (or deflation) of 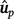 into
into 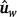 as phenotypes become available. Values greater than 1 indicate over-dispersion (or inflation) of
as phenotypes become available. Values greater than 1 indicate over-dispersion (or inflation) of 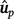 into
into 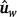 .
.
For bias and dispersion, we constructed 95% confidence intervals based on ±1.96 s.e. around the observed means across the 24 scenarios, i.e. 2 traits × 4 feedlots × 3 validation schemes.
Results and discussion
Phenotypes, fixed effects and covariates
Table 1 provides summary statistics for all phenotypes and covariates used in the analyses. For the REFE population, two steers had missing CWT and four had missing MSA-MARB. For the COMM population, the number of records with AUS-MARB scores of 1–9 was 36, 323, 817, 419, 337, 130, 44, 14, and 4 respectively.

|
For the REFE population, the fixed effects and covariates accounted for 77.9% and 38.6% of the variation in CWT and MSA-MARB respectively, and with all effects being highly significant (P < 0.001), except for slaughter age (P > 0.1), which was likely to have been captured by the effect of CGR. In comparison, for the COMM population, the fixed effects and covariates accounted for 62.9% and 42.1% of the variation in CWT and AUS-MARB respectively, and with all effects being highly significant (P < 0.001), except for DOF (P > 0.1), which was likely to have been captured by the effect of Feedlot and CGC. The average DOF (±standard deviation, s.d.) for Flot_1, Flot_2, Flot_3 and Flot_4 was 230.49 ± 8.03, 182.10 ± 8.77, 224.67 ± 47.18, and 275.81 ± 0.98. The longest DOF, with the smallest variation, was observed for Flot_4 due to steers being either 275 DOF (N = 271 steers) or 277 DOF (N = 185 steers). Table 2 presents the least-square means for CWT and AUS-MARB, across the four feedlots. Steers from Flot_4 had heavier CWT (P < 0.01) than those from the other three feedlots (reflecting additional DOF), which were not different from each other (P > 0.10). However, the ranking in CWT was not matched by the ranking in AUS-MARB, for which Flot_2 < Flot_4 = Flot_3 < Flot_1.

|
Fig. 1 shows the violin plots of the distribution of CWT observation in the REFE population and from each of the four feedlots represented in the COMM population. The apparent bimodality of the CWT records from the REFE population was attributed to some steers being short-fed (~100 days) and others being long-fed (~270 days) during the feedlot period.
|
|
Genotypes, genomic relationships and genetic parameters
Across the 45 364 SNPs, the correlation between the frequency of the first allele in the REFE and in the COMM population was very high at 0.996. In agreement with theoretical expectations, the 5890 diagonal elements of the genomic relationship matrix G created with the combined population averaged 1.001, with a standard deviation (s.d.) of 0.031, and ranged from 0.914 to 1.337. Meanwhile, the 17 343 105 off-diagonal elements of G averaged −0.000, with a s.d. of 0.025, and ranged from −0.112 to 0.657. These values are very similar to the ones reported by Reverter et al. (2021a) using a population of 3715 Angus steers and heifers that were progeny of ASBP sires. Also, the similarity in the variance of diagonal and off-diagonal elements indicates that both a sufficiently large number of SNPs was used to estimate relationships and the presence of a single-breed population (Simeone et al. 2011). Finally, the PCA of G did not show any clusters in the combined population, with the first three PCs accounting for only 0.79%, 0.52% and 0.43% of genomic diversity respectively. These results further confirmed the high Angus content of the steers in the COMM population.
On the basis of previously described approaches to estimate genomic breed composition (Reverter et al. 2020), using the 45 364 SNPs, the genomic estimate of the Angus content in the COMM population averaged 96.9% and ranged from 32.87% to 100%. Of the 2124 steers, 1703 (or 80.2%) were estimated to be 100% Angus, while a further 229 steers (10.8%) being estimated to have an Angus content <100% but ≥87.5% (or 7/8).
After fitting the bi-variate GBLUP model that treated the same trait (CWT or MARB) as a different trait in the two populations (REFE and COMM), the estimates (mean ± s.e.) of heritability (h2) for CWT were 0.419 ± 0.026 and 0.368 ± 0.038 for the REFE and COMM population respectively, and with a genetic correlation (rg) of 0.756 ± 0.068. For MARB, the same three parameter estimates were 0.357 ± 0.027, 0.340 ± 0.038 and 0.879 ± 0.073 respectively. Again, the similar h2 estimates for a given trait in the two populations coupled with the strong rg point towards the convenience of merging both populations into a single larger reference population.
Very similar to the h2 estimates reported here, the review of Ríos Utrera and Van Vleck (2004) reported average h2 estimates for CWT and MARB score of 0.40 and 0.37 respectively. However, using a subset of the Australian Angus cattle employed here, higher h2 estimates for CWT and MARB have been published, including the 0.75 ± 0.06 and 0.53 ± 0.05 respectively, of Duff et al. (2021), and the 0.63 ± 0.11 and 0.61 ± 0.09 respectively, of Reverter et al. (2021b).
There is a body of literature describing the strong relationship between different measures of marbling (for a recent account, see, for instance, Liu et al. (2021) and Martín et al. (2022)). Liu et al. (2021) reported a phenotypic correlation of 0.91 (P < 0.001) between AUS-MARB and MSA-MARB. Mateescu et al. (2015) reported a rg estimate of 1.00 ± 0.01 between marbling score and intramuscular fat content.
Genomic predictions and cross-validation results
The genomic prediction accuracies for both traits across four commercial feedlots are shown in Fig. 2. Averaged across all feedlots and based on both accuracy metrics (ACCT and ACCLR), genomic prediction accuracy for CWT increased from VAL1 (ACCT = 0.356; ACCLR = 0.475) to VAL2 (ACCT = 0.420; ACCLR = 0.524) to VAL3 (ACCT = 0.485; ACCLR = 0.546).
Similar to our previous findings (Reverter et al. 2021b), in the present study we observed a strong correlation between ACCT and ACCLR across the 24 measures (r = 0.603 ± 0.170), and, on average, the ACCLR accuracies were 15% higher than ACCT accuracies (0.511 vs 0.444) and less variable (s.d. = 0.038 vs 0.106).
The increase in prediction accuracy from VAL1 to VAL2 can be attributed in part to relationships between the steers from the feedlot being validated and the steers from the other feedlots, but also to an increase in the size of the new reference population, i.e. the original REFE population of 3766 steers plus all the steers from the other feedlots. However, the increase in accuracy from VAL2 to VAL3 can be mostly attributed to relationships between steers from the same feedlot to the one being validated. It is worth noting that the reference population for VAL3 comprised 4796 steers (the original 3766 steers from REFE plus a random 1030 steers from COMM), which is less than the number of steers in the reference populations for VAL2 (the original 3766 steers from REFE plus all the steers from COMM except those from the feedlot being validated). As commercial feedlot operators tend to source their steers from ‘preferred’ suppliers, the increase in accuracy observed in VAL3 relative to VAL2, and even with a smaller reference in VAL3, highlights the importance of having their own cattle represented in the reference population.
The 95% confidence interval for GEBV bias contained zero in 22 of the 24 scenarios considered (Fig. 3). The two anomalous scenarios correspond to CWT GEBV for Flot_2 steers being over-estimated. While further research is needed to ascertain the reason for this over-estimation, one possibility points towards the difficulty in modelling data from Flot_2 as it represents the largest sample size (720 steers compared with <500 for the other feedlots) across the largest number of suppliers (10 compared with the second-largest 6 for Flot_4). Nevertheless, this over-estimation vanishes at 99% confidence interval.
The 95% confidence intervals for the dispersion in GEBV showed a tendency for over-dispersion (or inflation), particularly for Flot_2 steers across both traits, and for Flot_3 steers in CWT and for Flot_1 steers in MARB. Again, while further research is needed to ascertain the reason for this inflation, a plausible reason is the use of an incorrect heritability, in this case higher for inflation, or the existence of a hidden trend in the data (Macedo et al. 2020). Similarly, this over-dispersion was observed in our previous study (Reverter et al. 2022) and attributed to higher h2 estimates when phenotypes of the validation cohort were treated as missing values compared with h2 estimates, using the whole dataset (Fig. 4).
Conclusions
Notwithstanding the importance of and difficulty in accurately modelling phenotypes from commercial operations, where data recording practices could be less stringent than in seedstock operations and research herds, the present study has highlighted the potential benefits of incorporating commercial data from Angus-based beef supply chain, which are independent of the ASBP and the Angus Australia reference population, into the existing reference population of Angus SteerSELECT genomic tool. In addition, the results have helped demonstrate to commercial beef producers the opportunity to apply genomic tools within commercial populations as part of routine management, since higher accuracies translate into an improved ability to predict performance, reducing the risk of steers not performing to expectation during short- or long-feeding regimes.
Data availability
The data that support this study may be shared upon reasonable request to the corresponding author.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
The authors acknowledge the vital in-kind support (steer access, data, personnel) provided by the participating feedlots of Bective (Whyalla Beef-NH Foods), Rangers Valley (Marubeni Corporation), Kerwee (Stockyard Beef) and Killara (Elders Rural Services). The technical assistance from Adrián López-Catalina and Fernanda Raidan is truthfully appreciated.
References
Alexandre PA, Porto-Neto LR, Hine B, Ingham A, Duff C, Samaraweera M, Reverter A (2022) Validation of HeiferSELECT genomic product using historical data. In ‘Proceedings of the 12th world congress on genetics applied to livestock production, 3–8 July 2022, Rotterdam, The Netherlands’. (Wageningen Academic Publishers)AUS-MEAT (2005) ‘Handbook of Australian meat international red meat manual.’ 7th edn. (AUS-MEAT: Sydney, NSW, Australia)
Bolormaa S, Pryce JE, Kemper K, Savin K, Hayes BJ, Barendse W, Zhang Y, Reich CM, Mason BA, Bunch RJ, Harrison BE, Reverter A, Herd RM, Tier B, Graser H-U, Goddard ME (2013) Accuracy of prediction of genomic breeding values for residual feed intake and carcass and meat quality traits in Bos taurus, Bos indicus, and composite beef cattle. Journal of Animal Science 91, 3088–3104.
| Accuracy of prediction of genomic breeding values for residual feed intake and carcass and meat quality traits in Bos taurus, Bos indicus, and composite beef cattle.Crossref | GoogleScholarGoogle Scholar |
Clark SA, Hickey JM, van der Werf JHJ (2011) Different models of genetic variation and their effect on genomic evaluation. Genetics Selection Evolution 43, 18
| Different models of genetic variation and their effect on genomic evaluation.Crossref | GoogleScholarGoogle Scholar |
Daetwyler HD, Villanueva B, Woolliams JA (2008) Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS ONE 3, e3395
| Accuracy of predicting the genetic risk of disease using a genome-wide approach.Crossref | GoogleScholarGoogle Scholar |
Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA (2010) The impact of genetic architecture on genome-wide evaluation methods. Genetics 185, 1021–1031.
| The impact of genetic architecture on genome-wide evaluation methods.Crossref | GoogleScholarGoogle Scholar |
de los Campos G, Vazquez AI, Fernando R, Klimentidis YC, Sorensen D (2013) Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genetics 9, e1003608
| Prediction of complex human traits using the genomic best linear unbiased predictor.Crossref | GoogleScholarGoogle Scholar |
de Roos APW, Hayes BJ, Goddard ME (2009) Reliability of genomic predictions across multiple populations. Genetics 183, 1545–1553.
| Reliability of genomic predictions across multiple populations.Crossref | GoogleScholarGoogle Scholar |
Druet T, Macleod IM, Hayes BJ (2014) Toward genomic prediction from whole-genome sequence data: impact of sequencing design on genotype imputation and accuracy of predictions. Heredity 112, 39–47.
| Toward genomic prediction from whole-genome sequence data: impact of sequencing design on genotype imputation and accuracy of predictions.Crossref | GoogleScholarGoogle Scholar |
Duff CJ, van der Werf JHJ, Parnell PF, Clark SA (2021) Redefining residual feed intake to account for marbling fat in beef breeding programs. Animal Production Science 61, 1837–1844.
| Redefining residual feed intake to account for marbling fat in beef breeding programs.Crossref | GoogleScholarGoogle Scholar |
Goddard M (2009) Genomic selection: prediction of accuracy and maximisation of long term response. Genetica 136, 245–257.
| Genomic selection: prediction of accuracy and maximisation of long term response.Crossref | GoogleScholarGoogle Scholar |
Habier D, Fernando RL, Dekkers JCM (2007) The impact of genetic relationship information on genome-assisted breeding values. Genetics 177, 2389–2397.
| The impact of genetic relationship information on genome-assisted breeding values.Crossref | GoogleScholarGoogle Scholar |
Habier D, Tetens J, Seefried F-R, Lichtner P, Thaller G (2010) The impact of genetic relationship information on genomic breeding values in German Holstein cattle. Genetics Selection Evolution 42, 5
| The impact of genetic relationship information on genomic breeding values in German Holstein cattle.Crossref | GoogleScholarGoogle Scholar |
Hine BC, Duff CJ, Byrne A, Parnell P, Porto-Neto L, Li Y, Ingham AB, Reverter A (2021) Development of Angus SteerSELECT: a genomic-based tool to identify performance differences of Australian Angus steers during feedlot finishing: phase 1 validation. Animal Production Science 61, 1884–1892.
| Development of Angus SteerSELECT: a genomic-based tool to identify performance differences of Australian Angus steers during feedlot finishing: phase 1 validation.Crossref | GoogleScholarGoogle Scholar |
Karaman E, Su G, Croue I, Lund MS (2021) Genomic prediction using a reference population of multiple pure breeds and admixed individuals. Genetics Selection Evolution 53, 46
| Genomic prediction using a reference population of multiple pure breeds and admixed individuals.Crossref | GoogleScholarGoogle Scholar |
Karoui S, Carabano MJ, Diaz C, Legarra A (2012) Joint genomic evaluation of French dairy cattle breeds using multiple-trait models. Genetics Selection Evolution 44, 39
| Joint genomic evaluation of French dairy cattle breeds using multiple-trait models.Crossref | GoogleScholarGoogle Scholar |
Legarra A, Reverter A (2018) Semi-parametric estimates of population accuracy and bias of predictions of breeding values and future phenotypes using the LR method. Genetics Selection Evolution 50, 53
| Semi-parametric estimates of population accuracy and bias of predictions of breeding values and future phenotypes using the LR method.Crossref | GoogleScholarGoogle Scholar |
Liu J, Pogorzelski G, Neveu A, Legrand I, Pethick D, Ellies-Oury M-P, Hocquette J-F (2021) Are marbling and the prediction of beef eating quality affected by different grading sites? Frontiers in Veterinary Science 8, 611153
| Are marbling and the prediction of beef eating quality affected by different grading sites?Crossref | GoogleScholarGoogle Scholar |
Macedo FL, Reverter A, Legarra A (2020) Behavior of the linear regression method to estimate bias and accuracies with correct and incorrect genetic evaluation models. Journal of Dairy Science 103, 529–544.
| Behavior of the linear regression method to estimate bias and accuracies with correct and incorrect genetic evaluation models.Crossref | GoogleScholarGoogle Scholar |
Martín NP, Schreurs NM, Morris ST, López-Villalobos N, McDade J, Hickson RE (2022) Meat quality of beef-cross-dairy cattle from Angus or Hereford sires: a case study in a pasture-based system in New Zealand. Meat Science 190, 108840
| Meat quality of beef-cross-dairy cattle from Angus or Hereford sires: a case study in a pasture-based system in New Zealand.Crossref | GoogleScholarGoogle Scholar |
Mateescu RG, Garrick DJ, Garmyn AJ, VanOverbeke DL, Mafi GG, Reecy JM (2015) Genetic parameters for sensory traits in longissimus muscle and their associations with tenderness, marbling score, and intramuscular fat in Angus cattle. Journal of Animal Science 93, 21–27.
| Genetic parameters for sensory traits in longissimus muscle and their associations with tenderness, marbling score, and intramuscular fat in Angus cattle.Crossref | GoogleScholarGoogle Scholar |
McGilchrist P, Polkinghorne RJ, Ball AJ, Thompson JM (2019) The meat standards Australia index indicates beef carcass quality. Animal 13, 1750–1757.
| The meat standards Australia index indicates beef carcass quality.Crossref | GoogleScholarGoogle Scholar |
Meuwissen T, Goddard M (2010) Accurate prediction of genetic values for complex traits by whole-genome resequencing. Genetics 185, 623–631.
| Accurate prediction of genetic values for complex traits by whole-genome resequencing.Crossref | GoogleScholarGoogle Scholar |
Misztal I, Legarra A (2017) Invited review: efficient computation strategies in genomic selection. Animal 11, 731–736.
| Invited review: efficient computation strategies in genomic selection.Crossref | GoogleScholarGoogle Scholar |
Pérez-Enciso M, Misztal I (2011) Qxpak.5: old mixed model solutions for new genomics problems. BMC Bioinformatics 12, 202
| Qxpak.5: old mixed model solutions for new genomics problems.Crossref | GoogleScholarGoogle Scholar |
Porto-Neto LR, Barendse W, Henshall JM, McWilliam SM, Lehnert SA, Reverter A (2015) Genomic correlation: harnessing the benefit of combining two unrelated populations for genomic selection. Genetics Selection Evolution 47, 84
| Genomic correlation: harnessing the benefit of combining two unrelated populations for genomic selection.Crossref | GoogleScholarGoogle Scholar |
Reverter A, Porto-Neto LR, Fortes MRS, McCulloch R, Lyons RE, Moore S, Nicol D, Henshall J, Lehnert SA (2016) Genomic analyses of tropical beef cattle fertility based on genotyping pools of Brahman cows with unknown pedigree. Journal of Animal Science 94, 4096–4108.
| Genomic analyses of tropical beef cattle fertility based on genotyping pools of Brahman cows with unknown pedigree.Crossref | GoogleScholarGoogle Scholar |
Reverter A, Hudson NJ, McWilliam S, Alexandre PA, Li Y, Barlow R, Welti N, Daetwyler H, Porto-Neto LR, Dominik S (2020) A low-density SNP genotyping panel for the accurate prediction of cattle breeds. Journal of Animal Science 98, skaa337
| A low-density SNP genotyping panel for the accurate prediction of cattle breeds.Crossref | GoogleScholarGoogle Scholar |
Reverter A, Hine BC, Porto-Neto L, Alexandre PA, Li Y, Duff CJ, Dominik S, Ingham AB (2021a) ImmuneDEX: updated genomic estimates of genetic parameters and breeding values for Australian Angus cattle. Animal Production Science 61, 1919–1924.
| ImmuneDEX: updated genomic estimates of genetic parameters and breeding values for Australian Angus cattle.Crossref | GoogleScholarGoogle Scholar |
Reverter A, Hine BC, Porto-Neto L, Li Y, Duff CJ, Dominik S, Ingham AB (2021b) ImmuneDEX: a strategy for the genetic improvement of immune competence in Australian Angus cattle. Journal of Animal Science 99, skaa384
| ImmuneDEX: a strategy for the genetic improvement of immune competence in Australian Angus cattle.Crossref | GoogleScholarGoogle Scholar |
Reverter A, Alexandre PA, Li Y, Hine BC, Duff CJ, Ingham AB, Porto-Neto LR (2022) Genomic prediction accuracy: how low can we go? In ‘Proceedings of the 12th world congress on genetics applied to livestock production, 3–8 July 2022, Rotterdam, The Netherlands’. (Wageningen Academic Publishers)
Ríos Utrera A, Van Vleck LD (2004) Heritability estimates for carcass traits of cattle: a review. Genetics and Molecular Research 30, 380–394.
Simeone R, Misztal I, Aguilar I, Legarra A (2011) Evaluation of the utility of diagonal elements of the genomic relationship matrix as a diagnostic tool to detect mislabelled genotyped animals in a broiler chicken population. Journal of Animal Breeding and Genetics 128, 386–393.
| Evaluation of the utility of diagonal elements of the genomic relationship matrix as a diagnostic tool to detect mislabelled genotyped animals in a broiler chicken population.Crossref | GoogleScholarGoogle Scholar |
Takeda M, Inoue K, Oyama H, Uchiyama K, Yoshinari K, Sasago N, Kojima T, Kashima M, Suzuki H, Kamata T, Kumagai M, Takasugi W, Aonuma T, Soma Y, Konno S, Saito T, Ishida M, Muraki E, Inoue Y, Takayama M, Nariai S, Hideshima R, Nakamura R, Nishikawa S, Kobayashi H, Shibata E, Yamamoto K, Yoshimura K, Matsuda H, Inoue T, Fujita A, Terayama S, Inoue K, Morita S, Nakashima R, Suezawa R, Hanamure T, Zoda A, Uemoto Y (2021) Exploring the size of reference population for expected accuracy of genomic prediction using simulated and real data in Japanese Black cattle. BMC Genomics 22, 799
| Exploring the size of reference population for expected accuracy of genomic prediction using simulated and real data in Japanese Black cattle.Crossref | GoogleScholarGoogle Scholar |
van Grevenhof IEM, van der Werf JHJ (2015) Design of reference populations for genomic selection in crossbreeding programs. Genetics Selection Evolution 47, 14
| Design of reference populations for genomic selection in crossbreeding programs.Crossref | GoogleScholarGoogle Scholar |
VanRaden PM (2008) Efficient methods to compute genomic predictions. Journal of Dairy Science 91, 4414–4423.
| Efficient methods to compute genomic predictions.Crossref | GoogleScholarGoogle Scholar |
Wientjes YCJ, Veerkamp RF, Calus MPL (2013) The effect of linkage disequilibrium and family relationships on the reliability of genomic prediction. Genetics 193, 621–631.
| The effect of linkage disequilibrium and family relationships on the reliability of genomic prediction.Crossref | GoogleScholarGoogle Scholar |
Wientjes YCJ, Calus MPL, Goddard ME, Hayes BJ (2015) Impact of QTL properties on the accuracy of multi-breed genomic prediction. Genetics Selection Evolution 47, 42
| Impact of QTL properties on the accuracy of multi-breed genomic prediction.Crossref | GoogleScholarGoogle Scholar |
Wray NR, Yang J, Hayes BJ, Price AL, Goddard ME, Visscher PM (2013) Pitfalls of predicting complex traits from SNPs. Nature Reviews Genetics 14, 507–515.
| Pitfalls of predicting complex traits from SNPs.Crossref | GoogleScholarGoogle Scholar |


