Investigation of methods for inclusion of systematic environmental effects in weaning and post-weaning weights for meat sheep in large-scale genetic evaluation
U. Paneru A B * , D. J. Brown
A B * , D. J. Brown  C , P. M. Gurman C and J. H. J. van der Werf A
C , P. M. Gurman C and J. H. J. van der Werf A
A School of Environmental and Rural Science, University of New England, Armidale, NSW 2351, Australia.
B Nepal Agricultural Research Council, Singhadurbar Plaza, Kathmandu, Bagmati 44600, Nepal.
C Animal Genetics and Breeding Unit (AGBU is a joint venture of NSW Department of Primary Industries and the University of New England), University of New England, Armidale, NSW 2351, Australia.
Handling Editor: Suzanne Mortimer
Animal Production Science 63(1) 41-50 https://doi.org/10.1071/AN21300
Submitted: 4 June 2021 Accepted: 15 June 2022 Published: 15 July 2022
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Genetic evaluation of Australian sheep is conducted for millions of animals for more than 100 traits. Currently, the Australian sheep genetic-analysis software (OVIS) applies a pre-adjustment of phenotype for fixed effects rather than fitting all fixed and random effects jointly in a linear mixed model to estimate breeding values. However, the current correction factors might be outdated and potential interactions among fixed effects not accounted for, which could lead to bias in estimated breeding values (EBVs).
Aims: This study aimed to assess whether correction factors used in OVIS for early bodyweights recorded in meat sheep breeds are appropriate, so as to explore whether the pre-adjustment method is still suitable and how this compares with a linear mixed model, and to estimate the significance of interactions between fixed effects.
Methods: Correlations between EBVs from different models and regression slopes from forward prediction were calculated, using weaning-weight data on 365 956 White Suffolk and 370 649 Poll Dorset sheep and post-weaning weight data on 292 538 White Suffolk and 303 864 Poll Dorset sheep.
Key results: The current OVIS procedure resulted in regression slopes of progeny performance on sire EBVs (averaged over breeds) of 0.37 and 0.35 for weaning and post-weaning weights respectively. Updated pre-adjustment factors improved the regression slopes to 0.40 and 0.38 respectively. Analysis with a linear mixed model produced significantly better regression slopes than did pre-adjustment (0.47 and 0.44 respectively). Further, regression slopes obtained from the linear mixed model with flock by sex by age interaction averaged over breeds were 0.48 for weaning and 0.46 for post-weaning weight respectively, which was a moderate improvement over the current OVIS model. Including a flock by sex by age interaction produced significantly better improvement in Poll Dorset sheep and modest improvement in White Suffolk sheep than did linear mixed model without interaction.
Conclusions: Using a linear mixed model with a flock by sex by age interaction significantly improves the utility of estimated breeding values for weaning and post-weaning weight in predicting the performance of future progeny.
Implications: To account for systematic environmental effects, a linear mixed model should be used in OVIS to jointly estimate the fixed effects and EBVs.
Keywords: accuracy, bias, estimated breeding values, interaction, linear mixed model, phenotype, pre-adjustment, regression slope.
Introduction
Genetic evaluation is conducted to provide information to breeders about the genetic merit of their animals in the form of estimated breeding values (EBVs) and selection-index values to assist them in their selection decisions. EBVs are predicted from best linear unbiased prediction (BLUP) by correcting phenotypes for these systematic environmental effects to allow fair genetic comparisons among animals. There are two common approaches to correct for these fixed environmental effects, namely (1) pre-adjustment of observed phenotypes for one or more systematic environmental effects before the genetic evaluation (Brown et al. 2000; Albuquerque and Meyer 2001) or (2) fitting these fixed effects in the mixed models to estimate them jointly with the breeding values (Laird and Ware 1982; Meyer 2004). The genetic evaluations for Australian sheep (OVIS) are conducted using the OVIS software, where phenotypes are corrected for fixed effects before prediction of EBVs (Brown et al. 2000). For bodyweight traits of lambs, these effects include the age of the animal at measurement, the age of the dam at lambing, birth type, and rear type. The only fixed effect directly fitted in an animal model in OVIS is the contemporary group (CG) which includes breed, flock, management group, sex, and year of measurement subclass (Brown et al. 2016). Further, new contemporary groups are created if the age of measurement exceeds 35 days in weaning weight and 70 days in post-weaning weight within the contemporary group (Brown et al. 2007).
Adjustment factors for systematic environmental effects are calculated by taking a subset of the data and calculating solutions for fixed effects from a mixed model analysis, with these adjustment factors later used in the conduct routine of genetic evaluations. In the case of meat traits important for Terminal-sire production systems such as weaning weight (Wwt) and post-weaning weight (Pwt), these adjustment factors have been estimated from a multi-breed dataset and are used to pre-adjust the observed phenotypes (Brown et al. 2000). The pre-adjusted phenotypes are then used in the main BLUP analysis, but are not re-calculated for each analysis. As they can become less accurate over time, new adjustment factors need to be calculated regularly to update the existing ones. Further, feedback from some breeders suggests that EBVs estimated from pre-adjustment are inconsistent with their perceived ranking, especially in flocks where their environment or management differs from those typically experienced in other flocks, and this concern should be addressed.
Theoretically, in predicting breeding values using BLUP, systematic environmental effects, including their interaction effects should be included in the mixed-model equations (Henderson 1982; Laird and Ware 1982; Henderson 1984; Meyer 1998). These estimates are expected to be better than pre-adjustment because fixed effect estimates may change. For example, the effect of age on bodyweight might change over time due to selecting for faster growth, with a linear mixed model being able to account for that change, whereas pre-adjustment cannot. However, estimating all effects jointly in the routine analysis would require significantly higher memory and increase the computational time. This could be prohibitive for large-scale genetic evaluations with millions of animals for many traits; however, with the availability of increased computing power and further advances in analysis algorithms, this issue is becoming less critical. Thus, it is important to find out empirically what the scale of the improvement would be and consider the feasibility of running a linear model in routine genetic evaluation. Further, there could be interaction effects between different fixed effects currently not accounted for, possibly leading to lower EBV accuracy.
Given these scenarios, this paper aimed to evaluate whether the adjustment factors currently used by OVIS are still applicable for Wwt and Pwt of the dominant breeds used in Terminal production systems and propose updated adjustment factors if required. We assessed whether the ranking of animals in some flocks is affected more than in other flocks when EBVs are estimated from pre-adjustment versus estimated from a linear mixed model. We examined the suitability and the advantage of using a linear mixed model in routine analyses conducted by OVIS over an evaluation system that uses pre-correction factors. Finally, the value of fitting interactions among systematic environmental effects in the linear mixed model was evaluated.
Materials and methods
Data
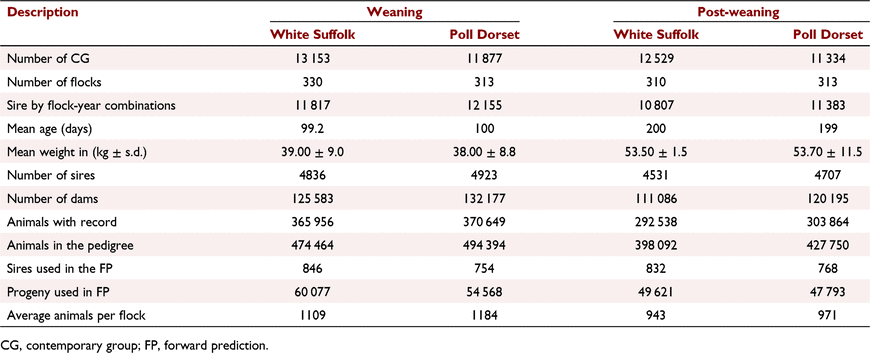
Data were retrieved from the LAMBPLAN database (Brown et al. 2007), consisting of bodyweight records for Australian and New Zealand sheep from 2009 to 2019. Two subsets of data were created by extracting weaning weight and post-weaning weight records from two meat breeds, White Suffolk and Poll Dorset. Data consisted of 356 956 White Suffolk and 370 649 Poll Dorset records for Wwt and 292 538 White Suffolk and 303 864 Poll Dorset records for Pwt. These two breeds account for about 70% of the LAMBPLAN Terminal sheep population. Data were filtered following the standard OVIS filters (Brown et al. 2000). Weaning weight records outside the bodyweight range of 15–60 kg and the age range of 15–165 days were removed, as well as Pwt records outside the bodyweight range of 25–90 kg and the age range of 105–345 days. Records with the age of the dam ranging outside of 0.8–12 years were also removed. Lambs were classified according to four birth types (singleton, twin, triplets and quadruplets) and four rear types (singleton, twin, triplets and quadruplets). Lambs with Birth type 5 were merged with the group of Birth type 4 and Rear type 5 were also merged with Rear type 4 for both Wwt and Pwt because of few animals with a birth/rear type of 5. All animals in the analysis had records on age at recording in days, birth type, rear type, dam age, and more than 90% of animals had sire and dam recorded. A concise summary of the final data sets and a summary of the fixed effects are shown in Table 1.
|
Variance component estimation
Variance components were estimated using a linear mixed model. The fixed effects in the model were contemporary group defined as combined flock, management group, sex (male, female), and year of measurement subclass. Additional fixed effects were birth type, rear type, adjusted age (observed age minus standard age), adjusted dam age (observed minus standard age of dam) and adjusted dam age squared. Data were modelled in ASReml ver. 4.1 (Gilmour et al. 2015) to estimate the mixed-effects model.
The linear mixed model used to estimate the fixed- and random-effects solutions was as follows:

where y is the vector of observations, b is the vector of fixed effects, a is the vector of estimated breeding values, m is the vector of maternal breeding values, mp is the vector of maternal permanent environmental effects, sfy is a vector of sire by flock–year interaction effects, and e is a vector of random residual. X is the incidence matrix relating b to y and Z1, Z2, Z3 and Z4 are incidence matrices relating a, m, mp and sfy to y and e is the vector of random residuals.
Calculation of pre-adjustment factors
From each data set, updated adjustment factors were estimated using a linear mixed model. To calculate multiplicative adjustment factors, variance components estimated from the data were then used to estimate best linear unbiased estimates (BLUE) for the mixed-model equations. Therefore, multiplicative adjustment factors were calculated from the linear adjustment factors as a ratio of mean weight of lambs for different effect classes. Separate factors were calculated for different effect classes for birth type and rear type. The multiplicative adjustment factors were calculated following the guidelines of OVIS (Brown et al. 2000). These updated pre-adjustment factors were compared with current OVIS pre-adjustment factors used in OVIS for the Terminal-breed genetic evaluation. Estimates of fixed effect solutions were compared with current adjustment factors.
Multiplicative adjustment for age is a non-linear adjustment method and was calculated from the solutions from a linear mixed model. Multiplicative pre-adjustment for age assumes that animals have their own growth curve such that the weight adjustment for age is based on the growth rate of the animal rather than an average growth rate. Every animal is assumed to have a predicted weight equal to zero at the ‘age intercept’ which is Ai. The age intercept is normally a negative value for weight traits, effectively being the age at which the weight equals zero. The age intercept was calculated by extrapolation of a linear regression line from the standard weight of animals to the x-axis (i.e. the ‘age at zero weight’). In a model without sex and age interaction, a single-sex regression line of weight on age was calculated, but in a model with sex and age interaction, two different regression lines (slope values) were calculated from the regression of weight on age, one for males and one for females.
If an animal attains an observed weight Yo at the age of Ao days, then the animal has grown by  kg per day. The weight Ya of the animal on the standard age of Aa days would then be predicted to be
kg per day. The weight Ya of the animal on the standard age of Aa days would then be predicted to be  times the growth per day, that is
times the growth per day, that is

Predicted weight at Aa can also be written as Aa − Ai times Yo/(Ao−Ai), which gives the following formula (Raymond 1982):

Age adjustment depends on the age intercept value; as the growth rate of animals increases, age intercept value decreases, and vice versa.
Dam age was fitted as the regression of weight on dam age with a second-order polynomial, i.e. with intercept, slope, and a quadratic term. Quadratic adjustment for dam age was made according to the formula used in OVIS (Brown et al. 2000):

where x is age of dam – average dam age (4.5 years); I is the intercept; L is the coefficient for the linear component and Q is the coefficient for quadratic component
The effectiveness of pre-adjustment factors was evaluated by correlating the observed (unadjusted) and adjusted phenotype (current OVIS and updated) values with the raw fixed effect covariate values for each animal. It is expected that once a trait is adjusted, its relationship with the fixed effect covariate values should be reduced close to zero.
To compare the effectiveness of age correction by using current OVIS adjustment factors with updated adjustment factors, we divided the age interval for the Pwt (115–345 days) into six classes consisting of 41-day intervals and calculated the average adjusted weight for each class from each method.
Correlation of EBVs
Spearman correlations were calculated between EBVs estimated from the linear mixed model and pre-adjustment methods to assess the magnitude of re-ranking of EBVs between the different methods. Spearman correlations of EBVs were estimated between linear mixed model and pre-adjustment by using updated adjustment factors for all animals in the data, top 10% of animals on EBV, young rams (born after 2016 and with few progeny), and young progeny (born after 2016). Correlations of EBVs were presented for young rams because young rams would have fewer progeny and their EBVs would be more influenced by their phenotypic adjustments. Similarly, EBVs of young progeny would also be affected by phenotypic adjustment to estimate the EBVs. The top 10% of animals are most relevant to understanding how well we can select animals for breeding purposes.
Interactions among fixed effects
The significance of interactions among fixed effects was tested by fitting in a linear mixed model. Identical fixed and random effects were fitted as in Model 1. The linear mixed model was expanded by adding an interaction effect sequentially. The interaction effects included sex by age, birth type by rear type, year of birth by age, flock by age, flock by sex by age and flock by birth type by rear type. Interaction effects that were observed to be significant were then used to build expanded linear models to be evaluated in forward prediction.
Regression of progeny performance on sire EBVs
Forward prediction was conducted to test the effectiveness of sire EBVs from the various models in predicting progeny performance. The breeding values of sires for Wwt and Pwt were estimated from the linear mixed models and pre-adjustment of the phenotypes from training data sets. Training data sets included individuals born before 2017 and progeny in the validation dataset were born after 2016. Sire EBVs were validated only if sires had progeny born after 2016. Progeny performance was corrected for all fixed effects by using solutions from a linear mixed model before progeny phenotype was regressed on sire EBVs. The expectation for the regression coefficient is 0.5, as offspring receive half of the additive genetic value from the sire. A lower value indicates an over-dispersion of sire EBVs relative to the variance observed in progeny performance data, while higher values reflect under-dispersion.
Variation among flocks in the effect of pre-adjustment
To investigate whether the effect of pre-adjustment is uniform across flocks, or is affected by time of recording, many flocks were tested that differed in age at recording. Each flock practices weight recording at their convenient time, and age at recording varies among flocks. For the purpose of the genetic analysis, weight measurements taken at the age interval of 15–165 days were assigned as weaning weight and that of 115–345 days were assigned as post-weaning weight. Many flocks were tested that differed in age at recording for Wwt and Pwt, but the results are presented with four representative flocks as case studies into the problem. Summary statistics of those four flocks are presented in Table 2.

|
Results
Variance components
Variance components are presented for Wwt and Pwt for both breeds by using linear mixed model (Table 3). Results for Wwt demonstrated that White Suffolk sheep have a significantly higher genetic variance (2.12) and heritability (0.08 ± 0.01) than was observed for the Poll Dorset sheep (1.41 and 0.05 ± 0.01 respectively). Similarly, White Suffolk have significantly higher genetic variance (4.52) and heritability (0.13 ± 0.01) than do Poll Dorset sheep (4.17 and 0.11 ± 0.01 respectively) for Pwt.

|
Comparison between pre-adjustment factors
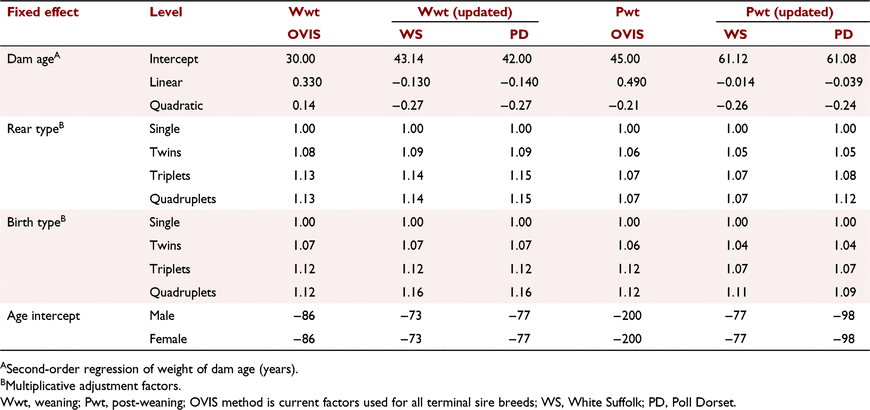
Comparison between adjustment factors for the weight traits estimated from the data (updated) and those currently used in OVIS for the Terminal-breed genetic evaluation are presented in Table 4. The updated adjustment factors for both Wwt and Pwt were different from the adjustment factors currently used in OVIS for age and dam age but were generally similar for birth type and rear type. The age intercept value for White Suffolk was estimated at −77 days, which was higher than the estimated age intercept value for Poll Dorset (−98 days). These values were much higher than those used in OVIS (−200 days) for Pwt. The overall means used to calculate the birth-type and rear-type adjustment factors for Pwt were 61.12 kg in White Suffolk sheep and 61.08 kg in Poll Dorset sheep. Results for Wwt were similar to those for Pwt.
|
The adjustment factors currently used in OVIS provided insufficient adjustment for younger animals and over-adjusted for older animals. The median adjusted Pwt of each subclass increased with age, even though it was age-adjusted in Fig. 1 (left). In contrast, there were no noticeable differences in the median weight of each class when using updated pre-adjustment factors (Fig. 1, right).
|
|
On the basis of updated adjustment factors, for both breeds, the correlations between adjusted weight and adjustor variables were close to zero (Table 5). For the age effect, correlations of −0.02 and −0.01 for Wwt and −0.01 and −0.01 for Pwt were observed for White Suffolk and Poll Dorset breeds respectively. The correlation between adjusted weight and dam age was also negligible after adjustment with updated pre-adjustment factors. Correlations much different from zero between adjusted weight with age and dam age were observed after adjustment when OVIS pre-adjustment factors were used.

|
Comparison between adjustment factors by regression
The regression coefficients of progeny phenotypes on sire EBVs derived using current OVIS and updated adjustment factors are presented in Table 6. Updated pre-adjustment factors resulted in regression coefficients closer to the expected value of 0.5 than did those for EBVs based on pre-adjustment factors currently used in OVIS. The current OVIS procedure resulted in regression slopes (averaged over breeds) of progeny performance on sire EBVs, 0.37 and 0.35 for Wwt and Pwt respectively. Updated pre-adjustment factors improved regression slopes across breeds to 0.40 and 0.38 respectively. When the regression slopes were estimated using EBVs derived using adjustment factors based on the average of the two breeds in each of the White Suffolk and Poll Dorset data sets, predictability of EBVs was not significantly different from that using breed-specific adjustment factors (result not shown).
Correlations between EBVs estimated from linear models and those based on pre-adjustment
Spearman correlations between EBVs estimated from a linear mixed model and those estimated using updated adjustment factors are presented for all animals, top 10% animals on EBVs, young rams, and young progeny (Table 7). Correlations were very strong for Wwt and Pwt in full, young progeny and young ram data sets (at least 0.98 in both breeds). Correlations of 0.92 and 0.94 were observed in the top 10% of the animals for Wwt for White Suffolk and Poll Dorset breed respectively. Correlations between EBVs for Pwt were similar to those for Wwt.
Evaluation of interaction among fixed effects
Interaction effects that were observed significant were: year of birth by age (P < 0.05), flock by birth type by rear type (P < 0.001), flock by age (P < 0.001), flock by sex by age (P < 0.001) for both Wwt and Pwt. Interaction effects of sex by age and birth type by rear type were non-significant.
Comparison between linear mixed models and pre-adjustment
When averaged across the breeds, the reference linear model (Model 1) produced a significantly (P < 0.001) better regression slope of progeny performance on sire EBVs for Wwt and Pwt (0.47 and 0.44 respectively) than did pre-adjustment of data using updated adjustment factors (0.40 and 0.38 respectively; Table 8). Regression slopes improved slightly more when flock by sex by age interaction was inclueded in the model, with average regression slopes across breeds of 0.48 and 0.46 for Wwt and Pwt respectively. Including flock by birth type by rear type interaction in the prediction model also increased the regression slope averaged across breeds, compared with the reference linear model for both traits. For Wwt, fitting the flock by sex by age interaction increased the regression slope slightly more than did fitting a flock by birth type by rear type interaction. We also fitted combinations of interaction effects, e.g. flock by birth type by rear type and flock by sex by age interaction, but this did not increase the predictability of EBVs and was discarded. Including the flock by sex by age interaction was significantly (P < 0.05) better than was the reference linear model in Poll Dorset sheep, but not for White Suffolk sheep (P > 0.05). Improvements in regression slopes from including the flock by sex by age interaction versus the reference linear model were 0.02 and 0.04 for Wwt and Pwt respectively for Poll Dorset sheep, and were 0.01 for both Wwt and Pwt respectively in White Suffolk Sheep. Regression slopes were closer to 0.5 in White Suffolk than in Poll Dorset sheep, particularly for linear mixed models that included flock by age or flock by sex by age interactions.
Variation among flocks in the effect of pre-adjustment
For the four Poll Dorset flocks, when EBVs were estimated from the pre-adjustment and compared with EBVs estimated from a linear mixed model, rank correlation of EBVs was observed to be lower than 1, indicating re-ranking of EBVs between these methods. Rank correlations between EBVs estimated from the two methods were much lower for Flocks 2 and 4 than for other flocks using OVIS adjustment factors for Pwt, which indicates high re-ranking of EBVs occurring in these flocks, which is more evident when only the top 10% of animals are considered (Table 9). Further, the relationship between mean age and mean weight from these flocks differed more from the relationship seen in the larger Poll Dorset data. Linear mixed model produced a regression slope close to expectation, which demonstrated that EBVs estimated from linear mixed model are better. Therefore, Flocks 2 and 4 could be problematic because of high re-ranking of EBVs that is occurring in these flocks. A similar trend was also observed in Wwt in using OVIS adjustment factors (result not shown).
Discussion
Genetic parameters
Genetic evaluation is based on accurate estimates of genetic parameters, and for this study, genetic parameters were re-estimated rather than using existing parameters used in OVIS. For Poll Dorset, heritability estimates from this study were similar to previous findings, with 0.05 for Wwt and 0.08 Pwt (Brown et al. 2009). Further, heritability parameters for Wwt and Pwt observed in this study were significantly different from those of earlier studies (Safari et al. 2005; Brown et al. 2016), where estimates were obtained without fitting sire by flock-year interaction effects in the model.
OVIS pre-adjustment versus updated pre-adjustment
Two adjustment factors were validated in the large-scale genetic evaluation for Australian sheep, namely, OVIS adjustment factors and updated adjustment factors. Updated age intercept values (−73 and −77 for White Suffolk and Poll Dorset sheep respectively) were observed to be higher than current value used in OVIS for Wwt (−86), showing that the pre-weaning growth rate of sheep has increased over time. Similarly, age intercept values (−77 and −98 for White Suffolk and Poll Dorset sheep respectively) were higher than those used in OVIS for Pwt (−200), also showing an increased growth rate to post-weaning assessment. This would be due to changes in data over time, as well as recording at an earlier age for both Wwt and Pwt. A higher age intercept value in the White Suffolk breed indicates that the growth rate of White Suffolk is higher than that of Poll Dorset sheep. However, when breed-specific adjustment factors were averaged, and the effect on EBVs on each breed was examined, it did not produce significantly different predictive ability when compared with breed-specific adjustment factors. Therefore, breed-specific adjustment factors are not needed for each breed. Updated pre-adjustment factors increased the regression slopes of progeny performance on sire EBVs compared with adjustment factors currently used in OVIS. The main reason for this difference was age correction because animals were selected for higher growth rate over the years. The age intercept value needs to be updated to better reflect current growth. However, this difference may be small because some of the age effects are captured by the contemporary group due to age slicing in the definition of the contemporary group. Further, adjustment factors used in OVIS cause high re-ranking of animals and it was observed that re-ranking of animals was flock-dependent. Results indicated that pre-adjustment factors currently used in OVIS do not adequately correct for fixed effects as well as the updated pre-adjustment factors from recent data. Therefore, it is recommended that updated pre-adjustment factors from multi-breed analysis be used in the OVIS evaluation.
Linear model vs pre-adjustment
The linear mixed model provided significantly better predictions of progeny performance from sire EBVs than when pre-adjustment of data was applied in estimating the EBVs. The main reason behind the linear model performing better than pre-adjustment could be due to the off-diagonal elements of the mixed model equation (X′Z and Z′X), which are absent in the pre-adjustment. Further, EBVs estimated from pre-adjustment are not consistent in some flocks. Therefore, it is better to use a linear mixed model than pre-adjustment to increase the accuracy of EBVs in predicting performance of future progeny if linear mixed models are feasible for computation. Ali and Mohammad (2017) also described that a perfect adjustment is nearly impossible. Paneru et al. (2021) also observed that the linear mixed model produced significantly improved regression slopes, over pre-adjustment, for ultrasound scan carcase traits in Australian sheep.
Correlation of EBVs
The correlation of EBVs estimated from the linear mixed model with those estimated from pre-adjustment was higher when updated pre-adjustment factors were used than with those currently used in OVIS. The correlation of EBVs from these two methods was not equal to 1 because the linear mixed model cannot make the multiplicative adjustment. Most of the multiplicative pre-adjustment factors considered assume a linear relationship for shorter intervals than additive pre-adjustment factors, which assume a linear relationship between variables from start to end (Raymond 1982). Results showed that ranking of the animals on the basis of EBVs are less affected when EBVs were estimated from pre-adjustment than from a linear mixed model. This is also true for young sire, which has less information source to estimate EBVs. More re-ranking on EBVs occurred for superior animals when EBVs were estimated from a linear mixed model than when pre-adjustment of data occurred. Therefore, pre-adjustment affects our ability to select outstanding animals for Wwt and Pwt and, eventually, affects the genetic gain from the breeding program. Further, pre-adjustment of data introduced more variance in the EBVs than did applying a linear mixed model to the data. Although we expect a slightly lower correlation in truncating data to the top 10% of animals, the still lower correlation indicates a significant re-ranking of EBVs between the two methods.
Inclusion of interaction fixed effects in the linear model
Regression of progeny phenotype on sire EBVs obtained from the model with either flock by age interaction or flock by sex by age interaction was slightly closer to 0.5 than were those obtained from a model without extra interaction effects for both weaning and post-weaning weights. Further, flock by sex by age interaction was significantly better than the reference linear mixed model in Poll Dorset sheep and non-significant in White Suffolk sheep. This suggests that age adjustment should differ between flocks and for males and females within these flocks because the growth rate of animals varies among flocks. Therefore, it may be better to use the flock by age interaction or flock by sex by age interaction to better account for flock and age effects. However, the use of interaction effects involving flock will use more degrees of freedom in the model, as well as more memory, and a significantly higher computation time to complete analyses, which may not be desirable for the current evaluation, with millions of animals in the analysis. A simple linear mixed model could be the best alternative. However, computing power is increasing at a fast pace, and it could be possible to incorporate the extra interaction effect in the future. Another consideration for fitting an extra interaction is that there should be enough observations in each subclass to be able to fit it. Otherwise, the estimate will be affected by sampling errors (Notter and Brown 2015). In the data used by this study, there were enough observations in each flock or flock by sex by age subclass to estimate the interactions effect well. Further, interaction effects should be consistent and predictable over time. When a subset of data was created by year of birth, this was confirmed. The ability to predict future progeny performance in Wwt and Pwt in Australian Terminal breeds from sire EBVs in this study was consistent with previous findings (Huisman et al. 2015).
Conclusions
Predictive ability of a model estimating EBVs using updated pre-adjustment factors was observed to be slightly better than current OVIS pre-adjustment factors used for weaning and post-weaning weights of Terminal breeds. Further, a linear mixed model brings significant improvements in the regression slopes in weaning and post-weaning weights compared with the pre-adjustment of data. Linear mixed models that included either flock by sex by age or flock by age interactions effects produced slightly better regression slopes of progeny phenotypes on sire EBVs than did the linear mixed model excluding interaction effects, in estimating breeding values. A linear mixed model with flock by sex by age interaction is recommended for future sheep genetic evaluation through OVIS if it is computationally feasible, although a linear mixed model without interaction is an alternative in the short term. These results allow industry and researchers to choose an appropriate model to account for systematic environmental effects in large-scale genetic evaluation for bodyweight traits recorded in young animals. As these findings were obtained from Terminal breeds, further investigation would be needed to identify whether they apply to a wider range of traits and to traits recorded in the Merino and Maternal breeds.
Data availability
Data used in this study were provided by the Sheep Genetics. Data were used on the condition that it will be kept confidential and cannot be shared publicly.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
This research was conducted using data provided by Sheep Genetics. The first author is supported by the University of New England (UNE) via International Postgraduate Research Award (UNE IPRA).
References
Albuquerque LG, Meyer K (2001) Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. Journal of Animal Science 79, 2776–2789.| Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle.Crossref | GoogleScholarGoogle Scholar | 11768105PubMed |
Ali M, Mohammad F (2017) Genetic evaluation of growth traits in Iranian Kordi Sheep using random regression model with homogeneous and heterogeneous residual variances. Genetika 49, 469–482.
| Genetic evaluation of growth traits in Iranian Kordi Sheep using random regression model with homogeneous and heterogeneous residual variances.Crossref | GoogleScholarGoogle Scholar |
Brown DJ, Tier B, Reverter A, Banks R, Graser HU (2000) OVIS: a multiple trait breeding value estimation program for genetic evaluation of sheep. Wool Technology and Sheep Breeding 48, 285–297.
Brown DJ, Huisman AE, Swan AA, Graser H-U, Woolaston RR, Ball AJ, Atkins KD, Banks RG (2007) Genetic evaluation for the Australian sheep industry. In ‘The proceedings of the association for the advancement of animal breeding and genetics’. (University of New England: Armidale, NSW, Australia)
Brown D, Swan A, Johnston D, Graser H (2009) Sire by flock year interactions for body weight in Poll Dorset sheep. In ‘The association for the advancement of animal breeding and genetics, South Australia’. (Association for the Advancement of Animal Breeding and Genetics: Brisbane, Qld, Australia)
Brown DJ, Swan AA, Gill JS, Ball AJ, Banks RG (2016) Genetic parameters for liveweight, wool and worm resistance traits in multi-breed Australian meat sheep. 1. Description of traits, fixed effects, variance components and their ratios. Animal Production Science 56, 1442–1448.
| Genetic parameters for liveweight, wool and worm resistance traits in multi-breed Australian meat sheep. 1. Description of traits, fixed effects, variance components and their ratios.Crossref | GoogleScholarGoogle Scholar |
Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R (2015) ‘ASReml user guide 4.1 functional specification.’ (VSN International Ltd: Hemel Hempstead, UK)
Henderson CR (1982) Analysis of covariance in the mixed model: higher-level, nonhomogeneous, and random regressions. Biometrics 38, 623–640.
| Analysis of covariance in the mixed model: higher-level, nonhomogeneous, and random regressions.Crossref | GoogleScholarGoogle Scholar | 7171692PubMed |
Henderson CR (1984) ‘Application of linear models in animal breeding.’ (University of Guelph: Guelph, ON, Canada)
Huisman AE, Brown DJ, Fogarty NM (2015) Ability of sire breeding values to predict progeny bodyweight, fat and muscle using various transformations across environments in terminal sire sheep breeds. Animal Production Science 56, 95–101.
| Ability of sire breeding values to predict progeny bodyweight, fat and muscle using various transformations across environments in terminal sire sheep breeds.Crossref | GoogleScholarGoogle Scholar |
Laird NM, Ware JH (1982) Random-effects models for longitudinal data. Biometrics 38, 963–974.
| Random-effects models for longitudinal data.Crossref | GoogleScholarGoogle Scholar | 7168798PubMed |
Meyer K (1998) Estimating covariance functions for longitudinal data using a random regression model. Genetics Selection Evolution 30, 221
| Estimating covariance functions for longitudinal data using a random regression model.Crossref | GoogleScholarGoogle Scholar |
Meyer K (2004) Scope for a random regression model in genetic evaluation of beef cattle for growth. Livestock Production Science 86, 69–83.
| Scope for a random regression model in genetic evaluation of beef cattle for growth.Crossref | GoogleScholarGoogle Scholar |
Notter DR, Brown DJ (2015) Effects of birth-rearing type on weaning weights in meat sheep are systematically associated with differences in mean performance among flocks. Genetics Selection Evolution 47, 57
| Effects of birth-rearing type on weaning weights in meat sheep are systematically associated with differences in mean performance among flocks.Crossref | GoogleScholarGoogle Scholar |
Paneru U, Brown DJ, Moghaddar N, Van der Werf JHJ (2021) Investigation of methods for inclusion of fixed effects for ultrasound scan carcasss traits in large scale sheep genetic evaluation. In ‘The association for the advancement of animal breeding and genetics.’ (University of Adelaide: Adelaide, SA, Australia)
Raymond CA (1982) ‘Systematic environmental effects on beef cattle growth (Master).’ (University of New England)
Safari E, Fogarty NM, Gilmour AR (2005) A review of genetic parameter estimates for wool, growth, meat and reproduction traits in sheep. Livestock Production Science 92, 271–289.
| A review of genetic parameter estimates for wool, growth, meat and reproduction traits in sheep.Crossref | GoogleScholarGoogle Scholar |
1 Each age class based on intervals of 41 days within the range 115–345 days for age at recording.






