The Modular Breeding Program Simulator (MoBPS) allows efficient simulation of complex breeding programs
Torsten Pook A B , Christian Reimer A B , Alexander Freudenberg C , Lisa Büttgen
A B , Christian Reimer A B , Alexander Freudenberg C , Lisa Büttgen  A B , Johannes Geibel
A B , Johannes Geibel  A B , Amudha Ganesan A , Ngoc-Thuy Ha A B , Martin Schlather B C , Lars Friis Mikkelsen D and Henner Simianer A B
A B , Amudha Ganesan A , Ngoc-Thuy Ha A B , Martin Schlather B C , Lars Friis Mikkelsen D and Henner Simianer A B
A University of Goettingen, Department of Animal Sciences, Animal Breeding and Genetics Group, Albrecht-Thaer Weg 3, 37075 Goettingen, Germany.
B University of Goettingen, Center for Integrated Breeding Research, Albrecht-Thaer Weg 3, 37075 Goettingen, Germany.
C University of Mannheim, Applied Stochastics Group, B6 26, 68159 Mannheim, Germany.
D Ellegaard Göttingen Minipigs, Sorø Landevej 300, 4261 Dalmose, Denmark.
E Corresponding author. Email: torsten.pook@uni-goettingen.de
Animal Production Science - https://doi.org/10.1071/AN21076
Submitted: 11 February 2021 Accepted: 27 August 2021 Published online: 23 September 2021
Journal Compilation © CSIRO 2021 Open Access CC BY-NC-ND
Abstract
Context: Breeding programs aim at improving the genetic characteristics of livestock populations with respect to productivity, fitness and adaptation, while controlling negative effects such as inbreeding or health and welfare issues. As breeding is affected by a variety of interdependent factors, the analysis of the effect of certain breeding actions and the optimisation of a breeding program are highly complex tasks.
Aims: This study was conducted to display the potential of using stochastic simulation to analyse, evaluate and compare breeding programs and to show how the Modular Breeding Program Simulator (MoBPS) simulation framework can further enhance this.
Methods: In this study, a simplified version of the breeding program of Göttingen Minipigs was simulated to analyse the impact of genotyping and optimum contribution selection in regard to both genetic gain and diversity. The software MoBPS was used as the backend simulation software and was extended to allow for a more realistic modelling of pig breeding programs. Among others, extensions include the simulation of phenotypes with discrete observations (e.g. teat count), variable litter sizes, and a breeding value estimation in the associated R-package miraculix that utilises a graphics processing unit.
Key results: Genotyping with the subsequent use of genomic best linear unbiased prediction (GBLUP) led to substantial increases in genetic gain (15.3%) compared with a pedigree-based BLUP, while reducing the increase of inbreeding by 24.8%. The additional use of optimum genetic selection was shown to be favourable compared with the plain selection of top boars. The use of graphics processing unit-based breeding value estimation with known heritability was ~100 times faster than the state-of-the-art R-package rrBLUP.
Conclusions: The results regarding the effect of both genotyping and optimal contribution selection are in line with well established results. Paired with additional new features such as the modelling of discrete phenotypes and adaptable litter sizes, this confirms MoBPS to be a unique tool for the realistic modelling of modern breeding programs.
Implications: The MoBPS framework provides a powerful tool for scientists and breeders to perform stochastic simulations to optimise the practical design of modern breeding programs to secure standardised breeding of high-quality animals and answer associated research questions.
Keywords: resource management, animal breeding, Göttingen Minipigs, optimum contribution selection, OGC, OCS.
Introduction
Breeding programs aim at improving the genetic characteristics of livestock populations with respect to productivity, fitness and adaptation, while controlling negative effects such as inbreeding or health and welfare issues. As breeding is affected by a variety of interdependent factors, the analysis of the effect of certain breeding actions and the optimisation of a breeding program are highly complex tasks. Although quantitative theory, such as the breeders’ equation (Falconer and Mackay 1996), can give approximations when considering single generations or relatively simple designs, this typically is not sufficient for todays’ complex breeding programs.
With increasing computing power, a relatively new approach to answer these questions is the execution of stochastic simulation by tools such as MoBPS (Pook et al. 2020). Stochastic simulations typically simulate each individual mating, including recombination events in the meiosis, and common breeding actions such as the phenotyping on a per individual basis. In comparison to a deterministic analysis based on quantitative genetic theory, such as implemented in ZPLAN+ (Täubert et al. 2010), stochastic simulations are computationally highly demanding, especially with respect to the simulation of meiosis and the estimation of breeding values.
While simulation tools have become more and more sophisticated and powerful, both research questions of scientists and practical design questions of breeders have become more complex at the same pace. Thus, simulation software frameworks constantly need to grow to allow for a larger population, to provide more modelling options for genetic traits, and to include new selection techniques, while still being accessible to a wide audience and not overwhelm the potential user by the sheer flood of parameter options. To help with those issues, Simianer et al. (2021) recently proposed a unifying concept to describe breeding programs in a comprehensive, unambiguous and reproducible way.
Most large-scale breeding programs use genotyping of at least some individuals to get a more accurate breeding value estimation, to control inbreeding rates, to confirm the pedigree, and to potentially reduce the generation interval (Meuwissen et al. 2001; Schaeffer 2006; Henryon et al. 2014). However, in small-scale breeding programs, genotyping still represents a substantial cost factor – and often it is not immediately clear whether the cost of genotyping is compensated by the benefits of genomic analysis.
In the present work, we will introduce various new features in the simulation framework MoBPS to more realistically model modern breeding programs and will display the potential of the framework to answer real-world breeding questions through simulation studies. To this end, we will exemplarily analyse the potential benefits of genotyping in the breeding program of Göttingen Minipigs (Reimer et al. 2020). Göttingen Minipig is the smallest commercially available minipig breed under a controlled breeding scheme, its breeding is globally organised in multiple isolated and independent colonies, and it is used in biomedical research as an animal model for various human disease areas and in preclinical toxicology and safety assessment studies (Pedersen and Mikkelsen 2019). The interested reader is referred to Simianer and Köhn (2010) for more details. Furthermore, we will introduce a new graphics processing unit (GPU)-based implementation to derive the genomic relationship matrix and to perform genomic best linear unbiased prediction (GBLUP) by solving the mixed model with known variance components, which massively reduces the computing time of this procedure.
Materials and methods
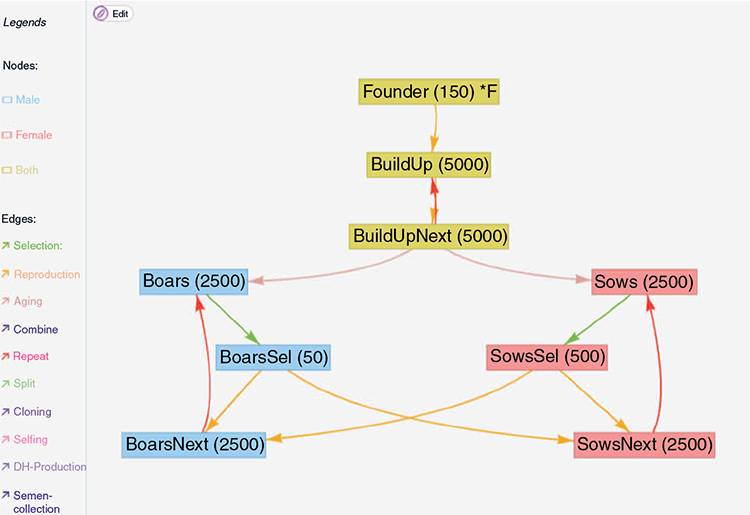
In this study, the R-package MoBPS (Pook et al. 2020) was used as the backend simulation software. To generate a realistic initial population, real genomic data of 150 Göttingen Minipigs genotyped with an Affymetrix Axiom™ Porcine Genotyping Array (600K) was used as a set of founders. On the basis of these individuals, a stock of an arbitrarily chosen size of 5000 animals was generated by randomly mating founder individuals. Furthermore, three generations of random mating within the flock were simulated to build up a basic pedigree structure. Founder individuals were assumed to be related according to a genomic relationship matrix derived following VanRaden (2008). In case no genomic data are available, a valid alternative would be the simulation of a far higher number of generations, say 1000, to build up a basic LD structure (function: founder.simulation() in MoBPS). For all matings, an average litter size of 5.6 was assumed, with the distribution of the litter size given in Table 1. For simplicity reasons, litter size was assumed to be independent from genetic components.

|
Three independent quantitative traits were simulated assuming 1000 underlying purely additive quantitative trait loci each, with effect sizes drawn from a Gaussian distribution and heritabilities of h12 = 0.3, h22 = 0.3 and h32 = 0.1 respectively. Traits were standardised to have an underlying true genetic variance of 100 and all animals were phenotyped for all three traits. Trait 1 can be thought of as a main growth trait (such as ‘smallness’, since a small body size is highly desirable for a porcine animal model), and Trait 3 represents a typical functional trait such as fertility. Phenotypes of the second trait were assumed to be observed in a discrete distribution to mimic a trait such as the teat count, with the distribution in the founder population given in Table 2. Note that the underlying trait still has a quantitative background and only the phenotypic expression is affected by this. An in-depth description of the generation of discrete value traits can be found in the MoBPS user guidelines (available at https://github.com/tpook92/MoBPS). In case real genomic and phenotypic data would be available, one could consider estimating quantitative trait loci effects via ridge regression BLUP to place marker effects onto known-effect regions (effect.estimate.add() in MoBPS).

|
A schematic overview of the breeding program itself is given in Fig. 1. The given breeding scheme can also be found as a template in the MoBPSweb application at www.mobps.de (Pook et al. 2021). In the following, we will consider five different selection strategies that require different amounts of genotyping:
|
-
Phenotypic selection
-
Pedigree BLUP (no genotyping)
-
Single-step genomic BLUP (10% genotyping)
-
Single-step genomic BLUP (25% genotyping)
-
Genomic BLUP (100% genotyping)
In case a breeding value estimation was performed, the animals of the last two generations were used with a pedigree-depth of 7. The genomic relationship matrix for the genotyped individuals was derived according to VanRaden (2008), and in cases in which not all individuals were genotyped, the combined relationship matrix for genotyped and non-phenotyped animals was derived via the single-step framework (Aguilar et al. 2010; Legarra et al. 2014).
The top 50 breeding boars and top 500 breeding sows were selected on the basis of a selection index, with equal weights on the three quantitative traits.
As traits were modelled to be uncorrelated and have the same overall genetic variance, single-trait models were used for the breeding value estimation and the selection index was a plain combination of the estimated breeding values. To handle more complex and realistic scenarios, both modelling of correlated traits and more complex selection indices that utilise the reliability of the estimated breeding values and correlation between traits are implemented in MoBPS (Hazel and Lush 1942; Miesenberger 1997).
Furthermore, we considered the use of optimum contribution selection (Meuwissen 1997) for the selection of the breeding boars. For this, the method introduced in Wellmann (2019), which is implemented in the R-package optiSel (Wellmann 2017), was used with the target function to maximise the breeding value (‘max.BV’), while limiting the increase in average kinship (‘ub.sKin’). This functionality is also implemented within the MoBPS framework and was tested as an alternative selection criterion in all scenarios, except plain phenotypic selection.
The described breeding cycle was repeated for 10 generations and averages of 50 independent simulations per scenario were used as results.
To reduce computing times, variance components were assumed to be known in the mixed model. Furthermore, the miraculix package was extended to utilise GPU resources. This GPU version relies on the cutlass and cuSolver libraries by NVIDIA (see https://github.com/NVIDIA/cutlass) for optimising memory latency and utilises bit compression to minimise memory transfers. By combining tailored two-bit matrix multiplication algorithms with instruction sets of state-of-the-art GPUs further optimises the actual computing times required for the breeding value estimation.
Results
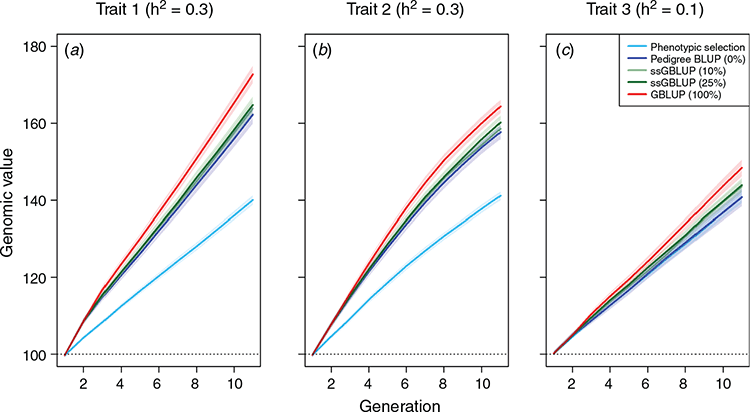
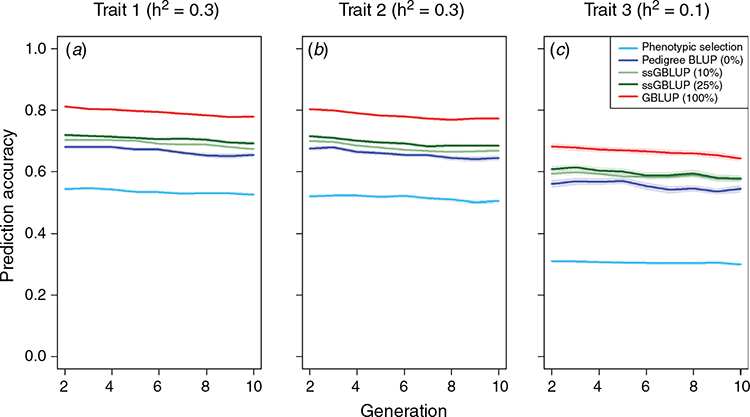
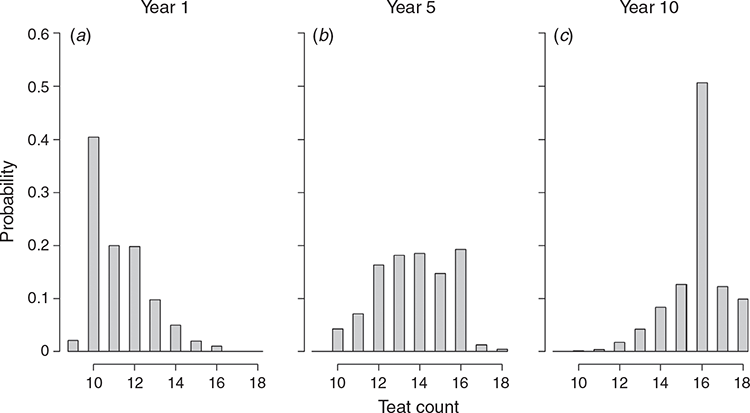
Across the different scenarios, we observed increasing prediction accuracy when a more sophisticated model was used for genomic prediction and/or the share of genotyped animals was increased. For example, the relative gain after 10 breeding cycles was 60.0% higher for the main growth trait when the phenotypic selection was replaced by a pedigree-based breeding value estimation (Fig. 2a). The relative gain when switching from pedigree BLUP (Scenario 2) to GBLUP (Scenario 5) was still substantial (15.3%), while further gains when using single-step BLUP were low. The genetic gain for the teat count trait was slightly lower than for the purely quantitative trait with the same heritability (Fig. 2b). Note that the discrete distribution was simulated with a maximum value of 18, which is reached by a substantial share of the animals (~10%, Fig. 3), hindering differentiation between top animals and, thus, also further genetic progress. Details on the obtained prediction accuracies are given in Fig. 4. As the additive genetic variance is going down slightly over time, while residual variances are simulated to remain the same, prediction accuracies slightly decrease over time. In practice, the introduction of new genetic variance and a larger training population over time will usually compensate for this.
|
In regard to analysing genetic diversity, average levels of kinship and inbreeding (Fig. 5) were calculated on the basis of the share of the genome in identity-by-descent (Donnelly 1983). As underlying points of recombination are known in MoBPS, this can directly be calculated. Note that this measure does not account for inbreeding occurring before the founder generation of the simulation and thus should be seen as an indicator for the increase of inbreeding only since the founder generation. Since the overall selection pressure is lowest when applying phenotypic selection, this results in by far the lowest increase in both kinship and inbreeding. Although genetic gains were highest in the scenario using genomic BLUP (Scenario 5), increases in inbreeding are lower than for all other BLUP-based scenarios, with GBLUP leading to a reduction of the average kinship of 24.8%, 22.5% and 18.3% compared with Scenarios 2, 3 and 4 respectively. Since GBLUP, by design, should be superior to pedigree-based methods to distinguish between close relatives (e.g. full sibs) and usually leads to the selection of animals from more families (Daetwyler et al. 2007), this should not be that surprising.

|
The performance of the optimum contribution selection for selecting breeding boars highly depends on the model parameter ‘ub.sKin’, which determines the maximum increase in average kinship per generation and can be interpreted as a weighting between genetic progress and genetic diversity. Across all scenarios, results were very similar; therefore, only Scenario 5 (GBLUP) is presented here. Overall, there are weightings that lead to both higher genetic gain and lower average kinship, hence being strictly better than the plain selection of the top breeding boars. For example, with similar genetic progress, we have a reduction in the average kinship by 15.2%, from 0.101 (plain selection) to 0.086 after 10 generations (Fig. 6). When restricting the increase in kinship to 0.005 per generation, this results in a genetic gain of 43.3 and an average kinship of 0.091 (compared with 42.3 and 0.101 in Scenario 5). When allowing for an extremely high increase in kinship, the short-term genetic gain is slightly increased, but after 10 generations, resulting gains are lower as genetic diversity has decreased heavily.

|
Depending on the scenario, a single simulation run took up to 21.9 min on a single core of an Intel Xeon Gold 6154 3.00GHz CPU. Thereof, 10.6 min were used for the generation of new animals, calculation of pedigree, single-step and genomic relationship matrices took 1.3, 3.2 and 0.7 min, and solving of the mixed model equations took 3.8 min. The whole process of a single breeding value estimation for a single trait including the calculation of the relationship matrix for 10 000 full genotyped individuals took 30 s (or 14 and 9 s when using 5 and 20 cores). The GPU implementation on a RTX 2080 Ti reduced the 30 s to less than 4 s (Schlather et al. 2021). In comparison, rrBLUP (Endelman 2011), which estimates also the variance components, would need 198 s. For a larger number of individuals, the traditional rrBLUP approach took ~100 times as long as the GPU-based approach via miraculix (Table 3). Although almost negligible in our scenarios, the computing times for solving the mixed model scales cubically with the number of individuals. Therefore, this is a critical bottleneck for large-scale simulation, as other computational factors such as the generation of individuals, scale approximately linear. The assumption of known heritability might not be true in practice; however, it is common practice to avoid re-estimating variance components for every new breeding value estimation. Especially for large-scale breeding programs, heritability estimates should be very accurate, so that the impact on the prediction accuracies should be only minimal.

|
Discussion
As expected, the use of genomic data improves the accuracy of genomic prediction and thus leads to higher genetic gain in the breeding program of Göttingen Minipigs. In a simulation study, we could quantify the expected gain to be ~15% between a pedigree-based and a fully genomic evaluation, while reducing gains in inbreeding by 25%. Note that one of the main breeding objectives in the Göttingen Minipig is a uniform reaction in medical tests and, thus, high genetic similarity among animals is actually desired, while negative effects of inbreeding must still be avoided. This is a particularly difficult breeding objective, as low genetic diversity usually means high inbreeding and vice versa.
The benefits of genotyping go even further, as it allows to validate the pedigree data and enables further downstream analyses such as genome-wide association studies. Furthermore, genotyping should be of even higher benefit when estimating breeding values for non-phenotyped animals to potentially save phenotyping costs and/or reduce the generation interval (Schaeffer 2006). Assuming genotyping costs of 25€ per animal, the yearly costs of genotyping will sum up to 125 000€. A breeding company needs to offset these costs against the potential benefits. Note that MoBPS could also answer follow-up questions and/or be used to assess more complex genotyping strategies by using different marker density arrays, use of (pooled) sequencing, and similar, which were neglected here. Furthermore, we can confirm that the use of optimal contribution selection can lead to strict improvements over the plain selection of top breeding boars with equal contributions and thus should be implemented in any case.
As a more general note, the present study has provided an exemplary case on the use of stochastic simulation to evaluate and compare breeding strategies. Without any doubt, our simulation study is a simplification of reality, as the underlying traits are usually much more complex, both in terms of genetic architecture and in how they are derived (e.g. the weight trait in the Göttingen Minipig is a weighted combination of multiple weight measurements at different age points; Köhn et al. 2007). As this, in the end, should still result in a trait that approximately corresponds to a Gaussian distribution, this should only have a small impact on the overall results.
In general, before setting up a simulation study, the most important factors influencing the simulation should be identified. The inclusion of any such factor should be well considered, as it might unnecessarily increase the complexity of the model. Note that many model extensions will affect different scenarios in similar ways. Thus, the estimation of the overall effects might be slightly off; however, the relative differences among scenarios will typically still be accurately estimated. As this is usually of interest in a simulation study, we generally recommend keeping a simulation study on an appropriate level of simplification. However, if a more complex design is needed after all, modern simulation software such as MoBPS provides a variety of features for modelling, such breeding programs (Büttgen et al. 2020) in a flexible but still highly efficient way.
The new features introduced to the MoBPS simulation framework allow for both more realistic modelling of common breeding actions (e.g. optimum contribution selection, adaptable litter sizes) and trait architectures (e.g. discretely distributed phenotypes), which, to our knowledge, are not implemented in any other stochastic simulation framework. Note that a variety of other features have been added since the initial release of MoBPS (Pook et al. 2020) to handle subpopulations, calculate average offspring performance, use different arrays for genotyping or features to automatically avoid fullsib/halfsib matings that are not relevant for the present study but further enhance the design options in the MoBPS framework. In combination with the graphical user interface (Pook et al. 2021), the variety of pre-implemented methods allows the simple use of the MoBPS framework not only for research but also for users without scripting experience, in industry, or to assist teaching of breeding program design. At the same time, the flexibility and modular structure allows researchers to assess new and experimental methodology, such as new selection techniques or a new breeding value estimation approach. MoBPS then only takes care of the background processes (e.g. meiosis, trait simulation, data storage) and enables the simulation of an even wider range of breeding programs. Additionally, the high computation efficiency of MoBPS in regard to both highly efficient storage (Pook et al. 2020) and faster computing than with other simulators enables the efficient simulation of a high number of runs of various scenarios.
Just a single simulation run for each considered scenario will usually not be enough to detect differences between designs unless they are of large effect. In contrast to real-world breeding programs, it is, however, possible to repeat simulations without requiring a large amount of time or financial effort (besides extended computational needs). Furthermore, external factors that potentially affect the outcome do not need to be controlled. This enables the extended statistical analysis of minor changes of a breeding scheme. In contrast to most deterministic simulations (Täubert et al. 2010) or analyses based on quantitative genetics and selection theory (Falconer and Mackay 1996), the use of stochastic simulation further allows for the estimation of the variability of the outcome. Variability can be accounted for by the calculation of confidence intervals, but also the direct analysis of individual simulations to make sure a certain breeding target is reached with a given probability. In particular, for large-scale breeding programs, mimicking all computational steps performed in practice for each generation in each run of each scenario computationally can be very costly, thus highlighting the need for both simplifications and highly efficient software. For the breeding value estimation, we recommend the use of known heritabilities, as resulting prediction accuracies are only mildly affected and variance components are at least approximately known (and in many practical breeding programs are not even estimated in each cycle either). As computing time of the breeding value estimation scales cubically, further simplifications, such as the use of approximate algorithms, such asthe algorithm for proven and young (Misztal 2016), or the down-scaling of cohort sizes, might be considered.
Data availability
The script used to perform the simulations can be found at https://github.com/tpook92/MoBPS/tree/master/Exemplary_scripts. Genomic data used in the simulations is available on reasonable request to the corresponding author (Torsten.pook@uni-goettingen.de).
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
References
Aguilar I, Misztal I, Johnson DL, Legarra A, Tsuruta S, Lawlor TJ (2010) Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. Journal of Dairy Science 93, 743–752.| Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score.Crossref | GoogleScholarGoogle Scholar | 20105546PubMed |
Büttgen L, Geibel J, Simianer H, Pook T (2020) Simulation Study on the Integration of Health Traits in Horse Breeding Programs. Animals (Basel) 10, 1153
| Simulation Study on the Integration of Health Traits in Horse Breeding Programs.Crossref | GoogleScholarGoogle Scholar |
Daetwyler HD, Villanueva B, Bijma P, Woolliams JA (2007) Inbreeding in genome‐wide selection. Journal of Animal Breeding and Genetics 124, 369–376.
| Inbreeding in genome‐wide selection.Crossref | GoogleScholarGoogle Scholar | 18076474PubMed |
Donnelly KP (1983) The probability that related individuals share some section of genome identical by descent. Theoretical Population Biology 23, 34–63.
| The probability that related individuals share some section of genome identical by descent.Crossref | GoogleScholarGoogle Scholar | 6857549PubMed |
Endelman JB (2011) Ridge regression and other kernels for genomic selection with R package rrBLUP. The Plant Genome 4, 250–255.
| Ridge regression and other kernels for genomic selection with R package rrBLUP.Crossref | GoogleScholarGoogle Scholar |
Falconer DS, Mackay TF (1996) ‘Introduction to quantitative genetics,’ 4th edn. (Longmans Green: Essex, UK)
Hazel LN, Lush JL (1942) The efficiency of three methods of selection. The Journal of Heredity 33, 393–399.
| The efficiency of three methods of selection.Crossref | GoogleScholarGoogle Scholar |
Henryon M, Berg P, Sørensen AC (2014) Animal-breeding schemes using genomic information need breeding plans designed to maximise long-term genetic gains. Livestock Science 166, 38–47.
| Animal-breeding schemes using genomic information need breeding plans designed to maximise long-term genetic gains.Crossref | GoogleScholarGoogle Scholar |
Köhn F, Sharifi AR, Malovrh S, Simianer H (2007) Estimation of genetic parameters for body weight of the Goettingen minipig with random regression models. Journal of Animal Science 85, 2423
| Estimation of genetic parameters for body weight of the Goettingen minipig with random regression models.Crossref | GoogleScholarGoogle Scholar | 17526674PubMed |
Legarra A, Christensen OF, Aguilar I, Misztal I (2014) Single Step, a general approach for genomic selection. Livestock Science 166, 54–65.
| Single Step, a general approach for genomic selection.Crossref | GoogleScholarGoogle Scholar |
Meuwissen THE (1997) Maximizing the response of selection with a predefined rate of inbreeding. Journal of Animal Science 75, 934–940.
| Maximizing the response of selection with a predefined rate of inbreeding.Crossref | GoogleScholarGoogle Scholar |
Meuwissen THE, Hayes BJ, Goddard ME (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.
| Prediction of total genetic value using genome-wide dense marker maps.Crossref | GoogleScholarGoogle Scholar |
Miesenberger J (1997) ‘Zuchtzieldefinition und Indexselektion für die österreichische Rinderzucht.’ (Universität für Bodenkultur Wien (BOKU)). Available at https://forschung.boku.ac.at/fis/suchen.projekt_uebersicht?sprache_in=de&menue_id_in=300&id_in=1265 [Verified 15 July 2021]
Misztal I (2016) Inexpensive computation of the inverse of the genomic relationship matrix in populations with small effective population size. Genetics 202, 401–409.
| Inexpensive computation of the inverse of the genomic relationship matrix in populations with small effective population size.Crossref | GoogleScholarGoogle Scholar | 26584903PubMed |
Pedersen HD, Mikkelsen LF (2019) Göttingen Minipigs as large animal model in toxicology. In ‘Biomarkers in Toxicology’. pp. 75–89. (Elsevier)
Pook T, Schlather M, Simianer H (2020) MoBPS: Modular Breeding Program Simulator. G3: Genes, Genomes. Genetics 10, 1915–1918.
| MoBPS: Modular Breeding Program Simulator.Crossref | GoogleScholarGoogle Scholar |
Pook T, Büttgen L, Ganesan A, Ha N-T, Simianer H (2021) MoBPSweb: a web-based framework to simulate and compare breeding programs. G3: Genes, Genomes. Genetics 11, jkab023
| MoBPSweb: a web-based framework to simulate and compare breeding programs.Crossref | GoogleScholarGoogle Scholar |
Reimer C, Ha N-T, Sharifi AR, Geibel J, Mikkelsen LF, Schlather M, Weigend S, Simianer H (2020) Assessing breed integrity of Göttingen Minipigs. BMC Genomics 21, 308
| Assessing breed integrity of Göttingen Minipigs.Crossref | GoogleScholarGoogle Scholar | 32299342PubMed |
Schaeffer LR (2006) Strategy for applying genome‐wide selection in dairy cattle. Journal of Animal Breeding and Genetics 123, 218–223.
| Strategy for applying genome‐wide selection in dairy cattle.Crossref | GoogleScholarGoogle Scholar | 16882088PubMed |
Schlather M, Erbe M, Skene F, Freudenberg A (2021) ‘miraculix: Algebraic and Statistical Functions for Genetics.’ R-package version 1.0.1. Available at https://github.com/tpook92/MoBPS
Simianer H, Köhn F (2010) Genetic management of the Göttingen Minipig population. Journal of Pharmacological and Toxicological Methods 62, 221–226.
| Genetic management of the Göttingen Minipig population.Crossref | GoogleScholarGoogle Scholar | 20570747PubMed |
Simianer H, Büttgen L, Ganesan A, Ha NT, Pook T (2021) A unifying concept of animal breeding programmes. Journal of Animal Breeding and Genetics 2021, 1–14.
Täubert H, Reinhardt F, Simianer H (2010) ZPLAN+, a new software to evaluate and optimize animal breeding programs. In ‘World Congress on Genetics Applied to Livestock’, 950. Available at https://www.uni-goettingen.de/de/document/download/dc6158ed8a8d81851a97da84dbf9b561.pdf/t%25C3%25A4ubert.pdf
VanRaden PM (2008) Efficient methods to compute genomic predictions. Journal of Dairy Science 91, 4414–4423.
| Efficient methods to compute genomic predictions.Crossref | GoogleScholarGoogle Scholar | 18946147PubMed |
Wellmann R (2017) ‘optiSel: optimum contribution selection and population genetics.’ R Package. version 0.9.1. Available at https://cran.r-project.org/web/packages/optiSel/index.html
Wellmann R (2019) Optimum contribution selection for animal breeding and conservation: the R package optiSel. BMC Bioinformatics 20, 25
| Optimum contribution selection for animal breeding and conservation: the R package optiSel.Crossref | GoogleScholarGoogle Scholar | 30642239PubMed |