Designing dairy cattle breeding schemes under genomic selection: a review of international research
J. E. Pryce A B and H. D. Daetwyler AA Biosciences Research Division, Department of Primary Industries, 1 Park Drive, Bundoora, Vic. 3083, Australia.
B Corresponding author. Email: jennie.pryce@dpi.vic.gov.au
Animal Production Science 52(3) 107-114 https://doi.org/10.1071/AN11098
Submitted: 3 June 2011 Accepted: 1 November 2011 Published: 9 December 2011
Journal Compilation © CSIRO Publishing 2012 Open Access CC BY-NC-ND
Abstract
High rates of genetic gain can be achieved through (1) accurate predictions of breeding values (2) high intensities of selection and (3) shorter generation intervals. Reliabilities of ~60% are currently achievable using genomic selection in dairy cattle. This breakthrough means that selection of animals can happen at a very early age (i.e. as soon as a DNA sample is available) and has opened opportunities to radically redesign breeding schemes. Most research over the past decade has focussed on the feasibility of genomic selection, especially how to increase the accuracy of genomic breeding values. More recently, how to apply genomic technology to breeding schemes has generated a lot of interest. Some of this research remains the intellectual property of breeding companies, but there are examples in the public domain. Here we review published research into breeding scheme design using genomic selection and evaluate which designs appear to be promising (in terms of rates of genetic gain) and those that may have unfavourable side-effects (i.e. increasing the rate of inbreeding). The schemes range from fairly conservative designs where bulls are screened genomically to reduce numbers entering progeny testing, to schemes where very large numbers of bull calves are screened and used as sires as soon as they reach sexual maturity. More radical schemes that incorporate the use of reproductive technologies (in juveniles) and genomic selection in nucleus herds are also described. The models used are either deterministic and more recently tend to be stochastic, simulating populations of cattle. A key driver of the rate of genetic gain is the generation interval, which could range from being similar to that in conventional testing (~5 years), down to as little as 1.5 years. Generally, the rate of genetic gain is between 12% and 100% more than in conventional progeny testing, while the rate of inbreeding tends to be lower per generation than in progeny testing because Mendelian sampling terms can be estimated more accurately. However, short generation intervals can lead to higher rates of inbreeding per year in genomic breeding programs.
Introduction
Genomic selection programs estimate a prediction equation in a reference population with genotype and phenotype data. This prediction equation can then be used to predict breeding values in animals without phenotype data (Meuwissen et al. 2001). Thus, selection decisions in dairy cattle breeding can now be made on young animals with higher accuracy than that of a parent average breeding value. This has substantial implications for the design of breeding schemes, because rather than waiting until a bull has daughters with phenotypic records, a process that typically takes 5–6 years, young bulls with no progeny can be used as sires. The development of high-throughput genotyping methods and reduced genotyping cost has made the application of genomic selection feasible.
Schaeffer (2006) presented a compelling argument of why dairy cattle breeding organisations should consider replacing conventional progeny-testing schemes with breeding schemes that use genomic selection. He modified a simple four-pathway selection model for progeny testing with accuracies predicted by Meuwissen et al. (2001) of 0.75 and reduced the generation intervals in the male pathways from 6–6.5 years down to 1.75 years. The selection intensities were kept the same as in progeny testing. Schaeffer’s genomic selection scheme resulted in an increase in response to selection by a factor of 2.17, compared with that in progeny testing. He also calculated that the costs of proving bulls could be reduced by 92%. Since then, breeding schemes that also alter the selection intensity in the pathways of selection have been tested, as well as more radical structures. However, breeding scheme design under genomic selection is still a new area of research. Most of the papers presented in the current review have been published in the past 5 years. In fact, it is quite likely that most of the breeding scheme designs that have been implemented are not in the public domain because of the competitive nature of commercial breeding companies. However, the papers already published should give an indication of the type of breeding schemes of the genomic era. Our intention is to highlight strategies that appear to be consistently promising ways to organise breeding schemes. Genomic selection is in its infancy and empirical evidence of the effect of this technology on the rates of genetic gain and inbreeding is sparse. Hence, we focus on papers using computer simulation. Although there are several papers that include the economic benefits of genomic selection at a breeding-company and industry level (e.g. Schaeffer 2006; König et al. 2009), the literature in this area is too sparse to draw firm conclusions.
Modelling breeding scheme designs
The models used to evaluate breeding schemes under genomic selection can be split into two types, namely deterministic or stochastic models. Deterministic models are flexible, have low computational requirements and are generally fast to run. So, a broad range of breeding schemes can be rapidly compared. Stochastic models are chosen instead of deterministic models because, by using them, it is easier to model two-stage selection and rates of inbreeding (de Roos et al. 2011). Stochastic models require populations to be simulated over a period of time that includes initially progeny testing and then genomic selection (Pedersen et al. 2009b; Winkelman and Spelman 2010; Buch 2011; de Roos et al. 2011; Lillehammer et al. 2011; Mc Hugh et al. 2011). There are two types of stochastic models. One is partially stochastic where populations are generated, but genomic breeding values are estimated assuming a known reliability and true breeding value (Winkelman and Spelman 2010; Buch 2011; de Roos et al. 2011). The advantage with this type of stochastic model is that it is computationally less demanding than the other type of stochastic model where genomes and single nucleotide polymorphisms (SNPs) are also simulated. However, stochastic models that simulate SNPs allow the accuracy of breeding values to change due to the estimation of SNP effects and the distance between the reference population and predicted population (Lillehammer et al. 2011; Mc Hugh et al. 2011). This is useful, because accuracies have been shown to reduce if marker effects are not re-estimated (e.g. Sonesson and Meuwissen 2009). However, one of the limitations with simulating SNPs as well as animals is that to balance the run-time with the output of results, the simulated population size is often small. Other limitations include the necessity to simulate the number of quantitative trait loci (QTLs) and the size of their effects, which could affect the results obtained.
Overview of schemes
Breeding schemes concentrate on changing three terms in the breeder’s equation,
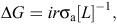
where ΔG is the genetic gain per year, i is the selection intensity, r is the accuracy of the selection, σa is the genetic standard deviation, and L is the generation interval. Assuming that the genetic variance is constant, one can calculate the rate of genetic gain by increasing the selection intensity and/or the accuracy of the selection, or by decreasing the generation interval. Genomic selection can potentially affect all three of these components at various points of the four pathways of selection found in dairy cattle. Most of the studies on breeding scheme design under genomic selection have compared rates of genetic gain and rates of inbreeding with those achieved in conventional progeny-testing schemes to allow for fair comparisons with current rates of genetic gain. This scheme will be referred to as CONV in the rest of the present paper. In progeny testing, it is generally assumed that either bull-dams are contract-mated to generate young bulls, or that young bulls are selected on their parent-average estimated breeding value (EBV). The selected bulls are then randomly mated to a population of progeny-tested cows with the objective of obtaining more than 80 daughters with records. On the basis of daughter and ancestor information, the bull’s set of EBVs can be estimated with a reliability of 80–90% at first-proof. Since the implementation of artificial insemination, progeny testing has been the method of choice to structure dairy cattle breeding schemes (Robertson and Rendel 1950).
Nicholas and Smith (1983) challenged conventional progeny testing with nucleus breeding schemes that used multiple ovulation and embryo transfer (MOET). They demonstrated that rates of genetic gain could be increased by 30% due to a reduction in generation intervals. Schemes using MOET were one of the few alternatives to progeny testing that had been implemented commercially, but had limited industry uptake partly because the accuracy of selection was considerably lower than that in conventional progeny testing (i.e. parent-average information).
One genomic breeding scheme design that has already gained popularity is partially replacing progeny testing with genomic selection (PRE-SCREEN) (see the section on implementation). Here, young bulls are genotyped and genomic breeding values are used to select and reduce the number of progeny-test candidates. The advantage with this scheme is that the number of bulls entering progeny testing is reduced, thereby offsetting the cost of genotyping young bulls.
Another approach is to screen a large number of bulls and then select the best 10–20 for widespread use as young sires (Pryce et al. 2010; Winkelman and Spelman 2010; Buch 2011; de Roos et al. 2011; Mc Hugh et al. 2011). We will refer to this scheme as a TURBO selection strategy, as in Buch (2011). Most studies assumed that bulls would be genotyped once. The exception was Winkelman and Spelman (2010) who also included schemes where bulls were pre-screened with a low-density SNP chip to identify candidates for the full-screen. The TURBO scheme is more aggressive than PRE-SCREENING and eliminates progeny testing completely.
Contract-mating of bull dams to generate bulls to enter progeny testing has been popular in CONV schemes. The role of bull dams could be reduced when it is possible for breeding companies to identify and genotype many more young bull calves on the basis of their parent-average. However, preferential treatment of bull dams may lead to over-inflation of parent-average and result in some erroneous selections of young bulls to genotype. The introduction of low-density SNP panels and the reduction in price of genotyping has made it more attractive to genotype females. The advent of low-density, inexpensive genotyping makes it inevitable that greater numbers of elite females will be genotyped. In fact, this is already being observed in the USA and Canada (B. J. Van Doormaal, pers. comm.). This should have a positive impact on bull-selection decisions, because the effect of preferential treatment of young bull dams on EBVs should be reduced and the reliability of genomic EBVs will be equivalent to several lactations of production. However, the risk of genotyping only elite females is that genetic evaluations will become biased, if these females become part of the reference population. Genotyping of females in both female pathways (dams of sires and dams of cows) are strategies that could increase the reliability of genomic EBVs and reduce bias in selection, provided commercial (non-elite) cows are genotyped as well as elite cows (Mc Hugh et al. 2011).
The highest selection intensity in female pathways is likely to be achieved through nucleus breeding schemes (NUCLEUS). Selection intensity can be increased further and generation intervals reduced by using reproductive technologies such as MOET or juvenile in vitro embryo transfer (JIVET) and sexed semen (Pedersen et al. 2009b; Pryce et al. 2010).
Rates of genetic gain and inbreeding achieved by altering breeding scheme designs
By using a PRE-SCREEN breeding scheme, it is possible to increase the rate of genetic gain by up to 30% (de Roos et al. 2011) when the genetic markers explain 100% of the genetic variation. These authors proposed that, currently, markers explaining 40% of the genetic variation (for a trait with a heritability of 0.3) is more realistic, because in this scenario, the overall reliability is 58% when phenotypic information is included in addition to direct genomic values. At this level, the response to selection was 12% more than that in conventional progeny testing. Similar results were obtained by Pryce et al. (2010) who used a deterministic model with a reliability of the genomically estimated breeding value (GEBV) of 60%. Here the rate of genetic gain achieved was 16% more than that in CONV. The rates of inbreeding per year in PRE-SCREEN ranged from 0.10% to 0.20% and were either very similar to or reduced compared with the rates of inbreeding in CONV (Buch 2011; de Roos et al. 2011; Lillehammer et al. 2011). These results showed that the rate of genetic gain can be increased or maintained through introducing GEBVs, but without making substantial alterations to the design of breeding schemes. Furthermore, the effect on annual inbreeding levels is small because generation intervals remain unchanged from CONV.
The next logical step is to market young bulls on the basis of their genomic proof. In fact, a combination of proven (i.e. graduates from progeny testing) and young bulls is the model currently being used by many breeding companies, because there is market demand for both proven and young genomically tested sires.
One of the dilemmas currently facing breeding companies is how far to reduce numbers of sires that undergo progeny testing, while achieving the same rate of genetic gain. De Roos et al. (2011) found that while proven bulls and cows are used as parents, the number of progeny-tested bulls can be reduced from 200 to 50 after screening 1000 bulls, and still maintain the same rate of genetic gain. If the market for proven bulls becomes small, then reducing the number of progeny-tested bulls is an option to decrease costs. As the reliability of genomic breeding values increases, the cost of cutting progeny testing reduces, because the best bulls can be accurately selected before progeny testing (de Roos et al. 2011). One argument in favour of keeping progeny testing is maintenance of a reference population to estimate SNP effects. However, it may be more cost-effective to update the reference population with females, provided these are not elite females with potentially biased EBVs.
TURBO or large-scale screening and use of young bulls could replace progeny testing completely. In the models reviewed, it was estimated that improvements in rates of genetic gain achievable could range between +28% and +108% over progeny testing (Table 1). The rate of genetic gain depends on the number of bulls genotyped versus the number selected as sires (selection intensity), the accuracy of selection and the generation interval. The highest selection intensity was 2.67 (König and Swalve 2009) and was achieved when the top 0.1% of animals were selected. Exactly the same selection intensity and response to selection can be achieved if the screened population is 10 000 and the best 100 are selected, which is probably a more realistic scenario. König and Swalve (2009) assumed that older females would be selected as parents, which is why the generation interval is longer than in other schemes. Harris et al. (2008) suggested that bulls should not be used widely until 2 years of age, so that congenital birth defects can be checked. However, reducing the generation interval will result in greater rates of genetic gain, as demonstrated by McHugh et al. (2011) who evaluated breeding schemes where bulls were parents at either 2 or 3 years of age. TURBO schemes resulted in the highest rates of inbreeding per year, ranging from 0.18% to 0.70%, mainly due to shortened generation intervals (Table 1).
The stochastic model used by Lillehammer et al. (2011) allowed the accuracy of genomic selection to vary according to the structure of the breeding scheme. They observed that in their TURBO schemes, the reference population used to estimate SNP effects consisted of grandsires and older relatives. This decreased the reliability when compared with other TURBO schemes, therefore stressing the importance of ensuring that the reference population is genetically similar to the population of young bulls.
With the advent of low-cost, low-density genotyping, it may be advantageous to use a genomic selection tool as a preliminary screen. Winkelman and Spelman (2010) assumed that many (1000) bull calves would be screened with a preliminary (lower-reliability) screen and the 200 bulls with the highest EBVs on the basis of the preliminary scan would then be screened with a higher-reliability scan. These authors also tested scenarios where either 1000 or 500 bulls were screened with just the secondary screen. However, they found that there was no benefit in using a preliminary and secondary screen, with the rate of genetic gain being 0.32 genetic standard deviations in most scenarios, which is a 29% improvement on CONV.
NUCLEUS breeding schemes where the male and female pathways are controlled are another option to structure breeding schemes. Pryce et al. (2010) considered a nucleus with 300 females selected for JIVET at 3 months and becoming parents at 1 year of age, and 20 sires selected, becoming parents at 2 years of age. The scheme referred to in Table 1 by de Roos et al. (2011) was actually a closed nucleus of 200 cows where each dam had 10 offspring, generating 1000 males and 1000 females. MOET was used in this scheme, so cows would be 3 years of age when their ET calves were born and the 20 selected sires would be 5 years old. The rate of inbreeding was 0.52% per year (Table 1), which was almost three times the annual rate of inbreeding under CONV.
Pryce et al. (2010) showed that using reproductive technologies aggressively could result in very high rates of genetic gain (double the rate of genetic gain of CONV). However, this was also associated with comparatively high rates of inbreeding, making implementation of this type of scheme less attractive.
Sexed semen is a reproductive technology that could be used to increase the rate of genetic gain. Pedersen et al. (2010b) used a stochastic model to study the effect of using sexed semen with and without MOET. Without MOET, there was a 6% increase in the rate of genetic gain through the use of sexed semen. However, when MOET was used, there was no additional benefit from using sexed semen in the nucleus population and only a small advantage in using sexed semen in both the nucleus and commercial populations. Interestingly, the increased rate of inbreeding per year that is observed when MOET is applied can be offset by the use of Y-sorted sexed semen in the breeding nucleus because this enables genomic selection to increase within-family selection. Thus, genomic selection could benefit from MOET, with only a small penalty in the rate of inbreeding.
Overview of impact of genomic breeding schemes on rates of inbreeding
The rate of inbreeding per year ranged between 0.07% and 0.70% (Table 1). The relatively low estimates of inbreeding per year reported by Pryce et al. (2010) were calculated using a deterministic model. While sufficient to compare schemes within their study, they are not directly comparable to estimates of inbreeding rate in other studies using stochastic methods.
The use of genomics will affect inbreeding. Whether this impact is positive or negative depends mainly, but not fully, on the inbreeding statistic considered. Most studies considered here have chosen to report both inbreeding per generation and inbreeding per year. It may be more appropriate to consider inbreeding per generation when comparing prediction methods, because the focus is on the accuracy of prediction and considering generation intervals would only serve to complicate the comparison. Another argument in favour of inbreeding per generation is that the processes that counteract inbreeding, such as mutation, also occur in each generation (Villanueva et al. 2000). However, in breeding programs, high selection intensities and large reductions in generation intervals may overwhelm these generally slow balancing processes, leading to losses in genetic variation. Thus, it may be prudent to concentrate on the inbreeding rate per year in breeding-program comparisons.
The inbreeding rate per generation was reduced by the use of genomic selection in the majority of scenarios considered, confirming earlier expectations (Woolliams et al. 2002; Daetwyler et al. 2007; Dekkers 2007). In the following paragraphs, papers that refer specifically to dairy cattle breeding programs are reviewed; for a broader discussion on the effect of genomic selection on inbreeding, refer to the above papers, as well as Pedersen et al. (2009a, 2010a) and Sonesson et al. (2010). The source of the increased accuracy of genomic selection over traditional methods is a better estimation of the Mendelian sampling term. This allows for a reduction in co-selection of relatives. Consider the selection of candidates for a progeny-test scheme, where two or more young full brothers will have the same set of EBVs. Therefore, under truncation selection, all the full brothers will be selected. In contrast, GEBVs will differ among full brothers and only the best will be selected. This leads to a reduction of inbreeding per generation, as seen in the PRE-SCREEN scenarios. The extent to which co-selection is improved depends on how well the Mendelian sampling terms can be estimated (i.e. the accuracy of genomic selection). Therefore, improvements in genomic prediction methods should decrease inbreeding per generation. It matters of course what genomic selection is compared with. In dairy cattle, progeny-test schemes already predict Mendelian sampling terms with high accuracy. Thus, when comparing TURBO to progeny-test schemes, the accuracy of young bull GEBVs is generally lower than the accuracy of progeny-test bull EBVs. This results in increased co-selection in the TURBO scheme versus the progeny-test schemes leading to higher inbreeding per generation in TURBO (de Roos et al. 2011; Mc Hugh et al. 2011). This trend is moderated if GEBVs are available on female selection candidates, resulting in less co-selection because the GEBVs will be more accurate than are traditional EBVs in cows (Schaeffer 2006; Daetwyler et al. 2007; Sorensen and Sorensen 2009).
Changes in selection intensity will affect inbreeding, regardless of whether one considers yearly or generational rates. In genomic selection, opportunities exist to screen large numbers of selection candidates and to select only the top animals. This increases selection intensity, but its effect on inbreeding is moderated if the number selected does not decrease substantially (Daetwyler et al. 2007). This strategy has been pursued to varying degrees (Tables 1 and 2). Realistically, this strategy is likely to be feasible only in the sires of sires, dams of sires, and sires of cows pathways, because generally most cow replacements are needed to maintain the herd size.
In addition to increasing accuracy through methodological advances of genomic selection, the accuracy of selection can be increased at the points of selection in the life cycle of dairy bulls and cows. These are the changes most often considered in breeding plan design. If the accuracy is increased by substituting genomic selection for traditional prediction, then inbreeding should be reduced. However, having accurate GEBVs early in life makes the selection of juveniles possible and reduces generation intervals substantially. In dairy cattle, this is likely the largest source of increased genetic gain per year, but it also increased the rate of inbreeding per year over traditional methods in some studies (Buch 2011; de Roos et al. 2011; Mc Hugh et al. 2011). While this is not due to a property of the genomic selection method itself, the potential reduction in genetic diversity is a direct result of its application and it should be taken seriously. The potential ways to counteract this trend exist already. One likely ad hoc strategy includes reducing the selection intensity of males and/or using a more genetically diverse set of bulls.
A possible outcome of genomic selection is that a higher number of bulls will be used, but individual bulls would have fewer daughters (Boichard et al. 2010). Such a trend could potentially be positive in terms of genetic diversity. A more theoretically based solution to control inbreeding is optimum contribution selection (OCS, Wray and Goddard 1994; Meuwissen 1997; Grundy et al. 1998). Its objective is to maximise genetic gain while restricting inbreeding levels through constraints on the co-ancestry of parents. Traditionally, pedigree-based relationships were used in OCS. Sonesson et al. (2010) compared using pedigree in OCS with using genomic relationships in OCS and evaluated pedigree and genomic inbreeding rates. They found that using genomic relationship in OCS was successful in keeping the genomic rate of inbreeding at the desired level and vice versa for pedigree OCS. However, when using pedigree OCS, the genomic rate of inbreeding was up to three times higher than that in genomic OCS. Pedigree OCS seemed less able to restrict inbreeding at sites with QTL of large effect, while genomic OCS resulted in a more even profile of inbreeding across the genome. This trend to higher inbreeding at QTL sites was also observed in a study by Pedersen et al. (2010a), which showed that genomic selection could result in large hitch-hiking effects. It may be necessary to re-evaluate guidelines for acceptable rates of inbreeding if it is measured genomically (Sonesson et al. 2010).
Implications for the reference population
Continuous re-estimation of marker effects in a genotyped reference population with accurate phenotypes is necessary for a successful genomic selection program (e.g. Habier et al. 2007). One risk with replacing progeny testing with breeding schemes that screen large numbers of young bulls and select only a small number of these for widespread use, is that fewer bulls will be added to the reference population on an annual basis than was the case in the past. This would decrease the accuracy of genomic prediction as the distance between the current dairy population and the majority of animals in the reference population increases (Lillehammer et al. 2011). Countries with small populations may be more affected by this issue than those with larger populations (McHugh et al. 2011). Considerable effort has gone into increasing the size of current reference populations and this effort must continue, to ensure that reference populations remain relevant to selection candidates. One of the strategies used to increase reference populations is to share genotypes. Currently, the Eurogenomics (founding partners include cattle breeding organisations from France, Germany, the Netherlands and the Nordic countries of Denmark, Norway and Sweden; Lund et al. 2010) and North American (USA and Canada) reference populations include ~20 000 and 12 000 males, respectively (Table 2).
Genotyping of cows is another way in which a larger reference population can be achieved. However, currently genotyping costs are too high for genotyping commercial dairy cows. This means that only high-merit (or elite) cows will be genotyped. High-merit cows may have been preferentially treated and therefore their phenotypes could be biased. Therefore, adding cows to the reference population could be, in some cases, detrimental. However, there are examples of research projects where females are being genotyped specifically to become part of the reference population. For example, in Australia the Dairy Futures Cooperative Research Centre’s 10 000 Holstein Cow Genomes project, where 10 000 cows (from commercial herds) will be genotyped to become part of the reference populations. In fact, collecting data on cows may actually be more important in the genomic era than ever before, because cows may become a key part of future reference populations. Decreasing genotyping costs may allow all females to be genotyped in the future. Buch (2011) compared using progeny-tested bulls in a reference population with using their genotyped daughters and phenotypes in the reference. The accuracy of genomic selection was higher when using cows because of a loss of information when using the progeny-tested bulls. This is possibly because the ‘phenotypes’ used for progeny-tested bulls are daughter-trait deviations that are the mean of a bull’s daughter group adjusted for fixed effects, thus ignoring variation around the mean. Whether this increase in accuracy alone warrants genotyping of very large numbers of cows remains to be investigated.
Another attractive aspect of having females in the reference population is that novel traits that are difficult or expensive to measure could be included in the breeding programs. Examples include health disorders, such as hoof-diseases recorded by hoof trimmers (Buch et al. 2011), residual feed intake (Pryce et al. 2011a), milk fatty acid composition (Soyeurt et al. 2011) or detailed recordings of reproductive measurements, such as pregnancy diagnosis data. One option could be to set up managed groups of information herds, selected for impeccable record-keeping.
Current-state of implementation of genomic selection
Several countries have started to implement genomic selection programs. National evaluations of genomic breeding values commenced in 2008 (Table 2), although before official national evaluations, some breeding companies were estimating genomic breeding values in-house, e.g. in 2006 for CRV in the Netherlands (S. de Roos, pers. comm.). The start date of genomic evaluations depends on the compilation of a large enough reference population and possibly also the pressure applied by enthusiastic domestic breeding companies.
The reference populations of Eurogenomics are shared (Lund et al. 2010), as are the reference populations of Canada and the USA. This means that higher reliabilities are realised in these countries. The variation in reliabilities in the Eurogenomics countries could be due to differences in methodology and the relatedness of the reference population to the predicted population. New collaborations, such as International Genomic Evaluation partnership (iGenoP), have been set up to facilitate dairy evaluation units to provide unbiased genomic evaluations through the sharing of genotypes and phenotypes. These should enable reference populations in other countries to grow and become competitive, as will the addition of females to the reference population. Adding females may be especially important to countries such as Australia and New Zealand where genotype by environment interactions between countries may be an issue in exchanging genotypes and moving to an international genetic evaluation system that includes genomic information, i.e. a genomic multiple-trait across country evaluations (GMACE) approach (VanRaden and Sullivan 2010).
Most countries start using young bulls in their AI programs from 14 to 20 months of age and large-scale screening to identify elite young sires appears to be the most popular method of selection, although there may be some screening of potential bull dams. In all countries included in Table 2, over half of the top 20 bulls were genomically evaluated with no daughters. Note that these bulls were reproductively capable, i.e. they were not young calves.
New Zealand is the only country to charge a premium of genomically tested sires. However, the cost of semen in New Zealand is low at an average of ~AU$13 per straw, for proven bulls.
USA–Canada and France currently screen most young bulls (>12 000 for each; Table 2). It is therefore unsurprising that in these countries young bulls occupy all of the top 20 places in bull rankings. France limits the number of inseminations of young bulls to try and counter the effects of large movements in bull proofs due to lower reliabilities, and other safe-guards may be in place for other countries. France is the only country where all breeding companies have stopped official progeny testing. The market share of genomically tested bulls is still only 30% because there is still a transition period from progeny-tested to genomically selected bulls. Eventually, bulls that were widely used as genomically tested sires will also be available as pseudo-progeny-tested bulls.
Genomic breeding values were released in Australia in April 2011 (at the time of writing); hence, the market share of genomically tested bulls in Australia is still to be realised. In the other countries presented in Table 2, the market share of genomically tested bulls ranges from 25% to 50%. The market share is likely to increase as the reliability of genomic evaluations increases and farmers become more confident in the technology.
Currently, many farmers purchase semen from proven bulls as they prefer high reliabilities. One option to achieve the same level of reliability as a proven bull is to combine records from daughters with a bull’s genomic-test results (König and Swalve 2009). For example, to achieve an accuracy of 0.8, for a trait with a heritability of 0.1 and accuracy of GEBV of 0.7, König and Swalve (2009) reported that records on 32 progeny would be required, compared with 70 when no GEBVs are available. However, it seems likely that the replacement of progeny testing by genomic selection is inevitable and, in this respect, the French appear to be taking the lead. Their rationale in this decision was illustrated by Boichard et al. (2010) who argued that the rate of inbreeding can be lower in a breeding scheme that uses young bulls only (i.e. a TURBO scheme) than in a scheme where 50% of sires are first-proofs and 50% are young bulls with only GEBVs, while the rate of genetic gain is almost the same.
Implementation in other dairy cattle breeds
We have concentrated on Holstein cattle because it is the dominant dairy breed globally. However, other dairy breeds would also benefit from implementing genomic selection. Unfortunately, they generally have lower population sizes and may be spread over several geographic regions. This has limited the size of reference populations and the resulting predictions are less accurate (Pryce et al. 2011b). In addition, some of these breeds have higher effective population sizes than do Holsteins (e.g. Simmental or Fleckvieh, Norwegian Red), which reduces genomic linkage disequilibrium and weakens associations between markers and QTL. One option is to develop across breed predictions. de Roos et al. (2008) estimated that at least 300 000 markers would be needed to achieve an accurate across-breed prediction using a multi-breed reference population, because of limited linkage disequilibrium across breeds. However, regenotyping at a higher density is expensive if animals are already genotyped with 50k SNP panels. One solution would be to genotype a subset of animals with a high-density (e.g. 800k) SNP panel and impute SNPs to the rest of the population genotyped with lower-density SNP panels (e.g. Browning and Browning 2009; Druet and Georges 2010; Daetwyler et al. 2011; Hickey et al. 2011; VanRaden et al. 2011). Another option is for breeds with populations in several countries to share genotypes to increase the size of reference populations. This strategy has been pursued in North America for the Jersey and Brown Swiss breeds and in Germany and Austria for Simmental. It is likely for this trend to continue as smaller breeds decide to take advantage of genomic technologies. Genomic selection is underway or planned for the following breeds: Ayrshire, Brown Swiss, Jersey, Montbeliarde, Normande, Norwegian Red, Simmental and Swedish Red.
Buch (2011) suggested that breeds other than Holsteins could differentiate themselves by selecting for traits that are closer to the breeding objective (novel traits, such as feed-conversion efficiency may be candidate traits).
Conclusions
Research into the best designs of genomic breeding programs in dairy cattle is well underway. All studies report increased genetic gain of genomic selection over non-genomic programs. In general, the advantage of genomic selection in terms of genetic progress depends on how aggressively it is pursued, with wide-spread use of young genomically tested bulls providing the best benefit. The substantial reduction in generation intervals may lead to increased annual rates of inbreeding, which will require tools, such as optimal contribution selection, to be implemented so that genetic diversity can be preserved. Further research is needed to determine the best use of cow genotypes in reference populations, as well as the best strategies to keep the reference population genetically close to selection candidates. Many countries have released national genomic breeding values and are currently in the midst of a transition to genome-assisted breeding. There is no doubt that during this transition research into improved genomic breeding programs will continue.
Acknowledgements
Funding is gratefully acknowledged from the Dairy Futures CRC, Melbourne, Australia (Jennie Pryce), and CRC for Sheep Industry Innovation, Armidale, Australia (Hans Daetwyler). We thank the following for assisting with the contents of Table 2: Kevin Beard and Gert Nieuwhof (ADHIS), Peter Thurn (Genetics Australia), Didier Boichard (INRA), Andrew Cromie (ICBF), Donagh Berry and Noirin McHugh (Teagasc), Sander de Roos (CRV), Richard Spelman and Anne Winkelman (LIC), Marie Lillehammer (Nofima Marin), John Cole and Tabitha Cooper (USDA), Morten Kargo (University of Aarhus), Gert Pedersen Aamand (Nordic Cattle Genetic Evaluation), Sven König (University of Kassel), and Fritz Reinhardt (VIT).
References
Boichard D, Ducrocq V, Fritz S, Colleau JJ (2010) Where is dairy breeding going? A vision of the future. Interbull Bulletin 41, 63–68.Browning BL, Browning SR (2009) A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated Individuals. American Journal of Human Genetics 84, 210–223.
| A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated Individuals.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXisFCrtL8%3D&md5=f35b8508f230a0710e68d56d2f433597CAS |
Buch LH (2011) Genetic improvement of functional traits in dairy cattle breeding schemes with genomic selection. PhD Thesis, Aarhus University, Denmark.
Buch LH, Sørensen AC, Lassen J, Berg P, Eriksson JÅ, Jakobsen JH, Sørensen MK (2011) Hygiene-related and feed-related hoof diseases show different patterns of genetic correlations to clinical mastitis and female fertility. Journal of Dairy Science 94, 1540–1551.
| Hygiene-related and feed-related hoof diseases show different patterns of genetic correlations to clinical mastitis and female fertility.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmvFeit7s%3D&md5=68474d38077d8a9a227a41a6bfc6fe32CAS |
Daetwyler HD, Villanueva B, Bijma P, Woolliams JA (2007) Inbreeding in genome-wide selection. Journal of Animal Breeding and Genetics 124, 369–376.
| Inbreeding in genome-wide selection.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD2sjjvFyhsQ%3D%3D&md5=5ba3cf2631fc8649c8ee5d81a416cc46CAS |
Daetwyler HD, Wiggans GR, Hayes BJ, Woolliams JA, Goddard ME (2011) Imputation of missing genotypes from sparse to high density using long-range phasing. Genetics 189, 317–327.
| Imputation of missing genotypes from sparse to high density using long-range phasing.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtlehsbvK&md5=e4d13a8264ab562e9b67c528d2066210CAS |
de Roos APW, Hayes BJ, Spelman RJ, Goddard ME (2008) Linkage disequilibrium and persistence of phase in Holstein–Friesian, Jersey and Angus cattle. Genetics 179, 1503–1512.
| Linkage disequilibrium and persistence of phase in Holstein–Friesian, Jersey and Angus cattle.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD1cvmsFeltw%3D%3D&md5=19f65e22eddf6efe5d7aa914e77a7a3cCAS |
de Roos APW, Schrooten C, Veerkamp RF, van Arendonk JAM (2011) Effects of genomic selection on genetic improvement, inbreeding, and merit of young versus proven bulls. Journal of Dairy Science 94, 1559–1567.
| Effects of genomic selection on genetic improvement, inbreeding, and merit of young versus proven bulls.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmvFeit7k%3D&md5=807608252a02edaad1fd5800bb7045d8CAS |
Dekkers JCM (2007) Prediction of response from marker-assisted and genomic selection using selection index theory. Journal of Animal Breeding and Genetics 124, 331–341.
| Prediction of response from marker-assisted and genomic selection using selection index theory.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD2sjjvFyiuw%3D%3D&md5=02eb2d1285b7c61038e0cbab1d4fdb2eCAS |
Druet T, Georges M (2010) A hidden Markov model combining linkage and linkage disequilibrium information for haplotype reconstruction and quantitative trait locus fine mapping. Genetics 184, 789–798.
| A hidden Markov model combining linkage and linkage disequilibrium information for haplotype reconstruction and quantitative trait locus fine mapping.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhsFOnurvN&md5=115ebea4006f5cc985537ecc2316ad79CAS |
Grundy B, Villanueva B, Woolliams JA (1998) Dynamic selection procedures for constrained inbreeding and their consequences for pedigree development. Genetical Research 72, 159–168.
| Dynamic selection procedures for constrained inbreeding and their consequences for pedigree development.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXmvVantQ%3D%3D&md5=622d19af4902941473e310a74db30513CAS |
Habier D, Fernando RL, Dekkers JCM (2007) The impact of genetic relationship information on genome assisted breeding values. Genetics 177, 2389–2397.
Harris BL, Johnson DL, Spelman RJ (2008) Genomic selection in New Zealand and the implications for national genetic evaluation. In ‘Proceedings of the 36th ICAR session’, Niagara Falls, NY. (Ed. JD Sattler) pp. 325–330. (ICAR, Via G. Tomassetti 3, 1/A, 00161 Rome)
Hickey J, Kinghorn B, Tier B, Wilson J, Dunstan N, van der Werf J (2011) A combined long-range phasing and long haplotype imputation method to impute phase for SNP genotypes. Genetics, Selection, Evolution. 43, 12
| A combined long-range phasing and long haplotype imputation method to impute phase for SNP genotypes.Crossref | GoogleScholarGoogle Scholar |
König S, Swalve HH (2009) Application of selection index calculations to determine selection strategies in genomic breeding programs. Journal of Dairy Science 92, 5292–5303.
| Application of selection index calculations to determine selection strategies in genomic breeding programs.Crossref | GoogleScholarGoogle Scholar |
König S, Simianer H, Willam A (2009) Economic evaluation of genomic breeding programs. Journal of Dairy Science 92, 382–391.
Lillehammer M, Meuwissen THE, Sonesson AK (2011) A comparison of dairy cattle breeding designs that use genomic selection. Journal of Dairy Science 94, 493–500.
| A comparison of dairy cattle breeding designs that use genomic selection.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXjslCms7w%3D&md5=87a49f6139c38713814092c57c639167CAS |
Lund MS, de Roos APW, de Vries AG, Druet T, Ducrocq V, Fritz S, Guillame F, Guldbrandsten B, Liu Z, Reents R, Schrooten C, Seefried M, Su G (2010) Improving genomic prediction by Eurogenomics collaboration. In ‘10th world conference of genetics applied to livestock production’, Leipzig, Germany. (German Society for Animal Science) p. 880. CD-ROM Communication paper.
Mc Hugh N, Meuwissen THE, Cromie AR, Sonesson AK (2011) Use of female information in dairy cattle breeding programs. Journal of Dairy Science 94, 4109–4118.
| Use of female information in dairy cattle breeding programs.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXpsVylurY%3D&md5=56199aac99229b6c68339bf5307725edCAS |
Meuwissen THE (1997) Maximizing the response of selection with a predefined rate of inbreeding. Journal of Animal Science 75, 934–940.
Meuwissen THE, Hayes BJ, Goddard ME (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.
Nicholas FW, Smith C (1983) Increased rates of genetic change in dairy-cattle by embryo transfer and splitting. Animal Production 36, 341–353.
| Increased rates of genetic change in dairy-cattle by embryo transfer and splitting.Crossref | GoogleScholarGoogle Scholar |
Pedersen LD, Sørensen AC, Berg P (2009a) Marker-assisted selection can reduce true as well as pedigree-estimated inbreeding. Journal of Dairy Science 92, 2214–2223.
| Marker-assisted selection can reduce true as well as pedigree-estimated inbreeding.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXlsFymsL8%3D&md5=e23d0b852d1658004096383d0fbc7f5dCAS |
Pedersen LD, Sørensen AC, Henryon M, Ansari-Mahyari S, Berg P (2009b) ADAM: a computer program to simulate selective breeding schemes for animals. Livestock Science 121, 343–344.
| ADAM: a computer program to simulate selective breeding schemes for animals.Crossref | GoogleScholarGoogle Scholar |
Pedersen LD, Sørensen AC, Berg P (2010a) Marker-assisted selection reduces expected inbreeding but can result in large effects of hitchhiking. Journal of Animal Breeding and Genetics 127, 189–198.
| Marker-assisted selection reduces expected inbreeding but can result in large effects of hitchhiking.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC3cvpsVOitA%3D%3D&md5=bc65f9f90bc432595bd429a55b29ece7CAS |
Pedersen LD, Sorensen MK, Berg P, Andersen JV, Sorensen AC (2010b) Using sexed semen has limited effect on genetic gain in a dairy cattle breeding scheme using genomic selection. In ‘10th world conference of genetics applied to livestock production’, Leipzig, Germany. (German Society for Animal Science) p. 714. CD-ROM Communication.
Pryce JE, Goddard ME, Raadsma HW, Hayes BJ (2010) Deterministic models of breeding scheme designs that incorporate genomic selection. Journal of Dairy Science 93, 5455–5466.
| Deterministic models of breeding scheme designs that incorporate genomic selection.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvVSjtQ%3D%3D&md5=f8d02320f524c9c2172ba33239724eb1CAS |
Pryce JE, Arias J, Bowman PJ, Macdonald KA, Waghorn GC, Wales WJ, Williams YL, Spelman RJ, Hayes BJ (2011a) Accuracy of genomic selection for residual feed intake and 250-day liveweight in dairy heifers using high-density (630k) SNP. Proceedings of the Association for Advancement of Animal Breeding and Genetics. 19, 367–370.
Pryce JE, Gredler B, Bolormaa S, Bowman PJ, Egger-Danner C, Fuerst C, Emmerling R, Sölkner J, Goddard ME, Hayes BJ (2011b) Genomic selection using a multi-breed, across-country reference population. Journal of Dairy Science 94, 2625–2630.
| Genomic selection using a multi-breed, across-country reference population.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvFCgt74%3D&md5=f859626fc4067fb0fbf8ad4316404129CAS |
Robertson A, Rendel JM (1950) The use of progeny testing with artificial insemination in dairy cattle. Journal of Genetics 50, 21–31.
| The use of progeny testing with artificial insemination in dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Schaeffer LR (2006) Strategy for applying genome-wide selection in dairy cattle. Journal of Animal Breeding and Genetics 123, 218–223.
| Strategy for applying genome-wide selection in dairy cattle.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD28vlvFCitA%3D%3D&md5=baf38b72655ef765385a0c797a65c8a6CAS |
Sonesson A, Meuwissen T (2009) Testing strategies for genomic selection in aquaculture breeding programs. Genetics, Selection, Evolution. 41, 37
| Testing strategies for genomic selection in aquaculture breeding programs.Crossref | GoogleScholarGoogle Scholar |
Sonesson AK, Woolliams JA, Meuwissen THE (2010) Maximising genetic gain whilst controlling rates of genomic inbreeding using genomic optimum contribution selection. In ‘World congress of genetics applied to livestock production’, Leipzig, Germany. (German Society for Animal Science) p. 892. CD-ROM Communication.
Sorensen AC, Sorensen MK (2009) Inbreeding rates in breeding programs with different strategies for using genomic selection. Interbull Bulletin 40, 94–97.
Soyeurt H, Dehareng F, Gengler N, McParland S, Wall E, Berry DP, Coffey M, Dardenne P (2011) Mid-infrared prediction of bovine milk fatty acids across multiple breeds, production systems, and countries. Journal of Dairy Science 94, 1657–1667.
| Mid-infrared prediction of bovine milk fatty acids across multiple breeds, production systems, and countries.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvFChtro%3D&md5=88f0183d5a851bd8a3297d96481389abCAS |
VanRaden P, Sullivan P (2010) International genomic evaluation methods for dairy cattle. Genetics, Selection, Evolution. 42, 7
| International genomic evaluation methods for dairy cattle.Crossref | GoogleScholarGoogle Scholar |
VanRaden PM, O’Connell JR, Wiggans GR, Weigel KA (2011) Genomic evaluations with many more genotypes. Genetics, Selection, Evolution. 43, 10
| Genomic evaluations with many more genotypes.Crossref | GoogleScholarGoogle Scholar |
Villanueva B, Bijma P, Woolliams JA (2000) Optimal mass selection policies for schemes with overlapping generations and restricted inbreeding. Genetics, Selection, Evolution. 32, 339–355.
| Optimal mass selection policies for schemes with overlapping generations and restricted inbreeding.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD2c%2Fms1Kquw%3D%3D&md5=2fd65359613cd6db3a61aa050ee54edcCAS |
Winkelman AM, Spelman RJ (2010) Response using genome-wide selection in dairy cattle breeding schemes. In ‘World congress for genetics applied to livestock production’, Leipzig, Germany. (German Society for Animal Science) p. 0290. CD-ROM Communication 714.
Woolliams JA, Pong-Wong R, Villanueva B (2002) Strategic optimisation of short- and long-term gain and inbreeding in MAS and non-MAS schemes. In ‘7th world congress of genetics applied to livestock production’, Montpellier, France. CD-ROM Communication no. 23–02.
Wray NR, Goddard ME (1994) Increasing long-term response to selection. Genetics, Selection, Evolution. 26, 431–451.
| Increasing long-term response to selection.Crossref | GoogleScholarGoogle Scholar |




