Spectral and wavelet analysis of gilgai patterns from air photography
A. E. Milne A , R. Webster A B and R. M. Lark AA Rothamsted Research, Harpenden, Hertfordshire AL5 2JQ, Great Britain.
B Corresponding author. Email: richard.webster@bbsrc.ac.uk
Australian Journal of Soil Research 48(4) 309-325 https://doi.org/10.1071/SR09189
Submitted: 26 October 2009 Accepted: 3 February 2010 Published: 16 June 2010
Abstract
Gilgais form repeating patterns that seem to be regular to some degree. We have analysed the patterns of gilgais as they appear on aerial photographs of the Bland Plain of New South Wales to discover to what degree they exhibit regularity and to estimate the spatial frequencies of the repeating patterns. We digitised rectangular sections of the photographs to produce grids of pixels at 0.063-mm intervals, equivalent to 1.3 m on the ground, with the optical density of each pixel recorded as a level of grey in the range 0 (black) to 255 (white). From the data we computed autocorrelograms and power spectra in both 1 and 2 dimensions and wavelet coefficients and wavelet packet coefficients and their variances.
Spectra of many of the individual rows of the grids contained peaks corresponding to wavelengths of ≈32 m (at Caragabal) and ≈52 m (at Back Creek). The 2-dimensional spectra have rings of relatively large power corresponding to these wavelengths in addition to their central peaks. The 1-dimensional wavelet variances have pronounced peaks at the 16–32 pixel scale, corresponding to 20–40 m on the ground. The 2-dimensional wavelet analyses revealed peaks in the variances in the same range. Back Creek has in addition a low-frequency feature caused by the much darker than average gilgais in one corner of the digitised rectangle, and this is equally evident in the 1-dimensional analyses of rows that cross this corner, where the largest contribution to wavelet packet variation is at wavelength 84–167 m. Where this feature is absent, the best wavelet packet basis indicates that variation at frequencies at or below the repeating pattern is consistent with an underlying stationary random variable, while higher-frequency components show more complex (non-stationary) behaviour. We conclude that the gilgai patterns we have examined have a regularity with wavelengths in the range 30–50 m.
Additional keywords: Bland Plain, correlogram, Fourier transform, stationarity, wavelet packet, wavelet variance, Daubechies wavelet.
Acknowledgments
This work was undertaken within Rothamsted Research’s programme in Computational and Mathematical Biology, which is funded by the Biotechnology and Biological Sciences Research Council (BBSRC).
Biswas A,
Si BC, Walley F
(2008) Spatial relationship between δ15N and elevation in agricultural landscapes. Nonlinear Processes in Geophysics 15, 397–407.
| Crossref | GoogleScholarGoogle Scholar |
showed that the 2-dimensional wavelet coefficients dM,1(x, y) are given by

where M is H for row, V for column or G for the diagonal coefficient and:
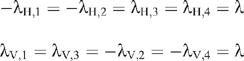
and
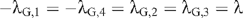
The wavelet variance is given by

where C(i, j) is the covariance between points pi and pj. If the underlying process is isotropic and stationary then we define the covariances at lags 0, 1 and 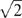 as C0, C1, and
as C0, C1, and 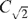 , respectively. This means that:
, respectively. This means that:
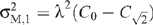
for M = H or V and:
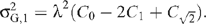
If the data are random noise then C0 = 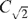 = 0 and the wavelet variances are equal. If, however, the data have a decreasing covariance function such that
= 0 and the wavelet variances are equal. If, however, the data have a decreasing covariance function such that

then σH,12 = σV,12 > σG,12. The wavelet coefficients dM,j (x, y) at j > 1 are calculated in a similar way to Eqn (12), except that in these cases pi is the scaled average of a 2j × 2j grid of data centred near x, y. Therefore similar arguments hold.


