Agronomic soil tests can be used to estimate dissolved reactive phosphorus loss
David Weaver A * , Robert Summers
A * , Robert Summers  B and Andreas Neuhaus C
B and Andreas Neuhaus C
A Department of Primary Industries and Regional Development, Western Australia, 444 Albany Highway, Albany, WA 6330, Australia.
B Department of Primary Industries and Regional Development, Western Australia, 45 Mandurah Terrace, Mandurah, WA 6210, Australia.
C CSBP Limited, Kwinana Beach Road, Kwinana, WA 6966, Australia.
Soil Research 61(7) 627-646 https://doi.org/10.1071/SR22167
Submitted: 18 July 2022 Accepted: 26 May 2023 Published: 15 June 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Phosphorus (P) use in agriculture can lead to eutrophication. Agronomic soil tests such as Colwell P and P buffering index (PBI) define critical soil P levels for pasture production. These tests have potential for re-use as environmental risk indicators of dissolved reactive P (DRP) loss from paddocks but are constrained because a 0–10 cm sample does not necessarily align with the dominant hydrological loss pathways of runoff or leaching.
Aims: To identify influences on the benchmark environmental measure of DRP (CaCl2-extractable P or CaCl2-P) by agronomic-based measures such as PBI, Colwell P and depth, and Colwell P to PBI ratio (P environmental risk index; PERI). To estimate CaCl2-P at any depth from a 0–10 cm sample, and the potential for change in DRP loss risk through the adoption of evidence-based fertiliser management based on soil testing.
Methods: Archives of 692 0–10-cm soil samples, along with 88 sites sampled at 0–10 cm and 0–1, 1–2, 2–5, 5–10, 10–20, and 20–30 cm were analysed for Colwell P, PBI, CaCl2-P, PERI, and P fertility index (PFI). Derived relationships between CaCl2-P and Colwell P for different PBI were applied to 30 981 0–10-cm samples to estimate the potential for DRP reduction resulting from the adoption of evidence-based fertiliser management.
Key results: CaCl2-P, Colwell P, PERI, and PFI decreased with depth, with an associated increase in DRP loss risk from surface soil. The CaCl2-P decreased with increasing PBI. The CaCl2-P, Colwell P, PERI, and PFI could be estimated at any depth from a 0–10 cm sample, with r2 > 0.77. The CaCl2-P was estimable from PERI, and soils with low PBI or with high PFI had high DRP loss risk. The CaCl2-P was positively correlated with Colwell P, with the slope decreasing with increasing PBI and becoming invariant when PBI > 100. When applied to the current soil Colwell P and estimated current CaCl2-P and compared to CaCl2-P at the critical Colwell P for different relative yields (RYs), DRP loss risk could be reduced by 24% for a RY target of 95%, and 59% for a RY target of 80%.
Conclusions: Because current Colwell P levels in soils exceed critical values, DRP loss risk can be substantially reduced by adopting evidence-based fertiliser management with little or no loss of utilised pasture.
Implications: Fertiliser management based on evidence of P requirements determined from soil testing has a significant role in reducing DRP loss risk.
Keywords: calcium chloride extractable P, Colwell P, dissolved reactive P, P environmental risk index, P fertility index, PBI, phosphorus, stratification.
Introduction
Phosphorus (P) is a primary plant nutrient that contributes to eutrophication in waterways through algal blooms, deoxygenation, and fish kills (Hodgkin and Hamilton 1993; Smil 2000). While a range of land use sectors contribute, diffuse agricultural sources often contribute the largest quantities of P because of its extensiveness (Kronvang et al. 2009). Reducing P loss is a priority to maintain beneficial uses of waterways, and to improve the efficiency and economics of limited farm inputs (Smil 2000; Ashley et al. 2011).
A range of factors contribute to the risk of P loss from agricultural soils, the forms of P that are lost, P mobilisation, and the pathways of P delivery to stream networks (Haygarth et al. 2005). These factors include but are not limited to landscape slope and shape, proximity to watercourses, depth to groundwater, the degree of waterlogging, soil P buffering, management factors (such as drainage, pasture type and cover, fertiliser rate and timing, soil test P and the degree of P saturation, and stocking rate), and factors beyond management control such as rainfall quantity and intensity.
Phosphorus loss risk indexes that account for one or more source, transport, and management factors have been developed to assist with nutrient management planning of agricultural land (Gburek et al. 2000; Birr and Mulla 2001; Eghball and Gilley 2001; Mallarino et al. 2002; DeLaune et al. 2004; Djodjic and Bergström 2005; Gourley et al. 2007; Heckrath et al. 2008). These indexes have been correlated with measurements of P loss (Sharpley et al. 2008), and most include agronomic soil test values (Olsen et al. 1954; Colwell 1965; Mehlich 1984) or measures of the degree of P saturation (DPS) (Nair et al. 2004) to contribute to the source component of the index. The DPS measures are most often based around molar ratios of P extracted in a soil test to the sum of iron (Fe) and aluminium (Al) extracted in the soil test, although ratios of other agronomic tests that mimic DPS have also been used. For example, in Sweden Blombäck et al. (2021) explored ratios of either Olsen P (Olsen et al. 1954) or ammonium lactate extractable P to the single point P sorption index of Bache and Williams (1971). They concluded that each of the DPS measures explored were equally capable of predicting dissolved P, and that well established agronomic tests could be used to determine soil fertility as well as the risk of P leaching. In Australia, Moody (2011) proposed a ratio of widely used agronomic tests such as Colwell P (Colwell 1965) and P buffering index (PBI) (Burkitt et al. 2002) as an environmental risk measure rather than introducing additional tests. This ratio of Colwell P to PBI is sometimes called the P environmental risk index (PERI). Moody (2011) demonstrated that PERI was strongly correlated with dilute CaCl2-extractable P (CaCl2-P), the benchmark method for the estimation of dissolved reactive P (DRP) leaving agricultural soils, and also identified a negative correlation between CaCl2-P and PBI. Similarly, strong positive relationships have been identified between DPS and P concentration in run-off (Nair et al. 2004; Tarkalson and Mikkelsen 2004; Withers et al. 2017; Dari et al. 2018), as have relationships between soil test P and surface runoff P concentrations in rainfall simulation experiments (Burkitt et al. 2010). McDowell and Condron (2004) identified strong correlations between CaCl2-P measured in soil extracts (0–7.5 cm) and DRP in subsurface flow, and demonstrated positive correlations between the ratio of Olsen P to P retention measures and CaCl2-P or H2O-extractable P, suggesting such ratios as a potential method to predict CaCl2-P or H2O-extractable P. Burkitt et al. (2010) developed empirical relationships between CaCl2-P and Olsen P for a soil with high PBI, while Moody (2011) found strong relationships between CaCl2-P and the ratio of Colwell P to PBI (R = 0.925); however, no empirical relationship between CaCl2-P and Colwell P or PERI was provided. Furthermore, Bloesch and Rayment (2006) explored the relationship between agronomic soil tests and the potential to release soluble P from soils in the Great Barrier Reef catchments. They identified that CaCl2-P declined with increasing soil PBI, and was correlated with the molar ratio of Mehlich-3 extractable P to Fe plus Al (R2 = 0.67). Bloesch and Rayment (2006) found poor correlations between CaCl2-P and Colwell P and suggested that separate relationships may be necessary for different land uses or different soil types but did not differentiate the data according to PBI or soil type. The authors concluded that CaCl2-P could be a useful tool to identify soluble P loss risk and suggested that values >2 mg kg−1 warranted further scrutiny from a nutrient management perspective, while Tyson et al. (2020) proposed an environmental threshold of 0.25 mg kg−1 based on the trigger values for water quality in ANZECC and ARMCANZ (2000).
The previously identified positive correlations between CaCl2-P and measures of DPS (McDowell and Condron 2004; Moody 2011) suggest that DRP loss risk will increase as legacy P stocks in soils increase (Burkitt et al. 2010; McCrackin et al. 2018). In addition, the nature of a quotient such as Colwell P to PBI ratio is that the risk of DRP loss increases as either Colwell P increases, or PBI decreases. It has been well documented for regions such as south-west Western Australia (SWWA), for example, that the soils have both low P buffering, and a high percentage (~75%) have Colwell P levels that exceed the requirement to achieve 90% or 95% of relative pasture yield (Weaver and Wong 2011; Rogers et al. 2021; Weaver and Summers 2021). This region therefore has a high risk of DRP loss, and DRP has been identified as the main P form lost from agricultural landscapes in this region (Summers et al. 2014; Weaver and Summers 2014). There is therefore significant potential through soil testing to inform the land manager to apply an evidence-based approach to fertiliser management, reduce legacy P stocks, and subsequently reduce DRP loss risk. This contrasts with a set-and-forget approach to fertiliser management in which the same nutrient application is applied year-in-year-out, and legacy P stocks and DRP loss risk have the potential to increase (Weaver and Summers 2021).
Agronomic soil samples for high rainfall pastures are typically collected from a single depth (0–7.5, 0–10, 0–15, or 0–20 cm) designed to represent the zone where plant roots will access most nutrients, as soil tests from these depths have been correlated with grass–legume pasture responses to nutrients (Gourley et al. 2019). Sampling depths designed for agronomic purposes, however, do not consider the dominant hydrological pathways of P transport, and hence use of agronomic sampling depths may limit the utility of these tests to identify locations and pathways of P loss risk. For example, studies show that P can be highly stratified in the soil (Ryan et al. 2017; Weaver and Summers 2021) with as much as 50% of the P stored to 1 m depth of soil found in the top 5 cm, and that stratified soil test P measured in shallow depths (0–5 cm) was better correlated with edge of field losses of dissolved and total P than sampling from 0–20 cm depth (Osterholz et al. 2020). When there is limited interaction of rainfall and runoff with the soil profile in inundated areas, or where there is strong stratification of P in the soil, soil tests derived from agronomic sampling depths may not provide an appropriate indication of DRP loss risk. Soils which have a highly-stratified P concentration in the top few centimetres of soil may desorb P into runoff water (Dougherty et al. 2006; Rivers 2012), particularly when there is a shallow water table and saturation excess, or during heavy rainfall and infiltration excess or in combination with steeper slopes (Zhang et al. 2019). A risk assessment based on an agronomic sampling depth of 0–10 cm may be misleading since the top few centimetres of soil with high DPS would be diluted by lower DPS values deeper in the collected sample. For example, a P-retentive clay soil which is strongly stratified with P in the surface when combined with a low infiltration rate may result in high soluble P in runoff due to P desorbing from P rich surface layers. A 0–10 cm soil sample would not directly identify this surface runoff risk. In contrast, a sandy, low P-retentive, P saturated soil would be identified as a P leaching risk with measures such as PERI derived from a 0–10 cm soil sample whereas a P stratified, poorly infiltrating, high P-retentive soil with potential for P runoff would fail to be identified.
It is possible, however, that P stratification in the soil profile may vary systematically, allowing analytes and derived variables at a specified depth to be estimated from a 0–10 cm agronomic sample. This is not an unreasonable expectation in undisturbed agricultural soils where P fertiliser is surface applied, and where ingress of P deeper into the soil profile is subject to the kinetics of P adsorption and desorption (Novak et al. 1975; Shah et al. 1975). Identification of systematic P stratification would increase the utility of agronomic samples, and when combined with knowledge of dominant hydrological pathways would provide a richer understanding of DRP loss risk from catchments.
This paper explores relationships between CaCl2-P, measures of DPS derived from agronomic soil tests (e.g. PERI, PBI, and soil P fertility), and stratification of P in the soil. Much of the data used here are from land that has been farmed for more than 50 years, allowing study of the impacts of long-term P fertilisation at low P rates (10–20 kg P ha−1 year−1) on soil P fertility and the resulting reductions in soil P sorption capacity (Weaver and Wong 2011) as measured by unadjusted PBI (Burkitt et al. 2008). The findings are applied to the catchments of the Peel Harvey, Leschenault, Vasse Geographe, Scott River and Lower Blackwood, Wilson Inlet, Torbay Inlet, and Oyster Harbour, which are areas at risk of losing DRP in SWWA. The following hypotheses are tested.
As soil depth decreases, CaCl2-P, Colwell P, PERI, and other soil P fertility indicators will increase, leading to a higher risk of DRP loss from surface soil layers under surface runoff conditions.
CaCl2-P will decrease as soil PBI increases and increase as Colwell P increases.
An empirical relationship can be established to predict CaCl2-P using PERI as the dependent variable, or Colwell P as the dependent variable for soils in a specified PBI range.
Soil properties such as CaCl2-P, PERI, soil P fertility, and Colwell P measured at 0–10 cm depth can predict the same properties at other depths.
Compliance with P fertiliser management based on critical Colwell P values will lead to a reduction in legacy stocks of Colwell P and DRP loss risk in SWWA.
Materials and methods
Climate, soils, and agriculture
The SWWA has a Mediterranean-type climate, with cool wet winters and hot dry summers. Most rainfall occurs between May and September, with 600–900 mm of rainfall annually. Mean maximum daily temperatures range from 12–20°C in July to 25–34°C in February. Many of the soils in SWWA have sandy surfaces, with profiles ranging from deep sands to sands over clays, as well as ironstone gravels. Around 8% of the surface soils (0–10 cm) have extremely low to low (<15) PBI values, one-third have moderately low (15–35) to medium (35–70) PBI values, and 46% have moderately high to high (70–280) PBI values (Rogers et al. 2021). Much of the area was cleared of native vegetation for agricultural pursuits in the 1950s and 1960s. The high rainfall zone of coastal plain sandy soils supports extensive rainfed annual pastures for grazing by beef and dairy cattle and sheep, of which beef is dominant. Rainfed annual pastures typically comprise a mixed sward of clover and ryegrass with an annual potential of 6–10 tonnes dry matter ha−1, and potential stocking rates of 15–25 dry sheep equivalents ha−1. Pasture nitrogen (N) requirements are often met by atmospheric fixation by clover; however, N application is common in dairy systems where ryegrass pastures are dominant or in beef farming for growing hay. When first cleared for agriculture, the soils were deficient in many nutrients, including P. Annual P applications of 10–20 kg ha−1 have remedied P deficiency for 75% of paddocks, while potassium (K) and sulfur (S) deficiency remain in part due to the mobility of these elements, and there is widespread soil acidity (Weaver and Reed 1998; Weaver and Wong 2011; Weaver and Summers 2021).
Sampling and chemical analysis
Soil samples were collected as part of routine soil testing programmes, during summer months following senescence of annual pasture, and at a depth of 0–10 cm. The samples were from paddocks that have been used for grazing for more than 50 years, many of which had received annual applications of P fertiliser and represented wide gradients of soil P fertility and P sorption capacity. These samples were composites of at least of 30 cores, obtained using a 19-mm pogo stick corer or 20-mm battery drill auger (Weaver et al. 2021), and were collected in accordance with Australian sampling guidelines (Gourley and Weaver 2019) to ensure that both micro- and macro-scale variations were taken into account (McAlpine and Birch 1985). There were 188 soil samples chosen randomly from samples collected in 2016/2017, 171 from samples collected in 2018/2019, 203 from samples collected in 2019/2020, 124 from 2020/2021, and 6 from 2021/2022.
In addition, 88 sites identified to represent gradients of PBI and soil P fertility levels from previous soil testing programmes were resampled concurrently to depths of 0–10, 0–1, 1–2, 2–5, 5–10, 10–20, and 20–30 cm. This depth-wise sampling therefore contained paired data for different depths that could be compared. Soil samples were collected at different depths, using different methods. Shallow samples (≤10 cm) were collected using a 15 cm × 5 cm scraper plate (Matsuda et al. 2015) in incremental depth intervals, while samples deeper than 10 cm were collected using a Geoprobe Macro-Core, hydraulic push sampling system, and a 50-mm tube. All samples were composites of six different locations within a paddock and were collected during the summer months following the senescence of pasture. The samples were dried at 40°C and passed through a 2-mm sieve before analysis. Each of the samples was analysed at the CSBP soil and plant laboratories (csbp.com.au) for texture using the hand bolus method (McDonald et al. 1990), Colwell P (Colwell 1965), Colwell K (Rayment and Lyons 2011), and PBI adjusted for Colwell P (PBI) (Burkitt et al. 2002). The PBI estimates a soil’s inherent P sorption capacity prior to P addition, while an unadjusted PBI (PBIu) can be determined to estimate the current P sorption capacity of the soil following P addition (Burkitt et al. 2008). To retain consistency with commonly used agronomic tests and with existing functions that estimate soil P status and requirements (Gourley et al. 2019), and to ensure that calculated DPS measures such as PERI used independent variables, PBI was used in preference to PBIu. Samples were also analysed for KCl40-S (Blair et al. 1991), (Rayment and Lyons 2011), and soil organic carbon (OC) using the heat of dilution method (Walkley and Black 1934). In addition, each sample was extracted using 0.01 M CaCl2, at a 1:5 ratio of soil to solution (Rayment and Lyons 2011) as the benchmark measure of DRP (Moody 2011).
In addition to the measured analytes, several derived measures were estimated. This included PERI or the ratio of Colwell P to PBI as a surrogate measure of DPS (Moody 2011) according to Eqn 1.
Phosphorus fertility index (Eqn 2) of samples was determined as the ratio of measured Colwell P to a critical Colwell P at 95% of relative yield (RY) (Rogers et al. 2021). While the P fertility index (PFI) was based on target Colwell P at 95% of RY, any RY target can be used, but most studies use a RY target of 90% or 95%. A range of P95 fertility index values were used as benchmark values when assessing and classifying the data. The PFI values of 0.5, 0.55, 0.63, 0.75, 1, 1.5, and >2 result in estimated RY of 78%, 80%, 85%, 90%, 95%, 99%, and 100% respectively (Gourley et al. 2019). These PFI and RY targets were selected to represent a range of conditions for pastures from P deficiency to P excess and cover the range of soil Colwell P levels where enterprise economic or agronomic goals could be optimised.
The stratification ratio (SR) of different soil analytes was also determined as the ratio of a value of an analyte at a surface layer to the value of that analyte in another soil layer (Franzluebbers 2002; Francaviglia et al. 2014; Deng et al. 2016). In this case, SR was determined in reference to soil test values found in an agronomic sample collected from 0–10 cm.
Data curation and analysis
The available data were presented as violin plots (Hintze and Nelson 1998) and scatterplots, stratified and symbolised by sampling depth, PBI, and CaCl2-P. In addition, linear, non-linear regression, analysis of covariance (ANCOVA), and Spearman rank correlation were undertaken using the exploratory data analysis and presentation tools RStudio (rstudio.com), DataDesk 8.3 (datadesk.com), and Igor Pro v9 (wavemetrics.com). The midpoint of depth ranges was used where depth was included as a variable. The ANCOVA was used to model linear relationships between CaCl2-P and Colwell P for overlapping PBI ranges, and to determine if systematic changes in the slopes of these relationships occurred with PBI. Overlapping PBI ranges were 0–5, 0–2.5, 2.5–7.5, 5–10, 7.5–15, 10–20, 15–30, 20–40, 30–80, 60–90, 80–120, 90–130, 100–150, 125–200, 175–250, 225–350, 300–400, 350–500, 450–700, 550–800, and 600–1200. Mean PBI within the overlapping PBI ranges was used as the dependent variable.
Data from the 88 soil profiles were presented by depth and symbolised by PFI and PBI. The paired 0–10 cm sample for each profile was classified into three PFI ranges (<0.5, 0.5–1.0, and >1.0) and three PBI ranges (<35, 35–280, and >280). Mean values of the corresponding paired data at each depth for the three PFI ranges and PBI ranges were overlain on the symbolised data to explore whether there were systematic changes in profile values based on a 0–10 cm soil sample. In addition, systematic changes in relationships for CaCl2-P, PERI, PFI, and Colwell P at different sampling depths as the dependent variable, and the paired 0–10 cm sample as the independent variable, were explored using ANCOVA. The CaCl2-P, PERI, PFI, and Colwell P were log transformed for this analysis.
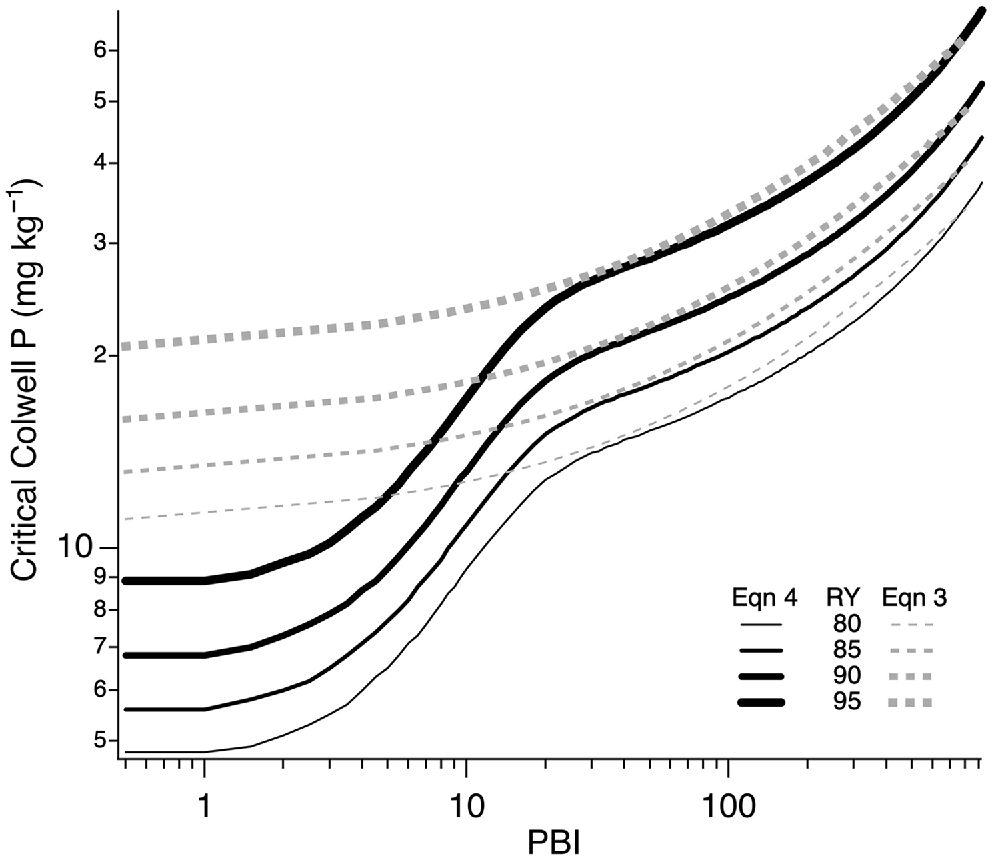
Tradeoffs between pasture productivity and DRP risk (measured as CaCl2-P) were modelled using a dataset of 30 981 geolocated 0–10 cm soil samples collected in SWWA during 2009–2022. This study established relationships between CaCl2-P and Colwell P for different PBI ranges, allowing estimation of CaCl2-P from Colwell P. The current DRP risk was determined from measurements of Colwell P and PBI in the dataset. Future DRP risk was estimated by predicting CaCl2-P levels in the same samples at critical Colwell P values to achieve 80–95% relative pasture yield in southern Australia (Gourley et al. 2019), and also for 97% and 98% RY (data not shown). Eqns 4 and 8 from Gourley et al. (2019) were used to predict critical Colwell P values (Fig. 1), with Eqn 8 being a modification of Eqn 4 to use lower critical Colwell P values when soil PBI < 15 (Yeates 1993; Moody 2007). These equations will be referred to as Eqns 3 and 4 in future references.
Relationship between soil PBI and critical Colwell P based on Eqns 3 (dashed lines) and 4 (solid lines). Line thickness shows critical values for different relative yield targets.
Mean CaCl2-P of samples that were geolocated within the soil groups of WA (Schoknecht and Pathan 2013) were determined to estimate both current and future DRP risk if Colwell P values were set to achieve 90% RY. The fractional change in CaCl2-P from current levels to those in catchments managed at 90% RY were estimated and mapped. The DRP leaching and runoff potential was distinguished by modelled soil measures at sampling depths of 0–10 and 0–1 cm respectively.
Results
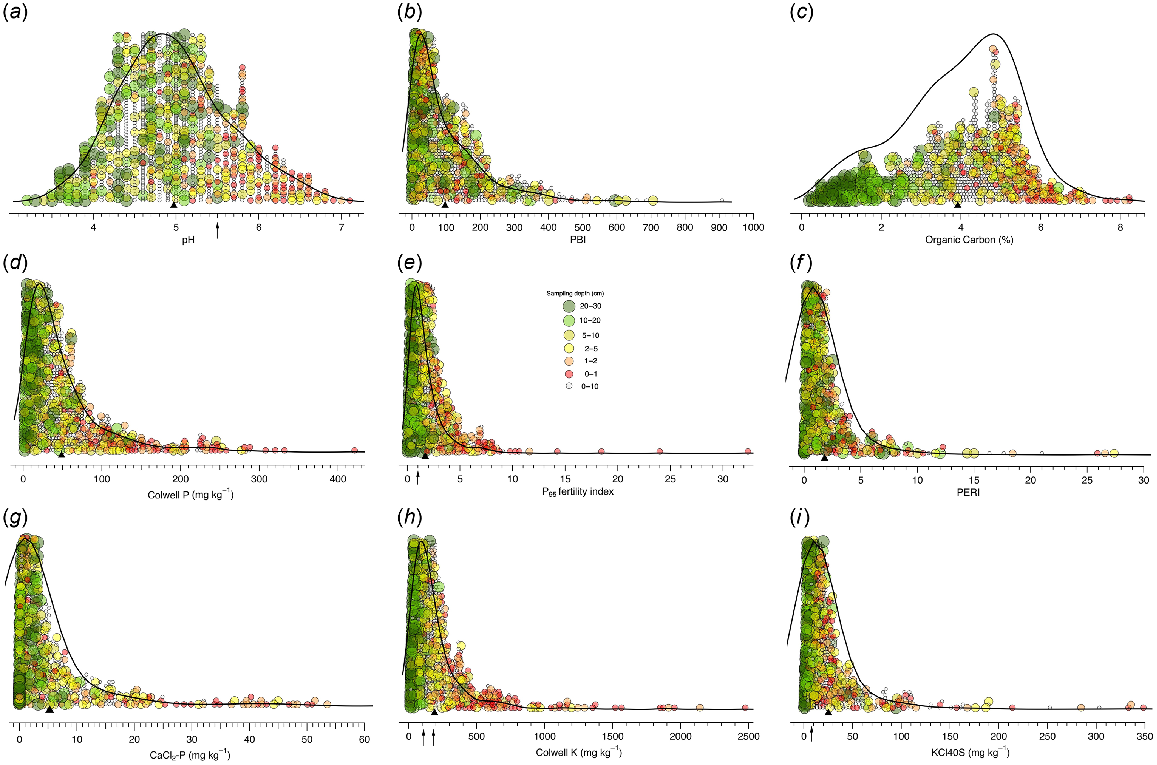
Mean pH (CaCl2) was 4.9, with range 3.2–7.1 (Fig. 2a), and decreased with depth (Table 1). Mean PBI was 97.3, with range 1–908 (Fig. 2b), and had no correlation with depth (Table 1). Soil OC had a mean of 3.9%, range 0.2–8.2%, and decreased with depth (Table 1). Samples collected from <5 cm tended to have OC > 5%, while those >10 cm tended to be <2%. The 0–10 cm OC values mostly decreased between the shallow and deeper samples (Fig. 2c). Of the 88 profiles, 81 had either uniform or two adjacent textures (sand, sandy loam, sandy clay loam, or clay loam). The remaining seven profiles had a mixture of three or four textures. No heavier textures were recorded.
Split violin plots showing the distribution of (a) pH, (b) PBI, (c) OC, (d) Colwell P, (e) P95 fertility index, (f) PERI, (g) CaCl2-P, (h) Colwell K, and (i) KCl40S. Different sample depths shown by symbol size and colour. Arrows identify critical values or ranges where appropriate. Black triangle shows mean value.
| Depth | PBI | CaCl2-P | Colwell P | P95 fertility index | PERI | OC | pH | Colwell K | |
|---|---|---|---|---|---|---|---|---|---|
| PBI | −0.098 | ||||||||
| CaCl2-P | −0.301 | −0.705 | |||||||
| Colwell P | −0.486 | 0.433 | 0.079 | ||||||
| P95 fertility index | −0.486 | 0.089 | 0.365 | 0.915 | |||||
| PERI | −0.255 | −0.716 | 0.828 | 0.257 | 0.591 | ||||
| OC | −0.582 | 0.120 | 0.317 | 0.451 | 0.461 | 0.216 | |||
| pH | −0.339 | 0.205 | 0.038 | 0.414 | 0.356 | 0.096 | 0.166 | ||
| Colwell K | −0.565 | 0.226 | 0.238 | 0.616 | 0.599 | 0.223 | 0.682 | 0.315 | |
| KCl40S | −0.394 | 0.242 | 0.097 | 0.500 | 0.474 | 0.121 | 0.519 | 0.291 | 0.445 |
Mean Colwell P was 49, with range 2–421, and decreased with sampling depth (Table 1). For samples collected from paired profiles, mean Colwell P in the 0–1 cm layer was 127 mg P kg−1, compared to 15 and 48 mg P kg−1 in the 20–30 and 0–10 cm layers, respectively (Fig. 2d). The SR of mean Colwell P20–30 cm: 0–10 cm was 0.32 and Colwell P0–1 cm: 0–10 cm was 2.7. The PFI95 of the samples ranged within 0.05–32.4, with mean of 1.7, and decreased with depth (Table 1). Mean PFI95 was 4.80, 1.76, and 0.64 in the 0–1, 0–10, and 20–30 cm layers, respectively (Fig. 2e), resulting in a SR of 0.36 and 2.7 for PFI20–30 cm: 0–10 cm and PFI0–1 cm: 0–10 cm, respectively.
Mean PERI in the 0–1 cm layer was 6.6, decreasing with depth (Fig. 2f, Table 1), consistent with a SR for mean PERI20–30 cm: 0–10 cm of 0.42 and 2.8 for PERI0–1 cm: 0–10 cm. Mean CaCl2-P in the 0–1 cm layer was 26.5 mg P kg−1, decreasing with depth (Table 1) and resulting in a SR of 4.9 for mean CaCl2-P0–1 cm: 0–10 cm and 0.18 for CaCl2-P20–30 cm: 0–10 cm (Fig. 2g).
Mean Colwell K in the 0–1 cm layer was 578 mg K kg−1, decreasing with depth (Table 1); 32% of 0–10 cm samples exceeded a critical Colwell K value of 161 mg P kg−1 for pastures grown on clay loam soils (Gourley et al. 2019). The KCl40-S decreased with depth (Table 1). Mean KCl40-S was 25.2 mg kg−1, well above the pasture critical value of 8 mg S kg−1 for 0–10 cm (Gourley et al. 2019).
All analytes were negatively correlated with depth (Table 1), supporting hypothesis 1, while there were also strong negative correlations of PBI with CaCl2-P and PERI. Strong positive correlations were identified of PBI with Colwell P, Colwell K, and KCl40-S; of CaCl2-P with PERI and PFI; of Colwell P with PFI and Colwell K; and of PFI with PERI and Colwell K. The OC was also positively correlated with PBI, CaCl2-P, Colwell P, PFI Colwell K, and KCl40-S.
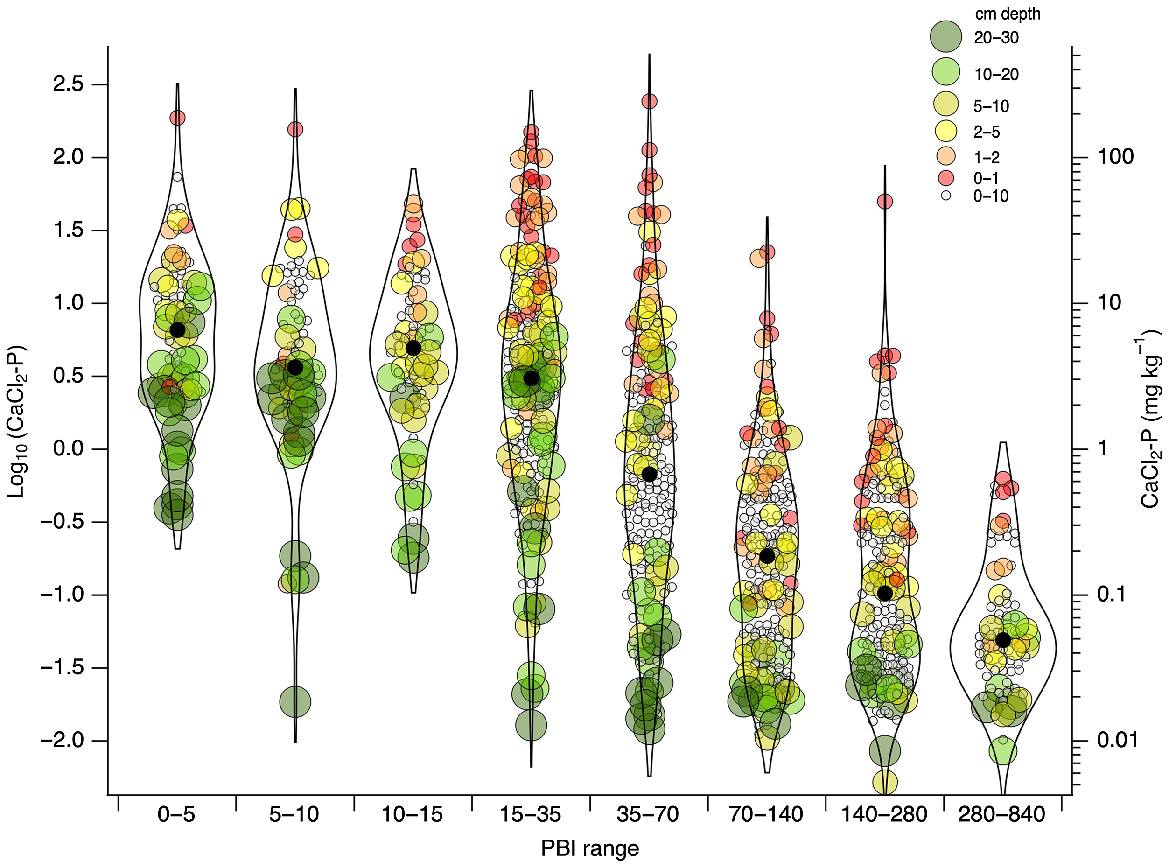
In support of hypothesis 2, CaCl2-P decreased with increasing PBI (Fig. 3). Mean values of CaCl2-P were 12.4, 9.4, 7.9, 11.3, 5.8, 0.64, 0.59, and 0.10 mg P kg−1 for the 0–5, 5–10, 10–15, 15–35, 35–70, 70–140, 140–280, and 280–840 PBI ranges, respectively. Within a PBI range, CaCl2-P tended to be lower for samples collected deeper in the profile. A distinct separation in CaCl2-P for specific depths was seen in the PBI range of 35–70, with samples from 0–5, 0–10, and 10–30 cm having a mean CaCl2-P of 22.1, 1.3, and 0.34 mg P kg−1, respectively.
Violin plots of CaCl2-P for different PBI classes. Size and colour of points represent sampling depth. Median values shown for each PBI group (●).
In support of hypothesis 3, log10CaCl2-P was linearly related with log10PERI (Fig. 4) with an r2 of 0.67. Soils with lower PBI tended to have higher PERI and CaCl2-P than soils with high PBI. Despite these tendencies, high CaCl2-P was not always restricted to shallow depths or when PBI was low.
CaCl2-P as a function of PERI (Colwell P to PBI ratio) for soils of different PBI and sampling depth. log10CaCl2P = 1.44 × log10PERI + 0.069; r2 = 0.67.
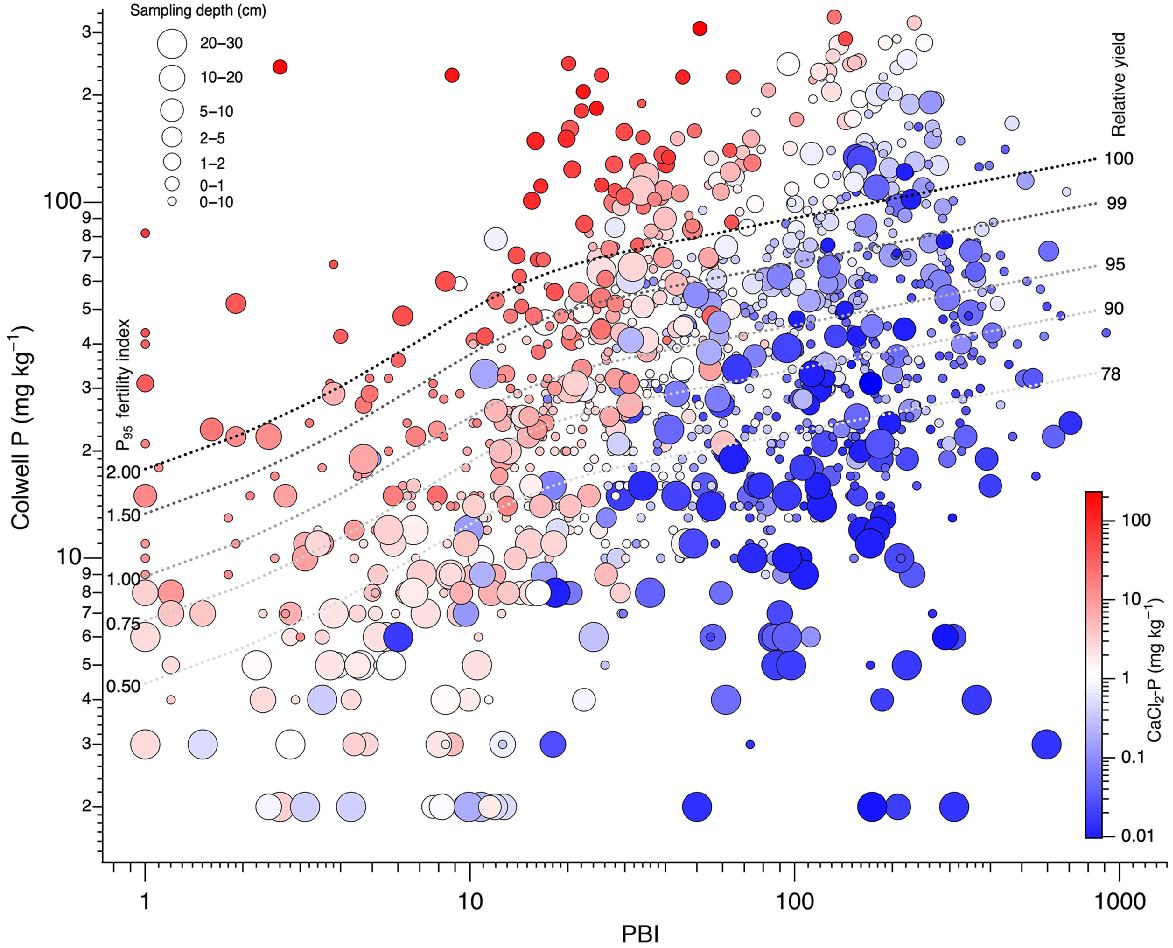
Colwell P of high PBI soils spanned a higher range than for low PBI soils (Fig. 5). Low PBI soils had high CaCl2-P, even when soil P fertility was low in subsoil layers. Low PBI soils had higher CaCl2-P than high PBI soils, although some high PBI soils sampled from shallow depths and with high Colwell P values also had high CaCl2-P. More of the high PBI soils had Colwell P values that exceeded a PFI95 of 1, where RY is nominally 95%. The CaCl2-P tended to be low for subsoil layers, particularly when soil PBI was high.
Colwell P as a function of PBI. Point colour represents CaCl2-P and size represents sampling depth. Line overlays show P95 fertility index and associated relative yields.
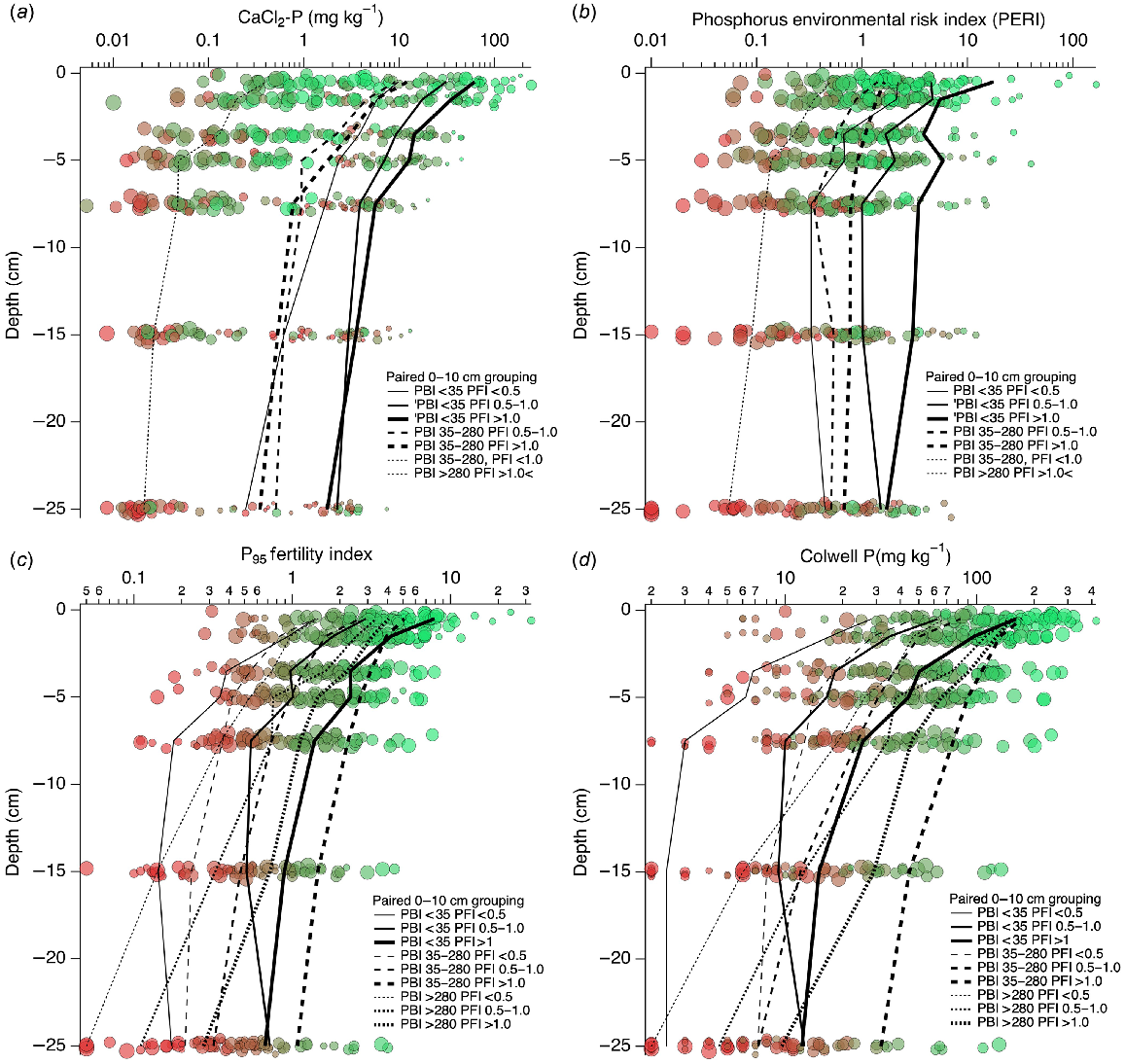
Compared to the raw data (Fig. 6), the SR (Fig. 7) showed less variation at the same depth. Based on the mean values, CaCl2-P was more strongly stratified with depth than PERI, PFI, or Colwell P. Mean CaCl2-P SR was 10.5, 4.2, 2.0, 0.71, 0.41, and 0.27; mean PERI SR was 2.9, 1.9, 1.2, 0.78, 0.67, and 0.56; mean PFI SR was 2.9, 1.9, 1.2, 0.71, 0.51, and 0.44; and mean Colwell P SR was 3.3, 2.1, 1.3, 0.71, 0.49, and 0.46 for the 0–1, 1–2, 2–5, 5–10, 10–20, and 20–30 cm depths, respectively.
Depth-wise changes in (a) CaCl2-P, (b) PERI, (c) P95 fertility index, and (d) Colwell P. Symbol colour shows the P95 fertility index ( <0.2,
<0.2,  0.2–0.4,
0.2–0.4,  0.4–0.6,
0.4–0.6,  0.6–0.8,
0.6–0.8,  0.8–1.0,
0.8–1.0,  1.0–2.0,
1.0–2.0,  2.0–3.0,
2.0–3.0,  3.0–5.0,
3.0–5.0,  >5.0), and symbol size shows the PBI range (small <5, 5–10, 10–15, 15–35, 35–70, 70–140, 140–280, and large 280–840). Plots overlain show mean values at each depth when categorised by specified PBI0–10 and PFI0–10 ranges. Gaussian noise has been added to depth to improve the visibility of overlapping data points.
>5.0), and symbol size shows the PBI range (small <5, 5–10, 10–15, 15–35, 35–70, 70–140, 140–280, and large 280–840). Plots overlain show mean values at each depth when categorised by specified PBI0–10 and PFI0–10 ranges. Gaussian noise has been added to depth to improve the visibility of overlapping data points.
Depth-wise changes in SR for (a) CaCl2-P, (b) PERI, (c) P95 fertility index, and (d) Colwell P. Symbol colour shows the P95 fertility index ( <0.2,
<0.2,  0.2–0.4,
0.2–0.4,  0.4–0.6,
0.4–0.6, 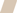 0.6–0.8,
0.6–0.8, 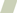 0.8–1.0,
0.8–1.0,  1.0–2.0,
1.0–2.0,  2.0–3.0,
2.0–3.0,  3.0–5.0,
3.0–5.0,  >5.0), and symbol size shows the PBI range (small <5, 5–10, 10–15, 15–35, 35–70, 70–140, 140–280, and large 280–840). Plots overlain show mean values at each depth. Gaussian noise has been added to depth to improve the visibility of overlapping data points.
>5.0), and symbol size shows the PBI range (small <5, 5–10, 10–15, 15–35, 35–70, 70–140, 140–280, and large 280–840). Plots overlain show mean values at each depth. Gaussian noise has been added to depth to improve the visibility of overlapping data points.
The CaCl2-P and CaCl2-P SR decreased with depth (Figs 6 and 7), and were generally associated with decreasing PFI95 down the profile. There were systematic changes in depth-wise mean CaCl2-P values when classified by the three PBI and PFI95 groups defined by the paired 0–10 cm sample, hereon described as PBI0–10 and PFI0–10. The CaCl2-P decreased as PFI0–10 decreased at every depth when PBI0–10 < 35, decreased further for PBI0–10 35–280 when PFI0–10 was 0.5–1 and >1, and further again for remaining classifications of PBI0–10 and PFI0–10.
The PERI and PERI SR (Figs 6 and 7) tended to decrease with increasing depth, had lower values associated with lower PFI0–10, and mean PERI values showed systematic changes in depth-wise values when classified by the three PBI0–10 and PFI0–10 groups. For PBI0–10 < 35 PERI decreased as PFI0–10 decreased to a depth of 7.5 cm and then remained relatively constant deeper in the profile. Mean PERI decreased further for PBI0–10 35–280 when PFI0–10 > 1, and further again for PFI0–10 0.5–1.0 and for remaining classifications of PBI0–10 and PFI0–10.
There were systematic changes in depth-wise and classified mean PFI95 values (Fig. 6). Depth-wise trends of PFI95 within a PBI0–10 group were similar and showed increasing mean PFI95 as PFI0–10 increased. When PBI0–10 > 280, PFI decreased more rapidly than for PBI0–10 < 35 or 35–280.
Colwell P and Colwell P SR decreased with depth and increased as PFI95 increased (Figs 6 and 7). There were systematic changes in depth-wise mean Colwell P values when classified by the three PBI0–10 and PFI0–10 groups. For PBI0–10 < 35, mean Colwell P at each depth decreased as PFI0–10 decreased. Below 10 cm depth, Colwell P was less variable for all PFI0–10 groups when PBI0–10 < 35. When PBI0–10 was >35, Colwell P continued to decrease with increasing depth.
The ANCOVA results exploring relationships between analytes at different depths are shown in Table 2. In support of hypothesis 4, linear relationships could estimate log10 of CaCl2-P, PERI, PFI, and Colwell P for a specified sampling depth based on the log10 of the same variable derived from a 0–10 cm sample. A common slope for each of the relationships for CaCl2-P, PERI, PFI, and Colwell P was identified; however, the intercepts varied systematically with midpoint sample depth as described by the equations and coefficients in Table 2.
| Dependent variable (y) | Independent variable (x) | Slope (m) | Intercept (b) | r2 of predicted vs actual | |
|---|---|---|---|---|---|
log10 CaCl2 − PDepth | log10 CaCl2-P0–10 cm | 0.836 | Y0 A b | −0.79 1.62 0.144 | 0.86 |
r2 = 0.99 | |||||
log10 PERIDepth | log10 PERI0–10 cm | 0.832 | Y0 A b | −0.364 0.756 0.210 | 0.78 |
r2 = 0.99 | |||||
log10 PFIDepth | log10 PFI0–10 cm | 0.859 | Y0 A b | −0.444 0.967 0.152 | 0.77 |
r2 = 0.99 | |||||
log10 Colwell PDepth | log10 Colwell P0–10 cm | 0.868 | Y0 A b | −0.381 1.074 0.137 | 0.79 |
r2 = 0.99 | |||||
Modelled depth-wise changes in CaCl2-P, PERI, PFI95, Colwell P, and SR for notional values of each analyte measured in a 0–10 cm sample are shown in Fig. 8. Similar to Fig. 7, the SR for CaCl2-P, PERI, PFI95, and Colwell P were less variable than the raw data. Higher values of each analyte measured in a 0–10 cm sample resulted in higher modelled values down the profile. The CaCl2-P was more strongly stratified than the other analytes. Even though the depth-wise SR for each analyte was similar for each of the modelled 0–10 cm values, the SR values were inversely related to the 0–10 cm values. That is, lower 0–10 cm values led to higher values of SR even though the SR range was narrow compared to the raw data. For example, modelled values of CaCl2-P SR ranged within 3–5 at a depth of 0.5 cm, while modelled CaCl2-P ranged within 5.2–64 when CaCl2-P in a 0–10 cm sample increased from 1 to 20 mg P kg−1. At 30 cm depth, CaCl2-P SR was in narrow range of 0.1–0.17 when CaCl2-P in a 0–10 cm sample increased from 1 to 20 mg P kg−1.
Modelled depth-wise changes in (a) CaCl2-P, (c) PERI, (e) P95 fertility index, (g) Colwell P, and (b, d, f, h) respective SR, using equations in Table 2 for example values of each variable measured in a 0–10 cm sample.
In further support of hypothesis 2, within a PBI range, CaCl2-P was linearly related with Colwell P, resulting in a systematic decrease in slope of these relationships as soil PBI increased (Fig. 9). The ANCOVA identified that the slope of regressions for overlapping PBI ranges significantly differed (P < 0.05) from 0 and decreased with increasing mean PBI within each PBI range (Fig. 9a). Slopes decreased rapidly from near 1 for PBI < 5 to around 0.2 at PBI 30, and 0.03 at PBI > 100. Small significant differences in intercept were found for PBI range of 10–80, but for other PBI ranges the intercept was close to 0. Inclusion of all interactions in this model accounted for 71% of the variation, while removing terms for varying intercepts reduced the variation accounted for to 69%. Subsequent modelled relationships between CaCl2-P and Colwell P assumed a zero intercept with a PBI dependent slope based on Fig. 9a.
(a) Curvilinear relationship between the slope of linear regressions between CaCl2-P and Colwell P for overlapping PBI ranges. Slope = 0.048 + 0.911 × 0.961PBI; r2 = 0.99. (b) Modelled relationships between CaCl2-P and Colwell P for soils of specific PBI from analysis of covariance of overlapping PBI ranges compared to 1:1 line. Coloured line overlays show different levels of soil P fertility index where a value of 1 is at the critical value for 95% relative yield. Lower (0.5) or higher fertility index (2, 3, and 4) values are multiples of the critical value of 1. Solid and dashed colour line overlays show P fertility index values based on Eqns 4 and 3, respectively.
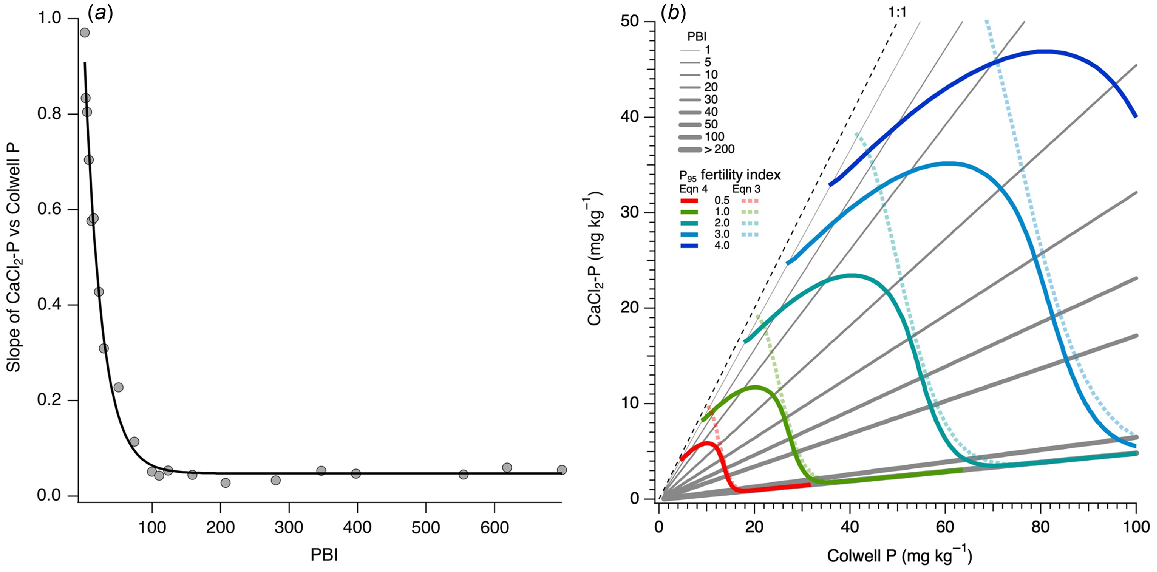
Modelled relationships between CaCl2-P and Colwell P were close to the 1:1 line when soil PBI = 1. The slope decreased as PBI increased (Fig. 9b), with little change in slope for PBI > 100. As PFI95 increased, CaCl2-P also increased. However, Eqn 3 resulted in CaCl2-P values for soils with low PBI that were double those of Eqn 4. As PBI approached 30, the difference between the two equations decreased, after which modelled CaCl2-P was similar.
The proportional change in current mean CaCl2-P within each PBI group from that based on RY targets determined from Eqns 3 to 4 is shown in Fig. 10a. For low PBI soils (<35), Eqn 3 led to an increase in mean CaCl2-P compared to Eqn 4 which showed a CaCl2-P decrease, but this depended on the target RY. Increases in CaCl2-P occurred when PBI < 35 at RY of 95%, PBI < 15 at RY of 90%, and PBI < 5 at RY of 85% for Eqn 3. For PBI > 35, both equations yielded similar results at all RY targets. That is, decreases in CaCl2-P for PBI range of 35–280, and some increases in CaCl2-P for PBI > 280, particularly when RY targeted ≥90%.
(a) Modelled proportional changes in mean CaCl2-P for PBI ranges when the target Colwell P is based on values to achieve 80%, 85%, 90%, and 95% pasture relative yield (RY). (b) Proportion of 30 981 samples collected during 2009–2022 in specified PBI ranges (bars, right hand y-axis) overlain by modelled contribution to change in mean CaCl2-P (lines, left hand y-axis) for PBI ranges when the target Colwell P is based on values to achieve 80%, 85%, 90%, and 95% pasture RY. Solid and dashed colour line overlays show P fertility index values based on Eqns 4 and 3, respectively. Total reduction in CaCl2-P annotated for each pasture RY.
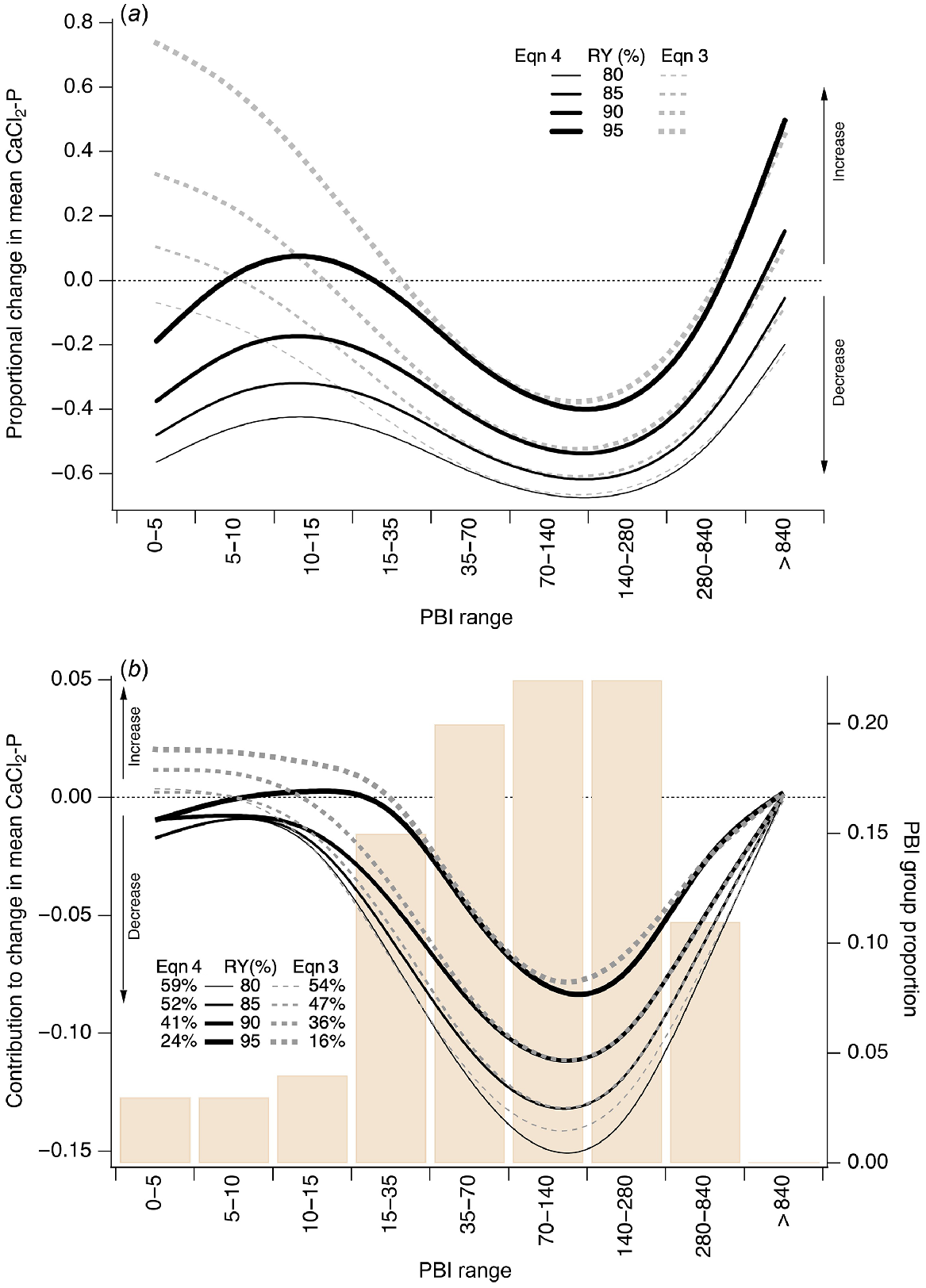
Of the 30 981 0–10-cm samples collected during 2009–2022, 80% fell into the PBI range 15–280, 8% into PBI < 15, and 12% into PBI > 280 (Fig. 10b). The greatest contribution to changes in mean CaCl2-P were for the PBI range 15–280. Eqn 4 resulted in greater changes in CaCl2-P than Eqn 3, which for PBI < 15 showed an increase in CaCl2-P. The choice of RY target also influenced the change in mean CaCl2-P within each PBI group, and the overall modelled change in CaCl2-P. The overall reduction in CaCl2-P at 95% RY was 24% and 16% using Eqns 4 and 3, respectively; these reductions increased to 59% and 54% at 80% RY (Fig. 10b). At 97% and 98% RY, the overall reduction in CaCl2-P was 11% and 0%, respectively, using Eqn 4 (data not shown). At 97% and 98% RY, the CaCl2-P reduced by 2% and increased by 9%, respectively, using Eqn 3 (data not shown).
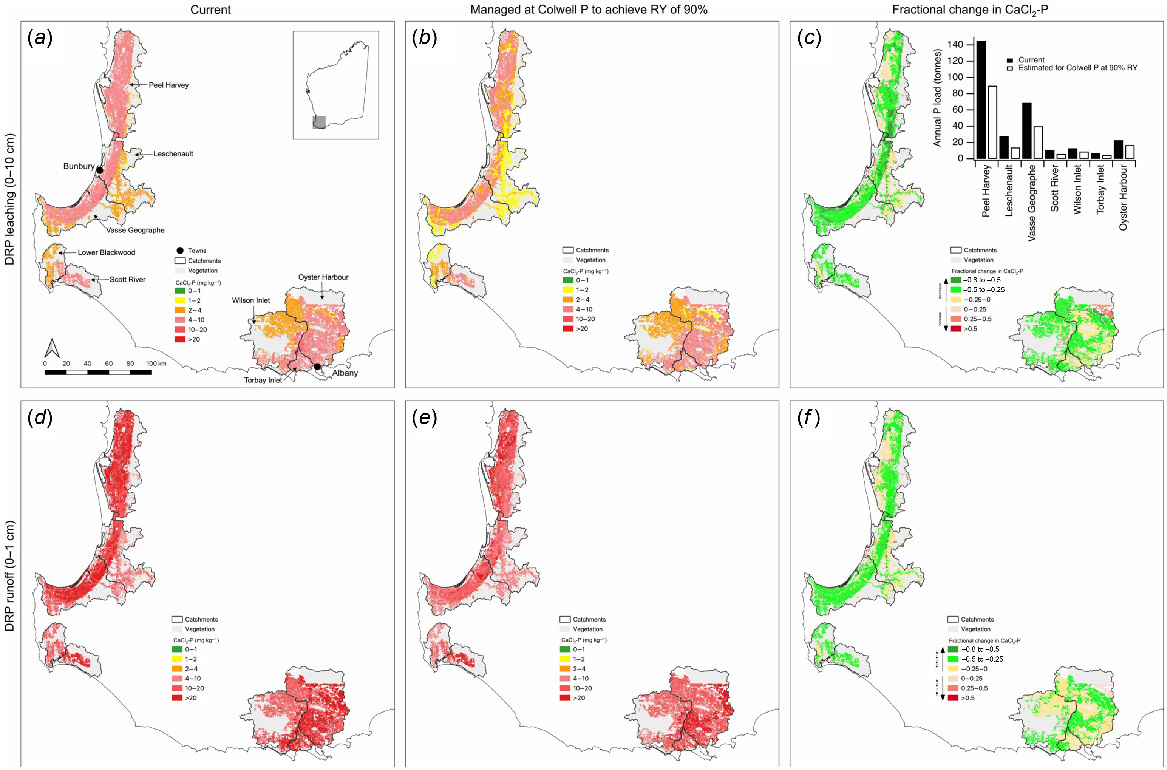
Current modelled CaCl2-P exceeded a threshold of 2 mg kg−1 for the study catchments based on 0–10 cm (Fig. 11a) and 0–1 cm (Fig. 11d) sampling depths, with much greater exceedance for the 0–1 cm depth. Modelled CaCl2-P reduced when Colwell P levels were reduced to achieve 90% RY for the 0–10 cm (Fig. 11b) and 0–1 cm (Fig. 11e) layers. Extensive areas in the study catchments had CaCl2-P below a threshold of 2 mg kg−1 for the 0–10 cm layer once the critical Colwell P levels for 90% RY were achieved (Fig. 11b), although extensive areas above the CaCl2-P threshold of 2 mg kg−1 also remained for the 0–10 and 0–1 cm layers (Fig. 11b, e). The mean fractional changes in CaCl2-P at both depths were extensive once the critical Colwell P levels for 90% RY were achieved (Fig. 11c, f), and were typically of the magnitude of 25–50%. The greatest fractional change from reducing the CaCl2-P to target 90% RY was in the areas near to the receiving estuarine waterbodies, especially the Peel Harvey, Leschenault, and Vasse Geographe catchments. These catchments also have high P loads in the runoff associated with high Colwell P in the soil (Fig. 11c, inset).
Spatial distribution of modelled (a, d) mean CaCl2-P within soil groups (Schoknecht and Pathan 2013) of 30 981 soil samples collected during 2009–2022 for the 0–10 and 0–1 cm layers, respectively; (b, e) mean CaCl2-P if soil Colwell P achieves RY of 90% (using Eqn 4) for the 0–10 and 0–1 cm layers, respectively; and (c, f) fractional change ( and respectively) in mean CaCl2-P within soil groups for the 0–10 and 0–1 cm layers, respectively. Inset bar chart in (c) shows current annual P loads (Ruprecht et al. 2013) in selected catchments and estimated annual P loads once critical Colwell P levels in soil for 90% RY have been achieved.
Discussion
Coarse-textured soils with low PBI are unlikely to be the sole source of water quality problems associated with DRP because DRP loss risk also increases (Fig. 3, Table 1) with shallow sampling depths for any PBI (Fig. 2). Soils with high PBI, particularly when sampled from shallow depths, also contain elevated Colwell P levels sufficient to support CaCl2-P at or above those of low PBI soils (Fig. 5). The implication is that soils of any PBI and texture subject to saturation excess or infiltration excess flow can contribute DRP, while coarse-textured soils with low PBI can also contribute DRP via leaching pathways. The DRP contribution of fine-textured high PBI soils should not be overlooked since they can sustain Colwell P levels of an order of magnitude higher than low PBI soils (Fig. 5). In addition, surface soil also likely contains elevated levels of Total P (Weaver and Summers 2021), which when eroded via surface runoff can contribute to particulate P losses.
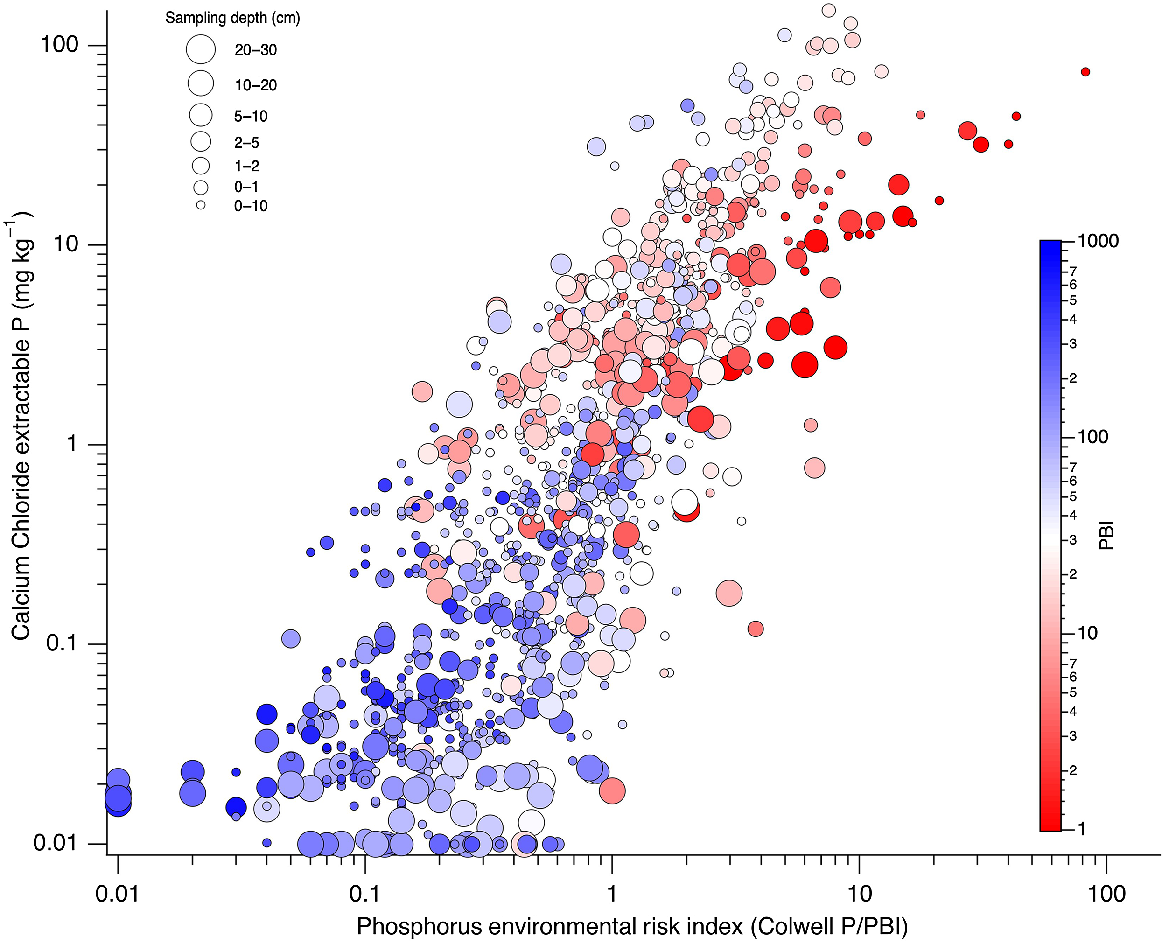
While analytes such as Colwell P and PBI can be utilised to estimate the risk of DRP loss (Fig. 4), a standardised agronomic sampling depth of 10 cm may limit their utility. Knowledge of DRP loss risk using a measure like PERI from an agronomic soil test alone is insufficient. Prior to sampling for the purpose of estimating DRP loss risk, consideration should be given to the dominant flow pathways for DRP transport since sampling at agronomic depths will not necessarily align with these flow pathways. Since Colwell P and CaCl2-P were highly stratified (Table 1), sampling to 0–10 cm will dilute the estimate of DRP loss risk compared to sampling to shallower depths. This is consistent with the findings of Osterholz et al. (2020) who identified a stronger relationship between shallow sampling depths and P concentrations in surface runoff and tile discharge than deeper sampling. For surface runoff, the exposure pathway aligns with the highest concentrations of soil P (0–1 cm) for soils of any PBI. For leaching situations, even though the zone of interaction between water and the volume of soil is expanded (0–10 cm), leaching usually occurs for coarse-textured soils with low PBI where opportunities for P sorption are limited. The result will be significant loss of DRP.
The risk of DRP loss, as determined by CaCl2-P, can be estimated by PERI, making use of existing agronomic analytes (Fig. 4), or from Colwell P and PBI (Fig. 9). However, to be useful as an estimate of DRP loss risk, sampling depth should be adjusted, or the soil test values estimated for a depth that matches the dominant flow pathway, for example 0–1 cm when surface runoff is dominant. This may only be possible for permanent pasture-based systems where the nutrient stratification profile remains undisturbed. Such adjustments can be made based on the equations and coefficients in Table 2, where CaCl2-P, PERI, PFI, and Colwell P at a specified soil depth can be estimated from the same analyte determined from a 0–10 cm sample (Fig. 8). For example, assume a 0–10 cm soil sample has been collected and analysed with a reported PBI of 10 and Colwell P of 25 mg kg−1, and hence a PERI0–10 of 2.5. Surface runoff has been identified as the dominant transport pathway and estimates of various soil parameters at a midpoint depth of 0.5 cm (0–1 cm sample) are required. Four approaches to estimate DRP loss risk using equations provided in this paper can be undertaken. Firstly, CaCl2-P0–10 can be estimated from PERI0–10 (Fig. 4), with adjustments of CaCl2-P to a midpoint depth using Table 2. Secondly, PERI0–10 can be adjusted to a midpoint depth of 0.5 cm using Table 2, with subsequent estimation of CaCl2-P from the depth-adjusted PERI value (Fig. 4). Thirdly, Colwell P0–10 can be adjusted to a midpoint depth of 0.5 cm using Table 2 with subsequent estimation of CaCl2-P from the depth-adjusted PERI value (Fig. 4). Fourthly, CaCl2-P0–10 can be estimated from the ANCOVA results (Fig. 9) based on the change in the slope of the relationship between CaCl2-P0–10 and Colwell P0–10 for different PBI. The resulting CaCl2-P0–10 can be adjusted to a midpoint depth of 0.5 cm using equations in Table 2.
The first approach estimated a CaCl2-P of 4.4 mg kg−1 for the 0–10 cm sample (Fig. 4), and therefore 18 mg kg−1 at midpoint depth of 0.5 cm (Table 2). A CaCl2-P SR of 4.1 identifies that the surface loss risk of DRP from the 0–1 cm layer is over four times that from leaching, assuming uniform leaching and no short-circuit loss pathways such as macropores. The second approach estimated a PERI of 4.4, a PERI SR of 1.8 at a midpoint depth of 0.5 cm (Table 2), and a CaCl2-P of 10 mg kg−1 (Fig. 4). The third approach estimated a Colwell P of 68, Colwell P SR of 2.7, PERI of 6.8 at a midpoint depth of 0.5 cm (Table 2), and a CaCl2-P of 33 mg kg−1 (Fig. 4). The fourth approach estimated a CaCl2-P0–10 of 16.5 mg kg−1 and CaCl2-P at a midpoint depth of 0.5 cm of 54.4 mg kg−1. While estimates from these approaches varied, they consistently provided higher values of CaCl2-P at shallow depths of around 2–4 times that of a 0–10 cm sample estimate (Fig. 8b). The approach to estimate DRP risk will depend on what soil test parameters are readily available, and multiple approaches are recommended with ground truthing dependent on application. There are also cases where soil P fertility is determined using other measures such as Olsen P, which for agronomic purposes does not require PBI for its interpretation (Gourley et al. 2019). While Olsen P and an equivalent PERI using Olsen P rather than Colwell P were not explored in this paper, the P loss risks and stratification are likely similar given the strong relationship between the two measures (Moody et al. 2013). It will therefore be as important for soils managed with Olsen P tests to comply with critical soil test values (Gourley et al. 2019) to minimise DRP loss risk. In addition, PBIu may be a useful adjunct measure where Olsen P is the default measure of soil P fertility to track changes in P sorption, particularly for soils at high risk of P leaching (Summers and Weaver 2022).
The study suggests that compliance with critical Colwell P values for fertiliser management can decrease legacy Colwell P and DRP loss. Hypothesis 5 is supported by the results, and the data in Fig. 10b illustrate the potential reduction under full compliance. The actual reduction in DRP, however, depends on several factors, some within the control of farm managers, agronomists, and fertiliser company decision support tools, and others not. Factors within control include the decision to use soil testing, the choice of equation to determine critical Colwell P values, the choice of RY targets, and the choice to modify P stratification in the soil profile. Factors such as rainfall amount and intensity, soil physical features such as texture and the dominance of surface runoff or leaching as primary transport pathways, as well as soil chemical properties such as PBI are less within the control of farm and catchment managers.
Soil testing, and adherence to critical Colwell P targets reduced DRP by a minimum of 16–24% at 95% RY, and up to 54–59% if lower RY were adopted (Fig. 10), while at 97% and 98% RY small decreases (2–11%) or increases (0–9%) occurred, respectively (data not shown). This is largely because critical Colwell P targets to achieve 90% or 95% RY were exceeded for a high percentage (~75%) of soils, except when PBI > 840 (Fig. 10a), in which case, applications of P are required, and CaCl2-P loss risk will increase. The very small proportion of these high PBI soils significantly limits the potential for overall DRP loss risk. For low PBI soils (<35), there is potential to reduce or increase DRP loss risk dependent on the equation used to determine critical Colwell P values. Use of Eqn 4, which includes lower critical Colwell P values for PBI < 15, reduced DRP loss risk while Eqn 3 increased DRP loss risk. Overall, the potential for DRP loss risk between the two equations for PBI < 15 did not greatly differ because of the small proportion of soils with PBI < 15. However, soils with PBI < 15 can be located close to estuaries, limiting the potential for assimilation of P as it is transported within the stream network (Weaver and Summers 2021), hence they have a proximity risk which should not be ignored and Eqn 4 is recommended.
The choice of RY target and the critical Colwell P associated with that has a much greater impact on DRP loss risk than the choice of equation used to determine critical Colwell P values (Fig. 10). From an agronomic perspective, there is little or no benefit in operating above 95% RY (Gourley et al. 2019; Rogers et al. 2021). At critical Colwell P values that support 95% RY, there is a minimum reduction of DRP loss of 16–24%. However, it is usually only dairy farms or hay paddocks that need to operate at 95% RY. Much of the pasture grown for livestock in SWWA is for beef and sheep grazing and, for many growers, other nutrient constraints such as K or soil acidity, pasture utilisation, and lifestyle choices reduce the need to operate at 95% RY. Operating at 80–85% RY is a more realistic proposition for many growers, meaning that the reduction in DRP loss may be closer to 50%. This is not an unreasonable estimate of DRP reduction for SWWA given that water-limited pasture yield in this high rainfall zone is around 9–10 tonnes of dry matter ha−1 year−1, based on a notional 15 kg dry matter mm−1 of growing season rainfall (Blumenthal and Ison 1993). Pasture utilisation on dairy farms in SWWA that have Colwell P levels in soil well above that which would support 95% RY has been measured at 4.5–6.5 tonnes ha−1 year−1 (Bolland et al. 2011). After accounting for the requirement to retain some residual pasture, RY targets are more likely in the range of 60–80%, and therefore a reduction in DRP of 50% is not unreasonable. In addition, the critical Colwell P values defined in Gourley et al. (2019) are based on growth response in a grass–legume system where clover is relied upon to fix nitrogen. Because clover has higher P requirement than grasses (Ozanne et al. 1969; Sandral et al. 2019), the potential for DRP reduction is likely to be greater for ryegrass-dominant pastures.
This estimate of DRP reduction was based on expected changes in CaCl2-P from 30 981 0–10-cm samples. However, CaCl2-P along with other soil analytes or derivates is highly stratified in the soil profile (Figs 6, 7, and 8), consistent with reports that repeated application of P to the topsoil has resulted in stratification of P (Dougherty et al. 2006; McLaughlin et al. 2011; Weaver and Summers 2021). The dominant transport pathway, leaching or runoff, and its interaction with stratified layers will therefore influence the magnitude of DRP loss and potential reduction. There is potential to interrupt these transport pathways and reduce stratification by burying P-saturated topsoil and bringing P-retentive soil to the surface, which must be considered against potential N or C losses. For example, Nash et al. (2007) reported that soil disturbance caused by laser levelling of irrigation bays resulted in 41% reduction in P loss to runoff and suggested that regular cultivation for pasture renovation decreases P export. On lower PBI soils (<35), the leaching pathway can be interrupted by amending the soil with P-retentive materials such as bauxite residue, which has been shown to reduce P leaching by more than 70% (Vlahos et al. 1989; Summers et al. 1993).
Despite the potential for up to 50% DRP reduction through the adoption of soil testing and evidence-based fertiliser management, it cannot be expected that these reductions will occur as soon as adoption of soil testing occurs, or that the magnitude of reduction will be correlated 1:1 with level of adoption. There are lags in the adoption of practices, time lags for practices to produce the required effect (Meals et al. 2010; Chen et al. 2019; McDowell et al. 2020; von Arb et al. 2021), and catchment feedbacks due to equilibrium P chemistry (Taylor and Kunishi 1971; Froelich 1988). These feedbacks mean that stream sediment will release P in response to reduced P concentrations from the edge of fields once practices are effective until a new in-stream equilibrium is established.
For practices to produce the required effect, a simplified paddock-based P balance example provides some insight into potential time lags. For a typical beef farm with annual P inputs from fertiliser of 10 kg P ha−1 and exports in animal products of 2 kg P ha−1 (Weaver and Wong 2011), the annual P balance excluding environmental losses is +8 kg P ha−1. If we assume that soil testing and evidence-based fertiliser management are now adopted, a cessation of P inputs would result in most cases because current soil Colwell P levels exceed critical values and P applications are not required. Annual P inputs from fertiliser are now 0 kg P ha−1 and animal products will contribute to an export of 2 kg P ha−1, resulting in a P balance of −2 kg P ha−1 until critical Colwell P levels are reached. The result is that under a fertilisation scenario, soil P levels will build at a faster rate than they will fall under a soil testing scenario with a complete cessation of P inputs (Schulte et al. 2010; Dodd et al. 2012; Tyson et al. 2020). This will likely lead to time periods for soil testing and evidence-based fertiliser management to have an effect that are greater than the time that was required to build soil P fertility to the current excessive levels. Similarly, typical P exports from sheep grazing of 1 kg P ha−1 will lead to longer lag times than beef grazing, and 7 kg P ha−1 for dairy shorter lag times, assuming a cessation of P inputs. These slow declines in legacy P stocks are supported by Bolland et al. (2011) who identified declines in Colwell P of 4.4–7.1 mg kg−1 year−1 following cessation of P inputs into pastures grazed by dairy cattle. More rapid declines in legacy P stocks may be achieved by excluding stock. Stock recycle 80–90% of the consumed P back to pastures (Hutton et al. 1967), while removing a 10 tonne hay crop from the farm and catchment would reduce legacy P stocks by 25–30 kg P ha−1 year−1 through phytomining (McDowell et al. 2020).
There are trade-offs between agricultural productivity and water quality. Based on the modelled estimates of current levels of CaCl2-P, these trade-offs do not currently favour water quality because legacy stocks of soil Colwell P exceed critical values, contributing to unnecessarily high losses of DRP. Neither do the trade-offs currently favour agriculture because Colwell P in excess of critical values provides no agronomic benefit. Reducing legacy stocks of soil Colwell P to the critical values results in no disbenefit to agriculture while significantly reducing the loss of DRP to waterways. Once critical Colwell P levels are achieved, a trade-off will likely remain, albeit significantly less than currently exists (Fig. 11c, inset), and which represents the cost of conducting optimal agriculture. The journey to achieve critical Colwell P levels will in most cases require a cessation of P inputs until soil testing suggests otherwise, and a change in fertiliser practice on arrival. Typically the change in fertiliser practice will be away from capital P applications, and towards maintenance P applications based around product P outputs when critical Colwell P levels are achieved (Barrow 2015).
Water quality improvement plans developed for at-risk catchments in SWWA (Environmental Protection Authority 2008; Department of Water 2010; Hugues-dit-Ciles et al. 2012; White 2012) specify current and target P loads. Target P loads are typically 30–60% lower than current annual P loads. Evidence-based fertiliser management based on soil testing and compliance with critical Colwell P levels can make a significant contribution to the required reduction in DRP and P loads (Figs 10 and 11). This could be achieved with minimal cost and likely increase in farm profit by reducing the cost of P fertiliser inputs and increasing productivity by diverting some of these savings to addressing other limiting factors.
Conclusions
Existing agronomic tests such as Colwell P and PBI, and the derived measure of PERI, or the slope of the relationship between CaCl2-P and Colwell P for a specified PBI are useful to estimate CaCl2-P, and when coupled with knowledge on the dominant hydrological pathways can provide a richer understanding of DRP loss risk. Data from a 0–10 cm sample collected for agronomic purposes can be used to estimate DRP loss risk from other depths. The risk of DRP loss is greater from near surface depths than deeper in the profile due to stratification. The DRP loss risk can be significantly reduced without loss of utilised pasture in SWWA because of already elevated levels of P fertility in soils. Soil testing and evidence-based fertiliser management such as use of Eqn 4 for P recommendations have a significant role in reducing DRP loss risk. The DRP loss risk could be reduced by as much as 60% through compliance with recommendations from soil testing, use of appropriate critical Colwell P values, and aiming for realistic and economical relative yields.
Data availability
The data that support this study cannot be publicly shared due to ethical or privacy reasons and may be shared upon reasonable request to the corresponding author if appropriate.
Declaration of funding
The soil samples collected and analysed in this project were supported by funding through the WA Government’s Royalties for Regions programmes: Regional Estuaries Initiative and Healthy Estuaries Western Australia, along with support from the Western Australian Department of Primary Industries and Regional Development.
Acknowledgements
Numerous staff of the WA Department of Primary Industries and Regional Development are acknowledged for their contribution to collecting and collating the dataset reported here. They include, but are not limited to Eric Dobbe, John Grant, Paul Matson, Peta Richards, David Rogers, and Fritz van der Schaaf.
References
ANZECC and ARMCANZ (2000) Australian and New Zealand guidelines for fresh and marine water quality. Available at https://www.waterquality.gov.au/anz-guidelines/resources/previous-guidelines/anzecc-armcanz-2000
Ashley K, Cordell D, Mavinic D (2011) A brief history of phosphorus: from the philosopher’s stone to nutrient recovery and reuse. Chemosphere 84(6), 737-746.
| Crossref | Google Scholar |
Bache BW, Williams EG (1971) A phosphate sorption index for soils. Journal of Soil Science 22, 289-301.
| Crossref | Google Scholar |
Barrow NJ (2015) Soil phosphate chemistry and the P-sparing effect of previous phosphate applications. Plant and Soil 397(1), 401-409.
| Crossref | Google Scholar |
Birr AS, Mulla DJ (2001) Evaluation of the phosphorus index in watersheds at the regional scale. Journal of Environmental Quality 30(6), 2018-2025.
| Crossref | Google Scholar |
Blair GJ, Chinoim N, Lefroy RDB, Anderson GC, Crocker GJ (1991) A soil sulfur test for pastures and crops. Soil Research 29(5), 619-626.
| Crossref | Google Scholar |
Bloesch PM, Rayment GE (2006) Phosphorus fertility assessment of intensively farmed areas of catchments draining to the great barrier reef world heritage area; 2: potential of soils to release soluble phosphorus. Communications in Soil Science and Plant Analysis 37(15–20), 2265-2276.
| Crossref | Google Scholar |
Blombäck K, Bolster CH, Lindsjö A, Hesse K, Linefur H, Parvage MM (2021) Comparing measures for determination of phosphorus saturation as a method to estimate dissolved P in soil solution. Geoderma 383, 114708.
| Crossref | Google Scholar |
Blumenthal MJ, Ison RL (1993) Water use and productivity in sub. clover and murex medic swards. I. Dry matter production. Australian Journal of Agricultural Research 44(1), 89-107.
| Crossref | Google Scholar |
Bolland MDA, Guthridge IF, Blincow G (2011) Response of intensively grazed ryegrass dairy pastures to fertiliser phosphorus and potassium. Nutrient Cycling in Agroecosystems 90(2), 281-298.
| Crossref | Google Scholar |
Burkitt LL, Moody PW, Gourley CJP, Hannah MC (2002) A simple phosphorus buffering index for Australian soils. Australian Journal of Soil Research 40, 497-513.
| Crossref | Google Scholar |
Burkitt LL, Sale PWG, Gourley CJP (2008) Soil phosphorus buffering measures should not be adjusted for current phosphorus fertility. Australian Journal of Soil Research 46, 676-685.
| Crossref | Google Scholar |
Burkitt LL, Dougherty WJ, Carlson SM, Donaghy DJ (2010) Effect of variable soil phosphorus on phosphorus concentrations in simulated surface runoff under intensive dairy pastures. Soil Research 48(3), 231-237.
| Crossref | Google Scholar |
Chen D, Zhang Y, Shen H, Yao M, Hu M, Dahlgren RA (2019) Decreased buffering capacity and increased recovery time for legacy phosphorus in a typical watershed in eastern China between 1960 and 2010. Biogeochemistry 144, 273-290.
| Crossref | Google Scholar |
Colwell JD (1965) An automatic procedure for the determination of phosphorus in sodium hydrogen carbonate extracts of soils. Chemical Industry 22, 893-895.
| Google Scholar |
Dari B, Nair VD, Sharpley AN, Kleinman P, Franklin D, Harris WG (2018) Consistency of the threshold phosphorus saturation ratio across a wide geographic range of acid soils. Agrosystems, Geosciences & Environment 1(1), 1-8.
| Crossref | Google Scholar |
DeLaune PB, Moore PA, Jr., Carman DK, Sharpley AN, Haggard BE, Daniel TC (2004) Evaluation of the phosphorus source component in the phosphorus index for pastures. Journal of Environmental Quality 33(6), 2192-2200.
| Crossref | Google Scholar |
Deng J, Sun P, Zhao F, Han X, Yang G, Feng Y, Ren G (2016) Soil C, N, P and its stratification ratio affected by artificial vegetation in subsoil, loess plateau China. PLoS ONE 11(3), e0151446.
| Crossref | Google Scholar |
Department of Water (2010) Vasse Wonnerup wetlands and geographe bay water quality improvement plan. Available at https://www.water.wa.gov.au/__data/assets/pdf_file/0017/3329/92284.pdf
Djodjic F, Bergström L (2005) Conditional phosphorus index as an educational tool for risk assessment and phosphorus management. AMBIO: A Journal of the Human Environment 34(4–5), 296-300.
| Crossref | Google Scholar |
Dodd RJ, Mcdowell RW, Condron LM (2012) Predicting the changes in environmentally and agronomically significant phosphorus forms following the cessation of phosphorus fertilizer applications to grassland. Soil Use and Management 28(2), 135-147.
| Crossref | Google Scholar |
Dougherty WJ, Nash DM, Chittleborough DJ, Cox JW, Fleming NK (2006) Stratification, forms, and mobility of phosphorus in the topsoil of a Chromosol used for dairying. Australian Journal of Soil Research 44(3), 277-284.
| Crossref | Google Scholar |
Eghball B, Gilley JE (2001) Phosphorus risk assessment index evaluation using runoff measurements. Journal of Soil and Water Conservation 56(3), 202-206.
| Google Scholar |
Environmental Protection Authority (2008) Water quality improvement plan for the rivers and estuary of the Peel-Harvey system – phosphorus management. Environmental Protection Authority, Perth, WA. Available at https://peel-harvey.org.au/wp-content/uploads/2018/02/Peel_Harvey_WQIP151208.pdf
Francaviglia R, Benedetti A, Doro L, Madrau S, Ledda L (2014) Influence of land use on soil quality and stratification ratios under agro-silvo-pastoral Mediterranean management systems. Agriculture, Ecosystems & Environment 183, 86-92.
| Crossref | Google Scholar |
Franzluebbers AJ (2002) Soil organic matter stratification ratio as an indicator of soil quality. Soil and Tillage Research 66(2), 95-106.
| Crossref | Google Scholar |
Froelich PN (1988) Kinetic control of dissolved phosphate in natural rivers and estuaries: a primer on the phosphate buffer mechanism. Limnology and Oceanography 33(4part2), 649-668.
| Crossref | Google Scholar |
Gburek WJ, Sharpley AN, Heathwaite L, Folmar GJ (2000) Phosphorus management at the watershed scale: a modification of the phosphorus index. Journal of Environmental Quality 29(1), 130-144.
| Crossref | Google Scholar |
Gourley C, Weaver D (2019) A guide for ‘fit for purpose’ soil sampling. Fertilizer Australia, Canberra, Australia. Available at https://fertilizer.org.au/Portals/0/Documents/Fertcare/Fertcare%20Soil%20Sampling%20Guide.pdf?ver=2019-06-17-095413-863
Gourley CJP, Melland AR, Waller RA, Awty IM, Smith AP, Peverill KI, Hannah MC (2007) Making better fertiliser decisions for grazed pastures in Australia. Victoria. Available at https://www.asris.csiro.au/downloads/BFD/Making%20Better%20Fertiliser%20Decisions%20for%20Grazed%20Pastures%20in%20Australia.pdf
Gourley CJP, Weaver DM, Simpson RJ, Aarons SR, Hannah MM, Peverill KI (2019) The development and application of functions describing pasture yield responses to phosphorus, potassium and sulfur in Australia using meta-data analysis and derived soil-test calibration relationships. Crop & Pasture Science 70, 1065-1079.
| Crossref | Google Scholar |
Haygarth PM, Condron LM, Heathwaite AL, Turner BL, Harris GP (2005) The phosphorus transfer continuum: linking source to impact with an interdisciplinary and multi-scaled approach. Science of The Total Environment 344(1-3), 5-14.
| Crossref | Google Scholar |
Heckrath G, Bechmann M, Ekholm P, Ulén B, Djodjic F, Andersen HE (2008) Review of indexing tools for identifying high risk areas of phosphorus loss in Nordic catchments. Journal of Hydrology 349(1–2), 68-87.
| Crossref | Google Scholar |
Hintze JL, Nelson RD (1998) Violin plots: a box plot-density trace synergism. The American Statistician 52(2), 181-184.
| Crossref | Google Scholar |
Hodgkin EP, Hamilton BH (1993) Fertilizers and eutrophication in southwestern Australia: setting the scene. Fertilizer Research 36(2), 95-103.
| Crossref | Google Scholar |
Hugues-dit-Ciles J, Kelsey P, Marillier B, Robb M, Forbes V, McKenna M (2012) Leschenault estuary water quality improvement plan. Department of Water, WA. Available at https://www.water.wa.gov.au/__data/assets/pdf_file/0016/3337/103743.pdf
Hutton JB, Jury KE, Davies EB (1967) Studies of the nutritive value of New Zealand dairy pastures. New Zealand Journal of Agricultural Research 10(3-4), 367-388.
| Crossref | Google Scholar |
Kronvang B, Rubæk GH, Heckrath G (2009) International phosphorus workshop: diffuse phosphorus loss to surface water bodies – risk assessment, mitigation options, and ecological effects in river basins. Journal of Environmental Quality 38(5), 1924-1929.
| Crossref | Google Scholar |
Mallarino AP, Stewart BM, Baker JL, Downing JD, Sawyer JE (2002) Phosphorus indexing for cropland: overview and basic concepts of the Iowa phosphorus index. Journal of Soil and Water Conservation 57(6), 440-447.
| Google Scholar |
Matsuda N, Mikami S, Shimoura S, Takahashi J, Nakano M, Shimada K, Uno K, Hagiwara S, Saito K (2015) Depth profiles of radioactive cesium in soil using a scraper plate over a wide area surrounding the Fukushima Dai-ichi Nuclear Power Plant, Japan. Journal of Environmental Radioactivity 139, 427-434.
| Crossref | Google Scholar |
McAlpine KW, Birch PB (1985) Spatial variability of total and bicarbonate extractable phosphorus and its relationship to sample size in two soils of the swan coastal plain, Western Australia. Department of Conservation and Environment, Perth, WA. Available at https://library.dbca.wa.gov.au/static/Journals/080239/080239-201.pdf
McCrackin ML, Muller-Karulis B, Gustafsson BG, Howarth RW, Humborg C, Svanbäck A, Swaney DP (2018) A century of legacy phosphorus dynamics in a large drainage basin. Global Biogeochemical Cycles 32(7), 1107-1122.
| Crossref | Google Scholar |
McDowell RW, Condron LM (2004) Estimating phosphorus loss from New Zealand grassland soils. New Zealand Journal of Agricultural Research 47(2), 137-145.
| Crossref | Google Scholar |
McDowell R, Dodd R, Pletnyakov P, Noble A (2020) The ability to reduce soil legacy phosphorus at a country scale. Frontiers in Environmental Science 8, 6.
| Crossref | Google Scholar |
McLaughlin MJ, McBeath TM, Smernik R, Stacey SP, Ajiboye B, Guppy C (2011) The chemical nature of P accumulation in agricultural soils – implications for fertiliser management and design: an Australian perspective. Plant and Soil 349(1), 69-87.
| Crossref | Google Scholar |
Meals DW, Dressing SA, Davenport TE (2010) Lag time in water quality response to best management practices: a review. Journal of Environmental Quality 39, 85-96.
| Crossref | Google Scholar |
Mehlich A (1984) Mehlich 3 soil test extractant: a modification of Mehlich 2 extractant. Communications in Soil Science and Plant Analysis 15(12), 1409-1416.
| Crossref | Google Scholar |
Moody PW (2007) Interpretation of a single-point P buffering index for adjusting critical levels of the Colwell soil P test. Australian Journal of Soil Research 45(1), 55-62.
| Crossref | Google Scholar |
Moody PW (2011) Environmental risk indicators for soil phosphorus status. Soil Research 49(3), 247-252.
| Crossref | Google Scholar |
Moody PW, Speirs SD, Scott BJ, Mason SD (2013) Soil phosphorus tests I: what soil phosphorus pools and processes do they measure? Crop & Pasture Science 64(5), 461-468.
| Crossref | Google Scholar |
Nair VD, Portier KM, Graetz DA, Walker ML (2004) An environmental threshold for degree of phosphorus saturation in sandy soils. Journal of Environmental Quality 33(1), 107-113.
| Crossref | Google Scholar |
Nash D, Webb B, Hannah M, Adeloju S, Toifl M, Barlow K, Robertson F, Roddick F, Porter N (2007) Changes in nitrogen and phosphorus concentrations in soil, soil water and surface run-off following grading of irrigation bays used for intensive grazing. Soil Use and Management 23(4), 374-383.
| Crossref | Google Scholar |
Novak LT, Adriano DC, Coulman GA, Shah DB (1975) Phosphorus movement in soils: theoretical aspects. Journal of Environmental Quality 4(1), 93-99.
| Crossref | Google Scholar |
Osterholz W, King K, Williams M, Hanrahan B, Duncan E (2020) Stratified soil sampling improves predictions of P concentration in surface runoff and tile discharge. Soil Systems 4(4), 67.
| Crossref | Google Scholar |
Ozanne PG, Keay J, Biddiscombe EF (1969) The comparative applied phosphate requirements of eight annual pasture species. Australian Journal of Agricultural Research 20(5), 809-818.
| Crossref | Google Scholar |
Rayment GE, Lyons DJ (2011) ‘Soil chemical methods – Australasia.’ (CSIRO Publishing: Collingwood, Vic.). Available at https://www.publish.csiro.au/book/6418/
Rogers D, Weaver D, Summers R, et al. (2021) Critical phosphorus values from the Better Fertiliser Decisions for Pastures project: early insights from validation trials. Crop & Pasture Science 72, 731-741.
| Crossref | Google Scholar |
Ruprecht J, Vitale S, Weaver D (2013) Nutrient export (phosphorus). Department of Agriculture and Food, Perth, WA. Available at https://www.agric.wa.gov.au/sites/gateway/files/2.9%20Nutrient%20export%20%28phosphorus%29.pdf
Ryan MH, Tibbett M, Lambers H, Bicknell D, Brookes P, Barrett-Lennard EG, Ocampo C, Nicol D (2017) Pronounced surface stratification of soil phosphorus, potassium and sulfur under pastures upstream of a eutrophic wetland and estuarine system. Soil Research 55(7), 657-669.
| Crossref | Google Scholar |
Sandral GA, Price A, Hildebrand SM, et al. (2019) Field benchmarking of the critical external phosphorus requirements of pasture legumes for southern Australia. Crop & Pasture Science 70(12), 1080-1096.
| Crossref | Google Scholar |
Schoknecht NR, Pathan S (2013) Soil groups of Western Australia: a simple guide to the main soils of Western Australia (4th edn). Department of Primary Industries and Regional Development. Available at http://researchlibrary.agric.wa.gov.au/rmtr/348/
Schulte RPO, Melland AR, Fenton O, Herlihy M, Richards K, Jordan P (2010) Modelling soil phosphorus decline: expectations of Water Framework Directive policies. Environmental Science & Policy 13(6), 472-484.
| Crossref | Google Scholar |
Shah DB, Coulman GA, Novak LT, Ellis BG (1975) A mathematical model for phosphorus movement in soils. Journal of Environmental Quality 4(1), 87-92.
| Crossref | Google Scholar |
Sharpley AN, Kleinman PJA, Heathwaite AL, Gburek WJ, Weld JL, Folmar GJ (2008) Integrating contributing areas and indexing phosphorus loss from agricultural watersheds. Journal of Environmental Quality 37(4), 1488-1496.
| Crossref | Google Scholar |
Smil V (2000) Phosphorus in the environment: natural flows and human interferences. Annual Review of Energy and the Environment 25, 53-88.
| Crossref | Google Scholar |
Summers R, Weaver D (2022) Lowering the water solubility of phosphorus fertilisers impacts leaching, plant growth and residual soil phosphorus. Soil Research 61, 20-36.
| Crossref | Google Scholar |
Summers RN, Guise NR, Smirk DD (1993) Bauxite residue (red mud) increases phosphorus retention in sandy soil catchments in Western Australia. Fertilizer Research 34, 85-94.
| Crossref | Google Scholar |
Summers R, Weaver D, Keipert N, Steele J (2014) Does riparian filtration reduce nutrient movement in sandy agricultural catchments? Environment and Natural Resources Research 4(4), 155-168.
| Crossref | Google Scholar |
Tarkalson DD, Mikkelsen RL (2004) Runoff phosphorus losses as related to phosphorus source, application method, and application rate on a Piedmont soil. Journal of Environmental Quality 33(4), 1424-1430.
| Crossref | Google Scholar |
Taylor AW, Kunishi HM (1971) Phosphate equilibria on stream sediment and soil in a watershed draining an agricultural region. Journal of Agricultural and Food Chemistry 19(5), 827-831.
| Crossref | Google Scholar |
Tyson J, Corkrey R, Burkitt L, Dougherty W (2020) Modelling changes in soil phosphorus when phosphorus fertiliser is reduced or ceases. Frontiers in Environmental Science 8, 93.
| Crossref | Google Scholar |
Vlahos S, Summers KJ, Bell DT, Gilkes RJ (1989) Reducing phosphorus leaching from sandy soils with red mud bauxite processing residues. Australian Journal of Soil Research 27, 651-62.
| Crossref | Google Scholar |
von Arb C, Stoll S, Frossard E, Stamm C, Prasuhn V (2021) The time it takes to reduce soil legacy phosphorus to a tolerable level for surface waters: what we learn from a case study in the catchment of Lake Baldegg, Switzerland. Geoderma 403, 115257.
| Crossref | Google Scholar |
Walkley A, Black IA (1934) An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Science 37(1), 29-38.
| Crossref | Google Scholar |
Weaver DM, Reed AEG (1998) Patterns of nutrient status and fertiliser practice on soils of the south coast of Western Australia. Agriculture, Ecosystems & Environment 67(1), 37-53.
| Crossref | Google Scholar |
Weaver D, Summers R (2014) Fit-for-purpose phosphorus management: do riparian buffers qualify in catchments with sandy soils? Environmental Monitoring and Assessment 186(5), 2867-2884.
| Crossref | Google Scholar |
Weaver D, Summers R (2021) Phosphorus status and saturation in soils that drain into the Peel Inlet and Harvey Estuary of Western Australia. Soil Research 59(7), 699-714.
| Crossref | Google Scholar |
Weaver DM, Wong MTF (2011) Scope to improve phosphorus (P) management and balance efficiency of crop and pasture soils with contrasting P status and buffering indices. Plant and Soil 349(1), 37-54.
| Crossref | Google Scholar |
Weaver D, Summers R, Rogers D, Richards P, Rowe D (2021) Assessment of soil sampling equipment for guiding fertiliser decisions. Resource management technical report 423. Department of Primary Industries and Regional Development, Western Australian Government. Available at https://library.dpird.wa.gov.au/rmtr/406/
White K (2012) Hardy Inlet water quality improvement plan: stage one – the Scott River catchment. Department of Water, WA. Available at https://www.water.wa.gov.au/__data/assets/pdf_file/0012/3261/103163.pdf
Withers PJA, Hodgkinson RA, Rollett A, Dyer C, Dils R, Collins AL, Bilsborrow PE, Bailey G, Sylvester-Bradley R (2017) Reducing soil phosphorus fertility brings potential long-term environmental gains: a UK analysis. Environmental Research Letters 12(6), 063001.
| Crossref | Google Scholar |
Yeates JS (1993) Changing fertilizer practices. Fertilizer Research 36, 135-140.
| Crossref | Google Scholar |
Zhang R, Li M, Yuan X, Pan Z (2019) Influence of rainfall intensity and slope on suspended solids and phosphorus losses in runoff. Environmental Science and Pollution Research 26(33), 33963-33975.
| Crossref | Google Scholar |


