Development and calibration of a soil carbon inventory model for New Zealand
Stephen J. E. McNeill A C , Nancy Golubiewski B and James Barringer AA Landcare Research, Box 69040, Lincoln 7640, New Zealand.
B Ministry for the Environment, PO Box 10362, Wellington 6143, New Zealand.
C Corresponding author. Email: mcneills@landcareresearch.co.nz
Soil Research 52(8) 789-804 https://doi.org/10.1071/SR14020
Submitted: 24 January 2014 Accepted: 8 September 2014 Published: 25 November 2014
Journal Compilation © CSIRO Publishing 2014 Open Access CC BY-NC-ND
Abstract
A soil organic carbon (SOC) and SOC change model for New Zealand is developed for use in national SOC inventory reporting. The foundation for the model is a generalised least-squares regression, based on explanatory variables of land use, soil–climate class, and erosivity. The SOC change model is based on the assumption that changes in SOC over a decadal timescale are usually restricted to transitions in land use. Improvements to the model are then considered that are intended to reduce the uncertainty of SOC changes through reduction of the standard error of the land-use effects. Stochastic gradient boosting is used to find data layers most strongly associated with SOC. The most influential of these were then used in a general least-squares model after stepwise refinement. The stepwise-refined model significantly reduced the standard error for SOC, but did not result in a consistent reduction in the standard error for land-use classes, nor did it result in an improvement in the SOC change model. The method of calculating SOC change from a transition between two land-use classes is described, along with the significance of the transition, by use of a multi-comparison significance procedure.
Additional keywords: carbon accounting, Kyoto Protocol, land-use change, soil carbon, soil inventory model, UNFCCC.
Introduction
New Zealand has been engaged with international climate change accords for 20 years, starting with signing and ratifying the United Nations Framework Convention on Climate Change (UNFCCC), which took effect in March 1994. In 1997, the Kyoto Protocol established legally binding obligations for countries to limit or reduce their greenhouse gas emissions. New Zealand ratified the Protocol in December 2002 and committed to reducing its emissions to 1990 levels, on average, over the 5-year commitment period (2008–12) or else to take responsibility for any emissions over these levels. To meet its obligations under the UNFCCC and Kyoto Protocol, New Zealand submits an annual emissions inventory to the UNFCCC, enabled by the Climate Change Response Act 2002. As part of these annual inventories, the Ministry for the Environment (MfE 2012) has created the Land Use and Carbon Analysis System (LUCAS), which is used to report on New Zealand’s land use, land-use change, and forestry sector in the greenhouse gas inventory.
LUCAS comprises three primary applications: the Geospatial System, the Gateway, and the Calculation and Reporting Application (CRA). These are used, respectively, for managing the land-use spatial databases, managing the plot and reference data, and combining the two sets of data to calculate the numbers required for reporting to the UNFCCC under the Kyoto Protocol. The Soil Carbon Monitoring System (the ‘Soil CMS’) has been developed for inventory of the soil organic carbon (SOC) pool. This paper addresses the design, development and calibration of the Soil CMS model that forms a central component of the greenhouse gas inventory for New Zealand.
In 1996, MfE initiated the development of the Soil CMS for reporting soil CO2 emissions resulting from land-use change. The system was designed to measure SOC stocks (Scott et al. 2002) by using country-specific land use, and it was stratified by soil type, climate, and land use. It was later used to estimate changes in SOC stock associated with present and future land-use changes (Tate et al. 2003a, 2003b) by employing a modified version of the model with an added erosivity index (slope × precipitation) variable. A default (Tier 1) methodology for this calculation is provided by the Intergovernmental Panel on Climate Change (IPCC) for countries with limited SOC data (Penman et al. 2003), but a country-specific (Tier 2) method is expected to provide a more accurate calculation, because such an approach is likely to reflect land-use change issues relevant to that country and would also be based on local SOC data.
The use of the Soil CMS model to estimate SOC change was based on the assumption that SOC values in the sample database represented equilibrium SOC values for each stratified soil, climate and land-use cell, and erosivity index, with samples removed where they were identified as being from disturbed sites (i.e. those where the land-use history was unreliable). Furthermore, it was assumed that changes in land use were the key drivers of change in SOC at the decadal scale, with all other changes due to soil, climate or erosivity assumed constant.
The Soil CMS model was refined through ongoing research (Tate et al. 2005), including three validation studies. First, the model was tested against detailed stratified soil sampling for 24 000 ha of South Island tussock land (unimproved pasture) (Scott et al. 2002). Second, the Soil CMS model results were compared with stratified SOC measurements (Tate et al. 2003a, 2003b) in an area of ~6000 ha in the South Island, suggesting that the national model systematically overpredicted the mean SOC for some soil–climate and land-cover categories in this region. Finally, a regional-scale test using one combination of soil–climate and land-use (temperate, volcanic soil in high-producing grassland) compared SOC values in the CMS database with values obtained from random field sampling, for which the means derived from random sampling were well within the 95% confidence limits of the model-predicted values (Wilde et al. 2004). More recently, a second regional-scale test (Hedley et al. 2012) used randomly sampled soils from a single combination of soil–climate and land cover of ~710 000 ha (high-activity clay mineralogy promoting long-term stabilisation of organic matter under low-producing grassland in a dry temperate New Zealand climate). This study showed no significant difference between the field-estimated value (67 ± 30 Mg C ha–1) and the mean value from the Soil CMS model (101 ± 41 Mg C ha–1).
The validation studies described above attempted to test for departures of field data from that described by the Soil CMS model. However, the limited number of samples employed means that the statistical power of these studies is low. At best, they suggest no compelling evidence that the model is wrong, but the studies are unable to prove the reverse (i.e. that the model is correct) because the uncertainty is high and only a few factor levels are tested. In this paper, we describe a method to provide high-power evidence of significance for a change in soil C arising from a change in land use, rather than the low-power equivalent (i.e. non-significance for a failure to detect soil C change arising from land-use change).
Since the inception of the Soil CMS model, changes have been made to the data used for fitting the model, to the source of the land-use and soil–climate information, and to the statistical methodology used for the model fitting. The original version of the model (Scott et al. 2002; Tate et al. 2003a, 2003b, 2005) used soil data from the National Soils Database alone, whereas later versions expanded the constituent soil data to include soils under indigenous forest and intensive cropland. Combining these data sources significantly improved the number of samples and their geographical distribution.
The early Soil CMS model (Scott et al. 2002; Tate et al. 2003a, 2003b, 2005) used as input a thematic classification that was partially descriptive of land cover and partially of land use, consisting of 13 land-use categories derived from a surrogate of vegetative cover. The vegetation cover was derived from the Vegetation Cover Map of New Zealand (Newsome 1987), with refined exotic forest boundaries and categorisation of indigenous forests. Later versions of the Soil CMS model used either a simplified set of six land-use classes (Baisden et al. 2006) derived from the Land Cover Data Base (LCDB-1; Landcare Research 2014) satellite classification, or a processed version of the LCDB in the form of the LUCAS Land Use Map (LUM) (Koordinates 2013) from thematically rich satellite land-cover classifications (McNeill et al. 2009).
Finally, there have been several developments to the statistical methodology used in fitting the Soil CMS model. Whereas the original CMS (Scott et al. 2002; Tate et al. 2003a, 2003b, 2005; Baisden et al. 2006) used the general linear model (hereafter called the LM), a later modification changed the fitting procedure to a generalised least-squares approach (GLS), with a correction for spatial autocorrelation (McNeill et al. 2009).
The combination of changes in the soil sample data available for fitting the Soil CMS model, changes in the source data for explanatory layers such as land use and soil–climate, and refinements to the statistical methodology employed make it difficult to separate and compare the effects of each of the developments to the model over time. Consequently, this paper sets out the considerations involved in refining the model and its underpinning assumptions as it is currently documented (McNeill 2013), rather than being a detailed historical account and justification of all of the changes that have been made.
This paper has three objectives. First, the Soil CMS model as it is currently used in New Zealand (McNeill 2013) is explained, along with the justification for key processing steps and the associated uncertainty model. Second, key steps are described that are important in determining whether or not the model can be used as the basis of a Tier 2 reporting option (use of country-specific data via the Soil CMS model) to report SOC stock changes in soils. Third, we seek to determine whether adding new covariate layers improves the degree of uncertainty in the land-use-effect estimates from the model, given the structural constraints in applying the model to give estimates of SOC change.
After the data sources have been defined, comprising the SOC data and the various model explanatory factors, the statistical methodology behind the current SOC inventory and inventory change model is developed, noting the shortcomings of the model form imposed as a result of one of the primary LUCAS applications (the CRA). In particular, we note that the SOC model can be optimised in terms of model complexity and the uncertainty of model estimates to minimise either the uncertainty of the SOC stocks or the uncertainty of the SOC stock change. The adopted model represents a pragmatic compromise between these two different models (SOC stock and SOC change). The uncertainty model of the Soil CMS is then developed, including several key assumptions involved in the fitting process and the assessment of the significance of the SOC change resulting from land-use change and its subsequent interpretation.
Potential alterations to the model are then considered, especially augmentation of the explanatory data by new national covariate data layers that might be associated with SOC. We show that these changes do result in a reduction in the standard error of the regression describing SOC, but that the addition of new layers (and additional complexity) does not result in a significant improvement in the model for SOC change resulting from land use.
In a regression to predict SOC, an implicit assumption is that the explanatory variables are measured without error. When the explanatory variables are subject to error during measurement, conventional regression procedures produce biased coefficient estimates, where the degree of bias depends on the degree of corruption of the explanatory variables. Several common environmental covariates have uncertainty or classification error associated with them (e.g. elevation model slope error, land-use misclassification), and we make the assumption that the degree of uncertainty in the various explanatory layers is not enough to warrant special regression procedures described elsewhere (Cheng and Van Ness 2001).
Materials and methods
Model basis
An inventory model for SOC change is inherently problematic compared with estimating the change associated with other C pools in the environment, such as vegetation. In principle, the parameters in a vegetation plot (e.g. species and diameter values for the same trees) can be remeasured on two separate dates some years apart, thus effectively eliminating the within-stratum variance (Coomes et al. 2002). The C measurement process in soil is destructive at a point, so the within-stratum variance cannot be eliminated by repeated-measurement, and thus many samples are required within a soil or climate stratum to reduce the pooled variance to acceptably low levels.
The operation of the Soil CMS model to produce SOC pool estimates involves applying a linear statistical model to key factors of land use, climate, and soil class, which together regulate net SOC storage. The model includes an additional environmental factor consisting of the product of slope and rainfall—a term used as a proxy for the potential for surface soil erosion to occur (‘erosivity’) (Giltrap et al. 2001). The key concept in the operation of the Soil CMS model is that land use affects SOC, and so estimates must be reported grouped by specified land-use classes. The model allows for an explanatory effect by land-use class, and this approach has some benefit if the variability between land-use classes is greater than the variability within a class. The SOC estimate is unbiased whether land-use class is included in the model or not, but the overall residual standard error is reduced by including the land-use class explanatory effect.
The uncertainty of the land-use effect in the Soil CMS model depends on two factors. One component of uncertainty relates to the inherent uncertainty of SOC knowledge, and a second depends on the number of field samples available. The nature of the field data is such that this latter component of uncertainty tends to be dominant.
An important consideration in the design of the Soil CMS model is that it includes several factors presumed to be associated with the variability in SOC stocks, although they may not be causally associated with those changes. Furthermore, these factors are not necessarily the only factors known to be associated with changes in SOC stocks. First, the total number of factors associated with variability in SOC stock is not known. Second, there are some physical and chemical properties of soil that are known to be highly influential predictors of SOC, but which are only available for a small number of samples and are not mapped at a national scale. Examples of such properties are soil specific surface area, cation exchange capacity, and the content of dithionite-extractable iron, which in previous studies have been shown to predict SOC content almost completely (Kahle et al. 2002). Therefore, the Soil CMS model development must represent a compromise between the collection of information available for all locations in the calibration dataset and the explanatory power of the variables for which representative information is available at a national scale.
The regression model underpinning the Soil CMS model is fitted using a set of soil measurements from several different sources gathered over decades. The soil sample locations, although important and relevant to the researchers at the time, are not the sites that might have been chosen if the study were to be designed afresh. Most standard statistical tests depend on random sampling or have some component of randomness imposed to satisfy the rigour of the subsequent statistical analysis (Lohr 1999), and soil samples that are in part historically derived do not satisfy this requirement. However, strict adherence to random sampling is not possible in the case of the Soil CMS model (in this case, circumscribed by the cost of acquiring a sufficient number of samples), but the inclusion of historical datasets chosen without bias or a particular intent (McCune and Grace 2002) allows researchers to achieve the aims of inventory analysis, while accepting that the derived model might require careful checking to detect possible sampling artefacts. Because of this approach, some soil–climate and land-use factors are under-represented while others are over-represented. To some extent, soil samples are correlated depending on the distance between them, which means that application of the Soil CMS model to the Soil CMS dataset results in predictions of SOC stocks that are biased from their true values. This effect was noted in earlier analyses (Kirschbaum et al. 2009), and the bias can be accounted for in the analysis (McNeill et al. 2009).
Soil C linear parametric model
The original model to estimate SOC in New Zealand (Scott et al. 2002) was similar to the approach used by IPCC at the time (IPCC 1996). This involves stratification of the New Zealand landscape by the key factors that influence soil carbon over time-scales of interest for national monitoring (soil group, climate, and land use or land cover).
The regression model for SOC in the 0–30-cm layer as a response variable uses explanatory variables of the soil–climate factor, the land-use class, and the slope–rainfall product. This model is represented as an equation for the SOC 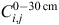 in land-use class i and soil–climate class j as:
in land-use class i and soil–climate class j as:

In Eqn 1, 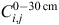 is the mean SOC in the 0–30-cm layer, and M is the mean SOC for the combination of the reference level of land use (low-producing grassland), the reference level for soil–climate (moist-temperate high-activity clay), and level ground; Li is the effect of the ith land use, specifying the difference in SOC relative to the reference land use (low-producing grassland) (in t ha–1); Sj is the effect of the jth soil–climate class relative to the reference level; and b is the additional SOC for each unit of erosivity (slope × rainfall), or SR (millidegrees × 10–1). The model uncertainty is encapsulated in ε, which is defined later.
is the mean SOC in the 0–30-cm layer, and M is the mean SOC for the combination of the reference level of land use (low-producing grassland), the reference level for soil–climate (moist-temperate high-activity clay), and level ground; Li is the effect of the ith land use, specifying the difference in SOC relative to the reference land use (low-producing grassland) (in t ha–1); Sj is the effect of the jth soil–climate class relative to the reference level; and b is the additional SOC for each unit of erosivity (slope × rainfall), or SR (millidegrees × 10–1). The model uncertainty is encapsulated in ε, which is defined later.
Equation 1 predicts a single value of SOC for one single site. If we denote 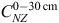 as the total New Zealand SOC stock, with ANZ, ALi, and ASj the area of New Zealand, the area in land use i, and the area in soil–climate class j, respectively, then the total SOC for New Zealand is found by using:
as the total New Zealand SOC stock, with ANZ, ALi, and ASj the area of New Zealand, the area in land use i, and the area in soil–climate class j, respectively, then the total SOC for New Zealand is found by using:

In Eqn 2, ANZ.M is the reference-soil SOC, characterising SOC for the low-producing grassland land-use class, moist-temperate high-activity clay soil–climate class, and flat land (i.e. slope of zero). The remaining terms adjust the reference value for other factors: Σj LiALi is the additive adjustment for the SOC in each land-use class other than low-producing grassland; Σj SjASj is the additive adjustment for the soil–climate relative to moist-temperate high-activity clay; and 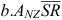 is the additive adjustment for rainfall and slope. The uncertainty ε in Eqn 2 is different from the uncertainty in Eqn 1, which uses the same symbol for convenience.
is the additive adjustment for rainfall and slope. The uncertainty ε in Eqn 2 is different from the uncertainty in Eqn 1, which uses the same symbol for convenience.
The quantities M, Li, and Sj, as well as the slope–rainfall coefficient b, are obtained by fitting a statistical model to the Soil CMS calibration dataset; all other quantities are obtained from other datasets or from separate analyses. For example, the mean value of the slope × rainfall must be obtained from national statistics of rainfall and a terrain slope map, which has been calculated from GIS layers as 39.1 millidegrees (Giltrap et al. 2001).
Although the choice of a reference level for land use (or indeed for soil–climate class) is arbitrary from a statistical viewpoint, there are good reasons why one might choose a specific reference class. In Tate et al. (2003a), ‘improved grassland’ was used as the reference because most land-cover changes considered at the time included improved grazing land; in addition, published reports suggested soil C for improved grassland could be assumed to be at steady-state. The present use of ‘low-producing grassland’ as a reference class is a continuation of the reasoning from Tate et al. (2003a).
The precise form of the regression model is not directly obvious from the form of Eqn 2. Although a linear model would be the obvious choice, it would not be appropriate because there is likely some spatial autocorrelation between points. In regions of high plot density, the local spatial correlation means that each additional sample of SOC tends to have a confirmatory effect on the existing value of SOC in that region and does not represent an independent estimate. Thus, the use of a linear model with a varying density of plots with spatial correlation may result in a bias of the estimated mean SOC (or the value after accounting for other explanatory variables) for some land-use classes and an underestimate of the uncertainty for the mean SOC. These issues can be expressed in terms of the basic assumptions of the linear regression model (e.g. see Bain and Engelhardt 1992, from p. 500).
SOC change model
Modelling of SOC with a regression approach essentially represents an intermediate step in the calculation of SOC change. Given, for example, the SOC model from Eqn 2, the SOC change ΔC1,2 between dates 1 and 2 is given by:

All other terms involving the soil–climate and the erosivity are assumed invariant over time and can be treated as constants. Since all other terms from Eqn 2 cancel, it seems as if refinement of SOC with additional explanatory factors is not worthwhile. However, refinements in the Soil CMS model to better explain SOC might be expected to alter the balance of the SOC variance explained by all factors (including land use) and be especially likely to alter the distribution of the SOC uncertainty in Eqn 2, and thus the uncertainty component of SOC change in Eqn 3.
The MfE CRA design is such that, currently, the SOC change model must accept as inputs each land-use class and the change in area associated with that land-use class, and these required inputs are compatible with the SOC change model in Eqn 3. Consider, however, a modification to Eqn 2 that transforms the Soil CMS model from a linear function to a non-linear function (f), which is invertible (inverse function f–1), such as log(C) or 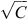 , both of which might be reasonable to apply to Eqn 1 to stabilise the variance of SOC and thus improve regression residual behaviour. In this case, the SOC change ΔC1,2 between dates 1 and 2 is given by:
, both of which might be reasonable to apply to Eqn 1 to stabilise the variance of SOC and thus improve regression residual behaviour. In this case, the SOC change ΔC1,2 between dates 1 and 2 is given by:
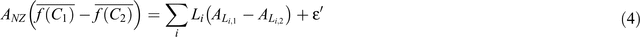
which cannot be inverted to produce 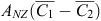 , and thus ΔC1,2, unless f is linear and ignoring issues concerning the transformation of the uncertainty component εʹ. Thus, the present design of the CRA precludes the use of a non-linear transformation of the SOC response function in Eqn 1.
, and thus ΔC1,2, unless f is linear and ignoring issues concerning the transformation of the uncertainty component εʹ. Thus, the present design of the CRA precludes the use of a non-linear transformation of the SOC response function in Eqn 1.
Soil data
Soil data for the Soil CMS model come from four sources. The first is the Historic Soils dataset, derived primarily from the National Soils Database, with a small number of samples from various supplementary datasets. The National Soils Database represents profile data collected for over 1500 soil pits scattered throughout New Zealand. These comprise the soil description following either the Soil survey method (Taylor and Pohlen 1979) or Soil description handbook (Milne et al. 1995), as well as physical and chemical analyses from either the Landcare Research Environmental Chemistry Laboratory or the Department of Scientific and Industrial Research (DSIR) Soil Bureau Laboratory. Soil properties were measured by horizon and then converted to fixed depth values by using a weighted average of fully and partially contained soil horizons (Baisden et al. 2006).
The second source, the Natural Forest Soils dataset, was gathered as part of MfE’s Natural Forest Survey, with soil samples taken by subsampling a regular, 8-km grid across the landscape, using fixed depths. The Natural Forest Soils were important in the development of the Soil CMS model because they provide spatial balancing in areas of New Zealand not adequately covered by other sources of soil data.
The third source of data is a set of intensively spatially sampled, high-producing grassland, annual cropland, and perennial cropland records, using fixed sampling depths and referred to as the Cropland dataset (Lawrence et al. 2008; Lawrence-Smith et al. 2010a, 2010b).
The fourth source of data comprises wetland soil data from a recent research effort to combine field data with analysis of the spatial distribution of current wetlands in New Zealand (A.-G. Ausseil, pers. comm.), consisting of 131 mineral and organic soils from wetlands. The soil cores in this dataset were typically 7 cm deep after removing surface living vegetation and litter; however, in most cases, the soils are homogeneous to 30 cm depth. These soils were recorded as soil C concentration and were converted to SOC stocks using either the bulk density for the sample or average bulk density of the wetland class for the sites where sample bulk density was not available. The soils were classed as organic by one of three rules. First, if the measured C concentration was >18%. Second, if the C concentration was not available, and thus estimated by assignment from a wetland class mean, the soil was classed as organic if the bulk density was <0.4. Finally, if the C concentration and the bulk density were both considered unreliable for classifying the soil sample, then expert knowledge of the site was used. The estimated SOC stocks were then extrapolated to the 0–30-cm layer and points with invalid or unknown map coordinates were discarded. Since organic soils classified in the above manner are treated separately in the Soil CMS model, these samples were discarded, resulting in 21 wetland mineral samples. Although this is only a small pool of samples compared with other data sources, it represents a large increase from the three wetland samples previously available from the National Soils Database alone.
Land-use information
Land-use information was derived from the MfE LUCAS LUM, which consists of New Zealand-wide land-use classes (12) nominally at 1 January 1990, 1 January 2008 and 31 December 2012 (Koordinates 2013); these date boundaries were dictated by the First Commitment Period of the Kyoto Protocol. The LUCAS classification from which the LUM was generated was produced from satellite imagery (Landsat-4, -5, or -7 or SPOT-5, depending on the LUM date), augmented by mapping and validation datasets from aerial- and satellite-based sources (Koordinates 2013). Two of the 12 LUM classes were not used because of lack of SOC data: open water (assumed 0, by definition) and settlements (assigned to low-producing grassland by convention).
The IPCC default assumption is that the SOC pool can be considered at steady-state 20 years after a land-use change known to cause a significant change in SOC (Penman et al. 2003). Following this rule, the Soil CMS model was built on the assumption that its constituent land-use classes have reached steady-state, and thus, classes that are in transition to steady-state should be removed from the model. Instead, these classes in transition should be assigned some portion of the steady-state pool of SOC. In particular, the pre-1990 and post-1989 forest classes should be separated because they are distinct populations; post-1989 forests generally lose SOC progressively over time (Beets et al. 2002), so pre-1990 forest would be expected to have lower SOC stocks than post-1989 forest. In calculations of SOC change, the pre-1990 forest class would be applied to the post-1989 forest soils, using a transition rate. For this reason, post-1989 forest samples were removed from the dataset.
Other explanatory layers
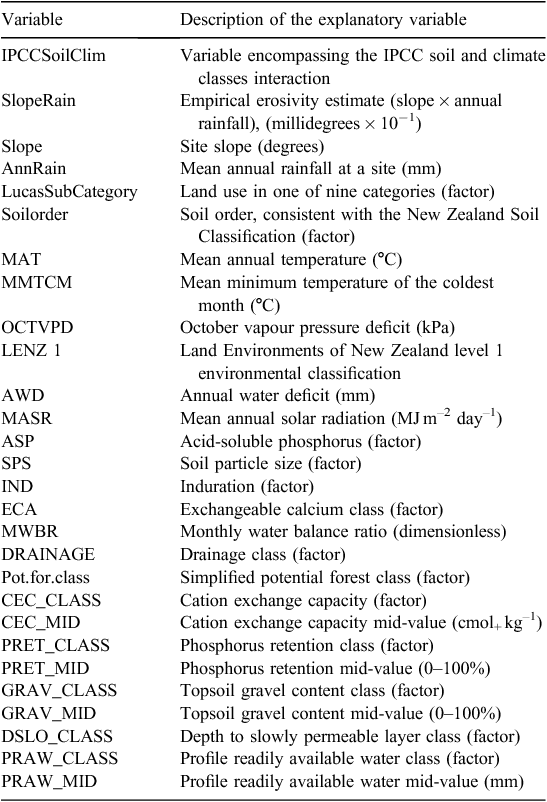
In order to investigate possible improvements to the model describing the relationship between SOC stock change and environmental variables, several other national-coverage layers were gathered as potential explanatory factors associated with SOC (Table 1).
|
The Land Environments of New Zealand (LENZ) provides numerical data layers describing various aspects of New Zealand’s climate, landforms, and soils, such as annual water deficit, monthly water balance ratio, or a factor defining the soil particle size (Leathwick et al. 2002). LENZ also provides a series of four hierarchical classifications that identify similar environments based on climate, landform, and soils, with 20, 100, 200, and 500 environments nationally for LENZ level 1, 2, 3, or 4. Only the LENZ level 1 classification is used (20 classes) in this study because the available soil sample data do not encompass the other classifications.
The Fundamental Soils Layer (FSL) is generated from a relational join of features from the New Zealand Land Resource Inventory (NZLRI) and the National Soils Database. The NZLRI is a national polygon database of physical land resource information. FSL provides GIS information of the expert-assessed classification of Soil Order, and other soil or landscape attributes over New Zealand, including, for example, an estimate of the mid-range value of the cation exchange capacity for a given polygon.
The S-map is a contemporary digital soil spatial information system for New Zealand (Lilburne et al. 2012), which provides information on the best available knowledge of classification of the Soil Order consistent with the New Zealand Soil Classification (NZSC; Hewitt 2010). Coverage by S-map is not available for all the land area, but it is available for regions of intensive agricultural use. The more-detailed S-map version of the Soil Order was used when available, and the version from the FSL when the S-map version was not available. In cases where only the FSL version was available, special FSL NZSC Orders corresponding to ‘town’, ‘estuary’, and ‘river’ were detected and the corresponding sample removed.
Topographic slope information was estimated from a digital elevation model generated from Land Information New Zealand topographic data layers at 1 : 50 000 scale (20-m contours, spot heights, lake shorelines and coastline), using Landcare Research in-house interpolation software, and using an interpolation process that enforced drainage from a national network of rivers.
Finally, the potential vegetation GIS layer is predicted from regressions relating the distributions of major canopy tree species to environment (Leathwick 2005). The layer is generated by a statistical modelling process that uses high-resolution environmental data from LENZ to reconstruct New Zealand’s potential vegetation pattern (Leathwick 2001), or the vegetation that could be expected in the absence of human activity. The layer provides two useful attributes: a code for the vegetation class, and a simplified version of the vegetation class. There are 26 unique classes in the vegetation and 16 in the simplified vegetation class; the latter is used in this analysis. It should be noted that this layer is subject to some uncertainty because it is the result of a modelling effort with relatively sparse prediction information. Nevertheless, it was considered a useful potential explanatory variable for SOC because it embodies the state of the vegetation in the environment before agricultural development and other land clearance, and thus might be considered a useful predictor when used in conjunction with LUM.
Data transformations
Some covariate layers corresponding to LENZ and FSL values were provided with convenient numerical types (e.g. mean annual temperature coded as 16-bit integer values in units of tenths of a degree Celsius) rather than floating-point values corresponding to physical units. Where this was the case, transformations were applied to transform the raw numbers to floating-point values in standard physical units. These transformations do not affect the analysis, but the use of physical units for covariates makes the analysis easier to understand.
Discrete explanatory variables (e.g. Soil Order, LENZ environmental class) were arranged as factors and ordered with respect to a common reference factor, as appropriate. For example, the soil–climate factor was referenced to moist-temperate high-activity clay, which happens to be the standard arrangement that had been used in previous analyses of this type (McNeill et al. 2009; McNeill 2010, 2012).
Non-parametric exploratory model
The SOC change model has evolved into a reliable method of regression based on explanatory factors of soil–climate, land use, and erosivity (slope × rainfall). To determine whether this model could be improved, various national data layers (Table 1) were sought as new explanatory factors. The intention was that the addition of one or more layers might reduce the uncertainty of the Soil CMS model, and therefore of SOC change. However, the large number of potential explanatory variables available for association with SOC means that the step-by-step processes of regression model evaluation and model selection for refinement is particularly difficult.
One possible approach is to use a non-parametric regression method, which is useful where there are many variables. These are sometimes referred to as data-mining methods or machine-learning methods, and they include regression trees, random forests, neural networks, bagging, and boosting (Hastie et al. 2009), of which the regression tree approach is perhaps the most well-known example.
Regression trees are powerful methods and much work has been done to improve the predictive ability of these tools through a variety of different methods, most notably by combining separate tree models into what is often called a committee-of-experts or ensemble approach. Random forests and stochastic gradient boosting are two of these newer techniques that use regression trees as basic building blocks. Of these methods, current practice favours stochastic gradient boosting as arguably the best method to use in a general application (National Research Council 2013), and this is the method used here (termed simply ‘boosting’) to predict SOC.
Machine-learning methods of regression are particularly suited for the regression-estimation of SOC for three reasons. First, the methods readily adapt to datasets where explanatory variables are available in some but not all records. Second, a non-linearity in the relationship between an explanatory variable and SOC is easily handled. Finally, interactions between explanatory variables can easily be tested, especially in cases where coverage of the variables in the dataset is sparse.
There are, however, several disadvantages of these methods when compared with parametric models (e.g. linear models). First, they are not so readily interpretable, although this may not be an important issue in practice. Second, they almost invariably assume that the fitting data are independent, which is unlikely to be the case for SOC data, given their strong spatial correlation. Thus, in this study, boosting is used as a way to rank the most influential explanatory variables, as well as to provide some understanding for the trend in the SOC response with different values of each explanatory variable. The failure of the method to directly account for spatial correlation of samples makes it likely that the uncertainty of the predictions is over-optimistic and, perhaps, biased towards regions of high density. Nevertheless, boosting is expected to shorten the time taken and simplify the process required to identify a suitable parametric model.
SOC change uncertainty calculation
The land-use effect for a transition in land use from low-producing grassland to one of the other land-use classes can be obtained by inspection of the coefficients of the appropriate SOC model (Table 2), noting that the various soil–climate class labels in Table 2 are defined in Scott et al. (2002). The land-use effect for a transition in land use from any arbitrary land-use class to a different land-use class can also be obtained by calculating the difference of the land-use effects from the origin and destination land use with respect to low-producing grassland. The uncertainty of the land-use effect (the change in SOC assuming the transition is stable) between two land-use classes in isolation is conceptually straightforward: two estimates of land-use effect are more likely to be significantly separated if their point estimates are farther apart after taking account of the covariance between the two land-use effects. The standard error, σi,j, of the land-use-effect change for a transition between two land-use classes with effects Li and Lj is then estimated from:

where Var(Li) is the variance of land-use effect i, and Cov(Li, Lj) is the covariance (see Table 6) between land-use effects Li and Lj.

|
Interpretation of comparison-wise significance
Although Eqn 5 provides a mathematically straightforward way to estimate the significance of a single transition from one land-use class to another (a comparison-wise significance), often there is need to determine whether several land-use classes are likely to be significantly different or essentially the same as an ensemble. As more comparisons are made between many different land-use types, it becomes more likely that at least one of the land-use-effect changes will appear to be different as a result of random chance alone, resulting in an increase in the Type 1 error. Thus, the significance of all possible land-use transitions must be calculated as a family of simultaneous comparisons (multiple-comparison significance), rather than calculated one at a time.
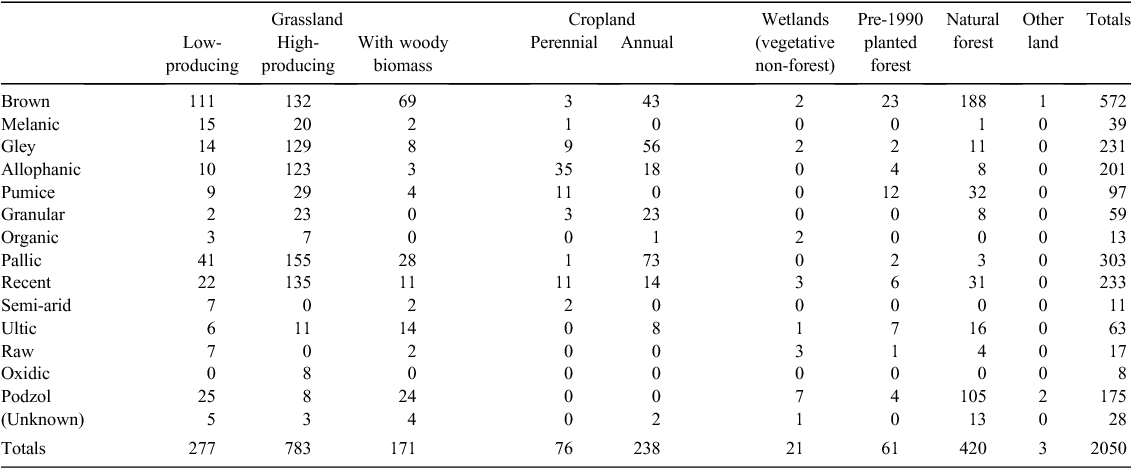
A variety of methods can be used to control the Type 1 error rate in multiple comparison significance testing, but the choice of which method is appropriate in a given situation is not straightforward (Bretz et al. 2010). The choice of a procedure depends partly on the type of problem. In addition, some methods are appropriate when the number of samples in each of the factor levels being compared is approximately equal; this is not the case for the number of samples in each LUCAS subcategory (Table 3).
|
For the SOC change model, what is required is the simultaneous testing of all possible combinations of the land-use classes for equality (a two-sided test), where the number of cases in each category is markedly different. We use a closed testing procedure test described by Marcus et al. (1976), which is a general method for performing several hypothesis tests simultaneously, implemented in the package multcomp in R (Bretz et al. 2010).
Results
Data selection
From the raw soil sample data, in total 2570 records were read. These were combined with the wetland data and then processed for later analysis where three conditions were true. First, each sample was assessed to pass quality-control checks from MfE, or verify that the sample was from the wetland dataset. Second, the soil sample was a mineral rather than an organic soil. Third, attributes defining the IPCC soil and climate type were defined for the sample. Finally, post-1989 planted forest samples were removed, as noted above.
One point from the SOC dataset was removed because it was located off the coastline of New Zealand; this point is likely to represent correct data but has had its map location entered incorrectly. One point from the wetland dataset was removed because it was duplicated within the National Soils Database. Finally, 15 points were removed from the dataset because they occurred at locations where the covariate values extracted from the combination of FSL and S-map were not valid. Subsequent analysis showed that these points are very close to the coastline, and because some of the layers extracted from the FSL are raster-based, the extracted covariate value was not valid so close to the coastline. After the data pruning, 2050 records remained for analysis.
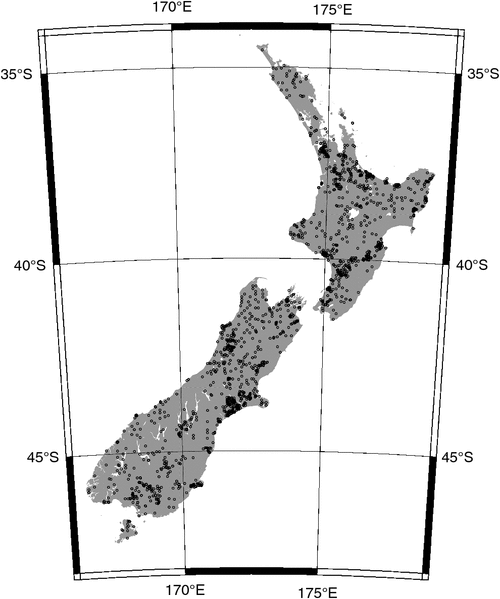
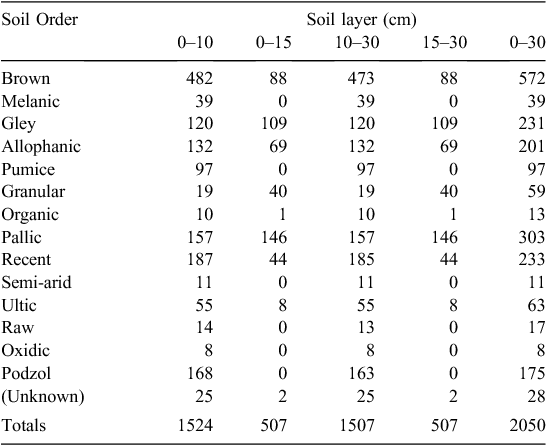
Together, the four combined datasets cover most of the land mass of New Zealand (Fig. 1), including Stewart Island, although coverage does not extend to the Chatham Islands and other offshore islands. Coverage is dense in areas of agricultural activity, and the density of points varies widely between different regions (Fig. 1). The density of plots varies from as low as 100 000 ha plot–1 to as high as 2 ha plot–1, or roughly four orders of magnitude difference. The SOC stock value is available for several different layer depths (Table 4), but the largest number of samples was for the 0–30-cm layer.
|
|
There is a wide variation in the number of records associated with the different land-use classes and Soil Orders (Table 3), with the largest land-use group (high-producing grassland) having 783 samples and the smallest (other land) only three samples. Thus, it would be reasonable to expect also considerable variability in the uncertainty of the estimated land-use effect for each of the different land-use classes, assuming all other things being equal. In addition, the large number of zero-valued cells means that it would be impossible to estimate the effect of an interaction between certain land-use and Soil Order categories (e.g. high-producing grasslands in semi-arid soils) (Table 3). Although certain combinations of these factors are unlikely, or even impossible, this constraint of zero cells effectively rules out an interaction between Soil Order and land-use category.
Parametric model
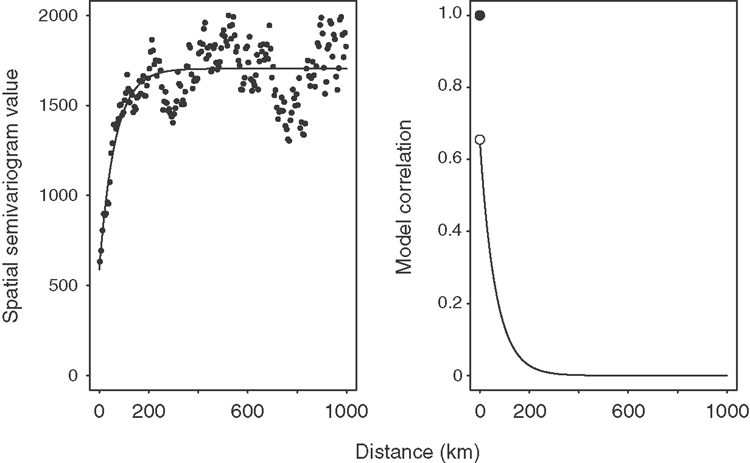
Figure 2 shows plots of the spatial semivariance of the sample data, along with a model estimate of the semivariance with a nugget and an exponential functional form. The corresponding spatial correlation model is also shown in Fig. 2, calculated from the fitted semivariance model. The correlation at zero distance must, of course, be one, but the correlation at an arbitrarily small distance from zero is 0.66, diminishing slowly to zero with increasing distance.
|
The residual standard error for the model is 42.1 t ha–1, and the corrected Akaike information criterion value (AICc) is 20 519.7. The spatial autocorrelation scale distance is 19.3 km, with a nugget of 0.46; these are values consistent with earlier analyses (McNeill et al. 2009; McNeill 2010, 2013). The use of the AICc as a model selection and comparison mechanism is widely supported in the literature in general, and soil modelling specifically (Burnham and Anderson 2002; Ogle et al. 2007; Elsgaard et al. 2012). All but one of the main land-use effect coefficients were significant (Table 2).
Non-parametric model
The use of the boosting model was intended to determine which of the explanatory variable layers would be strongly associated with SOC, and thus would form the basis of an improved SOC and (consequently) SOC change model. The package gbm (Ridgeway 2013) was used to implement the boosting model, with SOC as the response and the explanatory variables as listed in Table 1. A Laplace (absolute loss) distribution was used for the loss distribution as this has some resilience to outliers. Shrinkage (essentially the learning rate) was set at the recommended standard value of 0.001. Interactions of the explanatory variables were not permitted, because the dataset is sparse when interactions between factor variables are considered (Table 3). Five-fold cross-validation was specified to give an estimate of generalisation error, and 80 000 trees were fitted in total, a figure adopted after a trial to determine that the optimum number of trees had been covered. The optimal number of boosting iterations was chosen by cross-validation after fitting.
The LENZ level 1 environmental classification, NZSC Soil Order, IPCC soil–climate class, and the potential vegetation have (in descending order) the strongest influence on the prediction of SOC, whereas the profile readily available water class has precisely zero influence (Fig. 3). The influence measure needs to be interpreted with care, because the LENZ and IPCC soil–climate classes are both aggregate classifications of climate, and influence from the boosting regression (Fig. 3) describes the association of each variable with SOC after accounting for the effect of all other explanatory variables (Friedman 2001). No interactions between explanatory variables were permitted; therefore, the interpretation of explanatory-variable influence is straightforward, suggesting some value in including at least some of the variables with high influence, whereas others may be dropped.
Refined parametric model
Based on the results from the non-parametric boosting model, a refined parametric model using the GLS approach was then trialled, using the nine most-influential variables (Fig. 3) as well as the variables from the previous version of the parametric model (i.e. IPCC soil–climate, the various land-use classes, and erosivity). The result from this regression was inspected for non-significant explanatory variables. Then, the variable exhibiting non-significance was pruned from the model, which was then fitted again with GLS. This process was repeated until either the AICc no longer reduced or there were no longer any explanatory variables to prune. This is a manual type of backwards stepwise refinement procedure, and is preferred over automatic all-subset selection because it takes several hours to fit a given GLS regression model with a correction for spatial autocorrelation on a desktop PC.
The optimal model, reached when the AICc no longer decreased, dropped the annual rainfall and the mean annual temperature from the nine additional variables added as a result of the non-parametric regression. The AICc of the optimal model was 20 098.00, which is significantly reduced from the value of 20 519.7 of the original parametric model. The residual standard error of the optimal model decreased to 36.1 t ha–1 compared with 42.1 t ha–1 from the original parametric model.
Although the AICc and the residual standard error decreased for the optimal model, the values of the coefficients for the LUCAS subcategories (the various land-use classes) did not change by more than a few per cent, and the standard errors of the LUCAS subcategories increased in five of the eight classes (Table 5). In the three classes where the standard errors decreased in the optimal model (grassland with woody biomass, perennial cropland, and pre-1990 planted forest), the decrease was small (0.4%, 0.8% and 2.5%, respectively). Against the modest gains offered by the optimal model, a large increase in the complexity of the model is noted, involving some 80 coefficients, compared with the original parametric model with only 29 coefficients.
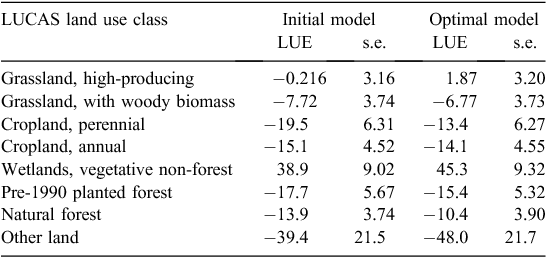
|
The relatively modest gains for the optimal model compared with the original parametric model (Eqn 1) shown in Table 5 suggest that the more parsimonious model from Eqn 1 would be preferred as the basis for an SOC change model. In the following sections, we abandon the use of the more complicated optimal model in favour of the original SOC model described in Eqns 1–3.
SOC change model uncertainty and significance
As noted in an earlier section, the marginal significance (the significance of a pre-planned land-use transition) can be determined from the covariance matrix Cov(Li, Lj) between any two land-use classes for the model, such as that fitted for Eqn 1. For the parametric GLS model of Eqn 1, the covariance matrix is given in Table 6, and the 95% confidence intervals for the land-use effects are provided in Table 7.

|
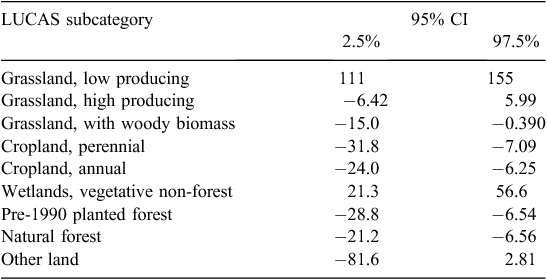
|
However, for the SOC change, the simultaneous testing of all possible combinations of the land-use classes is required for equality. The closed-testing procedure described by Marcus et al. (1976) is used, yielding point estimates and confidence intervals of a test statistic for each distinct combination of land-use transitions, and the critical test is whether the confidence intervals brace zero. All transitions involving ‘Other land’ are non-significant, and two other transitions are also non-significant: ‘Wetland, vegetative non-forest’ to ‘Cropland, annual’, and ‘Grassland, high producing’ to ‘Grassland, low producing’ (Fig. 4). Note that in Fig. 4, the test statistic does not depend on the order of the initial land-use change. Thus, the statistic from ‘Other land’ to ‘Cropland, annual’ is the same as the statistic for the reverse land-use change. These land-use-transition pairs contribute relatively little to land-use-induced SOC change calculations.

|
The transitions involving ‘Grassland, high producing’ to/from ‘Grassland, low producing’ comprise ~0.5% of all land-use change detected between 1990 and 2012. All land-use transitions involving ‘Other land’ make up ~0.8% of all land-use change detected between 1990 and 2012, and it can be noted that this category is used both to classify marginal land and to allow mapped areas to reconcile with national area, and C pools would not need to be assessed for the category except where overall consistency is to be checked (Penman et al. 2003). The transition between ‘Wetland, vegetative non-forest’ and ‘Cropland, annual’ has not been detected as a land-use change between 1990 and 2012 by LUCAS land-use mapping efforts. This would be expected from an ecological and land-management perspective as well as statistically, given the quite different SOC stocks of these two categories, and it is likely the lack of significance is an artefact of the distribution of the dataset.
Discussion
Adoption of a model for SOC change
The result from the non-parametric boosted model suggests several variables as strong predictors for SOC. The nine most influential variables were then used in stepwise-refinement of a parametric GLS model to predict SOC. For the stepwise-refined model, the size of the land-use effects is changed somewhat because of the new explanatory variables; a few (three of eight) decreased, but the changes are very small and none of the changes is significant. The size of the standard error decreased from 42.1 t ha–1 for the model fitted to Eqn 1 to the value for the stepwise-refined model of 36.1 t ha–1. Against this modest improvement of ~10% in the residual standard error for soil C and the lack of a consistent improvement in the standard error for the land-use effects in the stepwise-refined model, the complexity of this model is far higher (80 coefficients) than the simple model fitted from Eqn 1 (29 coefficients).
Although complexity of a model is in itself not bad, it is usually worth tolerating an increase in model complexity only if there is a worthwhile gain in model performance. The choice between the models fitted to Eqn 1 and the stepwise-refined model depends critically on how the model is to be used. If the intention is to use the model to predict SOC stocks, then the more complex model is the better choice, because it has a lower standard error and AICc. However, if the intention is to estimate SOC change, then the model adopted is the one that gave the estimate of the change with the smallest error. In both cases, however, model parsimony has some bearing, and simpler models are favoured over more complicated models if all other considerations are equivalent.
With respect to the selection of a suitable SOC change model, although the stepwise-refined model has a better residual standard error and AICc, the real interest is in reducing the size of the LUCAS subcategory standard errors so that the significance of the land-use-effect transitions can be improved, given the underlying premise that SOC change occurs due to land use. For this reason, the model fitted to Eqn 1 is favoured over the stepwise-refined model, despite the better overall performance of the latter in predicting SOC.
One of the reasons that the model fitted to Eqn 1 happens to be favoured here is that interactions between explanatory variables (particularly with land use) are ruled out, for reasons of ease of calculation of the SOC stock change in the MfE CRA. Similarly, using a transformed version of the SOC stock, in conjunction with interactions, would very likely reduce the standard error of the land-use coefficients, but at the expense of the complexity of the model and also violating the design requirements of the MfE CRA. Allowing interactions with land-use class and allowing a transformation of the SOC response variable would require the SOC stock to be separately mapped for each date, aggregating the map of SOC stock change to give a national estimate, and then calculating the difference to estimate the SOC change. By contrast, the current model can be directly formulated as a national inventory model and can be readily used within the CRA.
Interpretation of influential variables
The potential vegetation variable in the non-parametric boosted model encodes each location in a class describing the vegetation that might have been expected in the absence of human activity. All but one of the levels of the potential vegetation are significant compared with the reference class, but the uncertainty of the coefficient effect is such that the difference between pairs of classes is not likely to be significant except between those with the most extreme effect difference (Fig. 5), such as the difference between ‘Dunelands’ and ‘Scrub, tussock-grassland and herbfield above the treeline’, and to a lesser extent ‘Wetlands’.
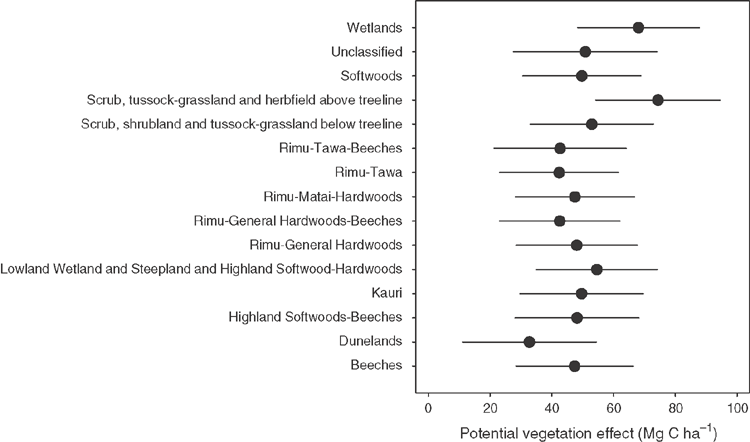
|
The high influence of potential vegetation in the regression of SOC (Fig. 3) can be understood in several different ways. One interpretation is that this variable encodes the level, or signature, of SOC that would have resulted from the long-term vegetation history in a location, which has subsequently been modified by land-use change, such as clearance for agricultural development. Another (equivalent) interpretation of the result is that the potential vegetation defines a legacy effect in SOC resulting from historical land cover after the effect of land use has been accommodated in the model. This latter explanation suggests that the land-use factor might be confounded by potential vegetation within one or more land-use classes. For example, the large effect of wetlands in the potential vegetation class (Fig. 5) could suggest that former wetlands (i.e. those wetlands that existed before agricultural development) now encoded in the high-producing grassland class have a different SOC than the remainder of the high-producing grassland class. This suggests that for an SOC model, potential vegetation is required in order to avoid the confounding effect or, alternatively, that one or more of the present land-use classes should be subdivided (cf. Gimmi and Bugmann 2013). However, as noted earlier, for an SOC change model, the inclusion of potential vegetation itself does not appear to change the land-use-effect coefficients or their significance.
Interpretation of the land-use-effects table
As noted earlier, the correct operation of the SOC change model involves fitting the model to the SOC dataset and then using the coefficients for the different land-use classes for a transition between two distinct land-use classes. The interpretation of the different land-use effects is subject to the consideration of multi-comparison significance. The GLS model is a minimum variance unbiased estimator (Draper and Smith 1998), so the SOC values, and the SOC changes as a result of a land-use transition, are unbiased if the coefficients are used in this manner. This approach is consistent with the physically based SOC model outlined in the literature (Scott et al. 2002; Tate et al. 2003a, 2003b, 2005; Baisden et al. 2006; Kirschbaum et al. 2009).
Having carried out the above calculation, it may turn out that some of the land-use transitions are not statistically significant in the multi-comparison sense, as noted earlier. However, this interpretation of significance does not alter the method of calculation of the SOC change resulting from land-use transition. In particular, it would not be correct to substitute a value of zero for the effect of a land-use transition where the transition itself is not significant in the multi-comparison sense, because if such a substitution were to be carried out, the calculation of the SOC would no longer be unbiased. Avoiding the bias in this manner also reduces the residual uncertainty of the SOC estimates. For this reason, the effect of all land-use transitions ought to be included in calculations of SOC change.
Interpretation of the land-use-change model
As noted in the previous section, the statistical model requires retention of all of the land-use classes in calculations of the SOC for a given land use, soil-climate, and erosivity (slope × rainfall), in order for the estimated SOC to be unbiased. When the SOC change model is used, the analyst is interested in the value of the SOC change for a given land-use-change combination, and the significance of the estimated change, assuming that the land-use classes have reached long-term stability. This calculation assumes there is no SOC change associated with soil–climate and erosivity (Eqn 3), because these factors are assumed constant.
The estimated level of SOC change for specified origin and destination land-use classes is given by Eqn 3, where the value of the coefficients is obtained using Table 2. The significance of the land-use transition in the multi-comparison sense (i.e. considering the ensemble of all possible land-use classes) is given by referring to Fig. 4, where all transitions involving ‘Other land’ are non-significant, as well as two other land-use transitions.
Significance of the result
The key contribution of this paper is the presentation of a statistical method that attempts to provide evidence for SOC change resulting from land-use change, where the evidence is considered among the ensemble of all possible land-use transitions. Prior work within the New Zealand context (Scott et al. 2002; Beets et al. 2002; Tate et al. 2003a, 2003b; Wilde et al. 2004; Hedley et al. 2012) has considered the evidence for SOC change for a restricted range of land-use transitions, or within a specific soil–climate class; these essentially provide evidence for marginal class transitions. The practical complications of the multi-comparison significance tests arise because the soil data from which the model is fitted are unbalanced, and hence the more common multi-comparison procedures are not appropriate. Marginal significance procedures provide low-power assessments of significance that are useful for testing the possible departure of the model (e.g. from Eqn 3) from the field data, but the procedures have limited utility for proving the correctness of the model.
The SOC and SOC change models developed in (Scott et al. 2002) and presented here in Eqns 1–3 represent a compromise arising from the limited amount of data available from previous soil surveys and some contemporary fieldwork to fill in certain soil–climate and land-use classes for which limited data exist. The models are straightforward, developed from a well-established methodology at the time of development (IPCC 1996), and use a simple set of explanatory variables that were accurately mapped.
Comparison with other work
Several studies in the literature have considered the SOC change as a result of land-use transition, within the context of a national or a regional sampling scheme (Callesen et al. 2003), as a meta-analysis (Poeplau et al. 2011, Bárcena et al. 2014), or as a national assessment within a single land use transition (Davis and Condron 2002). The assessment of the significance of the SOC change resulting from of all possible land-use transitions is methodologically difficult, because individual studies frequently do not provide the information required to carry out the required calculations (Bretz et al. 2010). Nevertheless, such calculations are important, because they establish the basic framework for high-power statistical evidence of SOC change, which is important for validation and verification.
There are various ways in the literature that SOC change can be estimated within a country as a whole, but two general approaches are dominant. In the first, experimental field data are used as the basis for SOC change inference (Houghton et al. 1999), but the precise methodology used varies from one study to another. A second approach is to use field data in conjunction with a theoretical model such as Century (Parton et al. 1987), DNDC (Li et al. 1994), or Roth C (Coleman and Jenkinson 1996) to build a process-based model for SOC, and thus SOC change.
There are advantages and disadvantages to the adoption of each approach to SOC change. Field-estimation of SOC change requires careful statistical sampling design in order to obtain results of adequate power, and in general, this approach requires more sampling effort than the approach where a theoretical model is used. By contrast, model-based SOC change estimation may require fewer field samples for fitting, but the assumptions inherent in the theoretical model must be justified, by laboratory studies or by validation efforts, and the models are more difficult to implement when conducting a national inventory (Ogle and Paustian 2005). In the end, the choice between these approaches depends on the national circumstances that apply in each case.
The New Zealand SOC change model might be considered an example of where SOC change is defined in an adopted theoretical (non-mechanistic) model, but the coefficients for estimating the change are calculated using extensive field data (largely gathered from historical sources). The simplicity of the theoretical model in the New Zealand case, compared with the more sophisticated models such as Century, DNDC, or Roth C, is a result of the fact that all land-use-class transitions must be modelled, rather than a subset. The complication in this model is that the significance of the SOC change must be determined for the ensemble of all classes for national inventory purposes; marginal class significance (Scott et al. 2002; Tate et al. 2003a, 2003b; Wilde et al. 2004; Hedley et al. 2012) can be useful for detecting gross departures from the model but do not address validation at a national level. This paper provides a method for validation of the model using a multi-comparison approach, providing direct evidence for the significance (or otherwise) of all transitions.
Combining the results of smaller, low-power studies for particular land-use transitions in a meta-analysis (Laganière et al. 2010) can provide useful high-power information at an international level. For the case of simultaneous land-use transitions, as addressed in this paper, it is not obvious how such studies would be combined.
Conclusions
An empirical model based on the GLS fitting of a linear model for SOC and SOC change has been described, based on explanatory variables of land use, soil–climate class, and erosivity, along with the associated uncertainty models. Possible improvements to the model for SOC have been considered as a way of reducing the uncertainty of SOC change estimates through a reduction in the standard error of the land-use effects. The improvements include the use of a stochastic gradient boosting non-parametric model to select data layers most strongly associated with SOC, and the fitting of a refined parametric SOC model using GLS with nine of the most influential explanatory variables from the boosting model and stepwise refinement. The stepwise-refined model has a significantly reduced standard error for SOC (36.1 t ha–1 compared with the original 42.1 t ha–1), but the standard errors for the different land-use classes are not consistently reduced, and the stepwise-refined model is considerably more complicated. The method of calculating SOC change resulting from the transition between two land-use classes is described by using the original GLS model, along with the significance of land-use effects by using a multi-comparison significance procedure.
Acknowledgements
We acknowledge funding for this project from the Ministry for the Environment. Cropland data were provided under an agreement between the Ministry for the Environment and Plant and Food Research.
References
Bain LJ, Engelhardt M (1992) ‘Introduction to probability and mathematical statistics.’ (Duxbury: Pacific Grove, CA, USA)Baisden WT, Wilde RH, Arnold GC, Trotter CM (2006) Operating the New Zealand carbon monitoring system. Landcare Research Contract Report LC0506/107 for the Ministry for the Environment, Wellington, New Zealand.
Bárcena TG, Kiaer LP, Vesterdal L, Stefansdottir HM, Gundersen P, Sigurdsson BD (2014) Soil carbon stock change following afforestation in Northern Europe: a meta-analysis. Global Change Biology 20, 2393–2405.
| Soil carbon stock change following afforestation in Northern Europe: a meta-analysis.Crossref | GoogleScholarGoogle Scholar | 24634314PubMed |
Beets PN, Oliver GR, Clinton PW (2002) Soil carbon protection in podocarp/hardwood forest, and effects of conversion to pasture and exotic pine forest. Environmental Pollution 116, S63–S73.
| Soil carbon protection in podocarp/hardwood forest, and effects of conversion to pasture and exotic pine forest.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XhsFel&md5=4977568b2ffb083d3dbe72fddba3277eCAS | 11833919PubMed |
Bretz F, Hothorn T, Westfall P (2010) ‘Multiple comparisons using R.’ (CRC Press: Boca Raton, FL, USA)
Burnham KP, Anderson DR (2002) ‘Model selection and multimodel inference: a practical information-theoretic approach.’ 2nd edn (Springer-Verlag: New York)
Callesen I, Liski J, Raulund-Rasmussen K, Olsson MT, Tau-Strand L, Vesterdal L, Westman CJ (2003) Soil carbon stores in Nordic well-drained forest soils - relationships with climate and texture class. Global Change Biology 9, 358–370.
| Soil carbon stores in Nordic well-drained forest soils - relationships with climate and texture class.Crossref | GoogleScholarGoogle Scholar |
Cheng C-L, Van Ness JW (2001) ‘Statistical regression with measurement error.’ (Arnold: London)
Coleman K, Jenkinson DS (1996) RothC-26.3: A model for the turnover of carbon in soil. In ‘Evaluation of soil organic matter models using existing, long-term datasets’. (Eds DS Powlson, P Smith, JU Smith) pp. 237–246. (Springer-Verlag: Heidelberg, Germany)
Coomes DA, Allen RB, Scott NA, Goulding C, Beets P (2002) Designing systems to monitor carbon stocks in forests and shrublands. Forest Ecology and Management 164, 89–108.
| Designing systems to monitor carbon stocks in forests and shrublands.Crossref | GoogleScholarGoogle Scholar |
Davis MR, Condron LM (2002) Impact of grassland afforestation on soil carbon in New Zealand: a review of paired-site studies. Australian Journal of Soil Research 40, 675–690.
| Impact of grassland afforestation on soil carbon in New Zealand: a review of paired-site studies.Crossref | GoogleScholarGoogle Scholar |
Draper NR, Smith H (1998) ‘Applied regression analysis.’ (Wiley: New York)
Elsgaard L, Görresa C-M, Hoffmann CC, Blicher-Mathiesen G, Schelde K, Petersen SO (2012) Net ecosystem exchange of CO2 and carbon balance for eight temperate organic soils under agricultural management. Agriculture, Ecosystems & Environment 162, 52–67.
| Net ecosystem exchange of CO2 and carbon balance for eight temperate organic soils under agricultural management.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhslWrurnN&md5=e9cd657f9311a8c3578f2061a7f3702fCAS |
Friedman JH (2001) Greedy function approximation: a gradient boosting machine. Annals of Statistics 29, 1189–1232.
| Greedy function approximation: a gradient boosting machine.Crossref | GoogleScholarGoogle Scholar |
Giltrap DJ, Betts H, Wilde RH, Oliver G, Tate KR, Baisden WT (2001) Contribution of soil carbon to New Zealand’s CO2 emissions. XIII: integrated general linear model and digital elevation model. Landcare Research, Forest Research Joint Contract Report JNT 9899/136 for the Ministry for the Environment, Wellington, New Zealand.
Gimmi U, Bugmann H (2013) Preface: integrating historical ecology and ecological modelling. Landscape Ecology 28, 785–787.
| Preface: integrating historical ecology and ecological modelling.Crossref | GoogleScholarGoogle Scholar |
Hastie T, Tibshirani R, Friedman J (2009) ‘The elements of statistical learning: data mining, inference and prediction.’ 2nd edn (Springer: New York)
Hedley CB, Payton IJ, Lynn IH, Carrick ST, Webb TH, McNeill S (2012) Random sampling of stony and non-stony soils for testing a national soil carbon monitoring system. Soil Research 50, 18–29.
| Random sampling of stony and non-stony soils for testing a national soil carbon monitoring system.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XisVyksb0%3D&md5=d3517b57370558e7d5a995fe499c3ab0CAS |
Hewitt AE (2010) ‘New Zealand Soil Classification.’ Landcare Research Science Series No. 1. 3rd edn (Manaaki-Whenua Press: Lincoln, New Zealand)
Houghton RA, Hackler JL, Lawrence KT (1999) The U.S. carbon budget: contributions from land-use change. Science 285, 574–578.
| The U.S. carbon budget: contributions from land-use change.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXltVSjsbw%3D&md5=f6e4749440d4cf375c80c0d397710098CAS | 10417385PubMed |
IPCC (1996) Chapter 5, Land-use change and forestry. In ‘Intergovernmental Panel for Climate Change. Revised 1996 Guidelines for National Greenhouse Gas Inventories: Reference Manual.’ pp. 5.6–5.75. (Intergovernmental Panel for Climate Change: Bracknell, UK)
Kahle M, Kleber M, Jahn R (2002) Predicting carbon content in illitic clay fractions from surface area, cation exchange capacity and dithionite-extractable iron. European Journal of Soil Science 53, 639–644.
| Predicting carbon content in illitic clay fractions from surface area, cation exchange capacity and dithionite-extractable iron.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXktVSlsQ%3D%3D&md5=4c1c783987d5ed9af68dca6f6d3ad5a6CAS |
Kirschbaum MUF, Trotter C, Wakelin S, Baisden T, Curtin D, Dymond J, Ghani A, Jones H, Deurer M, Arnold G, Beets P, Davis M, Hedley C, Peltzer D, Ross C, Schipper L, Sutherland A, Wang H, Beare M, Clothier B, Mason N, Ward N (2009) Carbon stocks and changes in New Zealand’s soils and forests, and implications of Post-2012 accounting options for land-based emissions offsets and mitigation opportunities. Landcare Research Contract Report LC0708/174 for MAF (now MPI), Wellington, New Zealand.
Koordinates (2013) LUCAS New Zealand land use map 1990–2008 (v011). Koordinates. Available at: http://koordinates.com/#/layer/4316-lucas-new-zealand-land-use-map-1990-2008-v011/ (accessed 21 July 2013)
Laganière J, Angers DA, Paré D (2010) Carbon accumulation in agricultural soils after afforestation: a meta-analysis. Global Change Biology 16, 439–453.
| Carbon accumulation in agricultural soils after afforestation: a meta-analysis.Crossref | GoogleScholarGoogle Scholar |
Landcare Research (2014) NZ Land Cover Database. Landcare Research. Available at: www.lcdb.scinfo.org.nz (accessed 24 January 2014).
Lawrence EJ, Beare MH, Tregurtha CS, Cuff J (2008) Quantifying the effects of soil and crop management history on soil quality. In ‘Carbon and nutrient management for agriculture’. Fertilizer & Lime Research Centre, Occasional Report No. 21. (Eds LD Currie, JA Hanly) pp. 23–28. (Massey University: Palmerston North, New Zealand)
Lawrence-Smith EJ, Tregurtha CS, Beare MH (2010a) Land Management Index data for use in New Zealand’s Soil Carbon Monitoring System. SPTS No. 4612. Plant & Food Research Client Report (Contract No. 25265) for the Ministry of the Environment, Wellington, New Zealand.
Lawrence-Smith EJ, Beare MH, Curtin D, Tregurtha C (2010b) Explaining variability in soil carbon stocks based on farm management factors. In ‘Food security from sustainable agriculture. Proceedings 15th Agronomy Conference’. 15–18 November 2010, Lincoln, NZ. (Eds H Dove, RA Culvenor) (Australian Society of Agronomy)
Leathwick JR (2001) New Zealands’s potential forest pattern as predicted from current species-environment relationships. New Zealand Journal of Botany 39, 447–464.
| New Zealands’s potential forest pattern as predicted from current species-environment relationships.Crossref | GoogleScholarGoogle Scholar |
Leathwick J (2005) ‘Predicted potential natural vegetation of New Zealand.’ CD of ArcGIS files. (Landcare Research: Hamilton, New Zealand)
Leathwick J, Morgan F, Wilson G, Rutledge D, McLeod M, Johnston K (2002) ‘Land environments of New Zealand: a technical guide.’ (Ministry for the Environment: Wellington, New Zealand)
Li C, Frokling S, Harriss RC (1994) Modeling carbon biogeochemistry in agricultural soils. Global Biogeochemical Cycles 8, 237–254.
| Modeling carbon biogeochemistry in agricultural soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXmtVCiu7s%3D&md5=b4e1f46643e7245a288aa3ea162dde0bCAS |
Lilburne LR, Hewitt AE, Webb TW (2012) Soil and informatics science combine to develop S-map: A new generation soil information system for New Zealand. Geoderma 170, 232–238.
| Soil and informatics science combine to develop S-map: A new generation soil information system for New Zealand.Crossref | GoogleScholarGoogle Scholar |
Lohr S (1999) ‘Sampling: design and analysis.’ (Duxbury Press: Pacific Grove, CA, USA)
Marcus R, Peritz E, Gabriel KR (1976) On closed testing procedures with special reference to ordered analysis of variance. Biometrika 63, 655–660.
| On closed testing procedures with special reference to ordered analysis of variance.Crossref | GoogleScholarGoogle Scholar |
McCune B, Grace JB (2002) ‘Analysis of ecological communities.’ (MjM Software Design: Gleneden Beach, OR, USA)
McNeill SJ (2010) Soil CMS model recalibration and uncertainty analysis. Landcare Research Contract Report LC93 for the Ministry for the Environment, Wellington, New Zealand.
McNeill SJ (2012) Respecification and reclassification of the MfE SoilCMS model. Landcare Research Contract Report LC975 for the Ministry for the Environment, Wellington, New Zealand.
McNeill SJ (2013) Respecification and Reclassification of the 2012 MfE Soil CMS Model. Landcare Research Contract Report LC1649 for the Ministry for the Environment, Wellington, New Zealand.
McNeill SJ, Forester G, Giltrap D (2009) Spatial autocorrelation analysis of data for the Soils CMS model. Landcare Research Contract Report LC0910/003 for the Ministry for the Environment, Wellington, NZ.
MfE (Ministry for the Environment) (2012) ‘Land use, land-use change and forestry. In ‘New Zealand’s Greenhouse Gas Inventory 1990–2010.’ Publication no. ME 1095. pp. 173–270. (Ministry for the Environment: Wellington, New Zealand)
Milne JDG, Clayden B, Singleton PL, Wilson AD (1995) ‘Soil description handbook.’ (Manaaki Whenua Press: Lincoln, New Zealand)
National Research Council (2013) ‘Frontiers in massive data analysis.’ (The National Academies Press: Washington, DC)
Newsome PFJ (1987) ‘The vegetative cover of New Zealand.’ Water and Soil Miscellaneous Publication No. 112. (National Water and Soil Conservation Authority: Wellington, New Zealand)
Ogle SM, Paustian K (2005) Soil organic carbon as an indicator of environmental quality at the national scale: Inventory monitoring methods and policy relevance. Canadian Journal of Soil Science 85, 531–540.
| Soil organic carbon as an indicator of environmental quality at the national scale: Inventory monitoring methods and policy relevance.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28Xjs1Ggug%3D%3D&md5=4e70f7204485fe8870eafe04150092fbCAS |
Ogle SM, Breidt FJ, Easter M, Williams S, Paustian K (2007) An empirically based approach for estimating uncertainty associated with modelling carbon sequestration in soils. Ecological Modelling 205, 453–463.
| An empirically based approach for estimating uncertainty associated with modelling carbon sequestration in soils.Crossref | GoogleScholarGoogle Scholar |
Parton WJ, Schimel DS, Cole CV, Ojima DS (1987) Analysis of factors controlling soil organic matter levels in Great Plains grasslands. Soil Science Society of America Journal 51, 1173–1179.
| Analysis of factors controlling soil organic matter levels in Great Plains grasslands.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXmtlGnsbw%3D&md5=83adee9d531a52b4c726cce830d3407cCAS |
Penman J, Gytarsky M, Hiraishi T, Krug T, Kruger D, Pipatti R, Buendia L, Miwa K, Ngara T, Tanabe K, Wagner F (Eds) (2003) ‘Good practice guidance for land use, land-use change and forestry.’ (Intergovernmental Panel on Climate Change: Kanagawa, Japan)
Poeplau C, Don A, Vesterdal L, Leifeld J, Van Wesemael B, Schumacher J, Gensior A (2011) Temporal dynamics of soil organic carbon after land-use change in the temperate zone—carbon response functions as a model approach. Global Change Biology 17, 2415–2427.
| Temporal dynamics of soil organic carbon after land-use change in the temperate zone—carbon response functions as a model approach.Crossref | GoogleScholarGoogle Scholar |
Ridgeway G (2013) gbm: Generalized Boosted Regression Models. package version 2.1. The R Project for Statistical Computing. Available at: http://CRAN.R-project.org/package=gbm.
Scott NA, Tate KR, Giltrap DJ, Smith CT, Wilde RH, Newsome PF, Davis MR (2002) Monitoring land-use change effects on soil carbon in New Zealand: Quantifying baseline soil carbon stocks. Environmental Pollution 116, S167–S186.
| Monitoring land-use change effects on soil carbon in New Zealand: Quantifying baseline soil carbon stocks.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XhsFCk&md5=9c1e23ebc7d1eaa34fabf40e7403a1f5CAS | 11837235PubMed |
Tate KR, Scott NA, Saggar S, Giltrap DJ, Baisden WT, Newsome PF, Trotter CM, Wilde RH (2003a) Land-use change alters New Zealand’s terrestrial carbon budget: Uncertainties associated with estimates of soil carbon change between 1990 and 2000. Tellus 55B, 364–377.
| Land-use change alters New Zealand’s terrestrial carbon budget: Uncertainties associated with estimates of soil carbon change between 1990 and 2000.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXktlSiu7Y%3D&md5=8b5d25138dfddb0291a8102845ffe261CAS |
Tate KR, Barton JP, Trustrum NA, Baisden WT, Saggar S, Wilde RH, Giltrap DJ, Scott NA (2003b) Monitoring and modeling soil organic carbon stocks and flows in New Zealand. In ‘Soil organic carbon and agriculture: Developing indicators for policy analysis’. Proceedings of an OECD Expert Meeting, Ottawa, ON, October 2002. (Ed. CA Scott-Smith) pp. 253–268. (Agriculture and Agri-Food Canada and Organisation for Economic Co-operation and Development: Paris, France)
Tate KR, Wilde RH, Giltrap DJ, Baisden WT, Saggar S, Trustrum NA, Scott NA, Barton JP (2005) Soil organic carbon stocks and flows in New Zealand: System development, measurement and modelling. Canadian Journal of Soil Science 85, 481–489.
| Soil organic carbon stocks and flows in New Zealand: System development, measurement and modelling.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28Xjs1GgsQ%3D%3D&md5=93925b0ff2ecd5c7487473fbbea6e74fCAS |
Taylor NH, Pohlen IJ (1979) ‘Soil survey method. A New Zealand handbook for the field study of soils.’ Soil Bureau Bulletin 25. (Department of Scientific and Industrial Research: Wellington, New Zealand)
Wilde H, Davis M, Tate K, Giltrap D (2004) Testing the representativeness of soil carbon data held in databases underpinning the New Zealand Soil Carbon Monitoring System. In ‘SuperSoil 2004. Proceedings 3rd Australian New Zealand Soils Conference’. 5–9 December 2004, University of Sydney, NSW. (The Regional Institute: Gosford, NSW) Available at: www.regional.org.au/au/asssi/



