The Brigalow Catchment Study: VI.† Evaluation of the RUSLE and MUSLE models to assess the impact of clearing brigalow (Acacia harpophylla) on sediment yield
J. Tiwari A , C. M. Thornton
A , C. M. Thornton  B and B. Yu A *
B and B. Yu A *
A School of Engineering and Built Environment, Australian Rivers Institute, Griffith University, Nathan, Qld 4111, Australia.
B Department of Resources, Mines, and Energy, PO Box 1762, Rockhampton, Qld 4700, Australia.
Soil Research 59(8) 778-793 https://doi.org/10.1071/SR21030
Submitted: 3 February 2021 Accepted: 27 May 2021 Published: 4 October 2021
© 2021 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution 4.0 International License (CC BY)
Abstract
Land clearing for cropping and grazing has increased runoff and sediment yield in Central Queensland. The Brigalow Catchment Study (BCS), was established to determine the effect of land clearing on water balance, soils, and productivity, and consisted of three catchments: brigalow forest, cropping, and grazing. Factors responsible for changes in and models for predicting sediment yield have not been assessed. Objectives of this study are to identify climatic, hydrological, and ground cover factors responsible for the increased sediment yield and to assess suitable models for sediment yield prediction. Runoff and sediment yield data from 1988 to 2018 were used to assess the Revised Universal Soil Loss Equation (RUSLE) and the Modified USLE (MUSLE) to predict the sediment yield in brigalow catchments. Common events among the three catchments and events for all catchment pairs were assessed. The sediment yield was approximately 44% higher for cropping and 4% higher for grazing than that from the forested catchment. The runoff amount (Q) and peak runoff rate (Qp) were major variables that could explain most of the increased sediment yield over time. A comparison for each catchment pair showed that sediment yield was 801 kg ha−1 or 37% higher for cropping and 28 kg ha−1 or 2% higher for grazing than for the forested catchment. Regression analysis for three different treatments (seven common events) and for different storm events (15 for forested, 40 for cropping, and 20 for grazing) showed that Q and Qp were best correlated with sediment yield in comparison with variations in ground cover. The high coefficient of determination (R2 > 0.60) provided support for using the MUSLE model, based on both Q and Qp, instead of the RUSLE, and Q and Qp were the most important factors for improving sediment yield predictions from BCS catchments.
Keywords: brigalow clearing, ground cover treatment, peak runoff rate, RUSLE and MUSLE, runoff, sediment yield, small dry catchments, storm events.
Introduction
Broad-scale clearing of native vegetation for agricultural systems, including grazing, has strongly affected hydrological processes and sediment yield in Australia and around the world (Siriwardena et al. 2006; Thornton et al. 2007; Ehigiator and Anyata 2011; Borrelli et al. 2017; Cheng and Yu 2019; Aghsaei et al. 2020). At the global level, soil erosion from the area of 125 million km2 covering ∼84.1% of Earth’s land surface has increased by 2.5% (baseline of 35 Pg year−1) due to spatial land use change occurring only in 3.3% of study area (Borrelli et al. 2017). In Australia, according to the Scientific Consensus Statement (Bartley et al. 2017), a three- and eight-fold increase in the total sediment yield has occurred across the Great Barrier Reef (GBR) catchments, depending on the region, of which approximately 80% could be attributed to changes in land cover. The Fitzroy Basin was identified as one of the major contributing areas for discharging large amounts of sediments into the GBR lagoon. The Brigalow Catchment Study (BCS) located near Theodore, Central Queensland, represents 36.7 Mha of brigalow bioregion of Queensland and northern New South Wales (Thornton and Yu 2016). Under the Land Development (Fitzroy Basin) Scheme, approximately 4.5 Mha of virgin brigalow forest was cleared for agriculture (including grazing), which has affected the water quality of the region (Elledge and Thornton 2017). The sediment story of the Fitzroy Basin reveals that the average current suspended sediment load exported from the Fitzroy River is between 1.5 and 2.0 Mt year−1 and a large quantity of load is generated due to the extensive clearing of brigalow lands since the 1950s (Lewis et al. 2015). The increase in sediment rates (∼1.5-fold) in sediment cores from the lagoons near Rockhampton also provide evidence for increased sediment loads from the Fitzroy River since European settlement (Bostock et al. 2006). The brigalow clearing of the Brigalow Land Development Fitzroy Basin Scheme represents 21% of all clearing in the brigalow bioregions and 32% of the Fitzroy Basin (Queensland Department of Primary Industries 1993).
The conversion of virgin brigalow to agricultural and grazing land has altered the hydrology of small catchments in the Fitzroy Basin (Thornton et al. 2007; Thornton and Yu 2016). Thornton et al. (2007) reported increases in runoff since 1982, at the BCS, as a result of broad-scale land clearing. The runoff coefficient (the ratio of total runoff over total rainfall) has increased from 5% for the virgin brigalow catchment to 11% for cropping, and 9% for grazing (Thornton et al. 2007). Similarly, Thornton and Yu (2016) reported that the peak runoff rate also increased from 5 to 8.3 mm h−1 for cropping and 2 to 5.6 mm h−1 for pasture catchment, after the development of the catchments. Moreover, a comparative study over a 25-year period from 1984 to 2010 of suspended sediment data for the three catchments revealed that the total suspended solids from the cropped catchment was 6.45 times greater, and from the grazed catchment was 1.46 times greater, than the virgin brigalow (2106 kg ha−1) (Elledge and Thornton 2017). Numerous studies around the world have shown the impact of land use change on sediment yield (Walling 1999; Santos et al. 2017; Gashaw et al. 2019; Aghsaei et al. 2020). Forest clearing since 1968 has led to a 1.8-fold increase in the annual sediment load of the Dnestr River at Sambur, Ukraine, in an 850 km2 catchment area (Walling 1999). Sediment yield increased 10 times due to conversion of a dry tropical forest into fully developed grassland based on an experimental 2.8 ha watershed in the semi-arid Upper Jaguaribe Basin, Ceara, Brazil (Santos et al. 2017). Recently, conversion of forest into irrigated agriculture in one of the subcatchments in the Anzali wetland catchment, Gilan, Iran, has led to a 169% increase in the mean annual sediment yield (Aghsaei et al. 2020). However, no study to date has clearly demonstrated changes in sediment yield at a small scale in dry areas, and no attempt to date has been made to evaluate factors that, either individually or collectively, have caused an increase in sediment yield due to clearing of virgin brigalow forest for cropping and grazing.
As the BCS catchments are contiguous, most of the physical catchment characteristics, such as topography, soil structure and texture, are considered to be similar and effectively static. However, other factors, such as rainfall, runoff, and vegetation cover, do vary with time and may be responsible for changes in the sediment yield among the three catchments. The Universal Soil Loss Equation (USLE) (Wischmeier and Smith 1978) and its derivatives, such as the Revised USLE (RUSLE; Renard et al. 1997) and the Modified USLE (MUSLE; Onstad and Foster 1975; Williams 1975), provide a framework to identify and test factors that have significantly affected the sediment yield at the BCS. These erosion prediction models are the most widely used around the world for different types of land cover, because of their simplicity and flexibility. The RUSLE, which considers the erosivity index (EI30) as its primary rainfall–runoff related factor, is the most commonly used model and is being applied in the Source Catchment/Dynamic SedNet modelling framework for hillslope erosion prediction for the GBR catchments (Yu 1998). The EI30 is the product of total amount of rainfall kinetic energy and maximum 30-min rainfall intensity (Wischmeier and Smith 1978). However, for the small dry catchments of the BCS, the EI30 would be essentially the same among the three different treatments. Therefore, if the RUSLE model were applied, the difference in the sediment yield would be attributed to changes in the cover and management factor (C) factor alone; C is defined as the ratio of soil loss from a field with a particular cover and management compared to a field under ‘clean-tilled continuous fallow’ (Wischmeier and Smith 1978). However, from previous studies (Thornton et al. 2007; Thornton and Yu 2016), runoff amount (Q) and peak runoff rate (Qp) could be major factors responsible for the variation in the sediment yield among the three catchments. Several previous studies have suggested that inclusion of Q and Qp could improve the capacity of the MUSLE model to predict the sediment yield compared with the USLE model (Kinnell 2004, 2010, 2016). Numerous studies have also suggested the appropriateness of the MUSLE model in improving sediment yield prediction under various conditions, due to inclusion of the runoff-related factors (Foster et al. 1982; Kinnell and Risse 1998; Erskine et al. 2002; Sadeghi and Mizuyama 2007; Kinnell 2010; Arekhi et al. 2012; Sadeghi et al. 2014). To test the relative contribution of Q, Qp, and cover factors, the USLE, as modified by Williams (1975) and Onstad and Foster (1975), will be used in this study to estimate the sediment yield from different land uses because they include runoff and peak runoff rate in addition to rainfall erosivity as the rainfall–runoff related factors. As mentioned above, the RUSLE was originally developed and is widely used to estimate soil loss from hillslopes. In this study, the measured sediment yield at the catchment outlet is assumed to equal the soil loss of the catchment. Soil loss is defined as the measured total suspended solids load from a catchment. This study, therefore, assumed that there is no sediment deposition in the catchment. At the very least, the delivery ratio is constant because it was assumed constant in the Dynamic SedNet model being applied to the GBR catchments for erosion predictions (Wilkinson et al. 2004). However, for large catchments, the RUSLE needs a separate sediment delivery ratio to estimate the sediment yield. In contrast, the MUSLE eliminates the need for a sediment delivery ratio because runoff and peak runoff rate are closely related to sediment detachment and transport for improved sediment delivery predictions (Williams 1975).
As such, the present study had three objectives:
-
to evaluate the effect of clearing brigalow for cropping or gazing on sediment yield for a subset of events over the period between 1988 and 2018,
-
to test whether the change in sediment yield occurred because of the change in runoff characteristics, rather than changes in ground cover, and
-
to test the applicability of using the RUSLE/MUSLE models to predict sediment yield from these small dry catchments in Central Queensland.
Materials and methods
Study area
This study was conducted in the three contiguous experimental catchments of the long-term BCS. The three catchments brigalow scrub (C1), cropping (C2), and grazing (C3) have contributing areas of 16.8, 11.7 and 12.7 ha, respectively. The BCS (24°48′S and 149°47′E) is a paired, calibrated catchment study located near Theodore in Central Queensland, Australia (Cowie et al. 2007). The study area is representative of the Brigalow Belt bioregion which covers an area approximately 36.7 Mha from Townsville in north Queensland to Dubbo in central-western New South Wales (Thornton et al. 2007). The Brigalow Belt bioregion has undergone extensive land clearing under the Queensland Government-sponsored Fitzroy Basin Land Development scheme, which operated between 1965 and 1985 (Cowie et al. 2007). The area experiences a semi-arid to subtropical climate with an average maximum monthly temperature for summer of 33.1°C, while the minimum temperature in winter averages 6.5°C. The average annual rainfall is 697 mm with a range of 246–1460 mm (Cowie et al. 2007). The land slope within the catchments varies from 1.8% to 3.5% and averages 2.5%. Soils in the experiment catchments mainly comprise fine-textured dark cracking clays (black and grey vertosols), some with gilgais and noncracking clays (black and grey dermosols), and subdominant soil of thin surfaced dark and brown sodic texture-contrast soils (black and brown sodosols) (Cowie et al. 2007). The detailed description of calibration and development of these catchments is given in Cowie et al. (2007). The location map of the study area is shown in Fig. 1.

|
Site history
The study has been divided into three distinct experimental stages (Table 1) (Thornton et al. 2010). Stage I, the calibration phase, commenced in 1965 with the three catchments retained in their virgin state for calibration purposes.

|
Stage II, the land development phase, commenced in March 1982 with C2 and C3 catchments cleared by bulldozer and chain. The fallen timber was burnt in situ in October 1982. In the C2 catchment, residual unburnt timber was raked to the contour line and burnt. Narrow-based contour banks at 1.5 m vertical spacing were then constructed and a grassed waterway later established. In the C3 catchment, unburnt timber was left in place, and in November 1982 the catchment was sown to improved pasture by throwing buffel grass seed (Cenchrus ciliaris cv. Biloela) on the soil surface. Stage II hydrology was not analysed in detail due its short duration, the marked changes in catchment condition, and a high incidence of equipment failure (Thornton et al. 2007).
During Stage III, the land use comparison phase, comparison of the effect of land use change commenced with cropping in C2 and grazing in C3. Sorghum was planted in C2 in September 1984 followed by nine annual wheat crops commencing in 1985. Fallow management in this period was entirely mechanical tillage. A minimum tillage and opportunity cropping philosophy was adopted in the early 1990s and has continued with either a summer (sorghum) or winter (wheat) crop sown whenever soil moisture was adequate. Grazing in C3 commenced in December 1983. Stocking rates varied between 0.29 and 0.71 head ha−1 (each beast typically 0.8 adult equivalents), adjusted to maintain pasture dry matter levels greater than 1000 kg ha−1. No feed supplementation was provided.
Application of the RUSLE and MUSLE models for sediment yield prediction
Regression analysis was performed by using observed sediment yield and the outputs from the models: USLE (Renard et al. 1997), MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975) models. This analysis was performed to test the capability of the models in sediment yield prediction. The primary factors of these three models differ from each other with all the other factors remaining the same. The RUSLE model contains EI30, the MUSLE (Williams 1975) model includes Q and Qp, and the MUSLE (Onstad and Foster 1975) model contains a combination of EI30, Q, and Qp.
The equations for three selected sediment yield models can be expressed as follows.
RUSLE model (Renard et al. 1997)
The soil loss equation for estimating average annual soil loss is expressed as follows:

In this study, this equation is used for estimating soil loss on event basis; therefore, it can be expressed as follows:

where A = average annual soil loss (t ha−1), Ae = estimated event sediment yield (t ha−1 event−1), R = average annual rainfall erosivity (MJ mm h−1 ha−1), EI30 = rainfall erosivity factor (MJ mm h−1 ha−1 event−1), K = soil erodibility factor (t ha−1 R−1), Ke = soil erodibility factor (t ha−1 EI30−1), L = slope length factor, S = slope steepness factor, C = cover management factor, and P = conservation support practice factor.
MUSLE model (Williams 1975)

where Ae = event sediment yield (t ha−1) by dividing runoff and peak runoff rate by catchment area and multiplying K by catchment area, Q = runoff (m3), Qp = peak runoff rate (m3 s−1), Ke = soil erodibility factor (t ha−1 EI30−1), and LS, C, and P are the same as for the RUSLE model.
MUSLE model (Onstad and Foster 1975)
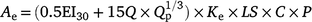
where Ae = sediment yield (t acre−1), EI30 = storm rainfall erosivity factor (foot tons per acre inches per hour), Q = storm runoff depth (in.), Qp = storm peak runoff rate (in. h−1), and Ke, LS, C, and P are the same as for the RUSLE model.
In this study, the Onstad and Foster (1975) MUSLE equation was converted to SI units using the conversions presented in (Foster et al. 1981). The equation in SI units can be expressed as follows:

where Ae = event sediment yield (t ha−1 event−1), EI30 = rainfall erosivity factor (MJ mm h−1 ha−1 event−1), Q = runoff (mm), Qp = peak runoff rate (mm h−1), and Ke, LS, C, and P are the same as for the RUSLE model.
Data inputs for models
In order to apply the RUSLE and MUSLE models in this study, estimations of rainfall erosivity (EI30), runoff (Q), peak runoff rate (Qp), sediment yield, ground cover data, cover management factor (C), and topographic factor (LS) are required. These parameters were determined on an event basis using BCS Stage III data from the hydrological years 1988–2018. The term sediment yield will be used throughout the paper because the present study is event based and assumed that the measured sediment yield equals the soil loss in the catchment outlet.
EI30
The R represents the effect of rainfall intensity and amount of rainfall on soil erosion (Wischmeier and Smith 1978). The EI30 is a function of kinetic energy (E) and maximum 30-min rainfall intensity (I30) (Wischmeier and Smith 1978). The BCS had two rain gauges, one sited at the discharge point of each catchment and one at the head point of all three catchments (Cowie et al. 2007; Thornton et al. 2007). The rainfall recorded at the head point of all three catchments was the most reliable and was selected as the source data to calculate EI30 for all three catchments. However, for some events with poor quality rainfall data, we used the rainfall data recorded from individual rain gauges installed in each catchment. In this study, storm energy (E) and 30-min rainfall intensity from 6-min rainfall data separated by an interval of 6 h were computed using the MetCal program ver. 1.7 developed by Yu (1998). MetCal uses the equation given by Renard et al. (1997) for calculating E for each storm event, and can be expressed as follows:
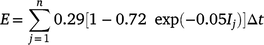
where Ij is the rainfall intensity for the time interval j (mm h−1), Δt is the time interval (h), and n is the number of time intervals of the storm.
Q and Qp
The Q and Qp observations for the BCS up to 2004 are presented in Thornton et al. (2007) and Thornton and Yu (2016), respectively. The data collection, manipulation, and storage methodologies described in both Thornton et al. (2007) and Thornton and Yu (2016) were continued for the period 2004–2019, as part of the core data collection of the long-term BCS. These data sets were summarised on an event basis to determine runoff and peak runoff rate for use in this study. The study event was defined as the longest event among the three catchments: forested, cropped, and grazed.
K-factor
The K refers to the erodibility of the soil, i.e. the resistance of the soil against the aggressiveness of raindrops, runoff, or both (Djoukbala et al. 2019). In the present study, K was calculated using the revised nomograph equation proposed by Loch and Rosewell (1992) for Australian soil based on the original equation developed by Wischmeier and Smith (1978), using the soil texture and organic matter content. The nomograph comprises five soil and soil-profile parameters, such as percent modified silt (0.002–0.1 mm), percent modified sand (0.1–2 mm), percent organic matter (OM), class for structure (s), and permeability (p) (Renard et al. 1997). The equation nomograph K in t ha h ha−1 MJ−1 mm−1 for soils with <70% silt can be expressed as follows:

where M = (%silt + %very fine sand)(100 − %clay), OM is percentage (%) organic matter, SS is soil structure code, and PP is profile permeability class.
Additionally, Ke was also estimated using the observed sediment yield data by applying regression method using model outputs of the RUSLE, the MUSLE (Williams 1975) and the MUSLE (Onstad and Foster 1975) models. This method is most reliable for the quantification of K because it accounts for the effect of changes occurred in natural condition and, therefore, can be used to calibrate the other K calculated using different methods.
LS-factor
Sediment yield is also influenced by the length of slope (L) and slope steepness factor (S), which is referred to as the topographic factor. Since the three catchments of the BCS are adjacent and have similar size and slope (Cowie et al. 2007), LS was considered to be the same for each catchment and event. The L and S layer for Queensland was downloaded from the Queensland Government’s Qspatial website (https://www.data.qld.gov.au/dataset/soils-universal-soil-loss-equation-series, accessed 1 October 2019). These layers have a resolution of 30 m × 30 m and were used as input dataset in the RUSLE model in source catchment framework for erosion predictions for the GBR catchments. The L and S layers for three catchments were extracted from the layer. The LS was then calculated by multiplying L and S. The average LS for the three catchments was calculated using the Raster analysis statistics tool available in QGIS and the value of LS was found to be 0.28 for forested, 0.32 for cropped, and 0.39 for grazed catchments. These values were supported by data from the LS spatial layer used in the Queensland Government’s EWater Source modelling program. (http://qldspatial.information.qld.gov.au/catalogue/custom/detail.page?fid={3F181365-702E-43FD-B54C-DD93F1A3B2CD}).
C-factor
For this study, C for forested (C1) and grazed (C3) catchments, and cover data for the cropping catchment (C2), were procured from Department of Environment and Science and were available on a 3-monthly basis (http://data.auscover.org.au/xwiki/bin/view/Product+pages/Landsat+Seasonal+Fractional+Cover). The C for forested and grazed catchments for each event was calculated as the average of the C of all the pixels located within each catchment. The C for cropped catchment was calculated by using average ground cover (%) and subfactors as advocated by Wischmeier and Smith (1978). The C can be expressed as follows:

where LU is a land use subfactor, CC is a crop canopy subfactor, SC is a surface cover subfactor, and SR is a surface roughness subfactor. In this study, LU = 0.45 (Rosewell 1993) and CC = 1 due to minimal effect of canopy, and SR = 1 for smooth surface. The cover subfactor SC is calculated as follows:

where bcov = 0.035 for croplands (Renard et al. 1997).
Crop conservation practice factor (P)
The P represents the effect of conservation practices on water erosion processes. It varies according to the conservation techniques practiced in the watershed from 0 in the zones well protected to 1 without any conservation practices. In this study, no significant practices were performed on the catchments over time; therefore, the value of P was assigned as 1.
Sediment yield
Sediment yield data from 1988 to 2010 are presented in Elledge and Thornton (2017). For runoff and peak runoff rate, the data collection, manipulation, and storage methodologies described in Elledge and Thornton (2017) were continued for the period 2004–2019, as part of the core data collection of the long-term BCS. These were summarised on an event basis to determine sediment yield for use in this study.
Comparison of sediment yield from three land uses using common events
The observed sediment yield was compared among different treatments, i.e. forested (C1), cropped (C2), and grazed (C3) catchments using common events. The term common events refers to the runoff events filtered from the set of measured events based on the data availability and are common among the three catchments. In addition to this, we set up three paired comparisons: forest and cropped, cropped and grazed, and forest and grazed. All the runoff events from 1988 to 2018 for which the measured sediment yield was available were selected for each comparison. The total runoff and sediment yield in each treatment were compared to identify the increase or decrease in sediment yield that occurred due to land clearing.
Identification of the potential factors affecting changes in sediment yield among different land uses and different storm events
The event-based temporal variation of sediment yield and variation in factors, such as EI30, Q, Qp, and C, were graphically represented for the common events to determine the potential factors that might have changed over time and could account for the changes in sediment yield among the three treatments.
Moreover, multiple correlation analysis was performed to detect the effects of EI30, Q, Qp, and C solely on sediment yield. The analysis was undertaken for two sets of events, first to determine the factors that explain the variation in sediment yield among different storm events and the second set of events was among different land uses. The first condition considers all common events among forest, cropping, and grazing, and the second condition considers all measured events from the three treatments.
The above-mentioned facts show that the three catchments are contiguous, share similar physical characteristics, and are exposed to the same climatic sequences, except post-land development which has different hydrology (Cowie et al. 2007; Thornton et al. 2007; Thornton and Yu 2016). Hence, the difference in the estimated sediment yield among the three catchments using the RUSLE model would be driven by differences in C. Use of the rainfall record from the common head point of the three catchments to determine EI30 across all catchments is considered appropriate due to the close proximity of the gauge to the catchment outlets, which averages 550 m downslope. Although the actual rainfall erosivity may vary spatially, there are no data to indicate the magnitude of the variations. Along with rainfall, EI30 is also affected by the wind and topography of the catchment. Nevertheless, LS is also quite similar among the three catchment, therefore, it can be assumed that EI30 would be the same among the three catchments. Thus, runoff and peak runoff rate would be the only factors able to explain the difference in the sediment yield among the three catchments. Consequently, the MUSLE model should provide a better understanding of the effect of flow processes on sediment yield. Assuming that no change in the other factors (EI30, K, LS, C, and P) occurred, the significant effect of change in hydrological factors was expected to alter the sediment yield in these catchments, suggesting that land clearing has affected the sediment yield.
Results
Sediment yield comparison among three land uses using common events
A total of seven common events for which all data were available were used to compare the runoff and sediment yield among the three treatments. Sediment yields (kg ha−1) from each treatment for the seven common events are summarised in box plots, with s.d. as error bars and mean in red (Fig. 2). The mean of sediment yields were 208 kg ha−1 (s.d. 267 kg ha−1 for forested, 299 kg ha−1 (s.d. 406 kg ha−1) for cropping, and 215 kg ha−1 (s.d. 336 kg ha−1) for grazing. The total runoff (mm), total event sediment yield (kg ha−1), and the increase in runoff and sediment yield in cropping and grazing, considering forest as the baseline, are presented in Table 2. The increase in runoff in cropping and grazing as a result of clearing was 35% and 34%, respectively. The total event sediment yield from cropping and grazing was 44% and 4% greater than for forested catchment, respectively. The difference in runoff amount between cropping and grazing catchment was almost negligible. In contrast, the cropping catchment exported 1.39 times higher loads of sediment than the grazing catchment.

|
Sediment yield comparison was performed using 13 common events from forested and cropping, 18 common events from cropping and grazing, and eight common events from forested and grazing. The results for total runoff (mm), observed event sediment yield (kg ha−1), and the increase in runoff and sediment yield for each paired comparison are presented in Table 3. The total runoff from cropped catchment was about 55% higher than the forested catchment (456 mm) and 46% higher than the grazing catchment (444 mm). Similarly, the total runoff in grazed catchment increased by 28% compared to forested catchment (370 mm). Total event sediment yield from cropping was 2945 kg ha−1, which was 1.37 times greater than that from brigalow scrub (2144 kg ha−1). The total event observed sediment yield from the cropped catchment was 525 kg ha−1 higher than that from grazing (1767 kg ha−1). Moreover, the paired study of eight common events between forested and grazing showed that the difference between the total observed sediment yield between the two treatments was approximately 28 kg ha−1.

|
Determination of the factors affecting changes in sediment yield among different storm events and land uses
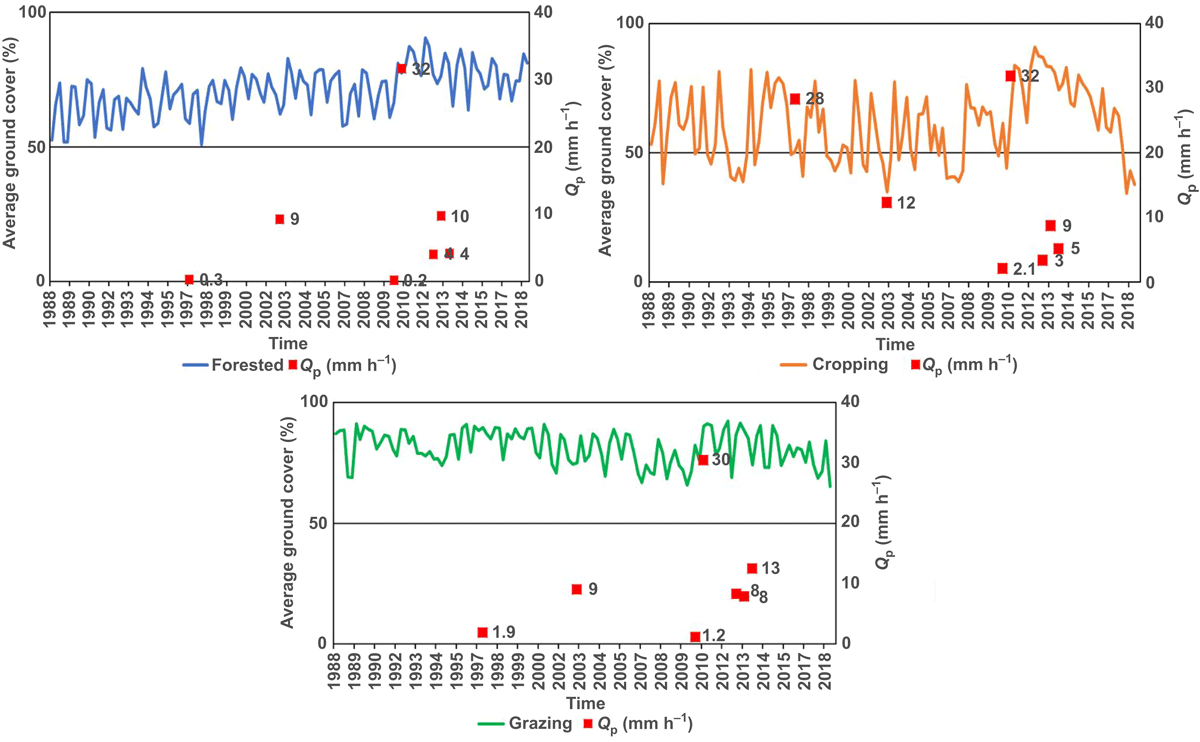
The event-wise variation in sediment yield and Q, Qp, EI30, and C for grazed catchment as an example is shown in Fig. 3. The figure shows that the sediment yield changed and increased with an increase in Q and Qp over time. The EI30 being the same among the three catchments, varied from event to event; however, the trend differed from the variation in sediment yield. The C was constant with time, which clearly was unrelated to the change in sediment yield. The temporal variation of average ground cover along with the common storm events for the three treatments from 1988 to 2018 is shown in Fig. 4.

|
|
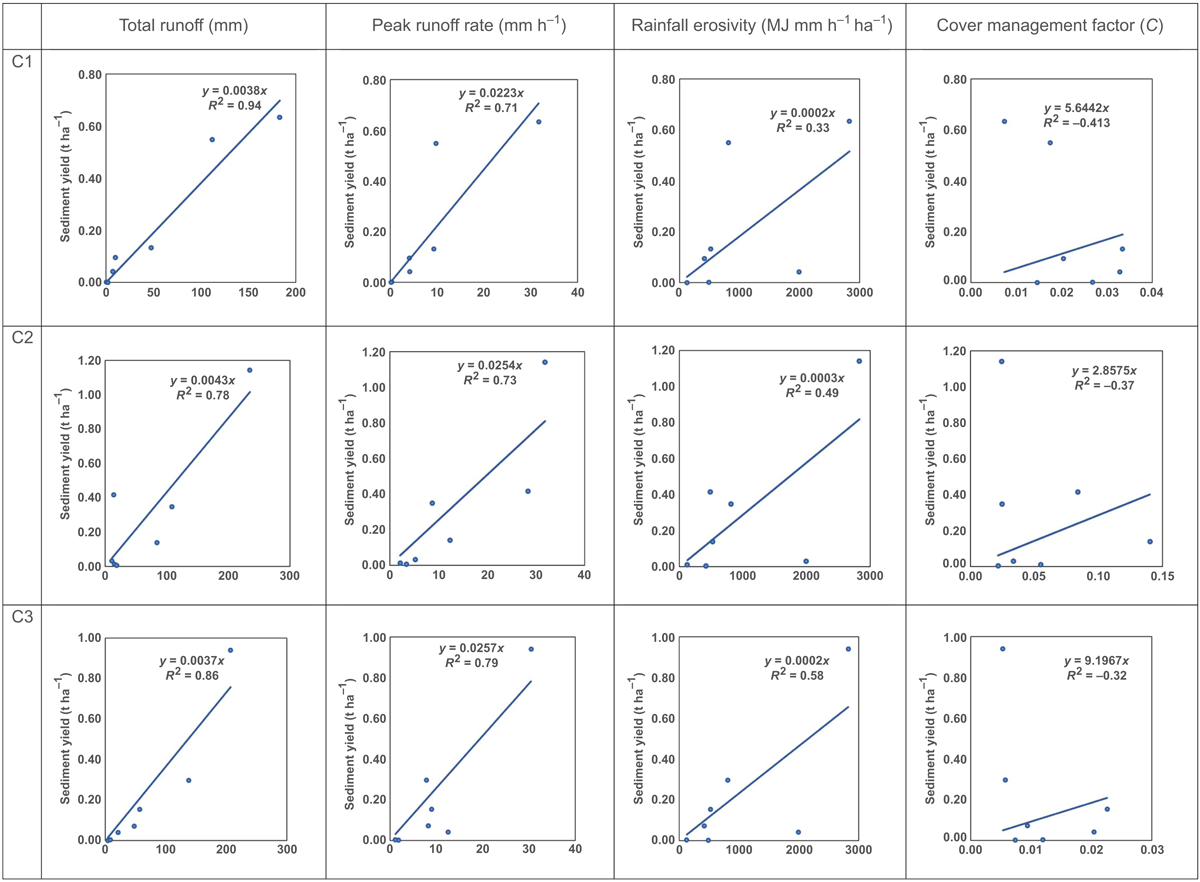
The correlation analysis performed between the observed sediment yield and Q, Qp, EI30, and C among different land uses indicated that Q and Qp were the best correlated factors among all factors. The correlation analysis results are presented in Fig. 5 and Table 4. The observed sediment yield was more sensitive to runoff (R2 > 0.78) for all the treatments in the case of common events; however, it was the most important in forested treatment (R2 = 0.94) followed by grazing (R2 = 0.86). Peak runoff rate was the second-best correlated factor (R2 > 0.71) among all three land uses. No significant correlation was found between C and event sediment yield (P > 0.32).
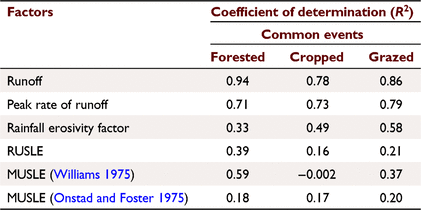
|
The results of regression analysis between the model outputs estimated from the RUSLE, MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975), and observed sediment yield, are shown in Fig. 6 and Table 4. The MUSLE model (Williams 1975), with factors Q and Qp, was the better correlated model for forested and grazing treatments. None of the models provided any relevant correlations for the cropping catchment. For forested and grazing, the MUSLE (Williams 1975) model with Q and Qp resulted in correlations of R2 = 0.59 and 0.37, respectively, which had the best performance among all three models. Using the model with best correlation, i.e. the MUSLE (Williams 1975) for forested and grazing and MUSLE (Onstad and Foster 1975) for cropping treatment, the K values were estimated. The estimated Ke was 0.043 for forested, 0.016 for cropping, and 0.059 for grazing treatment. The K calculated using the nomograph method was approximately 0.03 for all three BCS catchments. The calculated and estimated Ke along with s.e. are presented in Table 5. The results of total sediment yield and increases in sediment yield using the forested catchment as baseline calculated from each treatment using the estimated Ke obtained using the best correlated model are presented in Table 6. The total estimated sediment yield from cropping was about 1.22 and 1.11 times that of forested (1446 kg ha−1) and grazing (1590 kg ha−1), respectively. Total estimated sediment yield from grazing was about 1.10 times that of the forested catchment (1446 kg ha−1).

|

|

|
Among different storm events
Fifteen, 40, and 25 measured events were selected from forested, cropping, and grazing treatments for determination of the factors explaining the variation in sediment yield for different storm events. The correlation analysis between the observed sediment yield and factors Q, Qp, EI30, and C for the three treatments are shown in Fig. 7 and Table 7 (first four rows). The result shows that Q and Qp were the best correlated factors among all factors with high R2 value. The Qp had the highest R2, i.e. 0.61 for forested and 0.78 for cropping, followed by Q with R2 of 0.28 for forested, and 0.47 for cropping; whereas, for grazing, Q was better correlated with R2 = 0.83 followed by Qp with R2 = 0.54.
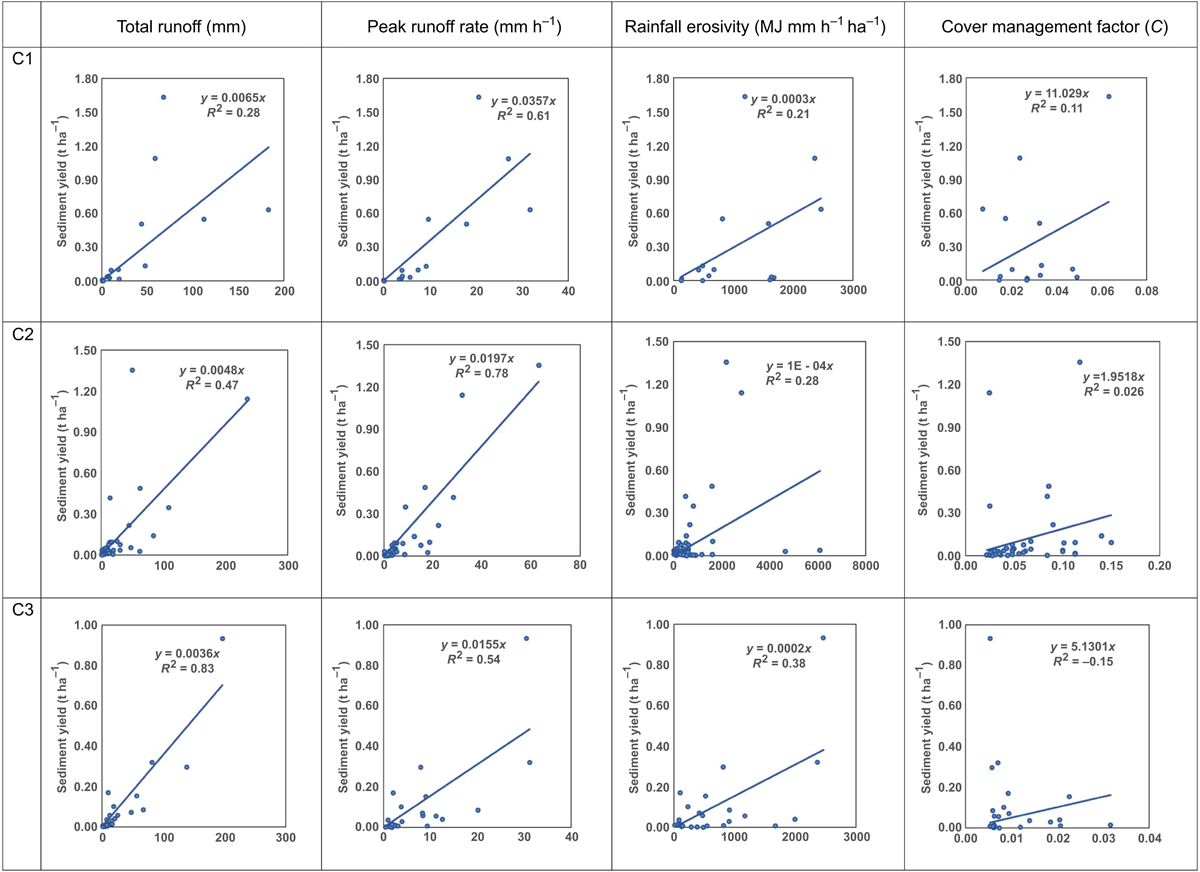
|

|
The regression analysis between the observed sediment yield in each treatment and the RUSLE, MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975) models revealed that the MUSLE model (Williams 1975) was the most appropriate for sediment yield estimation with higher R2 = 0.86 for forested, R2 = 0.62 for cropping, and R2 = 0.46 for grazing (Fig. 8 and Table 7). The Ke estimated using the best correlated model, i.e. the MUSLE model (Williams 1975), for the three treatments was 0.044 for forested, 0.0132 for cropping, and 0.0543 for grazing. These Ke were similar to the K estimated for these catchments using the common events among them.

|
Discussion
This study investigated the effect of clearing brigalow for cropping or grazing on sediment yield from 1988 to 2018 and tested whether the changes in sediment yield occurred because of the change in runoff characteristics, more so than changes in ground cover. In addition, applicability of the RUSLE/MUSLE models was tested to predict the sediment yield from these dry catchments in Central Queensland. The study assumed that the measured sediment yield was equal, or at least proportional, to the soil loss from the catchment.
Total event sediment yield from the cropped and grazed catchments had significantly increased due to conversion of brigalow forest to cropping and grazing. As illustrated in Table 2, the sediment yield from cropping and grazing was 44% and 4% higher than for forested catchment, respectively. Similarly, the comparative study between paired catchments (forested vs cropped, cropped vs grazed, and forested vs grazed) revealed that sediment yield from cropping increased by 37% and 30% compared with forested and grazed catchments, respectively. These findings were consistent with previous studies in that changes in land use and land cover could lead to an increase in sediment yield. For example, a study of the Dnestr River at Sambur, Ukraine, with a catchment area of 850 km2, showed that forest clearing in the catchment after 1968 led to a 1.8-fold increase in annual sediment load of the river (Walling 1999). The sediment yield from a 2.8 ha catchment in the semi-arid region Ceara, in the Upper Jaguaribe Basin, Brazil, increased 10 times due to conversion of a dry tropical forest in 2009 into full developed grassland by 2011 (Santos et al. 2017). A previous study at the BCS, Central Queensland, identified the effect of land use change on sediment loads exported from the catchment over 25 years, and showed that the total suspended solids from the cropped and grazed catchment was about 6.45 and 1.46 times greater than for virgin brigalow (2106 kg ha−1) (Elledge and Thornton 2017). The conversion of forest into irrigated agriculture in one of the subcatchments in the Anzali Wetland catchment, in Gilan, Iran, led to an increase of 169% in the mean annual sediment yield (Aghsaei et al. 2020). Although these studies conducted across the world have shown the increase in sediment yield due to land use change, the magnitudes of the increase in sediment yield due to land use conversion were somewhat different from the aforementioned previous studies. This is mainly because the present study was carried out on a very small paddock-scale area located in a semi-arid region. This study has clearly shown the increase in the sediment yield due to clearing of virgin brigalow forest for cropping and grazing, in small dry catchments over a relatively long period of time. The variability in the sediment yield was not only assessed among the three land uses but also among the different storm events. This variability of sediment yield was accompanied by temporal variations in other factors such as EI30, Q, Qp, and C; therefore, the present study has a limited number of common events for comparison purpose.
In this study, using the sediment yield models RUSLE and MUSLE, Q and Qp were shown to be the major potential factors or variables that caused the increase in the sediment yield in the cropped and grazed catchments after land clearing. The temporal variation in C was quite low and did not show a significant relationship with the increase in sediment yield. Rainfall erosivity cannot explain the variation in event sediment yield among the three catchments because the value of EI30 is the same for individual events among the three treatments, and therefore when using the MUSLE model, rainfall erosivity could not be related to the increase in sediment yield from cropping and grazing catchments. Therefore, it was only Q and Qp that varied and increased since clearing and have been the principal cause of the increase in sediment yield for these brigalow catchments. The results of the correlation analysis performed between the observed sediment yield and the factors Q, Qp, EI30, and C for the three catchments among the different land uses showed that Q and Qp were the best correlated factors to explain variations in the observed sediment yield with R2 > 0.78 and R2 > 0.71, respectively, for all treatments. Additionally, correlation analysis between the observed sediment yield and Q, Qp, EI30, and C for the three treatments among different storm events revealed that the effect of Q and Qp outweighed the effect of EI30 and C on sediment yield. The peak runoff rate, Qp, had a higher R2 value (>0.61) for forest and cropping and equal to 0.54 for grazing, whereas the runoff amount had the highest R2 (0.83) for grazing followed by cropping (R2 = 0.47) and forest (R2 = 0.28). The results were similar to the findings that sediment yield from catchments at three spatial scales (1 m2, 20 m2, and 2.80 ha) mainly depends on runoff, with R2 > 0.70 (Santos et al. 2017). Likewise, runoff explains 58% of the variance in sediment yield from the Magdalena catchment (257 438 km2), Colombia (Restrepo and Syvitski 2006).
The present study also illustrated that among the three sediment yield models, i.e. RUSLE, MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975), that the MUSLE (Williams 1975) model had the higher capacity to predict sediment yield from the BCS catchments, especially the grazed catchment. The results from the regression analysis between the model estimates from the RUSLE, MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975) models and observed sediment yield among the three treatments and different storm events suggested that, except for the cropped catchment, sediment yield was very sensitive to primary factors of the MUSLE (Williams 1975) model, i.e. Q and Qp. In addition, with regards to K, direct measurement of K is often quite expensive and time consuming (Loch et al. 1998). The USLE-based nomograph K, which is currently used in the eWater Source Catchments modelling framework of the GBR Paddock to Reef Integrated Monitoring, Modelling and Reporting Program for sediment yield modelling, is the best K to use for ungauged catchments without measured soil loss or sediment yield (Loch et al. 1998). Additionally, the estimated Ke obtained using the MUSLE model, either as it is or with some modifications with respect to the change in the real sediment yield data, can also be used to estimate sediment yield from the BCS catchments. For the cropped catchment, the estimated Ke was very close to the nomograph-based K; however, for the grazing catchment, the nomograph K needs some modifications with respect to real sediment yield data for use in the MUSLE model. Bosomworth et al. (2018) also indicated that the RUSLE-based nomograph K overestimated soil loss by approximately 50% in most cases of grazed soils. Although, adjustment is required, the difference between the nomograph and estimated Ke was not high enough to affect sediment yield estimation in any of these catchments. These observations provided support for the application of MUSLE (Williams 1975), with the inclusion of Q and Qp instead of EI30, for sediment yield prediction in BCS catchments.
As the RUSLE model does not consider Q and Qp for sediment yield estimation, any change in sediment yield among the three catchments will be related to either Ke or C, because EI30 was the same among the three treatments. However, Ke was estimated using the observed sediment yield; therefore, any change in other factors can only affect K. Hence, considering just change in C, we found that the ground cover in all three catchments was constantly higher with time and could not explain the increase in sediment yield. Therefore, we cannot use the USLE/RUSLE model to predict sediment yield for the three treatments. In contrast, it was observed that Q and Qp were the only factors that could be responsible for the change in sediment yield. The changes in Q and Qp due to the clearing of brigalow forest for cropping and grazing have been recorded in previous studies conducted by Thornton et al. (2007) and Thornton and Yu (2016). In the present study, Q and Qp dramatically increased due to land conversion. The effect of shear stress due to runoff factors has led to the detachment and transport of soil particles within the catchments. Therefore, the findings in the present study provide strong evidence that the increase in Q and Qp caused the increase in sediment yield among the three catchments over time. Moreover, the study clearly indicated that the MUSLE (Williams 1975) model was the most appropriate for sediment yield predictions in the BCS catchments. The reason behind the lack of capability of other two models, i.e. the RUSLE and MUSLE (Onstad and Foster 1975) models, was the small catchment area and also the lower amount of rainfall and rainfall intensity that produced low rainfall erosivity, which was insufficient to generate a modelled sediment yield.
The present study was based on the premise that there is no sediment deposition, i.e. the measured sediment yield at the catchment outlet was assumed to equal the soil loss from the catchment, where soil loss is defined as the measured total suspended solids load from a catchment. However, this assumption is inappropriate for large catchments, where the sediment delivery ratio needs to be considered explicitly for hillslope erosion prediction. For most of the Fitzroy Basin, the hillslope sediment delivery ratio (HSDR) was assigned a value of 0.1 in the dynamic SedNet model (Dougall et al. 2014). In contrast to the RUSLE model, the MUSLE model can be used directly for predicting sediment yield due to its consideration of runoff amount and the peak runoff rate, which eliminates the need for HSDR. However, for an ungauged catchment, the modified version of the USLE model can be used to estimate soil loss and sediment yield, and the combined sediment yield can be validated against the measured sediment data at the mainstream of the basin. Moreover, the ability of the USLE model can be improved by including the sediment transport capacity by stream flow process which leads to the estimation of soil loss or sediment yield at the catchment outlet. A modified version of USLE, i.e. USLE-M proposed by Kinnell and Rise (1998), which considers rainfall and runoff erosivity, has the capability to predict event soil loss better than USLE and, being a transport limited model, it can also predict the deposition occurring within a catchment (Kinnell 2015, 2016). The current study not only evaluated the effect of land clearing on sediment yield, but also assessed the alternative models, involving runoff characteristics for improved sediment yield predictions.
Conclusion
The aims of the present study were to evaluate the effect of land clearing for cropping and grazing in brigalow catchments on sediment yield, and to identify the factors or processes responsible for the increase in the sediment yield that occurred due to land use change. Moreover, the study examined the capability of sediment yield models, i.e. RUSLE, MUSLE (Williams 1975), and MUSLE (Onstad and Foster 1975), for estimating sediment yield from BCS catchments. The study involved the simple and direct comparison of observed total event sediment yield from different treatments and different storm events. The comparative study showed that the sediment yields significantly increased in cropped and grazed catchments following land clearing, and that the runoff amount and peak runoff rate were the main factors that changed over time and explained most of the variation and increase in sediment yield compared to the effect of ground cover. The regression analysis performed between the observed sediment yield and the factors Q, Qp, EI30, and C, revealed that the Q and Qp were the factors with best correlations and, thus, can be responsible for the changes in sediment yield from different land uses and different storm events. Moreover, the correlation between the observed sediment yield and the outputs of the three sediment yield models, each having a different model structure, revealed that the MUSLE (Williams 1975) model, which considers Q and Qp as its primary factors, was better able to appropriately predict sediment yield from the BCS catchments. This study clearly showed that the increased sediment yield was mostly caused by the increase in the runoff and peak runoff rate parameters Q and Qp. Previous studies conducted on the BCS catchments observed that changes in Q and Qp occurred due to conversion of brigalow forest to cropping and grazing, and the present study provides strong evidence that the inclusion of Q and Qp as the primary factors can improve sediment yield predictions from brigalow catchments.
Data availabilty
Data collected through the Brigalow Catchment Study can be accessed via the data portal (http://www.brigalowcatchmentstudy.com/BCSportal.html). Topography and ground cover data are available at (https://www.data.qld.gov.au/dataset/soils-universal-soil-loss-equation-series) and (http://data.auscover.org.au/xwiki/bin/view/Product+pages/Landsat+Seasonal+Fractional+Cover). Further details are available upon request to authors.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
The study was funded by Queensland Government, a Griffith University International Postgraduate Research Scholarship (GUIPRS), and a Griffith University Postgraduate Research Scholarship (GUPRS).
Acknowledgements
The authors would like to acknowledge Griffith University for the financial support provided through the Griffith University International Postgraduate Research Scholarship (GUIPRS) and the Griffith University Postgraduate Research Scholarship (GUPRS). The authors would like to thank Zhuo Cheng for helping with rainfall data analysis.
References
Aghsaei H, Dinan NM, Moridi A, Asadolahi Z, Delavar M, Fohrer N, Wagner PD (2020) Effects of dynamic land use/land cover change on water resources and sediment yield in the Anzali wetland catchment, Gilan, Iran. Science of the Total Environment 712, 136449| Effects of dynamic land use/land cover change on water resources and sediment yield in the Anzali wetland catchment, Gilan, Iran.Crossref | GoogleScholarGoogle Scholar |
Arekhi S, Shabani A, Rostamizad G (2012) Application of the modified universal soil loss equation (MUSLE) in prediction of sediment yield (case study: Kengir Watershed, Iran). Arabian Journal of Geosciences 5, 1259–1267.
| Application of the modified universal soil loss equation (MUSLE) in prediction of sediment yield (case study: Kengir Watershed, Iran).Crossref | GoogleScholarGoogle Scholar |
Bartley R, Waters D, Turner R, Kroon F, Wilkinson S, Garzon-Garcia A, Kuhnert P, Lewis S, Smith R, Bainbridge Z, Olley J, Brooks A, Burton J, Brodie J, Waterhouse J (2017) ‘Scientific Consensus Statement 2017: a synthesis of the science of land-based water quality impacts on the Great Barrier Reef. Chapter 2: Sources of sediment, nutrients, pesticides and other pollutants to the Great Barrier Reef’. (State of Queensland: Brisbane, Qld, Australia)
Borrelli P, Robinson DA, Fleischer LR, et al. (2017) An assessment of the global impact of 21st century land use change on soil erosion. Nature Communications 8,
| An assessment of the global impact of 21st century land use change on soil erosion.Crossref | GoogleScholarGoogle Scholar | 29222506PubMed |
Bosomworth B, Silburn DM, Eyles M, Shrestha K (2018) K-factor soil erodibility study on grazing lands: paddock to reef program: rainfall simulation program 2014 to 2018. Report to the Australian and Queensland Governments’ paddock to reef program. 53 pp. (Department of Natural Resources, Mines and Energy: Rockhampton, Qld, Australia)
Bostock HC, Ryan DA, Brooke BP, Packett R, Hancock G, Pietsch T, Revill A, Leeming P, Moss P, Harle K (2006). Sediment accumulation and Holocene evolution of the Fitzroy River lower floodplain, central Queensland, Australia. Cooperative Research Centre for Coastal Zone Estuary and Waterway Management. Technical report no. 48. Coastal CRC, Indooroopilly, Qld, Australia.
Cheng Z, Yu B (2019) Effect of land clearing and climate variability on streamflow for two large basins in central Queensland, Australia. Journal of Hydrology 578, 124041
| Effect of land clearing and climate variability on streamflow for two large basins in central Queensland, Australia.Crossref | GoogleScholarGoogle Scholar |
Cowie BA, Thornton CM, Radford BJ (2007) The Brigalow Catchment Study: I. Overview of a 40-year study of the effects of land clearing in the brigalow bioregion of Australia. Australian Journal of Soil Research Soil Research 45, 479–495.
| The Brigalow Catchment Study: I. Overview of a 40-year study of the effects of land clearing in the brigalow bioregion of Australia.Crossref | GoogleScholarGoogle Scholar |
Department of Environment and Heritage (2006) Databases and maps; information for decision making. Available at www.deh.gov.au/index.html. [Accessed 17 September 2007]
Djoukbala O, Hasbaia M, Benselama O, Mazour M (2019) Comparison of the erosion prediction models from USLE, MUSLE and RUSLE in a Mediterranean watershed, case of Wadi Gazouana (NW of Algeria). Modeling Earth Systems and Environment 5, 725–743.
| Comparison of the erosion prediction models from USLE, MUSLE and RUSLE in a Mediterranean watershed, case of Wadi Gazouana (NW of Algeria).Crossref | GoogleScholarGoogle Scholar |
Dougall C, McCloskey GL, Ellis R, Shaw M, Waters D, Carroll C (2014) Modelling reductions of pollutant loads due to improved management practices in the Great Barrier Reef catchments – Fitzroy NRM region, Technical report, vol. 6. Queensland Department of Natural Resources and Mines, Rockhampton, Qld, Australia.
Ehigiator OA, Anyata BU (2011) Effects of land clearing techniques and tillage systems on runoff and soil erosion in a tropical rain forest in Nigeria. Journal of Environmental Management 92, 2875–2880.
| Effects of land clearing techniques and tillage systems on runoff and soil erosion in a tropical rain forest in Nigeria.Crossref | GoogleScholarGoogle Scholar | 21783317PubMed |
Elledge A, Thornton C (2017) Effect of changing land use from virgin brigalow (Acacia harpophylla) woodland to a crop or pasture system on sediment, nitrogen and phosphorus in runoff over 25 years in subtropical Australia. Agriculture, Ecosystems & Environment 239, 119–131.
| Effect of changing land use from virgin brigalow (Acacia harpophylla) woodland to a crop or pasture system on sediment, nitrogen and phosphorus in runoff over 25 years in subtropical Australia.Crossref | GoogleScholarGoogle Scholar |
Erskine WD, Mahmoudzadeh A, Myers C (2002) Land use effects on sediment yields and soil loss rates in small basins of Triassic sandstone near Sydney, NSW, Australia. Catena 49, 271–287.
| Land use effects on sediment yields and soil loss rates in small basins of Triassic sandstone near Sydney, NSW, Australia.Crossref | GoogleScholarGoogle Scholar |
Estrepo JD, Syvitski JPM (2006) Assessing the effect of natural controls and land use change on sediment yield in a major Andean river: the Magdalena drainage basin, Colombia. Ambio: A Journal of the Human Environment 35, 65–74.
| Assessing the effect of natural controls and land use change on sediment yield in a major Andean river: the Magdalena drainage basin, Colombia.Crossref | GoogleScholarGoogle Scholar |
Foster GR, McCool DK, Renard KG, Moldenhauer WC (1981) Conversion of the universal soil loss equation to SI metric units. Journal of Soil and Water Conservation 36, 355–359.
Foster GR, Lombardi F, Moldenhauer WC (1982) Evaluation of rainfall–runoff erosivity factors for individual storms. Transactions of the ASAE 25, 0124–0129.
| Evaluation of rainfall–runoff erosivity factors for individual storms.Crossref | GoogleScholarGoogle Scholar |
Gashaw T, Tulu T, Argaw M, Worqlul AW (2019) Modeling the impacts of land use–land cover changes on soil erosion and sediment yield in the Andassa watershed, upper blue Nile basin, Ethiopia. Environmental Earth Sciences 78,
| Modeling the impacts of land use–land cover changes on soil erosion and sediment yield in the Andassa watershed, upper blue Nile basin, Ethiopia.Crossref | GoogleScholarGoogle Scholar |
Kinnell PIA (2004) Runoff, sediment concentration and predicting erosion on hill slopes within catchments. In ‘ISCO 2004 – 13th International Soil Conservation Organization conference, Brisbane, July 2004’. Conserving Soil and Water for Society: sharing solutions. Paper no. 132. (Eds SR Raine, AJW Biggs, NW Menzies, DM Freebairn, PE Tolmie) pp. 1–6. (Australian Society of Soil Science Incorported and International Erosion Control Association: Australasia) Available at https://scholar.google.com/scholar_lookup?title=Runoff%2C%20sediment%20concentration%20and%20predicting%20erosion%20on%20hillslopes%20within%20catchments&publication_year=2004&author=P.I.A.%20Kinnell
Kinnell PIA (2010) Event soil loss, runoff and the universal soil loss equation family of models: a review. Journal of Hydrology 385, 384–397.
| Event soil loss, runoff and the universal soil loss equation family of models: a review.Crossref | GoogleScholarGoogle Scholar |
Kinnell PIA (2015) Geographic variation of USLE/RUSLE erosivity and erodibility factors. Journal of Hydrologic Engineering 20, C4014012
| Geographic variation of USLE/RUSLE erosivity and erodibility factors.Crossref | GoogleScholarGoogle Scholar |
Kinnell PIA (2016) Comparison between the USLE, the USLE-M and replicate plots to model rainfall erosion on bare fallow areas. Catena 145, 39–46.
| Comparison between the USLE, the USLE-M and replicate plots to model rainfall erosion on bare fallow areas.Crossref | GoogleScholarGoogle Scholar |
Kinnell PIA, Risse LM (1998) USLE-M: empirical modeling rainfall erosion through runoff and sediment concentration. Soil Science Society of America Journal 62, 1667–1672.
| USLE-M: empirical modeling rainfall erosion through runoff and sediment concentration.Crossref | GoogleScholarGoogle Scholar |
Lewis S, Packett B, Dougall C, Brodie J, Bartley R, Silburn, M (2015) ‘Fitzroy sediment story’. (James Cook University: Townsville, Qld, Australia)
Loch RJ, Rosewell CJ (1992) Laboratory methods for measurement of soil erodibilities (K factors) for the universal soil loss equation. Australian Journal of Soil Research 30, 233–248.
| Laboratory methods for measurement of soil erodibilities (K factors) for the universal soil loss equation.Crossref | GoogleScholarGoogle Scholar |
Loch RJ, Slater BK, Devoil C (1998) Soil erodibility (Km) values for some Australian soils. Australian Journal of Soil Research 36, 1045–1056.
| Soil erodibility (Km) values for some Australian soils.Crossref | GoogleScholarGoogle Scholar |
Onstad CA, Foster GR (1975) Erosion modeling on a watershed. Transactions of the ASAE 18, 0288–0292.
| Erosion modeling on a watershed.Crossref | GoogleScholarGoogle Scholar |
Queensland Department of Primary Industries (1993) ‘The condition of river catchments in Queensland. A broad overview of catchment management issues.’ (Queensland Department of Primary Industries: Brisbane, Qld)
Renard KG, Foster GR, Weesies GA, McCool DK, Yoder DC (1997) Estimation of rainfall–runoff erosivity for individual storm events. In ‘Predicting soil erosion by water: a guide to conservation planning with the revised universal soil loss equation, RUSLE’. Agricultural handbook, no. 703. (Eds KG Renard, GR Foster, GA Weesies, DK McCool, DC Yoder) (United States Department of Agriculture: Washington, DC)
Rosewell CJ (1993) ‘SOILOSS: a program to assist in the selection of management practices to reduce erosion’. (Soil Conservation Service of NSW: Sydney, NSW, Australia)
Sadeghi SHR, Gholami L, Khaledi Darvishan A, Saeidi P (2014) A review of the application of the MUSLE model worldwide. Hydrological Sciences Journal 59, 365–375.
| A review of the application of the MUSLE model worldwide.Crossref | GoogleScholarGoogle Scholar |
Sadeghi SHR, Mizuyama T (2007) Applicability of the modified universal soil loss equation for prediction of sediment yield in Khanmirza watershed, Iran. Hydrological Sciences Journal 52, 1068–1075.
| Applicability of the modified universal soil loss equation for prediction of sediment yield in Khanmirza watershed, Iran.Crossref | GoogleScholarGoogle Scholar |
Santos JCND, Andrade EMD, Medeiros PHA, Guerreiro MJS, Palácio HADQ (2017) Land use impact on soil erosion at different scales in the Brazilian semi-arid. Revista Ciência Agronômica 46, 251–256.
| Land use impact on soil erosion at different scales in the Brazilian semi-arid.Crossref | GoogleScholarGoogle Scholar |
Siriwardena L, Finlayson BL, McMahon TA (2006) The impact of land use change on catchment hydrology in large catchments: the Comet river, central Queensland, Australia. Journal of Hydrology 326, 199–214.
| The impact of land use change on catchment hydrology in large catchments: the Comet river, central Queensland, Australia.Crossref | GoogleScholarGoogle Scholar |
Thornton CM, Cowie BA, Freebairn DM, Playford CL (2007) The Brigalow Catchment Study: II. Clearing brigalow (Acacia harpophylla) for cropping or pasture increases runoff. Australian Journal of Soil Research 45, 496–511.
| The Brigalow Catchment Study: II. Clearing brigalow (Acacia harpophylla) for cropping or pasture increases runoff.Crossref | GoogleScholarGoogle Scholar |
Thornton CM, Yu B (2016) The Brigalow Catchment Study: IV. Clearing brigalow (Acacia harpophylla) for cropping or grazing increases peak runoff rate. Soil Research 54, 749–759.
| The Brigalow Catchment Study: IV. Clearing brigalow (Acacia harpophylla) for cropping or grazing increases peak runoff rate.Crossref | GoogleScholarGoogle Scholar |
Thornton C, Radford B, Silburn M, Cowie B (2010) The Brigalow Catchment Study: more than 20 years of monitoring water balance and soil fertility of brigalow lands after clearing for cropping or pasture. In ‘Soil solutions for a changing world. Proceedings of the 19th World Congress of Soil Science; Soil Solutions for a Changing World, 1−6 August 2010, Brisbane, Australia’. (Eds RJ Gilkes, N Prakongkep) pp. 106–109. (International Union of Soil Sciences)
Trevithick R, Scarth P (2013) Estimating RUSLE C-factor values for Great Barrier Reef catchments using satellite derived ground cover estimates. In ‘MODSIM2013, 20th International Congress on Modelling and Simulation, 1−6 December 2013, Adelaide, Australia’. (Eds J Piantadosi, RS Anderssen, J Boland) pp. 3246−3252. (The Modelling and Simulation Society of Australia and New Zealand Inc)
Walling DE (1999) Linking land use, erosion and sediment yields in river basins. In ‘Man and river systems’. (Eds J Garnier, JM Mouchel) pp. 223–240. (Springer: Dordrecht, The Netherlands).
Wilkinson SN, Henderson AE, Chen Y (2004) ‘SedNet user guide. Client report for the cooperative research centre for catchment hydrology’. (CSIRO Land and Water: Canberra, ACT, Australia). Available at http://hdl.handle.net/102.100.100/184593?index=1
Williams JR (1975) Sediment-yield prediction with universal equation using runoff energy factor. In ‘Present and prospective technology for predicting sediment yields and sources’. pp. 244–252. (US Department of Agriculture, Agriculture Research Service: Washington, DC, USA)
Wischmeier WH, Smith DD (1978) ‘Predicting rainfall erosion losses: a guide to conservation planning’. (Department of Agriculture, Science and Education Administration: Hyattsville, MD, USA)
Yu B (1998) Rainfall erosivity and its estimation for Australia’s tropics. Australian Journal of Soil Research 36, 143–166.
| Rainfall erosivity and its estimation for Australia’s tropics.Crossref | GoogleScholarGoogle Scholar |
† Parts I–III, Australian Journal of Soil Research 45(7), 479–495, 496–511 and 512–523. Part IV, Soil Research 54(6), 749–759. Part V, Soil Research 59(2), 146–169.