Field-scale solute transport parameters derived from tracer tests in large undisturbed soil columns
Dirk MallantsCSIRO Land and Water, Waite Road - Gate 4, Glen Osmond, SA 5064, Australia. Email: Dirk.Mallants@csiro.au
Soil Research 52(1) 13-26 https://doi.org/10.1071/SR13143
Submitted: 4 May 2013 Accepted: 3 September 2013 Published: 5 February 2014
Abstract
Transport parameters obtained from laboratory tracer experiments were used to evaluate the stochastic form of the equilibrium convection–dispersion equation (CDE) in describing the transition of scale, i.e. from the column or local scale to a larger field scale. Local-scale solute breakthrough curves (BTCs) were measured in 1-m-long and 0.3-m-diameter undisturbed soil columns by means of time-domain reflectometry at six depths for a 79-h input pulse of chloride. The local-scale data were analysed in terms of the equilibrium CDE and the mobile–immobile non-equilibrium transport model (MIM). At the local scale, the MIM transport model better described the observed early breakthrough and the tailing of the BTC than did the CDE. A linear regression analysis indicated that the relationship between the hydrodynamic dispersion D and pore-water velocity v was of the form D = 31vl.92 (correlation ρv,D = 0.74). Averaging of the local-scale BTCs across the field produced a large-scale or field-scale mean BTC; at the greatest observation depth (0.8 m) the field-scale dispersivity <D>/<v> = λ equals 0.656 m. The results further showed that for large values of the mean dispersion coefficient, <D>, local-scale dispersion is an important mechanism for field-scale solute spreading, whereas the standard deviation, σD, and the correlation between v and D, ρvD, have negligible effects on field-scale transport. Stochastic stream tube models supplemented with statistical properties of local-scale transport parameters provide a practical and computationally efficient tool to describe heterogeneous solute transport at large spatial scales.
Additional keywords: convection–dispersion model, mobile–immobile model, stochastic stream tube model, time-domain reflectometry, parameter optimisation, contaminant transport.
Introduction
Protection of shallow groundwater systems will greatly benefit from our ability to accurately predict the field-scale transport of pollutants from the soil surface to the groundwater table. Remediation of shallow and deep vadose zones contaminated by organic and inorganic substances often depends on the success of delivery of surface-applied or injected amendments into the vadose zone. Field-scale solute transport modelling is indispensable for evaluating the feasibility of such clean-up methods (Brusseau et al. 2010; Zhang et al. 2012). However, field-scale solute transport is significantly influenced by the heterogeneous nature of flow and transport properties across the field (Jacques et al. 1998; Seuntjens et al. 2002; Mallants et al. 2011; Stauffer and Lu 2012). In the last three decades, research both theoretical and experimental has been carried out to investigate solute transport behaviour in field soils (Van Ommen et al. 1989; Ellsworth et al. 1996; Forrer et al. 1999; Ghodrati 1999; Dusek et al. 2008; Robinson et al. 2012). Theoretical investigations of solute transport in heterogeneous, stratified porous formations often rely on stochastic principles. For instance, the stream-tube model (STM) regards the field as a series of independent vertical stream tubes. The model parameters for each tube are viewed as realisations of a stochastic process. Bresler and Dagan (1981) investigated the combined effects of pore-scale dispersion and velocity variability on solute distributions in the field. Effects of local-scale transport parameters on field-scale transport for a variety of boundary and initial conditions were investigated by Toride and Leij (1996) assuming the convection–dispersion equation (CDE) in each stream tube. Ward et al. (1995) analysed the effects of variable layer thickness in a stochastic STM on solute spreading.
Testing of the predictive capacities of the above theoretical models is important and typically requires well-controlled flow conditions in the field, or alternatively, in the laboratory invoking flow conditions that mimic those in the field. Several studies have concentrated on the collection of field tracer data for this purpose (Jury 1982; Schulin et al. 1987a; Jaynes et al. 1988; Butters et al. 1989; Köhne and Gerke 2005). Solute transport at the field-scale, however, is known to be complicated by several processes, such as the presence of variable horizon thicknesses or tonguing (Van Wesenbeeck and Kackanoski 1991), and preferential flow (Roth et al. 1991; Zehe and Flühler 2001; Jarvis 2007). Furthermore, calibration and validation of theoretical models requires data collected from displacement experiments with well-controlled boundary conditions, which are often difficult to establish in field soils.
As a surrogate for actual field experiments, numerical experiments with hypothetical field soils have gained insight into the sensitivities of field-scale behaviour with respect to particular local-scale heterogeneities. For instance, Russo et al. (1989) investigated the influence of immobile water on solute transport subject to boundary conditions corresponding to cycles of infiltration, evaporation, and redistribution. Tseng and Jury (1994) compared the stochastic-convective log-normal transfer function model (CLT) and the CDE model to predict area-averaged transport in a hypothetical, two-dimensional heterogeneous field soil. Vanderborght et al. (1998) compared different approaches to calculate statistics of the solute travel time and displacement based on spatial covariance functions of the pore-water velocity. Based on simulated water flow in a two-dimensional, macroscopically homogeneous Miller-similar medium, Roth and Hammel (1996) demonstrated that the local structure of the velocity field (expressed by the form of the spatial autocorrelation function for the scaling factor) and the subscale hydrodynamic dispersion are of minor importance for the field-averaged transport process. Vogel and Roth (2003) proposed the ‘scaleway’ as a discrete hierarchical approach for modelling flow and transport, based on the explicit consideration of the full three-dimensional representation of the macro structure, while microscopic heterogeneities were averaged and replaced by effective descriptions.
In addition to field and numerical experiments, transport experiments for controlled laboratory conditions with undisturbed soil columns provide useful information on the local-scale solute behaviour if the natural layering is preserved (Schulin et al. 1987b; Seyfried and Rao 1987; Beven et al. 1993; Seuntjens et al. 2001). If the inherent spatial heterogeneity of the soil is represented by taking samples at different spatial locations across the field, and if the particular flow conditions at the local scale are also present at the field scale, e.g. steady-state vertical flow, then one should be able to evaluate the field-scale solute transport by appropriate averaging of the local-scale processes. Extrapolation of results obtained from laboratory experiments to field conditions may then yield satisfactory predictions.
This paper presents a solute-transport experiment carried out under controlled laboratory conditions using 14 undisturbed soil columns, 0.3 m in diameter and 1 m long, collected from a field transect. Local-scale solute breakthrough curves (BTCs) were measured at six different depths in the soil columns during steady saturated flow using time-domain reflectometry (TDR). The BTCs were analysed in terms of the one-dimensional CDE and the mobile–immobile non-equilibrium transport model (MIM). By assuming the field as a series of independent, vertical soil columns, field-scale mean transport was also analysed in terms of the STM with a stochastic pore-water velocity, v, and dispersion coefficient, D. The effect of the local-scale dispersion on field-scale transport was also discussed by considering the Peclet number, <v> x/D, in terms of the observation scale, x.
Materials and methods
Solute transport experiments
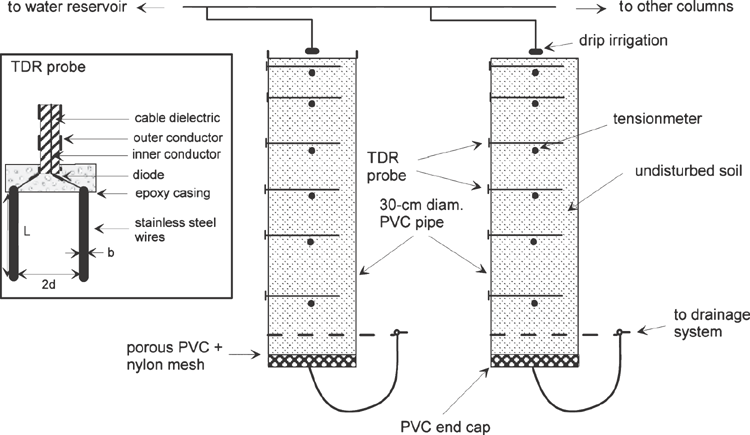
Thirty undisturbed soil columns, 0.3 m in diameter and 1 m in length (Fig. 1), were collected along a 31-m-long transect from the Bekkevoort experimental field, east of Leuven in central Belgium. The field plot was in an orchard, with the transect between two rows of trees. The surface between the trees was covered with permanent grass. The soil profile contained three different horizons: Ap, C1 and C2. The Ap and C1 horizon were pedogenetically identical, i.e. they had both developed on colluvial material. The C2 horizon was an old textural B horizon, which had been covered by erosion material. The average thickness of the Ap horizon was 0.25 m, whereas the mean thickness of the C1 and C2 horizons was 0.3 and 0.45 m, respectively, with a sharp boundary between all soil layers. Each layer had a fairly constant thickness along the transect. Physical and chemical properties of each soil horizon are listed in Table 1. The clay content increased from 12.7% in the Ap horizon to 16.6% in the Cl and 21.8% in the C2 horizon. The higher clay content in the C2 horizon is due to accumulation of migrating clay particles. The soil was classified as an Udifluvent (Eutric Regosol) (IUSS 2006) and contained a large number of macropores throughout the profile (Mallants et al. 1997). The macropores consisted mainly of decayed root channels and earthworm holes.

|
From the same field plot, additional 0.2-m-long, 0.2-m-diameter soil columns had previously been investigated to test the applicability of TDR for measuring transport processes at shallow depth (Mallants et al. 1994). The sampling locations were exactly between two wheel tracks so that the soil had not been compacted nor been in contact with any machinery. First, the soil was cleared of vegetation (grass) and the humus layer was removed. Sampling of the soil columns was done by means of polyvinyl chloride (PVC) cylinders. The PVC cylinders had an internal diameter of 0.3 m, and the inner wall was greased to have close contact between soil and the wall. The bottom end was provided with a sharp-edged steel ring to facilitate intrusion into the soil, and the cylinders were gently driven into the soil using a hydraulic jack. Once the cylinder was completely filled with soil, the soil around it was excavated gradually such that the column could be isolated and the bottom end cut off by means of a steel plate that was sharpened at one side. Next, a PVC end cap was placed on both ends of the cylinder. This unit was lifted hydraulically onto a truck and transported to the laboratory. Thirty undisturbed soil columns were sampled in this way with a separation distance of 1 m. At one location a sampling distance of 2 m was used because of difficulties in driving the cylinder into a locally compacted layer.
In the laboratory, a perforated 0.005-m-thick PVC plate was attached to the bottom end of the columns to prevent the soil from falling out. A nylon-type mesh was glued on top of the perforated plate to allow the application of a suction of up to 70 mbar (7 kPa). This assembly was attached to the bottom of the column together with an enclosed drainage system (Fig. 1). Drainage water from this column could be collected in small sampling bottles via a polyethylene (PET) tube. The set-up also allows a watertable to be maintained at the bottom of the column or a negative pressure to be imposed by means of a hanging water column. Solute-free water could be applied to the top of the columns by means of a constant-rate drip-irrigation system. A 0.01-m-thick fibre wool cover was put on top of the soil surface to reduce crust formation during irrigation. The top boundary condition was established by allowing water to pond for a maximum depth of 0.01 m. A spillway system diverted the excess water and secured a maximum water depth of 0.01 m. A second independent drip-irrigation line was constructed for the application of the tracer solution. In this way, it was easy to switch from solute-free water to tracer solution and vice versa. All columns were saturated from the bottom by stepwise increasing the water level in the small reservoir.
To ensure steady-state saturated flow, soil water content, θ, and pressure head, ψ, values were monitored by TDR and tensiometers installed at six different depths (0.05, 0.15, 0.3, 0.45, 0.6, and 0.8 m), i.e. two observation depths for each horizon. The TDR probes consisted of two parallel waveguides with a distance of 0.025 m between the centre of the rods. The diameter of the stainless steel rods was 0.0005 m. The 0.25-m-long stainless-steel probes were directly connected to the inner and outer conductor of a coaxial cable (see inset Fig. 1) in a way similar to the probe design of Ledieu et al. (1986). The volume of soil that is effectively sampled for water content using this probe design corresponds to an approximate cylinder with a diameter of 0.066 m. Details for the calculation of the sampling volume for TDR probes can be found in Knight (1992). Volumetric water contents were inferred from the travel time of an electromagnetic wave through a volume of wet soil. Travel times were obtained from the screen of a Tektronix 1502B cable tester (Tektronix Inc., Beaverton, OR, USA) and were converted to soil water content using the calibration relationships established by measuring travel times for repacked soil at known but different water contents. The pressure head was measured by pushing a hypodermic needle into a rubber membrane mounted on an air-filled reservoir. The needle was connected to a pressure transducer, which converted the pressure in the needle to a digital pressure value on a LCD screen (Thies-Clima, Göttingen, Germany).
The steady-state water contents, θ, as observed with TDR show little horizontal and vertical variation. Generally, water contents at 0.45 m depth are slightly smaller than those at 0.15 and 0.80 m. The maximum difference in water content between soil horizons is only ~5% by volume. The bulk density, ρb, also changes little horizontally, except for some fluctuations occurring near the surface. Hence, the effects of variable θ and ρb on the transport process are not considered further.
When the soil was saturated, solute-free water was applied through the drip irrigation system at a rate sufficient to maintain ponding. After establishing steady-state flow conditions, the application of solute-free water was interrupted and the remaining water allowed to infiltrate. Next, a 7 × 10–3 m CaC12 solution was applied continuously for a period of at least 79 h. This long application time guaranteed that, at least at the first observation depths (x = 0.05 m), the initial soil solution was completely displaced by the applied tracer solution (Mallants et al. 1996). For some extreme cases, solute had to be applied for as long as 664 h to saturate the soil at the first observation depth (x = 0.05 m). Such long application times resulted in an uncertain calibration, which would affect the derived transport parameter v and D (Mallants et al. 1996). Hence, only the columns with an application time, t0, of 79 h will be discussed for field-scale mean transport in this paper (14 in total). This still presents a sufficiently large dataset for testing field-scale transport processes. Finally, solute-free water was subsequently added again to the soil until all of the solute had leached out of the columns. Tracer concentrations at the six observation depths were obtained by converting estimates of the bulk soil electrical conductivity, ECa, to resident concentrations. The calibration methods for undisturbed soil were discussed in detail by Mallants et al. (1996). Values of ECa were estimated with TDR using procedures as discussed by several authors (Kachanoski et al. 1992; Wraith et al. 1993; Vanclooster et al. 1993; Mallants et al. 1994; Ward et al. 1994).
Local-scale transport
Solute transport in each soil column was analysed in terms of the CDE and the MIM models. The CDE for non-reactive tracers is given by:

where c is the resident concentration (g/cm3), D is the local-scale dispersion coefficient (cm2/h), v is the pore-water velocity (cm/h), defined as q/θ with q the Darcian flux density, x is depth (cm), and t is time (h).
The MIM model, which is often invoked to describe asymmetrical concentration distributions displaying early breakthrough and tailing, is given by:


where θ is the volumetric water content, α is a first-order mass transfer coefficient (day–1), and the subscripts m and im refer to the mobile and immobile liquid regions, respectively. The transport parameters in the CDE and MIM models were fitted to observed BTCs using an extended version of the CXTFIT non-linear parameter estimation program of Toride et al. (1995). Since the TDR only detected a relatively small region of the whole flow domain, this region may or may not include preferential flow channels. Following the approach of Mallants et al. (1994), independent estimates were first obtained of the pore-water velocities, v (for the MIM this is equivalent to vm θm/θ), from the first normalised temporal moment of the BTC (i.e. calculating time moments is independent from assuming any transport process model), and D was determined for the CDE, and Dm, θm/θ and α for the MIM. In so doing, the number of fitting parameters is reduced by one, which increases the uniqueness of the remaining fitting parameters. It was further assumed that TDR measures total resident concentration, i.e. cT = c for the CDE (Eqn 1) and cT = (θmcm + θimcim)/θ for the MIM (Eqn 2).
Field-scale mean transport
When the field is viewed as a set of homogeneous vertical stream tubes without exchange between the stream tubes, field-scale transport may be described by averaging local-scale concentrations over all stream tubes (Bresler and Dagan 1981; Simmons 1982). In order to investigate the effect of local-scale velocity and dispersion fluctuations on field-scale transport, the stream-tube concept was applied to the observed column BTCs. It was also assumed that the local-scale transport is described by the CDE (Eqn 1). The field-scale mean concentration, <c>, in terms of the STM with stochastic v and D is given by (Toride and Leij 1996):

where f(v, D) is the joint probability density function (pdf) for v and D, which may be described with the bivariate lognormal distribution:
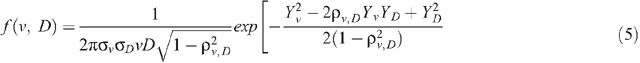
where:


in which µ is used for the mean and σ for the standard deviation of ln(v) or ln(D), and ρv, D is the correlation coefficient between Yv and YD. It is assumed that all random parameters are statistically stationary and obey the ergodicity principle. An average concentration across the field, obtained from a sufficient number of samples, is then identical to the area-averaged concentration:

where A denotes the area of the field and n is the number of samples. The approach, hence, assumes that horizontal field-averaged transport behaviour can be estimated from the local-scale column BTCs. When v and D are perfectly correlated, i.e. ρv, D = ± 1, the local-scale D can be expressed in terms of v (Toride and Leij 1996):
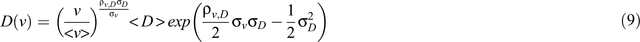
where <v> and <D> are ensemble averages of v and D, given as <v> = exp(µv + σ2v/2) and <D> = exp(µD + σ2D/2). A special case for Eqn 9 occurs when ρv, D = 1 with σv = σD, in which case Eqn 9 reduces to:

where <D>/<v> = λ, with λ the field-scale dispersivity (m). The relationship between D and v following Eqn 10 has been extensively used to express the dependence of D on v (e.g. for a review of D–v relationships see Beven et al. 1993; Vanderborght and Vereecken 2007). The field-scale mean concentration <c> can be obtained by substitution of the appropriate analytical solutions for the CDE and the pdf into Eqn 4 (Toride et al. 1995).
Results
Local-scale transport
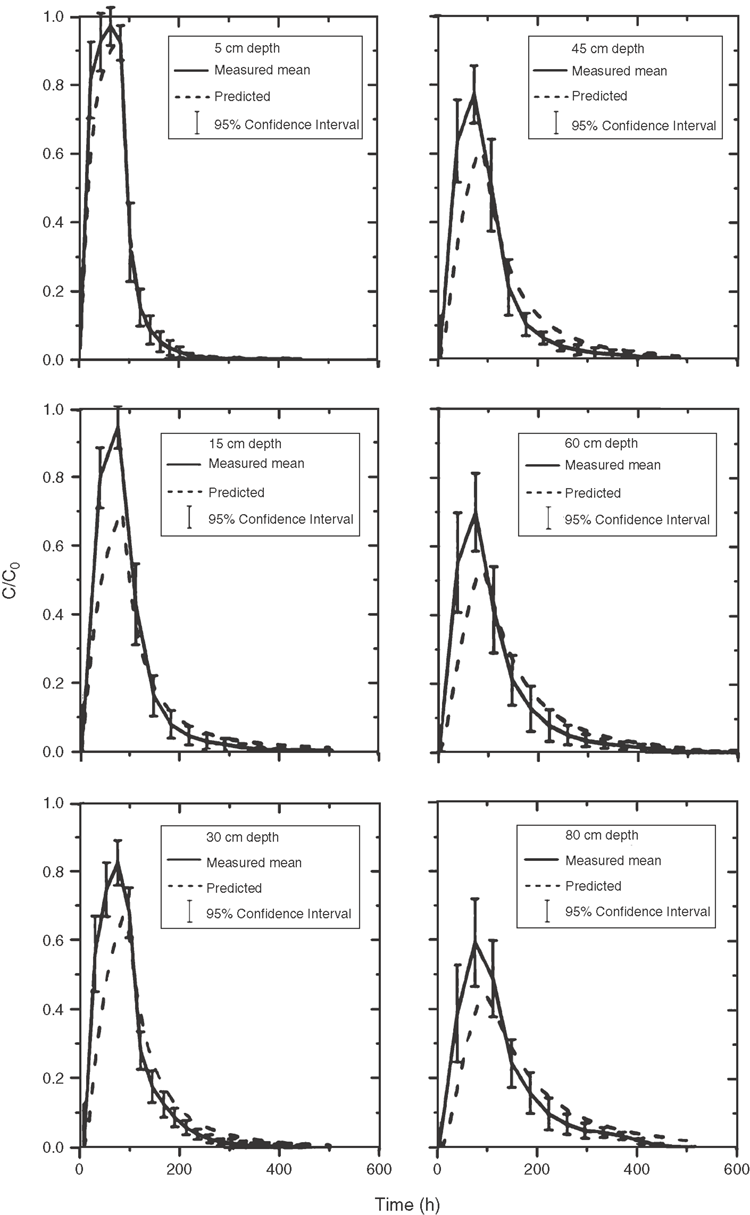
A typical example of measured local-scale BTCs in one single column together with the fitted local-scale CDE and MIM transport models is given in Fig. 2a–f for six observation depths. Note that the fitted transport parameters reflect the average properties from the surface to the observed depth. Table 2 presents fitted parameter values for the two models, together with the measured pore-water velocity at depth x, vo = q/θ, where θ is the steady-state water content at depth x. Since the pore-water velocity, v, was obtained from the first time moment of the observed BTC and subsequently fixed during parameter fitting for the CDE and MIM, the mean travel time τ to a given depth x is identical for the measured (by using time moments) and fitted curves. Comparison between vo and v for all depths indicates consistently larger values for the former compared with the latter, except at x = 0.8 m where the two values are relatively close. Values for v differed significantly between the first and second observation depth (0.87 and 2.73, respectively) whereas flow became more uniform deeper in the profile. As discussed by Mallants et al. (1994), the soil was more heterogeneous near the surface. The TDR probe at x = 0.05 m presumably could not detect all of the preferential flow channels that were present in the soil. As a result, mainly the slower transport regions may have been measured, resulting in a relatively symmetrical BTC with a fairly small value for v.

|

|
The dispersion coefficient D pertaining to the CDE varied considerably between the first three depths. From 0.45 m onwards, D became almost constant. The local-scale dispersivity, λ = D/v, was found to vary between 0.02 m at x = 0.05 m and 0.178 m for x = 0.8 m. Similar large values for λ have often been observed for undisturbed soils (Dyson and White 1987; Beven et al. 1993; Gelhar 1993; Vanderborght et al. 2001). Vanclooster et al. (1995), for example, reported a dispersivity λ = 0.31 m for their sandy soil in a 1-m-long lysimeter. Van Wesenbeeck and Kackanoski (1991) reported a maximum dispersivity of 4.81 m for a sampling depth of 1.83 m in a field test under ponding conditions.
The mobile-phase velocities, vm = v (θm/θ), were less variable compared with v, although vm was still somewhat smaller than vo. Fractions of mobile water, θm/θ, showed an increasing trend with depth except at x = 0.15 m, where nearly all of the water was mobile, i.e. θm/θ = 0.99. The fitted first-order mass transfer coefficient, α, indicates that deeper in the soil profile, less time is required to equilibrate the immobile phase concentration with respect to the mobile phase. That is, as the solute moved deeper in the soil profile, more solute mixing occurred between preferential pathways and bypassed flow regions.
Based on the values for the coefficient of determination, r2, the MIM model with three fitting parameters (Dm, θm/θ, and α) generally performed better than the CDE with a single fitting parameter (D). For observation depths greater than 15 cm, the CDE always underestimated the BTCs at small times, and overestimated the curves at large times. In order to compare the transport parameters between the CDE and the MIM, an effective dispersion coefficient, Deff, was evaluated, obtained from the MIM model parameters (Valocchi 1985; van Genuchten and Dalton 1986):

in which the first term is the hydrodynamic dispersion in the mobile phase, and the second term reflects the source–sink effects of solute transfer into and out of immobile zones. Note that the hydrodynamic dispersion is generally proportional to v, whereas in the second term, Deff is proportional to the square of v. Values of Deff, calculated with Eqn 11, for x = 0.6 and x = 0.8 m were, respectively, 74 and 48 cm2/h, whereas the CDE estimates of D in Table 2 were 38.7 and 34.1 cm2/h. The larger values for Deff are due to the solute exchange between mobile and immobile zones resulting in asymmetrical BTCs, which require a larger (effective) dispersion coefficient to describe it.
Parker and Valocchi (1986) indicated that transport in structured soils can be approached with the equilibrium CDE when the assumption of the local equilibrium (LE) is met. As the travel distance, x, increases, the mean residence time, xlv, becomes larger relative to the characteristic time for the solute exchange between mobile and immobile phases, 1/α. Validity of the LE assumption, therefore, improves as solute moves down. This LE effect could result in a good agreement between Deff and D for the CDE at 0.8 m. These results illustrate the potentials of describing solute transport at greater depths with the CDE using an effective D given by Eqn 11.
In addition to the LE effect, this close agreement between CDE and MIM at x = 0.8 m could be caused in part by the presence of a compacted soil layer, which was observed in some columns. When horizontal solute mixing increased in the compacted layer, solute transport could be described by means of the convective–dispersive process (Jury et al. 1991). In a few columns this compaction resulted in much lower peak concentrations at x = 0.8 m (results not further presented here).
To evaluate the relationship between the dispersion coefficient, D, and the pore-water velocity, v, for the CDE, linear regression was used to estimate the coefficient, λ, and the exponent, n, in the following equation:

where n is a parameter generally ranging from 1 to 2 (Saffman 1959; Bear 1972; Beven et al. 1993), although values <1 and >2 have also been reported (Bowman and Rice 1986; Jaynes et al. 1988). As discussed for Eqn 11, when hydrodynamic dispersion (the first term in Eqn 11) is the main spreading mechanism, n will be close to 1, while values of n close to 2 represent processes governed by intra-aggregate diffusion (the second term in Eqn 11). Results of the regression analysis between ln(D) and 1n(v) are given in Fig. 3 using all data from three soil horizons. Combining all data at the 0.8 m depth leads to a ‘field-scale’ dispersivity <D>/<v> = λ of 0.656 m, and n = 1.92 with the correlation coefficient, ρv, D = 0.74

|
This relatively high value for n indicates that non-equilibrium effects on solute spreading were dominant compared with the hydrodynamic dispersion in the mobile phase. Under ponded conditions, Biggar and Nielsen (1976) found a similar correlation between v and D for their soil, i.e. ρv, D = 0.795 (by combining data from all plots and all depths). Padilla et al. (1999) determined an n value of 1.99 and a value of 0.085 cm for λ based on the CDE model for a transport distance of 0.25 m. Of further note in Fig. 3 is the greater heterogeneity in the ln(v) data for the Ap horizon compared with ln(v) values for the deeper soil layers (Cl and C2). This likely reflects again the more homogeneous nature of the flow regime deeper in the soil profile.
Values of v and D from all depths were combined and used to construct fractile diagrams. The raw and log-transformed v and D values are shown in Fig. 4. The regression models are only used to determine whether the parameters are normally or log-normally distributed. The data seem to be adequately described by both the normal and log-normal distributions. Based on the complete dataset, v and D had <v> = 0.82 cm/h with σv = 0.62 cm/h, and <D> = 52.8 cm2/h with σD = 1.6 cm2/h, where σ is the standard deviation of the log-transformed variable as used in Eqn 5. The coefficient of variation (CV) = (exp(σ2) – 1)0.5 for a log-normally distributed v and D is, respectively, 68% and 350%. These results for λ lie in the range 0.15–1.56, which was compiled by Jury (1985) based on data in the literature. The 95% confidence intervals for v and D in terms of the log-normal distribution were 0.69–0.94 cm/h and 12.2–93.5 cm2/h, respectively. The larger confidence interval for the latter parameter indicates that D could be less accurately determined from the BTC data.

|
Values for the ensemble mean CDE parameters, together with the standard deviation for the log-transformed values for each depth, are given in Table 3. The relatively higher values for σv in the top layer demonstrate the reduced variability in the solute transport process at greater depths, with mean parameter values almost identical at 0.6 m and 0.8 m. Mean values for the MIM parameters are also listed in Table 4; parameter values at 0.6 m and 0.8 m are also identical as was found for the CDE. The fraction of mobile water increased with depth to a value of ~0.40. Judging from the results in Tables 3 and 4, a somewhat more homogeneous transport process occurred in the deeper layers compared with the near-surface layer.

|

|
Field-scale transport
The mean solute concentrations were evaluated for the 14 soil columns whose solute application time was 79 h. As shown in Eqn 8, it is assumed that the mean BTCs can be regarded as an area-averaged BTC across the horizontal plane. The procedure presented here considered flow and transport phenomena related to scale transition in undisturbed soil under identical boundary conditions (saturated and vertical flow). Measured field-scale BTCs and their 95% confidence limits (based on Student’s t distribution), together with the stream-tube predictions, given by Eqn 4, for all depths are presented in Fig. 5. Parameter values presented in Table 3 were used for the STM at each depth. The correlation coefficient, ρv, D = 0.74, as shown in Fig. 3, was used for all depths. Widest confidence limits are found (largest variances, see also Fig. 5) before and after the peak in the BTC. Although the STM parameters were obtained from the fitted local-scale parameters, the predicted and observed <c> distribution agree relatively well. However, the STM failed to predict the early arrival of solute and resulted in lower concentration peaks and longer tails. This result is caused primarily by the fact that the CDE does not describe accurately enough local-scale transport as was demonstrated in Fig. 2. Because the STM assumes a constant velocity with depth, it becomes clear from the above discussions that heterogeneities in the vertical direction cause predictions at greater depths based on parameters estimated at shallow depths to underestimate or overestimate the true field-scale solute distribution. Therefore, no attempt was made to evaluate the STM in this respect.
In addition to the mean concentration, the variance can be used to characterise fluctuations in the local-scale concentration at a particular depth. The variance in terms of the STM with stochastic v and D may be given by (Bresler and Dagan 1981):
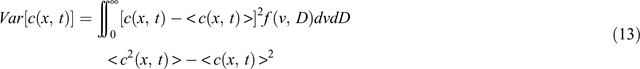
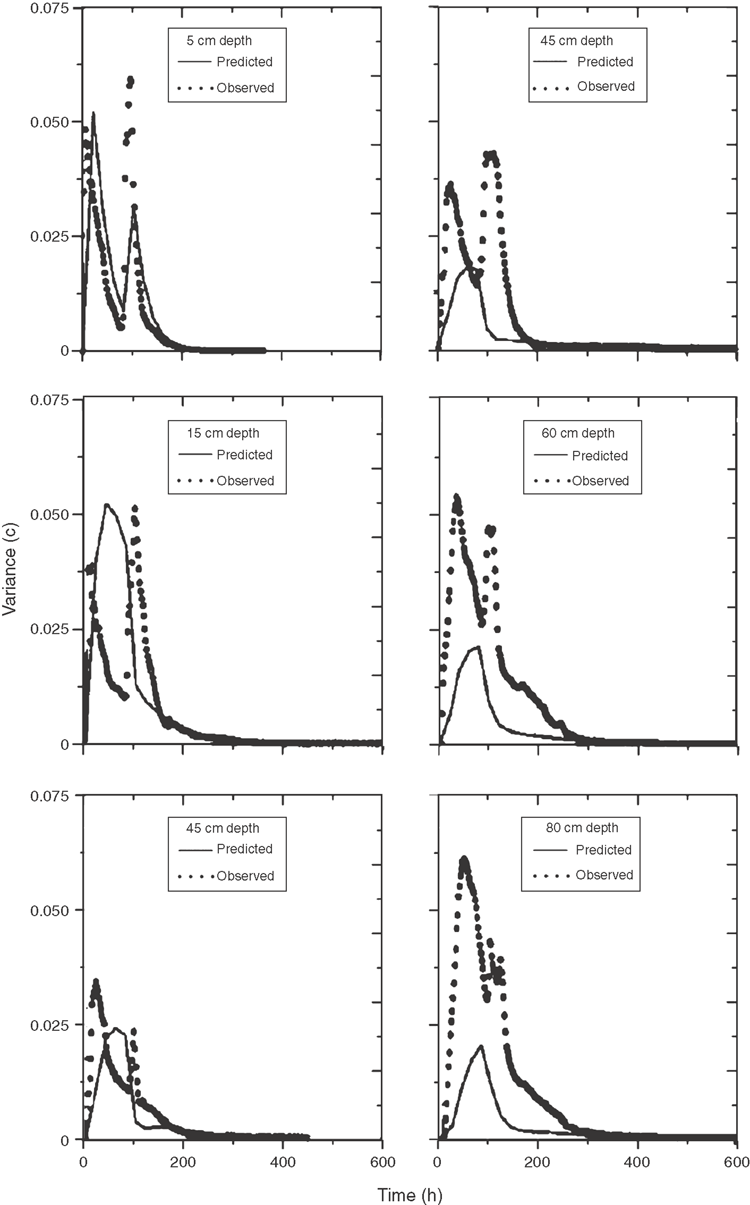
Field-scale variances were evaluated in a way similar to field-scale mean concentrations (Toride et al. 1995). The variance of the concentration characterises the degree of variation over the horizontal plane at a given depth x and time t. Figure 6 presents observed variances for 14 columns against time as well as predicted variances described with Eqn 13 using the same parameter values as in Fig. 5. Predicted and observed variances agree well at the first observation depth. Deeper in the profile, the predicted variance underestimates the observed variance and this difference increases with depth. The observed disparities at greater depths are probably the result of the relatively small number of observations used to calculate the transport parameter used in Eqn 5. Another reason is the observation that at greater depths the MIM is systematically better than the CDE model. In the calculation of the variances, a model was used that assumes the CDE is the governing local transport model. Because the CDE is not the best local-scale model, the variance estimations based on the CDE may explain in part the observed discrepancies.
Notice that the variance profile has a double peak with a relative minimum at the time peak concentration was observed. This bimodal behaviour for a pulse input was also demonstrated in a numerical study by Burr et al. (1994). At the time of the peak, the CV ranges from 8.9% at the first observation depth to 27% at x = 0.8 m. That is, relative variability in the local-scale peak concentrations are relatively small, and largest at the greatest observation depth. These small values of CV are the result of the relatively large solute application time. Continuous solute injection counteracted the horizontal concentration fluctuation caused by random solute transport and resulted in smaller variances (Toride and Leij 1996). The magnitude of the concentration variance itself only minimally decreases with increasing travel depth due to an increased mixing as the solute traverses through the medium.
Effect of the local-scale dispersion
Bresler and Dagan (1981) demonstrated that the effect of local-scale dispersion on field-scale transport is negligible compared with the effect of heterogeneous flow; most previous studies of stochastic transport have, therefore, neglected local-scale dispersion (Jury 1982; Destouni and Cvetkovic 1991). Toride and Leij (1996) discussed the STM using travel time moments. They concluded that the Peclet number, <v> x/<D> (= x/λ), in terms of the observation scale, x, is an index to determine whether or not local-scale dispersion can be neglected, while the effect of the standard deviation, σD, and the correlation coefficient, ρv, D, on solute spreading is relatively minor compared with the effect of <D>.
Bresler and Dagan (1981) assumed a local-scale dispersivity, λ, of 0.03 m. Their corresponding Peclet number was 26.7 at x = 0.8 m, whereas, as shown in Table 3, values for x/λ in our experiment are considerably smaller because of the large dispersion coefficient due to the mobile–immobile non-equilibrium effect. The following discussion demonstrates the effect of local-scale dispersion on field-scale mean transport using parameter values obtained at 0.8 m depth. At this depth, all heterogeneities are included in the BTCs.
First, comparison was made of the fitted BTC with the observed mean concentrations with two hypothetical cases: (1) a deterministic dispersion assuming σD = 0; (2) a constant dispersivity λ = <D>/<v> across the field, as shown in Eqn 10 assuming σD = σv, with a perfect positive correlation, ρv, D = 1. Figure 7 shows the mean BTCs at 0.8 m described with the STM using fitted and hypothetical parameter values. Fitted (case C) and hypothetical (case A and B) parameter values used in Fig. 7 are presented in Table 5. The observation that the predicted peak values are smaller than the mean observations indicates that the STM with parameters derived from a local-scale CDE model may not fully capture the extreme non-equilibrium effects observed in this soil.

|

|
The effect of σD and ρv, D on the mean solute concentration is almost negligible. In other words, the deterministic (σD = 0) and stochastic (σD = 0) dispersion process gave identical results. Similar results were found by Bresler and Dagan (1981), Amoozegar-Fard et al. (1982) and others, which also showed how little was the influence of fluctuations of local-scale dispersion on field-scale solute distribution. Hence, a constant dispersivity given by Eqn 10 is an acceptable simplification for practical applications of the STM model when little information is available on σD (Toride and Leij 1996).
In addition to σD and ρv, D, local-scale dispersion is often neglected for field-scale solute transport (e.g. Jury 1982; Destouni and Cvetkovic 1991). However, the relatively small Peclet numbers, <v>x/<D> = x/λ are around one for x > 0.05 m, as shown in Table 3, suggest that local-scale dispersion is important. We therefore evaluated the effect of <D> on the predicted field-scale BTC at 0.8 m depth assuming two additional hypothetical cases (case D and E in Table 5), whose local-scale dispersion is given by <D>/10 and <D>/100, respectively, where <D> is the fitted value. Figure 8 demonstrates that reduced dispersion leads to higher peaks and less spreading for relatively large <D>. Ignoring local-scale dispersion thus results in quite different field-scale solute distributions in cases where solute spreading is caused by physical non-equilibrium effects.

|
Conclusion
A transport experiment on 1-m-long undisturbed soil columns collected along a transect in the field was used to evaluate the stochastic representation of the CDE in terms of predicting field-scale transport. Local-scale transport parameters were obtained for the classical CDE model and alternatively for the non-equilibrium MIM transport model. The latter gave a better description of the observed early breakthrough and the tailing. The effective dispersion coefficient, Deff, in terms of the MIM model agreed relatively well at 0.8 m with D for the CDE. The assumption of the local equilibrium (LE) was nearly met as the travel distance approached the bottom of the column. Because of lateral solute mixing between mobile and immobile zones, estimated values for the CDE dispersion coefficient D were quite large.
Estimated transport parameters v and D varied significantly across the field with the coefficient of variation of 68% and 350%, respectively. A linear regression analysis between ln(v) and ln(D) resulted in D = 31v1.92 with a positive correlation of ρv, D = 0.74; the overall field-scale dispersivity value is 0.656 m. The exponent close to 2 indicates that intra-aggregate diffusion is the dominant mechanism compared with the hydrodynamic dispersion for the solute spreading. Values for σv decreased from 0.55–0.71 in the Ap horizon to 0.36–0.38 in the C2, indicating that flow and transport processes were more heterogeneous in the top horizon than the two deeper layers.
Field-scale transport was assumed to be described by averaging of the local scale BTCs. When field-scale mean transport was predicted by means of STM using transport parameters obtained from the local-scale BTC, the predicted BTC agreed relatively well with the observed BTC as a whole. However, peak concentrations were underestimated and the tails were overestimated.
A comparison between the measured and predicted concentration variances revealed that for the first observation depth, both agreed well. Deeper in the soil, the STM gave consistently smaller values for the standard deviation.
In order to demonstrate the effect of local-scale dispersion on field-scale transport, mean observed BTCs were compared with predicted BTCs assuming (1) deterministic dispersion (σD = 0), and (2) a constant dispersivity across the field (σD = σv and ρv, D = 1). The results showed that the contribution from local-scale dispersion to field-scale solute spreading was insignificant and suggest that solute spreading at the field-scale may be approximated using a heterogeneous flow field (stochastic v) and a constant dispersion coefficient <D>. However, values of <D> could not be ignored, as evidenced by the considerably larger concentration peaks and reduced spreading when 10 or 100 times smaller values of <D> were used in comparison with the mean fitted <D>. The large values of <D> correspond to small values of x/<λ> = <v> x/<D>. Using the latter index we demonstrated local-scale dispersion cannot be neglected where physical non-equilibrium dominates the transport process; this is often true for structured or macroporous soil such as these, where large values of the local-scale dispersion can be expected to have an important effect on field-scale solute spreading.
References
Amoozegar-Fard D, Nielsen DR, Warrick WW (1982) Soil solute concentration distributions for spatially varying pore-water velocities and apparent diffusion coefficients. Soil Science Society of America Journal 46, 3–9.| Soil solute concentration distributions for spatially varying pore-water velocities and apparent diffusion coefficients.Crossref | GoogleScholarGoogle Scholar |
Bear J (1972) ‘Dynamics of fluids in porous media.’ (Elsevier: New York)
Beven KJ, Henderson DE, Reeves AD (1993) Dispersion parameters for undisturbed partially saturated soil. Journal of Hydrology 143, 19–43.
| Dispersion parameters for undisturbed partially saturated soil.Crossref | GoogleScholarGoogle Scholar |
Biggar JW, Nielsen DR (1976) Spatial variability of the leaching characteristics of a field soil. Water Resources Research 12, 78–84.
| Spatial variability of the leaching characteristics of a field soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE28XhslyrtLg%3D&md5=99c62d8a880b63a84f8f09b3b5893c1bCAS |
Bowman RS, Rice RC (1986) Transport of conservative tracers in the field under intermittent flood irrigation. Water Resources Research 22, 1531–1536.
| Transport of conservative tracers in the field under intermittent flood irrigation.Crossref | GoogleScholarGoogle Scholar |
Bresler E, Dagan G (1981) Convective and pore scale dispersive solute transport in unsaturated heterogeneous fields. Water Resources Research 17, 1683–1693.
| Convective and pore scale dispersive solute transport in unsaturated heterogeneous fields.Crossref | GoogleScholarGoogle Scholar |
Brusseau M, Rohay VJ, Truex MJ (2010) Analysis of soil vapor extraction on data to evaluate mass-transfer constraints and estimate source-zone mass flux. Ground Water Monitoring and Remediation 30, 57–64.
| Analysis of soil vapor extraction on data to evaluate mass-transfer constraints and estimate source-zone mass flux.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhtFKqs7zJ&md5=0ceb5874e686c824cb4359eb712adea1CAS | 23516336PubMed |
Burr DT, Sudicky EA, Naff RL (1994) Nonreactive and reactive solute transport in three-dimensional heterogeneous porous media: Mean displacement, plume spreading, and uncertainty. Water Resources Research 30, 791–815.
| Nonreactive and reactive solute transport in three-dimensional heterogeneous porous media: Mean displacement, plume spreading, and uncertainty.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXisl2hu74%3D&md5=0f16933289e03247e97ec920e3ff0412CAS |
Butters GL, Jury WA, Ernst FF (1989) Field scale transport of bromide in an unsaturated soil. I. Experimental methodology and results. Water Resources Research 25, 1575–1581.
| Field scale transport of bromide in an unsaturated soil. I. Experimental methodology and results.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1MXlvFelsr4%3D&md5=1ffa51e35f90ecbe6236f6bbb185c5d8CAS |
Destouni G, Cvetkovic V (1991) The effect of heterogeneity on large scale solute transport in the unsaturated zone. Water Resources Research 27, 1315–1325.
| The effect of heterogeneity on large scale solute transport in the unsaturated zone.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXlvV2hu70%3D&md5=55dcebde4cf6e7f44a4bcf5dae10d00aCAS |
Dusek J, Gerke HH, Vogel T (2008) Surface boundary conditions in two-dimensional dual-permeability modeling of tile drain bromide leaching. Vadose Zone Journal 7, 1287–1301.
| Surface boundary conditions in two-dimensional dual-permeability modeling of tile drain bromide leaching.Crossref | GoogleScholarGoogle Scholar |
Dyson JS, White RE (1987) A comparison of the convection-dispersion equation and transfer function model for predicting chloride leaching through an undisturbed structured clay soil. Journal of Soil Science 38, 157–172.
| A comparison of the convection-dispersion equation and transfer function model for predicting chloride leaching through an undisturbed structured clay soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXkvFGrt74%3D&md5=f88f2321f82d0205bfb857b188edaf48CAS |
Ellsworth TR, Shouse PJ, Skaggs TH, Jobes JA, Fargerlund J (1996) Solute transport in unsaturated soil: Experimental design, parameter estimation, and model discrimination. Soil Science Society of America Journal 60, 397–407.
| Solute transport in unsaturated soil: Experimental design, parameter estimation, and model discrimination.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28Xitleqsrg%3D&md5=4018657ebe789f253f36ebbf2e0b892bCAS |
Forrer J, Kasteel R, Flury M, Flühler H (1999) Longitudinal and lateral dispersion in an unsaturated field soil. Water Resources Research 35, 3049–3060.
| Longitudinal and lateral dispersion in an unsaturated field soil.Crossref | GoogleScholarGoogle Scholar |
Gelhar LW (1993) ‘Stochastic subsurface hydrology.’ (Prentice Hall: Englewood Cliffs, NJ)
Ghodrati M (1999) Point measurement of solute transport processes in soil using fiber optic sensors. Soil Science Society of America Journal 63, 471–479.
| Point measurement of solute transport processes in soil using fiber optic sensors.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXks1ajtL4%3D&md5=e4442af0754611037f74bcb33ae32373CAS |
IUSS (2006) ‘IUSS Working Group WRB, 2006, World reference base for soil resources 2006.’ World Soil Resources Report No. 103. (FAO: Rome)
Jacques D, Kim DJ, Diels J, Vanderborght J, Vereecken H, Feyen J (1998) Analysis of steady state chloride transport through two heterogeneous field soils. Water Resources Research 34, 2539–2550.
| Analysis of steady state chloride transport through two heterogeneous field soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXmsF2lt7c%3D&md5=36a9edfb0fd876c0432a00d003282356CAS |
Jarvis NJ (2007) A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality. European Journal of Soil Science 58, 523–546.
| A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality.Crossref | GoogleScholarGoogle Scholar |
Jaynes DB, Bowman RS, Rice RC (1988) Transport of a conservative tracer in the field under continuous flood irrigation. Soil Science Society of America Journal 52, 618–624.
| Transport of a conservative tracer in the field under continuous flood irrigation.Crossref | GoogleScholarGoogle Scholar |
Jury WA (1982) Simulation of solute transport with a transfer function model. Water Resources Research 18, 363–368.
| Simulation of solute transport with a transfer function model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL38XitVCrtbc%3D&md5=7c3a91711afb7fc287cbee225af947a3CAS |
Jury WA (1985) Spatial variability of soil physical parameters in solute migration: A critical literature review. EA-4228 Project 2485-6. Electrical Power Research Institute, Riverside, CA.
Jury WA, Gardner WR, Gardner WH (1991) ‘Soil physics.’ 5th edn (John Wiley and Sons, Inc.)
Kachanoski RG, Pringle E, Ward A (1992) Field measurement of solute travel times using time domain reflectometry. Soil Science Society of America Journal 56, 47–52.
| Field measurement of solute travel times using time domain reflectometry.Crossref | GoogleScholarGoogle Scholar |
Knight JH (1992) Sensitivity of time domain reflectometry measurements to lateral variations in water contents. Water Resources Research 28, 2345–2352.
| Sensitivity of time domain reflectometry measurements to lateral variations in water contents.Crossref | GoogleScholarGoogle Scholar |
Köhne JM, Gerke HH (2005) Spatial and temporal dynamics of preferential bromide movement towards a tile drain. Vadose Zone Journal 4, 79–88.
| Spatial and temporal dynamics of preferential bromide movement towards a tile drain.Crossref | GoogleScholarGoogle Scholar |
Ledieu J, De Ridder P, DeClercq P, Dautrebande S (1986) A method of measuring soil moisture by time domain reflectometry. Journal of Hydrology 88, 319–328.
| A method of measuring soil moisture by time domain reflectometry.Crossref | GoogleScholarGoogle Scholar |
Mallants D, Vanclooster M, Meddahi M, Feyen J (1994) Estimating solute transport in undisturbed soil columns using time domain reflectometry. Journal of Contaminant Hydrology 17, 91–109.
| Estimating solute transport in undisturbed soil columns using time domain reflectometry.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXitlaiu7w%3D&md5=ec09a2e58d5fe3d9fb12658bea10fe71CAS |
Mallants D, Vanclooster M, Toride N, Vanderborght J, van Genuchten MTH, Feyen J (1996) Comparison of three methods to calibrate TDR for monitoring solute movement in undisturbed soils. Soil Science Society of America Journal 60, 747–754.
| Comparison of three methods to calibrate TDR for monitoring solute movement in undisturbed soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XjtFanu7w%3D&md5=0331acf19631e63c27ceb782fb1d8911CAS |
Mallants D, Mohanty BP, Vervoort A, Feyen J (1997) Spatial analysis of saturated hydraulic conductivity of a macroporous soil. Soil Technology 10, 115–131.
| Spatial analysis of saturated hydraulic conductivity of a macroporous soil.Crossref | GoogleScholarGoogle Scholar |
Mallants D, van Genuchten MTH, Simunek J, Jacques D, Seetharam S (2011) Leaching of contaminants to groundwater. In ‘Dealing with contaminated sites’. (Ed. F Swartjens) pp. 787–850. (Springer: Berlin)
Padilla IY, Yeh T, Jim C, Conklin MH (1999) The effect of water content on solute transport in unsaturated porous media. Water Resources Research 35, 3303–3313.
| The effect of water content on solute transport in unsaturated porous media.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXnsVWhs74%3D&md5=ee22a80b40db2f253aa128b75722e8c6CAS |
Parker JC, Valocchi AJ (1986) Constraints on the validity of equilibrium and first-order kinetic transport models in structured soils. Water Resources Research 22, 399–407.
| Constraints on the validity of equilibrium and first-order kinetic transport models in structured soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28XhslWqs74%3D&md5=bc821843a433d6013fac99ed6c924b21CAS |
Robinson BA, Chu S, Lu Z (2012) Simulation of radionuclide transport through unsaturated, fractured rock: Application to Yucca Mountain, Nevada. Vadose Zone Journal 11, 4
Roth K, Hammel K (1996) Transport of conservative chemical through an unsaturated two-dimensional Miller-similar medium with steady state flow. Water Resources Research 32, 1653–1663.
| Transport of conservative chemical through an unsaturated two-dimensional Miller-similar medium with steady state flow.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XjvV2gtL0%3D&md5=593c0e7dde66d4888331b6c193a070d8CAS |
Roth K, Jury WA, Flühler H, Aitinger W (1991) Transport of chloride through an unsaturated field soil. Water Resources Research 27, 2533–2541.
| Transport of chloride through an unsaturated field soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK38XitVejuw%3D%3D&md5=51109dd1e329f49bdcd150535c895326CAS |
Russo D, Jury WA, Butters GL (1989) Numerical analysis of solute transport during transient irrigation. 2. The effect of immobile water. Water Resources Research 25, 2119–2127.
| Numerical analysis of solute transport during transient irrigation. 2. The effect of immobile water.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXisVSis7s%3D&md5=1d786340b5b424c67521da81cbfc9e53CAS |
Saffman PG (1959) A theory of dispersion in a porous medium. Journal of Fluid Mechanics 6, 321–349.
| A theory of dispersion in a porous medium.Crossref | GoogleScholarGoogle Scholar |
Schulin R, van Genuchten MTH, Flühler H, Ferlin P (1987a) An experimental study of solute transport in a stony field soil. Water Resources Research 23, 1785–1794.
| An experimental study of solute transport in a stony field soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXmsVahsrk%3D&md5=e5fb0d1cedd6debe3cbd0c4ee21f598eCAS |
Schulin R, Wierenga PJ, Flühler H, Leuenberger J (1987b) Solute transport through a stony soil. Soil Science Society of America Journal 51, 36–42.
| Solute transport through a stony soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXhvFGgu7Y%3D&md5=cab0f563a9436aa4369bc8d15d82508eCAS |
Seuntjens P, Mallants D, Toride N, Cornelis C, Geuzens P (2001) Grid lysimeter study of steady-state chloride transport in two Spodosol types using TDR and wick samplers. Journal of Contaminant Hydrology 51, 13–39.
| Grid lysimeter study of steady-state chloride transport in two Spodosol types using TDR and wick samplers.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXlsFKis7k%3D&md5=192f1910ddfad4e4f4aa1a49ad61c73fCAS | 11530925PubMed |
Seuntjens P, Mallants D, Simunek J, Patyn J, Jacques D (2002) Sensitivity analysis of physical and chemical properties affecting field-scale cadmium transport in a heterogeneous soil profile. Journal of Hydrology 264, 185–200.
| Sensitivity analysis of physical and chemical properties affecting field-scale cadmium transport in a heterogeneous soil profile.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xot1ajs7k%3D&md5=b184880b004dbbf3b5b3d41a230b0fc5CAS |
Seyfried MS, Rao PSC (1987) Solute transport in undisturbed columns of an aggregated tropical soil: Preferential flow effects. Soil Science Society of America Journal 51, 1434–1444.
| Solute transport in undisturbed columns of an aggregated tropical soil: Preferential flow effects.Crossref | GoogleScholarGoogle Scholar |
Simmons CS (1982) A stochastic-convective transport representation of dispersion in one-dimensional porous media systems. Water Resources Research 27, 267–283.
Stauffer PH, Lu Z (2012) Quantifying transport uncertainty in unsaturated rock using Monte Carlo sampling of retention curves. Vadose Zone Journal 11,
| Quantifying transport uncertainty in unsaturated rock using Monte Carlo sampling of retention curves.Crossref | GoogleScholarGoogle Scholar |
Toride N, Leij FJ (1996) Convective-dispersive stream tube model for field-scale solute transport: I. Moment analysis. Soil Science Society of America Journal 60, 342–352.
| Convective-dispersive stream tube model for field-scale solute transport: I. Moment analysis.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28Xitleqsr4%3D&md5=ebf664916694f044e19d4642ccbba9e7CAS |
Toride N, Leij FJ, van Genuchten MTH (1995) The CXTFIT code for estimating transport parameters from laboratory and field tracer experiments. Research Report No. 137. U.S. Salinity Laboratory, Riverside, CA.
Tseng PH, Jury WA (1994) Comparison of transfer function and deterministic modelling of area-averaged solute transport in a heterogeneous field. Water Resources Research 30, 2051–2063.
| Comparison of transfer function and deterministic modelling of area-averaged solute transport in a heterogeneous field.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXmtFagsLY%3D&md5=42ba8622709725d201a26940f04f98bcCAS |
Valocchi AJ (1985) Validity of the local equilibrium assumption for modeling sorbing solute transport through homogeneous soils. Water Resources Research 21, 808–820.
| Validity of the local equilibrium assumption for modeling sorbing solute transport through homogeneous soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXlsVKktbk%3D&md5=8406bde193918988284719906753514cCAS |
van Genuchten MTH, Dalton FN (1986) Models for simulating salt movement in aggregated field soils. Geoderma 38, 165–183.
| Models for simulating salt movement in aggregated field soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28XlvFSjsrc%3D&md5=6d4f5f230678bd52592c8b195ac4eeccCAS |
Van Ommen HC, Dijksma R, Hendrickx JMH, Dekker LW, Hulshof J, van den Heuvel M (1989) Experimental assessment of preferential flow paths in a field soil. Journal of Hydrology 105, 253–262.
| Experimental assessment of preferential flow paths in a field soil.Crossref | GoogleScholarGoogle Scholar |
Van Wesenbeeck IJ, Kackanoski RG (1991) Spatial scale dependence of in situ solute transport. Soil Science Society of America Journal 55, 3–7.
| Spatial scale dependence of in situ solute transport.Crossref | GoogleScholarGoogle Scholar |
Vanclooster M, Mallants D, Diels J, Feyen J (1993) Determining local-scale solute transport parameters using time domain reflectometry. Journal of Hydrology 148, 93–107.
| Determining local-scale solute transport parameters using time domain reflectometry.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXhslaktLo%3D&md5=228b6f3169cdb88b5babd5aa63dca56eCAS |
Vanclooster M, Mallants D, Vanderborght J, Diels J, Van Orshoven J, Feyen J (1995) Monitoring solute transport in a multi-layered sandy lysimeter using time domain reflectometry. Soil Science Society of America Journal 59, 337–344.
| Monitoring solute transport in a multi-layered sandy lysimeter using time domain reflectometry.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXlt12qurg%3D&md5=8d86b99700efd745a0147f2e33d033ccCAS |
Vanderborght J, Vereecken H (2007) Review of dispersivities for transport modelling in soils. Vadose Zone Journal 6, 29–52.
| Review of dispersivities for transport modelling in soils.Crossref | GoogleScholarGoogle Scholar |
Vanderborght J, Mallants D, Feyen J (1998) Solute transport in a heterogeneous soil for boundary and initial conditions: evaluation of first-order approximations. Water Resources Research 34, 3255–3270.
| Solute transport in a heterogeneous soil for boundary and initial conditions: evaluation of first-order approximations.Crossref | GoogleScholarGoogle Scholar |
Vanderborght J, Vanclooster M, Timmerman A, Seuntjens P, Mallants D, Kim D-J, Jacques D, Hubrechts L, Gonzales C, Feyen J, Diels J, Deckers J (2001) Overview of inert tracer experiments in key Belgian soil types: Relation between transport and soil morphological and hydraulic properties. Water Resources Research 37, 2873–2888.
| Overview of inert tracer experiments in key Belgian soil types: Relation between transport and soil morphological and hydraulic properties.Crossref | GoogleScholarGoogle Scholar |
Vogel HJ, Roth K (2003) Moving through scales of flow and transport in soil. Journal of Hydrology 272, 95–106.
| Moving through scales of flow and transport in soil.Crossref | GoogleScholarGoogle Scholar |
Ward AL, Kachanoski RG, Elrick DE (1994) Laboratory measurements of solute transport using time domain reflectometry. Soil Science Society of America Journal 58, 1031–1039.
| Laboratory measurements of solute transport using time domain reflectometry.Crossref | GoogleScholarGoogle Scholar |
Ward AL, Kachanoski RG, von Bertoldi AP, Elrick DE (1995) Field and undisturbed-column measurements for predicting transport in unsaturated layered soil. Soil Science Society of America Journal 59, 52–59.
| Field and undisturbed-column measurements for predicting transport in unsaturated layered soil.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXjtlelsb8%3D&md5=b10015df4f4dc8724f9730a0d7733c48CAS |
Wraith JM, Comfort SD, Woodbury BL, Inskeep VP (1993) A simplified waveform analysis approach for monitoring solute transport using time-domain reflectometry. Soil Science Society of America Journal 57, 637–642.
| A simplified waveform analysis approach for monitoring solute transport using time-domain reflectometry.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXhtVGkt74%3D&md5=4602b73f79e995f3926b6427b9714b16CAS |
Zehe E, Flühler H (2001) Preferential transport of isoproturon at a plot scale and a field-scale tile-drained site. Journal of Hydrology 247, 100–115.
| Preferential transport of isoproturon at a plot scale and a field-scale tile-drained site.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXkvFartbc%3D&md5=19f2c489fe50f8b927c45444284b7922CAS |
Zhang ZF, Zhong L, White MD, Szecsody JE (2012) Experimental investigation of the eff effective foam viscosity in unsaturated porous media. Vadose Zone Journal 11,
| Experimental investigation of the eff effective foam viscosity in unsaturated porous media.Crossref | GoogleScholarGoogle Scholar |


 where
where  is the mean of yobs
is the mean of yobs