Popper and phylogenetics, a misguided rendezvous
Lars VogtInstitut für Evolutionsbiologie und Ökologie, Universität Bonn, An der Immenburg 1, D-53121 Bonn, Germany. Email: lars.m.vogt@gmail.com
Australian Systematic Botany 27(2) 85-94 https://doi.org/10.1071/SB14025
Submitted: 14 August 2014 Accepted: 14 August 2014 Published: 6 October 2014
Journal Compilation © CSIRO Publishing 2014 Open Access CC BY-NC-ND
Abstract
Popper’s falsificationism is frequently referred to as a general normative reference system in phylogenetics. Referring to falsificationism, phylogeneticists have made four central claims, including that frequency probabilities (1) cannot be used for inferring degrees of corroboration and (2) cannot be used in phylogenetics because phylogeny is a unique process, (3) likelihood methods represent verificationist approaches, and (4) the congruence test is a Popperian test. However, these claims are inconsistent with Popper’s theory. Moreover, phylogeneticists have proposed four strategies for dealing with the unfalsifiability of cladograms, including (1) interpreting re-interpretations of putative synapomorphy as homoplasy as Popperian ad hoc manoeuvres, (2) decoupling corroboration from falsification, (3) interpreting the tree with the highest likelihood as the most corroborated tree, and (4) interpreting tree hypotheses as Popperian probabilistic hypotheses that do not have to be falsifiable. These strategies are also inconsistent with Popper’s theory. Four fundamental problems and a problem with Popper’s formula for measuring degree of corroboration demonstrate that Popper’s theory does not live up to its own claims. Moreover, neither historical nor experimental sciences can be conducted in a way that is consistent with the principles of falsificationism. Therefore, phylogeneticists should stop referring to falsificationism when defending a specific methodological position.
Additional keywords: corroboration, falsificationism, likelihood, parsimony, testability.
Adventurous interpretations of Popperian falsificationism in phylogenetics
‘The trouble about people – uncritical people – who hold a theory is that they are inclined to take everything as supporting or ‘verifying’ it, and nothing as refuting it […] The proper counsel to the scientist is that he will always hold, consciously or unconsciously, a host of theories and that he is well advised to adopt a critical attitude towards them’ [Popper 1983, p. 233]
In the past, biologists repeatedly referred to Popper’s falsificationism to justify specific methodological and theoretical positions, including the superiority of phylogenetic systematics over evolutionary classification, and vice versa (e.g. Bock 1973; Wiley 1975; Kitts 1977; Cracraft 1978; Platnick and Gaffney 1978), and the superiority of parsimony over likelihood or Bayesian inference, and vice versa (e.g. Farris 1983, 2013; Kluge 1997a; Siddall and Kluge 1997; Faith and Trueman 2001; de Queiroz and Poe 2001; Helfenbein and DeSalle 2005; Randle and Pickett 2010). So as to adjust Popper’s theory to the needs and demands of phylogenetics, some phylogeneticists came up with more or less adventurous interpretations of his theory, which frequently disagreed with some of its core ideas.
Proponents of parsimony, for instance, have favoured parsimony over likelihood methods of numerical tree inference and argued in reference to falsificationism that statistical approaches, as for instance maximum likelihood, are inconsistent with falsificationism and that maximum parsimony represents the only known method of numerical tree inference that is ‘scientific’ in the Popperian sense. They have made the following four distinct claims (see also Vogt 2007):
-
Using frequency probabilities for inferring degrees of corroboration from the congruence test is inconsistent with falsificationism (Kluge 1997a, 1997b; Siddall and Kluge 1997; Farris 2000).
-
Frequency probabilities cannot be used for methods of tree reconstruction, because they require statistical reference classes, which are by definition general, and phylogeny is a unique process (Kluge 1997a, 1997b, 2002; Siddall and Kluge 1997; Grant and Kluge 2003).
-
When applied in phylogenetics, likelihood is a verificationist approach (Kluge 1997a, 1997b; Siddall and Kluge 1997).
-
The congruence-test tests tree hypotheses against observational evidence and is the most important Popperian test in phylogenetics, with the minimum-step tree representing the most corroborated tree (Kluge 1997a, 2002; Farris et al. 2001; Grant and Kluge 2003).
Interestingly, proponents of likelihood have countered these arguments explicitly in reference to falsificationsm and defended the statistical approach to numerical tree inference (Faith 1992, 1999; Faith and Trueman 2001; de Queiroz and Poe 2001, 2003). Whereas the persistency with which such contradicting positions are justified in reference to the same theoretical framework may astonish, it is at least safe to say that at the turn of the millennium Popper’s theory has taken the stage as the general normative reference system for epistemological and methodological questions in phylogenetics, although, obviously leaving much open to interpretation.
Accepting the role of falsificationism as a normative reference system for the sake of the argument, I have questioned the four claims of the proponents of parsimony and with them also the conclusion that parsimony would represent the only method of numerical tree inference that is truly ‘scientific’, because it would be the only one that is consistent with falsificationism, leaving the question of which method of numerical tree inference is the best open to empirical investigations rather than purely theoretical or epistemological considerations (Vogt 2007, 2008).
Claim I: frequency probabilities cannot be used for inferring degrees of corroboration
The first claim relates to the role of Popper’s concept of logical probabilities in his theory of falsificationism and his formula for degree of corroboration (see Eqn 1, further below). Some proponents of likelihood have argued that the probability terms in this formula refer to frequency probabilities (e.g. de Queiroz and Poe 2001), whereas some proponents of parsimony have claimed that they are logical probabilities and thus frequency probabilities may not be used for measuring degrees of corroboration (e.g. Siddall and Kluge 1997).
In this context, it is very important to distinguish between corroborability and degree of corroboration. According to Popper, the degree of corroborability or testability of a hypothesis equals its logical improbability (e.g. Popper 2005, p. 128), which is not equal to the actual degree of corroboration a hypothesis gains when successfully passing an empirical test, because corroborability indicates the highest possible degree of corroboration, describing the potential for corroboration and not the current status of corroboration of a hypothesis (Vogt 2007). Moreover, Popper himself noted that the probability terms of the formula can be interpreted in various ways, as long as they satisfy the mathematical calculus of probability (Popper 1983, p. 282), thus rendering the claim of the proponents of parsimony to limit them to logical probabilities an illegitimate reduction of Popper’s concept of corroboration (see also Vogt 2007).
Claim II: frequency probabilities cannot be used in phylogenetics because phylogeny is a unique process
The second claim confuses ontological with epistemological considerations. From a purely ontological point of view, one can rightfully claim that the frequency of a particular transformation process that already has occurred necessarily equals one. However, because of the possibility of parallel evolution, reductions and ‘overwriting’ subsequent transformations, we know that observable identity does not necessarily equal historical identity and distribution patterns of character states do not directly indicate monophyletic groups of species. Thus, whereas from a purely ontological point of view we believe that there is only one true phylogeny, talking about a specific phylogeny will always be a metaphysical statement, because we do not know the actual phylogenetic history (Vogt 2007). Therefore, we are talking about hypotheses about the true tree, and because we cannot infer the actual phylogenetic history, we are confined to inferring all possible histories and evaluate them against all relevant evidence, so as to be able to make a justified choice of the presently best corroborated hypothesis. Translated to the terminology of falsificationism, this means that it is likely that the amount of effectively accredited falsifiers of any given hypothesis of monophyly is significantly lower than the amount of its overall logical falsifiers and that this difference directly depends on the frequency of transformation processes that lead to structurally indistinguishable character states. The less frequent and thus the more improbable a set of processes that result in indistinguishable character states, the higher the evidential weight of the respective character state (see Vogt 2002, 2007).
In phylogenetics, we do not want to evaluate the propensity of the occurrence of a process that transforms one structure into another structure sometime in the future, nor do we want to give a prediction of future phylogenetic events or evaluate the process probability of single transformation events. We do want to evaluate, however, how good our reconstruction of past transformation events is, given the traces that phylogeny left behind. Consequently, it is reasonable to evaluate how often specific types of transformation processes may have occurred that potentially result in the same type of structure (especially with sequence data), and because types of processes do not represent particular processes, it is also reasonable to apply statistical methods and process frequencies to evaluate the diagnostic power of a particular character-state distribution (Vogt 2007). Therefore, from the three interpretations of the calculus of probability that Popper discussed for his formula of degree of corroboration (i.e. propensity, logical probability, frequency probability), only frequency probabilities can be reasonably applied in a phylogenetic framework (for a more detailed discussion see Vogt 2007).
Claim III: likelihood methods in phylogenetics represent verificationist approaches
The third claim, that likelihood methods in phylogenetics represent verificationist approaches, has already been countered by de Queiroz and Poe (2001), who pointed out that Fisher’s (1922) likelihood term p(e,hb) does not assign probabilities to hypotheses, but measures the probability of the evidence given the hypothesis. Therefore, it cannot be a measure of the probability of truth of the hypothesis and thus, does not represent a verificationist approach (see also Vogt 2007).
Claim IV: the congruence test is a Popperian test and the minimum-step tree is the most corroborated tree
The fourth claim, assuming that the congruence test is a Popperian test of phylogenetic tree hypotheses, is insofar misguided, as there exists no deductive and thus falsifiable link between the evidence of a character-state distribution and a given tree hypothesis in the congruence test, because with descent with modification as background knowledge, any character-state distribution can be explained by common ancestry (i.e. apomorphy) and independent evolution (i.e. homoplasy) alike, none of which necessarily contradicts any given tree hypothesis (Vogt 2008). The congruence test effectively accredits no potential falsifiers, because one cannot deduce a specific character-state distribution that is literally impossible to observe in case the tree hypothesis and the background knowledge were true – a given tree, in combination with descent with modification as background knowledge, does not prohibit any specific character-state distribution (Vogt 2008). As a consequence, and this is independent of the distinction of naïve ‘strict falsification’ and ‘methodological’ or ‘sophisticated falsification’, cladograms are not falsifiable in principle and thus not testable in a Popperian sense (for a detailed discussion see Vogt 2008; see also Hull 1983; Sober 1983; Rieppel 2003; contradicting Bock 1973; Cracraft 1978; Farris 1983, 2000; Kluge 1997a, 1997b, 2003; Farris et al. 2001).
Moreover, it is important to note that instead of being based on a deductive link between tree and character-state distributions, the congruence test is based on the deductive necessity that the distribution patterns of character states across OTUs must not overlap, indicating that congruence is testing sets of hypotheses of apomorphy instead of hypotheses of monophyly (i.e. tree hypotheses) – it would be logically circular to deduce from the congruence test the possibility to falsify specific hypotheses of monophyly, because a key presupposition of the congruence test is the a priori assumption that overlapping sets of monophyly are prohibited (Vogt 2002, 2008). Because the congruence test does not allow deductively identifying homoplasies (i.e. false apomorphies), the congruence test tests only whether all apomorphy hypotheses included in the test have been falsified as a set (for a detailed discussion see Vogt 2008).
Four strategies to save Popper for phylogenetics
If cladograms are unfalsifiable, their degree of testability and, therefore, also their degree of corroborability is necessarily zero in a Popperian framework. In other words, according to Popperian falsificationism, cladograms would possess no explanatory power and would thus not represent ‘scientific’ hypotheses. Although some phylogeneticists agreed with the lack of a deductive link between observations and tree hypotheses, they nevertheless wanted to provide a rational criterion for the choice of a presently preferred cladogram that is consistent with Popper’s falsificationism and therefore ‘re-interpreted’ Popper’s theory to meet their demands. Four different strategies of re-interpretation have been proposed (see also Vogt 2008).
Strategy I: re-interpreting putative synapomorphies as homoplasies represents a Popperian ad hoc manoeuvre
The first strategy shifts the attention from the condition of corroborability (= testability = falsifiability) to Popper’s methodological convention of renouncing all ad hoc manoeuvres, which is independent of Popper’s theory of falsification and corroboration. Some proponents of parsimony claimed that the congruence test would minimise ad hoc hypotheses of homoplasy, which rests on the assumption that any requirement of re-interpretation of putative synapomorphies as homoplasies because of incongruence with other putative synapomorphies would represent what Popper called an ad hoc manoeuvre (Farris 1983, 2000; Kluge 1997a, 1997b, 2001, 2002).
Popper characterised ad hoc manoeuvres as only having the purpose to save hypotheses from falsification and that they should be avoided (Popper 1983, pp. 133ff, 232, 1994, pp. 16, 48ff, 105), and if avoiding them is not possible, only those should be accepted that do not decrease the falsifiability of the system (Popper 1994, p. 51). Some proponents of parsimony have argued that incongruent putative synapomorphies would count evidentially against the respective tree hypothesis and that, therefore, the tree that inflicts the least amount of homoplasies would be the most corroborated tree, which is also the most parsimonious tree (e.g. Farris 1983, 2000; Kluge 1997a, 1997b, 2001, 2002). This conclusion is insofar problematic, with even Popper noting that his claim to renounce ad hoc manoeuvres represents a methodological convention that is independent of his concepts of falsification and corroboration and that only the degree of corroboration provides a measure for the acceptability of a hypothesis (Popper 1983, pp. 133ff, 232, 1994, pp. 16, 48ff, 105). In other words, one cannot justify the choice of the best tree hypothesis on grounds of minimising the number of ad hoc manoeuvres it implies (Vogt 2007).
Even more problematic, however, is the fact that the re-interpretation of putative synapomorphies as homoplasies does not qualify as a Popperian ad hoc manoeuvre, because the background knowledge of descent with modification already covers the two alternative explanations (i.e. apomorphy v. homoplasy) for the empirical phenomenon of indistinguishable traits between representatives of different species. The possibility of homoplasies is known prior to numerical tree inference and is a necessary consequence of the background knowledge. Therefore, hypotheses of homoplasy cannot represent Popperian ad hoc hypotheses, because they are not conceived after falsification takes place. Moreover, the ad hoc re-interpretation of a putative synapomorphy as a homoplasy in case of the falsification of a set of apomorphy hypotheses during the congruence test (see Claim IV) does not save the tested set of hypotheses, because the set remains to be falsified as a set, no matter how many putative synapomorphies are subsequently re-interpreted as homoplasies (for detailed discussion see Vogt 2008).
Strategy II: decoupling corroboration from falsification
The second strategy suggests to decouple corroboration from falsification and to take some degree of goodness-of-fit as the relevant evidence for tree hypothesis testing. Some proponents of the likelihood method suggested that the degree of corroboration of a tree hypothesis is primarily indicated by the improbability of data as fit-as-evidence, rather than by how well the hypothesis stood against attempts to falsify it (Faith 1992, 1999, 2004, 2006; Faith and Cranston 1992; Faith and Trueman 2001). In other words, not character-state distributions but goodness-of-fit serves as the evidence in a phylogenetic Popperian test, and instead of emphasising falsification, degree of corroboration is interpreted to depend on the improbability of evidence in the absence of the hypothesis, that is p(e,b) – the improbability of goodness-of-fit as evidence would significantly contribute to the corroboration of tree hypotheses (Faith 2004).
Unfortunately, Popper’s theory does not allow for decoupling falsification and falsifiability from corroboration and testability (see Vogt 2008), because Popper (1983, e.g. p. 231) closely related degree of corroboration to testability. According to Popper, corroborability is inversely proportional to absolute logical probability and equals testability, which equals empirical content, which is measured by the amount of potential falsifiers of the hypothesis and thus by its degree of falsifiability (Popper 1983, p. 245, 1994, pp. 84, 87). As a consequence, if a hypothesis is not falsifiable, it has no corroborability either, and corroboration cannot be decoupled from falsification (for a detailed discussion see Vogt 2008).
Strategy III: the tree with the highest likelihood is the most corroborated tree
The third strategy has been suggested by proponents of likelihood, who claimed that likelihood is not only consistent with Popper’s theory of corroboration, but that it represents its foundation, suggesting that the tree with the highest likelihood is also the most corroborated tree (de Queiroz and Poe 2001, 2003). So as to point out the connection between corroboration and Fisher’s (1922) likelihood term p(e,hb), Farris (2014) referred to Popper’s formula for the degree of corroboration C(h,e,b) of a hypothesis h by evidence e in the presence of some background knowledge b (e.g. Popper 1983, p. 240), as follows:

Farris argued that according to this formula ‘for given e and b, C increases monotonically with p(e,hb)’, that ‘the best corroborated tree is indeed the maximum likelihood tree – even though C itself is not a probability’, and that ‘in view of Popper’s formula for C, trees’ likelihoods correspond to degrees of corroboration’ (Farris 2014).
However, assuming a direct correspondence between likelihood values and degrees of corroboration is rather problematic. Popper himself seems to take a different position in this respect, as follows: ‘Thus we have proved that the identification of degree of corroboration or confirmation with probability (and even with likelihood) is absurd on both formal and intuitive grounds: it leads to self-contradiction’ (Popper 2005, p. 407).
Assuming that Farris’ claim is nonetheless correct, we would have to conclude that characters provide no significant support to phylogenetic tree hypotheses, because Popper claims that the ‘support given by e to h becomes significant only when… p(e,hb) – p(e,b) >> 1/2’ (Popper 1983, p. 240). Transferred to likelihood analyses in phylogenetics, the likelihood values obtained would have to be larger than 0.5 to provide significant support for a tree. Typical likelihood values obtained in phylogenetic analyses, however, are very small and are usually expressed as ln(L). They commonly range between –20 000 and –50 000 and are thus insignificant (for orientation: ln(0.5) is approximately –0.69, ln(0.00001) approximately –11.51).
Strategy IV: tree hypotheses are Popperian probabilistic hypotheses and, therefore, do not have to be falsifiable
Farris (2014) asserted that in likelihood methods phylogenetic tree hypotheses together with background models provide probability distributions and, therefore, represent Popperian probabilistic hypotheses, because otherwise trees could not assign likelihood values to evidence.
By referring to Popper’s treatment of probabilistic hypotheses, Farris redirected the discourse to a rather difficult subject, because the probability calculus itself is just a list of mathematical rules for calculating, with probabilities that can be interpreted in various ways. Popper distinguished the following two basic categories of interpretations: (1) objective interpretations that assume that the probability of a certain event ‘depends solely upon physical or similar conditions, and not upon the state of our knowledge’ and (2) subjective interpretations that ‘interpret the probability […] as being dependent upon the state of our (subjective) knowledge, or perhaps upon the state of our beliefs’ (Popper 1983, p. 288). Needless to say that Popper claimed that in science, probabilities must be interpreted objectively (Popper 2005, app. IX).
However, Popper himself obviously had problems with finding an adequate objective interpretation for his theory (Schroeder-Heister 1998). In his first edition of Logik der Forschung from 1935, the chapter about probabilities represents by far the longest chapter, and together with Supplements II, III and IV, which also discuss the concept of probability, it accounts for more than a quarter of the complete volume. Unfortunately, especially the passages in which Popper introduces and discusses his theory of statistical frequencies (in German: Häufigkeitswahrscheinlichkeit) seem to be provisional and incomplete (Schroeder-Heister 1998). This provisional character was not adjusted until the English edition of The Logic of Scientific Discovery (Popper 2005) was published, in which numerous footnotes and supplements were added that provide the necessary clarity.
By then, however, Popper also seemed to have realised that his initial frequency interpretation (a.k.a., statistical interpretation) of the probability calculus was flawed and that it had to be replaced by a propensity interpretation. The frequency interpretation explains a singular probability statement (e.g. ‘there is a probability of 1/6 that the next die roll will be a 6’) as merely formally singular (Popper 2005, section 71) and actually treats it as an element of a sequence of events with a relative frequency. Whereas the propensity interpretation, ‘attaches a probability to a single event as a representative of a virtual or conceivable sequence of events, rather than as an element of an actual sequence. It attaches to the event a a probability p(a,b) by considering the conditions which would define this virtual sequence: these are the conditions b, the conditions that produce the hidden propensity, and that give the single case a certain numerical probability. Only if we wish to test the ascribed numerical probability we shall have to realize a segment of the virtual sequence long enough to make it possible for us to apply to it a significant statistical test’ (Popper 1983, p. 287).
Thus, according to Popper, a probabilistic hypothesis hprob is described as the probability p of event a under conditions b that has the probability value r, as follows:

How is all this related to phylogenetics? Farris (2014) claimed that phylogenetic tree hypotheses do not have to be deductively falsifiable because they are Popperian probabilistic hypotheses. A phylogenetic tree hypothesis would thus be a hypothesis about a specific propensity of a certain event to occur under a defined set of conditions, comparable in its logical form to hypotheses such as ‘the probability of obtaining tail or head with the next tossing of this specific coin is 1/2’ (e.g. Popper 2005, section 50) or ‘the probability of throwing a five with the next throw of this specific die is 1/6’ (e.g. Popper 2005, section 71). If Farris is right, however, phylogenetic tree hypotheses must meet the defining criteria of Popperian probabilistic hypotheses (Eqn 2). As a consequence, a phylogenetic tree must entail more than just a tree topology, branch lengths and the phylogenetic relationships of operational taxonomic units, because all this information describes only an event a (= phylogeny), but not the conditions b and the probability value r for this event a to occur. Thus, b and r in Eqn 2 must be specified as well, to meet Popper’s definition for probabilistic hypotheses.
Farris (2014) argued that ‘if trees (together with background models) did not provide probability distributions, they could hardly assign probabilities p(e,hb) to evidence’. Maybe Farris took background models and thus stochastic models of evolution, like they are used in likelihood analyses, as the conditions b for his notion of probabilistic tree hypotheses. Then, these models would have to be considered to be entailed in phylogenetic tree hypotheses as well. However, it remains unclear which specific probability value r is tested in such a setting when conducting a likelihood analysis. Because, according to Popper, this r has to be tested by repeating the conditions b to obtain a sequence of events e1, e2, e3,…, ei from which we can extrapolate whether the propensity or frequency value r has been refuted or corroborated. Farris (2014) explicitly pointed out that r cannot be a certain likelihood value: ‘…likelihood values themselves are not the hypotheses tested, but then no competent theorist has ever supposed they were’ (Farris 2014, p. 6).
Unfortunately, Farris failed to specify the nature of r, and therewith the most central component of a Popperian probabilistic hypothesis. No later than when Farris referred to Popper’s formula for Eqn 1, it should have been obvious to him that when dealing with probabilistic hypotheses, one has to keep in mind that the h in Eqn 1 would have to take the form of hprob and, thus, ‘p(a,b) = r’. If phylogenetic tree hypotheses would represent probabilistic hypotheses sensu Popper, not only each tree itself would have to be tested, but the entire expression of Eqn 2, which would require the specification of r.
Anyhow, phylogenetic tree hypotheses cannot represent Popperian probabilistic hypotheses for several reasons, including the following:
-
Tree hypotheses do not specify any intrinsic propensity for a specific event or a sequence of events (= phylogeny) to occur. The probability of a tree is either 1 or 0, because it describes a singular event, which is the phylogeny of the respective operational taxonomic units, that either has taken place (p(a,b) = 1) or not (p(a,b) = 0). Phylogenetic analyses are not interested in testing the hypothesis that a particular phylogeny could be repeated with a probability of r if we could turn back time, although this indeed would represent a Popperian probabilistic hypothesis (‘What is the probability of Drosophila to evolve a second time if we could repeat evolution?’). In a likelihood analysis, we also do not repeat phylogeny several times, so as to use the resulting frequencies for testing a specific propensity of phylogeny.
-
Even if we would conceive phylogeny as a particular sequence of singular events, a phylogenetic tree hypothesis would still not represent a probabilistic hypothesis, because in phylogenetics, the particular sequence of singular events is essential, not the frequency of different event classes (e.g. what is the frequency or propensity of speciation events compared with insertion events?).
-
That trees together with evolutionary models can be used to calculate likelihood values (Farris 2014) is neither a surprise nor an argument supporting the probabilistic nature of tree hypotheses. Being able to assign probabilities to hypotheses does not make them probabilistic. Popper (2005, Suppl. 9) himself pointed out that statistical methods can be used for testing causal hypotheses (= non-probabilistic hypotheses) without turning the latter into probabilistic hypotheses. Anyhow, if Farris’ argument would be correct, it would have rather absurd consequences: Popper’s measure of degree of corroboration (Eqn 1) would be inapplicable to causal hypotheses, because Eqn 1 does require the assigning of probabilities p(e,hb) to evidence, which, according to Farris’ argument, can only be assigned if h is a probabilistic hypothesis.
The only hypotheses in likelihood analyses that somewhat resemble Popperian probabilistic hypotheses are the stochastic models of evolution themselves – not the tree hypotheses as such. The models specify one or more parameters that resemble probability values for certain events (e.g. a certain class of nucleotide substitutions) to occur. These parameters, thus, represent the r in Eqn 2, whereas a given tree with given branch lengths and a given character-state distribution at the nodes represents an event a, and the implicit assumptions for the applicability of the likelihood approach the conditions b. However, actual likelihood analyses do not test the parameters of an evolutionary model. If at all, the parameters are tested during a model test. This test, however, can hardly be called a Popperian test, as it tests different models against each other after estimating their model parameters from a given character matrix. This estimation represents an inductive step during which probability parameters are estimated and generalised from a limited set of data points. Because Popper’s falsificationism aims at excluding any inductive element (see below), model tests cannot be called Popperian tests.
Therefore, to sum it up, everything speaks against the interpretation of phylogenetic tree hypotheses as Popperian probabilistic hypotheses – at least if this interpretation should be based on Popper’s falsificationism.
Not only is the part about tree hypotheses being Popperian probabilistic hypotheses problematic about Farris’ claim. Although Farris (2014) admitted that the likelihood values obtained in likelihood analyses are not the hypotheses being tested, he nonetheless claimed that tree hypotheses do not have to be deductively falsifiable. Farris (2014) argued that ‘if trees cannot be logically (deductively) falsified, that scarcely matters. Probabilistic hypotheses are not supposed to be deductively falsifiable anyway’ (Farris 2014, p. 6). In other words, by claiming that phylogenetic tree hypotheses represent Popperian probabilistic hypotheses, Farris argued that they would not have to be falsifiable in the first place and could be analysed in a Popperian framework using the likelihood approach. Even if we assume that tree hypotheses were Popperian probabilistic hypotheses, Farris’ conclusion still is problematic and oversimplifies the issue.
At first glance, Farris seems to be right; according to Popper ‘[p]robability hypotheses do not rule out anything observable; probability estimates cannot contradict, or be contradicted by, a basic statement; nor can they be contradicted by a conjunction of any finite number of basic statements; and accordingly not by any finite number of observations either’ (Popper 2005, p. 181). Only an infinite conjunction of basic statements could falsify a probability hypothesis. This is because of the fact that any finite sequence of observations can be the product of accident, and, as such, it could represent the beginning section of a random infinite sequence that could possess any frequency limit value possible. Because we can perform only finitely many observations, every probabilistic hypothesis is therefore logically compatible with any observation sequence (Schroeder-Heister 1998). Consequently, because the dimension of a hypothesis is inversely proportional to its empirical content, probability hypotheses would have no empirical content.
As Farris (2014) pointed out himself, however, Popper asserted that a physicist ‘is usually quite well able to decide whether he ought to reject [some particular probability hypothesis] as “empirically confirmed”, or whether he ought to reject it as “practically falsified”, i.e., as useless for purposes of prediction’ (Popper 2005, p. 182). Farris, however, left unmentioned Popper’s conclusion, as Popper continued in the immediately following sentence that ‘[i]t is fairly clear that this “practical falsification” can be obtained only through a methodological decision to regard highly improbable events as ruled out – as prohibited. But with what right can they be so regarded? Where are we to draw the line? Where does this ‘high improbability’ begin?’ (Popper 2005, p. 182). Popper called it the problem of decidability, a problem that Farris would like to sweep under the curtain, so it seems.
Popper held that although probabilistic hypotheses cannot be falsified by a finite set of basic statements in the same way as Popper believed that non-probabilistic hypotheses can be falsified, some logical relations still hold between basic statements and probabilistic hypotheses that can be analysed in terms of ‘classical’ logical relations of deducibility and contradiction. Popper, therefore, made practical falsification dependent on a methodological rule to neglect the improbable (see also Falsifying Rule for Probability Statements, Gillies 1971). Popper proposed ‘that we take the methodological decision never to explain physical effects, i.e., reproducible regularities, as accumulations of accidents’ (Popper 2005, p. 192). This rule goes beyond Popper’s methodological rule to prohibit ad hoc hypotheses. The decision to ignore non-reproducible effects rests on the idea to consider them to be highly improbable. Popper reversed the argument and concluded that if something is highly improbable, it should be non-reproducible. As a consequence, he considered an improbable but reproducible effect to practically falsify a probabilistic hypothesis.
According to Popper, the function for corroboration C (Eqn 1) ‘can only be large […] if e is a statistical report asserting a good fit in a large sample’ (Popper 2005, p. 430). Popper continued that ‘the test-statement e will be the better the greater its precision… and consequently its refutability or content, and the larger the sample size n, that is to say, the statistical material required for testing e. And the test-statement e so constructed may then be confronted with the results of actual observations’ (Popper 2005, p. 430). Popper concluded that ‘[o]ne may see from all this the testing of a statistical [probabilistic] hypothesis is deductive – as is that of all other hypotheses: first a test-statement is constructed in such a way that it follows (or almost follows) from the hypothesis, although its content or testability is high; and afterwards it is confronted with experience’ (Popper 2005, p. 431), and ‘[t]hus our analysis shows that statistical methods are essentially hypothetico-deductive, and that they proceed by the elimination of inadequate hypotheses – as do all other methods of science’ (Popper 2005, p. 432).
Popper stuck to this notion of practical falsifiability of probabilistic hypotheses also after adopting the propensity interpretation of probability: ‘The probabilistic hypothesis predicts that the singular event has a certain propensity to be realized. This prediction can be tested by repeating the experiment under the conditions prescribed, and noting the frequency distribution in repeated experiments’ (Popper 1983, p. 289).
If phylogenetic tree hypotheses would represent probabilistic hypotheses and Farris wants to test them in a Popperian framework, he must address how to exactly apply Popper’s notion of practical falsifiability, because Popper obviously demanded very specific criteria to be met for testing probabilistic hypotheses. Farris ignored this aspect of Popper’s treatment of practical falsifiability.
Popper’s falsificationism is not a self-consistent theory
Measuring falsificationism by Popper’s own standards
Notably, Popper’s motivation often is not taken into account when phylogeneticists interpret his falsificationist approach for the needs, requirements and basic parameters of phylogenetics. This is insofar unfortunate, because there is the risk of emphasising aspects of his theory that are not specific to falsificationism (e.g. fallibility of hypotheses), while at the same time missing those aspects that distinguish his approach from alternative approaches (e.g. no inductive elements allowed). This includes the claims and premises that Popper himself held (Popper 1994), as for instance Reichenbach’s (1938, for a critical discussion see Hoyningen-Huene 2006) distinction of the context of discovery, which Popper identified as the psychological question of how to discover scientific hypotheses, and the context of justification, which Popper considered to be a logical–philosophical question of how to justify a scientific hypothesis. Popper thought only the latter to be of relevance for the scientific method and claimed that empirical sciences must be grounded in experience and that a theory of justification is central to the demarcation of empirical science against all kinds of pseudosciences that have been rather popular in the 1920s, such as Marxism and Freudian psychoanalysis. Popper compared the latter to Einstein’s theory of relativity, which he considered to be the poster child of empirical science.
With respect to phylogenetics, it is important to note that Popper’s poster child is a theory of experimental science, whereas phylogenetic tree hypotheses are hypotheses of historical science. There is a fundamental difference in the methodology used by historical and experimental science (e.g. Gee 1999, for falsificationism, and experimental v. historical science see Cleland 2001, 2002). Experimental scientists usually focus on a single hypothesis about a general class of repeatable events and attempt to repeatedly bring about the test conditions specific to the hypothesis, always eager to control for extraneous factors that could produce false positives and false negatives (Cleland 2001). They test their hypotheses by using controlled laboratory settings to generate certain effects predicted by the hypotheses. On the basis of modus tollens, they then compare the observed effects with the predicted effects, and the application of Popper’s falsificationism is in this regard straight forward. Historical scientists, however, usually focus on formulating multiple competing hypotheses about particular past events, always eager to find some smoking gun, that is, a trace left behind by the event that makes one of the competing hypotheses stand out as a better causal explanation for this trace than are the other hypotheses (Cleland 2001). As a consequence, historical scientists usually do not search for refuting evidence, but focus on finding positive evidence.
Moreover, Popper (1994) agreed with Hume (1993) that the prevailing inductive theories of justification suffered from the trilemma of (1) involving circular reasoning if induction is justified by the assumption of some principle of uniformity of nature, because this principle would have to be justified as well, resulting in induction being justified by induction; (2) leading to an infinite regress if induction is justified by a higher-order principle of induction, because this higher-order principle would have to be justified as well, requiring the next higher-order principle, and so on; or (3) having to revert to conventionalism or dogmatism or to resort to a priorism if the principle of induction is justified independent of experience. As a consequence, Popper realised that empirical scientific hypotheses cannot be verified in principle, i.e. one cannot prove their truth, and he concluded that a consistent theory of justification must be completely free of induction. He even went so far as to claim that including inductive elements in the foundation of the scientific method would be unscientific. Instead, Popper (1994) suggested a theory of justification exclusively based on deduction (more specifically: modus tollens), with falsifiability as the demarcation criterion between empirical science (e.g. Einstein’s theory of relativity) and pseudosciences (e.g. Marxism, Freudian psychoanalysis). Popper, thus, claimed that only those hypotheses are scientific that make predictions that can be contradicted by experience. This explains why, irrespective of the distinction of naïve ‘strict falsification’ and ‘methodological’ or ‘sophisticated falsification’, scientific hypotheses always must be falsifiable from a logical point of view, giving falsifiability a key position in Popper’s theory.
Therefore, it is essential when talking about Popperian tests in phylogenetics to specify the deductive link between evidence and hypothesis that shows how some evidence can potentially falsify the hypothesis when assuming that background knowledge and the falsifying observations were true. Furthermore, it is important to clarify that no inductive step has been involved in this test, because otherwise it cannot represent a Popperian test. Above I have argued why this does not apply to the congruence test in phylogenetics and tree hypotheses.
Basic problems with Popper’s falsificationism
Popper’s falsificationism has been criticised for various reasons (e.g. Salmon 1967, 1968, 1998; Lakatos 1968, 1970; Kuhn 1970; Putnam 1974; Grünbaum 1976; Mackie 1985; Sober 1988, 2000; Howson and Urbach 1989; Earman and Salmon 1992; McGuire 1992; Stamos 1996; Andersson 1998; Schurz 1998; Franklin 2001; Spohn 2001). The following problems challenge the foundation of Popper’s program (see also Vogt 2014):
-
Because of Popper’s claim of the theory-ladeness of perception-based statements, basic statements (i.e. perception-based statements that potentially falsify a hypothesis) cannot be verified by experience, but must be tested themselves against basic statements of a lower order or be accepted by an act of free decision (Popper 2005). This, however, leads to either infinite regress or some sort of conventionalism, a problem that Popper already had identified and criticised for the method of induction, which in its turn represented one of the main motivations for Popper to develop his falsificationist approach in the first place (see above).
-
According to the Duhem–Quine thesis, actual falsification is not possible because we cannot decide which component of the hypothetico-deductive setting is responsible for the deductive contradiction (Lakatos 1970; Thornton 2009). We can only conclude that the set as a whole, consisting of the tested hypothesis, background knowledge, ceteris paribus clause and basic statements, cannot be true. Therefore, because many of the auxiliary conditions of a test may affect the outcome of an experiment independent of the truth of the tested hypothesis and the number of auxiliary conditions can be practically infinite, attempting to falsify a given hypothesis is not a reasonable activity anymore, at least from a practical point of view. In this context, it is also worth mentioning that Popper’s position regarding ad hoc manoeuvres is also problematic. When looking at Popper’s poster child scientists, the classical experimental scientists, one must realise that they rarely reject their hypotheses in the face of failed predictions. In their experiments, they hold the test conditions constant while varying other experimental conditions, usually continuing to do so, even when previous experiments have resulted in failed predictions, thus resembling the activity that Popper stigmatised as ad hoc manoeuvre (see above) to save the hypothesis from refutation by denying an auxiliary assumption. Cleland proposed an alternative interpretation to this activity, because it might also be viewed as an attempt to ‘minimise the very real possibility of misleading confirmations and disconfirmations in concrete laboratory settings’ (Cleland 2002, p. 478). According to Cleland’s (2001, 2002) interpretation, classical experimental scientists are primarily concerned with protecting their hypothesis from false negatives and false positives rather than from falsification. This possibility seems to have escaped Popper’s attention.
-
Popper never provided any means of quantification for his concept of logical probabilities. Because Popper argued that the corroborability of a hypothesis and therewith its testability, its empirical content and its degree of falsifiability are inversely proportional to the absolute logical probability of the hypothesis (Popper 1983, 2005), corroborability and testability of a hypothesis are rather qualitative than quantitative concepts. The lack of a method of quantifying logical probabilities also makes the comparison of the corroboration of competing hypotheses rather problematic.
-
Popper’s concept of corroboration entails an inductive element (Vogt 2014), because Popper (2005) claimed that repeating a test that a hypothesis already successfully passed beforehand does not increase its degree of corroboration to the same extent as it did the first time. The underlying assumption of a logical relation between different instantiations of the same test can be justified only by assuming some general regularity underlying nature, which in its turn represents a principle of induction. This contradicts Popper’s claim that falsificationism must be free of any inductive element.
Popper’s measure of degree of corroboration contradicts core elements of falsificationism
Another fundamental problem concerns Popper’s Eqn 1 for measuring corroboration, which is the degree to which a hypothesis h has stood up in tests (Popper 2005, p. 434). As Rowbottom (2013) clearly demonstrated, Popper’s Eqn 1 is inconsistent with central claims of Popper’s own theory. Rowbottom argued that Popper repeatedly asserted that in an infinite universe, the absolute logical probability of a universal hypothesis h is zero relative to any finite set of basic statements (e.g. Popper 2005, pp. 375, 398, 433), as follows:

The underlying idea is that infinitely many alternative hypotheses will be compatible with any given finite set of basic statements and that those hypotheses must be assigned equal probabilities.
From the axioms of probability follows:

Rowbottom (2013) argued that from Eqn 3 and Eqn 4 follows for any universal hypothesis h:

If we apply Eqn 5 to Popper’s measure of corroboration (Eqn 1), we receive the following formula (Rowbottom 2013):
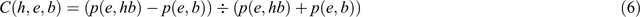
Eqn 6, however, shows why Popper’s formula does not provide a good measure of corroboration with respect to how well a universal hypothesis h withstood severe tests. This becomes clear when comparing two scenarios for two competing hypotheses h1 and h2, in which e1 and e2 have been found to be acceptable evidence. In the first scenario p(e1,h1b) = 1 and p(e1,b) = 0.1 and in the second p(e2,h2b) = 0.1 and p(e2,b) = 0.01. Following Eqn 6, h1 and h2 would be equally corroborated with a degree of corroboration of 9/11. This is absurd, because in the former scenario, e1 is entailed by h1 and b (with the consequence that the discovery of non-e1 would have falsified h1), whereas in the latter scenario, h2 makes no significant contribution to the prediction of e2 (with the consequence that the discovery of non-e2 would not have falsified h2). These two scenarios demonstrate that, whereas only the former satisfies Popper’s claim that ‘[t]he support given by e to h becomes significant only when… p(e,hb) – p(e,b) >> 1/2’ (Popper 1983, p. 240), both nonetheless receive the same degree of corroboration.
Rowbottom (2013) continued to argue that if all universal hypotheses possess an absolute logical probability of zero, they all would be equally testable, irrespective of their relative empirical content. This would apply even to the following two statements:
-
‘all A are X’, and
-
‘all A are X or Y’.
If the logical probability of each statement equals its degree of empirical content, then degree of empirical content of h relative to b cannot be equal to 1 – p(h,b) (a central claim of Popper’s notion of degree of testability, e.g. Popper 1983, p. 241), at least if degree of empirical content is defined as the class of its potential falsifiers (Popper 2005, p. 103), because the class of potential falsifiers of Statement 2 is a proper subset of those of Statement 1. Obviously, Popper’s measure of degree of corroboration is problematic and seems to contradict core ideas of Popper’s falsificationist theory.
Conclusions
Above, I have argued that the main claims of phylogeneticists regarding a falsificationist approach to phylogenetics are untenable; frequency probabilities can be used to measure degrees of corroboration and can be used in numerical tree inference although phylogeny is a unique process, likelihood methods in phylogenetics do not represent verificationist approaches, and the congruence test is not a Popperian test of tree hypotheses. Moreover, I have argued that cladograms are not falsifiable in principle and that all strategies that have been suggested for dealing with this fact contradict some of falsificationism’s core elements; re-interpreting putative synapomorphies as homoplasies does not represent a Popperian ad hoc manoeuvre, corroboration cannot be decoupled from falsification, the tree with the highest likelihood is not necessarily also the most corroborated tree, and tree hypotheses are not Popperian probabilistic hypotheses and Popperian probabilistic hypotheses are practically falsifiable. Moreover, Popper’s measure of degree of corroboration, to which phylogeneticists frequently refer to when arguing their case of how phylogenetic methodology is consistent with Popperian falsificationism, contradicts main ideas of Popper’s falsificationism.
I have briefly discussed four fundamental problems with falsificationism. These problems demonstrate that Popper’s falsificationism does not live up to its own claims. Measured by Popper’s own standards, one must conclude that neither historical nor experimental science is conducted in a way that is consistent with the principles of Popper’s falsificationist program. In its strict doctrine, falsificationism is practically inapplicable, and phylogeneticists should stop referring to falsificationism when they defend a specific methodological position (Vogt 2014). When talking to philosophers, they are always very surprised when I tell them that in phylogenetics many theoretical and methodological discussions are still based on Popper’s falsificationism, because shortcomings and inconsistencies of falsificationism are well known in philosophy. It is time that biologists start to realise that as well and take a look at alternative theories of justification.
References
Andersson G (1998) Basisprobleme. In ‘Karl Popper: Logik der Forschung. Klassiker Auslegen. Vol. 12’. (Ed. H Keuth) pp. 145–164. (Akademie Verlag: Berlin)Bock WJ (1973) Philosophical foundations of classical evolutionary classification. Systematic Zoology 22, 375–392.
| Philosophical foundations of classical evolutionary classification.Crossref | GoogleScholarGoogle Scholar |
Cleland CE (2001) Historical science, experimental science, and the scientific method. Geology 29, 987–990.
| Historical science, experimental science, and the scientific method.Crossref | GoogleScholarGoogle Scholar |
Cleland CE (2002) Methodological and epistemic differences between historical science and experimental science*. Philosophy of Science 69, 474–496.
| Methodological and epistemic differences between historical science and experimental science*.Crossref | GoogleScholarGoogle Scholar |
Cracraft J (1978) Science, philosophy, and systematics. Systematic Zoology 27, 213–216.
| Science, philosophy, and systematics.Crossref | GoogleScholarGoogle Scholar |
de Queiroz K, Poe S (2001) Philosophy and phylogenetic inference: a comparison of likelihood and parsimony methods in the context of Karl Popper’s writings on corroboration. Systematic Biology 50, 305–321.
| Philosophy and phylogenetic inference: a comparison of likelihood and parsimony methods in the context of Karl Popper’s writings on corroboration.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38zntVOgug%3D%3D&md5=c6c63694cf5cf6913dfa39d0276e8cefCAS | 12116577PubMed |
de Queiroz K, Poe S (2003) Failed refutations: further comments on parsimony and likelihood methods and their relationship to Popper’s degree of corroboration. Systematic Biology 52, 352–367.
Earman J, Salmon WC (1992) The confirmation of scientific hypotheses. In ‘Introduction to the Philosophy of Science’. (Eds MH Salmon, J Earman, C Glymour, JG Lennox, P Machamer, JE McGuire, JD Norton, WC Salmon, KF Schaffner) pp. 42–103. (Prentice Hall: Englewood Cliffs, NJ)
Faith DP (1992) On corroboration: a reply to Carpenter. Cladistics 8, 265–273.
| On corroboration: a reply to Carpenter.Crossref | GoogleScholarGoogle Scholar |
Faith DP (1999) Error and the growth of experimental knowledge Systematic Biology 48, 675–679. [Review]
Faith DP (2004) L.A.S. Johnson Review No. 1. From species to supertrees: Popperian corroboration and some current controversies in systematics. Australian Systematic Botany 17, 1–16.
| L.A.S. Johnson Review No. 1. From species to supertrees: Popperian corroboration and some current controversies in systematics.Crossref | GoogleScholarGoogle Scholar |
Faith DP (2006) Science and philosophy for molecular systematics: which is the cart and which is the horse? Molecular Phylogenetics and Evolution 38, 553–557.
| Science and philosophy for molecular systematics: which is the cart and which is the horse?Crossref | GoogleScholarGoogle Scholar | 16230031PubMed |
Faith DP, Cranston PS (1992) Probability, parsimony, and Popper. Systematic Biology 41, 252–257.
| Probability, parsimony, and Popper.Crossref | GoogleScholarGoogle Scholar |
Faith DP, Trueman JWH (2001) Towards an inclusive philosophy for phylogenetic inference. Systematic Biology 50, 331–350.
| Towards an inclusive philosophy for phylogenetic inference.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38zntVOnsg%3D%3D&md5=702ed20380225ba5d08390b30d5b3517CAS | 12116579PubMed |
Farris JS (1983) The Logical Basis of Phylogenetic Analysis. In ‘Advances in Cladistics 2’. (Eds NI Platnick, VA Funk) pp. 7–36. (Columbia University Press: New York)
Farris JS (2000) Corroboration versus ‘strongest evidence’. Cladistics 16, 385–393.
Farris JS (2013) Popper: not Bayes or Rieppel. Cladistics 29, 230–232.
| Popper: not Bayes or Rieppel.Crossref | GoogleScholarGoogle Scholar |
Farris JS (2014) Popper with probability. Cladistics 30, 5–7.
| Popper with probability.Crossref | GoogleScholarGoogle Scholar |
Farris JS, Kluge AG, Carpenter JM (2001) Popper and likelihood versus ‘Popper*’. Systematic Biology 50, 438–444.
| Popper and likelihood versus ‘Popper*’.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38zntVOntA%3D%3D&md5=63ed57f618a2416dcd46d738fdba3fd9CAS | 12116585PubMed |
Fisher RA (1922) On the mathematical foundations of theoretical statistics. Philosophical Transaction of the Royal Society of London A 222, 309–368.
| On the mathematical foundations of theoretical statistics.Crossref | GoogleScholarGoogle Scholar |
Franklin J (2001) Resurrecting logical probabilities. Erkenntnis 55, 277–305.
| Resurrecting logical probabilities.Crossref | GoogleScholarGoogle Scholar |
Gee H (1999) ‘In Search of Deep Time.’ (The Free Press: New York)
Gillies DA (1971) A falsifying rule for probability statements. The British Journal for the Philosophy of Science 22, 231–261.
| A falsifying rule for probability statements.Crossref | GoogleScholarGoogle Scholar |
Grant T, Kluge AG (2003) Data exploration in phylogenetic inference: scientific, heuristic, or neither. Cladistics 19, 379–418.
| Data exploration in phylogenetic inference: scientific, heuristic, or neither.Crossref | GoogleScholarGoogle Scholar |
Grünbaum A (1976) Is the method of bold conjectures and attempted refutations justifiably the method of science. The British Journal for the Philosophy of Science 27, 105–136.
| Is the method of bold conjectures and attempted refutations justifiably the method of science.Crossref | GoogleScholarGoogle Scholar |
Helfenbein KG, DeSalle R (2005) Falsifications and corroborations: Karl Popper’s influence on systematics. Molecular Phylogenetics and Evolution 35, 271–280.
| Falsifications and corroborations: Karl Popper’s influence on systematics.Crossref | GoogleScholarGoogle Scholar | 15737596PubMed |
Howson C, Urbach P (1989) ‘Scientific Reasoning: the Bayesian Approach.’ (Open Court Publishing Company: La Salle, IL)
Hoyningen-Huene P (2006) Context of discovery versus context of justification and Thomas Kuhn. In ‘Revisiting Discovery and Justification: Historical and Philosophical Perspectives on the Context Distinction’. (Eds J Schickore, F Steinle) pp. 119–131. (Springer: Dordrecht, the Netherlands)
Hull DL (1983) Karl Popper and Plato’s metaphor. In ‘Advances in Cladistics 2’. (Eds NI Platnick, VA Funk) pp. 177–189. (Columbia University Press: New York)
Hume D (1993) ‘An Enquiry Concerning Human Understanding.’ (Hackett Publishing: Indianapolis, IN)
Kitts DB (1977) Karl Popper, verifiability, and systematic zoology. Systematic Zoology 26, 185–194.
| Karl Popper, verifiability, and systematic zoology.Crossref | GoogleScholarGoogle Scholar |
Kluge AG (1997a) Testability and the refutation and corroboration of cladistic hypotheses. Cladistics 13, 81–96.
| Testability and the refutation and corroboration of cladistic hypotheses.Crossref | GoogleScholarGoogle Scholar |
Kluge AG (1997b) Sophisticated falsification and research cycles: consequences for differential character weighting in phylogenetic systematics. Zoologica Scripta 26, 349–360.
| Sophisticated falsification and research cycles: consequences for differential character weighting in phylogenetic systematics.Crossref | GoogleScholarGoogle Scholar |
Kluge AG (2001) Philosophical conjectures and their refutation. Systematic Biology 50, 322–330.
| Philosophical conjectures and their refutation.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38zntVOguw%3D%3D&md5=b48f853d8e731ee69ab0f7310da34cb2CAS | 12116578PubMed |
Kluge AG (2002) Distinguishing ‘or’ from ‘and’ and the case for historical identification. Cladistics 18, 585–593.
Kluge AG (2003) The repugnant and the mature in phylogenetic inference: atemporal similarity and historical identity. Cladistics 19, 356–368.
| The repugnant and the mature in phylogenetic inference: atemporal similarity and historical identity.Crossref | GoogleScholarGoogle Scholar |
Kuhn TS (1970) Logic of discovery or psychology of research? In ‘Criticism and the Growth of Knowledge’. (Eds I Lakatos, A Musgrave) pp. 1–23. (Cambridge University Press: Cambridge, UK)
Lakatos I (1968) Changes in the problem of inductive logic. In ‘The Problem of Inductive Logic’. (Ed. I Lakatos) pp. 315–417. (North-Holland Pub. Co.: Amsterdam, the Netherlands)
Lakatos I (1970) Falsification and the methodology of scientific research programmes. In ‘Criticism and the Growth of Knowledge. Vol. 4’. (Eds I Lakatos, I A Musgrave) pp. 91–96. (Cambridge University Press: Cambridge, UK)
Mackie JL (1985) ‘Logic and Knowledge.’ (Clarendon Press: Oxford, UK)
McGuire JE (1992) Scientific change: perspectives and proposals. In ‘Introduction to the Philosophy of Science’. (Eds MH Salmon, J Earman, C Glymour, JG Lennox, P Machamer, JE McGuire, JD Norton, WC Salmon, KF Schaffner) pp. 132–178. (Prentice Hall: Englewood Cliffs, NJ)
Platnick NI, Gaffney ES (1978) Systematics and the Popperian paradigm. Systematic Zoology 27, 381–388.
| Systematics and the Popperian paradigm.Crossref | GoogleScholarGoogle Scholar |
Popper KR (1983) ‘Realism and the Aim of Science; From the Postscript to the Logic of Scientific Discovery.’ (Routledge: London)
Popper KR (1994) ‘Logik der Forschung, 10. Auflage.’ (J.C.B. Mohr (Paul Siebeck): Tübingen, Germany)
Popper KR (2005) ‘The Logic of Scientific Discovery.’ (Routledge: London)
Putnam H (1974) The ‘corroboration’ of theories. In ‘The Philosophy of Karl Popper’. (Ed. PA Schilpp) pp. 221–240. (Open Court Publishing Company: La Salle, IL)
Randle CP, Pickett KM (2010) The conflation of ignorance and knowledge in the inference of clade posteriors. Cladistics 26, 550–559.
| The conflation of ignorance and knowledge in the inference of clade posteriors.Crossref | GoogleScholarGoogle Scholar |
Reichenbach H (1938) ‘Experience and Prediction.’ (University of Chicago Press: Chicago, IL)
Rieppel O (2003) Popper and systematics. Systematic Biology 52, 259–271.
| Popper and systematics.Crossref | GoogleScholarGoogle Scholar | 12746152PubMed |
Rowbottom DP (2013) Popper’s measure of corroboration and p(h|b). The British Journal for the Philosophy of Science 64, 739–745.
| Popper’s measure of corroboration and p(h|b).Crossref | GoogleScholarGoogle Scholar |
Salmon WC (1967) ‘The Foundations of Scientific Inference.’ (University of Pittsburgh Press: Pittsburgh, PA)
Salmon WC (1968) The justification of inductive rules of inference. In ‘The Problem of Inductive Logic’. (Ed. I Lakatos) pp. 24–43. (North-Holland Pub. Co.: Amsterdam, the Netherlands)
Salmon WC (1998) Rational prediction. In ‘Philosophy of Science: The Central Issues’. (Eds M Curd, JA Cover) pp. 433–444. (W.W. Norton and Company Inc.: New York)
Schroeder-Heister P (1998) Wahrscheinlichkeit. In ‘Klassiker Auslegen: Karl Popper, Logik der Forschung’. (Ed. H Keuth) pp. 185–213. (Akademie Verlag: Berlin)
Schurz G (1998) Das Problem der Induktion. In ‘Karl Popper: Logik der Forschung’, Klassiker Auslegen, Vol. 12. (Ed. H Keuth) pp. 25–40. (Akademie Verlag: Berlin)
Siddall ME, Kluge AG (1997) Probabilism and phylogenetic inference. Cladistics 13, 313–336.
| Probabilism and phylogenetic inference.Crossref | GoogleScholarGoogle Scholar |
Sober E (1983) Parsimony in systematics: philosophical issues. Annual Review of Ecology and Systematics 14, 335–357.
| Parsimony in systematics: philosophical issues.Crossref | GoogleScholarGoogle Scholar |
Sober E (1988) ‘Reconstructing The Past – Parsimony, Evolution, and Inference.’ A Bradford book. (The MIT Press: Cambridge, MA)
Sober E (2000) ‘Philosophy of Biology’, 2nd edn. (Westview Press: Oxford, UK)
Spohn W (2001) Vier Begründungsbegriffe. In ‘Erkenntnistheorie – Positionen zwischen Tradition und Gegenwart’. (Ed. T Grundmann) pp. 33–52. (Mentis: Paderborn, Germany)
Stamos DN (1996) Popper, falsifiability, and evolutionary biology. Biology and Philosophy 11, 161–191.
| Popper, falsifiability, and evolutionary biology.Crossref | GoogleScholarGoogle Scholar |
Thornton S (2009) Karl Popper. In ‘The Stanford Encyclopedia of Philosophy’. (Ed. EN Zalta) (The Metaphysics Research Lab, Stanford University: Standford, CA) Available at http://plato.stanford.edu/archives/win2011/entries/popper [Verified July 2014]
Vogt L (2002) Testing and weighting characters. Organisms, Diversity & Evolution 2, 319–333.
| Testing and weighting characters.Crossref | GoogleScholarGoogle Scholar |
Vogt L (2007) A falsificationist perspective on the usage of process frequencies in phylogenetics. Zoologica Scripta 36, 395–407.
| A falsificationist perspective on the usage of process frequencies in phylogenetics.Crossref | GoogleScholarGoogle Scholar |
Vogt L (2008) The unfalsifiability of cladograms and its consequences. Cladistics 24, 62–73.
| The unfalsifiability of cladograms and its consequences.Crossref | GoogleScholarGoogle Scholar |
Vogt L (2014) Why phylogeneticists should care less about Popper’s falsificationism. Cladistics 30, 1–4.
| Why phylogeneticists should care less about Popper’s falsificationism.Crossref | GoogleScholarGoogle Scholar |
Wiley EO (1975) Karl R. Popper, systematics, and classification : a reply to Walter Bock and other evolutionary taxonomists. Systematic Zoology 24, 233–243.
| Karl R. Popper, systematics, and classification : a reply to Walter Bock and other evolutionary taxonomists.Crossref | GoogleScholarGoogle Scholar |