Uncertainties in estimated phosphorus loads as a function of different sampling frequencies and common calculation methods
L. H. Defew A , L. May A C and K. V. Heal BA Centre for Ecology and Hydrology, Bush Estate, Penicuik, Midlothian EH26 0QB, Scotland, UK.
B School of GeoSciences, The University of Edinburgh, Crew Building, The King’s Buildings, West Mains Road, Edinburgh EH9 3JN, Scotland, UK.
C Corresponding author. Email: lmay@ceh.ac.uk
Marine and Freshwater Research 64(5) 373-386 https://doi.org/10.1071/MF12097
Submitted: 10 April 2012 Accepted: 21 January 2013 Published: 3 May 2013
Journal Compilation © CSIRO Publishing 2013 Open Access CC BY-NC-ND
Abstract
Water quality monitoring programs are often based upon low-frequency regular sampling regimes from which loads are estimated. In this study, stream flow (Q) and phosphorus concentrations (C) were measured at 2-hourly intervals over a 10-week period between October and December 2006 in a tributary of Loch Leven, Scotland. The dataset was deconstructed to emulate different weekly, daily and composite sampling strategies, the aim being to highlight the large amount of uncertainty and imprecision in estimating total (TP) and soluble reactive (SRP) phosphorus loads on the basis of commonly applied sampling strategies and calculation methods. When based on the full dataset, phosphorus (P) loads estimated from the 2-hourly data were 459 kg TP, 351 kg particulate P (PP) and 78 kg SRP. In contrast, P loads estimated from different weekly, daily and composite sampling regimes and determined by applying seven different calculation methods ranged from 22 to 5028 kg TP, 13 to 4588 kg PP and 7 to 286 kg SRP. The results of this study highlight the large amount of uncertainty and imprecision associated with estimating P loads and contributes to the body of evidence that high-frequency monitoring is necessary if P loads to standing water bodies are to be quantified accurately and the effects of nutrient management programs interpreted correctly.
Additional keywords: Diffuse pollution, phosphorus loads, regulatory monitoring, storm events.
Introduction
Eutrophication is a widespread problem caused by nutrient pollution. These nutrients enter a waterbody from point and diffuse sources within its catchment and, in many cases, phosphorus (P) is the main driver of the observed biological response, especially when the receiving waterbody is a lake (Schindler et al. 2008). Although inputs from point sources are relatively easy to quantify, determining P loads to waterbodies from diffuse sources is much more difficult. Nevertheless, it is important that the method of assessment used provides sufficient data to estimate these loads as accurately as possible. Catchment management decisions depend on the assumption that sampling programs provide an accurate estimate of ‘true’ P loads (Cassidy and Jordan 2011). Without this, the effectiveness of management measures that are aimed at improving water quality cannot be assessed (Johnes 2007) with a reliable degree of certainty.
When designing a program to estimate a pollutant load from a diffuse source accurately, two key issues need to be addressed (Rekolainen et al. 1991; Johnes 2007). These are (1) how often should stream flow (Q) and concentration (C) be measured, and (2) which method should be used to calculate a nutrient load from these values? The answers to these questions are influenced by a range of constraints such as financial budgets, project goals (concentration versus loads) and desired level of accuracy with respect to ‘true’ loads (Tate et al. 1999; King and Harmel 2003). Choosing an appropriate approach is difficult because of the lack of information available on different sampling strategies and their associated uncertainty and imprecision.
The most common sampling strategy used by regulatory authorities in the UK (Greig 2005) and other European Union (EU) countries (Kristensen and Bøgestrand 1996; Johnes 2007) is regular time-interval sampling at a very low frequency (i.e. monthly, or at best, weekly). Simple and cost-effective, low-frequency sampling was designed to characterise point-source pollution, which, historically, was the dominant source of P causing eutrophication. Since the introduction of the EU Urban Waste Water Treatment Directive, point sources of P have been reduced. Although sewage sources still appear to influence reactive P concentrations (Foy 2007), especially in spring–summer under low flow conditions (Jarvie et al. 2006), in general, total P input concentrations and loads in many rural catchments are now dominated by diffuse sources.
It is well established that diffuse P is delivered to water bodies predominantly during periods of heavy rainfall and subsequent storm events (Haygarth and Jarvis 1996; Evans and Johnes 2004). It has been reported widely that the highest P loads to standing waters in rural catchments are associated with high rainfall and surface runoff (e.g. Poinke et al. 1999; Haygarth et al. 2005; Bowes et al. 2009) and it is also well established that more than 80% of the annual P load to a waterbody is transported by just two or three large high-flow events (Sharpley 2008; Jordan et al. 2012).
Statistical sampling theory suggests that shorter sampling intervals produce more accurate estimates of P loads than longer intervals (Haan 2002; Harmel and King 2005), because high-frequency sampling captures important storm events that are responsible for the delivery of large quantities of diffuse source pollutants, especially P (Phillips et al. 1999; Jordan et al. 2005). In spite of this, there has been little progress in increasing sampling frequency in national monitoring programs across the EU, even though this could be vital in terms of meeting the regulatory requirements of the EU Water Framework Directive.
Several studies have tried to quantify the uncertainty and imprecision of P loads estimated using different calculation methods and sampling strategies (Walling et al. 2001; Johnes 2007; Bowes et al. 2009). Other studies have compared estimated P loads with ‘true’ P loads determined from high-frequency measurements of P concentration that capture the effects of storm events using automatic water samplers (7-hourly sampling: Jordan and Cassidy 2011) or in situ water quality monitoring equipment (Wade et al. 2012). The current study examined the effect of different calculation methods on P load estimates and compared estimated and ‘true’ P loads. High-frequency (2-hourly) sampling data that captured the influence of winter storm events on P dynamics were used to assess the uncertainty and imprecision of total P (TP), particulate P (PP) and soluble reactive P (SRP) load estimation as a result of (1) different sampling strategies (weekly, daily and composite sampling), (2) different interpolation and extrapolation calculation methods and (3) different sampling times. Uncertainty was determined by comparing estimated P loads to the ‘true’ TP, PP and SRP loads calculated from 2-hourly, paired measures of Q and C. The aim of this study was to highlight the inaccuracy and imprecision associated with different sampling frequencies and estimation methods because only when load estimates are accurate and reliable can the effectiveness of targeted nutrient-reduction programs be assessed correctly.
Materials and methods
Study site
Loch Leven is a shallow loch in lowland Scotland, UK, which has a surface area of 13.3 km2 and mean and maximum depths of 3.9 m and 25.5 m, respectively (Fig. 1). The loch has suffered from eutrophication problems for many years as a result of high P loads from the catchment (Bailey Watts and Kirika 1999; May and Spears 2012). Compared with other inland lochs of its size in Scotland, it has an unusually intensively farmed catchment with ~80% of the area being used for agricultural crops and livestock production, which are key diffuse sources of P to the loch. The Pow Burn, on which this study is focussed, is a 12.9-km-long second-order tributary that flows into Loch Leven. It drains a catchment area of 10.9 km2 and, during periods of heavy rainfall, transports large quantities of P in association with eroded soils and suspended sediment to the loch (Defew 2008).
|
Estimation of ‘true’ phosphorus loads
The objectives of this study were achieved by collecting high-frequency (2-hourly) stream flow (Q) and P concentration (C) data, deconstructing them to emulate different subdaily, daily, weekly and composite sampling regimes, and then calculating TP, PP and SRP loads for the 10-week study period using seven different calculation methods. ‘True’ P load, in this context, is defined as that obtained using the 2-hourly data.
The area of the UK in which this study was undertaken has an average annual rainfall of ~1000 mm, and high flows associated with short periods of intensive rainfall can occur at any time of year; there are no well defined wet or dry periods. The timing of the intensive sampling campaign was targeted at the period between October and December, when high-flow events tend to occur more reliably, because the impact of such events on load estimation was the focus of the study. However, the study period was not atypical of the year as a whole; it spanned 19% of the year and ~18% of the annual average rainfall fell over this period.
In detail, water samples were collected at the Pow Burn every 2 h from 10 October to 5 December 2006 inclusive using a Hach Lange® EPIC automatic sampler located on the bank of the stream. All water samples were analysed for TP, total soluble P (TSP) and SRP content within 48 h of collection following the methods of Eisenreich et al. (1975) and Murphy and Riley (1962). SRP concentrations in stream water samples with ‘low’ and ‘high’ initial SRP concentrations (~40 and 250 µg L–1, respectively) that had been stored in the polyethylene bottles of the automatic sampler under winter temperature conditions (0–7°C) were shown to be stable for up to 48 h (paired t-test, n = 3) (Defew 2008). Therefore, storage of samples for up to 48 h before analysis for SRP content was considered an acceptable method for this study. PP was calculated as PP = TP – TSP. Corresponding high-frequency flow data recorded at 15-min intervals by a continuous flow gauge were provided by the Scottish Environment Protection Agency. The ‘true’ TP, PP and SRP loads for the 10-week period were calculated from these data using Eqn 1:
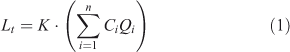
where Lt = estimated ‘true’ P load (kg), K = conversion factor to take account of time period of record, n = number of samples, Ci = instantaneous P concentration (µg L–1), and Qi = instantaneous discharge at time of chemical sampling (m3 s–1).
Sources of uncertainty
Three potential sources of uncertainty and imprecision were tested during this study. These were: calculation method, sampling strategy and sampling time.
Calculation method
Seven different calculation methods were used to estimate P loads (Table 1). These were the most commonly applied methods in the literature. Methods A–F are interpolation techniques that assume that the P concentration of a water sample is representative of conditions in the river for the period between two sampling occasions. In contrast, Method G is an extrapolation technique that describes a relationship between Q and C at the time of sampling. This relationship is then applied to continuous or high-frequency measures of Q to predict P concentrations between the sampling occasions. Phosphorus load is then calculated over the whole period of interest (Webb et al. 1997).
Sampling strategy
Eight different weekly sampling strategies were emulated by varying the start dates of the subsampling of the 2-hourly dataset as follows: 10, 11, 12, 13, 14, 15, 16 and 17 October. This created eight groups of data referred to, below, as weekly sampling Groups 1–8, respectively. Twelve additional datasets, emulating data collections at daily frequencies and starting at different times of each day, were also created. Finally, four different time-averaged composite water sampling strategies were constructed from the raw data using time-averaged values of C and Q calculated from samples that had been collected over the previous 6, 12, 24 or 48 h, respectively. The rationale for examining time-averaged composite datasets was that, if this sampling strategy yielded similar P load estimates to the loads calculated from 2-hourly sampling, it would reduce the resource required for water sample analysis when constructing loads.
Sampling time
The effect of sampling at different times of day was investigated. Load estimates were calculated from paired measures of Q and C collected at 01 : 00, 03 : 00. 05 : 00, 07 : 00, 09 : 00, 11 : 00, 13 : 00, 15 : 00, 17 : 00, 19 : 00, 21 : 00 and 23 : 00 hours during hypothetical weekly and daily sampling programs.
Calculating uncertainty
The uncertainty or accuracy of a load estimation procedure can be viewed as the difference between the actual (‘true’) load transported by a river and the estimated load (Webb et al. 1997; Johnes 2007). In this study, the error of each load estimate is presented as a percentage deviation from the ‘true’ load (Eqn 2). Positive percentage deviations indicated overestimations of P load, while negative percentage deviations indicated underestimated P loads.
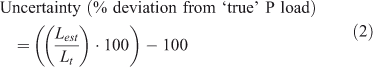
where Lest = the estimated P load based on a specific dataset, and Lt = the ‘true’ P load based on the high-frequency (2-hourly) dataset.
Data presentation
The uncertainty (as a measure of % deviation) generated in TP, PP and SRP load estimates by using different calculation methods, sampling strategies and sampling times, was compared using frequency distributions fitted to raw data using a ‘largest extreme value’ model in Minitab (ver. 15). Negative distributions highlighted underestimated P loads, whilst positive distributions showed overestimated P loads (as indicated by loc values). The spread of the frequency distribution tail described the precision of load estimates, which was characterised by the degree of dispersion generated by a given calculation approach. A greater degree of dispersion (as indicated by scale values) was interpreted as indicating a lower degree of precision and vice versa.
Statistical analyses
All tests were carried out at a 95% confidence level. Anderson–Darling normality tests were used to assess data distributions. Data were not normally distributed and were subsequently log10-transformed. One-way ANOVA and Tukey’s post hoc analyses were performed to determine whether there were statistical differences between data groups. For load estimates calculated from weekly data, calculation method (n = 7), sampling group (n = 8) and sampling time (n = 12) were the three factors tested. Calculation method (n = 7) and sampling time (n = 12) were the factors tested for daily sampling strategies. Differences between load estimates as a function of calculation method (n = 7) and sampling design (n = 4) were tested for composite sampling datasets.
Results
Nutrient concentrations and stream flow
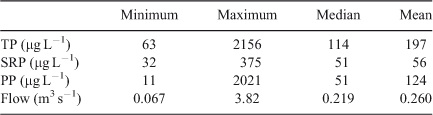
Fig. 2 shows the high temporal variability in stream flow and P concentrations in the Pow Burn during the period of the study. A summary of P concentrations and stream flows measured during the monitoring period are given in Table 2. Significant increases in P were closely associated with increasing stream flow during storm events.
|
‘True’ phosphorus loads
Based on 2-hourly measures of Q and C, ‘true’ P loads for the 10-week study period were calculated to be 459 kg TP, 78 kg SRP and 351 kg PP. Together, 10 high-flow events of varying size contributed 363 kg (79%), 49 kg (63%) and 295 kg (84%) of the ‘true’ TP, SRP and PP loads, respectively. The largest storm event alone, which occurred on 26 October 2006 (Fig. 2, Event D), contributed 157 kg (34%), 13 kg (17%) and 136 kg (39%) of the ‘true’ TP, SRP and PP loads, respectively, demonstrating the importance of storm events of varying magnitude in P mobilisation and delivery, and highlighting the need to capture such events during regulatory sampling programs.
Weekly sampling frequency
Sampling strategy
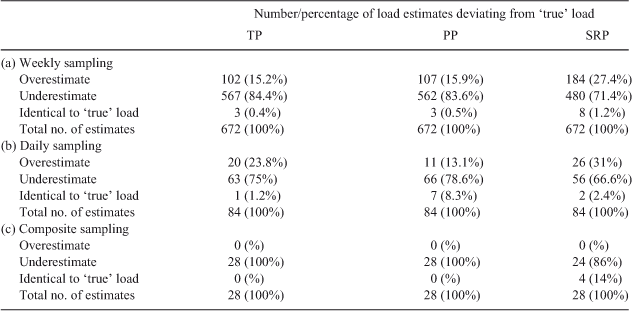
Phosphorus loads calculated using seven calculation methods over eight different weekly sampling programs, and 12 sampling times, ranged from 89 to 5028 kg TP, 35 to 4588 kg PP and 41 to 286 kg SRP. Frequency distributions for these datasets (Fig. 3) showed a tendency for TP, PP and SRP loads to be underestimated when determined from weekly datasets, with TP and PP having a greater negative bias compared with SRP. Table 3a summarises the accuracy of load estimates based on different weekly sampling strategies. Results suggest that most (>70%) of TP, PP and SRP load estimates are likely to be markedly underestimated as a result of this low sampling frequency. The number of estimates within ±10% of ‘true’ TP, PP and SRP loads was 48 (7%), 37 (6%) and 85 (13%), respectively (n = 672). In addition, there was a very low probability (<1%) that estimated P loads would be identical to the ‘true’ P loads, determined to the nearest whole number, when calculated using data collected at weekly intervals.

|
|
Calculation method
Negatively skewed frequency distributions indicated a clear tendency for all calculation methods to tend towards underestimating P loads (Fig. 3). There were statistical differences between P load estimates calculated using different methods (Table 4a). Tukey’s post hoc analysis showed that TP and PP loads calculated by Methods A, B and F were statistically different from those calculated by Method G. In this case, TP and PP loads were underestimated the most by Methods A, B and F, whilst Method G underestimated TP and PP loads the least and could be considered more accurate. However, Method G appeared to be less precise than Methods A, B and F, given that the dispersion of estimated loads was greater. Similarly, Methods C and D yielded the least precise load estimates. This was also true for estimates of SRP. However, patterns of accuracy and precision were slightly different for SRP than TP and PP. Methods A and F underestimated SRP loads the most and estimates were statistically lower than those from all other calculation methods; however, the extrapolation method (G) did not improve the accuracy associated with SRP load estimation compared with interpolation methods.

|
Sampling group
Frequency distributions for all weekly sampling groups (i.e. 1–8, as defined in the Methods section above) are presented in Fig. 3. The data show that TP, PP and SRP loads were most greatly underestimated in Sampling Groups 3 and 4. For TP and PP, the least uncertainty was associated with weekly Sampling Groups 1, 5 and 8. SRP loads were most accurate when calculated using data in Sampling Groups 1 and 8. However, there was a lower degree of precision associated with Groups 1, 5 and 8 compared with Groups 3 and 4. There were statistical differences between TP and PP load estimates using data from different sampling groups (Table 4). Sampling Groups [3 and 4], [1, 5 and 8], and [2, 6 and 7] were statistically different (Tukey’s post hoc analysis). For SRP load estimates, Groups [1 and 8], [3, 6 and 7], [2 and 5], and [4] were statistically different (Tukey's post hoc analysis). These results show that sampling day is an important factor affecting the accuracy of P load estimates.
Sampling time
Load estimate accuracy and precision were also notably influenced by the time at which weekly paired measures of C and Q were collected (Fig. 3). For TP and PP, there were statistical differences between load estimates calculated using data collected at different times of day (Table 4c). Loads calculated using values collected at 01.00 hours and 03.00 hours were estimated more accurately than loads calculated using C and Q values between 19.00 hours and 23.00 hours (Tukey’s post hoc analysis). Similarly, SRP loads calculated using values of C and Q measured between 13.00 hours and 19.00 hours were more accurate.
Daily sampling frequency
Sampling strategy
Estimated loads ranged from 22 to 1891 kg TP, from 13 to 1503 kg PP and from 7 to 276 kg SRP. The percentage deviation of P estimates calculated using daily measures of C and Q at different times of each sampling day, and using seven different calculation methods, is shown in Fig. 4. In comparison to weekly sampling strategies, P loads were mostly underestimated when calculated from daily data (Table 3b). Collecting data at a daily frequency did not result in any increase in the likelihood of the estimated P loads being identical to ‘true’ P loads (Table 3b). The number of estimates within ±10% of ‘true’ TP and PP loads was low, i.e. 9 (13%) and 8 (10%), respectively (n = 84). However, 37 (44%) of SRP load estimates were within ±10% of the ‘true’ load, a notable improvement in comparison with weekly sampling programs.
Calculation method
TP, PP and SRP loads were consistently underestimated by calculation Methods A and B when based on data collected at daily frequency (Fig. 4). TP and PP loads estimated by Methods A and B were found to be statistically different from loads estimated by all other methods (Table 4b). Frequency distribution analysis suggested that Method C resulted in the most accurate TP and PP loads (Fig. 5), although this method was the least precise. The extrapolation method (G) had the greatest precision, but still tended towards underestimating P loads. This method was particularly good for estimating SRP loads. Method G could be considered the best of the methods tested for estimating ‘true’ TP, PP and SRP loads if data are collected daily.

|
Daily sampling time
Results showed that sampling time affected the accuracy of P load estimates, even when sampling frequency was daily, and was an important factor influencing the accuracy of load estimates calculated using different methods (Fig. 4). Statistical analysis showed that there were significant differences between P loads estimated using different sampling times (Table 4b). TP and PP loads estimated from data collected between 23.00 hours and 05.00 hours were statistically different from loads calculated using data collected between 11.00 hours and 21.00 hours. Similarly, SRP loads calculated from data collected between 23.00 hours and 09.00 hours were statistically different from other sampling times (Tukey’s post hoc analysis). Frequency distribution analysis showed that loads calculated using values of C and Q measured in the afternoon were the most inaccurate (i.e. differed most from the 2-hourly load), but the most precise (Fig. 5). In contrast, loads were more accurate when calculated from data collected in the early hours of the morning, but these had low precision (Fig. 5).
Composite sampling design
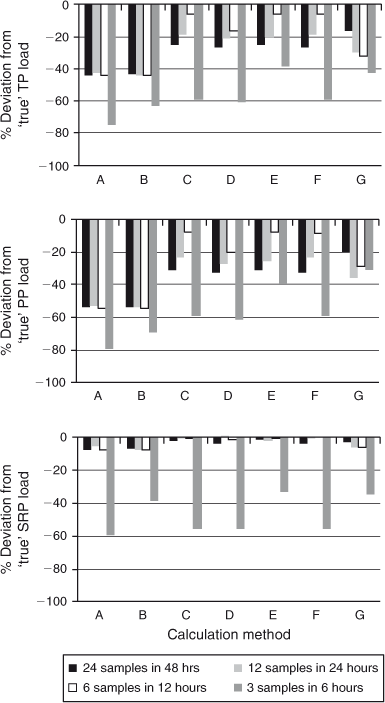
Fig. 6 shows percentage deviations of load estimates calculated by seven different methods using four different composite sampling strategies. Results indicate that TP, PP and SRP loads were consistently underestimated, regardless of increased sampling frequency or calculation method (Table 3).
|
Calculation method
Frequency distribution analysis showed that Methods A and B were the least accurate and underestimated P loads by the greatest amount, whilst loads were more accurate and precise when Methods E and G were applied to composite datasets (Fig. 7). TP and SRP load estimates were not significantly different as a result of using different calculation methods (Table 3). However, there were statistical differences between estimated PP loads; PP loads calculated using Methods E and G were significantly lower than those from Methods A and B.

|
Sampling strategy
In comparison to weekly and daily sampling regimes, TP and PP loads were consistently underestimated and highly unlikely to be identical to ‘true’ loads (Table 3c). Phosphorus loads calculated from a high-frequency composite sampling design were statistically different (Table 4); loads calculated from a composite sampling design of three samples collected over 6 h were statistically different from other composite sampling strategies. Frequency distribution analysis indicated that TP, PP and SRP loads were most grossly underestimated when based on values of Q and C calculated from three samples collected over 6 h (Fig. 7). Phosphorus loads estimated using average values of C and Q calculated from six samples collected over 12 h were found to be the most accurate (but still notably underestimated the ‘true’ load).
Overview of results
Increasing sampling frequency from weekly to daily paired measurements of C and Q reduced inaccuracy for all P fractions. Although more accurate than weekly sampling, it was clear that P loads were still, on average, underestimated by daily sampling regimes. However, daily sampling appeared to notably increase the likelihood of estimating SRP loads within 10% of ‘true’ loads. The time at which measures of C and Q were collected had a significant impact on the accuracy of P load estimates. For daily datasets, early morning sampling tended to result in overestimations, whilst late-night sampling resulted in underestimations. In comparison with daily sampling, composite sampling strategies increased the accuracy of TP and PP load estimates, but they were consistently underestimated. Again, composite sampling notably increased the likelihood of estimating SRP loads within 10% of ‘true’ loads. Interestingly, increasing the sampling frequency to three samples in 6 h resulted in a greater degree of underestimation of P loads compared with less frequent composite datasets.
Interpolation methods were most likely to underestimate P loads by the largest amount. Methods A and B, in particular, were notably inaccurate, particularly for TP and PP, regardless of sampling strategy. The log-log extrapolation method (Method G) increased the accuracy of P load estimates and improved precision, but still tended towards underestimation even with an increase in sampling frequency from weekly to daily or when composite datasets were applied.
Discussion
The accuracy and precision associated with different load-calculation methods and sampling strategies were investigated in this study. First, the results have highlighted the importance of high-flow events in delivering phosphorus to Loch Leven during the winter months, with 10 high-flow events contributing 79%, 84% and 63% of the winter TP, PP and SRP loads, respectively. The largest event alone contributed 34%, 49% and 17% of the ‘true’ TP, PP and SRP loads, respectively. Although intensive 2-hourly sampling was conducted in only one year, 2006 was not an unusual year in terms of rainfall and P loads. Rainfall measured in the northern part of the Loch Leven catchment in 2006 was 1200 mm, compared with an annual mean of 1061 mm (1992–2006), and catchment-wide monthly PP and SRP loads to Loch Leven for 2005 were highest in October and November 2005 (Defew 2008). The results support the findings of Jordan et al. (2005), who concluded that relatively few high-flow events deliver most of the P input to standing water bodies. So, accounting for the influence of high-flow events on P transport is crucial to estimating reliable P loads to a water body.
The results of this study confirm that different interpolation methods give different results and have a low degree of accuracy and precision. Methods A and B showed least variation between load estimates, but consistently and greatly underestimated P loads when based on weekly, daily and composite sampling strategies. This degree of underestimation was the result of using a time-weighted, rather than a flow-weighted, mean concentration value in the calculation procedure. Furthermore, it is likely that a flow-weighted composite sampling strategy would have yielded more accurate P load estimates than a time-weighted sampling strategy (Harmel et al. 2006). Interpolation Methods C, D and E showed a higher degree of accuracy but lower precision, as indicated by a wider range of over- and underestimated P loads. Notable overestimates by these three interpolation methods were specifically due to the inclusion of high-flow measures of Q and C in the calculation procedures. In general terms, although based on limited data, the results of this study tend to suggest that none of the common interpolation methods tested is capable of estimating P loads accurately or precisely, even when sampling frequency is increased to daily and datasets include high-flow events. They also raise concerns that the inclusion of storm event data can result in lower accuracy of calculated P loads if an inappropriate calculation method is used. It is, therefore, concluded that the use of interpolation methods is not the best approach to estimating P loads. Instead, sampling strategies should focus on collecting data that will enable the unique relationships between C and Q in different tributaries and catchments to be determined more accurately.
A commonly used alternative to interpolation methods has been the application of the log10-log10 regression method, together with a correction factor that was proposed by Stevens and Smith (1978) and Ferguson (1986) (Method G) to account for the variability in Q and C values between sampling occasions. This study found that this method resulted in more accurate values, but still resulted in load underestimation compared with that estimated from the 2-hourly sampling regime, despite application of the statistical correction factor designed to account for the inherent underestimation associated with the use of log-log linear regression models. Investigation of individual datasets showed that underestimation is a direct consequence of the specific range of Q and C values from which relationships were generated; daily data values explained the relationship between Q and C more precisely. These results support similar conclusions made by Webb et al. (1997), that frequency of sample collection is a key factor controlling the accuracy of P load estimates.
It has been suggested that storm chasing can increase the accuracy and precision of daily load estimates using extrapolation methods (Robertson and Roerish 1999; Soerens and Nelson 2002). The only datasets in this study to most accurately estimate loads were those comprising values of Q and C taken from the largest high-flow event (i.e. Fig. 2, event D) only. Datasets that included Q and C values from smaller high-flow events resulted in larger overestimations. This was due to an overestimation of P concentrations at higher flows, because P concentrations usually decline before discharge reaches its peak (Thomas and Lewis 1995; Bowes et al. 2009). The results from this study suggest that the log10-log10 extrapolation technique remains preferable to interpolation methods for generating the least inaccurate P load estimates for short periods and, to achieve the most accurate estimates of P loads, data should be collected at a minimum frequency of daily.
Interestingly, the results showed that the day and time of sampling affected the accuracy of the load estimates for weekly and daily sampling strategies, respectively. The implication of this for routine water-sampling programs is that the day and time of sampling should be varied to avoid systematic over- or underestimation of loads. Bowes et al. (2009) provide evidence that sampling was required at midday in the River Frome catchment in order to estimate P loads within 10% of ‘true’ loads. This study also supports the conclusion that daily sampling should be undertaken at a time of day that reflects nutrient-impacting activities in the catchment. However, although daily sampling did increase the accuracy of P load estimates for the Pow Burn, it was found that estimates were still unlikely to be within 10% of the ‘true’ load, particularly for PP and TP. This is a reflection of the relatively fast temporal changes in PP and TP concentrations that occur in response to increasing stream flow in contrast to SRP (see Fig. 2), perhaps reflecting small sewage point sources of SRP, as has been suggested in other UK rural catchments (e.g. Jarvie et al. 2006). Sampling protocols need to target the largest high-flow events to obtain the most reliable relationship between Q and C.
Conclusions
The results of this study show that commonly used interpolation methods and weekly sampling frequency are unlikely to give reliable estimates of P loads where temporal changes in stream flow and P concentrations happen very quickly in response to rainfall and surface runoff. In catchments where continuous stream flow data are available, the log10-log10 extrapolation method provides the most accurate load estimation on the basis of infrequent sampling. The accuracy of load estimates can be increased when using this extrapolation method by including C and Q values from the largest high-flow events, as the relationship between C and Q is better explained. Regulatory authorities should, therefore, begin to target high-flow events during their sampling programs if they cannot increase sampling frequency due to financial or resource constraints. However, there is little guidance or information available for determining suitable settings for high-flow monitoring in small watersheds (Harmel at al. 2003). It is recommended that, before the implementation of a sampling program, some knowledge be gained on the character of an individual catchment’s high-flow events (e.g. duration, flow ranges and pollutant behaviour). This information would aid the design and implementation of a successful monitoring program that is intended to provide a truly representative P load, whilst meeting financial constraints. This study also highlights the large degree of error that can occur when estimating P loads to water bodies and the difficulty that this may present when attempting to assess and interpret reductions in P loads as a result of nutrient reduction measures.
Acknowledgements
This work was funded by the Natural Environment Research Council (NERC) (Studentship no. NER/S/A/2004/12081) and the Scottish Environment Protection Agency (SEPA) Diffuse Pollution Initiative. The authors are grateful to SEPA for providing rainfall and river flow data, and for providing access to their sampling site.
References
Bailey-Watts, A. E., and Kirika, A. (1999). Poor water quality in Loch Leven (Scotland) since 1995 despite reduced phosphorus loadings since 1985: the influence of catchment management and inter-annual weather variation. Hydrobiologia 403, 135–151.| Poor water quality in Loch Leven (Scotland) since 1995 despite reduced phosphorus loadings since 1985: the influence of catchment management and inter-annual weather variation.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXjvFOrug%3D%3D&md5=59b320f6ef8fa6e551b89f9eae576caeCAS |
Bowes, M. J., Smith, J. T., and Neal, C. (2009). The value of high resolution nutrient monitoring: a case study of the River Frome, Dorset, UK. Journal of Hydrology 378, 82–96.
| The value of high resolution nutrient monitoring: a case study of the River Frome, Dorset, UK.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXht12htrjF&md5=ec9337002d2fbff437210e48efe6b88aCAS |
Cassidy, R., and Jordan, P. (2011). Limitations of instantaneous water quality sampling in surface-water catchments: comparison with near-continuous phosphorus time-series data. Journal of Hydrology 405, 182–193.
| Limitations of instantaneous water quality sampling in surface-water catchments: comparison with near-continuous phosphorus time-series data.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXoslCmsb8%3D&md5=2f931e6c3270e9cfc1fbea4fc9b4b661CAS |
Defew, L. (2008). The influence of high flow events on phosphorus delivery to Loch Leven, Scotland, UK. Ph.D. Thesis, University of Edinburgh.
Eisenreich, S. J., Bannermann, R. T., and Armstrong, D. E. (1975). A simplified phosphorus analytical technique. Environmental Letters 9, 43–53.
| A simplified phosphorus analytical technique.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE28XltlShurw%3D&md5=2fb88e7abd90e42d8bee52fe7746d395CAS |
Evans, D. J., and Johnes, P. J. (2004). Physico-chemical controls on phosphorus cycling in two lowland streams. Part 1 – the water column. The Science of the Total Environment 329, 145–163.
| Physico-chemical controls on phosphorus cycling in two lowland streams. Part 1 – the water column.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXlvVWmt7s%3D&md5=bab4f7d90c091c16369fa65b76173c6fCAS | 15262164PubMed |
Ferguson, R. I. (1986). River loads underestimated by ratings curves. Water Research 22, 74–76.
| River loads underestimated by ratings curves.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXksl2gsL0%3D&md5=76504d7d86c233f3276b61443867ecbaCAS |
Foy, R. H. (2007). Variation in the reactive phosphorus concentrations in rivers of northwest Europe with respect to their potential to cause eutrophication. Soil Use and Management 23, 195–204.
| Variation in the reactive phosphorus concentrations in rivers of northwest Europe with respect to their potential to cause eutrophication.Crossref | GoogleScholarGoogle Scholar |
Greig, S. M. (2005). Trends in diffuse pollution: data report to assist with the design and implementation of effective diffuse pollution monitoring programmes. Scottish Environment Protection Agency, Diffuse Pollution Initiative, Special Report 19.
Haan, C. T. (2002). ‘Statistical Methods in Hydrology.’ 2nd edn. (Iowa State University Press: Ames, IA.)
Harmel, R. D., and King, K. W. (2005). Uncertainty in measured sediment and nutrient flux in runoff from small agricultural watersheds. Transactions of the American Society of Agricultural Engineers 48, 1713–1721.
| 1:CAS:528:DC%2BD2MXht1OktLnO&md5=5e824c8bcdef9fd08e95af8ae614060dCAS |
Harmel, R. D., King, K. W., and Hauck, L. (2003). Automated storm water sampling strategies on small watersheds. Applied Engineering in Agriculture 19, 667–674.
Harmel, R. D., King, K. W., Haggard, B. E., Wren, D. G., and Sheridan, J. M. (2006). Practical guidance for discharge and water quality data collection on small watersheds. Transactions of the American Society of Agricultural and Biological Engineers 49, 937–948.
Haygarth, P. M., and Jarvis, S. C. (1996). Soil derived phosphorus in surface runoff from grazed grassland lysimeters. Water Research 31, 140–148.
Haygarth, P. M., Condron, L. M., Heathwaite, A. L., Turner, B. L., and Harris, G. P. (2005). The phosphorus transfer continuum: linking source to impact with an interdisciplinary and multi-scaled approach. The Science of the Total Environment 344, 5–14.
| 1:CAS:528:DC%2BD2MXktlCiur8%3D&md5=c23cec35c4565b276dffb464b5c9b57cCAS | 15907506PubMed |
Jarvie, H. P., Neal, C., and Withers, P. J. A. (2006). Sewage-effluent phosphorus: a greater risk to river eutrophication than agricultural phosphorus? The Science of the Total Environment 360, 246–253.
| Sewage-effluent phosphorus: a greater risk to river eutrophication than agricultural phosphorus?Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XjvFClsrg%3D&md5=a68914ea9ef92ff3a26615ac34e4d31bCAS | 16226299PubMed |
Johnes, P. (2007). Uncertainties in annual riverine phosphorus load estimation: impact of load estimation methodology, sampling frequency, baseflow index and catchment population density. Journal of Hydrology 332, 241–258.
| Uncertainties in annual riverine phosphorus load estimation: impact of load estimation methodology, sampling frequency, baseflow index and catchment population density.Crossref | GoogleScholarGoogle Scholar |
Jordan, P., and Cassidy, R. (2011). Technical Note: Assessing a 24/7 solution for monitoring water quality loads in small river catchments. Hydrology and Earth System Sciences 15, 3093–3100.
Jordan, P., Arnscheidt, A., McGrogan, H., and McCormick, S. (2005). High resolution phosphorus transfers at the catchment scale: the hidden importance of non-storm transfers. Hydrology and Earth System Sciences 9, 685–691.
| High resolution phosphorus transfers at the catchment scale: the hidden importance of non-storm transfers.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XktVOmsrs%3D&md5=bf58cd2e5dd54317b29998902e2968dbCAS |
Jordan, P., Melland, A. R., Mellander, P.-E., Shortle, G., and Wall, D. (2012). The seasonality of phosphorus transfers from land to water: implications for trophic impacts and policy evaluation. The Science of the Total Environment 434, 101–109.
| The seasonality of phosphorus transfers from land to water: implications for trophic impacts and policy evaluation.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38Xht1ahsr3E&md5=cdb38966e23b3adee066bf2441c3cc75CAS | 22425173PubMed |
King, K. W., and Harmel, R. D. (2003). Considerations in selecting a water quality sampling strategy. Transactions of the American Society of Agricultural Engineers 46, 63–73.
Kristensen, P., and Bøgestrand, J. (1996). ‘Surface Water Quality Monitoring.’ (EEA: Copenhagen.)
May, L., and Spears, B. (2012). Loch Leven: 40 years of scientific research – Understanding the links between pollution, climate change and ecological response. Developments in Hydrobiology 218. 132 pp.
Murphy, J., and Riley, J. P. (1962). A modified single solution method for the determination of phosphate in natural waters. Analytica Chimica Acta 27, 31–36.
| A modified single solution method for the determination of phosphate in natural waters.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF38XksVyntr8%3D&md5=5ea19289e2b04e8c9a62a02e1ed997fdCAS |
Ongley, E. D. (1973). Sediment discharge from Canadian basins into Lake Ontario. Canadian Journal of Earth Sciences 10, 146–156.
| Sediment discharge from Canadian basins into Lake Ontario.Crossref | GoogleScholarGoogle Scholar |
Phillips, J. M., Webb, B. W., Walling, D. E., and Leeks, G. J. L. (1999). Estimating suspended sediment loads in the LOIS study area using infrequent samples. Hydrological Processes 13, 1035–1050.
| Estimating suspended sediment loads in the LOIS study area using infrequent samples.Crossref | GoogleScholarGoogle Scholar |
Poinke, H. B., Gburek, W. J., Schnabel, R. R., Sharpley, A. N., and Elwinger, G. F. (1999). Seasonal flow, nutrient concentrations and loading patters in stream flow draining an agricultural hill-land watershed. Journal of Hydrology 220, 62–73.
Rekolainen, S., Posch, M., Kaemaeri, J., and Ekholm, P. (1991). Evaluation of the accuracy and precision of annual phosphorus load estimates from two agricultural basins in Finland. Journal of Hydrology 128, 237–255.
| Evaluation of the accuracy and precision of annual phosphorus load estimates from two agricultural basins in Finland.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK38Xms1Krtg%3D%3D&md5=adb3e14f005ff3de17d3dd6f181ce61cCAS |
Robertson, D. M., and Roerish, E. D. (1999). Influence of various water quality sampling strategies on load estimates for small streams. Water Resources Research 35, 3747–3759.
| Influence of various water quality sampling strategies on load estimates for small streams.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXit1yrtQ%3D%3D&md5=b8e20be2acc71b854f1e52664a4c124fCAS |
Rodda, J. C., and Jones, G. N. (1983). Preliminary estimates of loads carried by rivers to estuaries and coastal waters around Great Britain derived from the Harmonised Monitoring Scheme. Journal of the Institution of Water Engineers and Scientists 37, 529–539.
Schindler, D. W., Hecky, R. E., Findlay, D. L., Stainton, M. P., Parker, B. R., Paterson, M. J., Beaty, K. G., Lyng, M., and Kasian, S. E. (2008). Eutrophication of lakes cannot be controlled by reducing nitrogen input: results of a 37-year whole-ecosystem experiment. Proceedings of the National Academy of Sciences of the United States of America 105, 11254–11258.
| Eutrophication of lakes cannot be controlled by reducing nitrogen input: results of a 37-year whole-ecosystem experiment.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVShurrI&md5=cb3c4a57f8146cd9b5b23b7a0f688150CAS | 18667696PubMed |
Sharpley, A. N. (2008). Phosphorus loads from an agricultural watershed as a function of storm size. Journal of Environmental Quality 37, 362–368.
| Phosphorus loads from an agricultural watershed as a function of storm size.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXjsVWksLk%3D&md5=ed5b19d2e8fdafa63ea1bc703a42a448CAS | 18268298PubMed |
Soerens, T. S., and Nelson, M. A. (2002). Sampling strategies for determining nutrient loads in streams. In ‘Proceedings of the National Monitoring Conference, Monona Terrace Convention Centre, Madison, WI, 20–23 May 2002’. (National Water Quality Monitoring Council.)
Stevens, R. J., and Smith, R. V. (1978). A comparison of discrete and intensive sampling for measuring river loads of nitrogen and phosphorus in the Lough Neagh system. Water Research 11, 631–636.
Tate, K. W., Dahlgren, R. A., Singer, M. J., Allen-Diaz, B., and Atwill, E. R. (1999). Timing, frequency of sampling affects accuracy of water-quality monitoring. California Agriculture 53, 44–48.
| Timing, frequency of sampling affects accuracy of water-quality monitoring.Crossref | GoogleScholarGoogle Scholar |
Thomas, R. B., and Lewis, J. (1995). An evaluation of flow stratified sampling for estimating suspended sediment loads. Journal of Hydrology 170, 27–45.
| An evaluation of flow stratified sampling for estimating suspended sediment loads.Crossref | GoogleScholarGoogle Scholar |
Verhoff, F. H., Yakish, S. M., and Melfi, D. A. (1980). River nutrient and chemical transport estimates. Journal of the Environmental Engineering Division 10, 591–608.
Wade, A. J., Palmer-Felgate, E. J., Halliday, S. J., Skeffington, R. A., Loewenthal, M., Jarvie, H. P., Bowes, M. J., Greenway, G. M., Haswell, S. J., Bell, I. M., Joly, E., Fallatah, A., Neal, C., Williams, R. J., Gozzard, E., and Newman, J. R. (2012). From existing in situ, high-resolution measurement technologies to lab-on-a-chip – the future of water quality monitoring? Hydrology and Earth System Sciences 9, 6457–6506.
| From existing in situ, high-resolution measurement technologies to lab-on-a-chip – the future of water quality monitoring?Crossref | GoogleScholarGoogle Scholar |
Walling, D. E., and Webb, B. W. (1981). The reliability of suspended sediment load data. In ‘Erosion and Sediment Transport Measurement’. (Eds D. Walling and P. Tacconi.) IAHS Publication no. 133, pp. 177–194. (IAHS Press: Wallingford, UK.)
Walling, D. E., Russell, M. A., and Webb, B. W. (2001). Controls on the nutrient content of suspended sediment transport by British Rivers. The Science of the Total Environment 266, 113–123.
| Controls on the nutrient content of suspended sediment transport by British Rivers.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXhtFSmsrs%3D&md5=b18ad685b903e75bd932175f954049e8CAS | 11258807PubMed |
Webb, B. W., Phillips, J. M., Walling, D. E., Littlewood, I. G., Watts, C. D., and Leeks, G. J. L. (1997). Load estimation methodologies for British rivers and their relevance to the LOIS RACS programme. The Science of the Total Environment 194–195, 379–389.
| Load estimation methodologies for British rivers and their relevance to the LOIS RACS programme.Crossref | GoogleScholarGoogle Scholar |


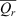 = mean discharge for period of record using continuous measures of Q (m3 s–1).
= mean discharge for period of record using continuous measures of Q (m3 s–1). 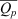 = mean discharge for interval between samples (m3 s–1). Cc = estimate of P concentration from continuous stream flow value. Qc = direct measurement or estimate of continuous stream flow (m3 s–1). m = slope of linear regression. b = intercept of linear regression
= mean discharge for interval between samples (m3 s–1). Cc = estimate of P concentration from continuous stream flow value. Qc = direct measurement or estimate of continuous stream flow (m3 s–1). m = slope of linear regression. b = intercept of linear regression


