Hierarchical variance decomposition of fish scale growth and age to investigate the relative contributions of readers and scales

Additional keywords: introduced species, measurement errors, sampling strategy, scalimetry.

Understanding patterns of natural variability is a major issue in evolutionary ecology, because variability can be described at the taxonomic, community, population, individual and evolutionary levels (Landres et al. 1999). However, populations have long been studied without concern for individual variability or inter-relationships within populations (Łomnicki 1999). With the rise of the holistic approach, most recent studies confound the organisational components of ecosystems from the individual level to the ecosystem organisational level. In particular, individuals in a population obviously differ in terms of behaviour, habitat use, reproduction or migratory strategy to optimise their fitness (Roff 1996; Fromentin et al. 2009).

Interindividual variability has attracted much attention during the past two decades because it could have severe consequences on the estimation of population dynamics. Thus, identifying sources of variability underlying interindividual differences is important for developing relevant sampling designs aimed at answering evolutionary questions with appropriate statistical power (Johnson et al. 2015). In this field, significant developments have been based largely on the use of mixed and individual-based modelling that explicitly considers individuals as variable entities (Baayen et al. 2008; Thorson and Minto 2015). As an example, in fish biology, as with many other taxa, individual growth is modelled using the von Bertalanffy growth function (VBGF). Growth parameters are highly dependent upon an accurate description of the individual age–length relationship (Hatch and Jiao 2016). Moreover, estimates of individual growth in population models can be significantly different while accounting for or failing to account for interindividual variability, leading to evolutionary misinterpretations or to inappropriate conservation decisions (Shelton and Mangel 2012; Vincenzi et al. 2014; Harris et al. 2018).

Teleost scales are an important and widely used tool in ichthyological studies (Goodrich 1907; Panfili et al. 2002). Among other applications, scales provide access to life history traits, such as age (Erickson 1983), growth (Kipling 1962; Ottaway 1978) and migration (Bagenal et al. 1973). Readings of the calcified structure can provide accurate estimates of growth and age at both daily and yearly scales. This offer a basis for recording growth patterns from the individual to the population level (Casselman 1990; Schreck and Moyle 1990). Over time, researchers have come to accept that analysing several scales from the same individual provides more reliable information (Panfili et al. 2002). On a theoretical basis, the number of scales required to determine growth and age depends on the species studied (Chilton and Beamish 1982), but the reason for using a given number of scales is rarely mentioned explicitly in the literature. In addition, inconsistency appears among studies dealing with the same fish species for the same purpose. Even if the accuracy of age data has been demonstrated in the published papers initially (Dahl 1907; Ward Cutler 1918; through mark–recapture datasets), Beamish and McFarlane (1983) pointed out that only a few consecutive studies have re-examined the methodology of those initial studies. Campana (2001) and Spurgeon et al. (2015) concluded that over the past 30 years the number of age validation studies has increased; however, there are still some deficiencies in integrating variability in models or in justifying the selected methods. Given the prominent importance of individual variation, the number of scales used for recording relevant individual life history (age, growth, migration) is a matter of interest. Setting up a sampling design with the minimum number of scales required is, indeed, a reasonable shortcut to avoid redundancy and a waste of resources. Variability in growth and age among individuals can be assessed by means of repeatability (characterised as the degree of agreement among measurements). By delineating annuli (yearly rings deposited during winter) and measuring the associated interannuli spacing, one can estimate an individual’s growth trajectory and migratory status (Elliott and Chambers 1996); however, measurements may vary across readers and scales. Therefore, establishing measurement repeatability is important in order to disentangle methodological from biological variance and to increase reliability in the study of evolutionary patterns.

To investigate to what extent biological variability in scale growth and age arises from either individual variation or methodological variation, the brown trout (Salmo trutta) was used as a case study. Variation in scale growth and age was decomposed in an explicit nested quantitative manner (i.e. extracting the respective contribution of readers, scales and individuals). Decomposition of variance is necessary to assess the sensitivity of growth and ageing measurements to realistic levels of scale or reader variability and to efficiently reallocate laboratory time to ecological issues.

The brown trout is a facultative anadromous salmonid species (Acolas et al. 2012; Dodson et al. 2013), with some individuals spending their entire life cycle in fresh water (resident fish), whereas others migrate to sea (anadromous fish). Among other salmonids, brown trout was successfully introduced into a dozen rivers in the subantarctic Kerguelen Islands between 1955 and 1979. This archipelago, located in the Southern Ocean (49°S, 70°E), was previously a fish-free landscape. The complete history of salmonid introduction to the islands is recounted in Lecomte et al. (2013). Since the introduction of fish to the Kerguelen Islands, long-term monitoring has been implemented for a better understanding of the causes and processes of colonisation (Labonne et al. 2013).

To test for the robustness of observations of the growth and age of captured brown trout, three streams with contrasting environments were selected, namely the Norvégienne, Manchot and Rohan rivers (Fig. 1), hereafter named Norvegienne, Manchot and Rohan respectively. The main characteristics of the streams are described in Table 1. Electro- and net fishing were conducted between 2010 and 2016. Because brown trout is a migratory species, resident and anadromous fish (hereafter referred to as ‘phenotype’) were primarily identified based on morphological criteria: length–weight relationship (Jonsson 1985) and colouration (Quigley et al. 2006). A total of 60 brown trout were analysed, with 20 individuals per site in a calibrated resident : anadromous fish ratio of 75% resident : 25% anadromous for Rohan and 55 : 45% for the two other streams (Table 2). The fork length (FL) of the fish at capture ranged from 88 to 770 mm (mean ± s.d., 333.2 ± 183.2 mm).

Fig. 1.  Locations of the studied streams in the Kerguelen Islands. The locations of the streams are shown on the right, with names and year of colonisation by salmonids.

Table 1.  Catchment details for the Rohan, Manchot and Norvegienne streams
The date of colonisation for each of the streams is given as year. Additional descriptions of the estuary and proximity to first neighbouring stream are provided

Table 2.  Details of fish sampled for the Rohan, Manchot and Norvegienne streams
Characteristics are given by phenotype (anadromous or resident) and stream. Unless indicated otherwise, data are given as the mean ± s.d.

Because the scales collected could be damaged and thus rendered useless by regeneration (Borgenson et al. 2014) and resorption (Kacem et al. 2013), numerous scales from each fish were removed from the optimal zone, specifically the second rank, below the dorsal fin and above the lateral line (Elliott and Chambers 1996). For each fish, four scales that were not regenerated nor resorbed were selected and investigated (Bereiter-Hahn and Zylberberg 1993). Selected scales were mounted and photographed (original scale in micrometres) under transmitted light using a stereomicroscope (Olympus SZX-16) and attached camera (Olympus DP72). Photographs were processed and saved using CellSens Entry microimaging software. Ageing and measurements were done by two readers (F. Guéraud and L. Aulus-Giacosa) with different degrees of expertise (2 v. 10 years’ experience) using ImageJ software (ver. 1.51u, National Institutes of Health, see https://imagej.net/Downloads; Abràmoff et al. 2004) on a total of 240 scales in a double-blind and independent manner.

Anadromous fish were distinguished from resident fish because the growth rate of brown trout in fresh water is generally less than the growth rate recorded at sea (Elliott and Chambers 1996; Jarry et al. 2018). Because scale growth is used as a proxy for somatic growth, an increase in the intercirculi spacing on scales is a good proximate indicator of migration. This criterion was used for anadromous fish to determine the size of scales at migration (measured from the core to the circulus corresponding to migration) and age at migration (counts of annuli until the intercirculi spacing increases).

Age was determined by counting the number of annuli on a scale (Borgenson et al. 2014) and total age (TA) was recorded. Freshwater age (FA) corresponds to the number of years spent in freshwater. For anadromous fish, FA was determined by counting the number of annuli before marine migration using the criterion of intercirculi spacing. For resident fish, FA was equal to TA.

Scale growth (interannuli spacing; µm) was measured along the main longitudinal axis from the core to the total radius (TR). The freshwater radius (FR) corresponds to freshwater growth. For anadromous fish, FR was measured on a scale from the core until the circulus before migration according to the criterion of intercirculi spacing. For resident fish, FR was equal to TR. The mean (±s.d.) position of the annuli for freshwater growth are given in Table 3. Further details on the mean position and mean freshwater growth by phenotype are given in Fig. S1, available as Supplementary material to this paper.

Table 3.  Mean position of annuli recorded on scales categorised by age at capture

Variance was decomposed hierarchically in a nested and crossed manner, namely fish–reader–scale (Fig. 2) to determine which levels account for the variance in growth and age. Sixty fish were sampled from three populations (Population) with samples taken from two phenotypes (Phenotype). For each fish (Fish), two readers (F. Guéraud and L. Aulus-Giacosa) (Reader) made independent readings on four selected scales (Scale) in a double-blind manner (i.e. two readers independently read each scale; this could be done on several scales for each fish).

Fig. 2.  Schematic drawing of the hierarchically crossed design of the study Fish–Reader–Scale.

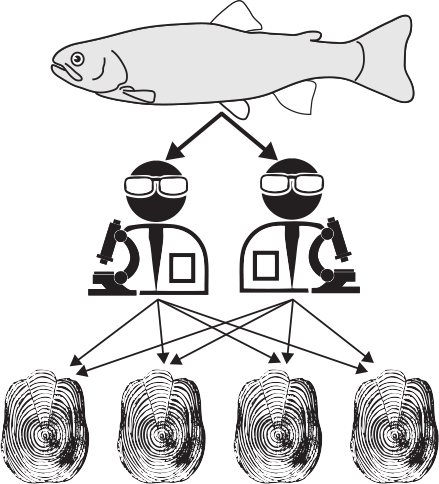
To decompose the variance, two response variables were examined through measurements of repeatability (r). The repeatability of scale measurements (an approximation of somatic growth) and age estimates was investigated. Repeatability ranges from 0 to 1 and expresses the proportion of variation explained by the considered level (Bell et al. 2009; Wolak et al. 2012). For each variable, the value taken by r is the proportion of variance explained by the variable and reflects its contribution to overall variance. To estimate repeatability, we used the newly developed method from Stoffel et al. (2017) as implemented in the rptR R package (ver. 0.9.21, see https://cran.r-project.org/web/packages/rptR/index.html; in R, ver. 3.4.4, R Foundation for Statistical Computing, Vienna, Austria). This package fits mixed-effects models by parametric bootstrapping (two Monte Carlo simulation steps) to quantify the uncertainty of repeatability. In our case, we simulated models with 1000 parametric bootstraps and tested the null hypothesis using a likelihood ratio test.

Population and Phenotype were both added as fixed effects in the variance decomposition. Fish, Reader and Scale were considered random variables to explain the variance of scale growth and age. Because growth is sharply contrasted between marine and freshwater habitats, we considered Phenotype as a fixed effect. Similarly, Population was considered a fixed effect because it maximised the log-likelihood.

In addition, we considered Reader as random because we hypothesised that readings subjectively correlated with scales and therefore should more widely reflect the inter-reader effect. Calculations considering Reader as a fixed effect were also performed and did not change the results (Fig. S2). To compare phenotype, we omitted the Phenotype fixed effect and accordingly divided the datasets into two parts, each of them being analysed as stated previously (focusing exclusively on Fish, Reader and Scale effects).

For the present study, variables related to age (FA and TA) were treated as Poisson-distributed data (Chi-Square goodness of fit for Poisson distribution, P = 1.70 × 10^–14 for TA and P = 1.00 × 10^–8 for FA) and scale growth was approximated and treated as Gaussian (D’Agostino normality test, P_{Skewness Test} = 2.55 × 10^–9, P_{Kurtosis Test} = 1.30 × 10^–1 for TR; P_{Skewness Test} = 1.10 × 10^–13, P_{Kurtosis Test} = 0.01 for FR). Codes and fully worked examples are available in SCRIPT.R and data.RData of the Supplementary material. The results for r are given with 95% confidence intervals (CI) and the P-value of the likelihood ratio test. For the Poisson-distributed data, the original scale approximations were used because they are the exact solution of the general linear mixed model (GLMM) compared with link scales approximations, which are approximations; however, in this study, the two approximations gave very similar results.

Population accounted for most of the variance (~40% for growth measures (TR, FR) and 15% for annuli counts (TA, FA)), highlighting an important contrast among the three localities in terms of growth and age.

Variance in growth as interpreted with scale measurements was primarily explained by interindividual differences. Exact values of repeatability are given in Table 4 with 95% CIs and P-values. Fish alone explained more than 96% of the phenotypic variance of TR (Fig. 3a) and 53% of FR (Fig. 4a). By contrast, the proportions of variance explained by Reader and Scale were not consistent in the decomposition of growth (Fig. 3b, c, 4b, c). For both TR and FR, the combined effect of Reader and Scale corresponded to <1% of the total variance and Reader for FR. In addition, growth was harder to decompose for anadromous fish. Although Phenotype was not consistent in accounting for the variance of TR (r = 4.55 × 10^–3; 95% CI 6.71 × 10^–4–1.36 × 10^–2), its effect on FR became greater (r = 0.364; 95% CI 0.202–0.536), reflecting the difficulty of locating the circulus corresponding to migration at sea.

Table 4.  Mean repeatability estimates (r) of scale growth (total and freshwater radii) according to Fish, Reader, Scale and Phenotype, with corresponding 95% confidence intervals (CIs) and P-values
Scale growth (interannuli spacing) was measured along the main longitudinal axis from the core to the total radius (TR); the freshwater radius (FR) corresponds to freshwater growth. Significant P-values are denoted by: ***, P ≤ 0.01; and **, 0.01 < P ≤ 0.05. There are no P-values for Phenotype because it was considered a fixed effect in the repeatability model and so was not included in the calculation of ratios of variance per se

Fig. 3.  Variance decomposition of measures made on the total radius of scales (TR). Symbols and dashed lines indicate the median of the repeatability estimates (r) for (a) Fish, (b) Reader and (c) Scale, with uncertainty (i.e. 95% confidence intervals) indicated, obtained over 1000 bootstraps.

Fig. 4.  Variance decomposition of measurements made on the freshwater radius (FR), which corresponds to freshwater growth. Symbols and dashed lines indicate the median of the repeatability estimates (r) for (a) Fish, (b) Reader and (c) Scale, with uncertainty (i.e. 95% confidence intervals) indicated, obtained over 1000 bootstraps.

Exact values of repeatability are given in Table 5, with 95% CIs and P-values. Fish explained the main proportion of the variance in ages read on scales: 53% for TA (Fig. 5a) and almost 40% for FA (Fig. 6a). By contrast, Reader and Scale were inconsistent factors for explaining the variance in TA and FA (Fig. 5b, c, 6b, c; Table 5). In addition, Phenotype explained 2% of the variance in TA and 6% in FA. Contrary to measures of growth (TR and FR), Phenotype explained a greater proportion of variance in age models (TA and FA), meaning that environmental conditions (i.e. freshwater v. marine) increase the difficulty of age readings, especially for anadromous fish, where an age at migration had to be determined. The number of annuli counted before migration (FA) was less repeatable than total age (TA) for Fish (r = 0.392 and 0.539 respectively; Fig. 5a, 6a).

Table 5.  Mean repeatability estimates (r) of age (total and freshwater) according to Fish, Reader, Scale and Phenotype, with corresponding 95% confidence intervals (CIs) and P-values
Total age (TA) was determined by counting the number of annuli on a scale (Borgenson et al. 2014); freshwater age (FA) corresponds to the number of years spent in freshwater. Significant P-values are denoted by: ***, P ≤ 0.01; and **, 0.01 < P ≤ 0.05. There are no P-values for Phenotype because it was considered a fixed effect in the repeatability model and so was not included in the calculation of ratios of variance per se

Fig. 5.  Variance decomposition of total age (TA). Symbols and dashed lines indicate the median of the repeatability estimates (r) for (a) Fish, (b) Reader and (c) Scale, with uncertainty (i.e. 95% confidence intervals) indicated, obtained over 1000 bootstraps.

Fig. 6.  Variance decomposition of freshwater age (FA), which corresponds to the number of years spent in fresh water. Symbols and dashed lines indicate the median of the repeatability estimates (r) for (a) Fish, (b) Reader and (c) Scale, with uncertainty (i.e. 95% confidence intervals) indicated, obtained over 1000 bootstraps.

The results obtained by separating Phenotypes are given in Table 6. Because TR was equal to FR and TA was equal to FA for resident fish, the results are the same for both pairs of variables. Variance decomposition was globally similar between resident and anadromous fish, with the notable exception of FA and, to a lesser extent, FR. The variance explained by Fish was reduced for FA and FR compared with TR and TA respectively for anadromous fish, highlighting the difficulty and subjectivity in locating the circulus corresponding to age at migration. The repeatability of interindividual differences in FA was sharply reduced for anadromous fish compared with resident fish (r = 0.167 and 0.584 respectively). In addition to the abovementioned fact that Phenotype has a noteworthy effect on FA decomposition, the proportion of variance in TR explained by Fish remains high for any phenotype, supporting our previous results that total scale growth is primarily explained by interindividual differences, regardless of Reader and Scale.

Table 6.  Mean repeatability estimates (r) for scale growth and age according to by Phenotype (resident v. anadromous)
Scale growth (interannuli spacing) was measured along the main longitudinal axis from the core to the total radius (TR); the freshwater radius (FR) corresponds to freshwater growth. Total age (TA) was determined by counting the number of annuli on a scale (Borgenson et al. 2014); freshwater age (FA) corresponds to the number of years spent in freshwater. CI, confidence interval

The motivating problem for our study was how to most effectively sample, based on biological variance, in order to appropriately model dynamics. Apart from the consensus acceptance that the correct zone for sampling scales in salmonids is the first rows around the lateral line between the pectoral and the anal fins (Ombredane and Richard 1990) and that measures have to be taken along the major scale axis (maximal length from the core of the scale to the border), the number of scales that need to be read to explain relevant individual information is still vague in the literature. Furthermore, a statistical issue in scalimetry is how many scales from fish should be used to improve precision in readings (Haraldstad et al. 2016).

Decomposition of repeatability on growth and age was performed and shows that most of the variability in repeatability is attributable to Fish. More generally, at least 50% of the interindividual variance is related to real interindividual variability, not to methodological or artefactual issues (Scale or Reader related), when investigating growth and TA. TR had the highest Fish repeatability, regardless of the reader and the chosen scale; therefore, increasing the number of scales examined is not necessary for capturing interindividual variability in growth because no significant effect has been recorded for Scale.

This study also suggests further issues associated with identifying migration. Compared with total variables (i.e. TR and TA), both freshwater variables (FR and FA) exhibited lower Fish repeatability, highlighting the difficulty and subjectivity in locating the migration point; however, the results arising from the global dataset encompass two distinct phenotypes. Consequently, when separating the phenotype into two datasets, we observed that the repeatability of Fish increased for FR (by a factor of 2) and decreased for FA (by a factor of 3). Those results globally confirmed that the determination of size through scale size and age at migration is a difficult task. Given the importance of this task to studies aiming to investigate ecological or evolutionary patterns of migration in many anadromous fish species, it is essential to quantify the uncertainty associated with locating the migration point.

In this paper, as in many others (Kimura and Lyons 1991), the percentage of agreement in age estimations between readers was reasonably low: 65 and 60% for TA and FA respectively. The difficulty for readers in ageing fish from multiple structures (scales, otoliths) has long been an issue in many species. To avoid a potential lack of precision, some studies have made the choice to only conserve scales where agreement between scales or readers was established. Nevertheless, by doing so, only a fraction of a fish’s life history may be selected and investigated. Consequently, the variability of life histories present in a population may be biased towards some more understandable pattern that does not necessarily reflect overall natural variability. Alternatively, one can estimate in a quantitative way the respective contributions of readers, scales and individuals to the precision of the information to be analysed. Quantifying the effect of those confounding factors allows extraction of relevant interindividual variability. Only such a decomposition can determine the legitimacy of ignoring scale-related variance. Even if methodological biases in interindividual variability are not significant in this study, they could be substantially reduced by appropriately quantifying reader variance by stream and environment (freshwater v. marine).

The present study provides a case study that quantifies the sources of variance in age and size. Because errors frequently arise either from disagreements between scales or between readers, associated variances should be explicitly integrated into admitting-errors models, such as growth models (Cope and Punt 2007; Shelton and Mangel 2012; Hatch and Jiao 2016). This is particularly true in an evolutionary context when the proper determination of fish length and age at migration, used as threshold traits in the decision to migrate, is necessary to produce reaction norms for migration (Dieckmann and Heino 2007; Hutchings 2011; Jonsson et al. 2016). Indeed, preliminary analysis to quantify errors should be a prerequisite to any study because it could provide valuable insights for accurate modelling of individual variability. Such understanding of interindividual variability should serve to better estimate population dynamics and could have several applications in stock assessment and conservation (Harris et al. 2018).

Inferring growth for fish or other taxa intrinsically depends on an accurate description of the age–length relationship, which may be undermined by measurement errors and ageing errors. Growth is an important life history trait potentially associated with fitness through sexual maturity and the mortality rate (Pettersson et al. 1996; Wysujack et al. 2009). In many taxa, such as mammals (English et al. 2012), birds (Tjørve and Tjørve 2010) or reptiles (Lehman and Woodward 2008), growth is widely modelled using the VBGF (Von Bertalanffy 1938). Not considering individual variability may lead to over- or underestimation of the VBGF parameters such as theoretical maximum length L_∞ and the growth coefficient k (Vincenzi et al. 2014, 2016; Harris et al. 2018; see Fig. S3; Table S1). Such errors affect our ability to understand the evolution of life history traits by comparing populations whose locations differ at different times.

A surprisingly high number of studies ignore the decomposition of variance and the implications of their methodologies on the estimation of parameters. Every researcher aims to answer a scientific issue while designing effective studies in terms of both time and funding. Not extending enough effort in data acquisition leads to underpowered analysis, whereas the reverse leads to overpowered analysis. The waste of resources can be considerable in both cases (Wolak et al. 2012; Johnson et al. 2015). Repeatability is an important feature in research, both to be able to reproduce our own studies and to compare with others (Cassey and Blackburn 2006). Unfortunately, the rationale for using a given scalimetric method in fish biology is rarely discussed, and even neglected; therefore, it is sometimes nearly impossible to access the precise methodology (numbers of scales or readers), precluding exact reproduction of experiments. In the present study, the data highlight the importance of individual variability within populations of brown trout in the Kerguelen Islands and enable us to avoid the unnecessary and time-consuming use of multiple scale readings (see Fig. S3; Table S1). In other contexts, the methodological approach (numbers of readers and scales by fish) should be similarly justified and discussed on a case-by-case basis.

In conclusion, decomposition of variance should be a prerequisite to any study aiming to quantify population dynamics through the growth of individuals. If neglecting methodological variance has an effect on the variables studied, the time spent in the laboratory cannot be adequately allocated to focus on biological variability. In addition, failing to disentangle the effects of biological and methodological variance could prevent the relevant investigation of ecological and evolutionary patterns.

The authors declare that they have no conflicts of interest.

This research did not receive any specific funding.