How large is the carbon isotope fractionation of the photorespiratory enzyme glycine decarboxylase?
Guillaume TcherkezLaboratoire d’Ecophysiologie Végétale, CNRS UMR 8079, Bâtiment 362, Université Paris XI, 91405 Orsay, France. Email: guillaume.tcherkez@ese.u-psud.fr
Functional Plant Biology 33(10) 911-920 https://doi.org/10.1071/FP06098
Submitted: 26 April 2006 Accepted: 2 August 2006 Published: 2 October 2006
Abstract
Despite the intense effort developed over the past 10 years to determine the 12C / 13C isotope fractionation associated with photorespiration, much uncertainty remains about the amplitude, and even the sign, of the 12C / 13C isotope fractionation of glycine decarboxylase, the enzyme that produces CO2 during the photorespiratory cycle. In fact, leaf gas-exchange data have repeatedly indicated that CO2 evolved by photorespiration is depleted in 13C compared with the source material, while glycine decarboxylase has mostly favoured 13C in vitro. Here I give theoretical insights on the glycine decarboxylase reaction and show that (i), both photorespiration and glycine decarboxylation must favour the same carbon isotope — the in vitro measurements being probably adulterated by the high sensitivity of the enzyme to assay conditions and the possible reversibility of the reaction in these conditions, and (ii), simplified quantum chemistry considerations as well as comparisons with other pyridoxal 5′-phosphate-dependent decarboxylases indicate that the carbon isotope fractionation favour the 12C isotope by ~20‰, a value that is consistent with the value of the photorespiratory fractionation (f) obtained by gas-exchange experiments.
Acknowledgments
This paper is dedicated to Prof. Christine Buffet who strongly supported me during the time of this work. I warmly thank Prof. Graham Farquhar for helpful discussions and the critical reading of the manuscript. I also thank the anonymous reviewers for their helpful comments.
Abell LM, O’Leary MH
(1988) Isotope effect studies of the pyridoxal 5′-phosphate dependent histidine decarboxylase from Morganella morganii. Biochemistry 27, 5927–5933.
| Crossref | GoogleScholarGoogle Scholar | PubMed |
simplifies to:

so that the observed isotope effect is given by:

As expected, the expression of the observed isotope effect given by Eqn A4 is identical to the usual formula used by O’Leary (1980).
If k3 is, on the contrary, very small, e.g. because of NAD+-limited conditions, and is then negligible compared with k–2, k3 disappears in the denominator of Eqn A2, and Eqn A1 rearranges to: v / *v = −1. This is a consequence of the steady-state condition imposed on M. In other words, we have an equilibrium system, and when the full equilibrium is reached, we have the following relationships:
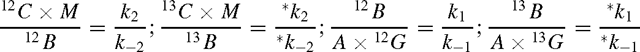
which may be combined to:
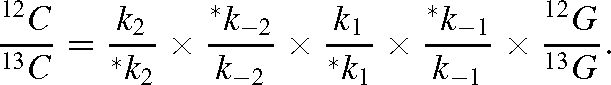
This gives, using the α notation of isotope effects for each individual reaction:

That is, using thermodynamic isotope effects:

with the additional relationships α1therm = α1/α−1;α2therm = α2/α−2.
Appendix 2. The relationship between the fractionation by GDC (g) and the photorespiratory fractionation (f)
Tcherkez et al. (2004) have shown that the carbon isotope fractionation by GDC (denoted as g) is related to the photorespiratory fractionation, f, as a consequence of the relationship giving the isotope ratio of net assimilated CO2:

where RA, R*, RC, RR are the isotope ratios of net assimilated CO2, Rubisco-fixed CO2, photorespired CO2, and day-respired CO2, respectively. φ is the ratio of oxygenation to carboxylation (vo / vc) and rd the ratio of day respiration to carboxylation. RC is given by:

where λ is a factor that depends on the fractionation by aldolase and transketolase, and may be written as 3 (1 + ϵ), where ϵ is in the per mil range. f is expressed with net assimilated CO2 as a source material, so that f = (RA − RC)/RC. Substituting Eqn B2 into Eqn B1 and using the ϵ notation for λ, neglecting day respiration (the rate of which is indeed very small), gives:
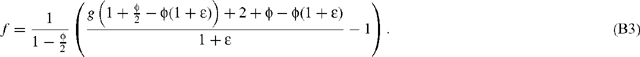
Using a limited development neglecting second order terms, this gives:
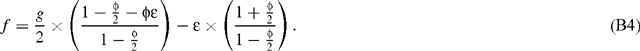
It can easily be seen from Eqn B4 that f is close to g / 2, provided ϵ is small. For usual photorespiration rates, it has indeed been shown by Tcherkez et al. (2004) that ϵ has a very slight effect on f, the difference between f and g / 2 being ~1‰. Because of the small value of ϵ, f and g are simultaneously positive or negative. In other words, photorespiration and the GDC reaction always favour the same carbon isotope.


