Carbon isotope effect predictions for enzymes involved in the primary carbon metabolism of plant leaves

We acknowledge valuable discussions with Dr Jill Gready and Dr J Andrews. GDF also wishes to acknowledge the Australian Research Council for its support through a Discovery Grant.

Abelson H, Hoering TC (1961) Carbon isotope fractionation in formation of amino-acids by photosynthetic organisms. Proceedings of the National Academy of Sciences USA 47, 623–632. with CO₂ and oxygen (competition between carboxylation and oxygenation). If RuBP is not limiting, the rate is:

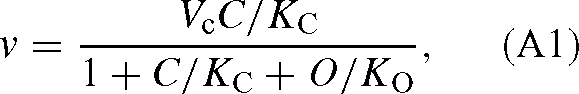
where O is the oxygen concentration, and K_C and K_O are the apparent Michaelis constants for CO₂ and O₂. V_c is the maximum velocity of the carboxylase. Similarly, with two ¹²C and ¹³C-isotopomers of CO₂, we have, neglecting oxygenation:

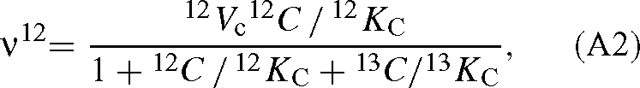
and the symmetrical expression for ¹³CO₂. The ratio of the velocities is then:

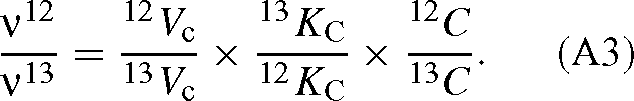
Dividing each side by ¹²C / ¹³C, we have the overall isotope effect of the reaction:

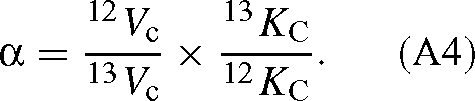
The values of K_C and V_c are (derived from the appendix of Farquhar 1979):

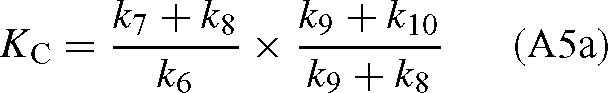
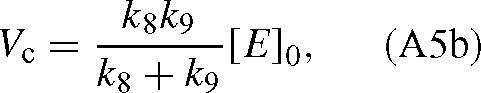
where [E]₀ is the total enzyme site concentration. Substituting the V_c and K_C values into eqn (A4) gives:

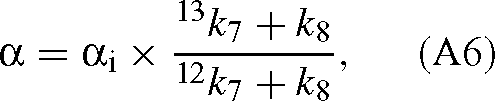
where α_i(= ¹²k₆ / ¹³k₆) is the ‘intrinsic’ isotope effect, that is, the isotope effect of the carboxylation step. k₈ is assumed to be similar with both isotopes because the corresponding step (hydration and cleavage of the C₆ intermediate) does not involve the carbon atom inherited from CO₂. This result is not modified when RuBP is limiting or when the oxygenation of RuBP is taken into account. If RuBP is limiting, the velocity is (Farquhar 1979):

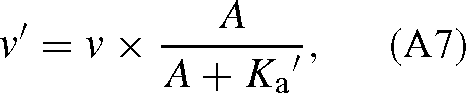
where K_a′ is the apparent Michaelis constant for RuBP and A is the concentration of RuBP. It is the same for ¹³C and ¹²C so that it cancels out in eqn (A3). When oxygenation is added, the denominator of v in eqn (A2) has the additional term O / K_O, and it has no effect on the ratio of eqn (A4).

Equation (A6) can be re-written with the relationship ¹²k₇ = (1 + ϵ₇)¹³k₇ (ϵ₇ is the discrimination associated with decarboxylation) and substituting k₇ using eqn (A5) as follows:

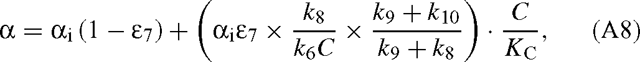
where C is the (overall) carbon dioxide concentration. The concentration C is here added in both the numerator and the denominator in order to recall that k₆C has the same dimension as k₈, and K_C has the dimension of a concentration.

The oxygen isotope effect that occurs when the O(O₂)–C₂(RuBP) is formed, as given by eqn (4) is not equal to the isotope effect that would be measured using the overall isotope ratio in O₂ compared with that of the oxygen that is fixed to the C-2 of RuBP. This is because of the symmetry of the O₂ molecule. The reaction is described as follows, where for clarity, the oxygen atoms are labelled with numbers:

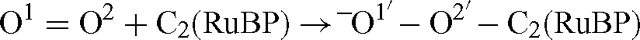
The fractionation given by eqn (4) is:

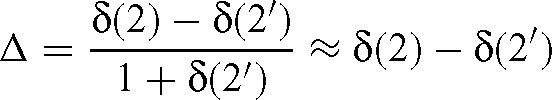
while the isotope fractionation that would be measured is as follows:

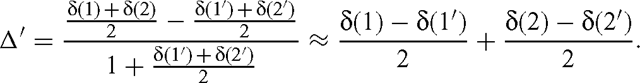
But the oxygen atom number 1 is not involved by the bond considered and so is not subjected to any isotope effect. So we have δ(1) = δ(1′) and the simple relationship: Δ′ = Δ / 2. As the isotope effect is given by α = Δ − 1, we have α′ = 1 + (α − 1)  / 2.

We assume here the following reversible reaction, with the reactants A and the product B:

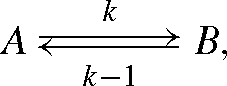
where the rate constants of the forward and backward reactions are k and k_–1, respectively_. For the ¹²C and ¹³C isotopes, we have: k¹², k¹³ and k_–1¹² and k_–1¹³. Mass balance equations are such that:

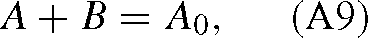
which is true for each isotope: A¹² + B¹² = A₀¹² and similarly for ¹³C. With a first order mechanism, we have the following differential equation:

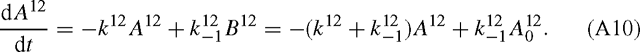
The same applies to ¹³C:

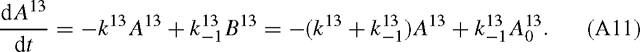
The solutions of (A10) and (A11) are exponential functions. For ¹²C, we have:

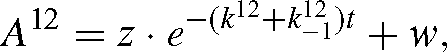
where z and w are obtained at t = 0 so that:

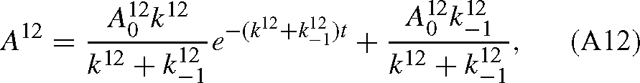
and the same for A¹³. Combining Eqns (A9) and (A12), we have:

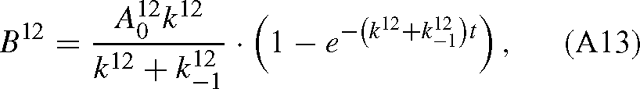
and similarly for B¹³. The isotope effect is defined by the isotope ratio of the reactants divided by that of the products, that is, with eqns (A12) and (A13):

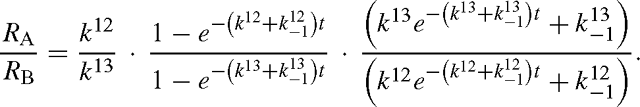
When t → 0, R_A / R_B tends towards k¹² / k¹³ and when t → +∞, it tends towards:

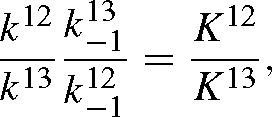
as the exponential term tends to zero.