Time–quefrency analysis of overlapping similar microseismic events
Koji NaganoMuroran Institute of Technology, Mizumoto 27-1, Muroran, Hokkaido 050-8585, Japan. Email: nagano@mmm.muroran-it.ac.jp
Exploration Geophysics 47(2) 133-144 https://doi.org/10.1071/EG15033
Submitted: 15 April 2015 Accepted: 18 April 2015 Published: 15 May 2015
Journal Compilation © ASEG 2016
Abstract
In this paper, I describe a new technique to determine the interval between P-waves in similar, overlapping microseismic events. The similar microseismic events that occur with overlapping waveforms are called ‘proximate microseismic doublets’ herein. Proximate microseismic doublets had been discarded in previous studies because we had not noticed their usefulness. Analysis of similar events can show relative locations of sources between them. Analysis of proximate microseismic doublets can provide more precise relative source locations because variation in the velocity structure has little influence on their relative travel times. It is necessary to measure the interval between the P-waves in the proximate microseismic doublets to determine their relative source locations.
A ‘proximate microseismic doublet’ is a pair of microseismic events in which the second event arrives before the attenuation of the first event. Cepstrum analysis can provide the interval even though the second event overlaps the first event. However, a cepstrum of a proximate microseismic doublet generally has two peaks, one representing the interval between the arrivals of the two P-waves, and the other representing the interval between the arrivals of the two S-waves. It is therefore difficult to determine the peak that represents the P-wave interval from the cepstrum alone. I used window functions in cepstrum analysis to isolate the first and second P-waves and to suppress the second S-wave. I change the length of the window function and calculate the cepstrum for each window length. The result is represented in a three-dimensional contour plot of length–quefrency–cepstrum data. The contour plot allows me to identify the cepstrum peak that represents the P-wave interval. The precise quefrency can be determined from a two-dimensional quefrency–cepstrum graph, provided that the length of the window is appropriately chosen. I have used both synthetic and field data to demonstrate that this method can be used to identify the cepstrum peak that represents the interval between the arrivals of successive P-waves.
Key words: cepstrum, microseismic events, quefrency, similar events.
Introduction
Analysis of similar earthquake events is a seismological tool that has been used to investigate the subsurface structure of the Earth (Poupinet et al., 1984). Events with similar waveforms occur at the same (or proximal) fractures and share a similar source mechanism. The similarity of their sources provides data that can be used to construct precise images of the subsurface fractures.
Analyses of similar seismic events have been used in many geophysical research fields. Cao and Romanowicz (2007) discussed scatterers in the mantle by analysing similar earthquakes. Danesi et al. (2007) reported using similar earthquakes beneath an Antarctic outlet glacier to show the structure of the glacier.
Similar microseismic events also occur during hydraulic injection in fractured reservoir systems, e.g. natural gas reservoirs (Rutledge and Phillips, 2003; Rutledge et al., 2004) and geothermal reservoirs (Moriya et al., 2002; Phillips, 2000). Eisner et al. (2006) reported similar microseismic events that were monitored during hydraulic fracturing in oil and gas fields. Analysis of similar microseismic events has revealed the detailed structure of fractured reservoirs, especially in geothermal fields.
Phillips (2000) analysed similar microseismic events that were induced by hydraulic stimulation of a hot-dry-rock (HDR) geothermal reservoir in the Rhine Graben near Soultz, France. The absolute location of a master event, which was one of the similar events, was calculated by the conventional arrival-time difference method in advance of the similar event analysis. Relative locations of the sources of events similar to the master event were then calculated by analysing the delay of the coherent frequency components of the similar events. The relative source locations provided a fine image of the fracture reservoir. Subsequently the relative source locations helped to define a fracture network and stress fields that governed fluid flow in the reservoir.
Moriya et al. (2002) used microseismic multiplet analysis in the Soultz HDR field and showed the spatial relationship between hypocenters for similar microseismic events. Combinations of the relative hypocenters of three or more similar events revealed fracture orientations. Moriya et al. (2002) reported that the estimated orientations of the fractures were consistent with the orientation of the tectonic stress field.
Time-dependent change of subsurface structures can also be examined by analyses using similar microseismic events (Poupinet et al., 1996; Yamawaki et al., 2004). Yamawaki et al. (2004) analysed cross-correlation coefficients of pairs of similar earthquakes. They showed that time-dependent cross-correlation patterns of S-waves differed among recording stations. The coefficients determined from two seismograph stations on the slope of Mt. Iwate in Japan decreased with elapsed time and their values became scattered. The coefficients for stations that were distant from Mt. Iwate were close to 1.0 and were less scattered. This analysis by Yamawaki et al. (2004) showed that the time-dependent cross-correlation patterns of S-waves in the similar earthquakes were indicative of subsurface structural changes caused by volcanic activity at Mt. Iwate.
Similar microseismic events
The analysis of similar microseismic events involves two factors, the difference of the source location and the change of the velocity structure. These two factors are connected to each other. A change of the velocity structure may introduce an error into the source location.
Some mechanisms, e.g. fracture growth, faulting, and metamorphism, will cause a change in the subsurface structure. The intervals between similar events for which analyses have been published in the seismological and geophysical literature range from several seconds to several days (Moriya et al., 2002; Poupinet et al., 1996; Yamawaki et al., 2004; Eisner et al., 2006). If the interval between arrivals is long, the velocity structure may have changed during the interval. For example, when hydraulic fracturing is carried out, fracture growth during the interval between similar events may change the subsurface structure. Block et al. (1994) applied a joint inversion method to monitor hydraulic fracturing. They estimated the velocity structure in combination with source locations by using a joint inversion method. Spreading sources of the microseismic events indicated an active fracture zone. They indicated in their paper that the microseismic events were induced by hydraulic fracturing, and that the velocity structure was changing while the data were collected. Therefore, the source locations should be computed using a time-variant velocity model that includes fracture growth when we analyse microseismic events due to hydraulic fracturing.
We need either P-wave propagation velocity or S-wave propagation velocity, or both, to estimate the relative location of similar sources. The propagation velocities in the field are estimated in advance of the analysis of the arrival-time differences for the source location. The estimation of the P-wave propagation velocity is more reliable than that of the S-wave propagation velocity. Therefore, in this paper, I used only P-wave information to estimate the relative source locations of between the similar microseismic events.
Proximate microseismic doublets
If a second event, with a similar waveform to an earlier event, arrives before complete attenuation of that earlier event, the two events overlap each other. I call such similar events within a short interval ‘proximate microseismic doublets’. The interval between proximate microseismic doublets ranges from several hundred milliseconds to several seconds. The interval can depend on the magnitude of an event. Big proximate doublets can have a long interval because of their long duration. The similarity between the two events of the doublet can be estimated from the cepstrum of the overlapping events. The cepstrum of the proximate doublets shows a high, sharp peak at quefrency of the interval, which is also estimated by rough observation of the waveform.
We had not previously used proximate microseismic doublets to derive relative source locations. I can offer some reasons why we had not analysed the proximate microseismic doublets. The first reason is that we had not read of the cepstrum method for estimating the interval. The second reason is the small number of proximate microseismic doublets. However, we can increase the number of estimated source locations by analysing such unused events. Moreover, the location of proximate microseismic doublet sources generally is more precise than that of similar events with a long interval between their origin times. Because the events in a proximate microseismic doublet have a short interval between them, time-dependent changes in the velocity structure should have little effect on the source locations. This possibility of errors for events separated by a long interval was indicated in the combined analysis of source locations and a velocity model by Block et al. (1994). Though proximate microseismic doublets are a small fraction of the events observed, their relative source locations are valuable.
It is difficult to estimate directly the interval between events in proximate microseismic doublets by using time-domain analysis. Bogert et al. (1963) introduced the cepstrum analysis to estimate interval between overlapping events with a similar waveform. The cepstrum shows a clear peak at the interval between similar events. Childers et al. (1977) summarised cepstrum analysis. When we apply cepstrum analysis to a proximate microseismic doublet, two peaks are apparent in their cepstrum. The two peaks are interpreted as the intervals between the P-wave arrivals and the S-wave arrivals. However, the cepstrum does not indicate which peak represents the interval between P-wave arrivals. The two peaks must be identified in order to locate the relative hypocenter. In this paper I present a new analytical method that combines variable length windows with cepstrum analysis to determine the interval between P-wave arrivals in proximate microseismic doublets.
In this paper, I have used microseismic data recorded at the Soultz HDR field during hydraulic fracturing in 1993. A total of 15089 events were located during this fracturing project, of which 6039 were identified as similar microseismic events (Moriya et al., 2002). The recording time for all data files was 1.638 s and the sampling frequency was 5000 Hz.
The cepstrum of a proximate microseismic doublet
In the analysis of the locations of the sources of similar microseismic events, the accuracy of the location of the source of the second event relative to the location of the first is more precise than that estimated by calculating independent source locations for each event (Moriya et al., 2002). The source locations of the first and second events are defined by (x1, y1, z1) and (x, y, z), respectively. The source location of the second event is also represented by the relative source location r = (Δx, Δy, Δz),

Figure 1 provides a schematic representation of the process described here for estimation of relative source location for similar microseismic events. The absolute source location of the first event, (x1, y1, z1), is calculated in advance by analysing arrival-time observations among recording stations. The source location, r, of the source of the second event relative to that of the first event is then calculated from station-to-station observations of arrival-time intervals for the second of the similar events (Ito, 1985).

|
Examples of proximate microseismic doublets examined in this study are shown in Figure 2. Importantly, the interval between the similar events in Figure 2 is shorter than the duration of a single event.
I found 230 pairs of proximate microseismic doublets in the 15089 events that were observed in the Soultz HDR field (Moriya et al., 2002). I selected waveforms in which two events overlapped by inspection, and made a rough estimate of the interval. We may observe overlapping events with a short interval but which occurred independently. Such overlapping events would not have similar waveforms. When the rough estimate of the interval was close to the quefrency of the peak in the cepstrum, I concluded that the waveform was likely to be a proximate microseismic doublet (Nagano and Ehara, 2008).
Cepstrum analysis is a method to estimate an interval between two similar event signals, such as in the proximate microseismic doublets. A composite signal consisting of a master wavelet h(t) and its slave signal is represented by

where ΔT is the delay between arrivals of the two signals and α is the magnitude ratio between the master and its slave. The power spectrum is

where H(f) and G(f) are Fourier transforms of h(t) and g(t), respectively. The logarithm of the power spectrum is

The inverse Fourier transform of the logarithm of the power spectrum is the cepstrum, which is a function of quefrency (Bogert et al., 1963; Childers et al., 1977; Brockwell and Davis, 2002). The dimension of quefrency is time. The cepstrum of Equation 2 shows a distinct peak at a quefrency of ΔT because there is an additive periodic component, log {1 + α2 + 2α cos (2π fΔT)}, in Equation 4.
Cepstrum analysis of proximate microseismic doublets is more complex than that represented by the pair of wavelets of Equation 2. Each seismic event has both a P-wave component and an S-wave component. Therefore, there are two pairs of overlapping seismic waves in proximate microseismic doublets. A composite signal y(t), which represents proximate microseismic doublets, is

where xP (t) and xS (t) are the P- and S-waves, respectively, of the first event, and ΔTP and ΔTS are intervals between P- and S-wave arrivals, respectively, for the two similar events. Fourier transforms of xP (t) and xS (t) are defined as XP (f) and XS (f), respectively. The logarithm of the power spectrum of y(t) in Equation 5 is

Therein, XP (f) = |XP (f)|exp {jθP (f)}, XS (f) = |XS (f)|\exp {jθS (f)}, and θP (f) and θS (f) are the phase spectra of the P- and S-waves, respectively. Equation 6 contains periodic components. Consequently, the cepstrum of Equation 5 will exhibit two peaks at intervals of ΔTP and ΔTS.
Figure 3 shows portions of the cepstra of two examples of proximate microseismic doublets. The sampling frequency constrains the quefrency resolution in the cepstrum. Because the sampling frequency is 5000 Hz in Figure 3, the quefrency resolution is 0.2 ms. Two peaks are clearly visible in the cepstra shown in Figure 3. For example, we can see the two peaks at 0.2998 s and 0.3006 s in Figure 3a. However, which peak represents the P-wave delay cannot be determined by using only the information shown in Figure 3.

|
Time–quefrency analysis
I have devised a further analysis or the cepstrum for proximate microseismic doublets. During the cepstrum analysis, it would be desirable to attenuate the peak that represents the S-wave interval to enhance the cepstrum peak of the P-wave interval. If the data after the arrival of the second S-wave were replaced with zeros, the S-wave signals would lose similarity. Consequently the cepstra of the modified data should show a decrease in the magnitude of the peak representing the interval between the S-waves.
I use a window function in the cepstrum analysis. The window function is intended to exclude the second S-wave and to suppress the similarity between the S-waves. The length of the window function is varied so that we can see the effect of the window length on the cepstra. Because the cepstrum is a non-linear transformation and there are two waves in the data, the effect on the cepstrum of the multiplied window function is not simple. We can discriminate the peak representing the S-wave interval from that representing the P-wave interval in the cepstra by repetitive application of this window function with varying window length. I call this method ‘time–quefrency analysis’. I use the Hamming window in my analysis to reduce bias due to spectral leakage in the estimation of the power spectrum (Percival and Walden, 1998).
Time–quefrency analysis performed as follows. Figure 4 illustrates time–quefrency analysis and ways of representing its results. The window begins at the start of the doublet record, but the end or terminal time (Tw) of the window is systematically shifted from before the second P-wave arrival to the end of the second S-wave. The contour plot in Figure 4 shows the cepstrum for each window terminal time and quefrency. Two notable cepstrum peaks are observed, one commencing at a terminal time of just over 7 s, and the second at a terminal time of just over 8 s. The cepstrum peak at a quefrency at ~4.004 s corresponds to the S-wave interval and the peak at ~4.000 s corresponds to the P-wave interval. The peak corresponding to the P-wave interval starts at ~7.2 s and continues to 12 s. On the other hand, the peak corresponding to the S-wave interval starts after ~8 s. It is because, for window lengths less than 8 s, the energy of the second S-wave is excluded by the multiplied window function and so does not contribute to the cepstrum.
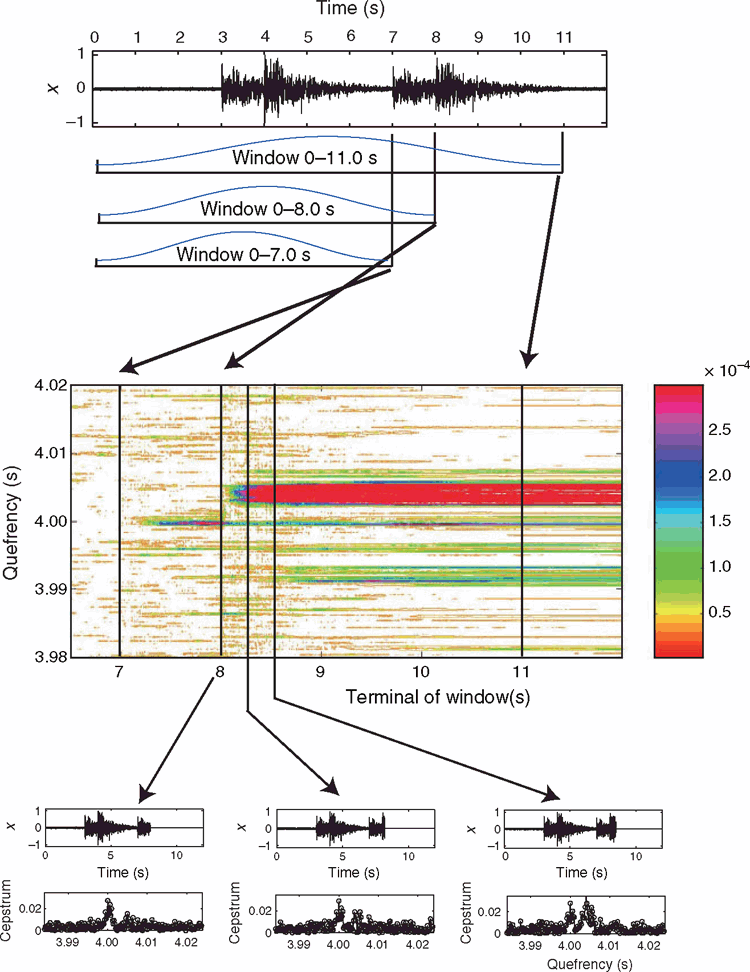
|
It is difficult to determine the precise quefrency of the P-wave interval from only the contour plot because a sharp top of the peak is not clearly visible in the contour plot. I therefore produced two-dimensional cepstrum–quefrency graphs from the three-dimensional time–quefrency–cepstrum data. The quefrency of the P-wave interval is conclusively determined in the cepstra as shown in the bottom panel of Figure 4.
The window length variation also affects the peak of the P-wave interval in the cepstra of a proximate microseismic doublet. The second S-wave arrives during the coda part of the second P-wave, so we observe both contributions simultaneously. When data after the arrival of the second S-wave are excluded, the contribution from the coda part of the second P-wave is also excluded. Therefore, the cepstrum peak due to the P-wave interval will be affected. Because the energy in the coda of the second P-wave is smaller than the energy in the initial part of the second S-wave, the S-wave interval peak is not greatly affected.
Computer simulation
I conducted time–quefrency analyses using synthesised signals that simulated proximate microseismic doublets. Figure 5 shows the waveform used for the numerical simulation together with the parameters that define the waveform. A signal simulating a microseismic event consists of two series of Gaussian random numbers that decreased exponentially. The two series simulate P- and S-waves, respectively. The Gaussian series are filtered to suppress high-frequency components because low-frequency components are dominant in a real seismic event. The cut-off frequency of the low-pass filter is 100 Hz. I then add a second signal, which is similar to the first signal, with a time lag to simulate a proximate microseismic doublet. I add another series of Gaussian random numbers to the simulated event to model background noise. Sampling frequency was set to 5000 Hz. The interval between P-waves was 4.000 s and that between S-waves was 4.004 s. The difference between these intervals is 20 sample points for a sampling frequency of 5000 Hz.

|
Figures 6 and 7 show spectra, cepstra and autocorrelations of the synthesised signals. The synthesised signal of Figure 6 has no noise, and its cepstrum shows distinct peaks at the quefrency corresponding to the interval between successive P-waves and that between successive S-waves (Figure 6c). Figure 7 shows the cepstrum of the synthesised signal with noise added. The cepstrum again has peaks at the quefrencies corresponding to the P-wave and S-wave intervals (Figure 7c); however, the peaks are wider and their forms less clear than those of the noise-free signals. Autocorrelation analysis also provides an interval between arrival-times for the synthesised signal; however, the resolution of this method is lower than that of cepstrum analysis because the spectra of the synthesised signals are not white (Brockwell and Davis, 2002).

|

|
Figure 8 shows the result of time–quefrency analysis for a synthesised signal with no noise. The contour plot of Figure 8b shows two main peaks at the quefrencies of 4.000 s and 4.004 s. The cepstrum peak at the earlier start time represents the interval between P-wave arrivals. The cepstra profiles of Figure 8c show the interval between the P-waves more precisely than in the contour plot (Figure 8b).
Some further peaks are visible in the contour plot, e.g. at the quefrencies of ~3.996 s, 3.992 s, and 3.985 s, when the window length is greater than 10 s. I can conclude the above mentioned peaks are artefacts because we cannot find any onsets of the events in Figure 8a at the starting time of the peaks in the contour plot of Figure 8b.
Figure 9 shows the time–quefrency analysis result for synthetic data with Gaussian noise. In the contour plot of Figure 9b, the relationship of the start times of the peaks is again confirmed. However, by when comparing Figure 9c with Figure 8c, we find that the true peaks corresponding to the intervals of P- and S-waves are contaminated by many noisy peaks. Therefore, it is difficult to recognise the true peaks from Figure 9c only. However, we can recognise them by comparing the contour plot of Figure 9b with Figure 9c. Using the cepstrum–quefrency graphs alone sometimes does not provide good results because of the noise contamination. Therefore, comparison the cepstrum–quefrency graphs with the contour plot is important for accurate recognition of the true peaks.

|
As shown in Figures 8 and 9, the cepstrum often has artefacts near true peaks. The cepstrum has higher-order components (Childers et al., 1977), which are artefacts of the true cepstrum peaks. However, the artefacts caused by the higher-order components are smaller than the true cepstrum peaks (Childers et al., 1977). For example, peaks shown at the quefrency of 3.996 and 3.992 s in Figure 8b and at the quefrency of 3.99 s in Figure 9b are the artefacts. The magnitudes of these peaks are smaller than the true peaks, however. We can get a rough estimate of the interval based on the observation of the waveform. We can isolate the artefacts in the contour plot by using both this rough estimate of the interval and the smaller amplitude property of the higher-order cepstrum components.
Field data analysis
I used the time–quefrency technique described above to analyse proximate microseismic doublets that were recorded at the Soultz HDR field. My aim was to detect the interval between P-waves within the recorded data. Figures 10–12 illustrate the results representing a contour plot and five cepstra for selected time window functions in each figure.
Application of the time–quefrency technique successfully determined the intervals between P-wave arrivals for the proximate microseismic doublets shown here, which were recorded at the Soultz HDR field. Two peaks and the difference of their start times were recognisable in the contour plots for the real data. The contour plot of Figure 10 shows peaks at quefrencies of 0.5264 s and 0.5275 s. The earlier peak represents the interval between P-wave arrivals in the contour plot of Figure 10. We can also recognise two peaks at quefrencies of 0.323 s and 0.324 s in the contour plot of Figure 11. The peak at the quefrency of 0.323 s starts earlier than another peak.
The shape of the peaks in the contour plot of Figure 12 differs from that of the peaks shown in Figures 10 and 11. Two peaks are again evident, at quefrencies of 0.4945 s and 0.4955 s before the window terminal time of ~1.37 s. It is difficult to recognise the two peaks after the window terminal time of 1.5 s in the contour plot of Figure 12b. However, we can see two peaks in the cepstrum of the Figure 12c. The peak at the quefrency of 0.4955 s starts at a smaller window terminal time than other peaks. Therefore, the peak at the quefrency of 0.4955 s represents the interval between successive P-waves.
As was the case for the synthetic data, the cepstrum–quefrency graphs for the real proximate microseismic doublets (Figures 10c, 11c, and 12c) allow more precise determination of the quefrency representing the interval between P-wave arrivals than the contour plots. The P-wave peaks are indicated by arrows in Figures 10c–12c.
It is important to set an appropriate length of the time window when the cepstrum–quefrency graphs, as shown in Figures 10c and 11c, are produced. For example, in Figure 11c, the cepstra of Tw = 0.940 s, 1.000 s, and 1.050 s show two peaks. But it is difficult to identify two peaks in the cepstra of Tw = 0. 839 s or 0.842 s. If we analyse only the cepstrum of Tw = 0. 839 s to determine exact quefrencies, we cannot determine them. Also, the peak in the cepstrum–quefrency graph might be poorly resolved if the window length is not appropriate for the data. Therefore, it is important to compare some cepstrum–quefrency graphs so that the appropriate length of the time window can be selected.
Conclusions
The interval between P-waves arrivals in proximate microseismic doublets can be detected by using time–quefrency analysis. In such an analysis, the cepstra show two peaks that represent the intervals between successive P-wave and S-wave arrivals. I examined some features of the time–quefrency analysis by computer simulation using synthesised signals, and then applied the technique to field data recorded at the Soultz HDR field.
My computer simulations showed that cepstra provide higher resolution estimates of arrival-time intervals than autocorrelations, and that noise added to the synthesised signal widens the cepstral peaks. The computer simulations also showed that cepstra derived from time–quefrency analysis, in which a window function is used to exclude the second S-wave, can identify the interval between two P-waves of proximate microseismic doublets. Even though the signal-to-noise ratio was low, and the cepstrum showed a broad peak that covered both the P-wave and S-wave intervals, I was able to identify the peak representing the interval between P-waves in contour plots of time–quefrency–cepstrum data.
I also applied my time–quefrency analysis to proximate microseismic doublets recorded at the Soultz HDR field and demonstrated that the technique can be successfully applied to real data.
We can determine the relative location of the sources of proximate microseismic doublets when the P-wave interval, which is determined by using the time–quefrency analysis, can be compared among four stations. Therefore, this paper has settled the first stage of the problem of relative source location for proximate microseismic doublets.
I have pointed out some practical techniques of time–quefrency analysis as we have applied it to synthesised and real data. The cepstrum of microseismic waveforms is often contaminated by artefacts and noisy peaks that are produced in the calculation of the cepstrum. To overcome the contamination and estimate precise interval with high resolution, it is important to do complementary analyses of the contour plot of the time–quefrency analysis, the cepstrum, and the waveform.
Acknowledgements
I thank staff at Socomine and Dr Hirokazu Moriya (Tohoku University) for their help and for providing access to the microseismic data used in this study. This work was carried out under a Japanese Ministry of Education, Culture, Sports, Science and Technology Grant-in-Aid (No. 20560753) for Scientific Research (C).
References
Block, L. V., Cheng, C. H., Fehler, M. C., and Phillipe, W. S., 1994, Seismic imaging using microearthquakes induced by hydraulic fracturing: Geophysics, 59, 102–112Bogert, B. P., Healy, M. J., and Tukey, J. W., 1963, The quefrency analysis of time series for echoes: cepstrum, pseudo-autocovariance, cross-cepstrum, and saphe cracking, in M. Rosenblatt, ed., Time series analysis: Wiley, 209–243.
Brockwell, P. J., and Davis, R. A., 2002, Introduction to time series and forecasting: Springer-Verlag.
Cao, A., and Romanowicz, R., 2007, Locating scatterers in the mantle using array analysis of PKP recursors from an earthquake doublet: Earth and Planetary Science Letters, 255, 22–31
| Locating scatterers in the mantle using array analysis of PKP recursors from an earthquake doublet:Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhvVGgtL0%3D&md5=07b242b870935cf2a72214e8e1b4e802CAS |
Childers, D. G., Skinner, D. P., and Kemerait, R. C., 1977, The cepstrum: a guide to processing Proceedings of the IEEE, 65, 1428–1443
| The cepstrum: a guide to processingCrossref | GoogleScholarGoogle Scholar |
Danesi, S., Bannister, S., and Morelli, A., 2007, Repeating earthquakes from rupture of an asperity under an Antarctic outlet glacier: Earth and Planetary Science Letters, 253, 151–158
| Repeating earthquakes from rupture of an asperity under an Antarctic outlet glacier:Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtlCkt7vF&md5=1728db8a78c7c0b2da082a047123728eCAS |
Eisner, L., Fischer, T., and Le Calvez, J. H., 2006, Detection of repeated hydraulic fracturing (out-of zone growth) by microseismic monitoring: The Leading Edge, 25, 548–554
| Detection of repeated hydraulic fracturing (out-of zone growth) by microseismic monitoring:Crossref | GoogleScholarGoogle Scholar |
Ito, A., 1985, High resolution relative hypocenters of similar earthquakes by cross-spectral analysis method: Journal of Physics of the Earth, 33, 279–294
| High resolution relative hypocenters of similar earthquakes by cross-spectral analysis method:Crossref | GoogleScholarGoogle Scholar |
Moriya, H., Nakazato, K., Niitsuma, H., and Baria, R., 2002, Detailed fracture system of the Soultz-sous-Forêts HDR field evaluated using microseismic multiplet analysis: Pure and Applied Geophysics, 159, 517–541
| Detailed fracture system of the Soultz-sous-Forêts HDR field evaluated using microseismic multiplet analysis:Crossref | GoogleScholarGoogle Scholar |
Nagano, K., and Ehara, D., 2008, Automatic detection of proximity AE doublets for relative location of subsurface fracture reservoir: Institute of Electrical Engineers of Japan Transactions on Electronics, Information and Systems, 128, 1005–1010
Percival, D. B., and Walden, A. T., 1998, Spectral analysis for physical applications: Cambridge University Press.
Phillips, W. S., 2000, Precise microearthquake locations and fluid flow in the geothermal reservoir at Soultz-sous-Forêts, France: Bulletin of the Seismological Society of America, 90, 212–228
| Precise microearthquake locations and fluid flow in the geothermal reservoir at Soultz-sous-Forêts, France:Crossref | GoogleScholarGoogle Scholar |
Poupinet, G., Ellsworth, W. L., and Frechet, J., 1984, Monitoring velocity variations in the crust using earthquake doublets: an application to the Calaveras fault, California: Journal of Geophysical Research, 89, 5719–5731
| Monitoring velocity variations in the crust using earthquake doublets: an application to the Calaveras fault, California:Crossref | GoogleScholarGoogle Scholar |
Poupinet, G., Ratdomopurbo, A., and Coutant, O., 1996, On the use of earthquake multiplets to study fractures and the temporal evolution of an active volcano: Annali di Geofisica, 39, 253–264
Rutledge, J. T., and Phillips, W. S., 2003, Hydraulic stimulation of natural fractures as revealed by induced microearthquakes, Carthage Cotton Valley gas field, east Texas: Geophysics, 68, 441–452
| Hydraulic stimulation of natural fractures as revealed by induced microearthquakes, Carthage Cotton Valley gas field, east Texas:Crossref | GoogleScholarGoogle Scholar |
Rutledge, J. T., Phillips, W. S., and Mayerhofer, M. J., 2004, Faulting induced by forced fluid injection and fluid flow forced by faulting: an interpretation of hydraulic-fracture microseismicity, Carthage Cotton Valley gas field, Texas: Bulletin of the Seismological Society of America, 94, 1817–1830
| Faulting induced by forced fluid injection and fluid flow forced by faulting: an interpretation of hydraulic-fracture microseismicity, Carthage Cotton Valley gas field, Texas:Crossref | GoogleScholarGoogle Scholar |
Yamawaki, T., Nishimura, T., and Hamaguchi, H., 2004, Temporal change of seismic structure around Iwate volcano inferred from waveform correlation analysis of similar earthquakes: Geophysical Research Letters, 31, L24616
| Temporal change of seismic structure around Iwate volcano inferred from waveform correlation analysis of similar earthquakes:Crossref | GoogleScholarGoogle Scholar |






