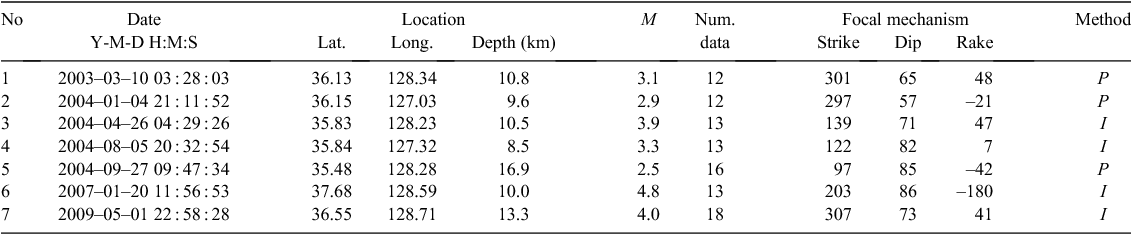
Direct simulation Monte Carlo method with a focal mechanism algorithm

Key words: direct simulation Monte Carlo (DSMC) method, focal mechanism, number of stations, receiver problem, seismic wave attenuation.

Seismic wave attenuation, usually expressed as Q^–1, is an indispensable parameter in understanding the interior state and tectonic history of the earth. In particular, regional information on Q^–1 of high-frequency waves in the lithosphere is very helpful, not only for scientific research, but also for the practical purpose of simulating earthquake ground motion in engineering seismology (Yoshimoto et al., 1993). After the observation of lithospheric Q^–1 at high frequency (Dainty, 1981), recent regional studies (e.g. Sato et al., 2012) have focused on the separation of the total seismic attenuation Q_t^–1 (another form of Q^–1), into Q_i^–1 and Q_s^–1, where Q_i^–1 represents the intrinsic absorption caused by the conversion of elastic energy to heat, and Q_s^–1 is the scattering attenuation caused by the redistribution of wave energy without any loss.

The most widely used approach to the separation into Q_i^–1 and Q_s^–1 is multiple lapse time window analysis (MLTWA), introduced almost simultaneously by Hoshiba et al. (1991) and Fehler et al. (1992). Based on the observations that the early portion of a seismogram is dominated by the direct S-wave whose amplitude is reduced by Q_t^–1, whereas the S-coda is composed entirely by scattered S-waves whose amplitude is reduced by Q_i^–1 but enlarged by Q_s^–1, MLTWA simulates the integral of the observed energy from multiple earthquakes in three successive time windows.

The simulated values, based on radiative transfer theory, were first obtained analytically by Zeng et al. (1991) and Sato (1993) using a model with a uniformly distributed scatterer in a homogeneous half-space and a source located at the origin. The simulated values were also obtained by the Monte Carlo method, using an improved model with isotropic layers and variable source depth (Hoshiba, 1997). The simulation method was further improved by the direct simulation Monte Carlo (DSMC) method (Yoshimoto, 2000) using a velocity gradient in the layer model. The DSMC method, which utilises a finite difference scheme for ray tracing, is expected to be applicable to a three-dimensional structure model due to the simplicity of the algorithm.

Despite the improvement of the simulation method, the MLTWA method generally displays a large observational scatter in the first window. The main cause of this scatter is known to be the different radiation pattern of each earthquake (e.g. Fehler et al., 1992). The regional alteration of local structure has also been thought of as one of the causes of the observational scatter (e.g. Giampiccolo et al., 2006). In addition, the different focal depth of each earthquake may cause significant scatter, because large variations of Q^–1 values of S-waves are well known in the crust and upper mantle (Mitchell and Xie, 1994; Mitchell, 1995). Recently, MLTWA, using single earthquake data, showed little observational scatter and presented reliable results despite the relative dearth of data (Asep et al., 2014).

To fit observation of the radiation pattern of an earthquake, the current study first attempts to implant a focal mechanism algorithm into the code of the DSMC method. As a comparison test, the same analysis is also performed using an unprocessed DSMC code. Hereafter, DSMC codes that are unprocessed and implanted with a focal mechanism are referred to as DSMC-1 and DSMC-2, respectively.

The DSMC-1 method (Yoshimoto, 2000) synthesises the waves coda envelope in three-dimensional scattering media by using the number of energised particles moving out from a point source with a take-off angle (θ) and an azimuthal angle (ϕ) (Figure 1), which are mutually independent, random variables with values in the range of [0, π] and [0, 2π], respectively.

Fig. 1.  Schematic diagram for an energised particle, starting from the source located at the origin of the Cartesian coordinate and drifting to a spherical-shaped receiver of volume ΔV, to count the number of the energised particles. Whereas the DSMC-1 used a torus-shaped receiver with the average radius proportional to the epicentral distance (), DSMC-2 replaced the torus with a hemisphere. Both receivers are located just beneath the free surface.

This method, however, assumes an isotropic source radiation and scattering of seismic waves with locally uniform coefficients of scattering and intrinsic . Consider that the particle propagates over distance v(z)Δt, where v(z) is the seismic velocity at depth z, and Δt is a short time interval. Then, the probability of a scattering event is represented by η_sv(z)Δt (Feynman et al., 1989), and the occurrence of scattering in the distance v(z)Δt is determined by the inequality:

where I is a random number between 0.0 and 1.0. If equation 1 is fulfilled, the particle moves to a different direction by the redetermination of θ and ϕ. In the x’–z plane (Figure 1), the particle location at time Δt follows the seismic ray theory expressed as the following:

where ϑ is the angle of particle propagation, initially ϑ = θ at the source, and satisfies the following differential equation (Cervený and Ravindra, 1971):

The finite difference method at interval time Δt = 0.2 s was used for the propagation of the particles, whose number at source is 10⁶ based on the Monte Carlo scheme.

Upon arrival in a receiver region with a volume element of ΔV, each particle was considered equivalent to a seismic energy packet. At the receiver, the energy of a particle at the source was reduced by exp (−η_iΔt). Torus volume, just beneath the free surface, was assumed as a receiver (Figure 1) because the isotropic assumption of source radiation and scattering of seismic waves signify a spherical symmetry of the DSMC-1 method. The size of torus volume, with the thickness of 7 km and with the radius of epicentral distance, is large enough to stabilise the number of arrived particles but small enough to retain temporal resolution.

The DSMC-1 method showed better results than those of the analytical solution by using a depth-dependent velocity model (Chung et al., 2010) and a source with a depth of 10 km (Chung, 2014).

Based on the code of DSMC-1, the DSMC-2 method incorporated the radiation pattern of both traverse SV and SH waves by using well-known relations (Aki and Richards, 1980) as in equations 4 and 5:

where φ_s, δ and λ represent the strike, dip and rake of the fault, respectively. This incorporation means an expanded application from the two-dimensional to the three-dimensional isotropic model, which was claimed as an advantage of the DSMC method over previous methods (Yoshimoto, 2000). The geometrical expansion, however, resulted in the torus volume being reduced to a small receiver with hemisphere volume (Figure 1), because a spherical symmetry of DSMC-1 was no longer available to DSMC-2.

In Figure 2, the amplitude of DSMC-2 is compared with DSMC-1 at a receiver with the hypocentral distance of 30 km. The azimuth of the receiver in DSMC-2 was 90° for the source at a depth of 10 km with focal mechanism parameters of strike = 180°, dip = 90° and rake = 90°. By considering the small volume of the receiver in DSMC-2, we shoot 2 × 10⁶ particles in DSMC-2, twice as many as those of DSMC-1, and shorten the interval time as Δt = 0.1 s. The envelopes of DSMC-2 are inflected around 12 s due to the anisotropic source radiation.

Fig. 2.  Comparison of the amplitude between DSMC-1 (grey line) and DSMC-2 (black dotted lines) at a receiver with the hypocentral distance of 30 km. The azimuth of the receiver in DSMC-2 was 90° for the source at a depth of 10 km with focal mechanism parameters of strike = 180°, dip = 90°, and rake = 90°.

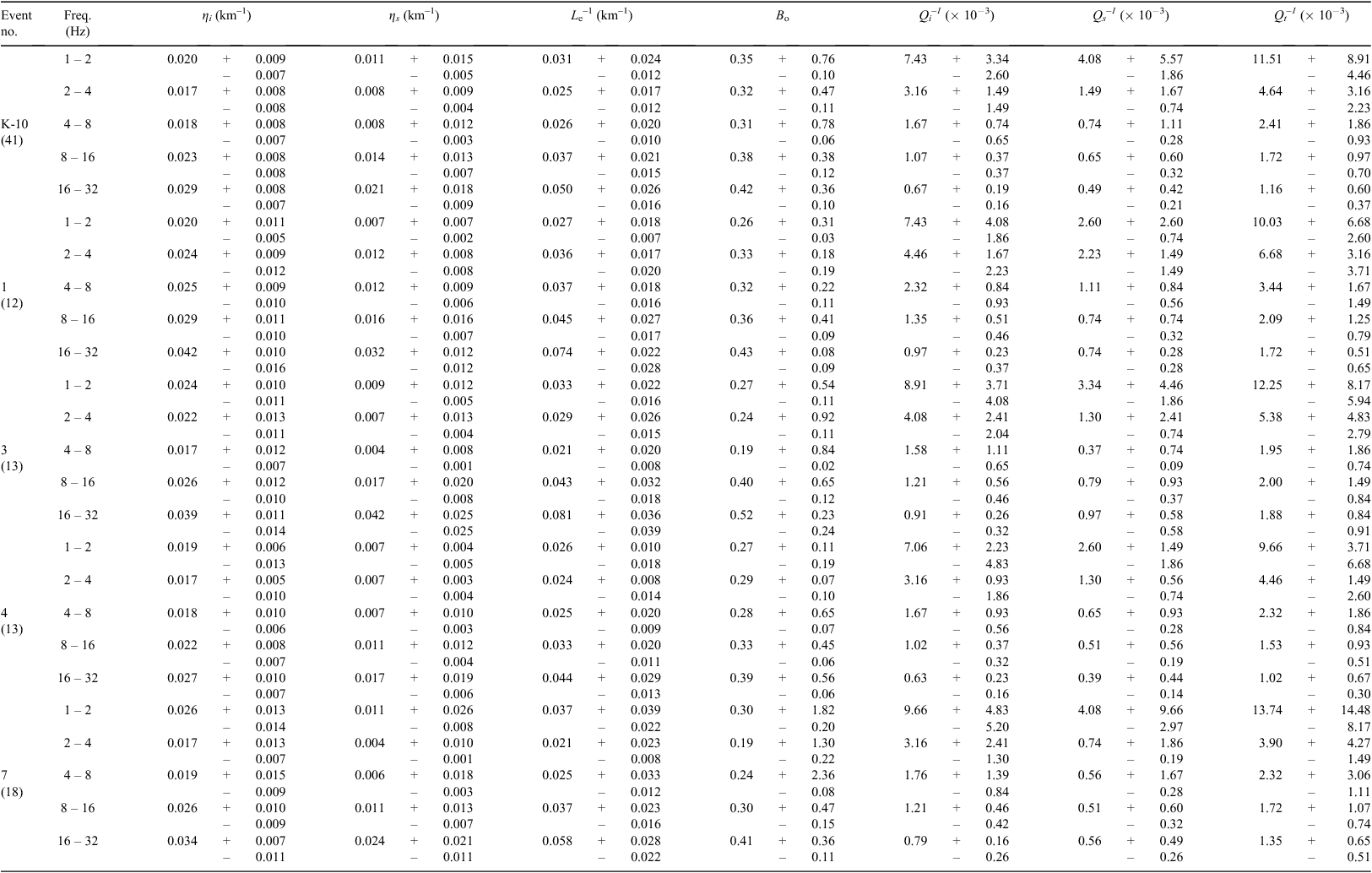
Our data are based on the study by Chung and Asep (2013), which used 41 events during the period of 1999 – 2009. Each event of depth and magnitude ranges from 6.1 to 16.9 km and from 2.0 to 4.8, respectively, which were recorded by 3 to 18 stations operated by the Korea Meteorological Agency (KMA) and the Korea Institute of Geoscience and Mineral Resources (KIGAM). From these events, DSMC-2 showed similar or smaller residuals – reliable results – than those of DSMC-1 for the events that have been recorded by 12 or more stations (see Tables 1 and 2). The results were obtained by MLTWA processing as follows. The MLTWA method was applied for each event with hypocentral distances less than 120 km. The first processing step was removing the trend and the mean values and the application of a 5% cosine taper to each end of the time series of a seismogram. Then, the seismogram was filtered by a four-pole Butterworth band-pass filter centred at five frequencies: 1.5 Hz, 3 Hz, 6 Hz, 12 Hz, and 24 Hz. The filtering used a low-pass Gaussian Nadaraya–Watson kernel regression smoother (R Development Core Team, 2006). After estimating the noise during the 5 s before the P-waves arrival, further processing was done for only seismograms with a signal/noise ratio greater than 2.

Table 1.  Earthquakes with more than 12 recorded stations. Focal mechanism parameters of events were obtained by Hong and Choi (2012), except event 5 (Park et al., 2007). In parameter evaluation, P denotes both the P-wave polarities and S/P amplitude ratios, and I denotes waveform inversion.

Table 2.  Comparison of M_sum between DSMC-1 and DSMC-2. The values in parentheses denote non-weighting values.

Table 3.  Range of MLTWA parameters and Q^–1 values for K-10 (Chung and Asep, 2013) and events 1, 3, 4, and 7, obtained by DSMC-1. Numbers in parentheses under the event number denote the number of record stations for the event.

From the three windows (Figure 3) for the processed seismograms, the seismic energies were obtained by integrating the squared amplitudes over time for the seismograms. The geometrical spreading effect was corrected by multiplication of 4πr², where r is the hypocentral distance. In addition, each integral was normalised by the coda spectral amplitude of a 10 s time window centred at 45 s to correct different sources and site effects (Hoshiba, 1993). Whereas the observed values of the envelope energy were obtained by the aforementioned procedure, the theoretical values were derived from the methods of DSMC-1 and 2 for the uniform velocity (= 3.5 km/s) model. For least-square estimates of the attenuation coefficients of intrinsic (η_i) and scattering (η_s), a grid-search with an interval of 0.001 km^–1 was done to find the minimum values of the misfit function M_f for each frequency f (Hoshiba, 1991):

Fig. 3.  An example of the seismogram used in this study. MLTWA processing was conducted by dividing three time windows (grey vertical line) with a length of 15 s starting from S-wave onset.

where k and j are the number of observations and time windows, respectively. EO_j (r_k) and EM_j (r_k) present the observed and theoretical energies, respectively. Comparisons of theoretical with observed values are exemplified in Figure 4. The sum of the misfit function, M_sum, is given by combining the misfit function for each frequency:

Because the radiation pattern is naturally a large influence near the source range, we empirically find weight factors for the residuals between observed and theoretical values, twice for distances less than 80 km. Through this distance-weighting, M_sum of DSMC-2 is decreased more than that of DSMC-1 (Table 2). The error intervals of the two attenuation coefficients for each frequency (Tables 3 and 4) were evaluated from the confidence contour using the F distribution test (Draper and Smith, 1998) as follows:

Fig. 4.  For event 7, observed energy values (grey symbols) and theoretical energy values (black symbols) are compared for three windows at the least M_sum for five frequency-bands.

Table 4.  Range of MLTWA parameters and Q^–1 values for K-10 (Chung and Asep, 2013) and events 1, 3, 4, and 7, obtained by DSMC-2. Numbers in parentheses under the event number denote the number of record stations for the event.

where is the minimum value of M_f (η_s, η_i), the number of model parameter is p = 2(η_s and η_i) and n is the number of observations. F₆₀ denotes the Fisher distribution function with a confidence level of 60%, which was also used by previous studies (Bianco et al., 2002, 2005; Giampiccolo et al., 2006). The ratios were depicted by the shading zones for the confidence areas (Figure 5). The seismic albedo, B₀ = η_s/(η_i + η_s), and the inverse of the extinction length, L_e^–1 = η_i + η_s, are also shown in Tables 3 and 4. The seismic albedo represents a dimensionless ratio of scattering loss to total attenuation, whereas, the inverse of the extinction length describes the inverse of the distance over which the primary S-wave energy is decreased by exponent (e).

Fig. 5.  Comparison of residual map of four events between DSMC-1 and DSMC-2, which were normalised to its minimum (✶) for five frequency-bands. The shaded areas represent a confidence zone of the F test at the 60% level. (a) Event 1, (b) event 4, (c) event 5, and (d) event 7.

Through application of distance weighting, DSMC-2 shows smaller M_sum than that of DSMC-1 for events 3 and 7, and similar M_sum for events 1 and 4 (Table 2). The focal mechanisms of events showing smaller or similar M_sum were considered as reliable, and only events 1, 3, 4 and 7 are exemplified in Figures 4 and 5 and Tables 3 and 4. In particular, event 7 shows significantly smaller M_sum of DSMC-2 than that of DSMC-1, even without the application of distance weighting. This reliability of event 7 seems to be related to the best azimuthal coverage among the data events (Figure 6). Although event 6 is the largest event, and the focal mechanism is well defined, the M_sum of DSMC-2 is larger than that of DMSC-1. This might be related to the topographic effect, whose contribution of amplitude variation is well known in rough terrain (Geli et al., 1988; Rodgers et al., 2010). The location of event 6 shows rough topography with a high mountainous area (Figure 6), which possibly caused amplitude errors in the waveform inversion using the simplified one-dimensional model.

Fig. 6.  Topographic maps of the events (triangles) with their focal mechanism solutions in Table 1 and recorded stations (circles). Events 1, 3, 4 and 7, which showed reliable results for DSMC-2, are denoted by yellow triangles connected by lines of colour (yellow, pink, purple and red, respectively), and with red numbers for focal mechanism. The other events 2, 5 and 6 are denoted by blue triangles connected by light blue, green and dark blue lines, respectively, and by blue numbers for focal mechanism.

Despite using the focal mechanism, however, improvements of M_sum were not significant for many events. This is thought to be due to the uncertainty of the focal mechanism, which is generally known to be large for small and shallow earthquakes, as in our data (Helffrich, 1997). The small magnitude of event 5 is attributed to larger M_sum of DSMC-2 than that of DSMC-1, in spite of the second-most numerous recorded stations. In Figure 7, the Q_s^–1 values for DSMC-2 are low compared with those for DSMC-1 and Chung and Asep’s (2013) results, which were also performed by DSMC-1. However, the Q_s^–1 values are consistent with the Q_s^–1 values obtained by Lee et al. (2010) in Kyeongsang Basin. The low Q_s^–1 values would imply that the intrinsic absorption predominates in our study region.

Fig. 7.  Comparison of Q⁻¹ values for K-10 (Chung and Asep, 2013) and events 1, 3, 4 and 7 obtained by DSMC-1 and DSMC-2. (a) 1/Q_t, (b) 1/Q_i, and (c) 1/Q_s.

The DSMC-2 method requires more computations than the DSMC-1 method to complement the small size of receivers. We increased the total number of particles and decreased the interval of time steps in the DSMC-2 process. These parameters should be determined to stabilise the number of arrived particles and retain temporal resolution.