S-wave reflection and surface wave surveys in liquefaction affected areas: a case study of the Hinode area, Itako, Ibaraki, Japan

Key words: artificial unconformity, Great Eastern Japan Earthquake, liquefaction, reflection method, S-wave, surface wave survey.

The Great East Japan Earthquake occurred on 11 March 2011 and caused serious damage to people’s lives and livelihoods, not only through direct damage from the ground motion but also from the subsequent tsunami, land subsidence, and liquefaction. In particular, liquefaction-related damage was experienced across a wide area of eastern Japan. The Tokyo Bay and Tone River downstream regions (Figure 1), the most highly developed and densely populated areas in Japan, were most seriously damaged by liquefaction (Komatsubara et al., 2014b).

Fig. 1.  Locations of Itako City and the Hinode area: (a) Location of Ibaraki prefecture, Japan; (b) location of Itako City, Ibaraki Prefecture; (c) location of the Hinode area, Itako City.

Estimating the liquefaction resistance of soil is quite important in the civil engineering field, especially in countries with frequent earthquakes (e.g. Japan). Estimates have conventionally been based on bore surveys and on laboratory tests of soil samples. A simplified procedure to estimate the liquefaction resistance of soil using the blow count (N value) of standard penetration tests (SPTs) was first developed by Seed and Idriss (1971). Stark and Olson (1995) determined a relationship between cone penetration test (CPT) tip resistance and liquefaction resistance. These kinds of approaches require invasive methods, such as bore surveys or penetration tests; thus, data are limited to drill-hole or penetration test locations, which provide only sparse spatial coverage.

In the Tokyo Bay and Tone River downstream region, both widespread earthquake damage and the high population and infrastructure density pose significant difficulties for using invasive methods. In such cases, simplified procedures for evaluating liquefaction resistance based on S-wave velocity (V_s) are applicable (Seed et al., 1983; Tokimatsu and Uchida, 1990; Andrus and Stokoe, 1997; Andrus et al., 1999; Andrus and Stokoe, 2000; Kayabali, 1996; Juang et al., 2001; Lin et al., 2004; Kayen et al., 2013). There are some examples in which evaluation of liquefaction in Japan has been based on V_s (Tokimatsu and Uchida, 1990; Hayashi et al., 2006). The V_s distribution can be obtained by non-destructive geophysical surveys, including reflection, refraction and surface wave surveys, and these can also solve spatial coverage problems because geophysical surveys can acquire data over a wider area, and even from subsurface locations that are difficult to reach using invasive methods (e.g. beneath paved roads).

In this study, we carried out both S-wave seismic reflection and surface wave surveys in the same areas, because each technique has advantages and disadvantages. Seismic reflection surveys are well suited to detecting layer boundaries and have a deeper survey capability. On the other hand, they performed poorly when obtaining information at extremely shallow depths because of their resolution limit. In contrast, surface wave surveys are better suited to assessing extremely shallow regions (< 5 m), although their results show ambiguity in the identification of layer boundaries and they have a limited survey depth. The relatively deeper portions of subsurface structures, which can be imaged by reflection surveys, are useful for predicting the local amplification of earthquake ground motions. The information can be used to predict maximum ground surface acceleration, which is necessary for accurately assessing liquefaction potential using V_s values. The distribution of V_s at shallow depths, which can be obtained by surface wave surveys, is useful for estimating liquefaction potential. By applying both techniques together, we derived more accurate subsurface information.

We performed seismic surveys in Itako, Ibaraki, Japan, with a particular focus on the Hinode area of Itako City, which has suffered from serious and widespread liquefaction damage (Figure 2; Komatsubara et al., 2014b). Our research complements other surveys carried out in the Hinode area, included boring (Itako City, 2014a, 2014b; Kazaoka et al., 2014; Tanabe et al., 2014), trenching (Komatsubara et al., 2014a), and direct-push type surveys (Jinguuji and Nakashima, 2014; Jinguuji and Toprak, 2016) in which measurements were carried out using CPT with several sensors attached to the CPT rod, Ram-sounding, and vibration probe penetration tests (VPT; Jinguuji et al., 2001, 2003, 2006). The basic concept of VPT is forcibly liquefying a liquefiable layer using artificial vibrations, and measuring the accompanying changes in physical properties.

Fig. 2.  Distribution map of liquefaction (sand boil) areas in the downstream Tone River area (modified from Komatsubara et al., 2014b).

We were able to extrapolate geological and hydraulic information obtained by boring and CPT by using the information on subsurface boundaries obtained from the reflection surveys and the V_s distribution obtained from the surface wave analyses as guides. On the basis of our results, the subsurface was classified into multiple layers, among which liquefaction occurred inside the uppermost artificial sandy soil layer, the spatial distribution of which was delineated using the V_s sections. By investigating the relationship between V_s and liquefaction potential, we confirmed that liquefaction prediction using V_s distribution is applicable to this area. The results of this study will assist in future subsurface imaging and liquefaction prediction for areas with limited numbers of drill holes.

The Hinode area (Figure 1) was once a lagoon called ‘Uchi-nasaka-ura’. The area was reclaimed in the 1940s in order to increase food production, and was used as water-filled paddy fields for 30 years. During this first land reclamation, an enclosure bank was created to discharge internal water. In the 1970s, further reclamation work was carried out. As a result, the lagoon became desiccated, the land was filled in for use as a housing site. During this second reclamation, sand pumping was used to in-fill the area (i.e. the area was filled with dredged soil sourced from surrounding lakes and rivers using pipes from dredger boats; Kazaoka, 2003; Itako City, 2014a, 2014b). At this time, an artificial unconformity was formed between the natural and artificial (human-made) strata. The artificial unconformity is significant from the viewpoint of geo-hazard prevention. Since artificial strata are younger than natural strata, they are generally unconsolidated and have greater porosity. The boundaries between artificial and natural strata can act as landslide surfaces because of the difference in their properties. When an earthquake occurs, ground motion tends to be amplified more in artificial strata because they are soft and their rigidity is low. Therefore, artificial ground with a high groundwater level is easily liquefied.

The regional strata that accumulated in the Holocene, include the Sawara Formation, the Hinode Mud Formation, and the artificial sandy dredged soil (Itako City, 2014a, 2014b; Tanabe et al., 2014). Figure 3 shows a schematic stratigraphic column of the Hinode area. The Sawara Formation is composed of alternate layers of sand and mud accumulated during a Holocene glacial retreat (i.e. marine transgression at ~5000–10 000 years BP). The Hinode Mud Formation contains muddy or silty sediments that accumulated during a regression period (~2000–5000 years BP) when the Hinode area was a lagoon. Beneath the Holocene layers (i.e. just below the Sawara Formation) is the Itako Mud Formation, which has a depositional age of about 40 000–60 000 years BP (Late Pleistocene).

Fig. 3.  Schematic stratigraphic column of the Hinode area. Wavy lines indicate unconformities.

Three survey lines were run across the Hinode and adjacent areas (Figure 4). Survey line GS13-ITK1 followed a road crossing the central portion of the Hinode area from east to west, while survey lines GS13-ITK2 and GS13-ITK3 ran north to south. The results of boring (Tanabe et al., 2014) and CPT (Jinguuji and Nakashima, 2014; Jinguuji and Toprak, 2016) close to the survey lines were used in this study (Figure 4). Survey lines GS13-ITK1, GS13-ITK2, and GS13-ITK3 were 1236 m, 1395 m, and 1634 m in length, respectively.

Fig. 4.  Survey lines of the S-wave reflection and surface wave surveys. A Geographical Survey Institute (GSI) map was used for the base map. A broken blue line indicates the boundary of the Hinode area. Boring locations are denoted by green circles and the locations of CPT are denoted by yellow circles.

Land seismic surveys generally use spiked geophones as receivers. Since they are firmly fixed to the ground, this type of receiver can acquire high quality data; however, in this study we used a land streamer receiver system (Inazaki, 1992). Although the data quality acquired by the land streamer system is generally lower than that of the spiked geophone system, deployment and movement of the whole spread was easier and greatly reduced the data acquisition time.

In the S-wave reflection survey (Table 1), we used a DAS-1 system (OYO-Geospace Co., Houston, TX, USA) for data recording. A horizontal impact perpendicular to a survey line made by a human powered sledgehammer onto a heavy plate was used as the primary SH energy source (i.e. the plank-hammering method). We also used a mechanical source (‘air-knocker’) using compressed air for some portions of the survey line. The standard shot interval was 1 m. For the 0–1000 m segment of survey line GS13-ITK2, and the 0–1030 m segment of survey line GS13-ITK3, the shot point interval was set to 2 m. The standard number of shots at each shot point (vertical stack number) was four. We attached 120 single-channel horizontal geophones perpendicular to a survey line with a natural frequency (f₀) of 14 Hz to the land streamer at intervals of 0.5 m. Receiver spread was ‘on end shooting’ and offset coverage was 3–62.5 m. The sampling rate was set to 0.5 ms and the total record length was 2.010 s.

Table 1.  Specifications of S-wave reflection data acquisition.

We carried out conventional S-wave reflection data processing based on common midpoint (CMP) stacking, and created S-wave reflection sections. In pre-processing, we eliminated surface wave energy and applied a static correction assuming V_s = 160 m/s. Then, we applied a whitening deconvolution filter. The normal moveout (NMO) stacking velocity was obtained by velocity analysis at every 250 m CMP location. The estimated NMO velocity was interpolated in the time-and-space direction, and a two-dimensional NMO stacking velocity table was created. We applied post-stack f-k migration to the NMO-stacked section. For the migration velocity, we used the NMO stacking velocity function smoothed in the survey line direction.

For the surface wave survey (Table 2), we used a DSS12 system (SUNCOH consultants Co., Tokyo, Japan) for data recording and a DigiPulse AWD-1 (GeoSurvey Systems Co., Conroe, TX, USA) as the energy source. This is a weight-drop-type energy source that generates an impulsive P-SV wave by striking a weight accelerated using the elastic energy of a rubber band and the potential energy of the weight, against a plate which is placed on the ground. The shot interval was 2 m and the standard number of shots at each shot point (vertical stack number) was two. We attached 96 single-channel vertical geophones with a natural frequency (f₀) of 4.5 Hz to the land streamer at intervals of 1 m. Receivers were in a ‘split-spread’ array, and offset coverage varied from 0–95 m to –47–48 m. The source shots from 0 to 48 m were performed with the position of the land streamer fixed. When the source had finished the 48 m shot position, the land streamer was moved 48 m forward. The sampling rate was set to 1 ms and the total record length was 4.010 s.

Table 2.  Specifications of surface wave survey data acquisition.

The surface wave survey data were processed using the multichannel analysis of surface waves (MASW; Park et al., 1999, 2001; Miller et al., 1999; Hayashi et al., 2001). We picked peaks on the colour contour panel of the frequency phase-velocity relationship and obtained the dispersion curves corresponding to the fundamental and higher modes. We used the f-k method (Capon, 1969; 1973) to obtain the relationship between frequency and phase-velocity. First, the f-k method obtained the power spectrum in frequency wavenumber (f-k) domain by the two-dimensional Fourier transform of the acquired data in time distance (t-x) domain, which were sorted into CMP gathers. Next, we obtained the power spectrum in frequency phase-velocity (f-v_ϕ) domain by converting the wavenumber to the phase-velocity () where v_ϕ is phase-velocity, ω is angular velocity, and k is wave number. Then we obtained the dispersion curve by picking the maximum amplitude on the power spectrum in the frequency phase-velocity (f-v_ϕ) domain. Using the picked values as inputs, we obtained the one-dimensional (horizontally layered) V_s structure by a nonlinear least-squares inversion (Hayashi et al., 2001), which simultaneously took fundamental and higher modes into consideration (see Appendix A for the necessity of this step and for justification of including higher modes in the inversion). During the inversion process, V_s models for a 15-layer structure were used. To stabilise the inversion, we kept layer thicknesses at constant values, and only the V_s value of each layer was estimated. The values of V_p, V_s, and density are necessary to define the Rayleigh wave velocity. However, if we try to estimate these values simultaneously, the inversion will become unstable. Moreover, occasionally such a procedure can result in a physically impossible model. Accordingly, in this study, we introduced the assumption that V_p and density values could be calculated from the V_s value in order to stabilise the inversion. Specifically, we estimated V_p and density values from empirical equations between those values and V_s. The equations were obtained by linear regression using experimental data (Sakai, 1968; Kitsunezaki et al., 1990; Society of Exploration Geophysicists of Japan, 1990). Finally, two-dimensional V_s sections were obtained by interpolating between the series of one-dimensional inversion results.

In the inversion procedure, we first created an initial velocity model by extracting rough estimations of the relationships between phase-velocity and depth from the obtained dispersion curve. First, by using the phase-velocity frequency relationship, we converted the phase-velocity into the wavelength at every frequency. Next, we plotted the phase-velocity at the depth corresponding to one-third of its wavelength. In this way, an apparent V_s structure was obtained, which was then used as the initial velocity model of the inversion after spatial smoothing. Finally, we created horizontal-layered initial models with 15 layers. We limited analysis to a maximum depth of 35 m.

Seed and Idriss (1971) proposed a simple approach for evaluating liquefaction potential. They introduced the external force of the earthquake as a cyclic stress ratio (CSR) and resistance to liquefaction in a soil deposit as cyclic resistance ratio (CRR), and assumed that the liquefaction occurred when the two values became equal (CRR = CSR). Since subsequent studies have shown that scaling by earthquake magnitude is necessary, a magnitude scaling factor (MSF) was also introduced (Andrus and Stokoe, 1997; Andrus et al., 1999). As a result, the boundary between liquefaction and no-liquefaction can be written using CSR, CSS, and MSF:

There are various ways to give the MSF value, as summarised in Table 2 of Andrus and Stokoe (1997). In this study, we used the values recommended for the upper-bound value in the National Center for Earthquake Engineering Research (NCEER) 1996 workshop (Youd and Idriss, 2001).

where M_w is the moment magnitude.

CSR is generally expressed as:

where σ_v is total overburden stress, σ^ʹ_v is initial effective vertical stress, g is acceleration of gravity, a_max is peak ground surface acceleration and r_d is a shear stress reduction factor to adjust for flexibility of the soil profile. For the value of r_d, we used (Liao et al., 1988):

where z is the depth below the ground surface in metres. Many empirical relationships concerning the boundary of liquefaction and no-liquefaction have been suggested using CRR and V_s (Seed et al., 1983; Tokimatsu and Uchida, 1990; Andrus and Stokoe, 1997; Andrus et al., 1999; Andrus and Stokoe, 2000; Kayabali, 1996; Juang et al., 2001; Kayen et al., 2013). In this study, we used the relationship for magnitude 7.5 earthquakes proposed by Andrus and Stokoe (1997), where the fine-grained fraction content is around 20%.

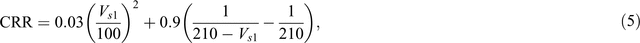
where V_s1 is stress corrected shear wave velocity, defined as:

where P_a is reference stress 100 kPa (approximately atmospheric pressure) and V_s is observed shear wave velocity.

We identified two notable reflection boundaries in the depth section of survey line GS13-ITK1 (Figure 5): (1) a relatively flat reflection boundary at a depth of about 10–15 m, which extended from the western end of the survey line for 700 m; and (2) a slightly west-dipping reflection boundary at a depth of about 15–30 m. A syncline (or pair of anticlines) was observed extending from the western end of the survey line for 500 m, at a depth of around 20–40 m.

Fig. 5.  Depth section of the S-wave reflection survey results along survey line GS13-ITK1. The reflection section is vertically exaggerated by 5 times.

For Line GS13-ITK2 (Figure 6), the interval between a point at a distance of 1000 m and the southern end of the survey line falls within the Hinode area. A relatively flat reflection boundary at a depth of around 10–15 m, which was observed extending from the northern end of the survey line to 800 m, rapidly increased in depth from the boundary of the Hinode area. From a point with a distance of about 1200 m to the southern end of the line, the deep reflection boundary was observed at a depth of around 50 m.

Fig. 6.  Depth section of the S-wave reflection survey results along survey line GS13-ITK2. The reflection section is vertically exaggerated by 5 times.

For Line GS13-ITK3 (Figure 7), a remarkable syncline (valley-like structure) was observed from the northern end of the survey line to approximately 400 m. The centre of the syncline was located at about 230 m from the northern end of the line, while the depth of the deepest part was about 42 m. Elsewhere, a reflection boundary with a gently changing depth (5–15 m) was observed between distances of 500 and 1500 m. The depth of the boundary gradually increased from the boundary of the Hinode area (at ~1000 m), reaching 25 m depth at the southern end of the survey line.

Fig. 7.  Depth section of the S-wave reflection survey results along survey line GS13-ITK3. The reflection section is vertically exaggerated by 5 times.

For survey line GS13-ITK1 (Figure 8), a layer with a V_s of around 180 m/s was observed at the ground surface. Just beneath the surface layer, a low-velocity layer with a V_s of about 150 m/s or lower was observed. This layer maintained a 15 m thickness from the western end of the survey line for 700 m, but rapidly thinned from this point towards the eastern end of the survey line. Where the low-velocity layer became thinner, the depth to the underlying high-velocity layer (V_s higher than 250 m/s) appeared to decrease.

Fig. 8.  S-wave velocity (V_s) distribution obtained from the surface wave survey results along survey line GS13-ITK1. The velocity section is vertically exaggerated by 20 times.

In the northern neighbouring zone of the Hinode area, covering the distance range of 0–1000 m along survey line GS13-ITK2 (Figure 9), the subsurface structure was classified into three parts. In the shallowest layer, a zone with a V_s of 180 m/s was intermittently observed. Below the uppermost zone, a low-velocity layer with a V_s of 150 m/s or slower was observed at depths of 1–5 m; and below a depth of 5 m, a layer with V_s of 250 m/s or higher was observed. The thickness of the second layer was almost constant within the zone. The Hinode area also had a three-layered structure. The uppermost layer (V_s of ~180 m/s) was horizontally continuous. The low-velocity second layer gradually increased in thickness from north to south, and rapidly thickened from ~1100 m.

Fig. 9.  S-wave velocity (V_s) distribution obtained from the surface wave survey results along survey line GS13-ITK2. The velocity section is vertically exaggerated by 20 times.

For survey line GS13-ITK3 (Figure 10), a triangle-shaped low-velocity zone (V_s of 150 m/s or lower) was observed in the shallow layer (0–10 m depth) at 0–270 m distance (near the northern end of the survey line). This low-velocity zone was located at almost the same position as a characteristic syncline structure observed in the reflection section of the same survey line (Figure 7). The subsurface structure to the south of this low-velocity layer showed almost the same trend as that observed on survey line GS13-ITK2 (Figure 9). At other points along the survey line, the features of the subsurface structures were similar to those seen in GS13-ITK2. The subsurface structure to the north of the Hinode area showed an almost horizontally layered velocity distribution. The surface layer had a V_s of about 180 m/s, the middle layer was low-velocity, while the deepest layer had a V_s of 250 m/s or more. Horizontal continuity of the surface layer was much better than that observed for survey line GS13-ITK2. In the Hinode area, the low-velocity layer gradually increased in thickness from north to south, rapidly becoming thicker from about 1500 m.

Fig. 10.  S-wave velocity (V_s) distribution obtained from the surface wave survey results along survey line GS13-ITK3. The velocity section is vertically exaggerated by 20 times.

We show the interpretation results for GS13-ITK1, GS13-ITK2 and GS13-ITK3 in Figures 11, 12 and 13, respectively. Each figure consists of three panels: (1) the reflection images obtained from the S-wave reflection survey (Figures 11a, 12a and 13a); (2) the V_s structures obtained from the surface wave survey (Figures 11b, 12b and 13b); and (3) geological interpretation (Figures 11c, 12c and 13c). The figures are vertically exaggerated by a factor of 10. The intersections of the survey lines, borehole locations and positions of CPT are also shown in the figures. The uppermost boundary between artificial sandy soil and the Hinode Mud Formation (broken green line) was interpreted in the V_s sections and overlaid on the S-wave reflection sections, while the other boundaries were interpreted in the S-wave reflection sections and overlaid on the V_s sections. In the Hinode area, the groundwater level is around 1–1.5 m below the ground surface.

Fig. 11.  Interpretation of the depth section along survey line GS13-ITK1. Broken green lines show the boundary between the artificial sandy soil and the Hinode Mud Formation. Broken blue lines show the boundary between the Hinode Mud Formation and the Sawara Formation. Broken red lines show the bottom of the Sawara Formation. A reflection boundary below the bottom of the Sawara Formation (within the Late Pleistocene) is denoted by the broken pink line. In the reflection and lithological interpretation sections, only the section below sea level is shown. (a) S-wave reflection depth section vertically exaggerated by 10 times. (b) V_s distribution vertically exaggerated by 10 times, with the groundwater level, geological column, N values and the q_c values overlaid. (c) Lithological interpretations.

Fig. 12.  Interpretation of the depth section along survey line GS13-ITK2. Broken green lines show the boundary between the artificial sandy soil and the Hinode Mud Formation. Broken blue lines show the boundary between the Hinode Mud Formation and the Sawara Formation. Broken red lines show the bottom of the Sawara Formation. A reflection boundary below the bottom of the Sawara Formation (within the Late Pleistocene) is denoted by the broken pink line. In the reflection and lithological interpretation sections, only the section below sea level is shown. (a) S-wave reflection depth section vertically exaggerated by 10 times. (b) V_s distribution vertically exaggerated by 10 times, with the groundwater level, geological column, N values and the q_c values overlaid. (c) Lithological interpretations.

Fig. 13.  Interpretation of the depth section along survey line GS13-ITK3. Broken green lines show the boundary between the artificial sandy soil and the Hinode Mud Formation. Broken blue lines show the boundary between the Hinode Mud Formation and the Sawara Formation. Broken red lines show the bottom of the Sawara Formation. A reflection boundary below the bottom of the Sawara layer (within the Late Pleistocene) is denoted by the broken pink line. The bottom of the relatively high-velocity layer near the surface, which is different from the artificial sandy soil, is denoted by the broken brown line. In the reflection and lithological interpretation sections, only the section below sea level is shown. (a) S-wave reflection depth section vertically exaggerated by 10 times. (b) V_s distribution vertically exaggerated by 10 times, with the groundwater level, geological column, N values and the q_c values overlaid. (c) Lithological interpretations.

As shown in Figure 11a, four reflection boundaries in the depth section of survey line GS13-ITK1 were interpreted. The top reflection boundary (green line) marked the boundary between the artificial sandy soil and the Hinode Mud Formation. The second reflection boundary (blue line) marked the boundary between the Hinode Mud and the Sawara Formations. The third reflection boundary (red line) marked the bottom of the Sawara Formation. We interpreted these three layers as nearly flat structures. Beneath these layers, from the western end of the survey line to a distance of about 300 m, an additional reflection boundary was observed and we interpreted this to represent an internal feature of the Late Pleistocene formation.

For survey line GS13-ITK1, we observed a ground surface layer (the artificial sandy soil) with V_s values of 150 to 180 m/s and q_c (CPT tip resistance) values obtained from CPT of more than 5 MPa (Figure 11b). Beneath this layer, we observed a low-velocity zone (the Hinode Mud Formation) with V_s values of 100–150 m/s and q_c values of less than 2 MPa. Below the low-velocity layer, we observed a high-velocity zone (the Sawara Formation) with V_s greater than 200 m/s and q_c values of over 10 MPa.

The two almost horizontal reflection boundaries corresponding to the bottom of the Hinode Mud Formation and the Sawara Formation were observed from the northernmost end of survey line GS13-ITK2 for about 500 m (Figure 12a). Between distances of 500 and 1000 m, three reflection boundaries were interpreted, consisting of the above-mentioned two reflection boundaries and the bottom of the subjacent Late Pleistocene layer, which dipped slightly to the north. Within the Hinode area, located to the east at a distance of 1000 m and greater, the inclination of the layered structure was large. In particular, the reflection boundary within the Late Pleistocene inclined significantly and its depth reached 50 m at the southern end of the survey line.

In the Hinode area (from 1000 m to the southern end of survey line GS13-ITK2; Figure 12b) we observed a three-layer V_s structure consisting of a relatively high-velocity surface layer (the artificial sandy soil) and subsiding low and high-velocity layers (the Hinode Mud and the Sawara Formations) similar to those observed in survey line GS13-ITK1. Outside the Hinode area, the surface layer was not observed; however, the low- and high-velocity layers were continuous towards the northern end of the survey line.

In the Hinode area (from 1000 m to the southern end of the survey line), three reflection boundaries were interpreted from survey line GS13-ITK3 (Figure 13a). The uppermost reflection boundary, representing the bottom of the dredged sandy soil, was delineated as an almost flat layer. The second reflection boundary, that between the Hinode Mud and the Sawara Formations, and the third reflection boundary, that at the bottom of the Sawara Formation were delineated as west-dipping reflection boundaries. To the north of the Hinode area (distance range of 0–1000 m) an additional reflection boundary was identified, which was observed to continue to the bottom of the characteristic syncline structure. Considering the depositional age of the Sawara Formation (~5000–10 000 years BP), we interpreted that the sediments between this additional reflection boundary and the one above accumulated during the Late Pleistocene. This depositional age was consistent with the results of the boring survey (Itako City, 2014a, 2014b; Tanabe et al., 2014). ‘Basal Gravel Beds of Alluvium’ are widely observed across Japan, including in the Kanto district, and are thought to have accumulated during the Last Glacial Maximum (~21 000 years BP during the Late Pleistocene). Thus, we interpreted the localised bottom reflection boundary to represent the top of the ‘Basal Gravel Beds’. Finally, from the depositional age and its characteristic shape, we interpreted the syncline structure to represent an erosional valley formed in the Pleistocene upland. Subterranean topography of this nature could locally enlarge earthquake ground motion and may be an important factor for future liquefaction predictions.

In the Hinode area (from 1000 m to the southern end of survey line GS13-ITK3; Figure 13b) we observed a three-layer structure similar to that seen in survey lines GS13-ITK1 and GS13-ITK2. The q_c and V_s values of each layer were almost the same as those along survey line GS13-ITK1. The thickness of the surface layer increased to the south, and as a result, the top depth of the low-velocity layer appeared to increase slightly to the south. The low-velocity layer also dipped towards the south, and the depth of the high-velocity layer increased accordingly. To the north of the Hinode area, a relatively high-velocity layer was observed at the ground surface within a distance range of 350–800 m. The origin of this high-velocity zone is not the reclamation because the area is located outside of the Hinode area; thus, we distinguished the layer from the dredged sandy soil. Just beneath the surface layer, we observed a low-velocity layer. We also observed a syncline structure filled with low-velocity sediment, extending from the northern end of the survey line to a point with a distance of about 300 m. The deepest point along the low-velocity layer was only approximately 12 m, whereas the depth of the ‘erosional valley’ (Figure 13a) was more than 40 m; however, their horizontal locations were identical. By considering the N values and velocities, we interpreted the low-velocity zone to be the same as that observed in the Hinode area. Over the distance range of ~290–330 m, a notable velocity anomaly was observed. It can be interpreted as a relic of Tone River bank; however in this study, we interpreted this to contain artefacts produced by the inversion procedure as a result of erroneous input values. These data were contaminated by noise (e.g. traffic, a waterway laid under the crossing road), which caused problems when picking the dispersion curve.

At some points, the trends observed in the q_c values obtained from CPT did not agree with those of the V_s obtained by our surface wave surveys (e.g. CPT2–26 on survey line GS13-ITK1; Figure 11b). Although the lowest-velocity portion of the low-velocity layer was observed at 2–3 m deep in the surface wave survey results, q_c values of less than 2 MPa at CPT2–26 occurred between depths of 3 and 5 m. This discrepancy may be explained by the difference in the survey position, with CPT2–26 located ~8 m south of the survey line GS13-ITK1. According to the result from survey line GS13-ITK3 (Figure 13b), the low-velocity layer at this position dips to the south, and the depth of first appearance of the layer is greater in the south. This observation explains the source of the discrepancy. We conclude that the appearance depth of the silt layer derived from the q_c value of CPT2–26 located south of survey line GS13-ITK1 was deeper than that derived from the surface wave survey results.

We compared the overall velocity trends for boreholes GS-ITK1 (survey line GS13-ITK3; Figure 14a) and GS-ITK2 (survey line GS13-ITK2; Figure 14b) obtained by suspension PS logging and extracted from the surface wave survey results, and found them to show similar velocity trends; although the surface wave survey results were much smoother. However, the inversion of dispersion curves using the surface wave survey data was unable to reconstruct the local low-velocity anomaly observed in the PS logging results. These two features originated from the differences between the V_s values obtained by the surface wave surveys and those obtained by PS logging. We also found that the surface layer velocities obtained from the surface wave survey results were higher. The distance between the drillholes and the survey line, which were metres apart, may explain this observation. Several other sources of this discrepancy are also possible. The V_s values of the surface layer obtained by the surface wave surveys may also have increased due to the existence of the high-velocity paved road and roadbed, which are just 1 m in thickness but may impact to a depth of up to 5 m. Inaccuracy of the suspension PS logging results in the shallowest layer (especially near the groundwater level) can also be a source.

Fig. 14.  Comparison of S-wave velocities (V_s) obtained by suspension PS logging and the surface wave survey: (a) V_s from borehole GS-ITK1; (b) V_s from borehole GS-ITK2.

We examined the liquefaction potential at CPT6–9 at a depth of 2.5 m (Figure 11b) based on CSR and CRR using Equations 1–6. For the values of total overburden stress (σ_v) and initial effective vertical stress (σ^ʹ_v) in Equations 3 and 6, we used the CPT survey result of CPT6–9. The earthquakes used for the examination were the Great East Japan Earthquake in 2011 (Mw = 9.0) and the Chiba-Ken-Toho-Oki (off the eastern coast of Chiba prefecture) Earthquake in 1987 (Mw = 6.1). Plotting V_s values obtained by the surface wave surveys on the horizontal axis and peak ground surface acceleration (a_max) on the vertical axis, the boundaries of liquefaction and no-liquefaction were delineated (Figure 15).

Fig. 15.  Liquefaction potential at the location of CPT6–9 at a depth of 2.5 m. The pink and light blue lines show the liquefaction and no-liquefaction boundary of the Great East Japan Earthquake (Mw = 9.0) and the 1987 Chiba-Ken-Toho-Oki Earthquake (Mw = 6.1), respectively. The blue and red arrows show the range of peak ground surface acceleration of the Great East Japan Earthquake and the Chiba-Ken-Toho-Oki Earthquake, respectively. The broken line indicates 155 m/s, which is the surface wave survey result at CPT6–9 at a depth of 2.5 m. Grey shading denotes V_s in the 150–180 m/s, which is equivalent to the V_s range of the artificial sandy dredged soil of the whole Hinode area.

According to Japan Meteorological Agency (2012) and National Institute for Land and Infrastructure Management (2011), the range of peak ground surface acceleration at CPT6–9 was 50–250 gal and 250–550 gal for the Chiba-Ken-Toho-Oki Earthquake and the Great East Japan Earthquake, respectively. The blue and red arrows on Figure 15 show the range of peak ground surface acceleration corresponding to each earthquake. A broken black line indicates 155 m/s, which is the surface wave survey result for CPT6–9 at a depth of 2.5 m. In addition, we added grey shading to show the V_s range (150–180 m/s) in the artificial sandy dredged soil of the whole Hinode area. The broken black line exists to the right of the blue arrow and to the left of the red arrow. If we assume that V_s values of this area have not changed since 1987, we can conclude from Figure 15 that the point (2.5 m deep at CPT6–9) did not liquefy during the Chiba-Ken-Toho-Oki Earthquake, but did liquefy during the Great East Japan Earthquake. Moreover, most of the grey shaded zone lies to the right of the blue arrow, but some of the dredged soil range is to the left of the red arrow. This implies that most of the artificial sandy dredged soil of the Hinode area did not liquefy during the Chiba-Ken-Toho-Oki Earthquake, but did liquefy during the Great East Japan Earthquake. These conclusions agree well with the geological facts. According to the National Institute for Land and Infrastructure Management and Building Research Institute (2011), only a few limited spots of the Hinode area were liquefied by the Chiba-Ken-Toho-Oki Earthquake. Since CPT6–9 is distant from these liquefied spots, it was assumed that liquefaction did not occur during the Chiba-Ken-Toho-Oki Earthquake at the location of CPT6–9. On the other hand, most of the Hinode area was liquefied during the Great East Japan Earthquake, including the location of CPT6–9.

According to previous research (Tanabe et al., 2014; Komatsubara et al., 2014a), large-scale liquefaction in 2011 occurred mainly in the artificial sandy soils. Our results suggest that the liquefied layer is represented by high V_s zones just beneath the ground surface. It can be assumed that this layer will again liquefy during future large-scale earthquakes. The existence of the silty-muddy Hinode Mud Formation, which lies just beneath the liquefiable artificial sandy soil, also plays a role in the liquefaction behaviour. The low permeability of the formation prevents groundwater from infiltrating the deeper subsurface. Therefore, the water content of the uppermost sandy layer is kept high. Consequently, we can say that the liquefaction probability of the layer is kept high because it is difficult to relieve the excess pore water pressure in the layer, brought about by an earthquake.

We performed S-wave seismic reflection and surface wave surveys in Itako, Ibaraki, Japan, an area that suffered from extensive liquefaction damage during the Great Eastern Japan Earthquake of 2011. We were able to image the subsurface structure and obtain the V_s distribution beneath the Hinode area and its surroundings. The relatively deeper subsurface structures imaged by the reflection surveys are useful for predicting the local amplification of the earthquake ground motion. The V_s distribution obtained by the surface wave survey showed that the survey area is mainly characterised by three layers: a relatively high-velocity surface layer, a low-velocity middle layer, and a high-velocity base layer. By comparing our results with data from drilling and other geological research we were able to interpret these layers as: (1) a relatively high-velocity surface layer (V_s of 150–180 m/s, q_c values greater than 5 and N values greater than 10), which represents the dredged sandy soil that experienced significant liquefaction; (2) a low-velocity layer (V_s of 100–150 m/s, q_c values lower than 2 and N values lower than 5), which represents the Hinode Mud Formation; and (3) a high-velocity layer (V_s of higher than 200 m/s, q_c values greater than 10 and N values greater than 20), which represents the sandy part of the Sawara Formation (alternating layers of sand and mud). The results of this study showed that geophysical (S-wave reflection and surface wave) surveys are economical approaches to quantifying liquefaction predictions with sufficient spatial coverage. Our results showed that V_s distribution can be used to efficiently map the distribution of artificial sandy soil, which is prone to liquefaction.

Understanding the relationship between liquefaction and seismic survey results is challenging. However, the results of this study showed that it is possible to identify the spatial distribution of liquefiable soil by comparing survey results with q_c values, N values and other geological data obtained by drilling and CPT. Furthermore, our results suggest that the V_s distribution is applicable for liquefaction prediction.