Multiple lapse time window analysis using solely single events in South Korea

Key words: Q_s^–1, Q_i^–1, flexible range window, MLTWA, wide single events.

Regional studies of scattering Q^–1 (Q_s^–1) and intrinsic Q^–1 (Q_i^–1) attenuation, separated from the total attenuation Q^–1 (Q_t^–1), have been carried out globally (Sato et al., 2012); these targeted studies are useful for making inferences about both the materials and the physical condition of the lithosphere. Q_s^–1 denotes the presence of heterogeneities that redistribute wave energy without any loss, and Q_i^–1 represents the anelasticity that changes vibrational energy to heat energy. High values of both Q_s^–1 and Q_i^–1 have been commonly reported from volcanic regions (Vargas et al., 2004), whereas high Q_i^–1 has been observed in regions of high heat flow (Abdel-Fattah et al., 2008). The availability of Q_i^–1 as an indicator of volcanic eruptions has been suggested based on the correlation of melt effects with magmatic activity (Chung et al., 2009).

Q_s^–1 and Q_i^–1 are generally separated by the method of multiple lapse time window analysis (MLTWA) (Hoshiba et al., 1991; Fehler et al., 1992), based on the technique by Wu (1985) of applying radiative transfer theory. The MLTWA method has been used with multiple earthquakes simultaneously, which is believed to be helpful for correcting the radiation pattern of each earthquake. Recently, Asep et al. (2015) subjected single earthquake data to MLTWA based on a report that the radiation pattern becomes insignificant for frequencies greater than 3 Hz (Kobayashi et al., 2015). The use of single earthquake data allows one to avoid the mixing of different earthquake parameters in MLTWA. Focal depth, in particular, is a critical parameter producing significantly different Q_s^–1 and Q_i^–1 for regionally identical locations (Del Pezzo et al., 2011; Chung and Asep, 2013). A study that considered focal depth produced higher Q_s^–1 and Q_i^–1 values in the crust than in the upper mantle, with a more distinctive discrepancy for Q_s^–1 (Badi et al., 2009).

MLTWA with single earthquake data has shown realistic results with more than eight observation stations (Asep et al., 2015). Based on the number of station observations, Asep and Chung (2016) obtained more reliable results by introducing the fitting curve of observations and first showed depth characteristics of crustal Q_s^–1 and Q_i^–1 values using quantitatively estimated earthquake focal depths. Higher values of Q_s^–1 were observed for shallower depths (bluish colours in Figure 1a) than for deeper depths (reddish colours). However, such variation was not clearly observable for Q_i^–1 (Figure 1b), but was slightly observable for Q_t^–1 (Figure 1c).

Fig. 1.  Comparisons of Q_s^–1, Q_i^–1, and Q_t^–1 by Asep and Chung (2016). In the right legend, the values in parentheses represent the median value (D_M) of the depth range, for which the symbols and lines identify shallow and middle/deep events by bluish colours and yellow/reddish colours, respectively. The values obtained by the combinations of events are connected by solid lines, whereas those obtained by single events are shown by dotted lines: (a) Q_s^–1, (b) Q_i^–1, and (c) Q_t^–1.

The results of Asep and Chung (2016), however, failed to include simulation with a single event for seven clusters of two or three events with similar depth (connected with solid lines in Figure 1); this was due to a lack of data in the MLTWA fitting range. A cluster combination with similar depth was ultimately performed for regionally distant events (Figure 2), due to few data being available for seismic stableness of the studied region. Because the analysis may be highly helpful if the combinations are separated as single data, in the present study, the fitting range in MLTWA was adjusted for single-event analysis of the clusters in the previous study.

Fig. 2.  Locations of studied events (Table 1) and seismic observatory.

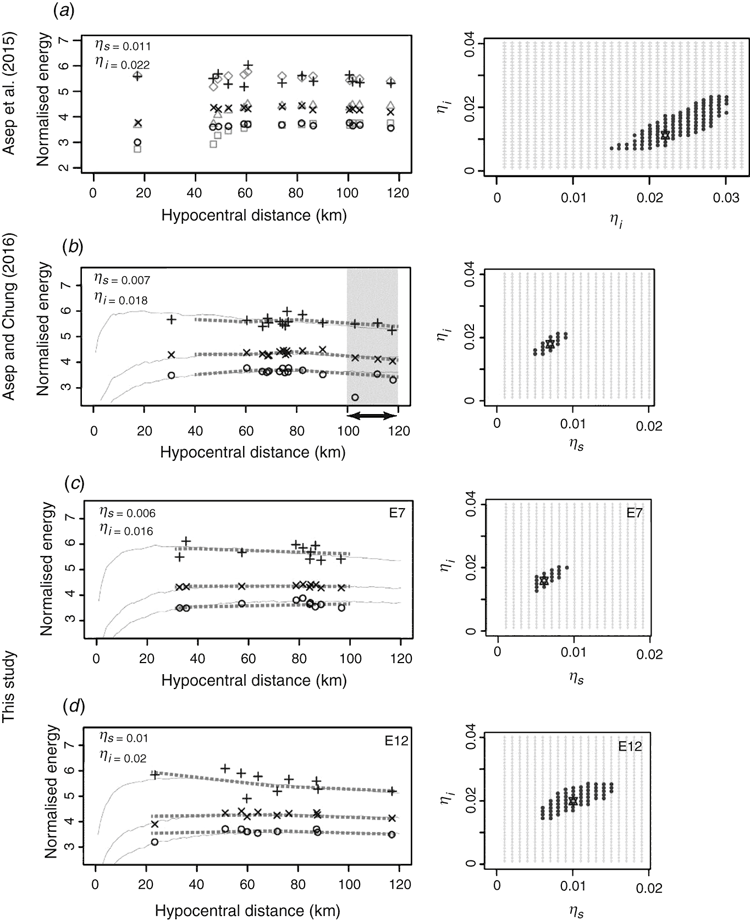
Asep and Chung (2016) processed vertical seismograms with hypocentral distances of less than 120 km for the MLTWA method as follows. Trend and mean values were removed from the seismograms and a 5% cosine taper was applied to each end of the time series. The data were then filtered by a four-pole Butterworth bandpass filter with central frequencies of 1.5, 3, 6, 12, and 24 Hz. Only seismograms with a signal-to-noise ratio greater than 2 were selected, by estimating noise in the 5 s before P-wave arrival. From three consecutive time windows of 15 s following the S-wave onset (Figure 3), the seismic energies (Figure 4a, b) were derived by integrating the squared amplitudes over time for the filtered seismograms and by multiplying by 4πr², where r is the hypocentral distance, as a geometrical spreading correction. To correct relative sources and site effects, each integral was normalised by the coda spectral amplitude (Aki, 1980) averaged in a 10-s window, the centre of which was a fixed reference time (t_C) at a lapse time of 45 s that was selected to be greater than 1.5 times that of the direct S-wave traveltime (Chung and Sato, 2001).

Fig. 3.  Typical vertical seismogram for MLTWA. Three time windows (0–15 s, 15–30 s, and 30–45 s) separated by dotted vertical lines start from the S-wave arrivals from the event with a hypocentral distance of 75 km. The origin time of the event (E12) is referenced in Table 1. The 10-s time bar (CNW) denotes the coda normalisation window, the centre of which (arrow with t_C) is the fixed reference time at the 45-s lapse time.

Fig. 4.  Comparison of MLTWA fitting (8–16 Hz) presented by (a) Asep et al. (2015), (b) Asep and Chung (2016), and (c, d) this study. In the normalised energy graphs (left panels), observed values (+, × , and ○) are obtained from the first, second, and third windows (see Figure 3), respectively. The theoretical fitting lines (dotted lines in b, c, and d) are derived from the window that requires at least two observational datasets in the range between 100 and 120 km (grey zone in b). In this study, the end range of window (c) was reduced from 120 to 100 km, and the range of window (d) was lengthened from 20 to 40 km. The confidence zone of the F-test, expressed by grey circles in the residual maps (right panels), is the 60% level for (a) and the 90% level for (b)–(d).

The corrected observations in the MLTWA for multiple events had been averaged over a spatial window of 4 km and reproduced as three curves to fit the theoretical curves (Chung et al., 2010). These curves, however, were not obtained for the first single-event MLTWA by Asep et al. (2015) due to the small number of observations (Figure 4a). By introducing a 15- or 20-km range window (Figure 4b), Asep and Chung (2016) showed that the three curves agreed well with observations.

The window, however, requires at least two observational datasets in the end range between 100 and 120 km (grey zone in Figure 4b) due to the significant influence of the end range for observational curves. The lack of datasets in the end range required that two or three events were combined for 11 events (Table 1).

Table 1.  Studied earthquakes.

To obtain the solution solely by single events, this study applied a flexible end range of the window by reducing the limit from 120 to 100 km (Figure 4c) or by lengthening the interval from 20 to 40 km (Figure 4d). These flexible windows secured at least two datasets in the end range and produced three observational curves, which were fitted with the theoretical values. For the theoretical energy values, the direct-simulation Monte Carlo (DSMC) method (Yoshimoto, 2000) was applied to a uniform velocity model with v = 3.5 km/s.

The intrinsic and scattering attenuation coefficients were obtained by following a grid search with an interval of 0.001 km⁻¹ to obtain the minimum values of the misfit function M_f for each frequency f (Hoshiba et al., 1991):

where k is the energy value of each distance and j is the number of curves. EO_j (r_k) and EM_j (r_k) denote the observed and the theoretical energies, respectively. The error intervals of the two obtained coefficients were obtained using the F distribution test (Draper and Smith, 1998):

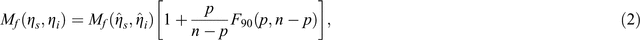
where is the minimum value of M_f (η_s, η_i), p is 2, the number of model parameters (η_s and η_i), and n is the number of energy values. F₉₀ denotes the Fisher distribution function with a confidence level at 90%; this value is more reliable than the previous value, 60% (Asep et al., 2015). The ratios of were plotted as the confidence area, as shown by the shaded zones (right panel in Figure 4a). An attenuation value was excluded as unreliable if its error was equal to or greater than the obtained value.

This study analysed 12 earthquakes (E1–12 in Table 1) treated not as single events but as combination events in Asep and Chung (2016). In addition, Table 1 also shows four single events from Asep and Chung (2016) (D1–4) because they were used as combination events in Figure 1. Using a crustal model constructed on the basis of refraction profiles (Cho et al., 2006, 2013), Asep and Chung (2016) obtained hypocentral parameters (latitude, longitude, and origin time) by a series of inversions while maintaining a fixed depth. For a suite of focal depths between 0 and 30 km at 0.5-km increments, the root mean square (RMS) residual times were calculated by using HYPO71 (Lee and Lahr, 1975), and the minimum value was chosen. Around the minimum RMS residual time, the depth range was defined as the interval with a difference between the minimum and the residuals of less than 0.05 s (Figure 5). The D_M value, the median of the depth range, was used as the event depth in the DSMC method for numerical fitting of MLTWA observations.

Fig. 5.  Example of residual curves showing depth range and median depth (D_M) for earthquakes E8 (grey line) and E11 (black line). The residuals with less than the minimum value plus 0.05 s were selected as the depth range, which is the width of the dotted portion in the residual curve. The median value of the depth range is D_M.

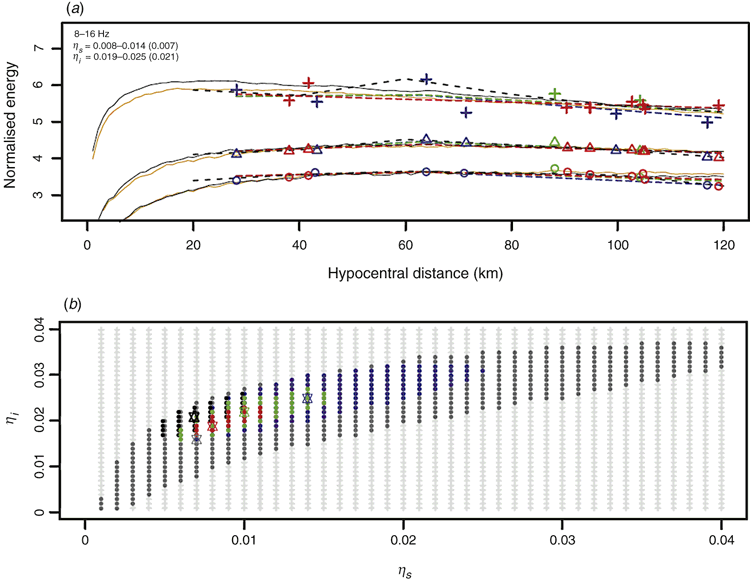
The flexible wide-range window enabled us to obtain the values of MLTWA for all single-event data. In addition, more reliable results than with Asep and Chung’s (2016) window were observed for a reduced number of data. As an example, event T1 was attempted for various numbers of observations, 6, 8, and 16, expressed as blue, green, and red symbols, respectively, in Figure 6a. The corresponding confidence zones of the F-test at the 90% level showed improved reliability with increasing number (Figure 6b). In particular, the blue zone was small compared with that of Asep and Chung’s (2016) window (grey colour), although the case of 16 observations showed similar sizes for the red and black colours. The observational lines (dashed lines with three colours in Figure 6a) were fitted by theoretical lines (solid lines with orange colour) using 0.008–0.014 and 0.019–0.025 for our windows of η_s and η_i, respectively, along with lines (black solid lines) of 0.007 and 0.0021 for Asep and Chung’s (2016) window of η_s and η_i, respectively. The ratio, , of the confidence areas for blue, green, red, grey, and black is 3.162, 2.154, 1.389, 3.162, and 1.389, respectively.

Fig. 6.  Comparison of the MLTWA fitting of this study (colour) and the window of Asep and Chung (2016) (black and grey) for event T1. (a) The number of observations of 6, 8, and 16 are expressed as blue, green, and red, respectively, for additional symbols. The observation lines (dashed lines) are fitted by the theoretical lines of this study (orange solid lines) and the window of Asep and Chung (2016) (black solid lines). (b) The corresponding residual map using the colours in (a). In addition, the black and grey area is for 16 and 6 observations, respectively. The other parameters and symbols for plotting are the same as in Figure 4.

The results of the MLTWA showed values similar to those of the combined events in Asep and Chung (2016) (Figures 1 and 7). However, the value of E1 showed anomalously lower Q_s^–1 than those of the combination with D1, which is explained by the small number of data (Table 1). In addition, several values at the frequency of 1.5 Hz were excluded because its error was greater than the value obtained.

Fig. 7.  Single event values separated from the event combinations in Figure 1. The previous values of single events are expressed as grey colours. The obtained Q^–1 values (right legend shows their depth) are connected by solid or broken lines for depth range (Table 1) smaller or greater than 5 km, respectively: (a) Q_s^–1, (b) Q_i^–1, and (c) Q_t^–1.

In Figure 7, the Q^–1 values are connected by solid or broken lines for depth ranges (Table 1) smaller or greater than 5 km, respectively. Asep and Chung (2016) showed a depth dependency of Q_s^–1 with high and low values corresponding to shallow (bluish colours) and deep (reddish colours) levels, respectively (Figure 1a). This depth dependency seems to correlate with our depth range classification, as shown in Figure 7a, in which bluish and reddish solid lines represent shallow (E3) and deep (E10, E11) events and show higher and lower values than those of broken lines (E4 and E12), respectively.

Additionally, as shown by Asep and Chung (2016), the depth dependency was not apparent for Q_i^–1 and was therefore weakened for Q_t^–1. The depth dependency of Q_s^–1 and Q_t^–1 values can be explained by the closure and healing of fluid-filled cracks in the brittle zone (Mitchell, 1991). This effect for Q_i^–1 appeared to be compensated for by increasing temperature, due to its heat sensitivity (Asep and Chung, 2016).

The use of single events in MLTWA is a robust tool for the study of crustal Q_s^–1 and Q_i^–1. This approach was first attempted by Asep et al. (2015), subsequently improved by Asep and Chung (2016), and finally completed in this study. This study showed a flexible range window to be successfully applied to solely single-event MLTWA. In particular, a more reliable constraint was obtained compared with the previous study, with a reduced number of data. Solely single-event MLTWA may be applicable for investigating seismically stable regions, due to the limitation of available combinations of similar depth events.