Not extinct yet: innovations in frequency domain HEM triggered by sea ice studies
Andreas A. Pfaffhuber 1 3 Stefan Hendricks 21 Norwegian Geotechnical Institute (NGI), Sognsveien 72, 0806 Oslo, Norway.
2 Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research (AWI), Bussestrasse 24, 27570 Bremerhaven, Germany.
3 Corresponding author. Email: aap@ngi.no
Exploration Geophysics 46(1) 64-73 https://doi.org/10.1071/EG14034
Submitted: 21 March 2014 Accepted: 21 August 2014 Published: 17 October 2014
Journal Compilation © ASEG 2015
Abstract
The last 15 years have brought major innovations in helicopter towed time domain electromagnetics (EM), while few further developments have been made within the classic frequency domain segment. Operational use of frequency domain EM for sea ice thickness mapping acted as a driving force to develop new concepts such as the system under our consideration. Since its introduction we have implemented new concepts aiming at noise reduction and drift elimination. We decreased signal noise base levels by one to two orders of magnitude with changes to the signal transmission concept. Further, we increased the receiver coil dynamic range creating an EM setup without the need for primary field bucking. Finally, we implemented control signals inside the receiver coils to potentially eliminate system drift. Ground tests demonstrate the desired noise reduction and demonstrate drift control, leading to essentially drift free data. Airborne field data confirm these results, yet also show that the procedures can still be improved. The remaining quest is whether these specialised system improvements could also be implemented in exploration helicopter EM (HEM) systems to increase accuracy and efficiency.
Key words: AEM, drift, frequency domain, HEM, sea ice.
Introduction
Using electromagnetic (EM) phenomena for geophysical exploration is a well established principle, dating (to our knowledge) back to the post-World War II era. Initiated by ground EM tests in 1947, the first airborne EM (AEM) system was flown in 1948 in Canada (Fountain, 1998). This first system operated by transmitting discrete frequencies (frequency domain EM, fdEM) into the ground. Signals where transmitted with a loop wound around a wooden aircraft and the signal’s interaction with the conductive ground was picked up by a corresponding receiver loop. Some 10 years later, time domain AEM (tdAEM) was introduced and was usually implemented on fixed wing platforms while fdEM systems then focused on towed, rigid structures operated from rotary wing aircraft (helicopter EM, HEM). In the decades leading towards the millennium both methods where further developed and refined, while the fundamental principles stayed untouched (Fountain, 1998). The new millennium saw the development of a trade off between the high resolution of fdEM and large penetration of tdEM, with the introduction of helicopter towed tdEM (HTEM) systems such as SkyTEM (Sørensen and Auken, 2004), AeroTEM (Balch et al., 2002) or VTEM (Witherly et al., 2004). As of today these HTEM systems are the by far most used platform and HEM has become a niche method for a limited number of applications that demand the comparably high frequencies and in-phase measurements possible with HEM. Development and innovation has thus been limited in the frequency domain but rather focused on the booming HTEM market. The classic HEM DIGHEM and RESOLVE systems have remained largely unchanged from their original concept besides of upgrades from analogue to digital systems and adaptations of frequencies and coil orientations (Hodges et al., 2010). The GEM-2A system by Geophex (Won et al., 2003) stands out from these developments with an innovation: a multi-frequency concept was implemented as an alternative to discrete frequency HEM.
The history of using AEM for sea ice thickness profiling dates back to first tests in the late 1980s, leading to purpose-built HEM systems through the 1990s and 2000s (Kovacs and Holladay, 1990; Haas et al., 2006). Acquiring sea ice thickness in the climatologically desired accuracy and precision (+/− 5 cm) posed a new challenge to HEM that illustrated the limitations of purpose-built, but traditional, systems (Pfaffling and Reid, 2009) and triggered new developments (Pfaffhuber et al., 2012a). In this work we discuss three discrete system innovations and improvements implemented in a system conceived in 2011, the Multi-method Airborne Sea Ice Explorer (MAiSIE). We provide detailed specifications of this device in Pfaffhuber et al. (2012a) and have presented first field data in Pfaffhuber and Hendricks (2012). The three improvements are in operation in the current version of MAiSIE. All modifications are aimed at achieving lower noise levels and an elimination of signal drift: (1) We apply a multi-frequency concept similar to the GEM-2A, that enables us to carry significantly more auxiliary payload to remove attitude effects by measuring bird movements with a dual-differential global positioning system (dGPS) combined with an inertial navigation system (INS) and on-board laser altimeter. Improvements in the digital signal generation have decreased the noise floor by one to two orders of magnitude. (2) Broadband, low-noise, ferrite-core receivers and data acquisition with sufficient dynamic range allow us to omit the originally designed active, digital bucking leading to a further decrease in harmonic noise and drift. (3) We report encouraging results based on an active drift control system, which permanently monitors receiver drift while acquiring survey data. This drift control has the potential to remove drift commonly seen in field data.
While the presented innovations where developed for high precision sea ice thickness surveys, we see potential use in traditional, larger scale systems. The drift control, especially, could have a major impact on other HEM systems that are commonly prone to drift problems. Further, the potential weight savings with a multi-frequency concept and small size receiver coils could (a) make HEM more competitive due to better manoeuvrability and less need for helicopter fuel and size and/or (b) open up to implementing piggy-back sensors such as multi-spectral scanners, gas sniffers and more. HEM has become a niche market, maybe the next natural step is to create truly niche systems adapted for the individual application.
Methods
In this work, we present system characteristics implemented in the period 2011–13 in an HEM system developed for polar research (Figure 1). This system, MAiSIE, is introduced and described in detail in Pfaffhuber et al. (2012a). In brief, MAiSIE is a small (3.5 m length) and broadband HEM system nominally operating from 500 Hz to 8 kHz. It is equipped with high accuracy, dual-dGPS and INS to track bird attitude and a laser altimeter with real time display to enable operational altitudes 10 to 15 m above ground. MAiSIE’s main target is sea ice thickness, internal structure and grounded pressure ridge keels. Here we focus on the improvements of signal quality through three specific system features (and adaptations).

|
Multi-frequency signal concept
The traditional HEM concept relies on sets of coils and capacitors that are tuned to resonate at discrete frequencies, both for transmitter and receiver coils (and usually a third set of coils to cancel, or buck, the primary field). This allows for large transmitter moments at low power needs. These systems are further robust towards external electromagnetic noise as the resonance coils act as narrow band-pass filters suppressing harmonic noise outside the desired frequencies. The multi-frequency concept implemented in the GEM-2A and MAiSIE systems uses one low-impedance transmitter coil that is used to transmit a digitally composed multi-frequency signal. Instead of several sets of transmitter- and receiver coils, only one set of coils is needed, significantly decreasing weight and system complexity. We use a rectangular, 100 × 30 cm transmitter loop with 14 turns (Figure 2). 14 turns were chosen so that the coil impedance matches the load capacity of the amplifier (1–8 Ω) within the primary frequency range (500 Hz – 4 (8) kHz) of the EM system. In order to avoid increased impedance caused by skin effects at higher frequencies (> 8 kHz), the transmitter coil is wound with litz wire. The transmitter coil current and voltage is continuously monitored by the control system during operations. To avoid the usual strong transmitter drift effects, we implemented an active current feedback system that keeps the actual transmitter current constant. Remaining changes in amplitude are handled by real time processing based on the actual, rather than nominal, transmitter moment (Pfaffhuber et al., 2012a). The maximum current supplied by the amplifier in the 500 Hz – 4 kHz frequency range is 16 A. This corresponds to a magnetic moment of 67 Am2. For frequencies above 4 kHz the electrical load in the transmitter coil is greater than the capacity of the amplifier, and as a result the maximum output current is divided in half for every doubling in frequency. Frequencies below 500 Hz would be possible with an additional resistor as the load of the transmitter coil is so small that the amplifier would perceive it as a short circuit, without an additional load. This means that though MAiSIE is set up for frequencies from 500 Hz to around 8 kHz, it would not be a major change to shift that bandwidth towards lower frequencies. Higher frequencies would demand changes to the analogue to digital (AD) conversion set-up due to the Nyquist limit at currently 12.5 kHz.

|
While noise characteristics where satisfactory for 4 kHz during the first field tests (Pfaffhuber et al., 2012b; Pfaffhuber and Hendricks, 2012) we saw room for improvement for the other frequencies used. Persistent 10 Hz noise (and harmonics) are evident in the raw data (Figure 3) both in the transmitter current and received magnetic fields. We identified two sources for that 10 Hz signal and successfully mitigated the effect:
-
The current feedback control loop calculates correction to the transmitter (TX) signal at a rate of 10 Hz based on real-time processed data derived from the streaming time series. These corrections generate small discrete steps in the TX signal 10 times a second. In the frequency spectrum, this will have a similar signature to that of a 10 Hz square wave. This effect is clearly visible in the TX current data (Figure 3). In the updated system control software the corrections to the TX signal have been synchronised so that the steps in the TX signal always happens in-between the 2500 sample bulks that are used to obtain the 10 Hz data streams (25 kHz sampling rate). In addition a Hanning window is applied to these data bulks before the Fast Fourier Transform (FFT) is calculated. These changes will not remove the 10 Hz square wave effect from the 25 kHz data, but they will make sure that there are no side effects of the TX corrections present in the 10 Hz data streams, potentially biasing the receiver readings. In other words, this effect is removed from the commonly used, real-time EM data supplied in parts per million (ppm) with 10 Hz sampling. The actual 10 Hz current feedback ‘step response’ still exists in the raw time series but has no significant effect on the processed data quality.
-
The multi-frequency TX waveform (a combination of sinusoids) is generated using 32-bit floating-point values. In order to match the resolution of the digital to analogue (DA) converter, the resolution of the combined signal has to be reduced to 16-bit integers before it is transmitted. This reduction introduces harmonic quantification errors generating peaks in the frequency spectrum dependent on the transmitted frequencies. When transmitting 4100 Hz we typically saw peaks on every second harmonic frequency of 100 Hz (100, 300, 500...), while transmitting 4110 Hz we would observe peaks at every second harmonic frequency of 10 Hz (10, 30, 50...). The magnitude of this noise appeared to be controlled by the least significant bit in the DA. We have implemented two techniques to reduce this effect: Installing a voltage divider on the DA’s output signal has reduced the effective gain of the TX amplifier. This allowed us to increase the magnitude of the TX signal, thus increasing the number of bits effectively in use from ~14 to 16. This will reduce the TX noise by a factor of 3.2. In addition, we implemented a dithering technique that involves adding white noise to the TX signal before this is converted from floating point to 16-bit integers. Adding white noise will transform most of the harmonic quantification errors into random noise. This will significantly reduce the peaks in the spectrum, but increase the white noise in the spectrum to equal the least significant bit of the DA (factor of 2). Dithering is a common practice in digital audio and image processing (for example, see Schuchman, 1964). The significant decrease in background noise (one to two orders of magnitude) due to these steps is evident in both the receiver and transmitter data (Figure 3). Note the drop of background noise for frequencies > 100 Hz. In addition to the discussed 10 Hz harmonics, ground based data also features a strong 50 Hz signal induced by the nearby power grid. This signal is evident in both receiver (RX) and TX data as the TX signal is measured directly on the transmitter coil, also picking up that frequency.
Abandoning the bucking concept
Frequency domain EM systems pose a certain technical challenge, as the comparably small secondary magnetic fields (in the ppm range) need to be acquired while the transmitter is sending the strong primary field. To avoid receiver saturation conventional systems employ bucking systems that cancel the primary field either by active or passive solutions. The conventional, passive method makes use of a second receiver coil that is cross-wired with the actual receiver coil directly subtracting the primary field from the acquired signal. Active solutions transmit bucking signals to cancel out the primary field at the receive coil position. The original MAiSIE concept employed digital, active bucking inside the receiver coils (Pfaffhuber et al., 2012a). We developed the first receiver coil version in cooperation with CNRS in France (Coillot et al., 2010). The assembly contains three individual coils oriented in three directions (X, Y and Z) each consisting of three separate set of windings around a common 4 mm diameter, biconical-shaped ferrite core (Figure 4). The primary winding consists of 16000 turns using 90 µm diameter wire. The secondary and tertiary windings both consist of 80 turns using 140 µm diameter wire. The primary winding is the main sensor element, and works as the receiver coil. The secondary winding was intended to be used as feedback coils in order to achieve a linear frequency response, but is left unconnected as the equivalent functionality was implemented using trans-impedance preamplifiers. Using trans-impedance RX amplifier ensures that the signals recorded are proportional to the magnetic field and that the frequency response is linear. The noise floor of the receiver coil/amplifier is less than 100 fT in the pass band. The tertiary winding is used as local transmitter, initially in order to cancel the primary field (active bucking) and later to monitor drift of the ferrite core (see below).

|
A temperature sensor is installed close to the receiver coil assembly. The active bucking system transmitted a small current to counter the direct field from the transmitter. The amplitude of the bucking signal was a function of the actual transmitter current. For most frequencies the bucking signal was comparably small as the primary fields where only marginally stronger than the receiver saturation limit. A combination of the receiver sensitivity improvements mentioned above and a minor decrease of transmitter current allowed us to skip the bucking effort. The dynamic range of the receiver system is sufficient to avoid saturation and still resolve the secondary EM field. The active bucking had one downside that we consequently avoided: the ferrite material has a temperature dependent susceptibility and it was evident in field data that the frequencies with the strongest bucking signals drifted most with temperature (Figure 5). We thus eliminated one drift source by skipping the active bucking concept. Comparing Figure 5 with Figures 6 and 7 illustrates the dramatic drift reduction for the 4 kHz signal from ~3–4 nT/h to a practically non-existent drift, below the ambient noise level (around 0.01 nT).

|
To perform real-time, airborne calibration checks, a calibration coil is placed close to the receivers (Figure 4). The calibration coil consists of 40 turns with 2 mm diameter wire around a glass fibre chassis with 76 mm diameter. The coil is oriented with a 45° tilt with respect to the X-, Y- and Z-axis to ensure a calibration signal on all receiver coils. The calibration coil is a passive device, and controlled by a relay switch to be either an open or a closed circuit. The signals from the (closed) calibration coil can be seen in the beginning and end of the 20 min time series in Figure 5.
Removing system drift
We avoid drift both actively during measurements as well as through post-processing by virtue of control frequency signals inside the receiver coils. The active feedback loop that controls the transmitter coil (described above) avoids undesired drift of the transmitter current that is often observed largely due to temperature changes of the transmitter coil cables. Minor, remaining short period drift that can occur, as the feedback loop needs to apply a certain lag to avoid resonance, are accounted for in real time processing as the actual voltage and transmitted current in the transmitter coil is logged continuously and is used to calculate the measured normalised fields (Pfaffhuber et al., 2012a).
Remaining drift can occur due to temperature changes and consequent changes of the magnetic susceptibility of the receiver ferrite cores. By transmitting reference frequencies on the secondary windings inside the receiver coils it is possible to continuously measure the changes in receiver sensitivity, as the temperature inside MAiSIE changes throughout a flight. These reference frequencies can be used to correct the EM data and remove most of the remaining drift with post processing (Figure 7). The processing steps involved are low pass filtering and scaling of the reference frequencies, before these are subtracted from the corresponding TX frequencies. Note that the drift is frequency dependent and thus control signals need to be included close to each transmitter frequency used. Also, note the significant decrease of drift magnitude comparing the data in Figures 5 and 6 due to the omitted bucking signal.
Results
We illustrate the introduced data quality improvements with two datasets. The first data was acquired during ground tests in 2013 immediately after the methods discussed above had been implemented. Note that we have already discussed various aspects of the ground test results in the Methods section, to better explain and illustrate the system improvements discussed there. The second example is real-world data from a field campaign in 2013, the first campaign applying the new solutions.
Ground tests
The aim of the ground test in winter 2012/13 was to assess the system improvements as laid out above in the Methods section. Would the dynamic range allow for measurements without bucking and would we be able to remove drift effects completely from the data? Alternatively, to what extent could we remove drift? Reducing the transmitter amplitude by typically 30% was sufficient to avoid saturation and the secondary magnetic fields where picked up clearly. The RMS noise estimates were smaller than in field campaigns in 2011 and 2012 but higher than during the first ground tests in 2011. We speculate that the reason for this is the location of the 2013 ground tests, closer to potential external noise sources (infrastructure) than in 2011. We successfully removed the ‘10 Hz noise’ as discussed in the section Multi-frequency signal concept and shown in Figure 3. The final question is to test the proposed drift removal strategy on the data. For this we acquired data throughout an 8 h period with system temperature changing from −7°C to −17°C (Figure 6) and used the reference signals to decrease the drift. The final receiver data is practically drift-free for all four frequencies (Figure 7).
Sea ice
The seasonal cycle of Arctic sea ice reaches its maximum in extent and thickness in mid-March. Airborne sea ice thickness surveys are therefore commonly conducted in March/April for scientific reason, but also due to a mix of favourable weather conditions and availability of daylight in the high latitude environment. Depending on location, air temperatures in Arctic spring may still range between −20°C and −40°C. Significant changes of the internal temperature of the airborne EM sensor are inevitable since sensor components such as the laser diodes, require a minimum temperature and thus pre-heating before take-off. The internal heat generation during flight is not sufficient though, to keep the system temperature on pre-flight levels and thus significant temperature drift can be expected under field conditions.
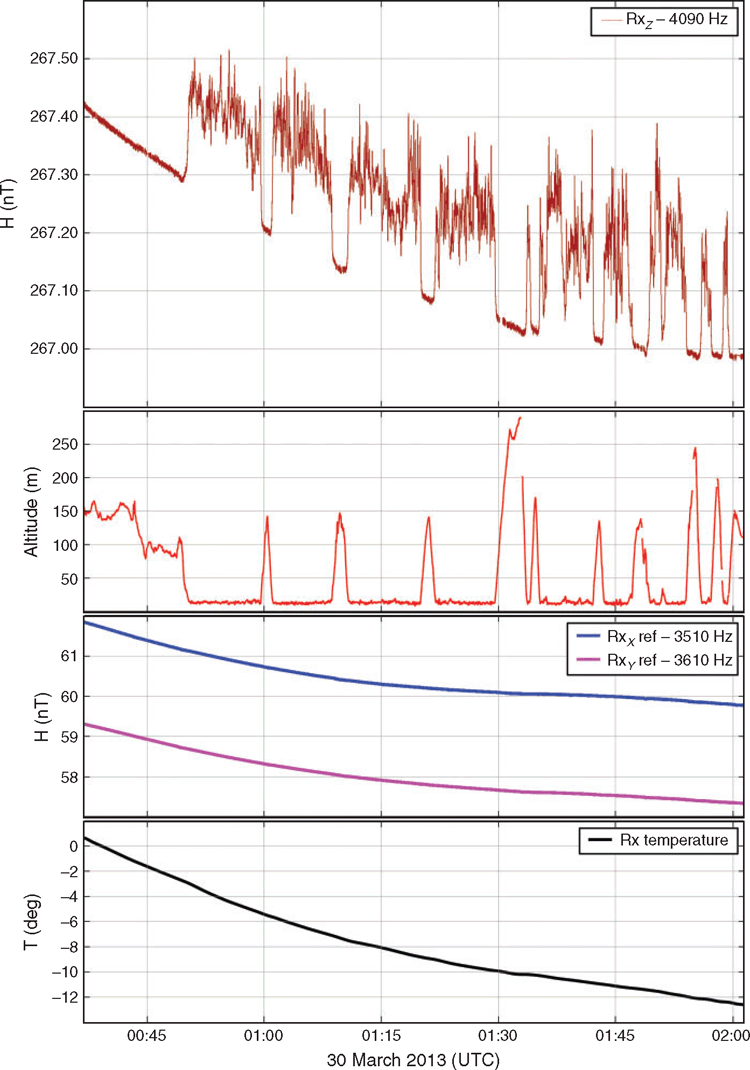
One example survey of sea ice thickness in the Beaufort Sea, on 30 March 2013, is shown in Figure 8. The time series starts with background data at high altitude and then continues with a series of data at survey altitude and repeated drift control ascends to high altitude (nominally 150 m or 500 ft). The outside air temperature was approximately −25°C and the internal temperature dropped by 12°C within 1.5 h. Measurements at high altitude consequently showed a signal drift of ~0.4 nT, comparable to the magnitude of the actual ocean response (readings at 12 m altitude versus 150 m altitude). In other words, after some hours without drift control, measurements at survey altitude would indicate a non-conducting full space. As a reference, an offset of 0.006 nT at production altitude (12 m) would offset the retrieved level ice thickness by 10 cm, the intended precision of HEM ice thickness sensors. Without any drift control, this would mean that the apparent sea ice thickness would drift by up to 150 m, from a purely theoretical point of view. The interval of ascends for drift control of 10 to 15 min reflect the need of sufficient data points for the non-linear signal drift without any reference information. Together with transfer to waypoints, 32% of the survey was spent at high altitude where no sea ice thickness information was obtained. We seek to decrease this percentage of ‘down-time’ significantly by virtue of near-real time drift correction using the reference signals inside the receiver coils.
The drift observed in the reference frequencies is correlated with temperature and to the drift in the transmitted frequencies, yet to remove drift from the receiver data scaling factors need to be determined for individual flights. We consider two scenarios to determine these scaling factors.
-
We use only three high altitude calibration nodes in the beginning, end and middle of the flight to scale the reference frequency signal to the observed drift of receiver amplitude. The scaling nodes are connected by a smoothing spline. We use then the remaining high altitude data as performance check for the drift correction. With this scenario we investigate the accuracy of drift post-processing using the reference frequencies at less high altitude calibration points.
-
The second scenario explores the accuracy of drift correction, that uses only a short training period with linear correlation only for the scaling between amplitudes of reference and receiver signals at the beginning of the flight and remains unchanged for the duration of the survey. This scenario is a feasibility study for a real-time correction of the drift and thus real-time sea ice thickness information, which might be of interest in operational hazard management in ice-covered areas.
The results of both scenarios are shown Figures 9 and 10, respectively. We chose values of 60 m and higher for the range of the laser altimeter as free-air measurements without the influence of the ocean. Changes in the transmitter moment as monitored by the current at the transmitter coil were found to be negligible during the entire survey. Therefore we assume that the drift in the receiver amplitude at 4 kHz is only controlled by temperature driven changes in the magnetic susceptibility of the ferrite cores. In the first scenario we find that the drift reconstruction from the two reference frequencies and the receiver temperature sensor capture the general trend of measurements at high altitude calibrations (H0, the magnetic field measured far away from any external electric conductor). But subtle differences can be found in the form of systematic offsets at high altitude calibrations that were not used for the scaling of the drift reconstruction data. The difference ΔH0 between all drift reconstructions and free-air receiver data though is below 0.04 nT, an order of magnitude less than the original receiver drift (0.4 nT). Mean values of ΔH0 are two orders of magnitude below the uncorrected drift, where the best performance is achieved by the reference frequency in the x-coil (mean ΔH0 = 0.0007 nT), followed by the reference frequency in the y-coil (–0.0017 nT) and the temperature sensor (–0.0025 nT). All these deviations from zero are well below the desired 0.006 nT to achieve 10 cm ice thickness accuracy. The standard deviation values of the ΔH0 distributions are in the order of 0.01 nT. The distributions, mean values and standard deviations are summarised in Figures 9 and 10 and Table 1.

|

|

|
The second scenario, with only initial linear correlation, shows significantly larger values of ΔH0 especially at the end of the survey (Figure 9 and Table 1). Consistently, mean and standard deviation of ΔH0 are higher than in scenario 1, with the exception of the y reference frequency, which not only produces a visual reasonable fit but shows the best result in both scenarios (mean ΔH0 = 0.0002 nT).
Discussion
A field experiment during Arctic spring conditions with air temperatures below −25°C and a change of receiver temperature of more than 12°C within less than 2 h showed that it is possible to reduce receiver drift by up to two orders of magnitude in post-processing and come close to the precision specification of 0.006 nT. In the experiment the drift reconstruction with the reference frequencies performed slightly better than using data from a temperature probe in the direct vicinity of the receiver ferrite cores. The usage of reference frequencies may therefore allow more efficient surveys, with less demand for high altitude drift controls to capture the non-linear signal drift. Also the development of a real-time correction envisaged for real-time sea ice thickness data appears realistic. The experiment though shows that the non-linearity in the scaling between reference and receiver signals in different coils and variable frequency range may require additional effort for a reliable real-time correction. For the drift-correction demonstration survey we discuss here, we did not transmit a reference signal in the z-coil but rather in the x- and y-coils. To simulate drift as well as possible, we transmitted the reference signals inside the x- and y-coil with equivalent amplitude as the received transmitter signal in the z-coil. The z-coil would have been over-saturated with a combination of two such strong signals. In a next system iteration, we shall transmit (smaller amplitude) references signals directly in the z-coil for better drift control. It is evident that the drift is not linear, neither in frequency nor temperature, as expressed in the variable correction results based on x- and y- signals, illustrating that the three individual coils don’t have the exact same drift behaviour.
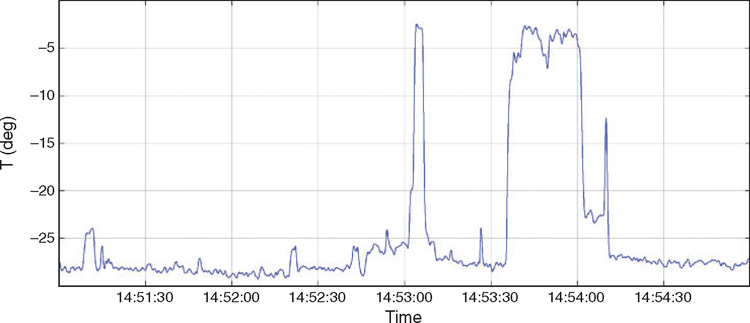
Another option to quantify signal drift at production altitudes, and therefore for both real-time and post-processing corrections is the automatic detection of sections of open water in the profile. These sections are common in most sea ice covered regions due to divergent movements of the ice pack due to atmospheric forcing. The so-called leads between ice floes are often used as an absolute calibration of the EM signal in terms of signal scaling and phasing since the conductivity of the ocean water is usually well known and constant in relevant depth due to turbulent mixing in the upper 10 to 20 m. Together with only minor surface waves, leads pose an ideal calibration target as a quasi-perfect homogenous half space. In the past, occurrence of leads had to be manually marked by the operator and used in post-processing for signal calibration. In the Arctic spring however, the surface temperature of the leads, even if covered by sea ice in the order of centimetres, is measurably warmer than the surface temperature of thicker and snow covered sea ice. In winter the water surface is always close to the freezing temperature of ocean water (approximately –1.8°C) while the surface of sea ice is close to the ambient air temperature. Sea ice will immediately form where the ocean is exposed to the cold atmosphere and this will reduce the surface temperature to a certain extent. But if the ice is thin enough it will dampen all remaining surface waves but still have a negligible effect on EM response, since the thickness is only in the order of a few centimetres and the conductivity contrast to the saline sea water is less than thicker sea ice. We therefore have integrated an infrared pyrometer (Heitronics KT19, Wiesbaden, Germany) into MAiSIE for automatic surface type classification in winter or spring time. Exemplary data of sea ice surface temperatures is shown in Figure 11. The data section corresponds to a surface profile of several kilometres in length, where two leads with very young sheet ice can be clearly identified due to the comparably high surface temperatures (approximately −3°C). The sections with thin ice clearly stand out compared to the cold (−27°C) snow surface of thicker sea ice and can be used for as drift corrections by calculating the HEM response for the altitudes indicated by the laser altimeter. This method of receiver drift correction is highly adapted for the case of sea ice thickness surveys in cold spring conditions, but here the need for abundant drift control points is the highest.
The remaining question to ask is whether the innovations implemented in MAiSIE can, or could be, extended to conventional HEM systems such as RESOLVE or DIGHEM. Especially the demonstrated drift reduction or possibly complete drift removal would be a milestone for frequency domain systems. Existing HEM systems tend to drift and a substantial amount of airtime could be saved if drift check ascends could be avoided or at least reduced. While the multi-frequency transmitter concept has its pros and cons (smaller moment, potentially more vulnerable to external EM noise), the broadband and small scale receiver coils may be just as useful for exploration systems due to their low noise floor and the possibility for control signals inside the coil.
Acknowledgements
The results we have described above are naturally a group effort and we first and foremost want to thank Yme Kvistedal and Erik Lied for their fabulous creativity, they are the major brains behind the innovations presented in this work. We want to further acknowledge the 12 individuals at NGI who worked on the creation of MAiSIE (please refer to Pfaffhuber et al. (2012b) for a full list of names). ‘Cheers’ to Andy Mahoney and Hajo Eicken from the University of Alaska, Fairbanks, for the organisation of the helicopter field surveys in Barrow, Alaska. These surveys were funded by the Seasonal Ice Zone Observation Network (SIZONet) on National Science Foundation award number 0632398. The dedicated assistance and field work with MAiSIE of Priska Hunkeler in Alaska is gratefully acknowledged. The pilots and mechanics of ERA helicopters have enabled the surveys with their professional dedication. We thank AWI and NGI for funding and permission to publish. Finally we are honoured by being invited by the AEM 2013 scientific committee to submit this manuscript. Two anonymous reviewers provided valuable comments on the manuscript.
References
Balch, S., Boyko, W., Black, G., and Pedersen, R., 2002, Mineral exploration with the AeroTEM system: 72nd Annual International Meeting, SEG, Expanded Abstracts, 9–12.Coillot, C., Moutoussamy, J., Lebourgeois, R., Ruocco, S., and Chanteur, G., 2010, Principle and performance of a dual-band search coil magnetometer: a new instrument to investigate fluctuating magnetic fields in space: IEEE Sensors Journal, 10, 255–260
| Principle and performance of a dual-band search coil magnetometer: a new instrument to investigate fluctuating magnetic fields in space:Crossref | GoogleScholarGoogle Scholar |
Fountain, D., 1998, Airborne electromagnetic systems – 50 years of development: Exploration Geophysics, 29, 1–11
| Airborne electromagnetic systems – 50 years of development:Crossref | GoogleScholarGoogle Scholar |
Haas, C., Goebell, S., Hendricks, S., Martin, T., Pfaffling, A., and von Saldern, C., 2006, Airborne electromagnetic measurements of sea ice thickness: methods and applications, in P. Wadhams, and G. Amanatidis, eds., Arctic sea ice thickness: past, present and future: European Commission, Climate Change and Natural Hazards series, 1–14 .
Hodges, G., Amine, D., and Annison, C., 2010, The power of frequency domain EM: principles and case histories: ASEG 2010 (Sydney), Extended Abstracts, 1–4.
Kovacs, A., and Holladay, J. S., 1990, Sea ice thickness measurement using a small airborne electromagnetic sounding system: Geophysics, 55, 1327–1337
| Sea ice thickness measurement using a small airborne electromagnetic sounding system:Crossref | GoogleScholarGoogle Scholar |
Pfaffhuber, A. A., and Hendricks, S., 2012, First data from MAiSIE, a multi-sensor airborne sea ice explorer: Remote Sensing Workshop (EAGE), Paris, France, 3–5 September, RS14.
Pfaffhuber, A. A., Hendricks, S., and Kvistedal, Y., 2012a, Progressing from 1D to 2D and 3D near surface airborne electromagnetic mapping with a multi-sensor airborne sea ice explorer: Geophysics, 77, WB109–WB117
| Progressing from 1D to 2D and 3D near surface airborne electromagnetic mapping with a multi-sensor airborne sea ice explorer:Crossref | GoogleScholarGoogle Scholar |
Pfaffhuber, A. A., Hendricks, S., Hunkeler, P., and Kvistedal, Y., 2012b, Introducing a new generation mulit-sensor airborne system for mapping sea ice cover of polar oceans: First Break, 30, 83–88
Pfaffling, A., and Reid, J. E., 2009, Sea ice as an evaluation target for HEM modeling and inversion: Journal of Applied Geophysics, 67, 242–249
| Sea ice as an evaluation target for HEM modeling and inversion:Crossref | GoogleScholarGoogle Scholar |
Schuchman, L., 1964, Dither signals and their effect on quantization noise: IEEE Transactions on Communication Technology, 12, 162–165
| Dither signals and their effect on quantization noise:Crossref | GoogleScholarGoogle Scholar |
Sørensen, K. I., and Auken, E., 2004, SkyTEM – a new high-resolution helicopter transient electromagnetic system: Exploration Geophysics, 35, 191–199
Witherly, K., Irvine, R., and Morrison, E. 2004, The Geotech VTEM time domain helicopter EM system: ASEG 2004, Extended Abstracts, 1–4.
Won, I. J., Oren, A., and Funak, F., 2003, GEM-2A: a programmable broadband helicopter-towed electromagnetic sensor: Geophysics, 68, 1888–1895
| GEM-2A: a programmable broadband helicopter-towed electromagnetic sensor:Crossref | GoogleScholarGoogle Scholar |