Numerical studies of information about elastic parameter sets in non-linear elastic wavefield inversion schemes
Akio SakaiJapan Petroleum Exploration Co. (Japex), 2-2-20 Higashi-shinagawa, Shinagawa, Tokyo 140-0002, Japan. E-mail: akios@japex.co.jp
Exploration Geophysics 38(1) 1-18 https://doi.org/10.1071/EG07011
Submitted: 1 August 2006 Accepted: 31 January 2007 Published: 5 April 2007
Abstract
Non-linear elastic wavefield inversion is a powerful method for estimating elastic parameters for physical constraints that determine subsurface rock and properties. Here, I introduce six elastic-wave velocity models by reconstructing elastic-wave velocity variations from real data and a 2D elastic-wave velocity model. Reflection seismic data information is often decoupled into short and long wavelength components. The local search method has difficulty in estimating the longer wavelength velocity if the starting model is far from the true model, and source frequencies are then changed from lower to higher bands (as in the ‘frequency-cascade scheme’) to estimate model elastic parameters. Elastic parameters are inverted at each inversion step (‘simultaneous mode’) with a starting model of linear P- and S-wave velocity trends with depth. Elastic parameters are also derived by inversion in three other modes – using a P- and S-wave velocity basis (‘VP VS mode’); P-impedance and Poisson’s ratio basis (‘IP Poisson mode’); and P- and S-impedance (‘IP IS mode’). Density values are updated at each elastic inversion step under three assumptions in each mode. By evaluating the accuracy of the inversion for each parameter set for elastic models, it can be concluded that there is no specific difference between the inversion results for the VP VS mode and the IP Poisson mode. The same conclusion is expected for the IP IS mode, too. This gives us a sound basis for full wavelength elastic wavefield inversion.
Key words: non-linear elastic wavefield inversion, frequency-cascade scheme, simultaneous mode, gas hydrate.
Akaike, H., 1974, New look at statistical-model identification IEEE Transactions on Automatic Control 19, 716–723.
| Crossref | GoogleScholarGoogle Scholar |
Bunks, C., Saleck, F. M., Zaleski, S., and Chavent, G., 1995, Multiscale seismic waveform inversion Geophysics 60, 1457–1473.
| Crossref | GoogleScholarGoogle Scholar |
Crase, E., Pica, A., Noble, M., McDonald, J., and Tarantola, A., 1990, Robust elastic nonlinear waveform inversion: Application to real data Geophysics 55, 527–538.
| Crossref | GoogleScholarGoogle Scholar |
Kolb, P., Collino, F., and Lailly, P., 1986, Pre-stack inversion of a 1-D medium Proceedings of the IEEE 74, 498–508.
Levander, A., 1988, Fourth-order finite-difference P-SV seismograms Geophysics 53, 1425–1437.
| Crossref | GoogleScholarGoogle Scholar |
Sakai, A., 1999, Velocity analysis of vertical seismic profile (VSP) survey at JAPEX/JNOC/GSC Mallik 2L–38 gas hydrate research well, and related problems for estimating gas hydrate concentration Geological Survey of Canada Bulletin 544, 323–340.
Tarantola, A., 1984, Inversion of seismic reflection data in the acoustic approximation Geophysics 49, 1259–1266.
| Crossref | GoogleScholarGoogle Scholar |
Appendix: Histogram class determination by Akaike’s Information Criterion
In taking histograms, it is important to define classes in a statistically plausible manner. Under the assumption that the probability of the relative errors in inverted data in each class is independent, a frequency of independent data trial takes a multinomial distribution. Currently, a histogram model M(a, r, b) is assumed that in the total number of classes c and frequencies n, with probability p(i) and frequency n(i), the number of classes at the ends are a and b and central data between the ends are classified into classes of the number of r as follows:
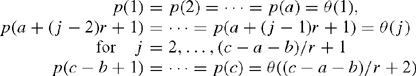
To estimate the most probable θ(j), for j = 1,…,(c – a – b)/r + 2, MAICE (minimum AIC) is used as the model selection criterion. AIC(a, r, b) approximates an expectation of unbiased average logarithmic likelihood and shows –2 multiplied by (maximum logarithmic likelihood of the model – the number of free parameters of the model) (Akaike, 1974).