Numerical modelling of electromagnetic waveguide effects on crosshole radar measurements
Hannuree Jang 1 2 Mi Kyung Park 1 Hee Joon Kim 11 Department of Environmental Exploration Engineering, Pukyong National University, Busan 608-737, Korea.
2 Corresponding author. Email: jhnree@pknu.ac.kr
Exploration Geophysics 38(1) 69-76 https://doi.org/10.1071/EG07008
Submitted: 8 December 2006 Accepted: 19 January 2007 Published: 5 April 2007
Abstract
High-frequency electromagnetic (EM) wave propagation associated with borehole ground-penetrating radar (GPR) is a complicated phenomenon. To improve the understanding of the governing physical processes, we employ a finite-difference time-domain solution of Maxwell’s equations in cylindrical coordinates. This approach allows us to model the full EM wavefield associated with crosshole GPR surveys. Furthermore, the use of cylindrical coordinates is computationally efficient, correctly emulates the three-dimensional geometrical spreading characteristics of the wavefield, and is an effective way to discretise explicitly small-diameter boreholes. Numerical experiments show that the existence of a water-filled borehole can give rise to a strong waveguide effect which affects the transmitted waveform, and that excitation of this waveguide effect depends on the diameter of the borehole and the length of the antenna.
Key words: crosshole, cylindrical coordinates, GPR, finite-difference time-domain.
Acknowledgments
This work was supported by the KOSEF-JSPS Cooperative Program (F01–2006–000–10248–0). We thank Dr Takao Kobayashi, Dr Jung-Ho Kim, and an anonymous reviewer for helpful comments and suggestions.
Alumbaugh, D., and Chang, P. Y., 2002, Estimating moisture contents in the vadose zone using cross-borehole ground penetrating radar: A study of accuracy and repeatability Water Resources Research 38, 1309.
| Crossref | GoogleScholarGoogle Scholar |
Moran, M. L., and Greenfield, R. J., 1993, Radar signature of a 2.5-D tunnel Geophysics 58, 1573–1587.
| Crossref | GoogleScholarGoogle Scholar |
Olsson, O., Falk, L., Forslund, O., Lundmark, L., and Sandberg, E., 1992, Borehole radar applied to the characterization of hydraulically conductive fracture zones in crystalline rock Geophysical Prospecting 40, 109–116.
| Crossref | GoogleScholarGoogle Scholar |
Tronicke, J., Holliger, K., Barrash, W., and Knoll, M. D., 2004, Multivariate analysis of cross-hole georadar velocity and attenuation tomograms for aquifer zonation Water Resources Research 40, W01519.
| Crossref | GoogleScholarGoogle Scholar |

Williamson, P. R., and Worthington, M. H., 1993, Resolution limits in ray tomography due to wave behaviour Geophysics 58, 727–735.
| Crossref | GoogleScholarGoogle Scholar |

Yee, K. S., 1966, Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media IEEE Transactions on Antennas and Propagation 14, 302–307.
| Crossref | GoogleScholarGoogle Scholar |

Zhou, C., Cai, W., Luo, Y., Schuster, G., and Hassanzadeh, S., 1995, Acoustic wave-equation traveltime and waveform inversion of crosshole seismic data Geophysics 60, 765–773.
| Crossref | GoogleScholarGoogle Scholar |

Appendix
Ampere’s law describes the relationship between magnetic field components along a closed elemental contour C, bounding the corresponding open element surface S, with the electric field distribution on that surface (Figure A1), and
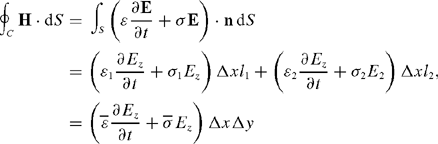
where
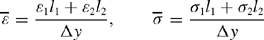
In particular, when l1 = l2 = Δy/2,


|

