Putting David Craig’s Legacy to Work in Nanotechnology and Biotechnology*
Jeffrey R. ReimersInternational Centre for Quantum and Molecular Structures, College of Sciences, Shanghai University, Shanghai 200444, China, and School of Mathematical and Physical Sciences, The University of Technology Sydney, Sydney, NSW 2007, Australia. Email: jeffrey.reimers@uts.edu.au
Australian Journal of Chemistry 69(12) 1331-1359 https://doi.org/10.1071/CH16489
Submitted: 27 August 2016 Accepted: 7 October 2016 Published: 4 November 2016
Abstract
David Craig (1919–2015) left us with a lasting legacy concerning basic understanding of chemical spectroscopy and bonding. This is expressed in terms of some of the recent achievements of my own research career, with a focus on integration of Craig’s theories with those of Noel Hush to solve fundamental problems in photosynthesis, molecular electronics (particularly in regard to the molecules synthesized by Maxwell Crossley), and self-assembled monolayer structure and function. Reviewed in particular is the relation of Craig’s legacy to: the 50-year struggle to assign the visible absorption spectrum of arguably the world’s most significant chromophore, chlorophyll; general theories for chemical bonding and structure extending Hush’s adiabatic theory of electron-transfer processes; inelastic electron-tunnelling spectroscopy (IETS); chemical quantum entanglement and the Penrose–Hameroff model for quantum consciousness; synthetic design strategies for NMR quantum computing; Gibbs free-energy measurements and calculations for formation and polymorphism of organic self-assembled monolayers on graphite surfaces from organic solution; and understanding the basic chemical processes involved in the formation of gold surfaces and nanoparticles protected by sulfur-bound ligands, ligands whose form is that of Au0-thiyl rather than its commonly believed AuI-thiolate tautomer.
Introduction
David Craig[1] pioneered many advances in the field of theoretical chemistry[2,3] and had a profound impact on the development of chemical and general scientific research in Australia through his roles in the Research School of Chemistry at the Australian National University,[4] the Australian Academy of Science,[5] and elsewhere. After his passing in 2015, he will be surely missed. In addition to his own works, he affected Australian and world science indirectly through the careers of his many students. Two of those include Ian Ross[6] and Gad Fischer[7] who were to become my Honours supervisors in 1978. His legacy continues through many people such as myself, and on through the careers of our own students and post-doctoral fellows. I was honoured to receive the David Craig Medal of the Australian Academy of Science in 2016.[8]
Some of the most fundamental papers in the history of the quantum description of chemistry are the ab initio electronic structure method based on Hartree–Fock theory,[9] the Born–Oppenheimer approximation that separates nuclear and electronic motion to define the concept of molecular potential-energy surfaces,[10] the Franck–Condon approximation that allows electronic spectra to be understood,[11] and its extension the Herzberg–Teller approximation that allows electronic and nuclear motions to couple.[12] However, the idea that it was possible to perform electronic structure calculations using methods with controllable levels of approximation that eventually led to the exact answer, i.e. the concept of ab initio, was first described by Parr, Craig, and Ross in 1950.[13] In that paper they performed the first ever calculation of electron correlation, the term neglected in the Hartree–Fock approximation to electronic structure, introducing the configuration-interaction (CI) method. Electron correlation has many consequences that are always significant but which sometimes can be ignored in basic thinking, e.g. in describing chemical bonds, and sometimes are critical, e.g. in understanding the London dispersion force that forms the attractive part of the van der Waals interaction, and in understanding exciton transport in light-harvesting proteins and materials. Similarly, while the 1920s Franck–Condon approximation provided the conceptual basis used for the next 20 years in interpreting molecular spectra, it was Craig who in 1950 performed the first ever quantitative calculation for a polyatomic molecule, determining the geometry of benzene in its excited electronic state.[14] Finally, while weak observed spectroscopic lines were for 20 years qualitatively interpreted in terms of the Herzberg–Teller principle and its associated symmetry selection rules, Craig in 1950 performed the first ever quantitative calculations, considering the excited states of benzene.[15] It was Craig that first realised that these weak transitions embodied a breakdown of the Born–Oppenheimer approximation[15] that, in modern language, resulted in entanglement[16] of the electronic and nuclear wave functions. Very little modern research in molecular spectroscopy, solar energy harvesting, chemical bonding theory, condensed-matter physics, and materials science does not flow from the advances made by Craig.
This review of my own contributions to science starts from Craig’s work and its impact on my career, combining this with classical and quantum simulation techniques[17–24] learned from my Ph.D. and postdoctoral supervisors Bob Watts,[25] Kent Wilson,[26] and Rick Heller,[27] my long-term collaborators Noel Hush[28,29] and Max Crossley,[29] as well as some of the contributions from the next generation. In terms of the development of theoretical chemistry in Australia, Hush’s contributions were also critical, both through the founding of the Theoretical Chemistry Department at The University of Sydney and through his seminal contributions to electron-transfer theory. That a close relationship existed between the works of Craig and of Hush was apparent from the Piepho–Krausz–Schatz quantitative model[30] of electron-transfer spectroscopy which applied Craig’s methods[15,31] to Hush’s revolutionary understanding of electron transfer.[32] Elmars Krausz had been recruited to the Research School of Chemistry by Craig. My work has focussed on the demonstration of this relationship and the power it gives to understanding modern problems in biotechnology and nanotechnology.
From Understanding Benzene in 1946 to Understanding Chlorophyll in 2013
Craig’s understanding of the spectrum of benzene,[14,15,33–35] general aromatic molecules,[36–40] and non-aromatic[41–43] molecules paved the way for understanding the properties of molecular spectroscopy and electronic structure in not only the gas phase but also condensed phases.[44–46] Perhaps the most important chromophore, however, is chlorophyll-a (Chl-a), yet its visible absorption spectrum was not authoritatively assigned until 2013.[47] The absorption, transport, and emission of light are critical to natural photosynthesis, and it is not possible to understand these processes without knowledge of the spectroscopic assignment. Natural photosynthesis has always been an important model system used in designing artificial devices for solar energy harvesting and conversion either into electrical energy or else to perform important functions such as carbon dioxide sequestration and solar hydrogen production.[48,49] Given that there is nothing fundamentally new in the spectra of Chl-a and modern light harvesting systems[50] (except for the direct primary charge-separation mechanism discovered by Hush[32]) that was not already apparent in Craig’s works, such a lengthy delay was not anticipated.
The basic understanding of the spectroscopic properties of the chlorophylls, porphyrins, and related functional molecules was established in the early 1960s by Gouterman[31,51–54] and is known as the ‘4-orbital’ model.[51] This model is just an adaption of Craig’s description of benzene: in benzene four orbitals are also critical, the doubly degenerate HOMO and LUMO orbitals, it is just that in porphyrins and chlorophylls the symmetry is lowered and degeneracies often removed. Craig focussed on the role of antisymmetric vibrations in providing intensity to transitions that are ‘forbidden’ by the Franck–Condon approximation[11] but allowed through Herzberg–Teller (vibronic) coupling.[12] Gouterman enhanced this by providing a mathematical formalism for the quantitative treatment of these effects, using it to consider three possible options for the interpretation of the available spectroscopic data for Chl-a and many other chlorophyllides, selecting one. A decade later Ross, who had then also moved to the Australian National University, developed the first method for deducing all of the parameters required by Gouterman’s formulae from a priori electronic structure calculations.[55,56] My honours project (published 1981) involved applying these methods to weak second-order effects on the spectrum of benzene not considered in Craig’s original treatments, showing that indeed every minute detail of the observed spectra could be understood from first principles analyses.[57] The highly distorted spectra of 1,5-naphthyridine also succumbed to quantitative analysis,[58] and it seemed that Craig’s ideas were invincible. It was at about the same time that Krausz at the Australian National University applied Craig’s and Gouterman’s ideas to provide[30] the first quantitative analyses in Hush’s new field of charge-transfer spectroscopy.[32] Nobody doubted the assignment that Gouterman had made 20 years earlier concerning the interpretation of the spectra of Chl-a, despite the observation of seemingly peripheral results that were yet to be interpreted.
However, this situation changed in 1982 when the first high-resolution spectra were measured for Chl-a by Avarmaa at Tartu University in Estonia.[59–62] These spectra were inconsistent with Gouterman’s original assignment of the spectrum of Chl-a and led to a new assignment, a different one to that of Gouterman’s original three possibilities. The basic issues are summarized in Fig. 1. The Gouterman 4-orbital model predicts that all chlorophyllides (and porphyrins) show four electronic absorptions in the visible (or near UV) region. These are known as the Qx and Qy transitions in the red-orange region and the Soret Bx and By transitions in the blue-UV region. A slight shifting of these transitions changes the perceived colour for purple in bacteriochlorophylls to green in chlorophylls to red in the related heme molecules. One or both Q bands can be weak while the Soret bands are always intense, these patterns arising as a result of strong electron correlation coupling individual transitions together. This critical effect was well known to Craig and Ross as their pioneering calculation of electron correlation in 1950 demonstrated this effect for benzene.[13] Modern nanotechnological applications to which electron correlation is critical will be discussed also in later sections.

|
Fig. 1 shows the observed[63] low-resolution Q-band absorption spectrum of Chl-a in the red–orange region and features three resolved bands: an intense band at low frequency followed by two progressively weaker bands shifted to higher frequency by 1400 and 2150 cm–1. Naively, both the Qx and Qy transitions were expected to show origin bands at low energy followed by a much weaker Franck–Condon allowed vibrational sideband in the range of +700 up to +1600 cm–1, while Qy was from all estimates expected to be an order of magnitude more intense than Qx. That the lowest-energy observed band is the Qy origin was a feature that was never in doubt. Two of Gouterman’s three possible assignments thus were (i) the observed band at +1400 cm–1 is the Qy vibrational sideband while that at +2150 cm–1 is the Qx origin, the assignment originally preferred,[10,13–16] and (ii) that +1400 cm–1 is made up of both the Qy vibrational sideband and the Qx origin, the revised assignment of Avarmaa.[59–61] Known to Gouterman were significant arguments favouring both assignments: the observed emission spectrum,[64] also shown in Fig. 1 after reflection about the Qy origin, is highly depleted in the +2150 cm–1 region, favouring assignment (i) as emission occurs only from Qy, whereas the observed magnetic circular dichroism spectrum,[63] again shown in Fig. 1, shows a negative signal indicating the presence of an x-polarized absorption centred at +1000 cm–1, favouring (ii). If the Qx origin is at +1000 cm–1 then this state will contribute significantly to all spectroscopic photosynthetic processes involving Chl-a, but if it is at +2140 cm–1 then its effect will be minimal. Hence the issue of the assignment is an important one concerning the understanding of natural photosynthesis. Analyses of photosynthesis have always used the traditional assignment,[65–68] one reason perhaps being that analyses of data based on the modern assignment never yielded basic properties like the Qx transition moment and its variation with environment. Without knowing these properties, it was very difficult to use the modern assignment to understand photosynthetic mechanisms.
During the 1980s to 1990s, many new experiments[63,69–71] were performed and interpreted in terms of the ‘modern’ assignment (ii), and this was backed up by density functional theory (DFT) calculations identifying that the +2150 cm–1 band was an absorption named S3 not anticipated by the Gouterman 4-orbital model and therefore never previously considered.[72,73] So in 2000 the situation again seemed clear, with the ‘modern’ assignment replacing the ‘traditional’ Gouterman one. However, neither assignment was actually able to explain all of the data and, as a result, experimentalists desiring a complete answer continued searching for a definitive experiment. In 2009 Freiberg at Tartu University performed new experiments[64] that were interpreted in terms of the modern assignment while a year later Krausz designed new experiments[67] interpreted in terms of the traditional assignment. After 50 years of research, the basic challenges to spectroscopic assignment still remained.
I became aware of the issue following the publication of linear dichroism spectra in 1989 that were clearly inconsistent with the traditional assignment.[69] Based on my previous experience applying the methods of Craig and Ross to benzene and naphthalene, I was confident that appropriate calculations would interpret all spectra and resolve the issues. I wrote a much enhanced version of the complete neglect of differential overlap (CNDO) code of Del Bene and Jaffè[74] including expansion to include intermediate neglect of differential overlap (INDO)[75] and multi-reference configuration interaction (MRCI). This failed to deliver the high accuracy required to be helpful in making the assignment, however, but the developed code today remains well used for understanding excited-state solvent shifts,[76–79] nanoparticle electronic structure,[80] and conduction between electrodes spanned by single molecules.[81] It is freely available on the NANOHUB with over 4000 registered users, applied to teach the basics of solar energy capture, charge transport, and photochemical charge separation.[82]
The advent of time-dependent density functional theory (TDDFT) a few years later offered the hope of performing calculations accurate enough to assign the spectrum of Chl-a. The first directly relevant publication was on porphyrin and claimed high accuracy,[83] but the assignment was inconsistent with the Gouterman 4-orbital model and to me seemed unrealistic. The influential subsequent works on Chl-a[42,43] had similar properties but now the deviation from the 4-orbital model was being used to assign the spectra. Believing something to be fundamentally wrong, I searched for simple ways of isolating and demonstrating the problem,[84] discovering a significant shortcoming of TDDFT when H2 was stretched (failure owing to ground-state instability),[85] that it failed when charge transfer was involved owing to the asymptotic potential error,[86] and most significantly that it failed for extended conjugation (including polyacetylene, porphyrins, and large acenes) despite many reports to the contrary.[87] The culmination of this work was the demonstration that all existing TDDFT methods predicted results for plant Photosystem-I that was starkly in contrast with experiment, showing that the non-Gouterman states must actually occur at much higher energies.[88] Realising the widespread significance of these result to modern technological applications, Kobayashi and Amos from the National Computational Infrastructure (NCI) recognized the potential of a proposed new computational method CAM-B3LYP[89] and programmed it into GAUSSIAN.[90] Together we showed that it indeed did work for extended conjugated molecules including chlorophylls.[91] Today this method is widely applied to chemistry, biotechnology, and nanotechnology applications, the method currently having over 3500 citations.
Over the next few years, we demonstrated that CAM-B3LYP could be used to interpret many sophisticated observations made concerning photosynthetic systems, including a priori prediction[68] of the visible absorption spectrum of Photosystem-I based on an optimized geometry for the 150 000-atom protein trimer that had previously been fully optimized using a linear-scaling DFT method we had developed.[92] Also, Freiberg was able, for the first time, to develop methods allowing comparison of both high-resolution absorption and emission spectra for chlorophyllides, obtaining results unprecedented in molecular spectroscopy, that CAM-B3LYP was able to predict to high accuracy.[93] However, three years’ work by Zhengli Cai attempting to use CAM-B3LYP to assign the spectrum of Chl-a produced no positive conclusions. The approach taken was to calculate the properties of some 32 chlorophyllides and their environments, comparing the predicted Qx–Qy spacing to that inferred by the traditional and modern assignments applied to each system. No correlation was found between the calculated data and either assignment,[47,94] suggesting that either they were both incorrect or else CAM-B3LYP was still not precise enough to be used for the evaluation of this property.
In 2012, Freiberg, Krausz, and myself got together to search for some key element that had possibly been missing from the research of the previous 50 years. Reviewing the extensive literature coming from both Eastern-Block and Western-Block countries, we found no significant error in logic or methods leading to conclusions favouring either the traditional or modern assignments. There was one remaining option, however: Gouterman had suggested three possible assignments but only two had been seriously advanced. The third assignment can be thought of as a quantum-mechanical supposition of the other two assignments, assignments based on application of the Born–Oppenheimer principle that allows Qx and Qy to be treated as independent potential-energy surfaces using say classical mechanics. Craig’s original works on aromatic molecules had shown that this was not strictly true and that breakdown of the Born–Oppenheimer approximation had significant repercussions on spectra.[15] Indeed, my honours project was based on quantifying these effects using CNDO calculations,[57,58] but the degree of breakdown was small and the effects only perturbative. Gouterman’s enhancements to Craig’s ideas[31,52] allowed for strong interactions and the complete breakdown of the Born–Oppenheimer equation. The great attraction of this possibility is that it can deliver two bands of x polarization, like what is seen in the MCD spectra in Fig. 1. However, if this effect were operative in Chl-a then it would also have consequences for all other chlorophyllides including highly categorized molecules like pheophytin-a and bacteriochlorophyll-a, and no trace of this effect had ever been reported in the spectra of these and many other chlorophyllides. Reviewing the literature, Gouterman’s argument against this assignment was as valid in 2012 as it was in 1962.
We reasoned that the missing bands must be there in the spectra of all these other chlorophyllides but be obscured by more intense features. Two data analysis methods were developed to reveal them, a computational method for fitting the observed spectra to Gouterman’s model appropriate for very strong coupling,[47] and an experimental method providing a new way of qualitatively interpreting data coming from MCD experiments.[95] Both approaches identified the missing bands in all species, with the fitting procedure delivering quantitative information concerning the unperturbed location of the Qx origin (the property deduced by electronic-structure calculations such as CAM-B3LYP), the Qx intensity, and the vibronic coupling strength between Qx and Qy. These results were in excellent agreement with the previous CAM-B3LYP calculations, and so a new assignment of the spectrum of Chl-a was established.[47]
The computational fitting procedure embodied a combination of the condensed-phase spectroscopic modelling techniques developed for liquid water and ice during my Ph.D. project with Bob Watts[17–20,96] with the time-dependent quantum dynamics techniques that I learnt from Eric Heller as a postdoctoral fellow[21] to aid[97] the design of NASA’s GALILEO probe to Jupiter.[98] The core infrastructure for this was built a decade earlier during work with Noel Hush to understand the nature of the special-pair radical cation produced after primary charge separation during bacterial photosynthesis.[99] This more complex problem involved four electronic states strongly coupled by 70 molecular vibrations,[100] with the highly quantum non-Born–Oppenheimer properties of the system controlling all observables including the (functionally critical) output voltage, spin distribution, electronic and infrared spectra, and Stark effect.[99,101,102] Our work on the bacterial reaction centre was also a long quest to understand perplexing experimental data, this time the observation of an apparently intervalence electronic transition peaking at 2700 cm–1 amongst the normal infrared lines.[103] It was clear that this spectrum could reveal the critical features controlling primary charge separation during photosynthesis, but its interpretation involved many aspects including reassignment of other observed band systems,[104] identifying other new band systems,[105] extensive simulations of mutagenesis effects,[106] and the identification of long-standing errors with the interpretation of electron-paramagnetic spectroscopy data.[101] This project was originally conceived as flowing from Hush’s classic theory of adiabatic electron transfer applied to intervalence spectroscopy,[32] but, as discussed in the next section, its relation to the works of Ross, Krausz, and Craig soon became apparent.[107,108]
The developed qualitative procedure for the interpretation of MCD spectroscopy involved finding a work around to a fundamental problem that limited the usefulness of the technique. Two independent spectra (absorption and MCD) are measured at n frequencies, while what is desired are component spectra depicting x and y polarization at each frequency, but two susceptibility parameters must also be determined from the spectroscopic data in order to construct an analytical data inversion. The data analysis problem is thus fundamentally underdetermined: there are 2n observables and 2n + 2 unknowns to evaluate. We showed that one of these unknowns can be determined based on other assumptions already used in the analysis, and that it was possible to construct a second unknown whose value acts to rescale component spectra but not significantly change their shape.[95] The result is a general method that can be used to get critical polarized bandshape information from MCD experiments. Had Gouterman had these simple equations in 1962, he would no doubt have immediately correctly assigned the spectrum of Chl-a.
One last problem remained for the acceptance of the strong vibronic-coupling assignment for the spectrum of Chl-a: high-resolution spectra measured in ether at low temperature, spectra whose qualitative features led to the initial rejection of the traditional assignment,[59,61] showed quantitative aspects that, from the beginning, were obviously incompatible with a strong-vibronic-coupling assignment. This issue was solved by Krausz and Freiberg who showed that the presence of trace water in the samples meant that the observed spectra were for an ether–Chl-a–water complex rather than for the presumed ether–Chl-a–ether complex.[109] Extensive free-energy simulations performed by Kobayashi then confirmed that indeed it is feasible for water to displace the solvent when doubly dilute with Chl-a in solution at low temperature.[110]
What emerges then is a rather unexpected description of photosynthetic machinery as working with an unusually quantum nature. Both the excited states of Chl-a critical for solar-energy harvesting and its transport and the primary charge separation unit from bacterial photosynthesis are subject to extreme failure of the Born–Oppenheimer approximation,[47,100] the idea that gives us the conceptual basis of modern chemistry. This obviously affects critical features such as the effect of environment and mutagenesis on output voltage,[100,101] spectra,[102] and excitonic energy flow.[47] However, there are many other fascinating consequences and associated features: Chl-a in protein environments is optimized to decohere Qx excitation as fast as could be possible,[47] asymmetry unprecedented in molecular spectroscopy is observed between absorption and emission of isolated electronic states,[93] and the intensity of the Qx transition varies by a factor of 7 as a function of chlorophyllide and solvent.[47]
A Basis for Chemical Understanding: Relationship of Craig’s Works to the Adiabatic Electron-Transfer and Chemical Reaction Theories of Hush
Some time after Craig moved to the Australian National University, Hush moved to Sydney University where he established the Department of Theoretical Chemistry. Their parallel teaching and research platforms in theoretical chemistry were to have a profound impact on chemistry research in Australia. Hush had pioneered many advances in understanding chemical reactivity, paralleling Craig’s work in spectroscopy. Although these research fields both involved breakdown of the Born–Oppenheimer and Franck–Condon approximations as core elements, their differences were sufficient for them to be considered as independent research fields.
To understand why this would be so, we need to trace the origin of Hush’s theories back to the beginnings of quantum mechanics and the understanding of chemical reactivity. The first treatise on reactivity was by London in 1928 using a diabatic description[111] in which simple potential-energy surfaces described the reactants and the products coupled together to make an adiabatic transition state. The London–Eyring–Polanyi (LEP) potential-energy surface[112] for general triatomic molecular reactions[113] was extended from this by Eyring and Polanyi in 1931, Horiuti and Polanyi made a similar extension for proton transfer reactions in 1935,[114] Wall and Glocker did the same for isomerization reactions in 1937,[115] and Hush fully generalized it in 1953, considering e.g. redox hydrogen transfer reactions.[116] Non-adiabatic reactions depicting failure of the Born–Oppenheimer approximation were similarly treated in 1932 by London,[117] with the more well known but more restricted treatment of Landau also appearing in that year.[11,12] Today diabatic models are widely used to depict most chemical processes including electron-transfer,[118–121] natural photosynthesis and organic photovoltaics,[122–133] chemical quantum computing,[134,135] racemization processes,[136,137] non-adiabatic photochemical reactions,[138–148] proton-transfer, hydrogen bonding, hydrogen-transfer, coupled electron–proton transfer reactions, general reactions,[149] and aromaticity.[150–154] An essential aspect of this modern pre-eminence is its connection with Hush’s adiabatic theory of electron transfer.[32,155–159] This approach differed significantly from other approaches to electron transfer such as that developed by Marcus[160] as Hush focussed on the physical properties of the involved transition states and the use of experimental and ab initio or a priori computational methods to quantify analyses. A centrepiece of Hush’s work was the assignment of the nature of unknown electronic transitions observed in mixed-valence species, leading to the field of intervalence spectroscopy.[32] This process was identified by Hush as producing primary charge separation, converting solar into electrical energy[161] and providing a basis for the subsequent understanding of the operation of natural photosynthesis and most processes involved in modern molecular-based artificial solar-energy harvesting systems.
It is Hush’s work on intervalence spectroscopy[32] that builds a bridge to Craig’s work. The connection was first realised by Krausz in his 1978 quantitative model for the shapes of intervalence transitions.[30] My first collaborations with Hush came through this connection when I started as an ARC Research Fellow at Sydney University in the late 1980s. Hush was collaborating with Michael Paddon-Row at the University of New South Wales, synthesizing, measuring (by Jan Verhoeven in The Netherlands) primary charge separation rates, and interpreting the data.[161] An unexpected result, questioning the conceptual understanding of the process, was that electronic symmetry-forbidden reactions were occurring only slightly slower than Franck–Condon allowed ones. My contribution was to apply the spectroscopic methods of Craig, Ross and Fischer to understand the kinetics process, showing that the observed fast rates were completely consistent with known spectroscopic properties.[162] This led to predictions of unusual properties that were later observed spectroscopically.[163] Ideas from spectroscopy were then imbedded into general theories for electron transfer,[164–166] resulting in the development of a chemical model[167–169] for interpreting Stark-effect measurements pioneered by Steven Boxer at Stanford for understanding charge transfer processes in general and photosynthetic function in particular,[102,170–175] as well as an understanding of electric-field driven molecular switches.[176] Parallel work included simulations of the effects of solvent dynamics on molecular spectra[78,79] and the importance of microheterogenuity in modifying electric fields and optical properties.[177]
However, the major focus of the decade became interpreting the spectroscopic and chemical properties of the special-pair radical cation from photosynthesis, as mentioned earlier. Hush’s original description of intervalence spectra[32] and Krausz’ computational model[30] had focussed on the reaction coordinate as the critical dimension controlling properties. Using the power of unitary transformations in quantum mechanics, I developed a way of transforming the full spectroscopic problem discussed initially by Craig in terms of the effects of symmetric[14] and antisymmetric[15] modes into the kinetics representation used by Hush, providing a complete description of the kinetics and spectroscopy of intervalence charge transfer.[107,108] This allowed the bacterial reaction centre cation to be understood completely,[99,102] facilitated assignment of the spectrum of Chl-a,[47] and led to the understanding of a range of phenomena where properties were determined by more than just the reaction coordinate, as has been recently reviewed.[178] It unified critical aspects of the works of Craig and of Hush, playing on the non-uniqueness of diabatic descriptions for chemical and spectroscopic phenomena.[179] Unification of basic theories for chemistry and spectroscopy touches the very foundations of chemical understanding. Traditionally, chemistry is taught in separate blocks using different nomenclatures and ideas, e.g. transition state theory, aromaticity, coordination compounds, crystal field theory, Walsh’s rules, valence-shell electron-pair repulsion theory (VSEPR), etc., and the teaching is quite different to approaches taken in condensed-matter physics for describing metals, insulator–conductor transitions, magnetism, etc. Yet inherently the same underlying principles apply.
Recently, we have been able to make progress in finding a unified approach to describing all these phenomena based on an underlying diabatic model, augmented where necessary for complicating effects.[180] This makes practical the dreams of the original 1920s–1930s developers of diabatic models. This work was done in conjunction with Ross McKenzie (Physics, University of Queensland) who brought his interest in valence-bond processes and quantum coherence, as well as his vast experience in studying coupled quantum nuclear-electronic problems in solid-state physics.[135,180–186] Many key advances in solid-state physics[187–189] were made at around the same time as Hush’s theory of adiabatic electron transfer was developed, and much was to be gained by merging results from the two disciplines. Also, much of the work was performed by our student Laura McKemmish as undergraduate research projects and during her honours year.[135,180–186,190]
Previously, diabatic models had been very successful only for electron-transfer theory. For it, a simple model with just two or three parameters could qualitatively describe a wide range of spectroscopic and kinetics properties.[180] Analogous quantitative treatments of chemical properties based on say pseudo Jahn–Teller approaches[19,94–96] have been very successful but require parameterization, often based on accurate ab initio calculations, for each property of interest. These approaches focus on two diabatic surfaces and the conical intersection that links them, by analogy to electron-transfer theory, but the deduced parameters are not transferrable either for the evaluation of different properties of the same system or else between similar systems. Hence they could describe important fine experimental details well but could not provide a fundamental basis for chemical understanding.
The central feature of electron-transfer theory not replicated in diabatic treatments of other systems was essentially the inability to transfer parameters. Fig. 2 shows the fundamental difference in electronic structure that caused this. Fig. 2a shows the situation for electron transfer, with an analogous one existing for hole transfer. Basically, it involves one electron (or hole) distributed amongst two orbitals, giving rise to two possible electronic states. Antisymmetric vibrations then couple the two resulting diabatic electronic states, producing all the kinetics and spectroscopic properties of electron-transfer theory.[30,32,107,108,156,159,167,168,180,191] General chemical reactions occur between closed-shell species, however, typically involving two electrons being redistributed amongst two orbitals, as sketched in Fig. 2b. This scenario leads naturally to three diabatic electronic states, the ground state G, the singly excited state S, and the doubly excited state D. Antisymmetric vibrations couple G to S in analogy to what happens in electron transfer, but the same vibrations necessarily also couple S to D. Therefore there exists one low-lying conical intersection seam for the G to S interaction and the process can be considered as a pseudo Jahn–Teller effect,[19,94–96] but there also exists a second seam linking S to D. This seam changes to properties of S significantly, just as the first seam affects G and S, and hence by an indirect mechanism D influences G. If one assumes that the vibronic coupling between S and D is the same as that between G and S (in practice small differences arise owing to the effects of electron correlation), then a renormalization of the full set of coupled equations is possible that allows the properties of the ground-state to be re-represented in terms of a simple two-state model analogous to electron-transfer theory.[180] This tells why two-state models involving only one conical intersection seam have been so successful in numerical applications, but it also indicates that the parameters appearing in such approaches get renormalized from a more basic set of parameters in different ways. Hence the underlying simplicity is lost and model parameters cannot be transferred.

|
For aromatic molecules, the HOMO and LUMO orbitals controlling chemistry and spectroscopy become either doubly degenerate (as is the case for benzene) or else nearly so. Fig. 2c sketches the scenario for benzene, it being possible to place the available four electrons in the four frontier orbitals in seven ways with singlet spin. Three of these ways are double excitations D, plus new triplet T and quadruple Q excitations are possible. If the three D states are replaced by one and the vibronic coupling connecting G to S, S to D, D to T, and T to Q are taken to be the same, then renormalizations of the five-state coupled problem in the strong coupling and weak coupling limits can be constructed that again map this problem involving many interacting conical-intersection seams back to a simple two-state one-seam situation.[180] The notion thus naturally appears that the ground state is ‘twinned’ to an excited state, just as the ground and excited states in electron transfer are intimately connected. This concept in regards to aromaticity has been highlighted for a long time by Shaik.[150–154] However, quantitative analysis akin to that applied in electron-transfer theory was never attempted. The reason for this is that Shaik mistakenly assumed that the excited state about which much was known, the singly excited state S, was the twin state whereas in fact it is the poorly characterized quadruply excited state Q; S indeed also has a twin state, but it is T not G.[180]
These results allow the theoretical description of aromaticity, general chemical reactions, and electron transfer to be unified.[180] Fig. 3 shows the situation for a closed-shell reaction involving isomerization, taking as an example the inversion reaction of ammonia.[135,180] The ground-state Born–Oppenheimer adiabatic potential-energy surface fitted to experimental data by Swalen and Ibers in 1962[192] (which is very similar to modern estimates[193,194]) is shown as green circles and fitted to a diabatic model. This model is described equivalently in the figure in two ways, (i) using the electron-transfer description of Hush as left (L), central (C), and right (R) localized diabatic potentials, and (ii) using the spectroscopic description of Craig, Ross, etc., of ground-state (G), single excited state (S), and double excited state (D) diabatic surfaces. Both diabatic approaches then yield identical descriptions of the ground-state (g), single-excited (s), and double excited (d) Born–Oppenheimer adiabatic surfaces. All potentials are specified by the parameters J (the resonance energy) and λ (the reorganization energy), as shown in the figure. The reorganization energy is related to the angle 21/2τm of the minimum of the localized diabatic L and R potentials through λ = 2kτm2, where k is the force constant. As atomic masses are rarely varied, knowing k is the same as knowing the vibration frequency ω for each of the diabatic potentials. The ammonia inversion reaction is a symmetric reaction between equivalent isomers, but symmetry is not an essential property. If the reaction is exothermic then a parameter E0 must be introduced to indicate the energy difference between the L and R diabatic minima. All chemical and spectroscopic properties are then determined from the four parameters J, λ, ω, and E0, including the transition state energy  shown in Fig. 3. For reactions involving general molecules, the specific torsional reaction coordinate τ used for the ammonia inversion reaction is replaced by a generalized dimensionless normal coordinate Q.
shown in Fig. 3. For reactions involving general molecules, the specific torsional reaction coordinate τ used for the ammonia inversion reaction is replaced by a generalized dimensionless normal coordinate Q.

|
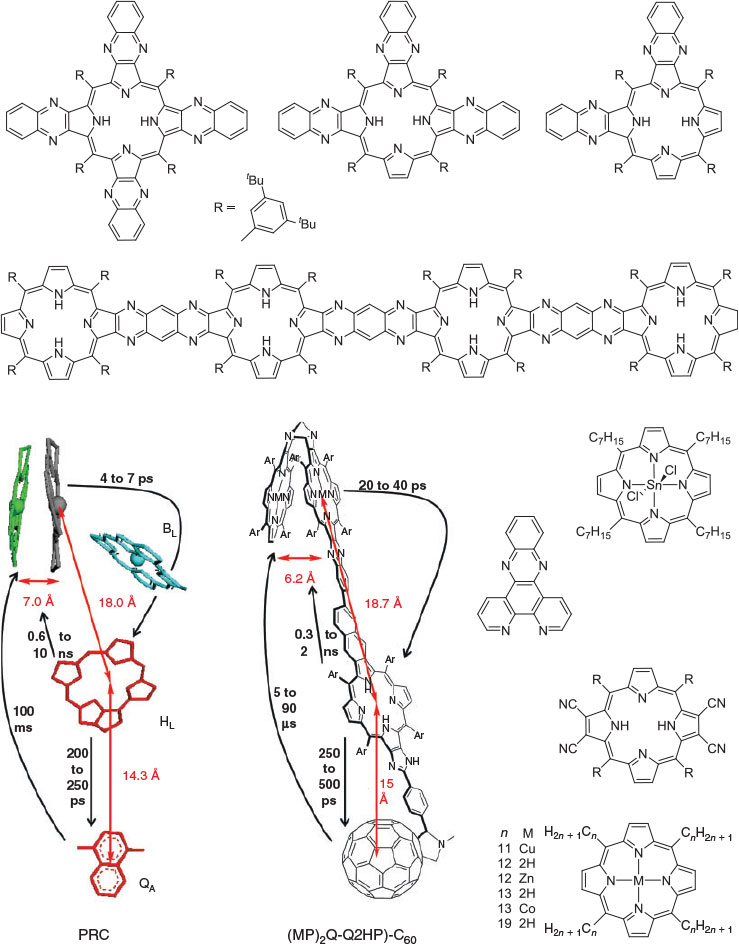
Fig. 4 and Table 1 depict 10 quite different applications of these ideas to modern chemical systems, including not just the ammonia inversion reaction[135,180,186] but also aromatic resonance in benzene,[135] breakdown of aromaticity in the triplet (π,π*) ground-state of pyridine (3PYR),[135,195] the Creutz–Taube ion in aqueous solution (CT),[196] possibly including an orthomethoxy substituent on the pyrazine ring (CT-OMe),[197] a variant of this in which pyrazine is replaced by a dipyridyl polyene (DPP),[198,199] the bacterial photosynthetic reaction centre from Rhodobacter sphaeroides (PRC),[99,100] gas-phase BNB,[200] pertinent to organic light-emitting diodes (OLED)s and artificial photovoltaics the fastest hole-transfer process in the β-phase crystal of the molecular conductor mer-tris(8-hydroxyquinolinato)aluminium(iii) (Alq3),[201,202] and a ferrocene–porphyrin–fullerene model triad molecule (FcPC60) designed by Crossley that undergoes long-range photochemical charge recombination.[203,204] Limitations of the application of the one-mode model to these molecular systems can be significant and are discussed elsewhere,[185] but the model does capture the critical chemical ideas.

|
Table 1 also presents five derived characteristic quantities depicting system properties. The ratio 2|J|/λ controls whether the ground-state Born–Oppenheimer surface is double welled (hence allowing reactions from one well to the other over the intervening transition state) or single welled (as in benzene, where the ground-state structure is a quantum resonance between two classical structures). For symmetric systems (E0 = 0) this parameter alone controls this localization or delocalization[205–207] and hence the class of a mixed-valence system,[208] but general expressions are also known.[184] For the molecules considered it ranges from 0.029 for the non-adiabatic electron transfer charge recombination process in FcPC60 to 0.8 in CT and ammonia to 3.3 in benzene. The parameter
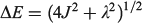
is a global measure of the electronic energy spacing, while  is the vibrational energy spacing, so the ratio
is the vibrational energy spacing, so the ratio  provides a basic guide to the suitability of the Born–Oppenheimer approximation, this becoming untenable as
provides a basic guide to the suitability of the Born–Oppenheimer approximation, this becoming untenable as  . In this limit, the Jahn–Teller effect most likely becomes important and so the inclusion of at least two vibrational modes becomes critical to providing a qualitatively useful description of the system. Of all the systems investigated, the PRC is the one most likely to suffer from Jahn–Teller effects, with
. In this limit, the Jahn–Teller effect most likely becomes important and so the inclusion of at least two vibrational modes becomes critical to providing a qualitatively useful description of the system. Of all the systems investigated, the PRC is the one most likely to suffer from Jahn–Teller effects, with  , though non-Condon effects are also known to be critical for CT.[196,209] The driving force of a reaction is best thought of in terms of the number of vibrational quanta involved,
, though non-Condon effects are also known to be critical for CT.[196,209] The driving force of a reaction is best thought of in terms of the number of vibrational quanta involved,  .
.
Born and Oppenheimer’s original consideration of ways to separate out nuclear and electronic motion employed an expansion in terms of the quarter root of the ratio of the electronic and atomic masses, a term roughly proportional to  . Failure of the Born–Oppenheimer approximation as the Jahn–Teller region is approached is therefore anticipated. It is also known that the Born–Oppenheimer approximation fails locally whenever diabatic surfaces become near degenerate, as is the case when
. Failure of the Born–Oppenheimer approximation as the Jahn–Teller region is approached is therefore anticipated. It is also known that the Born–Oppenheimer approximation fails locally whenever diabatic surfaces become near degenerate, as is the case when  . Hush, however, argued that the critical parameter was the diameter Qc of the cusp formed at the intersection point of the diabatic surfaces,[156] and we were recently able to quantify this effect.[185] For the simple one harmonic mode, two-state problem, the cusp diameter is given by
. Hush, however, argued that the critical parameter was the diameter Qc of the cusp formed at the intersection point of the diabatic surfaces,[156] and we were recently able to quantify this effect.[185] For the simple one harmonic mode, two-state problem, the cusp diameter is given by
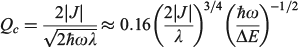
which unites the two basic ideas into one expression, with the Born–Oppenheimer approximation failing whenever Qc < 8–1/2 ≈ 0.35. Table 1 shows that, for classical chemical processes like aromaticity in benzene and ammonia inversion, the Born–Oppenheimer approximation holds well, with Qc = 12.6 and 6.34, respectively. Perhaps unexpectedly, it even appears useful for electron transport through Alq3 (Qc = 0.67). This process is, however, the fastest electron process found between molecules on different sites in an Alq3 crystal, with most other processes being much slower and hence smaller J and Qc, although the failure of non-adiabatic limit theories to describe the fast processes in the crystal has been noted.[202]
Simple spectroscopic quantities to flow from the equations are the electronic transition energies, dipole moment changes Δμ, and transition dipoles M. For symmetric reactions (E0 = 0) the electronic absorption vertical excitation energy is given by λ if 2|J|/λ < 1 and by 2|J| otherwise,[180] while
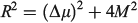
links the transition moment and dipole change (observable in Stark-effect measurements) to the distance R between centres in a charge-transfer application.[108,167] In the limit of weak coupling  this gives the transition moment as[32]
this gives the transition moment as[32]
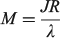
The vibrational frequency in the ground state is given by
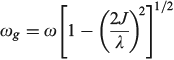
if the lower Born–Oppenheimer surface is double welled, while either the barrier frequency (if double welled) or the vibration frequency (if single welled) is given by
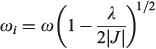
and the excited-state (the ‘twin state’) frequency is given by
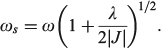
The most important kinetics property is the reaction barrier height  which is given in adiabatic electron-transfer theory for symmetric systems as
which is given in adiabatic electron-transfer theory for symmetric systems as
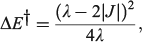
in the weak coupling non-adiabatic limit as[156,210]
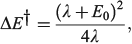
and in general is close to[185]
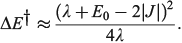
In the adiabatic limit the reaction rate is given by transition-state theory as[156]
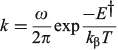
whereas in the non-adiabatic limit it is given by the Golden Rule[210,211] as
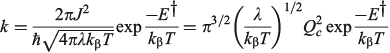
to emphasize the role of the cusp diameter.[185]
The one-mode two-state model is therefore characteristic of many chemical processes. It yields the above-mentioned analytical results plus many more,[101,108,167,168,180,185] and in addition can easily be solved numerically to high accuracy for any property without use of the Born–Oppenheimer approximation. Hence it can provide a means of assessing the reliability of computational schemes used in non-adiabatic calculations. Application of the Born–Oppenheimer approximation requires the neglect of three terms in the total nuclear-electronic Hamiltonian that scale with either the nuclear momentum or the nuclear kinetic energy. These are usually called the diagonal correction (DC), the first-derivative correction (FD), and the second-derivative correction (SD).[212,213] The one-mode two-state model leads to analytical expressions for these corrections[185] that are examples of known multi-mode relationships.[214,215] Their values depend on nuclear geometry but attain maxima of[185]
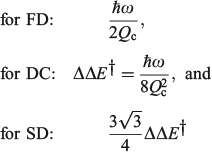
The FD term is thus lowest in order of 1/Qc and could therefore be expected to be the dominant correction as most of the time the Born–Oppenheimer approximation works well. However, this is not the case as Born–Oppenheimer breakdown is a specific example of a pitchfork bifurcation Cusp Catastrophe,[216–219] a phenomena known to be not treatable using such perturbation expansions as it embodies a fundamentally unstable mathematical description. These general conclusions have profound consequences when applied to the one-mode model that are easy to demonstrate. The DC term only acts to change the electronic energy levels, allowing wave functions to still be written as simple products of electronic wave functions and nuclear wave functions with retained adiabatic separation of variables. It can therefore be simply added to standard Born–Oppenheimer potential-energy surfaces as calculated by all electronic structure codes. This correction is very spiked at the cusp, which is located at or close to the transition state, and serves to increase the barrier for chemical reactions by the amount ΔΔE† given above. Values for the 10 chemical systems considered are given in Table 1, expressed relative to the vibrational energy spacing. What is clear is that in non-adiabatic reactions, ΔΔE† can be larger by far than the original activation energy ΔE†. Quantum tunnelling through the high but very narrow barrier generated by DC negates this effect to some extent, but we find that over the entire parameter space of the model there is no region in which inclusion of only the FD term leads to a reliable solution of the quantum dynamics equations depicting the reaction process.[185] Always all three corrections must be used to obtain reliable results. This observation is expected from general considerations of the cusp catastrophe but is contrary to standard practice for the determination of non-adiabatic reaction rates. Success over the last decades by methods including only FD has arisen owing to the accidental cancellation of large errors stemming from the use of an approximated Hamiltonian and its solution by semiclassical rather than full quantum treatments.
The usefulness of this unification of chemical and spectroscopic processes under the one diabatic umbrella is perhaps not so much in the description of important but nevertheless not typical non-adiabatic chemical processes but rather in its ability to unite standard chemical understanding. The difference between an isomerization process like the ammonia inversion reaction and aromaticity in benzene is seen to arise just through a change in the value of 2|J|/λ. This is > 1 in benzene so all C–C bond lengths are equal but < 1 in ammonia so the planar D3h structure is unstable and pyramidal structures form.[180] This suggests that the method can be used to provide an explanation of basic chemical structural properties from first principles.
The most fundamental approach to gaining insight into the structure of molecules like XY3 series such as NH3 to BiH3 is by application of Walsh's Rules[220–227] using understanding of how occupied orbitals change with molecular shape and electronegativity differences. Excited state properties can also be framed in this context[221,228] and reaction symmetry understood,[229–233] but the close connectivity[139,150–154,234,235] between ground-state and excited-state properties is lost. To apply the methods, one needs to know beforehand how orbitals behave as a function of geometry, something that may not always be intuitively obvious. A more widely applied but more empirical approach to describe bonding is VSEPR theory[236–239] and its origins.[240,241] This approach considers electron pairs associated with the same atom that repel each other, while being attracted to nuclei differently depending on electronegativity. It applies only to ground states and cannot depict excited-state properties. In its original form, VSEPR was applied like this: the XH3 series has four valence electron pairs and so they are presumed to be arranged tetrahedrally around the central atom making the expected HXH bond angle θ = 109.5° but compressed slightly as lone-pairs take more angular space than do bonding pairs owing to their contraction to the nucleus. Hence the observed HNH angle of 108° in ammonia is explained, but this argument does not explain why the bond angles in PH3 to BiH3 range between 93°–90°.[186] Traditionally, the empirical rule that second-row elements are always octahedral was therefore invented.[237,239] In the latest version of VSEPR theory, atomic radii are used for every pair of atoms, neglecting the traditional electronegativity arguments used in the earlier approach.[239] Essentially, VSEPR theory now parameterizes the answer for each problem into the method.
Diabatic descriptions instead offer the description of chemical structures in terms of fundamental properties: the resonance energy and the reorganization energy. It is the factors that control these quantities that control geometry. Considering orbital overlap with the diabatic references orbitals allows the diabatic bond angle in the absence of resonance to be determined. This process is illustrated in Fig. 5. For NH3+, the interaction involves one electron in two orbitals (the N lone pair orbital and the antibonding symmetric NH orbital). The diabatic orbitals are obtained by a 45° rotation of the adiabatic orbitals at the high-symmetry planar geometry, identifying them as sp hybrids (Fig. 5a). In the absence of resonance, the three NH bonding orbitals must be orthogonal to a single one of the two sp diabatic orbitals and so the bond angle becomes θ = acos[3sin2(atan(1/2))/2 – 1/2] = acos[–1/5] = 101.5° (Fig. 5b). Renormalization for the two-electrons in the two-orbitals case of NH3 increases the associated torsional angle by a factor of 21/2 and hence gives a bond angle of θ = acos[3sin2(21/2atan(1/2))/2 – 1/2] = 86.7°.[186] However, resonance drives both of these limiting structures towards the delocalized aromatic-like situation of a planar molecule with 120° angles, achieved whenever 2|J|/λ ≥ 1. Interpretations of the excited-state spectroscopic data of these molecules supported by ab initio calculations indicate that both the resonance energy and the reorganization energy are much larger for N compounds than for P–Bi compounds, but the effect on the resonance energy is second order so that the values of 2|J|/λ are 0.82 for NH3 but 0.48–0.36 for PH3–BiH3, respectively.[186] It is this discontinuity in 2|J|/λ that causes the geometry of NH3 to be tetrahedral while the other molecules are octahedral.

|
Understanding the sources of the large increases in the resonance energy and reorganization energy for N compounds therefore provides the way to understand the bonding from a fundamental perspective. As Fig. 3 shows, these quantities are not just properties of the ground state but are also excited-state properties. The nature of the excited states of molecules is thus intricately related to the properties of their ground states. To provide a good description of the ground-state potential-energy surface, computational methods must therefore also be able to describe the involved excited states. Unoccupied orbitals and their properties are just as important as occupied orbitals when it comes to understanding potential-energy surfaces.
The big difference between the orbital structures of NH3 and PH3 is an inverted ordering of the XH symmetric antibonding orbital σ*A and the lowest Rydberg orbital: in ammonia the Rydberg orbital is lowest in energy whereas in phosphine the valence orbital is lowest.[186] This change may not seem profound but the consequence is a change in orbital nodal pattern as the two orbitals interact to produce ‘bonding’ and ‘antibonding’ molecular orbitals. If σ*A is of lower energy then the interaction with the Rydberg orbital stabilizes it, spreading out the electrons over a larger volume, but if it is higher in energy then a nodal surface divides the two, compressing σ*A on top of itself (Chart 1).

|
This compression results in a large increase of electron–electron repulsion within the same electron pair, forcing up the energy and hence the resonance energy of two interacting sp hybrids. Hence the swap in order of the σ*A orbital and the lowest Rydberg orbital is responsible for the large change in properties between the first-row element N and the other elements of Group XV. The compression is clearly seen in Fig. 6 where the Hartree–Fock orbitals are shown for NH3 and AsH3 obtained using a STO-3G basis, as well as that when augmented by a single Rydberg s-type basis function. Adding the Rydberg orbital compresses the ammonia orbital significantly but has little effect on stilbene.

|
VSEPR theory provides no fundamental insight into chemical bonding, with its focus on bonding electron pairs causing it to not see the critical features that make first-row compounds different from those of later rows. Walsh’s rules allow ground-state and excited states to be simultaneously interpreted, but the interconnecting properties are omitted and one therefore must determine the key properties individually for each system. Only diabatic analysis can unify a wide range of spectroscopic and chemical properties to provide fundamental physical insight.[186]
Applications to the Nanotechnology Molecule of Crossley
Max Crossley at Sydney University has synthesized many molecules for application in molecular electronics, understanding photosynthesis, and biomedical applications, mostly based on porphyrin chemistry, see Fig. 7 for example. The essential element to the success of his work has been the ability to provide tight synthetic control over structure and function through making synthetically diverse but structurally rigid molecules. Such control allows theories to be developed to describe observed properties, as well as the application of high-level ab initio and density-functional computational methods. An example of this is FcPC60 highlighted in Fig. 4 and Table 1, presenting results obtained by combined synthesis, spectroscopic observation, and fundamental understanding. This and related molecules, at the time of original publication, achieved the longest-lived primary charge separation of any triad, up to 1 ms at room temperature in solution,[203] following earlier record-breaking performances of related dyad molecules.[204] Long-lived charge separation is a highly desired property in any artificial device that harvests solar energy and converts it into either electrical or chemical energy.
Recent advances on this technology include the synthesis of the tetrad molecule (MP)2Q-Q2HP-C60 (Fig. 7) with structural and functional properties that are the closest-known mimics to the bacterial photosynthetic reaction centre.[242] In parallel work, simpler compounds such as the tetracyanoporphyrin in Fig. 7 were designed and synthesized for use in organic solar cells, leading to discovery of the dominant mechanism of primary charge separation in poly[2-methoxy-5-(2′-ethylhexyloxy)-1,4-phenylenevinylene] (MEH-PPV) – [6,6]-phenylC61-butyric acid methyl ester (PCBM) blends,[243] the demonstration of optically controlled switching based on oligoporphyrin oligomers like the tetramer shown in Fig. 7,[244] the design of molecules like the dichlorotin porphyrin shown in Fig. 7 for reaction with and surface modification of the highly activated silica surfaces found in optical fibres,[245] the discovery of adatom-bound attachment of nitrogen bases based on 1,10-phenanthroline for the stabilization of gold surfaces and nanoparticles,[246] solar-energy upconverters 30 times more efficient than had previously been achieved[247,248] based on the cruciform, T-shaped, and elbow π-expanded porphyrins[249–252] (Fig. 7), and the development of molecules (see later) and methods for measuring the free energy of polymorphism of self-assembled monolayers on hydrophobic surfaces.[253]
That we were able to predict and design functional system properties for Crossley’s molecules[244,249,250,254–258] provided an important aspect to their success. These predictions integrated the traditional electron-transfer theories of Hush with the parallel understandings of Craig, as described in the preceding section. Some systems have been designed and shown to be synthetically feasible but not yet developed, however. This includes a molecular n-bit shift register made by the controlled synthesis of large porphyrin assemblies on substrates containing leads fabricated using current silicon device technology.[259] The established synthetic strategies involve scanning tunnelling microscopy (STM)-induced reactions of molecules[260–270] on silicon surfaces performed with atomic precision,[271,272] that are subsequently linkable to porphyrins.
Crossley’s molecules were also important in that they led to fundamental understanding of quantum-chemistry computational procedures now widely used in nanotechnology. The fundamental discoveries leading to the establishment of the CAM-B3LYP method programmed and championed by Kobayashi as part of the chlorophyll-assignment project (see earlier) were demonstrated using Crossley’s porphyrins.[87,91,244]
Molecular Electronics and Inelastic Electron Tunnelling Spectroscopy
The 1950s saw not only the advancement of Craig’s methods for spectroscopy and Hush’s methods for discrete electron transfer events but also the advent of the Landauer method[273,274] for understanding steady-state conduction through single molecules by coherent quantum transport. The importance of this work was recognized by Mark Ratner[275–277] (who had first proposed the use of single molecules as a replacement for silicon electronics in 1974),[278] Supiyro Datta,[279] and others. The approach was based on Keldysh Green’s function theory[280] and involved the green’s function G(E) = (H – E1)–1 where E is the energy of the transmitting electron, and H is the Hamiltonian of the molecule in the field of the semi-infinite external electrodes connecting to it, represented as the unperturbed molecular Hamiltonian plus self-energies ΓL and ΓR describing the external contacts to the left (L) and right (R) electrodes, see Fig. 8. Professor Hush and myself showed how this approach could be applied using a priori electronic structure calculations.[281] Through developments by Hong Guo, DFT implementations of this method combined with non-equilibrium Green’s function techniques[282] can now model the 14 nm technologies used in current silicon-chip manufacture more accurately than traditional empirical transistor models.[283] This field is enjoying a renaissance with, for example the recent discovery of a molecular rectifier switchable at 17 GHz.[284]
While calculation methods for molecular electronics are now well established, this was not always the case and indeed the whole field was once under a cloud in that it had never been shown that single molecules carrying currents of the order of μA remained chemically intact throughout the process. This situation changed in 2004 when two independent measurements[285,286] reported the vibrational spectrum of a conducting molecule, determined from the second-derivative of the current as a function of voltage in a process discovered at the Ford Motor Co. known as inelastic electron tunnelling spectroscopy (IETS).[287] Both spectra depicted vibrational levels at about the expected energies for the (very similar) molecules investigated, but the observed intensity patterns were completely different. A new method to understand the intensities in this type of spectra was required.
Our student Gemma Solomon quickly showed that the qualitatively different intensity patterns originated from different binding sites of the conducting molecule on the attached electrodes,[288] and Mark Ratner showed that the IETS experiment was more likely to emphasize totally symmetric molecular vibrations.[289,290] Such a discussion of symmetry was unprecedented in the field of molecular electronics, though it was one of the great successes of molecular spectroscopy decades earlier and a central feature of Craig’s works.[14,15,33–43] A reason for this is that it was reasoned that in general the junctions between arbitrarily positioned molecules and electrodes would not show symmetry. However, we demonstrated that the symmetry of the junction has only a minor effect[291] and can largely be ignored, allowing the full power of group theory to be applied to understand coherent elastic and inelastic electron transport through molecules.[292,293] Solomon showed that the appropriate point group was not that of the molecule but instead the molecular point group without any end-to-end symmetry as the applied voltage eliminates such symmetry elements. As a result, the symmetry of the electron-transport channels through the junctions can be defined, and the symmetry of the molecular vibrations utilized.
An example of this is shown in Fig. 8 for chemisorbed benzenedithiol spanning two gold electrodes. Current through the junctions and into the molecule is provided mostly by π-molecular orbitals of B1 symmetry, with coefficients on different atoms weighted as shown in the figure; however, σ channels of A1 symmetry also provide connection. Typically single channels dominate the junctions so if the same connector material is used on each side then the net product of the two junction symmetries must be totally symmetric and hence symmetric vibrations typically scatter the most.[289,290] However, knowing the ratios of the junction conductances of secondary channels to the dominant channel, scattering off asymmetric vibrations can occur and be quite intense, as illustrated in the figure.[292,293] The sensitivity of each particular vibration to scatter the transmitting electron is given by the vibronic coupling constants used by Craig to explain the spectra of benzene and related molecules, the same quantities that we showed also pertained to Hush’s electron-transfer theories. There is thus a very close connection between the understanding of molecular spectroscopy and the understanding of IETS phenomena.
Quantum Entanglement, Theories for Consciousness, and NMR Quantum Computing Design Rules
As previously described, central aspects of the works of Craig and of Hush involved the breakdown of the Born–Oppenheimer approximation. This was embodied in the work of Craig through vibronic coupling constants linking delocalized diabatic states or, equivalently, through electronic couplings linking localized diabatic states in the work of Hush (Fig. 3). A critical resulting feature is that the resultant electron-vibration system Eigenfunctions cannot be written as a simple product of electronic and vibrational wave functions. As a result, the electronic and vibrational motions become entangled.[16] Entanglement is the defining property of quantum systems, allowing them to store more information than could be encoded into an analogous classical system. This feature forms the basis of proposals for quantum information processing and hence chemical qubits based on electron-vibration entanglement that have been proposed for possible technological applications.[294] A qubit is a quantum memory storage device analogous to bits in modern digital computers.
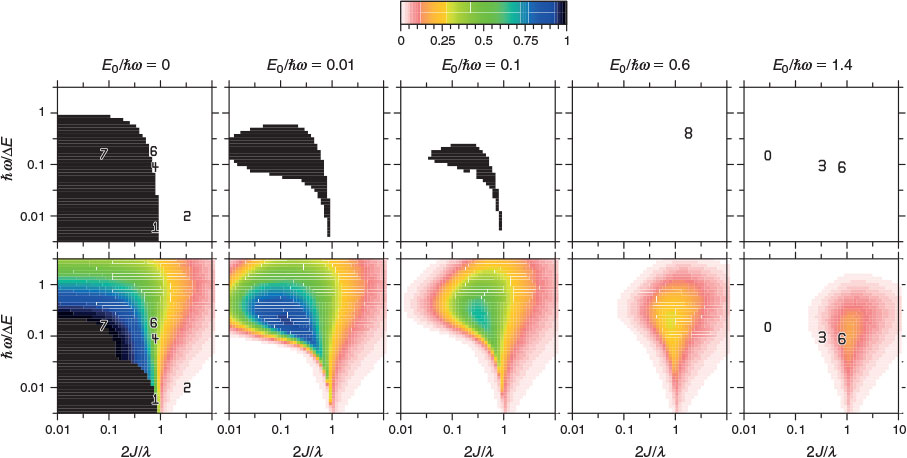
Our general model for chemical reactions developed in conjunction with Ross McKenzie and Laura McKemmish allows insight to be gained into what types of chemical processes may be useful as the basis of electron-vibration chemical qubits.[135,184] By varying the parameters ħω/ΔE, 2|J|/λ, and E0/ħω, it is possible to calculate the resulting entanglement and its stability with respect to external perturbations. The critical properties of a qubit are the amount of entanglement it generates, its ability to preserve that entanglement for long times during which quantum computations can occur through quantum coherence, and its ability to be read and written as classical states through intentional quantum decoherence. In essence, the requirements of quantum coherence during processes, which demands extreme isolation of the qubit from its environment, and easy read/write, which demands strong interactions with some part of the outside world, are seemingly mutually inconsistent, defining a central challenge in this research field. Entanglement can be measured as the von Neumann entropy S of the Eigenfunctions of the qubit, which varies from 0 for a classical system (in this case, a pure diabatic electronic state) and 1 when there is formed a phased 50–50 mixture of two such classical states.[135,184] At the simplest level of approximation, fluctuations in the environment modulate the energy difference E0 between the two diabatic states, making the sensitivity of the entanglement to variations in E0/ħω a quantity of primary interest.
Fig. 9 shows the entanglement as a function of ħω/ΔE and 2|J|/λ for three values of E0/ħω = 0, 0.01, and 0.1. To help understand these results, the figure also shows the bimodality index of the systems. Bimodality occurs when the ground-state Eigenfunction has a local maximum somewhere in its vibrational density profile. This can only happen when the Born–Oppenheimer adiabatic ground-state potential-energy surface has a double minimum that is sufficiently deep to support zero-point motion in each well. While entanglement occurs to some extent for all values of the parameters, it becomes large only when the ground-state density is bimodal, requiring at least 2|J|/λ < 1. However, as Fig. 9 shows, if the wells become very deep (2|J|/λ << 1) then small levels of asymmetry destroy the quantum interference, making the qubit extremely sensitive to environmental effects. A reasonable level of insensitivity is found in only a small region of the parameter space with 2|J|/λ only slightly less than 1 and ħω/ΔE only slightly less than 1. However, the single vibrational mode model that is used becomes invalid as ħω/ΔE → 1 because then Jahn–Teller effects can dominate. Hence finding a suitable chemical process for application as a quantum qubit is a very difficult challenge.[135,184]
|
Quantum entanglement may be of practical use in understanding quantum systems irrespective of its possible application to qubits in information processing. Relevant to information processing, the entanglement was described above in terms of diabatic states mimicking classical states to which experimental measurement could collapse quantum wave functions. No known experiment mimics collapse of non-adiabatic wave functions to Born–Oppenheimer states, but nevertheless the associated entanglement reveals significant insight into the Born–Oppenheimer approximation, indicating novel ways in which this could become manifest. Such insight is different to the commonly considered manifestations of breakdown in terms of say binding strengths, equilibrium geometries, transition energies, reaction probabilities, etc. What is found[184] is that the entanglement scales simply with the cusp diameter Qc and so provides a more intrinsic measure of the breakdown process than is provided by the other measures as these all amplify some particular aspect of the phenomenon. What becomes clear is that ways of calculating Born–Oppenheimer breakdown appropriate to one question of interest may not be appropriate for other properties of the same system. Indeed, the entanglement is the only property we have investigated that is dominated by the FD correction term, the DC term not contributing at all to entanglement with the SD term clearly being of secondary importance.
A dramatic possible manifestation of chemical quantum entanglement appears in the original ‘Orch-OR’ proposal of Penrose and Hameroff[295–299] that qubits based on this principle form in the tubulin dimers that constitute the microtubular primary structural supports in most cells. Their proposal is that such qubits can remain coherent on the neural timescale, being decohered only by quantum gravitational effects in some way which allows them to modulate neural cellular potentials and hence provide the essential element required for conscious thought. The search for such quantum processing contributions to neural activity stems from Penrose’s Lemma stating that electrochemical processes in neurons, as well as say the logic processes achievable in modern (classical) digital computers, are incapable of manifesting consciousness.[300,301]
All chemical quantum computing proposals involve coupling of electronic motion to vibrational motions that occur on the fs timescale. These, and all processes occurring on slower timescales, would have to remain quantum coherent on the ms neurological timescale for this process to be feasible in the Penrose–Hameroff ‘Orch-OR’ qubit proposal, something that would be extremely amazing, akin to superconductivity and Bose–Einstein condensation. Penrose and Hameroff evoked the possibility that an unobserved yet widely speculated phenomenon known as Fröhich condensation[302–304] could provide the required coherence. Fröhlich had considered a non-equilibrium steady-state scenario appropriate to biological environments in which energy flow from a source to a sink through an intervening oscillator system caused a dramatic non-equilibrium energy distribution amongst the oscillators that he likened to a Bose–Einstein condensate. However, we showed that Fröhlich’s equations indicate that in biological systems this effect only occurs after the energy of the non-equilibrium system, expressed as an average ‘temperature’, entered the range of 2000–1 000 000 K. We also showed that the effect was purely classical in nature and hence did not purvey quantum coherence.[182] Finally, we showed that the coherent vibrational oscillation specified in their proposal was in fact not a vibration at all but instead involved irreversible chemical reactions and the dismantling of the microtubules.[181] The original proposal was therefore untenable on a variety of biochemical, chemical, and physical principles. It has been withdrawn and the Penrose–Hameroff proposal restated[299] without specification of its central element, the vibrational qubit.[183] As a result, we concluded that there exists ‘no basis on which Orch-OR theory can be considered as a proposal worthy of further consideration’.[183]
On a more positive note, this work on the basics of chemical quantum computing led also to the development of qualitative tools as well as a simple computational model for predicting which gates can be successfully operated in an NMR-based quantum information processor.[190] This allows synthetic chemists to design new molecules with improved functionality, avoiding the huge supercomputing efforts demanded by the complicated quantum dynamics models used in current qubit simulations. It is based on the observation that the critical qualitative features of the complex experiments performed using NMR pulses shaped in the time domain are provided very easily by transforming the problem into the analogous frequency-domain representation. Some major results are yet to be published.
Strong But Highly Distributed Electron Correlation: The Van der Waals Force and Self Assembly
Craig’s heroic first calculation of electron correlation in 1950[13] opened the way for many modern research fields, from its dominance of the spectroscopy of aromatic molecules studied by Craig to subtle modifications to classical chemical bonding that facilitate many chemical processes to superconductivity to the London dispersion force that liquefies helium, causes oils to boil at high temperatures, controls biological and polymer structure, and allows sticking to ‘non-stick’ surfaces. While the qualitative effects of electron correlation have been recognized since the inception of quantum mechanics,[305] how to treat it efficiently in a priori or ab initio calculations has been a dominant theme of research over the past decades. Today there is much excitement concerning the possibility of applying 2D materials in electronics, nanotechnology, and biotechnology applications, with dozens of materials now known and thousands conceived.[306] These stack together by van der Waals forces, and understanding the ‘van der Waals gap’ that controls their properties is critical.[307]
Electron correlation is essentially a classical effect rather than a quantum one as it relates to how the instantaneous position of one electron affects the motion of others, although quantum effects do influence its manifestation. To put issues in perspective, Bohr’s semiclassical theory of electronic structure may be applied to molecules and is known to deliver more accurate results than comes from many modern sophisticated DFT approaches.[308–312] The advantage of Bohr’s approach is that it includes electron correlation simply and easily. Indeed, we have shown that a range of basic chemical phenomena like the nature of the valence states of transition-metal compounds, f-block chemistry, the basic description of NMR spectroscopy, relativistic effects in chemistry, etc., can be simply described at this level, providing an easy way to explain chemistry to freshman students.[313]
However, the dispersion force is an aspect of electron correlation that is purely quantum in origin. Classical mechanics specifies how permanent electrical charge distributions interact with each other and polarize their surroundings, but quantum mechanics adds something extra: the ability of systems to undergo spontaneous short-lived charge fluctuations as demanded by the uncertainty principle. After these fluctuations occur they interact with the environment in the same way as do permanent classical charges, meaning that the interactions take on a very different form if they occur in metals or in insulators, for example. Such classical aspects of a quantum phenomenon are mostly neglected in standard chemical thinking, despite being critical to understanding.
The reason for this of course is that molecules and proteins are not conductors and so the application of ideas coming from the classical electrostatics of insulators is almost always adequate. This leads to the idea that quantum fluctuations are restricted to occur on atoms, and that these fluctuations interact independently with the atoms in all surrounding pieces of matter. The net dispersion force between two molecules is then written simply as the sum over all inter-atomic interactions of terms scaling as r–6, where r is the interatomic distance. This generates London’s basic description of the dispersion force.
Consider, however, the situation shown in Fig. 10 in which particles are surrounded by a metallic conductor, and that this system then interacts with an external field. Gauss’ Law of classical electrostatics indicates that the metal conductor acts as a Faraday cage which prevents the electric field from penetrating inside, so the internal particles are screened from the external one and no interaction occurs. Gauss’ Law appears as a consequence of strong electron correlation in classical electrostatics. Another directly relevant feature of classical electron correlation is co-operativity in which a system of interacting polarizable centres interfere with themselves in a constructive manor, leading to much larger dipole moments than would otherwise have been expected. The increase in dipole moment of a water molecule from 1.8 Debye in the gas phase to 2.9 Debye in liquid water is an example of such a cooperative effect.

|
The same principles apply to the dispersion force.[314] Quantum fluctuations on an external molecule are screened by the Faraday cage and are not perceived by molecules inside the cage. Indeed, this effect has been recently demonstrated by Tsoi et al. for a system in which a silica surface is approached by an atomic force microscope with a silica tip.[315] Normally, a large dispersion force describable in terms of a sum over atoms as r–6 London energy contributions is found, and this force is maintained if a single layer of insulating fluorographene is inserted between the tip and surface. However, if conducting graphene is inserted instead, the tip and surface no longer experience van der Waals attraction! Instead, the field lines coming from a spontaneous dipole fluctuation inside the tip are reflected back off the graphene, generating interference patterns and possibly enhanced ‘antiscreening’ interactions with solvent or other matter nearby the tip.[314]
Expressed in a broad context of modern interests in biotechnology, surface chemistry, and nanotechnology, these issues have been clearly described recently by John Dobson from Griffith University.[314] His conclusions are presented in Table 2 concerning the dispersion interactions between objects of different shape in the asymptotic region of large separation as a function of the separation distance D. There, results from simple approaches to understanding inter-object dispersion as pairwise additive sums over interatomic London terms scaling as r–6, where r is the interatomic distance, are compared with the form determined using the sophisticated random-phase approximation (RPA).[314,316–322] Simple London-based approaches work well for intermolecular interactions, explaining their success in chemistry and biochemistry, and these also work for interactions between all 3D materials, but they fail for 1D and 2D conductors such as metallic nanotubes and graphene.

|
The screening interactions depicted in Fig. 10 are known as Dobson-B corrections[314] to pairwise-additive dispersion relationships. In addition, Dobson-C corrections involve quantum fluctuations that are not restricted to atoms but instead occur on length scales limited only by the finite duration of the fluctuations and the effective Fermi velocity of the metal. (In addition, the finite speed of light should also be considered, as in the Casimar effect,[323] but these influences are usually small.[316,318,324]) Hence quantum dipole fluctuations can spread over distances that are large compared with separations to neighbouring objects, possible up to lengths of 100 nm in order. As sketched in Fig. 11 for interactions between 1D conductors like nanotubes, this converts the usual quantum-fluctuation-dipole to induced dipole interaction described by the London force into something more like interacting quantum-fluctuation-charge to induced charge interactions. Such effects lead to the interactions between conducting nanotubes being very much stronger than expected, changing the asymptotic dependence from D–5 to D–2ln(D/D0)–3/2 in Table 2. In parallel 1D conductors, such fluctuations are perfectly aligned for maximum effect. Averaging over two dimensions reduces their impact, with fluctuations in the correct direction to have an effect becoming too improbable in three dimensions for there to be any major influence.

|
Computational methods that include dispersion by first-principle approaches are computationally demanding. This is highlighted in Table 3 where the scaling of various computational methods as a function of the number of electrons n is shown, as well as the scalings required to qualitatively describe different types of dispersion interactions. If only insulators are involved then n5 scaling is adequate whereas n6 scaling is required in general.[314] Ab initio methods like second-order Møller–Plessett perturbation theory (MP2) scale as n5 and hence are useful in chemical and biochemical applications but more expensive approaches like CI singles and doubles (CISD), coupled-cluster singles and doubles (CCSD), RPA, or TDDFT are required in general. However, these may not necessarily be applicable to conducting systems as they are single-reference in nature and so their multi-reference analogues are typically required. Traditional DFT methods using the local density approximation (LDA), the generalized-gradient approximation (GGA), or hybrid functionals fail completely, although scaled-down MP2-like dispersion is included in double-hybrid functionals. Note, however, that the scalings shown in the table are formal ones, not ones that may be achieved using some approximate yet very accurate implementation technique. Most significantly, a new TDDFT procedure has just been introduced with ~n4 scaling instead of n[6,325] and this method may prove very useful in the future.
Notwithstanding this, we have recently reviewed[326] many available options for accurate calculations, including multi-reference coupled-cluster,[327–337] embedded approaches,[332–334,337–343] mixed DFT–ab initio approaches,[324,337,340,344–349] and quantum Monte Carlo.[350,351] For most problems such approaches remain computationally unfeasible, however, and so empirical dispersion correction schemes to low-level GGA or hybrid DFT provide the most commonly used strategies. Of the currently available schemes, we recommend two: the D3 scheme of Grimme et al.[266,352–354] and the many-body dispersion (MBD) scheme of Tkatchenko et al.[267,355–360] The D3 scheme is based on pairwise sums of London terms and so suffers from the problems described in Table 2 for long-distance interactions, although a variant containing three-body interactions, D3(ABC), is available[352] and underused.[326] It also has older variants known as D and D2[266] but is most commonly applied in its form utilising Becke-Johnson damping, D3(BJ),[354] which herein is simply called just D3. The MBD scheme includes all many-body Dobson-B effects but does not allow for long-range Dobson-C fluctuations and hence also produces the wrong limits for long-range interactions. This scheme scales nominally as n3 in the number of atoms but the prefactor is large and the time required for MBD calculations can exceed that for the base GGA density functional by orders of magnitude. Hence this method can only be applied to small-to-medium-sized systems,[326] but the very efficient D3 scheme can be applied to any problem treatable by DFT. A promising alternate scheme to D3 and MBD is the exchange-hole dipole moment method (XDM)[361] that has recently undergone significant improvement.[362]
Both D3 and MBD have been shown to be very effective for many different types of problems, from ice cluster energies through crystal cohesion energies to basic chemistry and to surface adhesion to interactions with graphite and nanotubes.[260–270,341] This occurs despite fundamental limitations in the description of the interactions (Table 2). Success comes from the fact that these methods are designed to model interaction energies and geometries and are usually only applied for these purposes.
Our particular focus within this topic is self-assembly processes from solution. Such processes are important to, e.g. biology, polymerization, and nanotechnology. Two features of critical relevance are that processes are controlled by free energies not just binding energies, and that solvation effects act to dissolve self-assembled monolayers (SAMs). Our work has focussed on the self-assembly of tetraalkylporphyrin molecules synthesized by Max Crossley on highly ordered pyrolytic graphite (HOPG) surfaces from solution in 1-phenyloctane, octanoic acid, or n-tetradecane.[253,363–368] This involved measurement of STM images and the simulation[253,363,369] of the Gibbs free-energy of formation for a wide range of possible atomic structures for each image. The molecules considered are shown in Chart 2.

|
An important feature of this system is the observation of various polymorphs for shorter-chained molecules. Key aspects are shown in Fig. 12 and include grain boundary, a rare but informative feature of a polymorphic SAM. This boundary appears between different polymorphs and shows one row of molecular structures in the low density ‘L’ polymorph plus several interface ‘I’ rows that in their middle take on the structure of the medium-density ‘M’ polymorph.[368,369] The molecular structures determined from modelling of large areas of the L and M polymorphs are shown, as is how they seamlessly meld together to form the interface layers. The L polymorph is observed for all odd-length chain molecules studied (lengths m from 11 to 19)[253,363,366,368] but not for the even chain molecule studied, 2H-C12P,[364,365] while three M polymorphs[253,364,365,368] of quite different form named Ma, Mb, and Mc are observed for 2H-C11P, 2H-C12P, and 2H-C13P, respectively. The L structures have all four alkyl chains lying flat on the surface while the M polymorphs have two such chains with the other two somehow oriented into the solution. As there are many ways that molecules can orient in solution but only a few ways in which they can kink to lie flat on surface, a much greater variety of possible forms exists for the M polymorph compared with the L one. A high density polymorph with only one chain on the surface is also known for 2H-C11P.[368]

|
Atomic structures for the SAMs are determined by comparing calculated and observed structures. The calculated structures were obtained by optimizing five possible structures for the L polymorphs[363,366] and 40 possibilities for the M polymorphs.[363,369] These possibilities were obtained by considering various conformations of the chain kinks that occur as the alkyl chains come away from the porphyrin at an angle near 60° and must subsequently be bent back in order to lie flat on the surface. The 40 possibilities for the M polymorphs were obtained by varying kink-structure conformers and macrocycle rotation angles, first eliminating possibilities that cannot be shaped into a valid SAM. After optimization, only at most 22 stable SAMs were realised, named Ma to Mv. Structure assignment was made by comparing these structures to experiment, considering:[253,363,366,369]
-
Agreement of observed and calculated lattice parameters. To do this, new experimental techniques based on internal calibration and repeated measurements were developed to significantly reduce the experimental uncertainties in the lattice parameters, allowing for discrimination between the calculated structures.[253]
-
Agreement between observed and calculated chain hydrogen atom positions. It is common that images show resolved hydrogen atom locations for the alkyl chains, providing detailed information concerning the structure.
-
Agreement of the shape of the porphyrin-ring images. These images always have structure, typically eight resolved units coming from the pyrrole rings and the kinks in the alkyl chains, features that can be related to the calculated structures.
Always only one calculated structure matched all of the observed data, leading to a clear assignment. The observation of interface regions provides strong verification of the assigned structures as the L and M polymorphs must smoothly mesh into each other, a feature which is very difficult to obtain as it requires perfect alignment of many aspects of the structures.[369]
The calculations also yield the free energy of SAM formation.[253] This is evaluated using DFT in various forms. In one way, the B3LYP functional is used to describe the porphyrin and the kinks, with molecular mechanics force fields used to describe the porphyrin–porphyrin interactions and a specialized empirical graphite-alkane force field fitted to experimental enthalpy data used for the surface attraction, a QM/MM approach.[366] After optimization the vibration frequency of the SAM is determined, leading to evaluation of the zero-point energy and entropy of the SAM.[253] Solvation is then included using a self-consistent reaction-field approach that treats the dispersion interaction between the surface, molecule, and solvent as being simply proportional to the surface area exposed to the solvent.[253] The other approaches are based on using the Perdew–Burke–Ernzerhof (PBE)[370] density functional augmented by empirical dispersion corrections to describe all interactions.[253] The D3 and MBD empirical dispersion correction methods were both used.[326] Only optimized geometries and interaction energies were evaluated in this way, with the zero-point energy and entropy corrections determined by the QM/MM method simply added to these results.
A new method was also developed for estimating free energies of formation from experimental STM data.[253] Only a few measurements of free energies of SAM formation have ever been performed,[371] and while the error bars of our technique are large (of order a few kcal mol–1), they provide means for analysis of the calculated free energies. Comparison of observed and calculated values is made in Table 4. The observed values are about twice as large as the calculated ones, but the absolute differences in free energy of ~7 kcal mol–1 are small compared with the likely errors involved. The various computational methods are mostly in good agreement with each other.

|
The calculations provide insight into the factors controlling SAM polymorphism, as indicated in Fig. 13 for 2H-C13P. The strong (PBE-D3) binding to the surface of –148 and –100 kcal mol–1 for the L and M polymorphs is opposed by entropy effects of 37 and 25 kcal mol–1, respectively, combined with desolvation effects of 106 and 70 kcal mol–1, respectively, yielding free energies of formation of just –8 and –6 kcal mol–1, respectively. SAM formation is therefore associated with the near-complete cancellation of large SAM forming and SAM dissolving contributions, and subtle variations in this balance controls polymorphism.
As the L polymorph is observed to form at similar porphyrin concentrations over a wide range of chain lengths m, its free-energy of formation must change only slowly with m. In the asymptotic region of large m (> 15), the calculated chain-length dependences d(ΔG)/dm are shown in Table 5 evaluated using the QM/MM and PBE-D3 methods.[363] These dependences are also partitioned into the free-energy contributing components. As for the total free energies, these chain-length dependences show large cancelations between the contributing desolvation, entropy, and binding terms. Comparing the QM/MM and PBE-D3 methods, the QM/MM attraction term comes purely from the empirically fitted HOPG-alkane force field,[372] the AMBER inter-alkane force field,[373] the B3LYP description[374] of the intramolecular kinking energy, and the D3 dispersion contribution.[375,376] The empirical, AMBER, and B3LYP contributions would all be expected to be accurately determined. Hence the similar QM/MM and PBE-D3 results indicate that the D3 correction is also very reliable. The PBE-MBD method also gives similar results.[326] However, that these approaches predict very small total chain length dependences indicates that the explicit treatments used for the adsorbate–surface interactions compliment the dielectric-continuum calculations used to calculate the solvation of the molecule, bare surface, and SAM. These solvation calculations were based on the model of Floris et al.[377] and hence indicate that this implicit solvation formalism is highly compatible with D3 (and MBD).

|
In the broader context of Dobson’s description of dispersion forces in nanotechnology[314] described in Table 2, we note that this system involves large molecules with a delocalized central π system with attached alkane chains interacting with a metallic substrate. The molecules are essentially non-conductors, although when charged the central ring becomes internally conducting. According to Dobson’s analysis, methods like D3 based on summing interatomic London forces should be able to provide realistic descriptions of the chemistry, and the agreement found between D3, the empirical force field used that embodies screening, and the more general MBD approach supports this analysis. There are many applications in self-assembly that provide other examples of systems treatable by methods like D3. We have recently reviewed other applications elsewhere.[326]
Strong Localized Electron Correlation: Au–S Bonding, Gold Surface Protection, and Nanoparticle Synthesis
While the dispersion force was always known to be an example of electron correlation with profound consequences for molecular self-assembly, Craig’s first calculation of electron correlation has led in recent times to the discovery of new phenomena. The dispersion force between atoms scales somewhat in proportion to the product of the number of electrons on each atom, making it very important for heavy atoms. While such ideas have always been recognized in Pearson’s concept of hard/soft acids and bases,[378–381] that the dispersion force can be large enough to compete with covalent and ionic binding is just coming to be understood.[382,383] Sulfur-bound compounds SR stabilize gold surfaces and nanoparticles, and the chemical form has always been assumed to be AuI-thiolate, and many hemes are also stabilized in proteins by SR groups (like cysteines) that are assumed to be FeIII-thiolates, but ionic/covalent bonding is not necessary and Au0-thiyl or FeII-thiyl species are also possible. These are different chemical species, with different reactivities and spectroscopies. It has recently been shown that cytochrome FeII-thiyls can be formed,[383] and that Au0-thiyls are the species that actually protect gold surfaces and nanoparticles while AuI-thiolate production etches surfaces and inhibits nanoparticle formation.[382] The competition between covalent/ionic and van der Waals bonding is critical in each case, and Pearson’s ideas predict the main results as S and Au are soft while Fe can be either hard or soft. The Au–Au bond has always been regarded as anomalous, with the concept of ‘aurophilicity’ used to describe it,[384,385] but this is now known to be just the strong dispersion force acting on top of strong s–s interactions that make the gold atoms in a gold dimer more like those in gold metal than like isolated gold atoms.[386,387]
Understanding whether or not processes occur on the Au0-thiyl or AuI-thiolate potential-energy surfaces is essential to rationalizing the known synthetic chemistry and spectroscopy of gold surfaces and nanoparticles.[382] Work with Noel Hush (Sydney University) and Jens Ulstrup and Jingdong Zhang (Danish Technical University) has shown that gold (111) surfaces react with thiol or disulfide reagents to form initially ‘physisorbed’ species and then ‘chemisorbed’ ones (Scheme 1):

|
The SAM may take on two different types of atomic structure, either bound to gold adatoms above the surface or else bound directly to face centred cubic (FCC) surface sites, with the nature of the R group and the coverage determining which form.[388] For example, from among the butanethiol reagents, n-butanethiol,[389] iso-butanethiol,[390] and enantiomerically pure 2-butanethiol[391,392] bind to adatoms, but t-butanethiol binds to FCC sites[393,394] owing to strong steric repulsions in the adatom form and racemic 2-butanethiol shows both motifs in the same SAM[391,392] so as to maximize coverage; cysteamine in aqueous solution also binds to FCC sites owing to repulsion between the charged tail groups.[395]
Many properties of the two head-group arrangements are very similar despite the significant change in coordination, suggesting that the binding mechanism is similar in both cases. Also the binding strengths of the chemisorbed forms are not that much greater than those of the physisorbed forms[382,396] and are consistent with the binding of nitrogen and phosphorous bases to the surface, processes known to be controlled by the dispersion interaction. The postulate that both the ‘physisorption’ and ‘chemisorption’ processes depicted in the above reactions involve primarily dispersion forces and the Au0-thiyl valence state provides a consistent analysis of all of these data, including that for other chemical variations such as the replacement of Au with Ag or Cu and the replacement of S with O, Se, or Te.[382]
However, gold does not react with solutions containing thiolate anions RS–, but in an electrochemical cell in which AuI is produced at the anode and RS– at the cathode, the two species combine in solution to form AuI-thiolate compounds and thin films that then precipitate onto the surface (Scheme 2).[397]

|
AuI and thiolate ions are present as intermediates and their reaction produces an end product completely different to the protected SAM-covered surface produced by reactions with thiols and disulfides. Instead, this process parallels many known chemical reactions in solution that produce AuI-thiolate compounds and films and it is reasonable to assume that this is the type of chemistry that occurs whenever the AuI-thiolate potential-energy surface is engaged.
Sulfur protected gold nanoparticles can be formed using a range of synthetic conditions. We focus on what occurs under mild conditions in aqueous solution, and what occurs in the presence of excess strong reducing agents in non-aqueous media. In aqueous solution,[398] thiols reduce AuIII halide (X) salts to nanoparticles and cover them according to Scheme 3:
|
|
Thiolate anions are not reactants under these conditions, and, if the reaction follows known properties of the two-phase alternate Brust–Schiffrin synthesis[399] then the AuI intermediate [AuX2]– is implicated.[400–402] Of concern is how these results can be consistent with the details of the one-phase Brust–Schiffrin synthesis[403] in a 5 : 1 methanol/water solvent containing a large excess of the strong reducing agent NaBH4. AuI-thiolate molecular compounds can be isolated as intermediates that must be subsequently reduced by borohydride to form nanoparticles.[404] The only interpretation of these data consistent with the known Au(111) surface chemistry is that the one-phase Brust–Schiffrin reaction dominantly proceeds in three steps (Scheme 4):

|
This mechanism was verified by repeating the synthesis except for the omission of the AuIII salt.[382] The result was the conversion of the thiol used, hexanethiol, into hexanethiolate, showing that thiolate anions are indeed the active species in the reaction. Suggestions made during the Craig Lecture Tour by Sebastian Marcuccio from La Trobe University and Advanced Molecular Technologies that the produced thiolates complex the boron[405] as part of a thiolate storage mechanism,[406,407] even in solution in the reactive methanol solvent,[408] are currently being investigated. Under the mild conditions used in aqueous solution, radical pathways involving Au0-thiyl could dominate, whereas under conditions in which thiolate is produced, nanoparticles are not initially formed as the AuI-thiolate pathways lead to molecular compounds and films rather than stabilized nanoparticles.
In terms of bonding diagrams, the AuI-thiolate species involve covalent bonds formed between the s-electrons of isolated gold atoms and sulfur orbitals (Chart 3), whereas the Au0-thiyl species, prominent in compounds containing Au–Au bonds, involve strong interactions between filled Au d-orbitals and the sulfur (Chart 4) that affects bonding primarily through a strong Dobson-A effect, enhancing the dispersion interaction. The hybridization of the gold thus critically controls the bonding. When Au–Au bonds form, the resulting s–s interaction produces bonding and antibonding orbital combinations that are well removed from the Fermi energy and hence inaccessible to attacking reagents, making gold surfaces noble. In gold metal, the band broadening is sufficient to spread the occupied (‘valence’) and virtual (‘conduction’) bands so much that they weakly overlap, resulting in a low density of states at the Fermi energy that is responsible for the colour and conductivity of the solid.[385,409] For understanding chemical reactivity, the low density of states at the Fermi energy is the most critical property, however.

|

|
Sulfur bound to FCC sites clearly attaches to gold atoms having many Au–Au bonds, but the adatom-bound motif has traditionally[410–413] been drawn showing the adatom bound to only S and not to Au (Chart 5) and called the ‘staple’ motif.[414] In reality, there are also two direct Au–Au bonds (Chart 6) while superexchange through the S atoms makes for an effective four-bond system (Chart 7).[382] Hence the gold adatoms are tightly connected to the nanoparticle core and show similar broad s-bands.[382,415] While differences in the band structures of the adatoms do occur that are significant in terms of the total chemical structure, their similarity is enough for AuI-thiolates to be generally inhibited, becoming high-energy excited states of the protecting layer.

|

|

|
All spectroscopic studies clearly reflect the Au0-thiyl nature of the protecting layers of gold nanoparticles and surfaces. A direct experiment is X-ray photoelectron spectroscopy (XPS) which indicates that all atoms in the bulk and on the surface of gold nanoparticles are Au0 and not AuI.[399,404] Also the surface dipole moments measured for SAMs of SR groups and ammine groups on Au(111) have similar sign and magnitude, oriented so that the surface appears slightly negative and the ligands slightly positive.[416] For SR groups, this directionality arises because the only electropositive element in the interface is hydrogen and these atoms are located far from the surface, despite sulfur–gold bonds being polarized with slightly more bond electron density on sulfur than on gold.[416] This result follows directly from the Au0-thiyl nature of the surface and is opposite to that predicted if the surface was AuI-thiolate. Similarly, near-edge X-ray absorption fine structure (NEXAFS) measurements of SAMs[417] show electronic transitions to orbitals that are vacant in the Au0-thiyl description of the surface but already occupied in the AuI-thiolate description.[382] All DFT calculations show electronic structures of Au0-thiyl form,[415,417–426] with the sulfur orbitals mixing with gold d-orbitals as predicted only by the Au0-thiyl description.[415,417,421,427] Often DFT publications report the structure as being AuI-thiolate, however, reflecting not the nature of the orbitals generated but rather the most commonly used descriptions in the field at the time.
All chemical species involving Au–S bonds must show some degree of Au0-thiyl character and some degree of AuI-thiolate character as these two limiting valence forms mix via resonance in order to produce the ground and excited states of any system. The Au0-thiyl character must always be present as the dispersion interaction cannot be switched off, and the AuI-thiolate character must always be there as the gold s-band is continuous through the Fermi energy meaning that some covalent interactions with the s-orbitals must always occur. Also, in-equivalence of the gold and sulfur orbital energies means that some degree of ionic AuI-thiolate character must always be present through polarization effects. A simple way to understand the bonding is through an empirical partitioning scheme based on Hückel theory that partitions the binding energy into dispersion, covalent, and ionic contributions using a fitting parameter η specifying the hybridization of the gold orbital binding to the sulfur as d1-ηsη.[382] This yields values of η in the range of 0.75 to 1 for traditional AuI-thiolate molecular compounds, near 0.5 for reactive species likely to be seen in the early stages of nanoparticle growth, and below 0.2 for protected gold nanoparticles and surfaces. The elimination of AuI-thiolate character from the bonding is thus seen as a driving force for nanoparticle growth, this force resulting from the strength of the Au–Au bonds that form as the particles grow and become more noble in character.
Craig’s first calculation of electron correlation has led nearly 70 years later to the understanding that electron correlation does not just act to modify typical covalent and/or ionic bonds describable without it, nor just to provide the strong van der Waals force response for surface adhesion, protein structure, and other intermolecular interactions, but can also form bonds between atoms in its own right.
Conclusions
This article, describing the material presented in 26 lectures during 2016–17 as part of the David Craig Medal Lecture Tour, summarizes many of the important achievements of the later years of my life’s work, expressed in the context of advances made by David Craig, Noel Hush, Maxwell Crossley, Jens Ulstrup, and many others. It highlights that Craig’s Legacy remains alive and well in many current fields of Chemical Research.
* Jeffrey R. Reimers is the winner of the Australian Academy of Science David Craig Medal for 2016.
Acknowledgements
The author thanks the many senior scientists who have helped me in this work including: Roger Amos, George Bacskay, Evan Bieske, Steve Boxer, Pat Callis, Qijin Chi, Ron Clark, Charles Collyer, Paul Dastoor, Aldo Di Carlo, Hans Elemans, Marcus Elstner, Gad Fischer (honours supervisor), Mike Ford, Paul Franzon, Thomas Frauenheim, Arvi Freiberg, Shunichi Fukuzumi, Ken Ghiggino, Hong Guo, Casey Hynes, Rick Heller (postdoctoral supervisor), Mark Hersam, Karl Kadish, Bruce King, Rika Kobayashi, Michael Klein, Tony Lacey, Tony Larkum, Peter Lay, Len Lindoy, Alan Mark, Ross McKenzie, Josef Michl, Sture Nordholm, Fabian Pauly, Richard Payne, Alessandro Pecchia, Peter Politzer, Kei Ohkubo, Margus Rätsep, Alistair Rendell, Ian Ross (honurs supervisor), Greg Scholes, Phil Smith, Pali Thordarson, David Tozer, Adam Trevitt, Bob Watts (PhD supervisor), Paul Wormell, Kent Wilson (postdoctoral supervisor), and Jingdong Zhang, and the many students and postdoctoral fellows he has worked with including Ante Bilić, Ian Blake, Zhengli Cai, Peter Cafe, Peter Canfield, Ying Chin, Simon Craw, Mats Dahlbom, Deanna D’Alessandro, Olle Falköf, Chris Foster, Alessio Gagliardi, Lars Goerigk, Lachlan Hall, Jennifer Hayward, Jason Hughes, Michael Hutter, Tony Khoury, Nicholas Lambropoulos, Allan Larsen, Jimmy Lee, Laura McKemmish, Patty Nieuwenburg, Dwi Panduwinata, Runhai Ouyang, Wei Ren, Karina Sendt, Warwick Shapley, Paul Sintic, Gemma Solomon, Johan Visser, Brett Wallace, Yun Wang, Peter Weber, Asaph Widmer-Cooper, Soren Wohlthat, Shuwei Xia, Shiwei Yin, and Jun Zeng.
References
[1] https://en.wikipedia.org/wiki/David_P._Craig. Accessed 23 October 2016.[2] https://www.science.org.au/learning/general-audience/history/interviews-australian-scientists/professor-david-craig-1919-2015. Accessed 23 October 2016.
[3] http://www.iaqms.org/members/craig.php. Accessed 23 October 2016.
[4] http://chemistry.anu.edu.au/about-us/history. Accessed 23 October 2016.
[5] https://www.science.org.au/news-and-events/news-and-media-releases/vale-former-academy-president-david-craig. Accessed 23 October 2016.
[6] G. Fischer, R. G. Gilbert, Hist. Rec. Aust. Sci. 2009, 20, 91.
| Crossref | GoogleScholarGoogle Scholar |
[7] http://academic.research.microsoft.com/Author/53681842/gad-fischer. Accessed 23 October 2016.
[8] https://www.science.org.au/opportunities-scientists/recognition/honorific-awards/career-awards/david-craig-medal. Accessed 23 October 2016.
[9] V. Fock, Z. Phys. 1930, 62, 795.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaA3cXkvVehsA%3D%3D&md5=092e37fd81607632dd65efa86f12dfe1CAS |
[10] M. Born, R. Oppenheimer, Ann. Phys. 1927, 389, 457.
| Crossref | GoogleScholarGoogle Scholar |
[11] E. U. Condon, Phys. Rev. 1928, 32, 858.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaB1MXit1CisQ%3D%3D&md5=501ff5098c2553229e7413f89a9962d5CAS |
[12] G. Herzberg, E. Teller, Z. Phys. Chem. 1933, 21, 410.
[13] R. G. Parr, D. P. Craig, I. G. Ross, J. Chem. Phys. 1950, 18, 1561.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3MXjsV2rtQ%3D%3D&md5=5fae7d574a5bd63f1f90d89f1f9cab96CAS |
[14] D. P. Craig, J. Chem. Soc. 1950, 2146.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3MXlsF2h&md5=d770ca99664399c542285a4a7f6da26cCAS |
[15] D. P. Craig, J. Chem. Soc. 1950, 59.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3cXis1Omsw%3D%3D&md5=fff71f6e39167a9150cd78c3fd6ecb65CAS |
[16] M. A. Nielsen, I. L. Chuang, Quantum Computation and Quantum Information 2000 (Cambridge University Press: New York, NY).
[17] J. R. Reimers, R. O. Watts, M. L. Klein, Chem. Phys. 1982, 64, 95.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL38XptF2ltA%3D%3D&md5=6c55d4f9758b804eda5d51d31d5cc92cCAS |
[18] J. R. Reimers, R. O. Watts, Chem. Phys. 1984, 85, 83.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2cXhsVGgsLc%3D&md5=5f8db2c702504f856cfcd6bcbdb5a6a2CAS |
[19] J. R. Reimers, R. O. Watts, Mol. Phys. 1984, 52, 357.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2cXks1SnsLY%3D&md5=6160a2e3e00665e69afb33c27c105a8bCAS |
[20] J. R. Reimers, R. O. Watts, Chem. Phys. 1984, 91, 201.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXltFWmsw%3D%3D&md5=2a741974aaf33c92127937277ecb2598CAS |
[21] J. R. Reimers, K. R. Wilson, E. J. Heller, J. Chem. Phys. 1983, 79, 4749.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3sXmt1Wmsbo%3D&md5=63e40acee026e4c07eeecd75cf492cfdCAS |
[22] J. P. Bergsma, J. R. Reimers, K. R. Wilson, J. T. Hynes, J. Chem. Phys. 1986, 85, 5625.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXpslGq&md5=b74b61fe966d44b12b0564e1e8627b4cCAS |
[23] E. J. Heller, J. R. Reimers, G. Drolshagen, Phys. Rev. A 1987, 36, 2613.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXmtVGntb0%3D&md5=70cdb4828d23aebb3e5a374015e29bf3CAS |
[24] J. R. Reimers, E. J. Heller, J. Phys. Chem. 1988, 92, 3225.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXit1Ojsbc%3D&md5=ccf2f39c26cd70fe66aee7c96966e35bCAS |
[25] http://academic.research.microsoft.com/Author/24242960/robert-o-watts. Accessed 23 October 2016.
[26] http://ucsdnews.ucsd.edu/archive/newsrel/science/mcwilson.htm. Accessed 23 October 2016.
[27] https://en.wikipedia.org/wiki/Eric_J._Heller. Accessed 23 October 2016.
[28] https://en.wikipedia.org/wiki/Noel_Hush. Accessed 23 October 2016.
[29] http://academic.research.microsoft.com/Author/18374060/maxwell-j-crossley. Accessed 23 October 2016.
[30] S. B. Piepho, E. R. Krausz, P. N. Schatz, J. Am. Chem. Soc. 1978, 100, 2996.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE1cXktFCgt74%3D&md5=71830163a6519b504098cebcbeaf12b8CAS |
[31] R. L. Fulton, M. Gouterman, J. Chem. Phys. 1961, 35, 1059.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF38Xkt1enug%3D%3D&md5=7e632994a62a2c8198de849225cbf00fCAS |
[32] N. S. Hush, Prog. Inorg. Chem. 1967, 8, 391.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF1cXhtVSjsbY%3D&md5=ac192973eb8ec1da596eef8eedf3072eCAS |
[33] D. P. Craig, J. Chem. Phys. 1950, 18, 236.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3cXis1Omsg%3D%3D&md5=7208092d0aff3c75c73abd411c980378CAS |
[34] C. W. L. Bevan, D. P. Craig, Trans. Faraday Soc. 1951, 47, 564.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3MXlvFWisw%3D%3D&md5=686b9930de5fba08c3fbc0bf1146492bCAS |
[35] D. P. Craig, L. E. Lyons, Nature 1952, 169, 1102.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG38XlvFOnuw%3D%3D&md5=2f8196c4d27eb63e4dc6054ddce79ebcCAS |
[36] D. P. Craig, Nature 1946, 158, 235.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH28Xjt1Oqsw%3D%3D&md5=39eed99c9b755b32900e2a09921798d3CAS |
[37] D. P. Craig, J. Chem. Phys. 1949, 17, 1358.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3cXis1CltQ%3D%3D&md5=a4989cd41a97a5584210a6fe22eba478CAS |
[38] D. P. Craig, L. E. Lyons, J. Chem. Phys. 1952, 20, 1499.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG38XmsFCnsA%3D%3D&md5=e4bf54219d6738228b1bee2494a313f9CAS |
[39] D. P. Craig, P. C. Hobbins, Nature 1953, 171, 566.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3sXktlOjtA%3D%3D&md5=0778e617bcbd483e34ce08d76e09c86fCAS |
[40] D. P. Craig, N. L. Paddock, Nature 1958, 181, 1052.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG1cXhtVeksbY%3D&md5=d541cf5ff2744ce8a6f4c146ec3c3ae7CAS |
[41] D. P. Craig, J. Chem. Phys. 1948, 16, 158.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH1cXhs1yqtw%3D%3D&md5=6cd5dc58550896aee76c65b11181ecd8CAS |
[42] D. P. Craig, A. Maccoll, Nature 1948, 161, 481.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH1cXitV2lsA%3D%3D&md5=1037bed005ec8ef9fea1bcc70abb05aeCAS | 18933225PubMed |
[43] D. P. Craig, A. Maccoll, J. Chem. Soc. (Resumed) 1949, 964.
| Crossref | GoogleScholarGoogle Scholar |
[44] D. P. Craig, J. R. Walsh, J. Chem. Phys. 1956, 25, 588.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG2sXlslM%3D&md5=09a24208147dee2cd11d623eb07119a3CAS |
[45] D. P. Craig, J. R. Walsh, J. Chem. Phys. 1956, 24, 471.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG28XjtFSmug%3D%3D&md5=93d5926d9038b05b6c52e60a538929a6CAS |
[46] D. P. Craig, J. R. Walsh, J. Chem. Soc. (Resumed) 1958, 1613.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG1cXotV2juw%3D%3D&md5=0b2b31b9a8274cb8b54f3752eb7f847eCAS |
[47] J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg, E. Krausz, Sci. Rep. 2013, 3, 2761.
| Crossref | GoogleScholarGoogle Scholar | 24067303PubMed |
[48] G. D. Scholes, G. R. Fleming, A. Olaya-Castro, R. van Grondelle, Nat. Chem. 2011, 3, 763.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXht1ajurzF&md5=a6037749fddd54f4d23ecf0354684ae8CAS | 21941248PubMed |
[49] R. E. Blankenship, Molecular Mechanisms of Photosynthesis (2nd edn) 2014 (Wiley-Blackwell: Oxford).
[50] J. R. Reimers, M. Biczysko, D. Bruce, D. F. Coker, T. J. Frankcombe, H. Hashimoto, J. Hauer, R. Jankowiak, T. Kramer, J. Linnanto, F. Mamedov, F. Müh, M. Rätsep, T. Renger, S. Styring, J. Wan, Z. Wang, Z.-Y. Wang-Otomo, Y.-X. Weng, C. Yang, J.-P. Zhang, A. Freiberg, E. Krausz, Biochim. Biophys. Acta, Bioenerg. 2016, 1857, 1627.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XhtFSgt7bJ&md5=43e5111f62210668dd98eccf8f9cb4f3CAS |
[51] M. Gouterman, G. H. Wagnière, L. C. Snyder, J. Mol. Spectrosc. 1963, 11, 108.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF3sXkslaltLg%3D&md5=3480e38f93a630d8603a4f8d44891404CAS |
[52] R. L. Fulton, M. Gouterman, J. Chem. Phys. 1964, 41, 2280.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF2cXkslektLs%3D&md5=2102a9e662e4fa1b35631517f4febc96CAS |
[53] M. Gouterman, in The Porphyrins (Ed. D. Dolphin) 1978, Ch. 1, pp. 1–165 (Academic Press: New York, NY).
[54] M. Gouterman, J. Chem. Phys. 1965, 42, 351.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF2MXhvFKrug%3D%3D&md5=573bb76268bf55e3313d035dd02334c3CAS |
[55] I. G. Ross, Isr. J. Chem. 1975, 14, 118.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE28Xhsl2gu7o%3D&md5=08b76ae33cfcd8131a6585ef8bd1f55dCAS |
[56] G. Fischer, Vibronic Coupling 1984 (Academic Press: London).
[57] G. Fischer, J. R. Reimers, I. G. Ross, Chem. Phys. 1981, 62, 187.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL38Xis1GgtQ%3D%3D&md5=0ea04cd4d2b92be940ebecf54405cf6eCAS |
[58] P. J. Chappell, G. Fischer, J. R. Reimers, I. G. Ross, J. Mol. Spectrosc. 1981, 87, 316.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3MXksFWrt7c%3D&md5=dab55ec13d0b000a60bf56efd44c4d87CAS |
[59] K. K. Rebane, R. A. Avarmaa, Chem. Phys. 1982, 68, 191.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL38Xks1ems70%3D&md5=02142b56e85d4fd6d19e312a0751f2e3CAS |
[60] R. A. Avarmaa, A. Suisalu, Opt. Spectrosc. 1984, 56, 54.
[61] R. A. Avarmaa, K. K. Rebane, Spectrochim. Acta A 1985, 41, 1365.
| Crossref | GoogleScholarGoogle Scholar |
[62] I. Renge, K. Mauring, P. Sarv, R. Avarmaa, J. Phys. Chem. 1986, 90, 6611.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28XmtVKns7s%3D&md5=6d537f3144645e6b5ad933b0ec2c273bCAS |
[63] M. Umetsu, Z.-Y. Wang, M. Kobayashi, T. Nozawa, Biochim. Biophys. Acta, Bioenerg. 1999, 1410, 19.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXht1KmsLs%3D&md5=fa288aa738276e0eee82ff994a15c541CAS |
[64] M. Rätsep, J. Linnanto, A. Freiberg, J. Chem. Phys. 2009, 130, 194501.
| Crossref | GoogleScholarGoogle Scholar | 19466837PubMed |
[65] Y. Nonomura, S. Igarashi, N. Yoshioka, H. Inoue, Chem. Phys. 1997, 220, 155.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXkt1Sit74%3D&md5=37eaf9ae5bdb2c02a0eb9059a28bfe3bCAS |
[66] M. Helfrich, B. Bommer, U. Oster, H. Klement, K. Mayer, A. W. D. Larkum, W. Rüdiger, Biochim. Biophys. Acta, Bioenerg. 2003, 1605, 97.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXlvFyit7o%3D&md5=5784506a0197521cd513a3f08d1a44a6CAS |
[67] J. L. Hughes, B. Conlon, T. Wydrzynski, E. Krausz, Phys. Procedia 2010, 3, 1591.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXisl2lsbo%3D&md5=3ea51acf401c228c5c02309cda643df7CAS |
[68] S. Yin, M. G. Dahlbom, P. J. Canfield, N. S. Hush, R. Kobayashi, J. R. Reimers, J. Phys. Chem. B 2007, 111, 9923.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXotlOjtLs%3D&md5=7b1f2b8265e194f2c93433e12886b5eaCAS | 17672486PubMed |
[69] M. Fragata, B. Norden, T. Kurucsev, Photochem. Photobiol. 1988, 47, 133.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXnt1ertA%3D%3D&md5=87380b52a3f22d4b5f5c9a1e4ca26023CAS |
[70] M. Umetsu, Z.-Y. Wang, T. Nozawa, Recent Res. Dev. Phys. Chem. 2001, 5, 185.
| 1:CAS:528:DC%2BD38XivFyiu7k%3D&md5=274b87d0a1a06ce67606dfc7182cd72aCAS |
[71] M. Umetsu, Z.-Y. Wang, K. Yoza, M. Kobayashi, T. Nozawa, Biochim. Biophys. Acta, Bioenerg. 2000, 1457, 106.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXisFKisrw%3D&md5=affe26a09de9d9b483d89c84f0dc13c8CAS |
[72] D. Sundholm, Chem. Phys. Lett. 1999, 302, 480.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXhvV2gtLs%3D&md5=6eba87049e02fed68971612b5adadc6fCAS |
[73] D. Sundholm, Chem. Phys. Lett. 2000, 317, 545.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXhtFahtrs%3D&md5=66b511e45b70b01e109d8b46e0329c14CAS |
[74] J. D. Bene, H. H. Jaffè, J. Chem. Phys. 1968, 48, 1807.
| Crossref | GoogleScholarGoogle Scholar |
[75] M. C. Zerner, G. H. Loew, R. F. Kirchner, U. T. Mueller-Westerhof, J. Am. Chem. Soc. 1980, 102, 589.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3cXosFSkug%3D%3D&md5=e0eda80a485a8cde7a227fb5854fb516CAS |
[76] J. Zeng, N. S. Hush, J. R. Reimers, J. Am. Chem. Soc. 1996, 118, 2059.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XovFGjtA%3D%3D&md5=38b896df83c13ab24ca97075071b5a4bCAS |
[77] J. Zeng, N. S. Hush, J. R. Reimers, J. Phys. Chem. 1996, 100, 19292.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XntVWmt78%3D&md5=cff565ba062514c7c44857bba7a494e7CAS |
[78] N. S. Hush, J. R. Reimers, Coord. Chem. Rev. 1998, 177, 37.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXjtV2qsw%3D%3D&md5=8f8b18d737a2a40245e943e20808e2d0CAS |
[79] N. S. Hush, J. R. Reimers, Chem. Rev. 2000, 100, 775.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXms1Gn&md5=6669a15dc323ce5fe93e5339cea203eaCAS | 11749250PubMed |
[80] J. R. Reimers, N. S. Hush, J. Phys. Chem. B 2001, 105, 8979.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXlslyqu7c%3D&md5=94fe1125997899696964f1bd2a29accdCAS |
[81] G. C. Solomon, J. R. Reimers, N. S. Hush, J. Chem. Phys. 2004, 121, 6615.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXotVKms74%3D&md5=7eef4ab949e7b13a11bb5a5616b2cc0cCAS | 15473716PubMed |
[82] B. Tejerina, J. Reimers, nanoHUB 2008. Available at www.nanohub.org. Accessed 23 October 2016.
[83] R. Bauernschmitt, R. Ahlrichs, Chem. Phys. Lett. 1996, 256, 454.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XksFWltrs%3D&md5=ce3afb1a4b786d601824ba48f4430c9eCAS |
[84] J. R. Reimers, Z.-L. Cai, A. Bilic, N. S. Hush, Ann. N. Y. Acad. Sci. 2003, 1006, 235.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXpvVaquw%3D%3D&md5=3f136935e7d10432d047ed0d92eb6b69CAS | 14976022PubMed |
[85] Z.-L. Cai, J. R. Reimers, J. Chem. Phys. 2000, 112, 527.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXit12quw%3D%3D&md5=2e0f6ca184092d05309818cae96aaa12CAS |
[86] Z.-L. Cai, D. J. Tozer, J. R. Reimers, J. Chem. Phys. 2000, 113, 7084.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXnsFSrtrY%3D&md5=1fd39166b879760cd91679d9f0865d6aCAS |
[87] Z.-L. Cai, K. Sendt, J. R. Reimers, J. Chem. Phys. 2002, 117, 5543.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XmvVSgsr8%3D&md5=ea9f56607cb330c57ed9ad13ff057f14CAS |
[88] M. G. Dahlbom, J. R. Reimers, Mol. Phys. 2005, 103, 1057.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXjsF2mtrc%3D&md5=70c6642cd5c92143d621b3b55db27051CAS |
[89] T. Yanai, D. P. Tew, N. C. Handy, Chem. Phys. Lett. 2004, 393, 51.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXlsFKgtbs%3D&md5=b62eb59c694a178aa43858fe34ac9f1eCAS |
[90] R. Kobayashi, R. D. Amos, Chem. Phys. Lett. 2006, 420, 106.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28Xhslyqs7s%3D&md5=4978b043cf893a5d569851edabcf17bbCAS |
[91] Z.-L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi, R. D. Amos, J. Phys. Chem. B 2006, 110, 15624.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XmvFWhtr4%3D&md5=1d6c83386d5e710cfffb8b8a1b05a75fCAS | 16884287PubMed |
[92] P. Canfield, M. G. Dahlbom, J. R. Reimers, N. S. Hush, J. Chem. Phys. 2006, 124, 024301.
| Crossref | GoogleScholarGoogle Scholar | 16422577PubMed |
[93] M. Rätsep, Z.-L. Cai, J. R. Reimers, A. Freiberg, J. Chem. Phys. 2011, 134, 024506.
| Crossref | GoogleScholarGoogle Scholar | 21241119PubMed |
[94] J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg, E. Krausz, AIP Conf. Proc. 2014, 1618, 18.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhslartL%2FO&md5=8eb46df6bee003a980de71985431f878CAS |
[95] J. R. Reimers, E. Krausz, Phys. Chem. Chem. Phys. 2014, 16, 2315.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXlvF2itA%3D%3D&md5=94fcd118d3314637957dc8f5d4e07dcfCAS | 24346310PubMed |
[96] J. R. Reimers, R. O. Watts, Chem. Phys. Lett. 1983, 94, 222.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3sXotVyhtw%3D%3D&md5=62076375428e831bfc8aad288244f698CAS |
[97] J. R. Reimers, K. R. Wilson, E. J. Heller, S. R. Langhoff, J. Chem. Phys. 1985, 82, 5064.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXkt12gs7c%3D&md5=21e27d28cebd3f02c554c7c3ea00f5c7CAS |
[98] http://science.nasa.gov/missions/galileo/. Accessed 23 October 2016.
[99] J. R. Reimers, N. S. Hush, J. Am. Chem. Soc. 2004, 126, 4132.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXitValsr0%3D&md5=ea3d6c98858b9c9c4d36a8fdb83c0c93CAS | 15053603PubMed |
[100] J. R. Reimers, N. S. Hush, J. Chem. Phys. 2003, 119, 3262.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXlvVWksrc%3D&md5=6ca509d429e19ccac39ed449b671f818CAS |
[101] J. R. Reimers, J. M. Hughes, N. S. Hush, Biochemistry 2000, 39, 16185.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXotl2ns7w%3D&md5=fc4a0d2d6ca48a30fab01a9cecb6bd03CAS | 11123947PubMed |
[102] O. Kanchanawong, M. G. Dahlbom, T. P. Treynor, J. R. Reimers, N. S. Hush, S. G. Boxer, J. Phys. Chem. B 2006, 110, 18688.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28Xoslyjs7s%3D&md5=eca7f013f3bf65150f583777bc0b48ebCAS |
[103] J. Breton, E. Nabedryk, W. W. Parson, Biochemistry 1992, 31, 7503.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK38XltVygtb4%3D&md5=6fb97be3703473ef1db0220ef954e490CAS | 1510937PubMed |
[104] J. R. Reimers, N. S. Hush, J. Am. Chem. Soc. 1995, 117, 1302.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXjtF2qsLo%3D&md5=0e5854c172f5c9204e15d17d5ceb74ceCAS |
[105] J. R. Reimers, W. A. Shapley, N. S. Hush, J. Chem. Phys. 2003, 119, 3240.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXlvVWksrk%3D&md5=81d383605cad3fcbd831cbca990ab563CAS |
[106] J. M. Hughes, M. C. Hutter, J. R. Reimers, N. S. Hush, J. Am. Chem. Soc. 2001, 123, 8550.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXlslCktrc%3D&md5=b155d14787f1663b6260009a8df2cb7dCAS | 11525663PubMed |
[107] J. R. Reimers, N. S. Hush, Chem. Phys. 1996, 208, 177.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28Xkt12rsbg%3D&md5=0a707da2216335e60df4f76b901998d8CAS |
[108] J. R. Reimers, N. S. Hush, Chem. Phys. 2004, 299, 79.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhslWhtbk%3D&md5=9916f2edd5300e6dcb17ce5a0a619808CAS |
[109] J. R. Reimers, Z.-L. Cai, R. Kobayashi, M. Rätsep, A. Freiberg, E. Krausz, Phys. Chem. Chem. Phys. 2014, 16, 2323.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXlvF2itw%3D%3D&md5=a84cd90a87de143d713c80ffe4e95b11CAS | 24352346PubMed |
[110] R. Kobayashi, J. R. Reimers, Mol. Phys. 2015, 16, 928.
[111] F. London, Z. Phys. 1928, 46, 455.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaB1cXhtlSmsA%3D%3D&md5=ccc05298dc2819f0c34ccf9bc9c14d67CAS |
[112] H. Eyring, M. Polanyi, Z. Phys. Chem. Abt. B 1931, 12, 279.
| 1:CAS:528:DyaA3MXjtF2msw%3D%3D&md5=92ceecf97f9b3179c4fc69a2b271edbdCAS |
[113] M. G. Evans, M. Polanyi, Trans. Faraday Soc. 1938, 34, 11.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaA1cXitVWisg%3D%3D&md5=b35fc37261d53efd1dbb7a1fb60c4489CAS |
[114] J. Horiuti, M. Polanyi, J. Mol. Catalysis A 2003, 199, 185. [translation of Acta Physicochimica U.R.S.S. 1935, 2, 505].
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXjsVGmu7w%3D&md5=137674abb3619afb54736c72c8c0a8adCAS |
[115] F. T. Wall, G. Glockler, J. Chem. Phys. 1937, 5, 314.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaA2sXjt1KntA%3D%3D&md5=fd1f34e9a05e16a62608c72e77554cd6CAS |
[116] N. S. Hush, J. Polym. Sci., Polym. Phys. Ed. 1953, 11, 289.
| 1:CAS:528:DyaG2cXitVyltA%3D%3D&md5=b4ff1d508461ed9390348a753d9ac661CAS |
[117] F. London, Z. Phys. 1932, 74, 143.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaA38XjtVWqtg%3D%3D&md5=bbb3a22c036ba106ef579dcd5fa54ad7CAS |
[118] C.-H. Yang, C.-P. Hsu, J. Chem. Phys. 2013, 139, 154104.
| Crossref | GoogleScholarGoogle Scholar | 24160497PubMed |
[119] C. Butchosa, S. Simon, L. Blancafort, A. Voityuk, Phys. Chem. Chem. Phys. 2014, 16, 17154.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhtVOnurvN&md5=9b3ae3661c8ba9c16b280a010e383ff5CAS | 25010229PubMed |
[120] A. A. Voityuk, Phys. Chem. Chem. Phys. 2012, 14, 13789.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38Xhtl2ru7fI&md5=acfa89b0383af703881e87a4b10c2e8fCAS | 22513425PubMed |
[121] S. Hammes-Schiffer, Energy Environ. Sci. 2012, 5, 7696.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XptVWrsLs%3D&md5=675e463803e074ec1fe8eec76ff276bbCAS |
[122] R. A. Marcus, N. Sutin, Biochim. Biophys. Acta 1985, 811, 265.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXltFygs78%3D&md5=b2ad270dfef9603bb5bee958d43dfc8cCAS |
[123] M. K. Johnson, R. B. King, D. M. Kurtz Jr, C. Kutal, M. L. Norton, R. A. Scott, Electron Transfer in Biology and the Solid State 1989 (American Chemical Society: Washington DC).
[124] A. A. Kornyshev, M. Tosi, J. Ulstrup, Electron and Ion Transfer in Condensed Media 1997 (World Scientific: Singapore).
[125] S. Isied, Electron Transfer Reactions 1997 (American Chemical Society: Washington DC).
[126] A. Kutnetsov, J. Ulstrup, Electron Transfer in Chemistry and Biology 1999 (Wiley: Hoboken, NJ).
[127] V. Balzani, Electron Transfer in Chemistry. Principles, Theories, Methods and Techniques 2001 (Wiley-VCH: Hoboken, NJ).
[128] A. Nitzan, Annu. Rev. Phys. Chem. 2001, 52, 681.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXksFKlsLk%3D&md5=e5b00322dfdc91b4310c9400d58e0e9dCAS | 11326078PubMed |
[129] D. M. Guldi, Chem. Soc. Rev. 2002, 31, 22.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xhslenuro%3D&md5=674029cfceafe75b8085974a564abc1dCAS | 12108980PubMed |
[130] T. W. Marin, B. J. Homoelle, K. G. Spears, J. T. Hupp, L. O. Spreer, J. Phys. Chem. A 2002, 106, 1131.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xns1KltQ%3D%3D&md5=ae6a24c530f578c5230b14273139653aCAS |
[131] E. A. Plummer, J. I. Zink, Inorg. Chem. 2006, 45, 6556.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XnsFemu78%3D&md5=dd39a2c773c594c53f6b660717a0afefCAS | 16903698PubMed |
[132] S. F. Nelsen, Adv. Phys. Org. Chem. 2006, 41, 183.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXmslOjsL8%3D&md5=0834fdab711db40e0a38d7f730dbf053CAS |
[133] V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey, J. L. Brédas, Chem. Rev. 2007, 107, 926.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXjt1ymsb8%3D&md5=9b42f711f56d28ec98b3ab95b75d96daCAS | 17378615PubMed |
[134] A. P. Hines, C. M. Dawson, R. H. McKenzie, G. J. Milburn, Phys. Rev. A 2004, 70, 022303.
| Crossref | GoogleScholarGoogle Scholar |
[135] L. K. McKemmish, R. H. McKenzie, N. S. Hush, J. R. Reimers, J. Chem. Phys. 2011, 135, 244110.
| Crossref | GoogleScholarGoogle Scholar | 22225147PubMed |
[136] Z. Vager, Chem. Phys. Lett. 1997, 273, 407.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXkslaqsbY%3D&md5=44e5de6ee794ed492a03407140f2cbaeCAS |
[137] J. Trost, K. Hornberger, Phys. Rev. Lett. 2009, 103, 023202.
| Crossref | GoogleScholarGoogle Scholar | 19659202PubMed |
[138] J. C. Polanyi, A. H. Zewail, Acc. Chem. Res. 1995, 28, 119.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXjvFOkt7g%3D&md5=a2255fd3024e41940f2b1de73a8f1329CAS |
[139] I. B. Bersuker, Chem. Rev. 2001, 101, 1067.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXhslagsLY%3D&md5=72325426a68c44c31c86e7700007e2b8CAS | 11709858PubMed |
[140] I. B. Bersuker, Chem. Rev. 2013, 113, 1351.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXms1yisg%3D%3D&md5=43d4ff3a7a6b0531728afbf83fbebdaeCAS | 23301718PubMed |
[141] J. Ma, X. Zhu, H. Guo, D. R. Yarkony, J. Chem. Phys. 2012, 137, 22A541.
| 23249078PubMed |
[142] X. Xu, K. R. Yang, D. G. Truhlar, J. Chem. Theory Comput. 2013, 9, 3612.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXpsVOnu7w%3D&md5=a10f04ff3b18bba1eaa36f4510269118CAS | 26584115PubMed |
[143] X. Zhu, D. R. Yarkony, J. Chem. Phys. 2014, 140, 024112.
| Crossref | GoogleScholarGoogle Scholar | 24437870PubMed |
[144] J. Dillon, D. R. Yarkony, J. Phys. Chem. A 2013, 117, 7344.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXmt1emt78%3D&md5=3daecc7df2afdfcc8ad46b7d8d40fbc3CAS | 23600519PubMed |
[145] K. R. Yang, X. Xu, J. Zheng, D. G. Truhlar, Chem. Sci. 2014, 5, 4661.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXht1yltLzJ&md5=0769b35fbb2d47dc088d36b641bbca7cCAS |
[146] L. Zhou, B. Jiang, D. Xie, H. Guo, J. Phys. Chem. A 2013, 117, 6940.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhslOls7jF&md5=4509941c224e5dcc109bc5b1c5f261c4CAS | 23210666PubMed |
[147] C. Xie, J. Ma, X. Zhu, D. H. Zhang, D. R. Yarkony, D. Xie, H. Guo, J. Phys. Chem. Lett. 2014, 5, 1055.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXjvFSjtLs%3D&md5=ab8aaa29bccd3ba51fe9869fd60f87b8CAS | 26274448PubMed |
[148] W. Eisfeld, O. Vieuxmaire, A. Viel, J. Chem. Phys. 2014, 140, 224109.
| Crossref | GoogleScholarGoogle Scholar | 24929376PubMed |
[149] P. Politzer, J. R. Reimers, J. S. Murray, A. Toro-Labbe, J. Phys. Chem. Lett. 2010, 1, 2858.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhtFGhsbvM&md5=ec593f245d85680c1c90c9ecfcd44fccCAS |
[150] S. Zilberg, Y. Haas, D. Danovich, S. Shaik, Angew. Chem. Int. Ed. 1998, 37, 1394.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXjvFGjt74%3D&md5=571ebade13d549b371e3b129002cb156CAS |
[151] S. Shaik, S. Zilberg, Y. Haas, Acc. Chem. Res. 1996, 29, 211.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XisVymurc%3D&md5=912d198965ddebc356b918ac59f36421CAS |
[152] S. Shaik, A. Shurki, D. Danovich, P. C. Hiberty, J. Am. Chem. Soc. 1996, 118, 666.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XitFSmuw%3D%3D&md5=23d7aa76e11ab67329af06f8da0c47d7CAS |
[153] S. Shaik, A. Shurki, D. Danovich, P. C. Hiberty, Chem. Rev. 2001, 101, 1501.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXis1Sqtrc%3D&md5=227be37398d52e172619dc2aa2a38aedCAS | 11710231PubMed |
[154] S. Zilberg, Y. Haas, J. Phys. Chem. A 2011, 115, 10650.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtFSmt7vO&md5=b38219d2ff0cd701f7991bea037826acCAS | 21851061PubMed |
[155] N. S. Hush, Z. Elektrochem. Angew. Phys. Chem. 1957, 61, 734.
| 1:CAS:528:DyaG2sXovFCqtw%3D%3D&md5=170d46a4a478c99d4d2ce79e84f8dee0CAS |
[156] N. S. Hush, J. Chem. Phys. 1958, 28, 962.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG1cXptFKitA%3D%3D&md5=fe0264481c4e69072ae01a448208a3b3CAS |
[157] N. S. Hush, Discuss. Faraday Soc. 1960, 29, 113.
| Crossref | GoogleScholarGoogle Scholar |
[158] N. S. Hush, in Soviet Electrochemistry: Proceedings of the Fourth Conference on Electrochemistry 1956 (Ed. A. N. Frumkin) 1961, Vol. 1, pp. 99–100 (Consultants Bureau: New York, NY).
[159] N. S. Hush, J. Electroanal. Chem. 1999, 460, 5.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXhs1Sls7c%3D&md5=6a31270971192e75302681f4d56212ffCAS |
[160] R. A. Marcus, Annu. Rev. Phys. Chem. 1964, 15, 155.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF2cXkslaksro%3D&md5=ce7e78457a63e868120acad200b101cfCAS |
[161] J. M. Warman, M. P. d. Haas, M. N. Paddon-Row, E. Cotsaris, N. S. Hush, H. Oevering, J. W. Verhoeven, Nature 1986, 320, 615.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28Xkt1Wru74%3D&md5=8a4242635f268a485cdb79832d677d72CAS |
[162] J. R. Reimers, N. S. Hush, Chem. Phys. 1990, 146, 105.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXjt1ylsA%3D%3D&md5=083c05ae0d0243a725693984eb5895a0CAS |
[163] J. R. Reimers, N. S. Hush, D. Sameth, P. R. Callis, Chem. Phys. Lett. 1990, 169, 622.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXls1Wmt7s%3D&md5=646025680bdfe50ceafe6d7fa47c94ddCAS |
[164] J. R. Reimers, N. S. Hush, Chem. Phys. 1989, 134, 323.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1MXlvVWrsrc%3D&md5=5a42f7522dfb69432cc7d321df5a120fCAS |
[165] J. R. Reimers, N. S. Hush, J. Photochem. Photobiol. Chem. 1994, 82, 31.
| Crossref | GoogleScholarGoogle Scholar |
[166] J. R. Reimers, N. S. Hush, Chem. Phys. 1990, 146, 89.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXmtFyqtrw%3D&md5=a90d4c058fadebb8821c3c0634a40205CAS |
[167] J. R. Reimers, N. S. Hush, J. Phys. Chem. 1991, 95, 9773.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXms1Gktr4%3D&md5=cb1e9273e8d9b748a4466c603c3e9d7aCAS |
[168] J. R. Reimers, N. S. Hush, in Mixed Valence Systems: Applications in Chemistry, Physics, and Biology (Ed. K. Prassides) 1991, Ch. 2, pp. 29–50 (Kluwer Academic Publishers: Dordrecht).
[169] N. S. Hush, J. R. Reimers, J. Phys. Chem. 1995, 99, 15798.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXosVKqtro%3D&md5=b3e7548156cf086a7004624b680c6dc7CAS |
[170] D. J. Lockhart, S. G. Boxer, Biochemistry 1987, 26, 664.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXmsVCmtQ%3D%3D&md5=c87e8ac8b08f6022fb8f9bced8a63a71CAS |
[171] D. J. Lockhart, R. F. Goldstein, S. G. Boxer, J. Phys. Chem. 1988, 89, 1408.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXlsVKnurg%3D&md5=1d6e5b9336b7bb9fd9264116cbe89348CAS |
[172] M. A. Steffen, K. Lao, S. G. Boxer, Science 1994, 264, 810.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXjtF2lt78%3D&md5=2a4cbaa5b48392b94258cc95ed28f4a6CAS | 17794722PubMed |
[173] K. Lao, L. J. Moore, H. Zhou, S. G. Boxer, J. Phys. Chem. 1995, 99, 496.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXivVeqt7Y%3D&md5=2795af2c44dd31ff271660ade6753674CAS |
[174] L. M. P. Beekman, M. Steffen, I. H. M. van Stokkum, J. D. Olsen, C. N. Hunter, S. G. Boxer, R. van Grondelle, J. Phys. Chem. B 1997, 101, 7284.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXlsVSnu7c%3D&md5=bc586d42d27eb8df04a4c60a29fd9d86CAS |
[175] S. D. Fried, S. Bagchi, S. G. Boxer, Science 2014, 346, 1510.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXitV2gtrzN&md5=b09ca4d403f6fe7f47206e956385e009CAS | 25525245PubMed |
[176] N. S. Hush, A. T. Wong, G. B. Bacskay, J. R. Reimers, J. Am. Chem. Soc. 1990, 112, 4192.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXit1ensLY%3D&md5=966574b8526c046461897ab4a0965655CAS |
[177] J. R. Reimers, L. E. Hall, J. Am. Chem. Soc. 1999, 121, 3730.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXit1aks7c%3D&md5=8e39e362a78ea7ebed8a7f7cde385ba8CAS |
[178] J. R. Reimers, Aust. J. Chem. 2015, 68, 1202.
| 1:CAS:528:DC%2BC2MXht1OnsrfP&md5=3e06b85911df2017e06c0a667d1cb6c3CAS |
[179] T. Van Voorhis, T. Kowalczyk, B. Kaduk, L.-P. Wang, C.-L. Cheng, Q. Wu, Annu. Rev. Phys. Chem. 2010, 61, 149.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXmt1WrsbY%3D&md5=a4b8caf3c57910efe607eb1168d874b5CAS | 20055670PubMed |
[180] J. R. Reimers, L. McKemmish, R. H. McKenzie, N. S. Hush, Phys. Chem. Chem. Phys. 2015, 17, 24598.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtFemu7bL&md5=fcf6d8de99b8609ebf9cf4be8669b4f5CAS | 26193994PubMed |
[181] L. K. McKemmish, J. R. Reimers, R. H. McKenzie, A. E. Mark, N. S. Hush, Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009, 80, 021912.
| Crossref | GoogleScholarGoogle Scholar | 19792156PubMed |
[182] J. R. Reimers, L. K. McKemmish, R. H. McKenzie, A. E. Mark, N. S. Hush, Proc. Natl. Acad. Sci. USA 2009, 106, 4219.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXjslChuro%3D&md5=7bb18897c53fb4408b222e27dc7eefeeCAS | 19251667PubMed |
[183] J. R. Reimers, L. K. McKemmish, R. H. McKenzie, A. E. Mark, N. S. Hush, Phys. Life Rev. 2014, 11, 101.
| Crossref | GoogleScholarGoogle Scholar | 24268490PubMed |
[184] L. McKemmish, R. H. McKenzie, N. S. Hush, J. R. Reimers, Phys. Chem. Chem. Phys. 2015, 17, 24666.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtFemu7bF&md5=ba53a5d96187cf15ae0cf16699017588CAS | 26204101PubMed |
[185] J. R. Reimers, L. McKemmish, R. H. McKenzie, N. S. Hush, Phys. Chem. Chem. Phys. 2015, 17, 24640.
[186] J. R. Reimers, L. McKemmish, R. H. McKenzie, N. S. Hush, Phys. Chem. Chem. Phys. 2015, 17, 24618.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtFemu7bK&md5=3c2a435451a3c8470e60005a074c939bCAS | 26190514PubMed |
[187] N. F. Mott, M. J. Littleton, Trans. Faraday Soc. 1938, 34, 485.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaA1cXivFaksg%3D%3D&md5=751da7d998ef051a3e82a3c740b49998CAS |
[188] T. Holstein, Ann. Phys. 1959, 8, 343.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF3cXpsFejtg%3D%3D&md5=2a397f4cdeeaa8b29d2075d05177a3d6CAS |
[189] T. Holstein, Ann. Phys. 1959, 8, 325.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF3cXpsFejsQ%3D%3D&md5=d6c1182e1781222fbc33268c644b5de6CAS |
[190] L. K. McKemmish, D. J. Kedziora, G. R. White, N. S. Hush, J. R. Reimers, Aust. J. Chem. 2012, 65, 512.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38Xns1yrsLo%3D&md5=0a9d27b017a66ab8c37ea52526d8f0d8CAS |
[191] N. S. Hush, Trans Faraday Soc. 1961, 57, 557.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF3MXhtV2ksrg%3D&md5=d6f0832f3f5ff353cd0c3c5d7bd6cdf3CAS |
[192] J. Swalen, J. Ibers, J. Chem. Phys. 1962, 36, 1914.
| Crossref | GoogleScholarGoogle Scholar |
[193] S. N. Yurchenko, R. J. Barber, J. Tennyson, W. Thiel, P. Jensen, J. Mol. Spectrosc. 2011, 268, 123.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtVyntL%2FE&md5=71924489ec8a0db8b2ef7b358e74e475CAS |
[194] X. Huang, D. W. Schwenke, T. J. Lee, J. Chem. Phys. 2011, 134, 044320.
| Crossref | GoogleScholarGoogle Scholar | 21280738PubMed |
[195] Z.-L. Cai, J. R. Reimers, J. Phys. Chem. A 2000, 104, 8389.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXlslWktrY%3D&md5=582d644d29912e776af808a2692d70e2CAS |
[196] J. R. Reimers, B. B. Wallace, N. S. Hush, Philos. Trans. R. Soc. A 2008, 366, 15.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsVCgsr0%3D&md5=86e80bf31635eed4fbc7b2ce1e616b99CAS |
[197] N. S. Hush, in Mechanistic Aspects of Inorganic Reactions (Eds D. B. Rorabacher, J. F. Endicott) 1982, Vol. 198, Ch. 13, pp. 301–332 (American Chemical Society: Washington DC).
[198] S. Woitellier, J. P. Launay, C. W. Spangler, Inorg. Chem. 1989, 28, 758.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1MXoslCitg%3D%3D&md5=cbe2fdf4be30002ff6e183c0be205296CAS |
[199] J. R. Reimers, N. S. Hush, Inorg. Chem. 1990, 29, 3686.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXlsVWiurg%3D&md5=35031d7eb0c005f0d8887ce00cda34ceCAS |
[200] J. F. Stanton, J. Chem. Phys. 2010, 133, 174309.
| Crossref | GoogleScholarGoogle Scholar | 21054034PubMed |
[201] M. Brinkmann, G. Gadret, M. Muccini, C. Taliani, N. Masciocchi, A. Sironi, J. Am. Chem. Soc. 2000, 122, 5147.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXjtV2mtbo%3D&md5=252b21b8be1b955b3963137b812e31c1CAS |
[202] S. Yin, L. Li, Y. Yang, J. R. Reimers, J. Phys. Chem. C 2012, 116, 14826.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XosFekur4%3D&md5=faf77802922b8040c6ae4d3409ae1039CAS |
[203] S.-H. Lee, A. G. Larsen, K. Ohkubo, Z.-L. Cai, J. R. Reimers, S. Fukuzumi, M. J. Crossley, Chem. Sci. 2012, 3, 257.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhsFeju7bE&md5=553422b36b3c131d66d3b0110ce74b1cCAS |
[204] D. Curiel, K. Ohkubo, J. R. Reimers, S. Fukuzumi, M. J. Crossley, Phys. Chem. Chem. Phys. 2007, 9, 5260.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtV2itL3I&md5=75d5884be219592d4d7549018a62b64cCAS | 19459289PubMed |
[205] N. S. Hush, Chem. Phys. 1975, 10, 361.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE2MXmtFWis7c%3D&md5=b134cc5eb947516fbc35afdb030ba1cbCAS |
[206] N. S. Hush, NATO Adv. Study Inst. Ser., Ser. C 1980, 58, 151.
| 1:CAS:528:DyaL3MXlslaiuw%3D%3D&md5=045398eb7fac00b2b8a148d075dd2e19CAS |
[207] U. Öpik, M. H. L. Pryce, Proc. R. Soc. Lond. A: Math. Phys. Sci. 1957, 238, 425.
| Crossref | GoogleScholarGoogle Scholar |
[208] M. B. Robin, P. Day, Adv. Inorg. Chem. Radiochem. 1967, 10, 247.
| 1:CAS:528:DyaF1cXovF2isA%3D%3D&md5=147fc9884e6f384dde363aca8ea268d9CAS |
[209] S. B. Piepho, J. Am. Chem. Soc. 1990, 112, 4197.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXit1emtrs%3D&md5=c3cace4f79b599d0fee0d1a3cb321eb6CAS |
[210] R. Kubo, Y. Toyozawa, Prog. Theor. Phys. 1955, 13, 160.
| Crossref | GoogleScholarGoogle Scholar |
[211] V. G. Levich, R. R. Dogonadze, Dokl. Akad. Nauk. SSSR Ser. Fiz. Khim. 1959, 124, 123.
| 1:CAS:528:DyaF3MXmtFA%3D&md5=032c370b276c9c65e2815e86836aff4eCAS |
[212] M. Born, K. Huang, Dynamical Theory of Crystal Lattices 1954 (Clarendon: Oxford).
[213] C. J. Ballhausen, A. E. Hansen, Annu. Rev. Phys. Chem. 1972, 23, 15.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE3sXmsVehug%3D%3D&md5=6b73ee3406ead771d599cd50137458caCAS |
[214] B. K. Kendrick, C. A. Mead, D. G. Truhlar, Chem. Phys. 2002, 277, 31.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XhtlOjsb4%3D&md5=1096308cd99f540abb1d1632439a75a7CAS |
[215] A. W. Jasper, B. K. Kendrick, C. A. Mead, D. G. Truhlar, Adv. Ser. Phys. Chem. 2004, 14, 329.
| 1:CAS:528:DC%2BD2cXkvFKjtbo%3D&md5=ffc24cb745966a34f6d00481d022d997CAS |
[216] P. T. Saunders, An Introduction to Catastrophe Theory 1980 (Cambridge University Press: Cambridge).
[217] F. Xu, Z. Phys. Chem. 1990, 166, 79.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXhvVKrtr0%3D&md5=af9f2141dc2698ba14cd143955b77f62CAS |
[218] X. Krokidis, B. Silvi, C. Dezarnaud-Dandine, A. Sevin, New J. Chem. 1998, 22, 1341.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXpt1en&md5=5430f05d728db33d66615835d6d7b479CAS |
[219] D. J. Wales, Science 2001, 293, 2067.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXntVCisL0%3D&md5=8ff41911d4e9eac0ab9a7c8df0801369CAS | 11557887PubMed |
[220] R. S. Mulliken, Rev. Mod. Phys. 1942, 14, 204.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH3sXnvFKg&md5=c53d2261dd3b447998b4a4edf3ec01beCAS |
[221] A. D. Walsh, J. Chem. Soc. 1953, 2296.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3sXntVOlug%3D%3D&md5=2cefb3ce9b61495638fd6ac995f41307CAS |
[222] A. D. Walsh, Photoelec. Spectrom. Group Bull. 1961, 13, 348.
[223] B. M. Gimarc, J. Am. Chem. Soc. 1971, 93, 593.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE3MXmsl2isw%3D%3D&md5=f6fb1921d781deaae99a475369ff23d9CAS |
[224] K. Mislow, R. D. Baechler, J. Am. Chem. Soc. 1971, 93, 773.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE3MXhtFWnsb4%3D&md5=f93d7b1ec888c8e139cfdb5663c0fdf2CAS |
[225] A. H. Pakiari, F. Nazari, J. Mol. Struct. THEOCHEM 2005, 717, 189.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhvF2ltrg%3D&md5=28a2c7bf47eed5546b7da1172287da96CAS |
[226] Y. Arasaki, K. Takatsuka, K. Wang, V. McKoy, Phys. Rev. Lett. 2003, 90, 248303.
| Crossref | GoogleScholarGoogle Scholar | 12857232PubMed |
[227] R. G. Pearson, Chem. Phys. Lett. 1971, 10, 31.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE3MXltVWgtLc%3D&md5=6a8a08a6b211f64f5607a15b020e578cCAS |
[228] A. D. Walsh, P. A. Warsop, Trans. Faraday Soc. 1961, 57, 345.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF3MXhtV2rtrg%3D&md5=7e01fe2b7f377751914358cd58eaa333CAS |
[229] R. F. W. Bader, Can. J. Chem. 1962, 40, 1164.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF38XksVSntro%3D&md5=0117e244aaba9641576c9c8f5c23c780CAS |
[230] L. Salem, J. S. Wright, J. Am. Chem. Soc. 1969, 91, 5947.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF1MXlt12htro%3D&md5=e51e654c6ebed0599f589d5ebe078e7fCAS |
[231] R. G. Pearson, J. Am. Chem. Soc. 1969, 91, 4947.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF1MXkslCitb8%3D&md5=2a47a29e2fa272e773f4186e9217b279CAS |
[232] R. G. Pearson, Acc. Chem. Res. 1971, 4, 152.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE3MXhtlSmt74%3D&md5=fc80efa0e979de07c73e8ed8eef7ebccCAS |
[233] C. C. Levin, J. Am. Chem. Soc. 1975, 97, 5649.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE2MXlvVeqsLw%3D&md5=8fd693eedc0f00018f192fbbbc6ed7a0CAS |
[234] I. B. Bersuker, Adv. Quantum Chem. 2003, 44, 1.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhsVSmu70%3D&md5=be6579c016579ea985150300e58bb134CAS |
[235] Y. Liu, I. B. Bersuker, W. Zou, J. E. Boggs, J. Chem. Theory Comput. 2009, 5, 2679.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtFOks7fM&md5=2d22ca4ae6fff000dba9163a00865ae8CAS | 26631781PubMed |
[236] R. J. Gillespie, R. S. Nyholm, Q. Rev. Chem. Soc. 1957, 11, 339.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG1cXivFSjug%3D%3D&md5=fec0c758642cf2dcbbce35f21e8c158aCAS |
[237] R. J. Gillespie, E. A. Robinson, Angew. Chem. Int. Ed. Engl. 1996, 35, 495.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XhvVOlu74%3D&md5=9a00eac0fbd60d58854a15078b0e10a1CAS |
[238] R. J. Gillespie, Coord. Chem. Rev. 2000, 197, 51.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXitVSms7c%3D&md5=2058e61837e900a4d3cc93ff00d9cbe7CAS |
[239] R. J. Gillespie, Coord. Chem. Rev. 2008, 252, 1315.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXlvFyntr0%3D&md5=5ddfba002bc845df556a4ed708509df5CAS |
[240] N. V. Sidgwick, H. M. Powell, Proc. R. Soc. Lond. A 1940, 176, 153.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH3MXotVKn&md5=165eddc80f4113f3fb844973b72b5b04CAS |
[241] J. A. Pople, Proc. R. Soc. Lond. A 1950, 202, 323.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3MXjsVKgsg%3D%3D&md5=02e736558aed4502b2ee5375015c0097CAS |
[242] S.-H. Lee, I. M. Blake, A. G. Larsen, J. A. McDonald, K. Ohkubo, S. Fukuzumi, J. R. Reimers, M. J. Crossley, Chem. Sci. 2016, 7, 6534.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XpvFeisLo%3D&md5=b0ec14361949b24326cedd0a7188a919CAS |
[243] P. C. Dastoor, C. R. McNeill, H. Frohne, C. J. Foster, B. Dean, C. J. Fell, W. J. Belcher, W. M. Campbell, D. L. Officer, I. M. Blake, P. Thordarson, M. J. Crossley, N. S. Hush, J. R. Reimers, J. Phys. Chem. C 2007, 111, 15415.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtFSmsLnK&md5=ce6bf9c0d014d61bd28d5ea967feaf56CAS |
[244] K. Sendt, L. A. Johnston, W. A. Hough, M. J. Crossley, N. S. Hush, J. R. Reimers, J. Am. Chem. Soc. 2002, 124, 9299.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xltlais7w%3D&md5=a6d40e177b50e896822bfe8edcfd0eb5CAS | 12149038PubMed |
[245] C. Martelli, J. Canning, J. R. Reimers, M. Sintic, D. Stocks, T. Khoury, M. J. Crossley, J. Am. Chem. Soc. 2009, 131, 2925.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhs1Sls70%3D&md5=f1f3732b8ad78b75dacf6678a09b274fCAS | 19203267PubMed |
[246] P. F. Cafe, A. G. Larsen, W. Yang, A. Bilic, I. M. Blake, M. J. Crossley, J. Zhang, H. Wackerbarth, J. Ulstrup, J. R. Reimers, J. Phys. Chem. C 2007, 111, 17285.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXht1eitrvP&md5=717ac34447e10ced1f2910a32ddeebfaCAS |
[247] R. B. Piper, M. Yoshida, D. J. Farrell, T. Khoury, M. J. Crossley, T. W. Schmidt, S. A. Haque, N. J. Ekins-Daukes, RSC Adv. 2014, 4, 8059.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhtlagsLs%3D&md5=90323d8ec932ec8df3007a1f45720a62CAS |
[248] Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley, T. W. Schmidt, Phys. Chem. Chem. Phys. 2010, 12, 66.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhsFektbjK&md5=44769f1f7d5ba91f60b7b86db37bc8c9CAS | 20024445PubMed |
[249] P. J. Sintic, W. E, Z. Ou, J. Shao, J. A. McDonald, Z.-L. Cai, K. M. Kadish, M. J. Crossley, J. R. Reimers, Phys. Chem. Chem. Phys. 2008, 10, 268.; this article was unfortunately duplicated later in 10(4) P515–527, their note 10 P7328.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVGksL8%3D&md5=692a3351eccedc6402252cadf888634dCAS | 18273994PubMed |
[250] W. E, K. M. Kadish, P. J. Sintic, T. Khoury, L. J. Govenlock, Z. Ou, J. Shao, K. Ohkubo, J. R. Reimers, S. Fukuzumi, M. J. Crossley, J. Phys. Chem. A 2008, 112, 556.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXitFaqsg%3D%3D&md5=259df1defa3929cc91cffd92409e9dd2CAS | 18171032PubMed |
[251] M. J. Crossley, C. S. Sheehan, T. Khoury, J. R. Reimers, P. J. Sintic, New J. Chem. 2008, 32, 340.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsFyqt70%3D&md5=8913fff7f54a5a656954939f9a21ce68CAS |
[252] K. M. Kadish, W. E, P. J. Sintic, Z. Ou, J. Shao, K. Ohkubo, S. Fukuzumi, L. J. Govenlock, J. A. McDonald, A. C. Try, Z.-L. Cai, J. R. Reimers, M. J. Crossley, J. Phys. Chem. B 2007, 111, 8762.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXnsV2rsLo%3D&md5=3146c01a7d57f4463cfd1a12efbde583CAS | 17608523PubMed |
[253] J. R. Reimers, D. Panduwinata, J. Visser, Y. Chin, C. Tang, L. Goerigk, M. J. Ford, M. Sintic, T.-J. Sum, M. J. J. Coenen, B. L. M. Hendriksen, J. A. A. W. Elemans, N. S. Hush, M. J. Crossley, Proc. Natl. Acad. Sci. USA 2015, 112, E6101.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhsleksbbN&md5=7f32bbb197215464b218ef2fb8dd6dc5CAS | 26512115PubMed |
[254] T. X. Lü, J. R. Reimers, M. J. Crossley, N. S. Hush, J. Phys. Chem. 1994, 98, 11878.
| Crossref | GoogleScholarGoogle Scholar |
[255] J. R. Reimers, T. X. Lu, M. J. Crossley, N. S. Hush, Nanotechnology 1996, 7, 424.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXjtVWlt78%3D&md5=f9c1d8b9395e5d3b733f06e822d31764CAS |
[256] J. R. Reimers, L. E. Hall, M. J. Crossley, N. S. Hush, J. Phys. Chem. A 1999, 103, 4385.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXjtVCntbs%3D&md5=b2a3e1caf0c3f38206c0d89f0af535a8CAS |
[257] J. R. Reimers, N. S. Hush, M. J. Crossley, J. Porphyr. Phthalocyanines 2002, 06, 795.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXhsFWmtr4%3D&md5=f076c092254d7fb5444fd6a3a3dfec87CAS |
[258] J. R. Reimers, A. Bilic, Z.-L. Cai, M. Dahlbom, N. A. Lambropoulos, G. C. Solomon, M. J. Crossley, N. S. Hush, Aust. J. Chem. 2004, 57, 1133.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhtVGns73K&md5=9fcaa1f31d901b71b37c588c3a251c6aCAS |
[259] N. A. Lambropoulos, J. R. Reimers, M. J. Crossley, N. S. Hush, K. Silverbrook, Nanotechnology 2013, 24, 505202.
| Crossref | GoogleScholarGoogle Scholar | 24270608PubMed |
[260] C. Yelgel, J. Appl. Phys. 2016, 119, 065307.
| Crossref | GoogleScholarGoogle Scholar |
[261] A. A. Tonkikh, E. N. Voloshina, P. Werner, H. Blumtritt, B. Senkovskiy, G. Güntherodt, S. S. P. Parkin, Y. S. Dedkov, Sci. Rep. 2016, 6, 23547.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XkvVCrtr8%3D&md5=99b8cf2b54b5a9845925a43fedf5dbbbCAS | 27009238PubMed |
[262] J. Tesch, P. Leicht, F. Blumenschein, L. Gragnaniello, M. Fonin, L. E. M. Steinkasserer, B. Paulus, E. Voloshina, Y. Dedkov, Sci. Rep. 2016, 6, 23439.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xks1CrurY%3D&md5=0daec7fb1014ae80e23e1f44c32d1030CAS | 27002297PubMed |
[263] P. Singla, M. Riyaz, S. Singhal, N. Goel, Phys. Chem. Chem. Phys. 2016, 18, 5597.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XpsVWhsQ%3D%3D&md5=f92aff332a146be071e1bbfe9eef773fCAS | 26863069PubMed |
[264] M. Muruganathan, J. Sun, T. Imamura, H. Mizuta, Nano Lett. 2015, 15, 8176.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhvVWru7rK&md5=b1757201d4c0029bee3f1035e834424dCAS | 26562749PubMed |
[265] J. Moreno, S. Aspera, M. David, H. Kasai, Carbon 2015, 94, 936.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXht1KgtrfP&md5=3d8ee79da68fb7500f803632f9f7061cCAS |
[266] D. Mollenhauer, C. Brieger, E. Voloshina, B. Paulus, J. Phys. Chem. C 2015, 119, 1898.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtFyltLc%3D&md5=870db1f441e4e0a8937061ad2a1b1bc9CAS |
[267] R. J. Maurer, V. G. Ruiz, A. Tkatchenko, J. Chem. Phys. 2015, 143, 102808.
| Crossref | GoogleScholarGoogle Scholar | 26374001PubMed |
[268] W. Gao, A. Tkatchenko, Phys. Rev. Lett. 2015, 114, 096101.
| Crossref | GoogleScholarGoogle Scholar | 25793829PubMed |
[269] Y. S. Dedkov, E. N. Voloshina, M. Fonin, Phys. Status Solidi B 2015, 252, 451.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXktVGqtbc%3D&md5=94cb58275edbdd5852629b356490acfdCAS |
[270] Y. S. Dedkov, E. N. Voloshina, J. Phys. Condens. Matter 2015, 27, 303002.
| Crossref | GoogleScholarGoogle Scholar |
[271] B. Wang, X. Zheng, J. Michl, E. T. Foley, M. C. Hersam, A. Bilic, M. J. Crossley, J. R. Reimers, N. S. Hush, Nanotechnology 2004, 15, 324.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXlslalurc%3D&md5=300cbcefc2c2d5e277e9c29d3cdcd437CAS |
[272] S. A. Saraireh, P. V. Smith, B. V. King, J. R. Reimers, B. J. Wallace, M. J. Crossley, J. Phys. Chem. C 2009, 113, 16094.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtVSgtbvK&md5=59804668bd598e05f32ab3bdf3f4a7f7CAS |
[273] R. Landauer, IBM J. Res. Develop. 1957, 1, 223.
| Crossref | GoogleScholarGoogle Scholar |
[274] Y. Meir, N. S. Wingreen, Phys. Rev. Lett. 1992, 68, 2512.
| Crossref | GoogleScholarGoogle Scholar | 10045416PubMed |
[275] A. Cheong, A. E. Roitberg, V. Mujica, M. A. Ratner, J. Photochem. Photobiol. Chem. 1994, 82, 81.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXmvV2gtbg%3D&md5=7d60ff7b85533c2620609978452be90bCAS |
[276] M. Kemp, V. Mujica, M. A. Ratner, J. Chem. Phys. 1994, 101, 5172.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXmsVaktb8%3D&md5=44fb1a3aab72d30fcaaea39d88ec5341CAS |
[277] M. Kemp, A. Roitberg, V. Mujica, T. Wanta, M. A. Ratner, J. Phys. Chem. 1996, 100, 8349.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XisFKgu70%3D&md5=83d8e1b7266f9d90e60350abfce871b1CAS |
[278] A. Aviram, M. A. Ratner, Chem. Phys. Lett. 1974, 29, 277.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE2MXhs1Cjtbw%3D&md5=2ed4ea2b259e7f87640a1e46af6e6582CAS |
[279] S. Datta, Electronic Transport in Mesoscopic Systems 1997 (Cambridge University Press: Cambridge).
[280] L. V. Keldysh, Sov. Phys. JEPT 1965, 20, 1018.
[281] L. E. Hall, J. R. Reimers, N. S. Hush, K. Silverbrook, J. Chem. Phys. 2000, 112, 1510.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXitlantA%3D%3D&md5=b9ba772590d9c79e677909b082dd18daCAS |
[282] J. Taylor, H. Guo, J. Wang, Phys. Rev. B 2001, 63, 245407.
| Crossref | GoogleScholarGoogle Scholar |
[283] L. N. Zhang, F. Zahid, Y. Zhu, L. Liu, J. Wang, H. Guo, P. C. H. Chan, M. S. Chan, IEEE Trans. Electron. Dev. 2013, 60, 3527.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhslGnsrfK&md5=9bf374628505a580e45fc6ac7335c6deCAS |
[284] J. Trasobares, D. Vuillaume, D. Théron, N. Clément, Nat. Comm. 2016, 7, 12850.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xhs1amtLzM&md5=fdb4991ba0848d881cd05bfa8a3fe063CAS |
[285] W. Wang, T. Lee, I. Kretzschmar, M. A. Reed, Nano Lett. 2004, 4, 643.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhvFWlur4%3D&md5=16dad14c6e6e51148314b142cbad5ea8CAS |
[286] G. Kushmerick, J. Lazorcik, C. H. Patterson, R. Shashidhar, Nano Lett. 2004, 4, 639.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXitFeqsLw%3D&md5=c61dfa320ac73f741aa5f2d7e32c22c9CAS |
[287] R. C. Jaklevic, J. Lambe, Phys. Rev. Lett. 1966, 17, 1139.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF2sXktFCnsg%3D%3D&md5=a0687e94927d6f3732efd3df4c9d7c5aCAS |
[288] G. C. Solomon, A. Gagliardi, A. Pecchia, T. Frauenheim, A. Di Carlo, J. R. Reimers, N. S. Hush, J. Chem. Phys. 2006, 124, 094704.
| Crossref | GoogleScholarGoogle Scholar |
[289] A. Troisi, A. Ratner Mark, Phys. Rev. B 2005, 72, 033408.
| Crossref | GoogleScholarGoogle Scholar |
[290] A. Troisi, A. Ratner Mark, A. Nitzan, J. Chem. Phys. 2003, 118, 6072.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXitlemtr4%3D&md5=b48e42101e4f94f2df7aba6c585054acCAS |
[291] G. C. Solomon, A. Gagliardi, A. Pecchia, T. Frauenheim, A. Di Carlo, J. R. Reimers, N. S. Hush, J. Chem. Phys. 2006, 125, 184702.
| Crossref | GoogleScholarGoogle Scholar | 17115774PubMed |
[292] A. Gagliardi, G. C. Solomon, A. Pecchia, T. Frauenheim, A. Di Carlo, N. S. Hush, J. R. Reimers, Phys. Rev. B 2007, 75, 174306.
| Crossref | GoogleScholarGoogle Scholar |
[293] J. R. Reimers, G. C. Solomon, A. Gagliardi, A. Bilic, N. S. Hush, T. Frauenheim, A. Di Carlo, A. Pecchia, J. Phys. Chem. A 2007, 111, 5692.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXlvVWjtL0%3D&md5=caf0f4e34f57a5f4d993cfd0f1b19818CAS | 17530826PubMed |
[294] A. J. Ferguson, P. A. Cain, D. A. Williams, G. A. D. Briggs, Phys. Rev. A 2002, 65, 034303.
| Crossref | GoogleScholarGoogle Scholar |
[295] R. Penrose, S. R. Hameroff, J. Conscious. Stud. 1995, 2, 99.
[296] S. Hameroff, R. Penrose, Math. Comput. Simul. 1996, 40, 453.
| Crossref | GoogleScholarGoogle Scholar |
[297] S. Hameroff, Philos. Trans. R. Soc. A 1998, 356, 1869.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXmtVygsLw%3D&md5=db8ab2018c38e429ed254fd9636af892CAS |
[298] S. Hagan, S. R. Hameroff, J. A. Tuszynski, Phys. Rev. E: Stat. Nonlin. Soft Matter Phys. 2002, 65, 061901.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38vktlCisg%3D%3D&md5=7b1b275079cb22b56b4583bf6e390d54CAS |
[299] S. Hameroff, R. Penrose, Phys. Life Rev. 2014, 11, 39.
| Crossref | GoogleScholarGoogle Scholar | 24070914PubMed |
[300] R. Penrose, The Emperor’s New Mind 1989 (Oxford University Press: Oxford).
[301] R. Penrose, Shadows of the Mind 1994 (Oxford University Press: New York, NY).
[302] H. Fröhlich, Int. J. Quantum Chem. 1968, 2, 641.
| Crossref | GoogleScholarGoogle Scholar |
[303] H. Fröhlich, Phys. Lett. A 1968, 26, 402.
| Crossref | GoogleScholarGoogle Scholar |
[304] H. Fröhlich, Nature 1970, 228, 1093.
| Crossref | GoogleScholarGoogle Scholar | 5483165PubMed |
[305] E. U. Condon, G. H. Shortley, The Theory of Atomic Spectra 1935 (Cambridge University Press: London).
[306] A. K. Geim, I. V. Grigorieva, Nature 2013, 499, 419.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhtFKnu7rN&md5=8f91b4f5c8c42a9774e3c220230694b5CAS | 23887427PubMed |
[307] A. Allain, J. Kang, K. Banerjee, A. Kis, Nat. Mater. 2015, 14, 1195.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhvVOlsr3K&md5=6cb1b4e5a52be349dc9b296d917c4864CAS | 26585088PubMed |
[308] A. A. Svidzinsky, M. O. Scully, D. R. Herschbach, Proc. Natl. Acad. Sci. USA 2005, 102, 11985.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXps1yrur8%3D&md5=4670ee38f1cebfca02c1d7e6edbcca22CAS | 16103360PubMed |
[309] G. Chen, Z. Ding, S. B. Hsu, M. Kim, J. Zhou, J. Math. Phys. 2006, 47, 022107.
| Crossref | GoogleScholarGoogle Scholar |
[310] A. A. Svidzinsky, S. A. Chin, M. O. Scully, Phys. Lett. A 2006, 355, 373.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XltV2hurs%3D&md5=e84cd3e88eec1ddac59c7e75e98f1cafCAS |
[311] D. Ben-Amotz, J. Phys. Chem. B 2006, 110, 19861.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XmvFGjsbk%3D&md5=32e60c55e352982df4a72e1c2a52e912CAS | 17020371PubMed |
[312] G. Chen, Z. Ding, C. S. Lin, D. Herschbach, M. O. Scully, J. Math. Chem. 2010, 48, 791.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhtFaitLvE&md5=86ab3eec93e2bf3484ea577bb77e0ce4CAS |
[313] G. B. Bacskay, J. R. Reimers, S. Nordholm, J. Chem. Educ. 1997, 74, 1494.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXnslShu70%3D&md5=63628b9ff373c3e04340b1852b634f9dCAS |
[314] J. F. Dobson, Int. J. Quantum Chem. 2014, 114, 1157.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXislCgsLg%3D&md5=65ba4f70431b7f832be8a36021c2c411CAS |
[315] S. Tsoi, P. Dev, A. L. Friedman, R. Stine, J. T. Robinson, T. L. Reinecke, P. E. Sheehan, ACS Nano 2014, 8, 12410.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhvFKqurbJ&md5=1d1356d6eb8ff587b7af1c1909b4fe9eCAS | 25412420PubMed |
[316] J. F. Dobson, A. White, A. Rubio, Phys. Rev. Lett. 2006, 96, 073201.
| Crossref | GoogleScholarGoogle Scholar | 16606085PubMed |
[317] S. Lebègue, J. Harl, T. Gould, J. G. Ángyán, G. Kresse, J. F. Dobson, Phys. Rev. Lett. 2010, 105, 196401.
| Crossref | GoogleScholarGoogle Scholar | 21231187PubMed |
[318] J. F. Dobson, T. Gould, G. Vignale, Phys. Rev. X 2014, 4, 021040.
| Crossref | GoogleScholarGoogle Scholar |
[319] R. F. Liu, J. G. Angyan, J. F. Dobson, J. Chem. Phys. 2011, 134, 114106.
| Crossref | GoogleScholarGoogle Scholar | 21428606PubMed |
[320] M. Boström, B. E. Sernelius, Phys. Rev. B 2000, 61, 2204.
| Crossref | GoogleScholarGoogle Scholar |
[321] D. B. Chang, R. L. Cooper, J. E. Drummond, A. C. Young, Phys. Lett. A 1971, 37, 311.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE38Xns1GmtA%3D%3D&md5=96de4f758fa26ccfbe564363e819980cCAS |
[322] V. V. Gobre, A. Tkatchenko, Nat. Commun. 2013, 5, 2341.
[323] R. Jaffe, Phys. Rev. D: Part. Fields Gravit. Cosmol. 2005, 72, 021301.
| Crossref | GoogleScholarGoogle Scholar |
[324] A. J. Misquitta, B. Jeziorski, K. Szalewicz, Phys. Rev. Lett. 2003, 91, 033201.
| Crossref | GoogleScholarGoogle Scholar | 12906414PubMed |
[325] J. Erhard, P. Bleiziffer, A. Görling, Phys. Rev. Lett. 2016, 117, 143002.
| Crossref | GoogleScholarGoogle Scholar | 27740821PubMed |
[326] J. R. Reimers, M. Li, D. Wan, M. J. Ford, in Noncovalent Interactions in Quantum Chemistry and Physics: Theory and Applications (Eds A. Otero de la Roza, G. DiLabio) 2017, in press (Elsevier: Amsterdam).
[327] A. Grüneis, J. Chem. Phys. 2015, 143, 102817.
| Crossref | GoogleScholarGoogle Scholar | 26374010PubMed |
[328] Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki, M. Kállay, J. Chem. Phys. 2013, 139, 094105.
| Crossref | GoogleScholarGoogle Scholar | 24028100PubMed |
[329] E. Voloshina, Phys. Rev. B 2012, 85, 045444.
| Crossref | GoogleScholarGoogle Scholar |
[330] D. Usvyat, L. Maschio, M. Schütz, J. Chem. Phys. 2015, 143, 102805.
| Crossref | GoogleScholarGoogle Scholar | 26373998PubMed |
[331] M. Del Ben, J. Hutter, J. VandeVondele, J. Chem. Phys. 2015, 143, 102803.
| Crossref | GoogleScholarGoogle Scholar | 26373996PubMed |
[332] H. Stoll, B. Paulus, P. Fulde, Chem. Phys. Lett. 2009, 469, 90.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXpvFSjsQ%3D%3D&md5=ad9f9e3bc731f245aa87b95fb88ca3b9CAS |
[333] B. Paulus, Phys. Rep. 2006, 428, 1.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XjtVOiu7Y%3D&md5=98482464f1e01b4df2a7c24247ef4f49CAS |
[334] C. Muller, B. Paulus, Phys. Chem. Chem. Phys. 2012, 14, 7605.
| Crossref | GoogleScholarGoogle Scholar | 22373600PubMed |
[335] M. Marsman, A. Grüneis, J. Paier, G. Kresse, J. Chem. Phys. 2009, 130, 184103.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD1MzltlajsA%3D%3D&md5=d1f25725f481323d7ed0bd81c1d43257CAS | 19449904PubMed |
[336] E. Voloshina, B. Paulus, J. Chem. Theory Comput. 2014, 10, 1698.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXivFyrsrk%3D&md5=f994edcbc1cd574939afc58fbbe7e40fCAS | 26580378PubMed |
[337] M. P. de Lara-Castells, R. Fernandez-Perea, F. Madzharova, E. Voloshina, J. Chem. Phys. 2016, 144, 244707.
| Crossref | GoogleScholarGoogle Scholar | 27369533PubMed |
[338] H. Stoll, Phys. Rev. B 1992, 46, 6700.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK38XlvFyrsrk%3D&md5=416d5521c11be474a5b8f6b6ffc76155CAS |
[339] H. Stoll, J. Chem. Phys. 1992, 97, 8449.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3sXmsl2iuro%3D&md5=f39084e437e8f5cd49c441a3e2d61efdCAS |
[340] M. P. de Lara-Castells, A. O. Mitrushchenkov, H. Stoll, J. Chem. Phys. 2015, 143, 102804.
| Crossref | GoogleScholarGoogle Scholar | 26373997PubMed |
[341] M. J. Gillan, D. Alfè, P. J. Bygrave, C. R. Taylor, F. R. Manby, J. Chem. Phys. 2013, 139, 114101.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC2c7ivFWjuw%3D%3D&md5=5e20afdfde3ea90bfb37c8a630f25f4eCAS | 24070273PubMed |
[342] G. H. Booth, A. Grüneis, G. Kresse, A. Alavi, Nature 2013, 493, 365.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhvV2ntbbL&md5=891d84478d228ee8a3303988643c98f1CAS | 23254929PubMed |
[343] L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer, G. Kresse, Nat. Mater. 2010, 9, 741.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhtVGlsr%2FK&md5=ee95c1db8c53e2b8be34df1c304c5038CAS | 20657589PubMed |
[344] M. P. de Lara-Castells, H. Stoll, B. Civalleri, M. Causa, E. Voloshina, A. O. Mitrushchenkov, M. Pi, J. Chem. Phys. 2014, 141, 151102.
| Crossref | GoogleScholarGoogle Scholar | 25338874PubMed |
[345] M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov, H. Stoll, J. Chem. Phys. 2015, 143, 194701.
| Crossref | GoogleScholarGoogle Scholar | 26590547PubMed |
[346] A. Heßelmann, G. Jansen, M. Schütz, J. Chem. Phys. 2005, 122, 014103.
| Crossref | GoogleScholarGoogle Scholar |
[347] A. Heßelmann, J. Chem. Phys. 2008, 128, 144112.
| Crossref | GoogleScholarGoogle Scholar | 18412428PubMed |
[348] M. Pitoňák, A. Heßelmann, J. Chem. Theory Comput. 2010, 6, 168.
| Crossref | GoogleScholarGoogle Scholar | 26614329PubMed |
[349] C. Tuma, J. Sauer, J. Chem. Phys. 2015, 143, 102810.
| Crossref | GoogleScholarGoogle Scholar | 26374003PubMed |
[350] Y. S. Al-Hamdani, M. Ma, D. Alfè, O. A. von Lilienfeld, A. Michaelides, J. Chem. Phys. 2015, 142, 181101.
| Crossref | GoogleScholarGoogle Scholar | 25978876PubMed |
[351] G. H. Booth, A. J. W. Thom, A. Alavi, J. Chem. Phys. 2009, 131, 054106.
| Crossref | GoogleScholarGoogle Scholar | 19673550PubMed |
[352] S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 2010, 132, 154104.
| Crossref | GoogleScholarGoogle Scholar | 20423165PubMed |
[353] S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 2011, 32, 1456.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXjsF2isL0%3D&md5=738d507a3e0a68831e1f4257fbe0c764CAS | 21370243PubMed |
[354] A. D. Becke, E. R. Johnson, J. Chem. Phys. 2007, 127, 154108.
| Crossref | GoogleScholarGoogle Scholar | 17949133PubMed |
[355] A. Tkatchenko, R. A. Distasio, R. Car, M. Scheffler, Phys. Rev. Lett. 2012, 108, 236402.
| Crossref | GoogleScholarGoogle Scholar | 23003978PubMed |
[356] V. G. Ruiz, W. Liu, A. Tkatchenko, Phys. Rev. B 2016, 93, 035118.
| Crossref | GoogleScholarGoogle Scholar |
[357] A. Tkatchenko, Adv. Funct. Mater. 2015, 25, 2054.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXitVWhu7nM&md5=0fc1e47fbee2c0711bed9a4cb15a292aCAS |
[358] A. M. Reilly, A. Tkatchenko, Chem. Sci. 2015, 6, 3289.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXlsVyjs7Y%3D&md5=cf6b908a6788beafee8adbcd8a59c16aCAS |
[359] A. Ambrosetti, N. Ferri, R. A. DiStasio, A. Tkatchenko, Science 2016, 351, 1171.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xjs12gtrk%3D&md5=722f620d9d4c35f8227abd952c78456dCAS | 26965622PubMed |
[360] T. Bucko, S. Lebegue, T. Gould, J. G. Angyan, J. Phys. Condens. Matter 2016, 28, 045201.
| Crossref | GoogleScholarGoogle Scholar | 26753609PubMed |
[361] E. R. Johnson, in Noncovalent Interactions in Quantum Chemistry and Physics: Theory and Applications (Eds A. Otero de la Roza, G. DiLabio) 2017, submitted (Elsevier: Amsterdam).
[362] M. S. Christian, A. Otero-de-la-Roza, E. R. Johnson, J. Chem. Theory Comput. 2016, 12, 3305.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XptVOjs70%3D&md5=33904b4097e6518b0fd31242a88eccfdCAS | 27253340PubMed |
[363] J. R. Reimers, D. Panduwinata, J. Visser, Y. Chin, C. Tang, L. Goerigk, M. J. Ford, M. Sintic, T. J. Sum, M. J. J. Coenen, B. L. M. Hendriksen, J. A. A. W. Elemans, N. S. Hush, M. J. Crossley, J. Phys. Chem. C 2016, 120, 1739.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xis1Gqtg%3D%3D&md5=f727f58360434cabff664c9ee2e73504CAS |
[364] J. Visser, N. Katsonis, J. Vicario, B. L. Feringa, Langmuir 2009, 25, 5980.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXjvF2gtrw%3D&md5=c5d670089c54305ba5a29f19c7b5d20bCAS | 19341279PubMed |
[365] N. Katsonis, J. Vicario, T. Kudernac, J. Visser, M. M. Pollard, B. L. Feringa, J. Am. Chem. Soc. 2006, 128, 15537.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtFCjtb3O&md5=406433a1f40d57528a81675a2235d1b4CAS | 17132021PubMed |
[366] Y. Chin, D. Panduwinata, M. Sintic, T. J. Sum, N. S. Hush, M. J. Crossley, J. R. Reimers, J. Phys. Chem. Lett. 2011, 2, 62.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhs1SrsLzO&md5=77c6c19d9453326590bd82cb27893351CAS | 26295522PubMed |
[367] B. Hulsken, R. Van Hameren, P. Thordarson, J. W. Gerritsen, R. J. M. Nolte, A. E. Rowan, M. J. Crossley, J. A. A. W. Elemans, S. Speller, Jpn. J. Appl. Phys. Part 1 2006, 45, 1953.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XkvFSltbg%3D&md5=765fbe0bc5a0d569df51664947022144CAS |
[368] M. J. J. Coenen, D. den Boer, F. J. van den Bruele, T. Habets, K. A. A. M. Timmers, M. van der Maas, T. Khoury, D. Panduwinata, M. J. Crossley, J. R. Reimers, W. J. P. van Enckevort, B. L. M. Hendriksen, J. A. A. W. Elemans, S. Speller, Phys. Chem. Chem. Phys. 2013, 15, 12451.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhtVyks7bF&md5=1c8a5a0a9d2c21462a8c081a48a33222CAS |
[369] J. R. Reimers, M. J. Ford, L. Goerigk, Mol. Simul. 2016, 42, 494.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhvVamu7rN&md5=7575b47143e781815422dc78adba1c68CAS |
[370] J. P. Perdew, W. Burke, M. Ernzerhof, Phys. Rev. Lett. 1996, 77, 3865.
| 1:CAS:528:DyaK28XmsVCgsbs%3D&md5=80e9e7f93c4d868c24426c2d2790225cCAS | 10062328PubMed |
[371] U. Mazur, K. W. Hipps, Chem. Commun. 2015, 51, 4737.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtF2qt7g%3D&md5=90830b83b0bb2b327f14856f19993adfCAS |
[372] L. Battezzati, C. Pisani, F. Ricca, J. Chem. Soc., Faraday Trans. II 1975, 71, 1629.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE2MXlvVCjsr8%3D&md5=8aa0f9f5214995f45cf9d1a5d7d2c30bCAS |
[373] S. J. Weiner, P. A. Kollman, D. A. Case, U. C. Singh, C. Ghio, G. Alagona, J. S. Profeta, P. Weiner, J. Am. Chem. Soc. 1984, 106, 765.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2cXmsVCgug%3D%3D&md5=7dc8c68f84ed5dde8a274ef1f1154126CAS |
[374] J. P. Perdew, Y. Wang, Phys. Rev. B 1992, 45, 13244.
| Crossref | GoogleScholarGoogle Scholar |
[375] S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 2010, 132, 154104.
| Crossref | GoogleScholarGoogle Scholar | 20423165PubMed |
[376] S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 2011, 32, 1456.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXjsF2isL0%3D&md5=738d507a3e0a68831e1f4257fbe0c764CAS | 21370243PubMed |
[377] F. M. Floris, J. Tomasi, J. L. Pascual Ahuir, J. Comput. Chem. 1991, 12, 784.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXls1Ort74%3D&md5=9734e4692d5e4d079e456a04cbb7c0b9CAS |
[378] R. G. Pearson, J. Chem. Educ. 1968, 45, 581.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF1cXltVShs74%3D&md5=46ada80ae14abbca3751f85ec08d71f0CAS |
[379] R. G. Pearson, Coord. Chem. Rev. 1990, 100, 403.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXksFWgsLo%3D&md5=e01b86bd323d24fb039afd0ba7240af7CAS |
[380] P. W. Ayers, R. G. Parr, R. G. Pearson, J. Chem. Phys. 2006, 124, 194107.
| Crossref | GoogleScholarGoogle Scholar | 16729803PubMed |
[381] B. Selinger, Chemistry in the Marketplace 1999 (Allen & Unwin: Sydney).
[382] J. R. Reimers, M. J. Ford, A. Halder, J. Ulstrup, N. S. Hush, Proc. Natl. Acad. Sci. USA 2016, 113, E1424.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xjt12hsLk%3D&md5=e9bd331ec8897f072b3fef80f7938f5fCAS | 26929334PubMed |
[383] P. K. Das, S. Samanta, A. B. McQuarters, N. Lehnert, A. Dey, Proc. Natl. Acad. Sci. USA 2016, 113, 6611.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28XptFWgsbY%3D&md5=e43c9828e4bb69c2e7200e2cc0b467b9CAS | 27302948PubMed |
[384] H. Schmidbaur, A. Schier, Chem. Soc. Rev. 2008, 37, 1931.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVOitb3O&md5=5e62131995a9457f97f1498ddb0543daCAS | 18762840PubMed |
[385] P. Pyykko, Angew. Chem. Int. Ed. 2004, 43, 4412.
| Crossref | GoogleScholarGoogle Scholar |
[386] M. H. McAdon, W. A. Goddard, J. Chem. Phys. 1988, 88, 277.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXhslersr0%3D&md5=b1a19ea82c5a0cc7928e533eda780b7dCAS |
[387] M. H. McAdon, W. A. Goddard, J. Phys. Chem. 1988, 92, 1352.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1cXhtF2iurw%3D&md5=45cb1f9543faec4421b04460bce28570CAS |
[388] Y. Wang, Q.-J. Chi, J.-D. Zhang, N. S. Hush, J. R. Reimers, J. Ulstrup, J. Am. Chem. Soc. 2011, 133, 14856.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtFaks7vJ&md5=a790d836b015fa77430e2b3caf950835CAS | 21859147PubMed |
[389] Y. Wang, Q. Chi, N. S. Hush, J. R. Reimers, J. Zhang, J. Ulstrup, J. Phys. Chem. C 2011, 115, 10630.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXlslKjtLo%3D&md5=48e58615013ddfc2704591351ecaf48cCAS |
[390] Y. Wang, Q. Chi, N. S. Hush, J. R. Reimers, J. Zhang, J. Ulstrup, J. Phys. Chem. C 2009, 113, 19601.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXht1CrsrfI&md5=c5e43af5b57ad48090117312129f8f90CAS |
[391] J. Yan, R. Ouyang, P. S. Jensen, E. Ascic, D. A. Tanner, B. Mao, J. Zhang, C. Tang, N. S. Hush, J. Ulstrup, J. R. Reimers, J. Am. Chem. Soc. 2014, 136, 17087.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhvFKqtbfO&md5=af0257f153d0e0ca4c0521736982650aCAS | 25407476PubMed |
[392] R. Ouyang, J. Yan, P. S. Jensen, E. Ascic, S. Gan, D. A. Tanner, B. Mao, L. Ni, J. Zhang, C. Tang, N. S. Hush, J. R. Reimers, J. Ulstrup, ChemPhysChem 2015, 16, 928.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXks1yrtrc%3D&md5=a539e0eb00ad8a04488bed372b0d1fabCAS | 25648513PubMed |
[393] Q. Chi, J. Zhang, J. Ulstrup, J. Phys. Chem. B 2006, 110, 1102.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtlClsbzF&md5=ebb9a5ab1f6415ef50889addaa6ddec8CAS | 16471649PubMed |
[394] Y. Wang, N. S. Hush, J. R. Reimers, J. Phys. Chem. C 2007, 111, 10878.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXntVCqt7o%3D&md5=af86cb082b2b0341d7bf8d547720838eCAS |
[395] J. Zhang, A. Bilic, J. R. Reimers, N. S. Hush, J. Ulstrup, J. Phys. Chem. B 2005, 109, 15355.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXmtlSgu7o%3D&md5=98dd51acbcd263da43becda134d9ac1eCAS | 16852948PubMed |
[396] Y. Wang, N. S. Hush, J. R. Reimers, J. Am. Chem. Soc. 2007, 129, 14532.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXht12gsrfJ&md5=d7851a1a7570bfc9c30d42ec30ddb6c6CAS | 17988124PubMed |
[397] R. K. Chadha, R. Kumar, D. G. Tuck, Can. J. Chem. 1987, 65, 1336.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXmt1Crtbc%3D&md5=c2c6a54428fdac8943a96d0f5a062dd2CAS |
[398] Y. Negishi, T. Tsukuda, J. Am. Chem. Soc. 2003, 125, 4046.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXhvF2lsbk%3D&md5=3fc565ad4e6a8990ad976ece103082aeCAS | 12670215PubMed |
[399] M. Brust, M. Walker, D. Bethell, D. J. Schiffrin, R. Whyman, J. Chem. Soc. Chem. Commun. 1994, 801.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXjtVCmurk%3D&md5=91a6fadea8db439ffc208bd6ec6c5d90CAS |
[400] P. J. G. Goulet, R. B. Lennox, J. Am. Chem. Soc. 2010, 132, 9582.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXnvVKqtb4%3D&md5=f707f4ed5fb19731548e4c5b8847e09dCAS |
[401] Y. Li, O. Zaluzhna, Y. J. Tong, Langmuir 2011, 27, 7366.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmtlyms7k%3D&md5=77341b36215a2dd169de40e7dbada098CAS | 21598931PubMed |
[402] L. Zhu, C. Zhang, C. Guo, X. Wang, P. Sun, D. Zhou, W. Chen, G. Xue, J. Phys. Chem. C 2013, 117, 11399.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXmvFyrtbg%3D&md5=0b14bd9f94e1d6c1b21f2cb96e00798cCAS |
[403] M. Brust, J. Fink, D. Bethell, D. J. Schiffrin, C. Kiely, J. Chem. Soc. Chem. Commun. 1995, 1655.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXns1yksrs%3D&md5=83ea52d685f7970a528530c9662926c4CAS |
[404] M. K. Corbierre, R. B. Lennox, Chem. Mater. 2005, 17, 5691.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtFSjt7%2FO&md5=e9b16434c02c90a2e4d5618204e5efb6CAS |
[405] E. A. Romero, J. L. Peltier, R. Jazzar, G. Bertrand, Chem. Commun. 2016, 52, 10563.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xht1ygtrbO&md5=244acc1681d872a30c9564a635abcc58CAS |
[406] M. G. Civit, X. Sanz, C. M. Vogels, C. Bo, S. A. Westcott, E. Fernández, Adv. Synth. Catal. 2015, 357, 3098.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhs1elurzP&md5=56a04c9e9c2255be33e1521c37f08f63CAS |
[407] C. Solé, E. Fernández, Angew. Chem. Int. Ed. 2013, 52, 11351.
| Crossref | GoogleScholarGoogle Scholar |
[408] R. E. Davis, J. A. Gottbrath, J. Am. Chem. Soc. 1962, 84, 895.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF38Xnslyntg%3D%3D&md5=f2c52ffbd05dff7ce54b792447900eecCAS |
[409] T. Rangel, D. Kecik, P. E. Trevisanutto, G.-M. Rignanese, H. Van Swygenhoven, V. Olevano, Phys. Rev. B 2012, 86, 125125.
| Crossref | GoogleScholarGoogle Scholar |
[410] P. Maksymovych, D. C. Sorescu, J. T. Yates, Phys. Rev. Lett. 2006, 97, 146103.
| Crossref | GoogleScholarGoogle Scholar | 17155271PubMed |
[411] R. Mazzarello, A. Cossaro, A. Verdini, R. Rousseau, L. Casalis, M. F. Danisman, L. Floreano, S. Scandolo, A. Morgante, G. Scoles, Phys. Rev. Lett. 2007, 98, 016102.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD2s7lvVGmtg%3D%3D&md5=ad7e2885c93553554108e97a4500bff9CAS | 17358489PubMed |
[412] A. Cossaro, R. Mazzarello, R. Rousseau, L. Casalis, A. Verdini, A. Kohlmeyer, L. Floreano, S. Scandolo, A. Morgante, M. L. Klein, G. Scoles, Science 2008, 321, 943.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXpslWrtb8%3D&md5=5fddb40776aeeb5625374115d7247d8fCAS | 18703737PubMed |
[413] P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell, R. D. Kornberg, Science 2007, 318, 430.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtFOjtb%2FP&md5=ae7f9586aca151450f7c347955a891afCAS | 17947577PubMed |
[414] D.-E. Jiang, M. L. Tiago, W. D. Luo, S. Dai, J. Am. Chem. Soc. 2008, 130, 2777.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsF2rtLk%3D&md5=bdc1c856c031c7620112e6fcd6ae4215CAS | 18257572PubMed |
[415] J. R. Reimers, Y. Wang, B. O. Cankurtaran, M. J. Ford, J. Am. Chem. Soc. 2010, 132, 8378.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXmvFarsrs%3D&md5=6ccf308578d16c7d6e85310688740d75CAS | 20518461PubMed |
[416] E. de la Llave, R. Clarenc, D. J. Schiffrin, F. J. Williams, J. Phys. Chem. C 2014, 118, 468.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXhvFSqsLrN&md5=7804915a4544e05b0a57df2a3f6c77c8CAS |
[417] A. Chaudhuri, M. Odelius, R. G. Jones, T. L. Lee, B. Detlefs, D. P. Woodruff, J. Chem. Phys. 2009, 130, 124708.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD1M3ltFOgsg%3D%3D&md5=6a5b76769fdd23d187e86ed5f228a70cCAS | 19334873PubMed |
[418] M. Konopka, R. Rousseau, I. Stich, D. Marx, J. Am. Chem. Soc. 2004, 126, 12103.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXnt1GmsbY%3D&md5=d6aeeea2829aa17cbb2bda6d2f95029aCAS | 15382946PubMed |
[419] J. A. Rodriguez, J. Dvorak, T. Jirsak, G. Liu, J. Hrbek, Y. Aray, C. Gonzalez, J. Am. Chem. Soc. 2003, 125, 276.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XovFygtbk%3D&md5=fe5cdd723f4777f14bf7a2cd87186f42CAS | 12515530PubMed |
[420] V. De Renzi, R. Rousseau, D. Marchetto, R. Biagi, S. Scandolo, P. U. Del, Phys. Rev. Lett. 2005, 95, 046804.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD2MvkvFOgtw%3D%3D&md5=c2c14bbdd05ec89f942887b7247c0e03CAS | 16090833PubMed |
[421] A. Bilic, J. R. Reimers, N. S. Hush, J. Chem. Phys. 2005, 122, 094708.
| Crossref | GoogleScholarGoogle Scholar | 15836163PubMed |
[422] H. Grönbeck, J. Phys. Chem. C 2010, 114, 15973.
| Crossref | GoogleScholarGoogle Scholar |
[423] T. Zhang, Z. Ma, L. Wang, J. Xi, Z. Shuai, Philos. Trans. R. Soc., A 2014, 372, 20130018.
[424] M.-C. Bourg, A. Badia, R. B. Lennox, J. Phys. Chem. B 2000, 104, 6562.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXkt1Gru74%3D&md5=4ff2115cd88dd88bdd1fd511a927b396CAS |
[425] H. Grönbeck, A. Curioni, W. Andreoni, J. Am. Chem. Soc. 2000, 122, 3839.
| Crossref | GoogleScholarGoogle Scholar |
[426] P. C. Rusu, G. Brocks, J. Phys. Chem. B 2006, 110, 22628.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtVKiur%2FL&md5=5284b8472772ecedf374d88b91b3ee49CAS | 17092010PubMed |
[427] Y. Li, G. Galli, F. Gygi, ACS Nano 2008, 2, 1896.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVWmu73E&md5=db0c67b24c2ccf0a9f3afdd1e1572e9bCAS | 19206430PubMed |
[428] http://www.gaussian.com/g_whitepap/thermo/thermo.pdf. Accessed 23 October 2016.


 ) of NH3 (green circles) fitted up to a torsional angle of τ = 44° (NHN bond angle θ = 77°) by a three-state three-parameter diabatic-potential model (
) of NH3 (green circles) fitted up to a torsional angle of τ = 44° (NHN bond angle θ = 77°) by a three-state three-parameter diabatic-potential model ( = 4.13 eV, λ = 10.55 eV, τm = 25.1°, RMS error 1.2 meV): purple- resulting adiabatic ground-state (g), singly valence-excited state (s), and doubly valence-excited state (d) (the ‘twin state’); red - localized representation of two of the diabatic potentials; blue - delocalized representation of the two of the diabatic potentials (both
= 4.13 eV, λ = 10.55 eV, τm = 25.1°, RMS error 1.2 meV): purple- resulting adiabatic ground-state (g), singly valence-excited state (s), and doubly valence-excited state (d) (the ‘twin state’); red - localized representation of two of the diabatic potentials; blue - delocalized representation of the two of the diabatic potentials (both  ). Reproduced from ref. [180] with permission of the PCCP Owner Societies.
). Reproduced from ref. [180] with permission of the PCCP Owner Societies.
 and its three orthogonal s1/2p5/2 bondable hybrid orbitals at a torsional angle of τ = 26.6° and HXH bond angle θ = 101.5°.). Reproduced from ref. [186] with permission of the PCCP Owner Societies.
and its three orthogonal s1/2p5/2 bondable hybrid orbitals at a torsional angle of τ = 26.6° and HXH bond angle θ = 101.5°.). Reproduced from ref. [186] with permission of the PCCP Owner Societies.