Implementation of network embedding strategy on proteome datasets from multi-source cancers to demonstrate marker proteins of cancers
Dezhi Sun A B # , Ruzhen Chen A # , Shuaikang Ma C , Yuqi Zhang A C and Dong Li
A B # , Ruzhen Chen A # , Shuaikang Ma C , Yuqi Zhang A C and Dong Li  A *
A *
A State Key Laboratory of Proteomics, Beijing Proteome Research Center, National Center for Protein Sciences (Beijing), Beijing Institute of Lifeomics, Beijing 102206, China.
B Department of Pharmaceutical Sciences, Beijing Institute of Radiation Medicine, Beijing 100850, China.
C College of Life Sciences, Hebei University, Baoding 071002, China.
Handling Editor: Mibel Aguilar
Australian Journal of Chemistry 76(8) 437-447 https://doi.org/10.1071/CH22176
Submitted: 10 August 2022 Accepted: 22 November 2022 Published: 19 January 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
The rapid production of high-throughput cancer omics data provides valuable data resources for revealing the pathogenesis, prognosis prediction and treatment strategies of cancers. However, the huge data scale brings great challenges to data analysis. Therefore, we applied the representation learning method to the joint analysis of biomedical network and omics data. According to the protein expression profile of patients with early-stage hepatocellular carcinoma, 15 dimensional embedding vectors of 101 samples were obtained. Unsupervised learning was then used to cluster the embedded vectors of the samples, and we found that the clustering of the embedded vectors of the samples was consistent with the clustering of the original data. Therefore, the spatial distribution of embedded vectors can maintain the similarity of samples. New pan-cancer subtypes were obtained by joint embedding the expression profile of pan-cancer proteomic and pathway network data. Nine hunded and forty four proteins such as KIF2C, AURKA, ATP1B1, BDH1 and C6ORF106 were found to be significantly related to these subtypes, and 143 biological pathways or processes such as p53 signaling pathway, nucleotide synthesis, immune diseases, metabolism, cholesterol synthesis and transportation were found to be significantly related to these subtypes. These results show that the representation learning system developed can realize the seamless connection between the omics data and the pathway network. Our method is expected to help mine the biological knowledge contained in the omics data and provide a new perspective for further explanation of the molecular mechanism.
Keywords: biological pathway, network embedding, pan-cancer analysis, proteomics, representation learning.
Introduction
High throughput quantitative proteomics technology is widely used for studying proteomics, which reflect the existing state of biomolecules in the sample at a specific time and state, such as expression level, modification, etc. The purpose of proteomics analysis is to explore the relationship between biomedical entities (such as sample–protein, protein–protein, sample–sample relationship). However, traditional analysis strategies usually ignore the interactions between proteins, which makes it difficult to discover the potential knowledge contained in the proteomics data. Pathway networks contains a lot of priori knowledge, such as protein–protein interactions in pathways, which can supplement the information in the omics data. The combination of the two cannot only make full use of the corresponding relationship between the samples and molecules in the omics data, but also retain as much as possible the correlation information between the molecules in the networks, which is conducive to the full development of knowledge excavate. Therefore, it is necessary to combine pathway networks with omics data.
Network embedding is a method of representation learning, which aims to express the associated entities and their relationships in the low dimensional semantic space. Specifically, it uses mathematical methods to represent the associated entities and their relationships with vectors in the low dimensional space, while retaining the structural information of the original data set. This low dimensional space is called embedded space.[1] In this way, in the embedded space, the nodes and edges of the network can be expressed as low dimensional embedded vectors, and then such vectors can be input into typical and mature machine learning methods such as neural network, support vector machine (SVM) and decision tree for training. This makes the classical machine learning model able to learn from network data, which was impossible before. Omics data can be regarded as an adjacency matrix of networks composed of samples and molecules.[2] Omics data representation learning technology is essentially a dimensionality reduction method, which has no requirements for the original distribution of data. At present, some work has applied representation learning to the analysis of omics data. For example, Hou et al.[3] proposed a new unsupervised feature selection method based on joint embedded learning and sparse regression (JELSR). Later, LJELSR[4] enhanced the JELSR algorithm by adding L₁-norm constraints to the regularization term, and applied it to identify differentially expressed genes and cluster samples of different genomic data. Embedding methods above have some shortcomings. On the one hand, they are linear dimensionality reduction. On the other hand, they only embed the omics data without involving priori knowledge. Therefore, for highly complex omics data, the amount of information is not fully utilized. Single Cell Rep- resentation Learning (SCRL) method[5] embedded the single-cell transcriptome data with the pathway networks to obtain the embedding vector that could maintain the cell similarity. However, there is no algorithm for the joint embedding of proteomic data and pathway network data. Therefore, we developed a new tool for non-linear dimensionality reduction of proteomic data based on network embedding.
Results and discussion
Sample–protein network embedding preserving sample–sample relationship
We first used the protein expression profile data set of samples from patients with early-stage hepatocellular carcinoma published by Jiang et al.[6] to evaluate the model. This data set contains the expression data of 9252 proteins in tumor and adjacent non-tumor tissues of 101 patients. Jiang divided the 101 samples into three subtypes: S-I, S-II and S-III. We first filtered out the proteins expressed in less than 25% of the samples (remaining 7207 proteins), and then selected the top 25% proteins with the largest variance of expression value in the samples (1802 proteins). We then integrated the profile into a sample–protein network, containing 1903 nodes (101 sample nodes, 1802 protein nodes) and 90 694 edges reflecting the expression relationship between these nodes. The weight of the edges represented the expression level.
We downloaded the human pathway data set from the IntPath database. Protein–protein interactions of 583 human pathways were collected from KEGG,[7] WikiPathways,[8] BioCyc,[9] etc. We integrated the pathways into a protein–protein interaction network. The network contained 3081 protein nodes and 15 281 edges that reflected the interaction between these nodes.
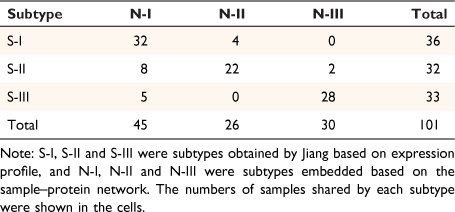
The embedding vectors of 1903 entities were obtained by sample–protein network embedding, including the embedding vectors of 101 samples and 1802 proteins. In order to intuitively observe the distribution of the corresponding embedding vectors of the samples in the embedding space, we showed them in three-dimensional space by principal components analysis (PCA). The samples in the respective subtypes of S-I, S-II and S-III tended to be distributed in the adjacent areas in the embedding space (Fig. 1a). In order to verify whether the embedded vector could reflect the similarity of the original samples. We used consistent clustering to cluster the embedded vectors of samples. Each class in the clustering results was regarded as a subtype. After consistent clustering, samples could be grouped into three subtypes: N-I, N-II, N-III (Fig. 1b). Jiang found that the non-negative matrix factorization method (NMF) can effectively divide the early-stage HCC cohort into subtypes with different clinical outcomes, therefore we next compared our method based on embedded vectors with the NMF method based on expression matrices. The number of samples in the repeated part between each classification was counted (Table 1). Obviously, the distribution of samples in these three categories was highly consistent with the results of Jiang. The embedding vector learned by our model maintained the similarity between samples.
|
Joint network embedding to discover new pan-cancer subtypes
The embedding of the sample–protein network can only objectively reflect the distribution of the protein expression level of the sample. Therefore, we implemented the joint network embedding, combining the prior knowledge (protein–protein network) with the proteomic profiles. We used the pan-cancer proteomics profile,[10] an expression profile data set of 2000 proteins containing 532 cancer samples from five tissue sources to construct the sample–protein network. The sample–protein network contained 2532 nodes (including 532 sample nodes and 2000 protein nodes) and 804 760 edges reflecting the expression relationship between these nodes, and the weight of the edges was the expression level. In the same way, the pathway data were integrated into a protein–protein network, which contained 3276 protein nodes, and 15 332 edges that reflect the interaction between these nodes.
The above two networks were input into our joint embedding model, after which the embedding vectors of 4922 entities were obtained, including the embedding vectors of 532 samples, 2000 proteins and 2390 pathway proteins. In order to intuitively observe the distribution of the corresponding embedding vectors of the samples in the embedding space, they were represented in the three-dimensional space (Fig. 2a). As can be seen, samples from different tissue sources were mixed together in the space, which provides a good basis for distinguishing pan-cancer subtypes.
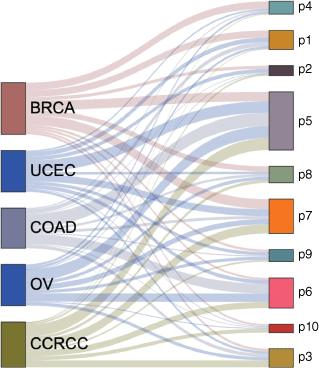
We performed consensus clustering on low dimensional embedding vectors of 532 tumor samples trained with joint embedding. The samples were divided into ten clusters, and each cluster represented a pan-cancer subtype (Fig. 1b). Because prior knowledge (pathway information) was added in the process of network embedding, it was named as prior based clusters, and these pan-cancer subtypes were hereinafter referred to as P1, P2… P10 (Table 2). We found that each subtype contained cancer samples from different tissue sources, and different subtypes may also contain cancer samples from the same tissue source. Most subtypes were dominated by three or less tumor tissue sources. For example, the vast majority of P1 are BRCA, COAD and UCEC samples (83%), P6 is dominated by CCRCC, COAD and OV (81%), P7 is dominated by BRCA, CCRCC and UCEC samples (76%) and P4 is dominated by BRCA (58%). P5 is the subtype with the largest sample size, and the samples from five tissue sources account for the same proportion in P5 (Fig. 3).

|
|
Discovery of pan-cancer subtypes related proteins based on embedded vector similarity
In the vector embedding training, we first assigned a random embedding vector to each entity, including samples and proteins, and then modified the parameters of the embedding vector by optimizing the loss function. In fact, the optimization process is to make the embedding vectors closer between entities with larger association weight in each network, and vice versa (Fig. 4). Depending on this premise, the sample vectors and protein vectors are comparable in the same space.
First, the embedding vectors of all samples in each pan-cancer subtype were averaged into a central vector to represent the pan-cancer subtype. Spearman correlation analysis was carried out between all proteins and this central vector, and proteins with the most significant correlation were selected as the related proteins of this subtype. In this way, a total of 944 proteins related to these 10 subtypes were obtained (Fig. 5a). In order to explore the significance of the correlation between the proteins and subtypes, the average standardized expression values (mean s.d.) of these proteins in pan-cancer subtype samples were extracted (Fig. 5b). Comparing Fig. 5a, b, it can be found that in most cases, the closer the protein is to the center of the subtype in the embedding space, the higher the protein’s average expression value in the samples of this subtype is, and vice versa. This shows that a large part of the similarity between the embedding vector of samples and proteins in embedding space comes from the expression value of proteins in the proteomic profile. Of course, another part comes from the connection between pathway proteins and samples generated by protein–protein association in the pathway network.
The GO entry enrichment analysis of the top 100 proteins most related to each subtype by David shows that the related proteins in P1 are mainly concentrated in extracellular exosomes, which were related to calcium binding function. The related proteins in P2 are concentrated on the cell membrane and are related to protein binding, immune regulation and other functions. P3 related proteins are concentrated in the cytoplasm and are related to ATP binding, innate immune response and other functions. P4 related proteins are mainly concentrated in cytoplasm and nucleoplasm, and are related to cell division. The related proteins in P5 are mainly concentrated on the cytoplasmic membrane and are related to cell apoptosis, transportation, cell adhesion and other functions. The related proteins in P6 are mainly concentrated in the extracellular matrix, which is related to adhesive plaque. P7 related proteins are mainly concentrated in the extracellular space, which is related to cell adhesion. P8 and P9 related proteins are related to extracellular exosomes, and P9 related proteins are enriched into integrin mediated signaling pathways; P10 related proteins are mainly enriched in the components of the membrane. Using DisGeNET (https://www.disgenet.org/home/) analysis found that 19 of the top 30 proteins associated with these 10 subtypes have been reported to be associated with these five tissue-derived tumors. For example, the protein most related to P4 is KIF2C, which has been reported to be significantly related to the invasive characteristics of breast cancer,[11] and AURKA has also been reported to promote the proliferation and survival of breast cancer cells.[12] The other 11 are new genes that have not been reported to be related to these five cancers, such as the protein C6ORF132 most related to P5, which has not been reported to be related to these five cancers before, and it is not significantly related to any subtype by traditional protein expression profile difference analysis. At present, there are few studies on the function of C6ORF132 protein, but some studies have shown that the high expression of C6ORF132 is detrimental to the prognosis of pancreatic cancer.[13]
Discovery of pan-cancer subtype related pathways based on embedded vector similarity
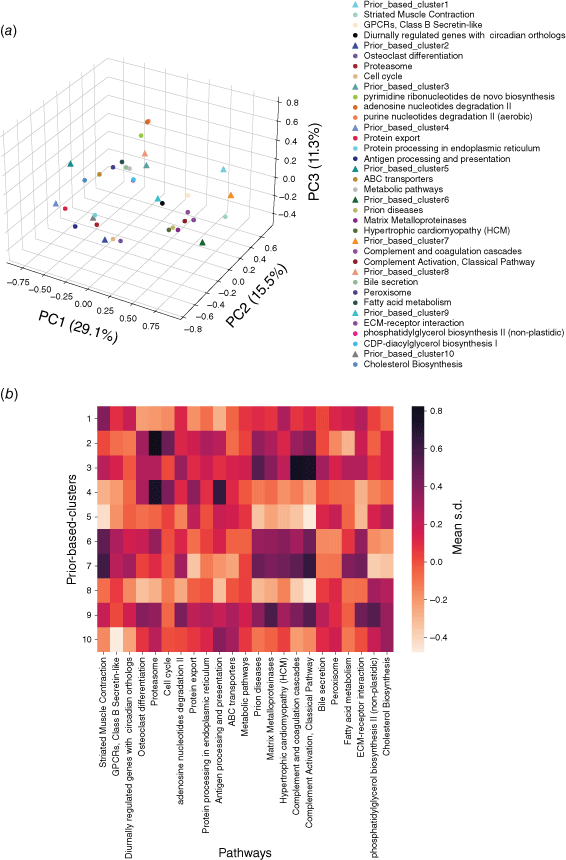
Using a similar principle, the embedding vectors of all proteins in each pathway were averaged into a central vector to represent the pathway. Then Spearman correlation analysis was carried out between the center vector of each subtype and each pathway. The pathways with the most significant correlation (P < 0.05) were selected as the correlation pathway of this subtype, so a total of 143 pathways related to these 10 subtypes were obtained. Fig. 6a visualizes the center vectors of pan-cancer subtypes and the first three pathways related to each subtype in three dimensions. In order to explore the significance of the correlation between pan-cancer subtype related pathways and subtypes, we calculated the average standardized expression value (mean s.d.) of the proteins in each pathway in each pan-cancer subtype (Fig. 6b). Comparing Fig. 6a, b, it is also found that the closer the center of the pathway is to the center of the subtype in embedding space, the higher the average expression value in the samples of this subtype is, and vice versa. This is because we have fully considered the expression relationship in the expression profile when embedding the networks, and some related pathways whose average expression values are not significantly up-regulated relative to other subtypes will also be found by our model, such as the Bile secretion pathway significantly related to P8.
|
After analyzing the pathways significantly related to each subtype, we described these subtypes as follows: P2 is mainly related to the activation of p53 signaling pathway to promote the start of cell cycle. Previously, it was reported that TP53 mutation is a driving mutation in some samples of breast cancer and endometrial cancer,[14] indicating that the samples in P2 may have the same characteristics. P3 is mainly related to nucleotide synthesis and metabolism. Endometrial cancer samples account for the largest proportion of P3 (38%), and increased nucleotide synthesis is conducive to the proliferation of endometrial cancer cells.[15] P4 is a subtype related to immune diseases, and the immune system plays an important role in inhibiting tumor development,[16] so immune system defects may be characteristic of samples in P4. The functional characteristics of P5 and P8 are mainly reflected in metabolism and transportation. The activation of oncogenes and the loss of tumor suppressors promote the metabolism of tumor cells, thereby improving the intake of nutrients, thus providing energy and material basis for the growth and proliferation of tumor cells.[17] The representative pathway related to P6 and P7 is matrix metalloproteinase. Due to its large up-regulation in malignant tumors and its unique ability to degrade extracellular matrix components, matrix metalloproteinase is considered to be an ideal target for tumor therapy.[18] Meanwhile P10 is related to cholesterol synthesis and transportation. Some tumor cells have a high demand for cholesterol. Blocking the synthesis and uptake of cholesterol has an inhibitory effect on the formation and growth of tumors.[19] P10 may be very sensitive to the treatment strategy for cell cholesterol homeostasis.[20]
Experimental
Workflow
The basic idea of the model was to combine the proteomic data with the prior knowledge in pathway network, to learn the low dimensional vector representation of samples and proteins. Samples with similar protein expression patterns (converged with pathway networks) should be mapped to adjacent regions in the embedding space. The method included two steps: network construction and network embedding. First, we converted the profile matrix into the form of triples, and then integrated them into the sample–protein network. Next, we downloaded human pathway data from IntPath,[21] a public pathway data set integrated by experts, and integrated them into a protein–protein network in pathways. The above two networks were used as input data and submitted to the training program developed for joint embedded learning. Theoretically, the purpose of embedding learning is to make the similarity of embedding vectors in the embedding space consistent with that of corresponding entities in the network. For this purpose, we built a workflow to implement embedding training, and output the embedding result vector of each entity for downstream analysis (Fig. 7).

|
Integration of sample protein network and pathway protein network
Sample–protein network: given an expression data set of S samples and P proteins, for each expression value vij in the set, the corresponding sample and protein was denoted by si and mi. We used a binary (si, mj) to represent them, and vij is the weight of the binary. In this way, a sample–protein network Esm was constructed by using the weighted binary extracted from the expression profile: if the corresponding expression value |vij| > 0, an edge with weight of vij was added between sample si and protein mj.
Protein–protein network: given a priori pathway network, if protein pi and protein mj were directly connected in the network, we used a binary (pi, mj) to represent them. In this way, we used the binary extracted from the network to construct a pathway protein–protein network Epm: If the protein pi and protein mj were directly connected, an edge would be added with a weight of one between the protein pi and protein mj.
Establishment of loss function
Let S be the number of samples, M the number of proteins and P the number of proteins not included in the sample–protein network (pathway protein). And s was a sample, m was a protein and p was a pathway protein. The index of samples, proteins, pathway proteins were i = 1, 2, …, S, j = 1, 2, …, M and j* = 1, 2, …, P. The low dimensional embedding vector of si, mj, pj* were 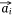 ,
, 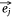 ,
, 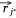 . vij was the expression value of protein mj in sample si in omics data, and wj*j was the weight of pathway protein pj* and protein mj in the priori network. And
. vij was the expression value of protein mj in sample si in omics data, and wj*j was the weight of pathway protein pj* and protein mj in the priori network. And 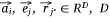 was the dimension of embedded vector.
was the dimension of embedded vector.
We used the following loss function (Eqn 1) to evaluate the embedding effect of the sample protein network:
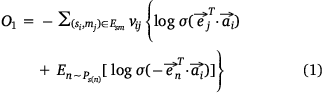
We used the following loss function (Eqn 2) to evaluate the embedding effect of the pathway protein network:
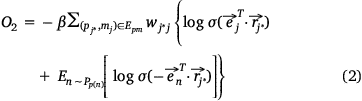
where, 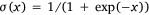 was the sigmoid function,
was the sigmoid function, 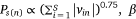 was the weight of priori knowledge in model training, usually set to one.
was the weight of priori knowledge in model training, usually set to one.
When the embedding vectors 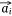 and
and 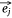 corresponding to a pair of entities si and mj in Esm were close to each other in the embedding space, then their contribution to O1 decreased and vice versa. If the embedding vectors of all entity pairs in Esm conform to this distribution, O1 should be the minimum. Similarly, the design of O2 was also based on this purpose. Therefore, in the process of joint embedding, the following function (Eqn 3) should be optimized:
corresponding to a pair of entities si and mj in Esm were close to each other in the embedding space, then their contribution to O1 decreased and vice versa. If the embedding vectors of all entity pairs in Esm conform to this distribution, O1 should be the minimum. Similarly, the design of O2 was also based on this purpose. Therefore, in the process of joint embedding, the following function (Eqn 3) should be optimized:

Ojoint was the loss function of our model theory.
Using negative sampling technique to simplify loss function
Negative samples were defined as pairs of entities that do not exist in the network. In practice, we found that the direct optimization of the objective function Ojoint had a high calculation cost, because when calculating the loss value of each pair of positive samples 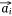 ,
, 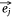 we also needed to calculate all the negative samples with
we also needed to calculate all the negative samples with 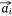 as the head entity. However, negative sampling[22] helped simplify the original loss function to the proxy objective function of binary classification, which had the same parameters but low computational complexity. Specifically, Eqns 1, 2 can be rewritten as Eqns 4, 5:
as the head entity. However, negative sampling[22] helped simplify the original loss function to the proxy objective function of binary classification, which had the same parameters but low computational complexity. Specifically, Eqns 1, 2 can be rewritten as Eqns 4, 5:
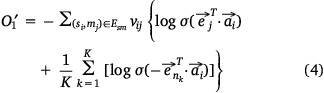
where, 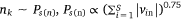 , K was the number of negative samples.
, K was the number of negative samples.
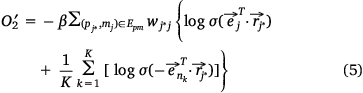
where, 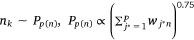 , K was the number of negative samples.
, K was the number of negative samples.
Improving training efficiency by using redesigned edge sampling technique
In the process of model training, we randomly selected an edge (si, mj) from the sample protein network, and the corresponding K negative edges, and their embedded vectors were used to calculate the losses. The stochastic gradient descent (SGD) method was then used to calculate the gradient first, and the gradient was multiplied by the weight of the edge to correct the vector parameters. But such a design would lead to a ‘gradient explosion and vanishing’ problem. To overcome this problem, the edge sampling technique proposed by Tang[23] was adopted. Its basic idea was to divide the edge with weight into several edges with weight of one, and then used the protein expression value in the sample as the probability to sample. However, this method had two shortcomings: first, some omics data, such as pan-cancer omics data that had been standardized many times, contained a large number of negative values; Secondly, this method tended to train the protein with high absolute expression value, but did not pay attention to the protein whose expression was significantly inhibited, which was not comprehensive for the study of protein expression changes in samples. Therefore, we redesigned the edge sampling technique: If the weight of edge (si, mj) was vij, we transformed this edge into |vij| edges with the weight of 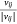 . Eqns 4, 5 were redesigned to give Eqns 6, 7:
. Eqns 4, 5 were redesigned to give Eqns 6, 7:
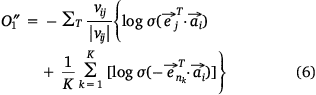
where, 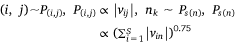 , K was the number of negative samples, T was the maximum training epochs.
, K was the number of negative samples, T was the maximum training epochs.
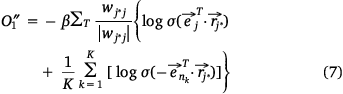
where, 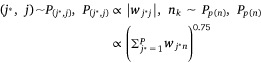 , K was the number of negative samples, T was the maximum training times.
, K was the number of negative samples, T was the maximum training times.
In this way, the loss function can be rewritten as Eqn 8:
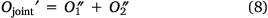
Model training steps
In practical operation, we trained the model by minimizing the loss function to Ojoint′ according to the following steps:
Algorithm 1 Model training steps
Input: Esm, Epm
System parameter: total training epochs T, number of negative samples K, embedded dimension D, priori knowledge weight
Output: low dimensional embedding vectors of all entities in Esm, Epm
1: function TRAINING(Esm, Epm)
2: From the uniform distribution of [−1,1], initialize a D-vector representation for all entities in Esm and Epm randomly
3: while iter < T do
4: One edge is randomly selected from Esm, and K negative edges are randomly selected from Ps(n) to update the sample embedding vector and protein embedding vector
5: One edge is randomly selected from Epm, and K negative edges are randomly selected from
noise distribution Pp(n) to update the pathway protein embedding vector and protein embedding vector
6: end while
7: Output all D-dimensional vectors
8: end function
Sample–protein network embedding
In order to verify the effectiveness of our method, the sample–protein network was first embedded without adding priori knowledge (pathway network). We set the weight parameters of the pathway protein–protein network β Set to zero. The sample–protein network was input into the model for 15-dimensional vector embedding, training 1 million epochs with five negative samples per epoch. In order to intuitively observe the distribution of the corresponding embedding vectors of the samples in the embedding space, we showed them in three-dimensional space by PCA.
Joint network embedding
We carried out the joint network embedding so that the embedding vector of the sample doesnt just reflect the protein expression level. The priori knowledge (pathway network) was added to the model and jointly embedded with the sample–protein network. The weight parameters of the pathway protein–protein network β was set to one. The embedding dimension was set to 15, the number of negative samples was five, and the training epoch 1 million.
Conclusions
We established a learning method for representation of omics data based on the embedding of pathway networks, which can represent the entities in omics data and pathway networks as a low dimensional embedding vector. The distribution of the embedding vector in space is able to maintain the similarity between entities, which achieves a seamless bridging of omics data and prior knowledge.
Using our method to learn the pan-cancer protein expression profiles derived from five tissues, we obtained ten pan-cancer subtypes based on the embedded vectors and found 944 proteins and 143 pathways significantly associated with the pan-cancer subtypes, such as ATP1B1, BDH1, MMPs and ABC transporters.
Biological networks are expected to play an important role in the field of biomedical research, but their potential remains to be explored, and there are still some issues to be considered. The future development of our network embedding methods may incorporate the following aspects:
The entities and relationship types in the protein–protein network are relatively single, our method was applied only to tumor data. In future work, we will further optimize the methodology to enable its extended application to other research areas including fibrosis and to more heterogeneous networks.
The basic idea of our paper is to combine the proteomic data with the prior knowledge in pathway networks to discover biological insights. The reason why we focus on proteomics is that proteins play direct roles in pathways, and the integration with pathway data is more reasonable in biology. The Cancer Genomics Atlas (TCGA) contains proteomic data derived from the reverse phase protein array, which contains limited proteins and there is only a very small overlap between the genes corresponding to proteins in the TCGA and the genes in the biological pathway. Therefore, we did not try our method in the TCGA datasets. Of course, we will improve the method and apply it to the proteomic datasets of TCGA in future work. In addition, multi-omics data has inconsistencies and up- and downstream regulatory relationships between different omics molecules may be implied in the biological networks. This provides an idea of intelligent integration of multi-omics data, but at present, there is much to break through in this area.
Supplementary material
Trained embedding matrices and program codes were available and freely accessible online in https://github.com/1300060609/PPRL. Supplementary material is available online.
Data availability
The models and data generated in this study are available from lidong.bprc@foxmail.com on reasonable request.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This work was supported by the National key Research and Development Program of China, grant number 2021YFA1301603 and 2020YFE0202200. This work was also funded by the National Natural Science Foundation of China, grant number 32088101 and 31871341.
Acknowledgements
The authors sincerely appreciate the help from Ed Nice for this work, who is our long-time friend and collaborator. They are very honored to contribute this paper to celebrate his 75 years birthday.
References
[1] H Cai, VW Zheng, CC Chang, A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans Knowl Data Eng 2018, 30, 1616.| A comprehensive survey of graph embedding: Problems, techniques, and applications.Crossref | GoogleScholarGoogle Scholar |
[2] H Xu, L Gao, M Huang, R Duan, A network embedding based method for partial multi-omics integration in cancer subtyping. Methods 2021, 192, 67.
| A network embedding based method for partial multi-omics integration in cancer subtyping.Crossref | GoogleScholarGoogle Scholar |
[3] C Hou, F Nie, X Li, D Yi, Y Wu, Joint embedding learning and sparse regression: a framework for unsupervised feature selection. IEEE Trans Cybern 2014, 44, 793.
| Joint embedding learning and sparse regression: a framework for unsupervised feature selection.Crossref | GoogleScholarGoogle Scholar |
[4] S-S Wu, M-X Hou, C-M Feng, J-X Liu, LJELSR: A strengthened version of jelsr for feature selection and clustering. Int J Mol Sci 2019, 20, 886.
| LJELSR: A strengthened version of jelsr for feature selection and clustering.Crossref | GoogleScholarGoogle Scholar |
[5] X Li, W Chen, Y Chen, et al. Network embedding-based representation learning for single cell RNA-seq data. Nucleic Acids Res 2017, 45, e166.
| Network embedding-based representation learning for single cell RNA-seq data.Crossref | GoogleScholarGoogle Scholar |
[6] Y Jiang, A Sun, Y Zhao, W Ying, H Sun, X Yang, B Xing, W Sun, L Ren, B Hu, C Li, L Zhang, G Qin, M Zhang, N Chen, M Zhang, Y Huang, J Zhou, Y Zhao, M Liu, X Zhu, Y Qiu, Y Sun, C Huang, M Yan, M Wang, W Liu, F Tian, H Xu, J Zhou, Z Wu, T Shi, W Zhu, J Qin, L Xie, J Fan, X Qian, F He, Chinese Human Proteome Project (CNHPP) Consortium. Proteomics identifies new therapeutic targets of early-stage hepatocellular carcinoma. Nature 2019, 567, 257.
| Proteomics identifies new therapeutic targets of early-stage hepatocellular carcinoma.Crossref | GoogleScholarGoogle Scholar |
[7] M Kanehisa, M Furumichi, Y Sato, M Ishiguro-Watanabe, M Tanabe, KEGG: Integrating viruses and cellular organisms. Nucleic Acids Res 2021, 49, D545.
| KEGG: Integrating viruses and cellular organisms.Crossref | GoogleScholarGoogle Scholar |
[8] M Martens, A Ammar, A Riutta, A Waagmeester, DN Slenter, K Hanspers, et al. WikiPathways: Connecting communities. Nucleic Acids Res 2021, 49, D613.
| WikiPathways: Connecting communities.Crossref | GoogleScholarGoogle Scholar |
[9] PD Karp, R Billington, R Caspi, CA Fulcher, M Latendresse, A Kothari, et al. The BioCyc collection of microbial genomes and metabolic pathways. Brief Bioinform 2019, 20, 1085.
| The BioCyc collection of microbial genomes and metabolic pathways.Crossref | GoogleScholarGoogle Scholar |
[10] F Chen, DS Chandrashekar, S Varambally, CJ Creighton, Pan-cancer molecular subtypes revealed by mass-spectrometry-based proteomic characterization of more than 500 human cancers. Nat Commun 2019, 10, 5679.
| Pan-cancer molecular subtypes revealed by mass-spectrometry-based proteomic characterization of more than 500 human cancers.Crossref | GoogleScholarGoogle Scholar |
[11] G Jiang, X Zhang, Y Zhang, L Wang, C Fan, H Xu, Y Miao, E Wang., A novel biomarker C6orf106 promotes the malignant progression of breast cancer. Tumour Biol 2015, 36, 7881.
| A novel biomarker C6orf106 promotes the malignant progression of breast cancer.Crossref | GoogleScholarGoogle Scholar |
[12] Y Zou, WS Henry, EL Ricq, ET Graham, et al. Plasticity of ether lipids promotes ferroptosis susceptibility and evasion. Nature 2020, 585, 603.
| Plasticity of ether lipids promotes ferroptosis susceptibility and evasion.Crossref | GoogleScholarGoogle Scholar |
[13] F Pontén, K Jirstrm, M Uhlen, The human protein atlas—a tool for pathology. J Pathol 2008, 216, 387.
| The human protein atlas—a tool for pathology.Crossref | GoogleScholarGoogle Scholar |
[14] C Kandoth, MD McLellan, F Vandin, K Ye, B Niu, C Lu, M Xie, Q Zhang, JF McMichael, MA Wyczalkowski, M Leiserson, CA Miller, JS Welch, MJ Walter, MC Wendl, TJ Ley, RK Wilson, BJ Raphael, L Ding, Mutational landscape and significance across 12 major cancer types. Nature 2013, 502, 333.
| Mutational landscape and significance across 12 major cancer types.Crossref | GoogleScholarGoogle Scholar |
[15] R Teng, Z Liu, H Tang, W Zhang, Y Chen, R Xu, L Chen, J Song, X Liu, H Deng, HSP60 silencing promotes warburg-like phenotypes and switches the mitochondrial function from ATP production to biosynthesis in ccRCC cells. Redox Biol 2019, 24, 101218.
| HSP60 silencing promotes warburg-like phenotypes and switches the mitochondrial function from ATP production to biosynthesis in ccRCC cells.Crossref | GoogleScholarGoogle Scholar |
[16] ML Disis, Immune regulation of cancer. J Clin Oncol 2010, 28, 4531.
| Immune regulation of cancer.Crossref | GoogleScholarGoogle Scholar |
[17] LK Boroughs, RJ DeBerardinis, Metabolic pathways promoting cancer cell survival and growth. Nat Cell Biol 2015, 17, 351.
| Metabolic pathways promoting cancer cell survival and growth.Crossref | GoogleScholarGoogle Scholar |
[18] LM Coussens, B Fingleton, LM Matrisian, Matrix metalloproteinase inhibitors and cancer—Trials and tribulations. Science 2002, 295, 2387.
| Matrix metalloproteinase inhibitors and cancer—Trials and tribulations.Crossref | GoogleScholarGoogle Scholar |
[19] (a) H Xu, S Zhou, Q Tang, H Xia, F Bi, Cholesterol metabolism: New functions and therapeutic approaches in cancer. Biochim Biophys Acta Rev Cancer 2020, 1874, 188394.
| Cholesterol metabolism: New functions and therapeutic approaches in cancer.Crossref | GoogleScholarGoogle Scholar |
(b) S Ehmsen, MH Pedersen, G Wang, MG Terp, A Arslanagic, BL Hood, et al. Increased cholesterol biosynthesis is a key characteristic of breast cancer stem cells influencing patient outcome. Cell Rep 27, 3927.
| Increased cholesterol biosynthesis is a key characteristic of breast cancer stem cells influencing patient outcome.Crossref | GoogleScholarGoogle Scholar |
[20] (a) PMR Cruz, H Mo, WJ Mcconathy, N Sabnis, AG Lacko, The role of cholesterol metabolism and cholesterol transport in carcinogenesis: A review of scientific findings, relevant to future cancer therapeutics. Front Pharmacol 2013, 4, 119.
| The role of cholesterol metabolism and cholesterol transport in carcinogenesis: A review of scientific findings, relevant to future cancer therapeutics.Crossref | GoogleScholarGoogle Scholar |
(b) OF Kuzu, R Gowda, MA Noory, et al. Modulating cancer cell survival by targeting intracellular cholesterol transport. Br J Cancer 2017, 117, 513.
| Modulating cancer cell survival by targeting intracellular cholesterol transport.Crossref | GoogleScholarGoogle Scholar |
[21] H Zhou, J Jin, H Zhang, B Yi, M Wozniak, L Wong, IntPath--an integrated pathway gene relationship database for model organisms and important pathogens. BMC Syst Biol 2012, 6, S2.
| IntPath--an integrated pathway gene relationship database for model organisms and important pathogens.Crossref | GoogleScholarGoogle Scholar |
[22] Mikolov T, Sutskever I, Kai C, Corrado G, Dean J. Distributed representations of words and phrases and their compositionality. In: Burges CJ, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors. Advances in neural information processing systems 26; 2013.
[23] Tang J, Qu M, Wang M, Zhang M, et al. LINE: Large‐scale information network embedding. Proceedings of the 24th international conference on world wide web; 2015. pp. 1067–1077.
| Crossref |.






