Analysis of Nanoconfined Protein Dielectric Signals Using Charged Amino Acid Network Models

Protein dynamics covers multiple spatiotemporal scale processes, including slow motions (microsecond to second), which are not much understood because they are difficult to measure, even though they are underlying protein folding and protein functions.^[1–3]

Fast motions (femtosecond to nanosecond) concern local atomic motions (vibration, amino acid side chain motions) and are measured by ultra-fast techniques such as ultra-fast NMR spectroscopy, femtosecond simulated Raman spectroscopy, ultra fast transient Infra Red spectroscopy, or ultra resolution X-ray crystallography and X-ray laser.^[4–13] Molecular dynamics (MD) simulations have atomic resolution and can now also cover motions up to a millisecond thanks to the ANTON super computer.^[1] However, MD simulations at high resolution are limited in terms of size and it remains hard to assess motions slower than the microsecond range.^[14,15]

Slow motions concern the collective motions of many atoms within areas of large size such as secondary and tertiary structural elements (microsecond to millisecond) up to domains or chain (millisecond to second).^[3] The slow fluctuation dynamics is monitored by lower spatial resolution techniques such as atomic force microscopy (AFM) or fluorescence spectroscopy (e.g. Förster resonance energy transfer, FRET), where the detailed MDs are generally lost.^[16–18] The slow motions are also investigated with network models and integrative approaches combining experimental and multiple theoretical approaches.^[19–30] They are particularly successful in monitoring the slow motions involved in protein assembly and pore formation.^[28,31–33]

Broadband dielectric spectroscopy (BDS), although not often used on proteins, can monitor protein MDs in the frequency range from 1 Hz to 10⁶ Hz where the slow motions from microseconds to seconds involved in protein folding and protein functions take place.^[34–37] The advantage of BDS is the capacity to characterise dipole features both at the local scale (dipole environment) with the temperature at maximum signal, and at a larger scale through fluctuations of collective motions exhibiting a characteristic relaxation tau (τ), defined as the inverse of the frequency. However, as for other biophysics methods such as fluorescence spectroscopy, the measurement is performed at the macroscopic scale where responses come from the bulk composed of many protein and solvent molecules containing many dipoles.

To overcome some of these limits, the dynamics of the cholera toxin B pentamer (CtxB₅) was measured by BDS after different thermal treatments, but under nanoconfined and dehydrated conditions.^[37] Thus, no bulk water contributed to the dielectric signal and attograms (considering a density of ~1 g cm⁻³, 1 attogram is ~10 nm × 10 nm × 10 nm) of matter were probed, approaching the characteristic dimension of one protein.^[37] The nanoconfinement, initially developed to analyse attograms (1 attogram = 10⁻¹⁸ g) and zeptograms (1 zeptogram = 10⁻²¹ g) of matter, allows one to investigate the dielectric behaviour of matter on a length-scale comparable with the molecular dimensions.^[38,39] In our study, the BDS signal was found to probe protein conformations that arise from the toxin thermal unfolding.^[37] Based on knowledge on the scale of protein dynamics and on toxin unfolding mechanisms, a model of the toxin thermal unfolding monitored by BDS was proposed where two non-native pentamers and toxin assembly intermediates were captured.

Nevertheless, because the sample was a mixture of protein, phosphate buffered saline (PBS), and adsorbed water, the global dielectric signal was not de-convoluted in terms of distinct dipolar relaxation.

Here, we use network-based models to infer the protein dipoles present in the native toxin pentamer and network based analyses to show that, consistently with our model, the toxin interfaces are distinguishable dielectrically and thermally.

We have recently shown that the dielectric signals of CtxB₅ measured by BDS in nanoconfined and dehydrated conditions evolved with the thermal treatments of the toxin at 60, 100, 140, and 180°C, probing for the toxin thermal unfolding.^[37] However, because the protein sample was a mixture of three compounds – the protein, phosphate buffer saline (PBS), and protein adsorbed-water – it was impossible to analyse the global dielectric signals in terms of individual dipolar relaxations. In fact, understanding the individual contribution of each compound and how the individual signals combine together to give rise to the global signal is intractable.

Instead, we proposed a model of the thermal toxin unfolding where the global dielectric signal was interpreted based on the knowledge on protein dynamics from MD simulations and from experimental investigations of protein assembly and disassembly under macroscopic conditions where non-native pentamers and CtxB assembly intermediates were identified.^[39–42] Protein assembly can be described by two mechanisms, the induced fit mechanism where the protein monomer folds before assembling and the fly-casting mechanism where the folding and assembling are concomitant.^[40,43–45] Protein disassembly involves transitions from native oligomers to either folded monomers or non-native oligomers.^[46–49] In the model, the three distinct MDs detected by BDS, referred to as MD₁, MD₂ and MD₃, were assigned to two different non-native pentamers (MD₁ and MD₃) and to toxin assembly intermediates (MD₂), suggesting that the dielectric signal probed the toxin interfaces.^[37]

Here, we use network-based models to describe the dipoles present at the toxin interface and to test this hypothesis.

As the sample is composed of three compounds, water, salt (PBS), and protein, the first issue is to determine whether the MDs are the water, PBS, and protein respective individual dielectric signals.

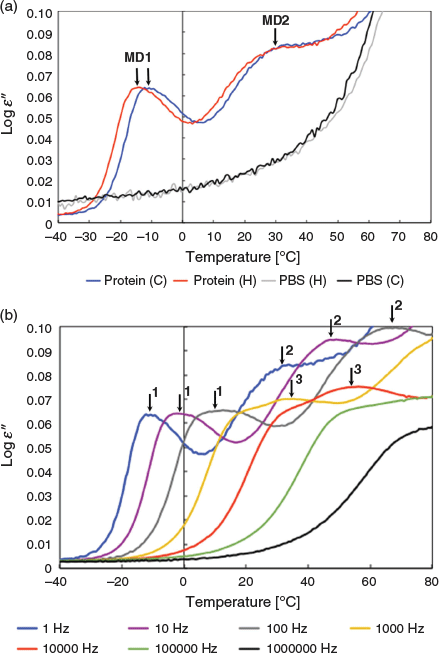
First, the dielectric behaviour of the toxin is investigated after three hours incubation at 80°C during which the toxin unfolds. Toxin samples are deposited in the nanomembrane and the dielectric loss ϵ′ is measured by BDS (see Experimental). After thermal treatment for 3 h at 80°C, the dielectric loss ϵ′ is measured as a function of temperature going from 80 to −80°C (cooling) and from –80 back to 80°C (heating). The dielectric loss ϵ′ of the samples during the cooling ramp is shown in Fig. 1 for frequencies ranging from 1 to 10⁶ Hz.

Fig. 1.  Dielectric loss as a function of temperature after 3 h of thermal treatment at 80°C. (a) Dielectric loss as a function of temperature for the cholera toxin B pentamer and for the PBS buffer control at 1 Hz. The signals for the heating (H) and cooling (C) temperature ramps are shown. The cooling ramp goes down to −80°C but the signal remains flat already below −40°C. The relaxation processes corresponding to the molecular dynamics peaks MD₁ and MD₂ are indicated by arrows. (b) Dielectric loss as a function of temperature for the cholera toxin B pentamer at frequencies from 1 to 10⁶ Hz. The three molecular dynamics peaks (MD₁, MD₂, and MD₃) are observed corresponding to three relaxation processes. The relaxation processes corresponding to the molecular dynamics peaks MD₁, MD₂, and MD₃ are indicated by arrows. The MD letters have been removed for clarity.

The cooling and heating curves show similar dielectric signals demonstrating that the proteins under study are stabilised in a state where no bulk water is present anymore (i.e. no more water evaporation) (Fig. 1a). In the previous study, it was shown that the protein sample contains adsorbed water.^[37] As observed in our previous study, the protein spectra can be described by three relaxation processes, which give rise to three peaks in the spectra of the dielectric loss (Fig. 1b). The PBS buffer control shows only a conductivity contribution under the same conditions indicating that the signal in the protein sample is protein dependent (Fig. 1a).

The absence of MD for the PBS buffer control indicates that the individual dielectric signals of the water, the salt (PBS), and the protein are non-additive and the Havrialiak–Negami functions cannot be applied to de-convolute the global signal. The three MDs are not the respective individual dielectric signal of the water, the salt, and the protein but their coupled responses.

The second issue is to determine how many sets of dipoles are associated with the three MDs.

The main relaxation process, referred to as MD₁ (molecular dynamics peak 1), is identified by a narrow peak and it is the fastest, with a maximum dielectric loss ϵ′ at temperature θ_max equal to −14°C at 1 Hz. MD₁ is detected for frequencies from 1 to 10⁵ Hz. The second relaxation process, referred to as MD₂, has a broader peak and is slower with θ_max equal to 30°C at 1 Hz. The broadness of MD₂ suggests a relaxation process associated with a more heterogeneous population of average toxin conformations compared with the average toxin conformations associated with the narrower MD₁ peak. This leads to the assumption that MD₂ is associated with more thermally perturbed toxin conformations than MD₁ and CtxB assembly intermediates (tetramer, trimer, and dimer). Unfolding leads to loss of atomic interactions such that MD₂, which is detected only at low frequencies from 1 to 10² Hz and therefore exhibits fluctuations of larger-scale atomic motions (domain or chain) than the faster frequencies of 10³ Hz and above observed in MD₁, is in a more unfolded state than MD₁.^[3] The third relaxation process, referred to as MD₃, has a narrow peak as MD₁ but appears only at frequencies higher than 100 Hz indicating the loss of the dipoles detected at low frequencies in MD₁ and so a more unfolded state than the average conformations associated with MD₁. Because MD₃ has fast motion dipoles and smaller-scale motions than the slow dipoles detected in MD₂, it is in a less unfolded state than MD₂. Thus as reported previously for thermal treatments at higher temperatures, three unfolding toxin intermediates can be associated with the BDS signal, two non-native pentamers, MD₁ and MD₃, and toxin assembly intermediates with MD₂.^[37]

For the three MDs, the positions of the maximum dielectric signals (θ_max) shift to higher temperatures with increasing frequencies. The temperature dependencies of the relaxation times tau (τ), which are the inverse of the frequency (τ = 1/f), can be followed by plotting τ against the temperature at the maximum signal for the respective frequency (Fig. 2).

Fig. 2.  Temperature dependencies of the relaxation times for the three relaxation processes MD₁, MD₂, and MD₃ identified for the cholera toxin B pentamer after thermal treatments at 80°C. On the x axis the temperature (T) is θ_max. Dipoles changing frequencies across relaxation processes are highlighted with vertical arrows. Dipoles changing environment but not relaxation times are indicated with horizontal arrows. The data fit with exponential curves that are indicated by straight lines with their respective R² values.

The relaxation times follow an Arrhenius linear temperature dependency indicating that dipoles fluctuating at different frequencies are independent from one another (see Experimental). This is true for the three relaxation processes. The relaxation times become longer from MD₁ to MD₃ to MD₂ (Fig. 2, vertical arrows).

Longer relaxation times mean dipole fluctuations involving larger collective motions consistently with more advanced stage of the toxin unfolding. The temperatures at maximum signals (θ_max) shift to higher temperatures (lower 1000/T) for dipoles with similar relaxation times from MD₁ to MD₃ and for MD₁ to MD₂ (Fig. 2, horizontal arrows). This shift means that thermal unfolding also leads to changes in the vicinity of dipoles (changes in the temperature at maximum signals) with no impact on the dipole relaxation time (no change in tau) or that different sets of dipoles (changes in the temperature at maximum signals) with similar fluctuation scales (no change in tau) are probed.

MD₁ and MD₂ have dipoles with slow motions but not with the same temperatures at maximum signals, indicating that two different sets of dipoles are detected in MD₁ and MD₂. This is confirmed by the loss of the MD₁ slow fluctuations dipoles in MD₃, interpreted as an intermediate unfolding stage between MD₁ and MD₂. The set of dipoles with fast motions in MD₁ is detected as well in MD₃ but with slightly slower motions indicating larger collective motions probably due to further unfolding (Fig. 2, vertical arrows). This set of dipoles is no more detected in the MD₂, probably because the area unfolded further and the resulting motions fall out of the measured frequency range. Native dipole fluctuations are unlikely to be detected as they fall within time scales equal or below nanoseconds.^[1,3] According to other experiments and MD simulations, slow motions (millisecond to second) are large domains and chains, while fast motions (microsecond to millisecond) involve smaller areas such as secondary and tertiary structural elements.^[1,3]

In summary the MD₁ is associated with two sets of dipoles, one with slow fluctuations and the other one with fast fluctuations. The set with fast motions is also detected in MD₃ and a third set of dipoles with slow motions is detected in MD₂. The dipoles with fast motions in MD₁ and MD₃ could be detected in MD₂ but with slower motions due to a more advanced toxin unfolding. However, because the motions in MD₂ are a thousand times slower it is unlikely that such larger unfolding leads to no change in the local environment of the dipoles (no change in the temperature at maximum signals). It is more reasonable to consider that MD₂ is associated with a third set of dipoles which has similar temperatures at maximum signals than the set of dipoles with fast fluctuations in MD₁ and MD₃. Thus, two sets of dipoles with slow motions are detected and one set with fast motions.

The BDS data indicate that three sets of dipolar relaxations are detected and the model of the toxin thermal unfolding assumes that MD₁ and MD₃ are non-native pentamers while MD₂ is associated with assembly intermediates, implying that the toxin interfaces are probed by the BDS signal.

Hence, for the model to be valid, the toxin interfaces need to be dielectrically detectable, thermally sensitive, and be composed of three different sets of dipolar relaxations with distinct thermal sensitivity.

To investigate such a possibility, network-based models are used to study the toxin interfaces in terms of stability and dielectric features. The steps to build the different networks are schematised in Fig. S1 (Supplementary Material).

An intermolecular interaction network, referred to as a 4D-network, was built based on the X-ray structure of the toxin native pentamer to describe the toxin interface (see Experimental). The nodes of the network are amino acids which belong to different chains and which can be connected because they have at least one pair of atoms within a threshold distance of 5 Å. The links are weighted according to the exact number of pairs of atoms, one per chain that are within a threshold distance of 5 Å. The 4D-network models intermolecular atomic and amino acid interactions, namely the interactions involved in the toxin interface. As an approximation of the interface stability, the number of amino acid and atomic interactions involved in the 4D-network are computed.

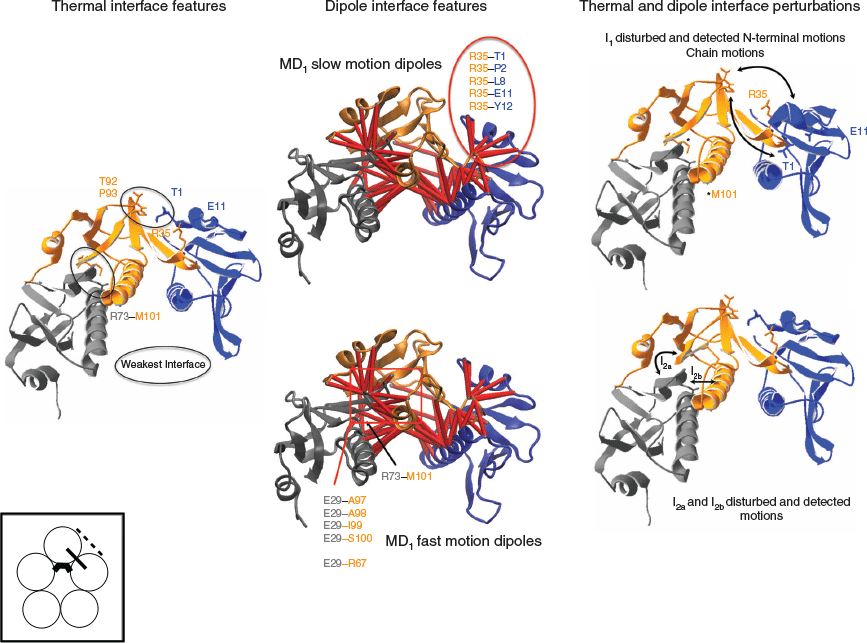
The toxin interface is rather complex and made of three physically distinct domains, I₁, I₂, and I₃ (Fig. 3).

Fig. 3.  The toxin interface. The cholera toxin B pentamer has a complex chain-interface made of mainly three sub-interfaces: I₁, I₂, and I₃, that are shown on a trimer of the X-ray structure of the toxin for simplicity (left). The chain F is in dark grey, the chain E in orange and the chain D in blue. I₁ is sub-divided into two interfaces: I_1a made of residues 1 to 3 of chain E interacting with residues 92 and 93 on the adjacent chain F, and I_1b made of residues 1 to 12 of chain E interacting with residues 28 to 39 on chain F. I₂ is also sub-divided into three interfaces: I_2a made of residues 25 to 32 of chain E interacting with residues 88 and 96 to 103 on chain D, I_2b made of residues 28 to 39 of chain E interacting with residues 58 to 68 on the adjacent chain D, and I_2c made of residues 101 to 103 of chain E interacting with residues 73 to 77 on the adjacent chain F. I₃ is a tripartite interface composed of residues 58 to 81 of chain M (e.g. E) interacting with residues 58 to 81 on chain M – 1 (D) and M + 1 (F). The electrostatic networks, made using VMD 3D-representations are on the left, with the 4D-charged network at the top and the 4D-induced charged network at the bottom (see Experimental). The dipoles are represented by red sticks. A schematic of the three interfaces in the native pentamer are shown in the left side bottom corner.

For simplicity, in Fig. 3, I₁, I₂, and I₃ sub-domain interfaces are shown on a trimer of the toxin instead of a pentamer involving the chains D, E, and F. I₁ is the N-terminal sub-domain interface domain of the toxin, it involves residues 1 to 12 of chain E and interacts with two sub-domains on the adjacent chain F. The residues 1 to 3 of chain E interact with residues 92 and 93 on chain F and constitute a weak patch (I_1a) of the sub-domain interface I₁ with only 5 amino acid pairs and 46 atomic interactions (Table 1). The sub-domain interface I_1b is made of residues 1 to 12 of chain E and residues 28 to 39 of chain F and constitutes a moderate interface composed of 19 amino acid pairs and 137 atomic interactions (Table 1). I₂ constitutes the main sub-domain β-interface of the toxin and is composed of the β-strand number 3 (residues 25 to 39) and the β-strand number 6 (residues 96 to 103). The residues 25 to 32 of chain E interact with the residues 88 and 96 to 103 on chain D (I_2a) and constitute a strong interface (I_2a) with 26 amino acid pairs and 198 atomic interactions (Table 1). The residues 28 to 39 of chain E interact with some of the residues 58 to 68 of the central helix (residues 58 to 81) of chain D, constituting a moderate interface (I_2b) with 19 amino acid pairs and 136 atomic interactions (Table 1). Finally, there is a weak interface patch (I_2c) involving interactions between residues 101 to 103 of chain E and residues 73, 76–77 on the adjacent chain F with only 5 amino acid pairs and 22 atomic interactions (Table 1). I₃ is the central α-helix sub-domain interface, composed of residues 58 to 81 of chain E interacting with residues 58 to 81 on the adjacent chains D and F. This is a tri-partite interface as it involves interactions between chain E and F as well as between chain E and D (Fig. 3), but it still constitutes a single interface with two ‘sticky’ moieties. The central α-helix sub-domain interface I₃ is the strongest interface with 24 amino acid pairs and 214 atomic interactions (Table 1).

Table 1.  Interface interaction and dipole features inferred from amino acid network based models

Based on the number of atomic and amino acid interactions, the toxin stability of the sub-domain interfaces can be ranked as follows: I_1a and I_2c are the weakest, I_1b and I_2b are moderate, and I_2a and I₃ are the strongest (Table 1).

In order to assess the dielectric properties of the toxin interface, an intermolecular charged amino acid network and an intermolecular induced charged amino acid network were built (see Experimental). The former is referred to as the 4D-charged network and the latter as the 4D induced charged network. The 4D-charged network is a sub-network of the 4D-network where only charged amino acids are retained (see Experimental). The pairs of charged residues are called ionic dipoles. The 4D induced charged network is initially built as the 4D-charged network but the non-charged amino acid neighbours in the 4D-network of the nodes are added. The pairs of non-charged residues are called induced dipoles. The construction of the different networks is schematised in Fig. S1 (Supplementary Material).

The choice of these two types of networks to model the dipoles in the native state of the toxin pentamer and infer dipoles which are detected by BDS is supported by the following reasons. First, protein structures and protein dynamics rely on non-specific hydrophobic interactions (van der Waals) and specific electrostatic interactions (e.g. salt bridges, charged-dipoles), the latter are contributing more to the dielectric signal as they involve Coulomb forces. Moreover, the electrostatic interactions are key to the folding and the stability of a protein and are believed to play a major role in the protein thermal stability.^[43] Second, charged residues and their proximal neighbours are the major constituents of the electrostatic interactions in proteins.^[50] Third, the electrostatic interactions in protein structures depend on the pH and the salt conditions, such that considering interactions between charged residues as an approximation of the coupling between protein, water, and salt (PBS) dipoles is relevant.^[50] Because the pH is 6.9 and based on disassembly and reassembly pH-dependency studies, the N- and C-terminals, lysine and arginine residues are considered protonated while glutamic and aspartic acids are considered deprotonated and hence participating in the 4D-charged network.^{[40,46,51–53]}

Based on the 4D-charged network and the 4D-induced charged network, the dielectric properties of the different interface sub-domains are deduced (Table 1) (Fig. 3). I_1a and I_2c are dielectrically invisible and weakly visible, respectively, as they have no charged residues but I_2c has two induced dipoles. I_1b and I_2b have two ionic dipoles (pair of charged residues) and some induced dipoles (charged–non charged pairs). I_2a is invisible dielectrically as it has no charged residues but it can be detected through the induced dipoles in the environment of the charged residue Glu29 (Table 1). I₃ is the strongest dielectric interface domain of the toxin with 13 ionic dipoles and 5 induced dipoles.

Based on the dielectric and stability features of the toxin interface, we can draw the following conclusions on the dipoles that are participating to the BDS signal. The I_1a and I_2c domains are the weakest and ranked as the most temperature-sensitive domains but they cannot be detected by BDS or only weakly through induced dipoles (Table 1). The thermal perturbation of I_1a will be detected when I_1b is thermally perturbed as well through the ionic dipoles T1–R35 and E11–R35 (Table 1) (Fig. 4). Likewise, the thermal perturbation of the I_2c domain will be detected via the perturbation of the induced dipoles and the ionic dipoles involving Glu29 when I_2a and I_2b are thermally disturbed (Table 1) (Fig. 4). Because I_1b is a moderate interface in terms of amino acid and atomic interactions compared with I_2a, I_1b unfolding is likely to occur before the unfolding of I_2a and so I_1b is associated with the slow motion dipoles detected in MD₁ but lost in MD₃. It follows that I_2a and I_2b are associated with the fast motion dipoles observed in MD₁ and MD₃. The slow dipoles of MD₂ are associated with the I₃ interface sub-domain as this domain has the strongest stability and the highest number of ionic dipoles and would be detected in the most unfolded stage of the toxin. In MD₂, the toxin conformations would have lost the I₁ and I₂ sub-domain interfaces, their dipoles being no more detected by BDS such that the chain dissociation would occur as only an I₃ destabilised interface remains (slow motion = large fluctuation).

Fig. 4.  Toxin interface state and dipole detected in MD₁. MD₁ is associated with the interface state closest to the native pentamer. The weakest interfaces I_1a and I_2c are thermally disturbed leading to I_2a and I₁ interface fluctuations (left and middle structures). I_1b is weaker than I_2a so it is associated with the slowest relaxation times of MD₁ (ten milliseconds to second) while I_2a and I_2b’s fluctuations are associated with the fastest relaxation times of MD₁ (microsecond to millisecond). The charged dipoles participating in the MD₁ signals are shown on the right structures. The box in the left bottom corner is a schematic of the toxin interface state in MD₁.

The thermal unfolding perturbation and the dipoles detected in MD₁ are schematized in Fig. 4.

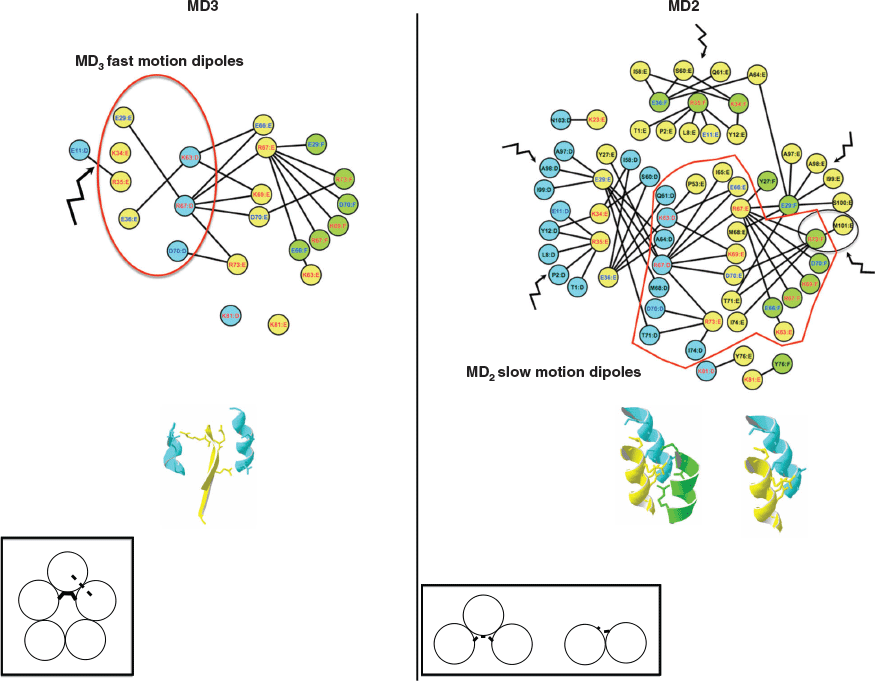
The weak interfaces unfold, leading to the perturbation of the I₁ N-terminal interface detected by dipoles with slow motions and to the perturbation of the I₂ β-interface detected by dipoles with fast motions. The dipoles detected in MD₃ and MD₂ are shown on the 4D-charged network and the 4D-induced charged network, respectively on Fig. 5. The interface I₂ further unfolds in MD₃ where the dipoles involving the residues Glu29 and Glu36 and the residues Lys63 and Arg67 on the adjacent chains are detected. In MD₂, the N-terminal I₁ interface and the I₂ interface are unfolded and not detected anymore, while only dipoles from the central helix I₃ interface are still detected.

Fig. 5.  Toxin interface state and dipole detected in MD₂ and MD₃. The MD₃ interface state is shown on the left panel. The charged network of the whole interface is shown for a toxin trimer with the nodes (charged residues) of chain D in cyan, of chain E in yellow, and of chain F in green. The residue name and sequence positions are indicated within the nodes, with non-charged residues written in black, positively charged residues in red, and negatively charged residues in blue. MD₃ has lost the slow motion dipoles associated with the N-terminal interface, which is considered damaged and not detected (jagged arrows). Consequently, the I_2b interface becomes destabilised and detected (red box) with dipoles E29–R67 and E36–K63 shown as linked on the charged network. The structure of the I_2a and I_2b interfaces detected in MD₃ are shown below the network. The box in the left bottom corner is a schematic of the toxin interface state in MD₃. The MD₂ interface state is shown on the right panel. MD₂ is associated with the most destabilised interface state of the toxin. Only the central α-helix interface I3 is assumed to be still present. The induced-charged network of the whole interface is shown for a toxin trimer with the nodes (charged residues) of chain D in cyan, of chain E in yellow, and of chain F in green. The damage interfaces are indicated with jagged arrows while the red box indicates the destabilised I₃ interface and the maximum dipoles detected in MD₂. The structure of the I₃ interfaces detected in MD₂ is shown below the network. The box in the left bottom corner is a schematic of the toxin interface state in MD₂.

This novel network approach to analyse dielectric signals, using network-based models and infer toxin interface dielectric and stability properties from the X-ray structure, supports the hypothesis that BDS probes the thermal perturbation of the toxin interfaces. The toxin interface is composed of three sub-domains that have distinct dielectric and stability features as expected from the model of the toxin thermal unfolding. Moreover, the scale of the motions detected by the BDS is also in good agreement with the unfolding stage of the toxin: the I₁ N-terminal unfolding likely leads to chain motion and the detected slow fluctuations (millisecond to second), in MD₂ only the I₃ sub domain interface is connecting two chains which is likely to lead to chain dissociation and the detected slow fluctuations, the fast motions involving the I₂ interface perturbation is a smaller scale fluctuation involving secondary structure element motions.

Our study is not an exhaustive investigation of the dipoles involved in the BDS signal, and intramolecular contributions are probably also taking place, a possibility that can be explored in the future using charged intramolecular networks instead. Nevertheless, the results allow the pinpointing of some residues potentially important for the toxin unfolding and detected dielectrically, such as the charged pair R35–E11 in the I₁ interface, the charged dipoles E29–(A97, A98, I99, S100) and R73–M101 in the I₂ interface and several charged pairs K63–E66, R67–D70, and D70–R73 in the central α-helix. The results also suggest that the I₃ interface is the most stable and most dielectrically detectable interface in the toxin. Thus, based on the results, toxin mutants can be proposed to test the roles of these amino acids both in the dielectric signals and in the toxin thermal unfolding. This integrative approach could also be used to investigate protein sequence variants and rank them according to dynamics perturbations. The network analysis combined with the experimental molecular dynamics measured by BDS in nanoconfined conditions offers a powerful approach to investigate the relation between local perturbations and global protein conformational changes.

Lyophilized cholera toxin B pentamer purchased from Sigma Aldrich (C9903) was diluted in phosphate buffered saline (PBS; 10 mM sodium phosphate, 150 mM sodium chloride, pH 7.4) at a final concentration of 2.6 mg mL⁻¹. This bulk toxin preparation was aliquoted and kept at −20°C, and thawed and frozen two times at most, when used for the dielectric measurements. Concentrated PBS solutions were purchased from BIOSOLVE and diluted 10 times in distilled water to prepare the PBS used in the bulk toxin solution. In addition, the PBS solution was filtered by 22 μm filters to limit impurity contamination. The aluminium oxide (AAO) films on Al were purchased from InRedox. The AAO membrane dimensions were 10 mm × 10 mm, and they contained nanopores of 40 nm diameter and 10 µm length, with 12 % porosity. The AAO membrane containing the nanopores is referred to as the nanomembrane. Before use, the nanomembranes were plasma-treated for 20 min to remove organic impurities.

Protein sample preparation. For the dielectric measurement, a protein sample at 0.025 mg mL⁻¹ was used. This protein sample was prepared by diluting 2 μL of the bulk toxin solution at 2.6 mg mL⁻¹ in 204 μL of deionised water (final pH 6.9). Since the bulk protein is prepared in PBS, the sample for the dielectric measurement contains protein, deionised water, and PBS. A 200 μL drop of sample was deposited on the nanomembrane using the drop technique, and then heated at 50°C (323 K) for 15 min to evaporate the bulk water and allow proteins to enter the pores. The sample was cooled to 30°C (303 K) for 5 min with a speed of 2 K min⁻¹, placed between two Al electrodes of 7 and 40 mm diameter, respectively, and placed in the cell holder for measurement. The procedure was the same for the control samples.

Dielectric measurements. The dielectric measurements were performed on a broadband dielectric spectrometer Novocontrol Alpha analyser over a frequency range from 1 to 10⁶ Hz and a temperature range from –80 (193) to 80°C (353 K). The temperature ramps were carried out at a rate of 2 K min⁻¹ and a voltage of 0.2 V was applied. The dielectric loss ϵ′, the imaginary part of the complex dielectric permittivity, was measured as a function of temperature at different frequencies. For the temperature control, a flow of pure nitrogen gas was used in a closed cryostat, providing water-free and oxygen-free experimental conditions. The sample was first heated to 80°C (353 K) for 3 h, and to −80°C (193 K) (cooling, C) and maintained for 30 min before being heated back to 80°C (heating, H). A cycle was composed of the cooling (C) and the heating (H) temperature ramp. The curves of the cooling and heating signals were very similar for the protein sample (Fig. 1a). This demonstrates that the proteins under study were stabilised in a state where no bulk water is present anymore and where the amount of adsorbed water is stabilised as well. It also shows that the protein remains in a steady-state across the measurement and undergoes thermal unfolding mainly during the 3 h incubation time. The PBS buffer control showed no molecular dynamics and only had conductivity after treatment at 80°C (Fig. 1a). The dielectric signals are therefore from the protein.

Dielectric data. The temperature dependence of the relaxation processes was modelled by an Arrhenius equation expressed as Eqn 1:^[34,35]

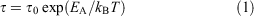
where τ is the relaxation time, τ₀ the relaxation time at high temperatures, T the temperature, E_A the activation energy, and k_B the Boltzmann constant.^[45]

Control experiments. The dielectric response of the empty nanomembrane was measured for 10 min at 60°C and from 60 to −80°C to control that no dielectric dispersions were detected. The dielectric response of nanopores filled with a 200 μL drop of deionised water was measured for 10 min at 60°C and from 60 to −80°C to control that the deionised water used to prepare the sample show no dielectric dispersions too. Finally, the dielectric response of nanopores filled with a 200 μL drop of PBS buffer control was measured following a complete temperature ramp experiment as for the protein sample. The PBS buffer control was prepared with 2 μL of PBS diluted in 204 μL of deionised water (no protein was added). This concentration was equivalent to the concentration used to prepare and measure the protein sample. This control experiment was carried out to investigate the dielectric response of PBS mixed with deionised water in the same conditions as the protein.

To make sure the toxin was in a native state when a dielectric experiment is performed, the toxin pentameric state was checked by Trp-fluorescence beforehand.^[45] The sample could not be recovered from the nanopores after the BDS experiment so it was not possible to control the state of the toxin after.

The toxin interfaces were modelled by a network of the amino acids that belong to different chains and had at least one pair of atoms within a 5 Å distance, so-called hotspots.^[24] The amino acid network (AAN) of the whole pentamer was built first and the intermolecular amino acid network was generated after by selecting only intermolecular interactions. The networks were created using the Python Biograph module, available at https://github.com/rodogi/biographs, or directly with the script available at https://github.com/lorpac/network_vmd. Briefly this was done using the atomic coordinates of the toxin structure (PDB: 1EEI) freely available from the RCSB website (https://www.rcsb.org/) and computing intermolecular atomic distances between amino acids that belong to different chains (nodes). Hotspots were linked when their respective atoms were close enough for a chemical interaction using 5 Å distance as a threshold. Such spatial networks based on Euclidian distances between nodes are classically used in proteins to infer atomic and amino acid interactions intractable otherwise due to the size of the system.^[2,22,54] From the intermolecular amino acid network of the toxin, simple network measures such as number of hotspot pairs, number of atomic interactions, number of charged amino acid pairs, and number of charged dipole pairs within the interfaces were computed. A charged dipole pair was a charged amino acid interacting with a polar or hydrophobic amino acid. The intermolecular amino acid networks were referred to as a 4D-network for simplicity, 4D corresponds to the quaternary structure of proteins, namely the number of chains present in a protein oligomer.

The intermolecular charged amino acid networks were sub-networks of the intermolecular amino acid networks where only charged amino acids are kept as nodes of the network. The charged amino acid networks model the Coulomb interactions with charged–charged interactions within the toxin interface and were used to analyse the protein dielectric signals which result from such interactions. The intermolecular charged amino acid networks were referred to as the 4D-charged network for simplicity. The orientation of the dipoles was not taken into account in the model although it could cancel out the contribution to the dielectric signal of some of the dipoles considered in the model when dipoles of equal strength had opposite orientation. Nevertheless, the amino acid neighbourhood was sufficiently anisotropic for this to be unlikely, making the approximation locally reasonable. The isoelectric point (pI) of the toxin pentamer was around pH 5.6 such that at pH 6.9 the global charge was negative and a global dipolar moment was expected, consistent with having a dielectric signal. It also supported the approximation at the global scale of the entire protein.

The intermolecular induced charged amino acid network was as the intermolecular charged amino acid network but with the addition of the non-charged amino acids located in the chemical vicinity of the charged hotspots. This network models the Coulomb interactions as well as the ion-dipole interactions with the charged non-charged amino acid pairs, present at the toxin interface. The intermolecular induced charged amino acid networks were referred to as 4D-induced charged network for simplicity.

Mathematically, if the network of all amino acid interactions is represented by a graph G(V, E) with set of nodes V (Vertices) and set of edges (E), then the 4D-network is represented by a graph 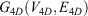with nodes

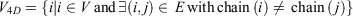
and edges

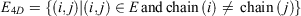
The 4D-charged network is then represented by a graph 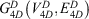with nodes

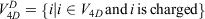
and edges

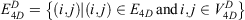
and the 4D-induced charged network is represented by a graph 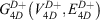with nodes

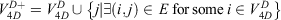
and edges

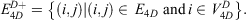
The construction of the networks is shown in Fig. S1 (Supplementary Material).

All networks were generated by manipulating the amino acid network of the toxin using the Python package NetworkX.^[46] Two-dimensional network representations were produced using the Gephi software^[48] and three-dimensional network representations were produced using the Python scripts available at https://github.com/lorpac/network_vmd and visualised with the VMD software.^[49] For simplicity, the toxin pentamer having a central symmetry, only links between nodes involved in the interfaces between chain E and D and between chain E and F are represented.

A schematic of the network construction flow is available on the Journal’s website.

LB and LP performed research and analysed data; AS designed research, analysed data, and wrote the manuscript; CL designed research, analysed data, and wrote the manuscript.

The authors declare no conflicts of interest.