A Derivation of the Gibbs Equation and the Determination of Change in Gibbs Entropy from Calorimetry*
Denis J. Evans A , Debra J. Searles B C and Stephen R. Williams D EA Department of Applied Mathematics, Research School of Physics, Australian National University, Canberra, ACT 0200, Australia.
B Australian Institute for Bioengineering and Nanotechnology, University of Queensland, Brisbane, Qld 4072, Australia.
C School of Chemistry and Molecular Biosciences, University of Queensland, Brisbane, Qld 4072, Australia.
D Research School of Chemistry, Australian National University, Canberra, ACT 0200, Australia.
E Corresponding author. Email: swilliams@rsc.anu.edu.au
Australian Journal of Chemistry 69(12) 1413-1419 https://doi.org/10.1071/CH16447
Submitted: 1 August 2016 Accepted: 14 November 2016 Published: 1 December 2016
Abstract
In this paper, we give a succinct derivation of the fundamental equation of classical equilibrium thermodynamics, namely the Gibbs equation. This derivation builds on our equilibrium relaxation theorem for systems in contact with a heat reservoir. We reinforce the comments made over a century ago, pointing out that Clausius’ strict inequality for a system of interest is within Clausius’ set of definitions, logically undefined. Using a specific definition of temperature that we have recently introduced and which is valid for both reversible and irreversible processes, we can define a property that we call the change in calorimetric entropy for these processes. We then demonstrate the instantaneous equivalence of the change in calorimetric entropy, which is defined using heat transfer and our definition of temperature, and the change in Gibbs entropy, which is defined in terms of the full N-particle phase space distribution function. The result shows that the change in Gibbs entropy can be expressed in terms of physical quantities.
Introduction
The Gibbs equation is essential for applications of thermodynamics in chemistry, and is referred to as the ‘fundamental equation’ in many standard texts on physical chemistry. It determines how the internal energy, U, of a system depends on system variables. For a system whose composition does not change and which undergoes pV work only, these system variables are the temperature (T), entropy (S), pressure (p), and volume (V) of a system, and the Gibbs equation is 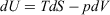 . In this manuscript, we show that the Gibbs equation can be derived directly from microscopic arguments. In order to establish the framework in which the derivation is carried out, we first establish how systems relax towards equilibrium, consider how the properties of a system vary under quasi-static processes, and discuss the Clausius’ equality for quasi-static processes. By a ‘quasi-static process’ we mean that the process is undertaken sufficiently slowly that the system can be considered to be at equilibrium at any point in time. Many of the arguments and derivations presented in this paper have also been presented therein;[1] however, these are repeated in the present study and discussed in more detail.
. In this manuscript, we show that the Gibbs equation can be derived directly from microscopic arguments. In order to establish the framework in which the derivation is carried out, we first establish how systems relax towards equilibrium, consider how the properties of a system vary under quasi-static processes, and discuss the Clausius’ equality for quasi-static processes. By a ‘quasi-static process’ we mean that the process is undertaken sufficiently slowly that the system can be considered to be at equilibrium at any point in time. Many of the arguments and derivations presented in this paper have also been presented therein;[1] however, these are repeated in the present study and discussed in more detail.
Relaxation to Equilibrium
In 2009, we gave a derivation of the relaxation to thermal equilibrium that clarified when and how relaxation occurs.[2] We have refined this discussion in subsequent papers, e.g. see the study therein.[3] In the present proof, we consider a system as a collection of particles whose positions (q1, q2, …) and momenta (p1, p2, …) are represented by the phase space vector, 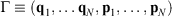 whose trajectory is determined by time-reversible classical equations of motion. As an example of a simple process, we consider a system that is initially at equilibrium at a given temperature
whose trajectory is determined by time-reversible classical equations of motion. As an example of a simple process, we consider a system that is initially at equilibrium at a given temperature 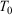 . The system is placed in contact with a thermostatting bath, whose temperature is changed over a certain period after which it is fixed at a final temperature,
. The system is placed in contact with a thermostatting bath, whose temperature is changed over a certain period after which it is fixed at a final temperature, 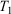 . At this stage, we define the ‘temperature’ of the heat bath by its equipartition value, which is expressed in terms of the peculiar kinetic energy of the bath per degree of freedom. If the system relaxes to equilibrium, then under some conditions the system will eventually attain the final temperature of the thermostatting bath and have the properties of an equilibrium system at the new temperature. In our model, a Nosé–Hoover thermostat[4] was used to represent the heat reservoir though any other mathematical representation of a time reversible thermostat could be used, such as a Gaussian isokinetic thermostat, to derive essentially identical results. For realistically modelled systems of interest in which correlations decay quickly enough (i.e. are T-mixing†) and in contact with a Nosé–Hoover thermostat with a target temperature T, we proved that in the long time limit, averages of smooth phase functions
. At this stage, we define the ‘temperature’ of the heat bath by its equipartition value, which is expressed in terms of the peculiar kinetic energy of the bath per degree of freedom. If the system relaxes to equilibrium, then under some conditions the system will eventually attain the final temperature of the thermostatting bath and have the properties of an equilibrium system at the new temperature. In our model, a Nosé–Hoover thermostat[4] was used to represent the heat reservoir though any other mathematical representation of a time reversible thermostat could be used, such as a Gaussian isokinetic thermostat, to derive essentially identical results. For realistically modelled systems of interest in which correlations decay quickly enough (i.e. are T-mixing†) and in contact with a Nosé–Hoover thermostat with a target temperature T, we proved that in the long time limit, averages of smooth phase functions 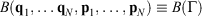 (where
(where 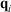 is the position of particle i, and
is the position of particle i, and 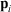 refers to the momentum of particle i) approach their equilibrium canonical averages:
refers to the momentum of particle i) approach their equilibrium canonical averages:
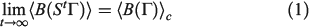
where the ensemble average on the left is over the initial distribution function (in our example this will be the distribution function for the system at temperature 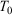 ). In this equation,
). In this equation, 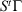 is the phase space vector obtained by evolving the system forward in time for a duration t from the phase vector
is the phase space vector obtained by evolving the system forward in time for a duration t from the phase vector 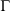 at
at 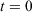 . Eqn 1 states that in the long time limit, the properties of the system relax towards their canonical equilibrium values. The canonical average
. Eqn 1 states that in the long time limit, the properties of the system relax towards their canonical equilibrium values. The canonical average 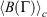 is defined as
is defined as
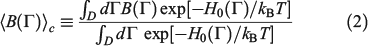
where H0 is the total energy (kinetic and interparticle potential) of the atoms comprising the system. In Eqn 2, D is the ostensible phase space domain (i.e. all the possible phase space configurations that the system can adopt) with particle coordinates ranging over some physical volume V and momenta spanning over an infinite range from –∞ to +∞, kB is Boltzmann’s constant, and T is the temperature of the equilibrium system. We can model a system undergoing a change in temperature using the Nosé–Hoover equations of motion[4] for the system:
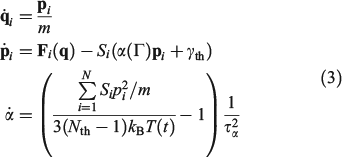
In Eqn 3, 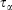 is the Nosé–Hoover time constant, Nth is the actual number of thermostatted particles, and m is the particle mass.
is the Nosé–Hoover time constant, Nth is the actual number of thermostatted particles, and m is the particle mass. 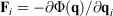 is the total force exerted on particle i by all the other particles, Si = 0, 1 is a switch controlling which particles are subject to the thermostat, and the fluctuating force γth is chosen to fix the total momentum of the thermostatted particles at zero. Additionally, in Eqn 3,
is the total force exerted on particle i by all the other particles, Si = 0, 1 is a switch controlling which particles are subject to the thermostat, and the fluctuating force γth is chosen to fix the total momentum of the thermostatted particles at zero. Additionally, in Eqn 3, 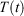 is the possibly time-dependent, target temperature appearing in the equation of motion for the Nosé–Hoover thermostat. As the system relaxes towards a time-independent equilibrium state, we know that
is the possibly time-dependent, target temperature appearing in the equation of motion for the Nosé–Hoover thermostat. As the system relaxes towards a time-independent equilibrium state, we know that 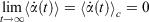 and therefore using Eqn 3, the equilibrium thermodynamic temperature is indeed related, as we said above, to its equipartition value.
and therefore using Eqn 3, the equilibrium thermodynamic temperature is indeed related, as we said above, to its equipartition value.
This set up, Eqn 3, allows us to model the thought experiment we discussed above using a parametric change in the Nosé–Hoover target temperature of the thermostat. In this thought experiment, the thermostat is always in thermal contact with the system of interest, whose response we wish to understand. We note that in theory, the thermostatted particles could be made arbitrarily near or far from a system of interest (the two may be separated by arbitrarily thick, realistically modelled walls whose particles, similarly to the particles in the system of interest itself, have 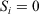 in Eqn 3). Thus, the results obtained below could be generalized and would be independent of the precise mathematical details of our thermostat.
in Eqn 3). Thus, the results obtained below could be generalized and would be independent of the precise mathematical details of our thermostat.
Our equilibrium relaxation theorem for systems in contact with a heat reservoir also shows that for T-mixing systems, the analytic equilibrium distribution function is in fact unique, and any deviation from this distribution function (even in the momenta) will cause dissipation, which tends to be strictly positive,[7] and the deviated distribution cannot be stationary in time.[2] This means that the same result will be obtained even if the initial state of the system is not just at a different temperature, but could be in a non-equilibrium state. The relaxation theorems do not imply that the full N-particle distribution actually relaxes to the canonical distribution (Eqn 2); in contrast, ensemble averages of physical phase variables (e.g. energy, pressure, specific heat etc.) relax. These averages are exact functionals of the low-order 1-, 2-, 3-particle distribution functions obtained by integrating over N –1, N – 2, N – 3, … particle coordinates and momenta, respectively (note that different low-order distributions are obtained depending on which variables are integrated out). These low-order distribution functions do relax to their canonical forms in the long time limit as they can be written as ensemble averages of phase variables.[8] Therefore, using the fact that the analytic equilibrium distribution function is unique, the ensemble averages of the low-order distribution functions must relax to their equilibrium values.
The equilibrium relaxation theorems also show that if the parametric change in the Nosé–Hoover target temperature is halted at a certain time 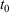 , so that the target temperature is
, so that the target temperature is 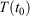 and the system is T-mixing, then the properties of the system, including the low-order equilibrium distribution functions, will relax towards their values with the equilibrium thermodynamic temperature being
and the system is T-mixing, then the properties of the system, including the low-order equilibrium distribution functions, will relax towards their values with the equilibrium thermodynamic temperature being 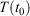 .
.
Clausius’ Equality for Quasi-Static Processes and the Gibbs Equality
In 2011, we gave a mechanical proof[9] of Clausius’ inequality for heat transferred to a heat reservoir in a cyclic process, 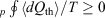 , where
, where 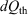 is the heat absorbed by the thermostatting reservoir from the system of interest. The Clausius inequality only applies if a system, subject to a periodic protocol, settles down to a periodic ensemble-averaged response – hence the subscript ‘p’ in front of the integral. This proof used generalizations[10] of the Crooks fluctuation theorem[11] and the Jarzynski equality.[12] It stands in contradistinction to Clausius’ ‘proof’, which is based on the axiom ‘that heat cannot by itself flow from a colder to a warmer body’ (see p. 277 in Clausius (1867)[13]). Furthermore, our approach unambiguously defines the temperature appearing in the inequality, as discussed below. Our proof is based on the laws of classical mechanics and the axiom of causality.[7]
is the heat absorbed by the thermostatting reservoir from the system of interest. The Clausius inequality only applies if a system, subject to a periodic protocol, settles down to a periodic ensemble-averaged response – hence the subscript ‘p’ in front of the integral. This proof used generalizations[10] of the Crooks fluctuation theorem[11] and the Jarzynski equality.[12] It stands in contradistinction to Clausius’ ‘proof’, which is based on the axiom ‘that heat cannot by itself flow from a colder to a warmer body’ (see p. 277 in Clausius (1867)[13]). Furthermore, our approach unambiguously defines the temperature appearing in the inequality, as discussed below. Our proof is based on the laws of classical mechanics and the axiom of causality.[7]
For quasi-static (qs) processes (also referred to as reversible process), the forward and reverse integrals 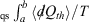 have equal magnitude and opposite sign. Thus, the Clausius inequality reduces to Clausius’ equality:
have equal magnitude and opposite sign. Thus, the Clausius inequality reduces to Clausius’ equality: 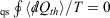 . The integral
. The integral 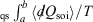 for quasi-static processes (and only for quasi-static processes!), where soi refers to system of interest, was defined by Clausius as the change in the equilibrium entropy,
for quasi-static processes (and only for quasi-static processes!), where soi refers to system of interest, was defined by Clausius as the change in the equilibrium entropy, 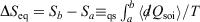 , and therefore Clausius’ entropy is a state function. This means that
, and therefore Clausius’ entropy is a state function. This means that 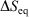 will be independent of the actual pathway between equilibrium states a and b.
will be independent of the actual pathway between equilibrium states a and b.
Note that the strikethrough on the differential for the heat denotes the fact that the heat is not a state function, and many textbooks state that 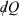 is an ‘imperfect’ differential. Additionally, textbooks often state that the reciprocal of the absolute temperature is the ‘integrating factor for the heat, thereby turning
is an ‘imperfect’ differential. Additionally, textbooks often state that the reciprocal of the absolute temperature is the ‘integrating factor for the heat, thereby turning 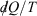 into a perfect differential i.e. dS’, meaning that its integral gives the change in a state function, namely the equilibrium calorimetric entropy,
into a perfect differential i.e. dS’, meaning that its integral gives the change in a state function, namely the equilibrium calorimetric entropy, 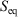 . We also follow the conventional notation used in classical thermodynamics wherein dX denotes a quasi-static, so-called virtual change, in the arbitrary variable X. We could replace each dX by dX/dt; however, conventionally this has not been done.
. We also follow the conventional notation used in classical thermodynamics wherein dX denotes a quasi-static, so-called virtual change, in the arbitrary variable X. We could replace each dX by dX/dt; however, conventionally this has not been done.
Close to equilibrium, an intensive quantity such as the hydrostatic pressure, which is a purely mechanical property,[14] behaves as follows:
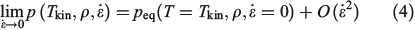
where Tkin is the kinetic temperature of the non-equilibrium system (or in fact, any other phase function whose equilibrium average is the equilibrium thermodynamic temperature), T is the equilibrium thermodynamic temperature appearing in the equilibrium canonical distribution function (Eqn 2).[2] It is the equilibrium thermodynamic temperature the system will relax towards (as in Eqns 1 and 2) if the dilation rate is set instantaneously to zero 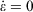 , and we simply allow the relaxation processes to run their courses. In Eqn 4,
, and we simply allow the relaxation processes to run their courses. In Eqn 4, 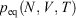 is the equilibrium pressure. In the so-called, quasi-static limit where rates of executing non-equilibrium processes go to zero, we can calculate changes using the equilibrium values for thermodynamic variables. This is possible because integration times for the process scale like the reciprocals of the rates (e.g.
is the equilibrium pressure. In the so-called, quasi-static limit where rates of executing non-equilibrium processes go to zero, we can calculate changes using the equilibrium values for thermodynamic variables. This is possible because integration times for the process scale like the reciprocals of the rates (e.g. 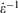 ), while the errors incurred by replacing the actual non-equilibrium values with their equilibrium counterparts (Eqn 4) scale like the square of the rates. This means that the non-equilibrium contributions to the time-integrated changes vanish as
), while the errors incurred by replacing the actual non-equilibrium values with their equilibrium counterparts (Eqn 4) scale like the square of the rates. This means that the non-equilibrium contributions to the time-integrated changes vanish as 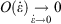 at sufficiently slow rates, and the quasi-static changes can be expressed in terms of the properties of the equilibrium systems.
at sufficiently slow rates, and the quasi-static changes can be expressed in terms of the properties of the equilibrium systems.
One can now combine the conservation of energy for our system of interest with the definition of the change in equilibrium entropy to obtain the Gibbs equation for quasi-static changes in the internal energy, U. The equilibrium entropy 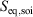 and the volume V of the system of interest are related to the temperature T, and the equilibrium pressure,
and the volume V of the system of interest are related to the temperature T, and the equilibrium pressure, 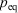 , by the following equation:
, by the following equation:
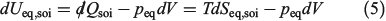
where we have assumed the system is macroscopic and fluctuations are negligible. This is the key equation of classical equilibrium thermodynamics and it was first written down for single-component systems by Clausius and generalized to mixtures by Gibbs. Currently, even the single-component version is known as the Gibbs equality.[15] Because we are able to derive the Clausius equality from the mechanical equations of motion and use this to derive the Gibbs equality as shown above, the result gives a derivation of the Gibbs equality based on mechanical dynamics.
There is an alternative derivation of the Gibbs equation, Eqn 5, which obviates the need to introduce the generalized Crooks and Jarzynski relations. The Helmholtz free energy (Ac) of an equilibrium, canonical system in the thermodynamic limit (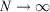 ) is:
) is:
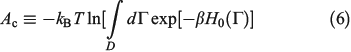
In Eqn 6, 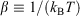 , with the temperature being the usual thermodynamic temperature of the equilibrium system. The equilibrium Helmholtz free energy is the logarithm of the partition function (the normalisation factor appearing in the equilibrium canonical distribution (Eqn 2)). The Helmholtz free energy is obviously a property of the equilibrium system and is a function of N,T,V.
, with the temperature being the usual thermodynamic temperature of the equilibrium system. The equilibrium Helmholtz free energy is the logarithm of the partition function (the normalisation factor appearing in the equilibrium canonical distribution (Eqn 2)). The Helmholtz free energy is obviously a property of the equilibrium system and is a function of N,T,V.
If we subject our system to a quasi-static (equilibrium) cyclic change in temperature, from the definition of the Helmholtz free energy of the equilibrium canonical system, we see that for quasi-static changes,‡
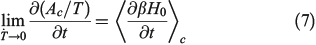
In Eqn 7, 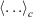 denotes a canonical average (Eqn 2). When deriving Eqn 7, we are assuming that the Helmholtz free energy is given by the canonical expression Eqn 6 at all times. We are thus computing the derivatives in the infinitely slow limit as shown in Eqn 7.
denotes a canonical average (Eqn 2). When deriving Eqn 7, we are assuming that the Helmholtz free energy is given by the canonical expression Eqn 6 at all times. We are thus computing the derivatives in the infinitely slow limit as shown in Eqn 7.
We can therefore compute the cyclic integral of the quasi-static rate of change in the Helmholtz free energy due to temperature changes in the thermodynamic limit:
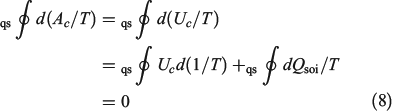
The first line is obtained from Eqn 7, noting that 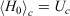 . In going from the first to the second line in Eqn 8, we use the chain rule and the fact that for this transformation, by construction, the change in the internal energy is caused solely by exchange of heat.
. In going from the first to the second line in Eqn 8, we use the chain rule and the fact that for this transformation, by construction, the change in the internal energy is caused solely by exchange of heat.
The cyclic integral of the change in the Helmholtz free energy divided by the temperature of our quasi-static (equilibrium) cycle is zero because, by definition, in a cyclic, quasi-static process, the system returns to its initial equilibrium state after one cycle. Similarly, both the internal energy and the temperature (our definition) are state functions; hence, 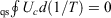 .
.
Substituting the latter expression into Eqn 8 shows that
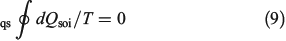
This result again shows that for quasi-static changes, the equilibrium entropy is a state function. We can then invoke energy conservation and the definition of the equilibrium entropy changes to derive the Gibbs equality (Eqn 5), as we did before.
The property T was not explicitly defined for non-equilibrium processes in the original statements of Clausius’ inequality. In our work,[7,9] we showed that if T is interpreted as the temperature the non-equilibrium system would relax to if all the driving forces were removed, then the inequality can be proven. However, one might question whether there is more than one temperature that would satisfy the inequality in general. This is not the case – the integrating factor for the heat (apart from a simple scaling) is unique. It cannot be replaced by any other monotonic function of the reciprocal temperature such as 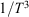 . This is because it comes directly from the algebraic form for the canonical equilibrium distribution function (Eqn 2) and then the associated form for the corresponding Helmholtz free energy (Eqn 6). For T-mixing systems in contact with a heat reservoir, the analytic equilibrium distribution is unique as well as the ‘integrating factor’ for the heat. Thus, the integrating factor for the heat is in fact the instantaneous temperature of the canonical distribution of states through which the system evolves during a quasi-static process.
. This is because it comes directly from the algebraic form for the canonical equilibrium distribution function (Eqn 2) and then the associated form for the corresponding Helmholtz free energy (Eqn 6). For T-mixing systems in contact with a heat reservoir, the analytic equilibrium distribution is unique as well as the ‘integrating factor’ for the heat. Thus, the integrating factor for the heat is in fact the instantaneous temperature of the canonical distribution of states through which the system evolves during a quasi-static process.
There is another important consequence of this new, much simpler derivation of the Gibbs equation in Eqn 5. This simpler derivation confirms observations by Tatiana Ehrenfest (see the preface (p. 54) to ‘The Conceptual Foundations of the Statistical Approach to Statistical Mechanics’ by Paul and Tatiana Ehrenfest[16]) whereby the so-called Gibbs equality (Eqn 5) can be derived without any reference to irreversibility. It is a statement that only concerns equilibrium processes or non-equilibrium processes considered in the quasi-static limit. The Gibbs equality (Eqn 5) ‘is completely independent of the direction of time’.[16]
Clausius’ Inequality and Calorimetric Entropy
We note that our mechanical proof of Clausius’ inequality[9] is valid for periodic processes that are irreversible. The temperature that appears in our inequality at any point in a cycle is the Nosé–Hoover target temperature appearing in the equations of motion (Eqn 3) at that same point in the cycle. At any point in the cycle, that temperature is the equilibrium temperature appearing in the canonical distribution that characterises the canonical averages of phase functions that the system will relax towards if the execution of the cycle is halted and the relaxation towards equilibrium is allowed as in Eqns 1 and 2.
The change in equilibrium entropy defined by Clausius refers to quasi-static processes and leads to the entropy being a state function. We now introduce a new entropy that we refer to as the change in the calorimetric entropy 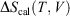 of the system of interest where we do not require the change to be quasi-static:
of the system of interest where we do not require the change to be quasi-static:
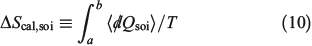
The change in the calorimetric entropy will depend on the path from state a to state b and therefore it is not a state function. However, in the quasi-static limit, the values for the change in calorimetric and equilibrium entropies become the same. Using this definition, we can show that changes in the calorimetric entropy of the system of interest and of the thermostat computed for reversible or even irreversible processes are equal and opposite, with the sum of their changes being precisely zero 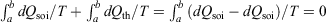 . Our thermodynamic temperatures for the reservoir and system of interest are obviously instantaneously equal to one another because by construction, the reservoir and the system of interest are always in thermal contact with each other. This shows that the change in the calorimetric entropy of the universe is zero for any process, which is inconsistent with Clausius’ famous statement: ‘the entropy of the Universe tends to a maximum’.[13] Clausius’ statement is problematic because the universe is not always in quasi-static equilibrium; furthermore, for non-equilibrium systems, Clausius’ entropy is not defined. Often, the requirement for systems to be at equilibrium at the beginning and end of a process for Clausius’ statement to apply is overlooked. The temperature as Clausius defined it,
. Our thermodynamic temperatures for the reservoir and system of interest are obviously instantaneously equal to one another because by construction, the reservoir and the system of interest are always in thermal contact with each other. This shows that the change in the calorimetric entropy of the universe is zero for any process, which is inconsistent with Clausius’ famous statement: ‘the entropy of the Universe tends to a maximum’.[13] Clausius’ statement is problematic because the universe is not always in quasi-static equilibrium; furthermore, for non-equilibrium systems, Clausius’ entropy is not defined. Often, the requirement for systems to be at equilibrium at the beginning and end of a process for Clausius’ statement to apply is overlooked. The temperature as Clausius defined it, 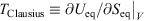 , is obviously undefined for non-equilibrium systems. At equilibrium, there are infinitely many phase functions whose ensemble average equals the equilibrium thermodynamic temperature (e.g.
, is obviously undefined for non-equilibrium systems. At equilibrium, there are infinitely many phase functions whose ensemble average equals the equilibrium thermodynamic temperature (e.g.  (where
(where 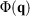 is the total interatomic potential energy of all the atoms in our system[17]). When we deviate from equilibrium, these different expressions each generally have different ensemble-averaged values. Reading through Clausius’ papers, it appears that he thought that the temperature of an ideal gas is always well defined. However, this is in fact not the case as we deviate from equilibrium. The logical inconsistencies inherent in Clausius’ strict inequality for a system of interest have been known for over 100 years.[18]
is the total interatomic potential energy of all the atoms in our system[17]). When we deviate from equilibrium, these different expressions each generally have different ensemble-averaged values. Reading through Clausius’ papers, it appears that he thought that the temperature of an ideal gas is always well defined. However, this is in fact not the case as we deviate from equilibrium. The logical inconsistencies inherent in Clausius’ strict inequality for a system of interest have been known for over 100 years.[18]
As we deviate from equilibrium, we cannot use the known equilibrium temperature of a second ideal gas reservoir system to determine the temperature of a non-equilibrium steady-state because there is no zeroth law for the equality of the temperature of a non-equilibrium system in thermal contact with an equilibrium system. As we have shown using the fluctuation theorem and the second law inequality, if there is a system of interest in equilibrium with an ideal gas, then the system of interest is driven away from equilibrium by application of a field – heat will simply flow from the non-equilibrium system to the ideal gas (formerly) equilibrium system on average.[19] This flow, close to equilibrium, would be interpreted as occurring in response to a temperature gradient. Further from equilibrium, the temperature under Clausius’ definition remains undefined.
Relationship between Gibbs Entropy and the Calorimetric Entropy
In this section, we show that our calorimetric entropy is completely consistent with Gibbs’s observation – in an autonomous Hamiltonian system, the fine-grained Gibbs entropy, 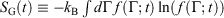 , is a constant of the motion.[20] There have been many discussions of Gibbs (Boltzmann) entropy and its relationship to thermodynamics; for examples see the references therein.[21–27] Here, we use a different approach.
, is a constant of the motion.[20] There have been many discussions of Gibbs (Boltzmann) entropy and its relationship to thermodynamics; for examples see the references therein.[21–27] Here, we use a different approach.
We now consider the instantaneous rate of change of the Gibbs entropy for a possibly irreversible process:
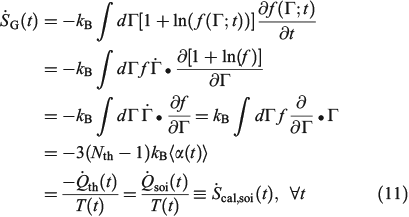
In Eqn 11, 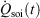 denotes the rate of heat gain or loss for the system of interest and
denotes the rate of heat gain or loss for the system of interest and 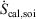 denotes the possibly irreversible change in the calorimetric entropy of the system of interest. This extension of the notion of calorimetric entropy to irreversible processes is made possible by our extension of the definition of temperature to such systems. Eqn 11 expresses the rate of change in Gibbs entropy in terms of heat transfer and equilibrium temperature that could be measured calorimetrically, at least for some experimental setups, rather than phase space properties such as the distribution function and phase space contraction rate. The relationship between the phase space contraction and the heat transfer used to obtain the final equality is valid for field-driven thermostatted systems and for the systems undergoing temperature changes discussed above, see reference therein.[9] Under other conditions, such as field-driven isoenergetic systems, the relationship can differ but the change in Gibbs entropy may still be expressed in terms of measureable properties.
denotes the possibly irreversible change in the calorimetric entropy of the system of interest. This extension of the notion of calorimetric entropy to irreversible processes is made possible by our extension of the definition of temperature to such systems. Eqn 11 expresses the rate of change in Gibbs entropy in terms of heat transfer and equilibrium temperature that could be measured calorimetrically, at least for some experimental setups, rather than phase space properties such as the distribution function and phase space contraction rate. The relationship between the phase space contraction and the heat transfer used to obtain the final equality is valid for field-driven thermostatted systems and for the systems undergoing temperature changes discussed above, see reference therein.[9] Under other conditions, such as field-driven isoenergetic systems, the relationship can differ but the change in Gibbs entropy may still be expressed in terms of measureable properties.
We note that in order to determine the sign of the Clausius inequality, one has to employ a fluctuation relation such as the Crooks fluctuation relation,[11] as we have done previously.[9]
In going from line 2 to line 3 of Eqn 11, we have assumed that Nth particles are subject to a Nosé–Hoover thermostat in 3 Cartesian dimensions, as in our equations of motion (Eqn 3). However, one could thermostat just one Cartesian dimension. In this case, the factor 3 in line 3 would be changed to 1. This makes no difference to the final result. The result is also completely independent of the Nosé–Hoover time constant 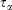 appearing in the equations of motion (Eqn 3) and the actual number of thermostatted particles, Nth. The factor
appearing in the equations of motion (Eqn 3) and the actual number of thermostatted particles, Nth. The factor 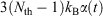 is thus completely nominal. The only quantities that are independent of how the thermostatting is carried out are the rate of heat gained by the system of interest
is thus completely nominal. The only quantities that are independent of how the thermostatting is carried out are the rate of heat gained by the system of interest 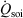 and the equilibrium thermodynamic temperature the system will relax to
and the equilibrium thermodynamic temperature the system will relax to 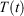 if at time t, the protocol execution is halted and the system is allowed to relax towards equilibrium. This temperature is, in this case, always the target temperature of the Nosé–Hoover thermostat at time t,
if at time t, the protocol execution is halted and the system is allowed to relax towards equilibrium. This temperature is, in this case, always the target temperature of the Nosé–Hoover thermostat at time t, 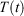 (Eqn 3). This target temperature is completely independent of the Nosé–Hoover time constant, the actual number of thermostatted particles, or indeed whether the thermostat operates on all Cartesian momentum components or just some of them. We note that the non-equilibrium distribution of states at time t,
(Eqn 3). This target temperature is completely independent of the Nosé–Hoover time constant, the actual number of thermostatted particles, or indeed whether the thermostat operates on all Cartesian momentum components or just some of them. We note that the non-equilibrium distribution of states at time t, 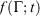 , is highly dependent on the Nosé–Hoover time constant and the precise number of particles that are directly thermostatted. It is only the underlying equilibrium temperature that is independent of the thermostatting details.
, is highly dependent on the Nosé–Hoover time constant and the precise number of particles that are directly thermostatted. It is only the underlying equilibrium temperature that is independent of the thermostatting details.
Eqn 11 gives a generalized expression for the rate of change of Gibbs entropy. It is valid for reversible and irreversible processes and shows that the change in Gibbs entropy, defined in terms of the phase space distribution function, is in fact related to physical properties i.e. the heat transfer and the underlying equilibrium temperature of the possibly non-equilibrium system.
The reversible and irreversible Gibbs and calorimetric entropies are instantaneously equal. The key to understanding Eqn 11 is our definition of the temperature – the temperature of the underlying equilibrium state that any non-equilibrium system will relax to if it was so allowed. Every T-mixing non-equilibrium system is in a sense ‘attracted’ to a unique equilibrium state. The equilibrium temperature of this attracting state is the temperature that appears in Eqn 11.
If the process is not quasi-static, the change in the entropy that would be computed using Eqn 11 is not path independent. This means that if the process is irreversible, the calorimetric entropy is not a state function and because Clausius’ entropy must be a state function, the definition of the temperature, 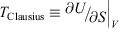 , is as we noted above, not well defined.
, is as we noted above, not well defined.
We note that for a quasi-static process, transforming a system from equilibrium state 1 to equilibrium state 2, 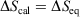 , where
, where 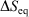 is the difference of equilibrium entropies of the equilibrium states. However, if the transformation is carried out irreversibly,
is the difference of equilibrium entropies of the equilibrium states. However, if the transformation is carried out irreversibly, 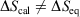 . This reflects the fact that only the equilibrium entropy is a state function. It also reflects the fact that the change in the Gibbs entropy calculated using Eqn 11 incorporates the details of the underlying distribution that will never reach the equilibrium distribution of state 2 in finite time, although the physical properties of the system will relax towards their equilibrium values to within any desired accuracy.
. This reflects the fact that only the equilibrium entropy is a state function. It also reflects the fact that the change in the Gibbs entropy calculated using Eqn 11 incorporates the details of the underlying distribution that will never reach the equilibrium distribution of state 2 in finite time, although the physical properties of the system will relax towards their equilibrium values to within any desired accuracy.
For a non-equilibrium system, only the Gibbs and calorimetric entropies are defined. Eqn 11 provides a very simple example of how these non-equilibrium entropies are singular by considering a system undergoing constant energy dynamics (possibly using an ‘ergostat’, which has a similar function to a thermostat but fixes the energy rather than the temperature). If we start with a microcanonical equilibrium distribution in the thermodynamic limit and such a system evolves using Hamiltonian dynamics (Newtonian), then there is no need to apply an ergostat, and Eqn 11 shows that the Gibbs entropy does not change. However, if we apply a dissipative field to the system, an ergostat will be required to keep the energy fixed. Eqn 11 gives the rate of change of the Gibbs entropy of the system of interest, even in the presence of the dissipative field. After sufficient time (several periods equal to the time required for relaxation of stress in the system, or ‘Maxwell times’), we assume the system relaxes into a ‘pseudo non-equilibrium steady state’[6]. By this, we mean that the system has relaxed to a state whose properties do not change with time within some arbitrarily small tolerance). The non-equilibrium steady state can be approached arbitrarily closely by extending the time over which the field is applied.
In the pseudo-steady state, the ensemble-averaged value of the ergostat multiplier ( ) is approximately constant, i.e. independent of time. However, Eqn 11 shows that this means that the Gibbs entropy of the system diverges towards negative infinity at a constant rate. Now consider what happens if, after some long but finite time t, we set the dissipative field back to zero and let the T-mixing system relax at constant energy towards microcanonical equilibrium.[28] In this relaxation process, the Gibbs entropy of the system does not change because it is now an autonomous Hamiltonian system following Newtonian dynamics.[20,29] No thermostat is required to keep the energy constant, and therefore
) is approximately constant, i.e. independent of time. However, Eqn 11 shows that this means that the Gibbs entropy of the system diverges towards negative infinity at a constant rate. Now consider what happens if, after some long but finite time t, we set the dissipative field back to zero and let the T-mixing system relax at constant energy towards microcanonical equilibrium.[28] In this relaxation process, the Gibbs entropy of the system does not change because it is now an autonomous Hamiltonian system following Newtonian dynamics.[20,29] No thermostat is required to keep the energy constant, and therefore 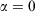 . After a Maxwell time (or several Maxwell times), the averages of all physical phase functions converge towards the same microcanonical values they had at time zero. However, the Gibbs entropy of the final state determined from Eqn 11 can be made arbitrarily more negative than the initial entropy by simply extending the duration t of the non-equilibrium pseudo-steady state to arbitrarily large values! Obviously, if we attempt to find the temperature of this second state by applying Clausius’ definition to this irreversible process,
. After a Maxwell time (or several Maxwell times), the averages of all physical phase functions converge towards the same microcanonical values they had at time zero. However, the Gibbs entropy of the final state determined from Eqn 11 can be made arbitrarily more negative than the initial entropy by simply extending the duration t of the non-equilibrium pseudo-steady state to arbitrarily large values! Obviously, if we attempt to find the temperature of this second state by applying Clausius’ definition to this irreversible process, 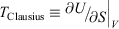 , we can obtain an infinite range of values depending on how long we stayed in the non-equilibrium pseudo-steady state. Although the physical properties will converge towards their equilibrium values, the path integral of the rate of change in Gibbs entropy computed along non-equilibrium paths using Eqn 11 can be made arbitrarily different from its equilibrium value.
, we can obtain an infinite range of values depending on how long we stayed in the non-equilibrium pseudo-steady state. Although the physical properties will converge towards their equilibrium values, the path integral of the rate of change in Gibbs entropy computed along non-equilibrium paths using Eqn 11 can be made arbitrarily different from its equilibrium value.
We note that if after an irreversible process of arbitrary duration, the system is allowed to relax towards equilibrium and the equilibrium entropy differences can be computed arbitrarily accurately. For example, the equilibrium entropy difference 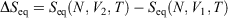 can be computed as an equilibrated path integral using the Maxwell relation
can be computed as an equilibrated path integral using the Maxwell relation 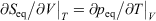 as
as 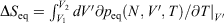 . (Note:
. (Note: 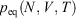 is obtained to arbitrary accuracy from the non-equilibrium pressure by using Eqn 4.) This does not contradict our statement above that the entropy is not a state function for irreversible processes. This is because the Maxwell relations, upon which this approach is based (via equality of two expressions for
is obtained to arbitrary accuracy from the non-equilibrium pressure by using Eqn 4.) This does not contradict our statement above that the entropy is not a state function for irreversible processes. This is because the Maxwell relations, upon which this approach is based (via equality of two expressions for 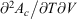 ), are ultimately based on the Gibbs equation (Eqn 5) and Eqn 9, both of which are valid for equilibrium states only. Both of these equations, as we have already noted, have nothing to do with irreversibility.
), are ultimately based on the Gibbs equation (Eqn 5) and Eqn 9, both of which are valid for equilibrium states only. Both of these equations, as we have already noted, have nothing to do with irreversibility.
The Gibbs entropy, which is instantaneously equal to the calorimetric entropy, is a function of the unphysical and generally unmeasurable N-particle phase space probability distribution function. A true equilibrium distribution can never be reached in finite times.[2] Therefore, by introducing the T-mixing condition, we concentrate on the relaxation of averages of physical phase functions, thereby ignoring the intricacies of the full N-particle phase space distribution functions.
Conclusion
We can summarise the relationships between the change in equilibrium entropy (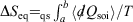 ), change in calorimetric entropy (
), change in calorimetric entropy (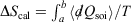 ), Gibbs entropy
), Gibbs entropy 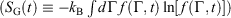 and equilibrium Gibbs entropy
and equilibrium Gibbs entropy 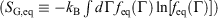 as follows:
as follows:
-
Quasi-static processes:
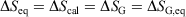
-
Quasi-static cyclic processes:
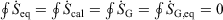
-
Irreversible processes that start and end at equilibrium:
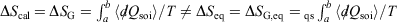
-
Irreversible processes that start or end out of equilibrium
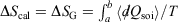 and
and 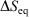 and
and 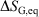 are undefined
are undefined -
For reversible or irreversible processes,
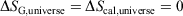
We note that for irreversible processes that start and end in equilibrium states, the change in Gibbs free energy is not equal to the difference in Gibbs free energies of the equilibrium state that the system starts in and relaxes towards i.e. 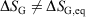 . Although this seems counterintuitive, the inequality occurs because though the state functions of the system will have relaxed to their equilibrium values, the distribution function continues to evolve and will never reach the equilibrium distribution. The Gibbs entropy is a function of the distribution function itself, and therefore the Gibbs entropy of the evolved state will never be equal to the Gibbs entropy of the equilibrium state that is being approached. The equilibrium Gibbs entropy,
. Although this seems counterintuitive, the inequality occurs because though the state functions of the system will have relaxed to their equilibrium values, the distribution function continues to evolve and will never reach the equilibrium distribution. The Gibbs entropy is a function of the distribution function itself, and therefore the Gibbs entropy of the evolved state will never be equal to the Gibbs entropy of the equilibrium state that is being approached. The equilibrium Gibbs entropy, 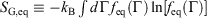 , is a state function. However, in general, the Gibbs entropy,
, is a state function. However, in general, the Gibbs entropy, 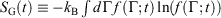 , is not an average of a phase function and is not a state function. In summary, therefore,
, is not an average of a phase function and is not a state function. In summary, therefore, 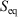 and
and 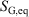 are state functions, whereas, in general,
are state functions, whereas, in general, 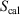 and
and 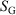 are not.
are not.
Because the thermostat in Eqn 3, with Nosé–Hoover target temperature 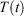 , is not applied directly to the system of interest, our treatment may appear to be highly non-local. We thus consider the heat transferred to the system of interest and the temperature that is controlled by the thermostat, which is external to the system of interest. However, the zeroth ‘Law’ of thermodynamics (see our recent mechanical proof[19]) shows that the equilibrium temperature to which the entire system will relax, if it is so allowed, is in fact spatially uniform across the entire thermal system (the system of interest, the walls (if any) and the thermostatting particles). This makes the temperature of the underlying or attracting equilibrium state uniform across the entire thermal system. This in turn means that our results can be expressed entirely in terms of variables that are local to the system of interest because our newly defined temperature is in fact a global property.
, is not applied directly to the system of interest, our treatment may appear to be highly non-local. We thus consider the heat transferred to the system of interest and the temperature that is controlled by the thermostat, which is external to the system of interest. However, the zeroth ‘Law’ of thermodynamics (see our recent mechanical proof[19]) shows that the equilibrium temperature to which the entire system will relax, if it is so allowed, is in fact spatially uniform across the entire thermal system (the system of interest, the walls (if any) and the thermostatting particles). This makes the temperature of the underlying or attracting equilibrium state uniform across the entire thermal system. This in turn means that our results can be expressed entirely in terms of variables that are local to the system of interest because our newly defined temperature is in fact a global property.
Finally, we point out that there have recently been many related developments regarding the foundations of statistical thermodynamics. A succinct summary is available in a recently published book therein.[1]
References
[1] D. J. Evans, D. J. Searles, S. R. Williams, Fundamentals of Classical Statistical Thermodynamics, Dissipation, Relaxation and Fluctuation Theorems 2016 (Wiley-VCH Verlag: Weinheim).[2] D. J. Evans, D. J. Searles, S. R. Williams, J. Stat. Mech.: Theory Exp. 2009, 2009, P07029.
| Crossref | GoogleScholarGoogle Scholar |
[3] D. J. Evans, S. R. Williams, D. J. Searles, L. Rondoni, J. Stat. Phys. 2016, 164, 842.
| Crossref | GoogleScholarGoogle Scholar |
[4] D. J. Evans, G. P. Morriss, Statistical Mechanics of Non-Equilibrium Liquids 1990 (Academic: London).
[5] S. R. Williams, D. J. Searles, D. J. Evans, Mol. Simul. 2014, 40, 208.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXitVWisrfO&md5=837641100daf044359eb2207bac6e98cCAS |
[6] (a) D. J. Evans, D. J. Searles, S. R. Williams, J. Chem. Phys. 2008, 128, 014504.
| Crossref | GoogleScholarGoogle Scholar |
(b) D. J. Evans, D. J. Searles, S. R. Williams, J. Chem. Phys. 2008, 128, 249901.
| Crossref | GoogleScholarGoogle Scholar |
[7] D. J. Evans, D. J. Searles, Adv. Phys. 2002, 51, 1529.
| Crossref | GoogleScholarGoogle Scholar |
[8] P. M. Morse, H. Feshbach, Methods of Theoretical Physics Vol. II 1953 (McGraw-Hill: New York, NY).
[9] D. J. Evans, S. R. Williams, D. J. Searles, J. Chem. Phys. 2011, 134, 204113.
| Crossref | GoogleScholarGoogle Scholar |
[10] J. C. Reid, E. M. Sevick, D. J. Evans, EPL 2005, 72, 726.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtlehurrJ&md5=2d002070341ce72ee2219a953511ef5eCAS |
[11] G. E. Crooks, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999, 60, 2721.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXls1Cltrc%3D&md5=7157580c180e569ca7eb9a2db91ca24aCAS |
[12] C. Jarzynski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1997, 56, 5018.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXntFGht7c%3D&md5=83c878f3b11cc34a8b97f06243d5540fCAS |
[13] R. Clausius, The Mechanical Theory of Heat with Its Applications to the Steam-Engine and to the Physical Properties of Bodies 1867 (Taylor and Francis: London).
[14] J. H. Irving, J. G. Kirkwood, J. Chem. Phys. 1950, 18, 817.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG3cXlsFSmtg%3D%3D&md5=1a71ae8cfa3431d0987708812142b776CAS |
[15] I. Muller, A History of Thermodynamics 2007 (Springer: Heidelberg).
[16] P. Ehrenfest, T. Ehrenfest, The Conceptual Foundations of the Statistical Approach to Statistical Mechanics 1990 (Dover: Mineola, NY).
[17] B. D. Butler, O. Ayton, O. J. Jepps, D. J. Evans, J. Chem. Phys. 1998, 109, 6519.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXmsFCrurg%3D&md5=cf7f0ee7a7301245c82289e7d3de4d55CAS |
[18] (a) J. L. F. Bertrand, Thermodynamique 1887 (Gauthier-Villars: Paris).
(b) W. M. Orr, Phil. Mag. Ser. 6 1904, 8, 509.
| Crossref | GoogleScholarGoogle Scholar |
(c) E. Buckingham, Philos. Mag. Ser. 6 1905, 9, 208.
| Crossref | GoogleScholarGoogle Scholar |
(d) M. Planck, Philos. Mag. Ser. 6 1905, 9, 167.
| Crossref | GoogleScholarGoogle Scholar |
[19] D. J. Evans, S. R. Williams, L. Rondoni, J. Chem. Phys. 2012, 137, 194109.
| Crossref | GoogleScholarGoogle Scholar |
[20] J. W. Gibbs, Elementary Principles in Statistical Mechanics 1981 (Ox Bow Press: Woodbridge, CT).
[21] J. L. Lebowitz, Phys. Today 1993, 47, 115.
[22] F. Bonetto, J. L. Lebowitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2001, 64, 056129.
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD38%2FivFSgsw%3D%3D&md5=d50267ca9212b49f8e9333fe85806feeCAS |
[23] R. Luzzi, A. R. Vasconcellos, J. R. Ramos, Braz. J. Phys. 2006, 36, 97.
| Crossref | GoogleScholarGoogle Scholar |
[24] D. Sands, Eur. J. Phys. 2008, 29, 129.
| Crossref | GoogleScholarGoogle Scholar |
[25] S. Hilbert, P. Hänggi, J. Dunkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2014, 90, 062116.
| Crossref | GoogleScholarGoogle Scholar |
[26] D. Frenkel, P. B. Warren, Am. J. Phys. 2015, 83, 163.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2MXhtFKntbk%3D&md5=827d9f7bb8b539e02746d0dec4f004a1CAS |
[27] R. de Miguel, J. M. Rubi, J. Phys. Chem. B 2016, 120, 9180.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC28Xht12jsbzM&md5=8a29dfd5da04e68739e61d221dd7f430CAS |
[28] D. J. Evans, D. J. Searles, S. R. Williams, in Diffusion Fundamentals III (Eds C. Chmelik, N. Kanellopoulos, J. Karger, T. Doros) 2009, Vol. 11, pp. 367–374 (Leipziger Universitatsverlag: Leipzig).
[29] H. R. Brown, W. Myrvold, arXiv:0809.1304 [physics.hist-ph] 2008. Available at: https://arxiv.org/abs/0809.1304 (accessed 15 November 2016).
∗ Denis J. Evans was the 2015 recipient of the David Craig Medal of the Australian Academy of Science.
† For T-mixing systems, time integrals of transient time-correlation functions of zero-mean physical phase functions converge to finite values in the long time limit.[5] Thus,
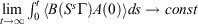 ; using the dissipation theorem[6]
; using the dissipation theorem[6] 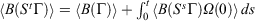 implies
implies 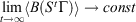 .
.‡ Note: There is a typographic error in our derivation of Eqns 7 and 8 in our recent book[1] (eqns 5.57 and 5.58).


