Evidence for widespread torsion–vibration interaction in substituted toluenes
Jason R. Gascooke A and Warren D. Lawrance
A and Warren D. Lawrance  A *
A *
A
Abstract
The torsional constant (F) is a parameter extracted from spectroscopic analyses of molecules possessing a methyl group. Its value depends primarily on the methyl structure. Widely varying F values have been reported for substituted toluenes in their ground electronic state, first excited singlet electronic state or the ground electronic state of the cation. Conventionally, this variability is assumed to indicate significant changes in the methyl structure with substituent, its position on the ring and the electronic state. However, when the large amplitude methyl torsion interacts with other, small amplitude vibrations, this interpretation is misleading as the torsional states are shifted to lower energy, resulting in a reduced, ‘effective’ F being determined. We have observed coupling between methyl torsion and the low frequency, methyl group out-of-plane wag vibration in toluene, p-fluorotoluene, m-fluorotoluene and N-methylpyrrole, leading us to postulate that, since such motion will be present whenever the methyl group is attached to a planar frame, this type of interaction is widespread. This is tested for a series of substituted toluenes by comparing the methyl group structure calculated by quantum chemistry with the experimental torsional constants. The quantum chemistry calculations predict little variation in the methyl structure across a wide range of substituents, ring positions and electronic state. The wide variation in F values observed in experimental analyses is attributed to the torsion–vibration interaction affecting the torsional band structure, so that measured F values become ‘effective constants’. Comparisons between calculated and experimental torsional constants need to be cognisant of this effect.
Keywords: ab initio calculations, internal rotation, large amplitude motion, methyl torsion, rotational spectroscopy, structure elucidation, torsion–vibration interaction, torsion–vibration coupling.
Introduction
A theme running through Brian Yates’ research career has been the use of computational chemistry to provide insights into chemical processes. In the spirit of the special issue celebrating his contribution to Australian chemistry, this paper takes an analogous approach, whereby the insights into molecular behaviour provided by quantum chemistry are explored in the context of a large amplitude motion (LAM), internal rotation of the methyl group, also referred to as methyl torsion.
Large amplitude motion is central to chemistry. Chemical change usually involves molecules undergoing a rearrangement in their atomic connectivity, the expulsion of atoms or fragments or the exchange of atoms or fragments between molecules. These atomic motions happen far from the well understood simple harmonic vibrations of molecules with well-defined structures.1 Methyl torsion is regarded as a well understood LAM,2 with the number of papers reporting the analysis of microwave spectra for molecules containing a methyl group recently being estimated to exceed 1000.3 Microwave studies observe transitions between rotational states rather than observing the transitions between the torsional states directly but, nonetheless, constants describing the torsional motion, particularly the torsional potential, can be determined when fitting the observed line positions.2,4–7 Although there are many fewer studies of methyl torsion using electronic spectroscopy, studies of supersonically cooled gas phase samples have allowed torsional states to be observed directly (see Ito8 and Breen et al.9 for early examples). Here, fits to the torsional energies allow the constants describing this motion to be determined. An advantage of these studies is that the torsional constant (F), which is related to the methyl group structure, is routinely extracted along with the torsional potential parameters. Although F can be determined in fits to microwave spectra when lines for multiple torsional states are fitted simultaneously,6,7 it is not routinely determined. Spectroscopic analyses assume that the large amplitude torsional motion can be separated from the remaining small amplitude vibrations.2,4–7 In the case of microwave spectra, this assumption is unavoidable as spectra can be fitted equally well with torsion–vibration interaction included or excluded, with the difference being the value of the constants extracted (vide infra), as has been explicitly demonstrated for toluene.10
Despite the widespread success in spectroscopic fitting using the assumption that torsion can be separated from the remaining vibrations, evidence has emerged in the past few years that, in cases where the methyl group is attached to a planar frame, the large amplitude torsional motion is affected by the small amplitude vibrations that involve an out-of-plane methyl group wagging motion. To date, this coupling has been observed and analysed in detail in toluene,11–13 p-fluorotoluene,14 m-fluorotoluene15 and N-methylpyrrole.16 Earlier studies by Weisshaar’s group also noted isolated resonances due to coupling between torsional and torsion–vibration states in o-chlorotoluene,17 2-fluoro-6-chlorotoluene18 and 2,6-difluorotoluene19 (see table VIII of Richard et al.17 for a summary). We have previously discussed how torsion–vibration interaction and methyl group precession are both manifestations of a torsion angle-dependent tilting of the methyl group, and shown that the analyses of rotational spectra for a number of ‘small’ molecules with planar frames require precession terms to fit the line positions, suggesting torsion–vibration interaction is also present in these molecules.20 These observations have led us to postulate that the interaction between methyl torsion and methyl group in- and out-of-plane wagging is pervasive when the methyl group is attached to a planar frame.15 This has important implications for intramolecular energy flow, as torsion–vibration interaction increases the rate of intramolecular vibrational energy redistribution significantly.14,21,22
Some 60 years ago, Kirtman discussed the issue of torsion–vibration interaction in the context of the analysis of microwave spectra and concluded that, provided the interaction can be adequately treated using a perturbation approach (specifically, a van Vleck transformation in Kirtman’s discussion), analyses can ignore it but the torsional constants determined are ‘effective’ constants and no longer retain their unperturbed, physical meaning.23 Thus, the success of the torsional model used in spectroscopic analyses is not necessarily a reflection of the validity of the approximation that torsion and small amplitude vibrations can be separated but, instead, may reflect situations where torsion is interacting with vibration and the constants extracted are effective constants, as demonstrated for toluene.10
One of the key torsional constants is the internal rotation constant, now generally denoted by F, although B has also been used, which depends on the structure of the methyl group and the frame to which it is attached, as is discussed below. The value of F is reduced when torsion–vibration interaction is present. This occurs because the torsion–vibration interaction couples torsional states within the one quantum vibrational level with those in the zero quantum level. The lower torsional states in the zero quantum level are shifted to lower energy by this interaction, thus requiring a smaller value of F to reproduce the observed energies12 (see fig. 6 of Gascooke et al.12 for a schematic). Another way this interaction is manifested is through methyl group precession, which again leads to a reduced value of F.24 With structural calculations using quantum chemistry codes now routine, it is clearly important to understand the role of torsion–vibration interactions, so that it can be determined when an experimental F value truly pertains to the molecular structure or when it is simply an effective value.
Experimental techniques such as two-dimensional laser induced fluorescence (2D-LIF)25 and far infrared absorption spectroscopy13 have proven successful in revealing the interaction between methyl torsion and methyl group wagging motions.11–16 However, experimental acquisition and analysis is time consuming and, in the short term, it becomes impractical to apply the techniques to a large series of molecules to explore how widespread this type of interaction is. It would thus be useful to have a means to screen existing data sets to ascertain if torsion–vibration interaction involving the methyl group wagging modes is largely ubiquitous as we have proposed. One means to do this is to use quantum chemistry structure calculations to determine F values and compare these with experimentally determined values. If torsion–vibration interaction is present, the experimental F values will be effective values, and smaller than those predicted, for the reasons discussed above. This is the goal of the present work.
It is usually the case in microwave analyses that the number of torsional states considered is limited and an experimental value of F is not determined. This is changing, with analyses using codes such as BELGI6 and RAM367 incorporating multiple torsional states and determining F values, generally for small molecules. We recently considered several examples and showed that torsion–vibration interaction, manifest through methyl group precession, was likely present and affecting the F values extracted.20 By contrast, there is a comparatively large compendium of F values available through the analysis of electronic spectra measured in supersonic free jet expansions. Excitation spectra allow the study of torsional states within the first excited electronic singlet state, S1, whereas dispersed fluorescence from selected S1 states allows observation of the torsional states in the ground electronic state, S0. Ionisation from intermediate S1 states allows the torsional states within the lowest electronic state of the associated cation, , to be observed by zero electron kinetic energy (ZEKE) spectroscopy. Owing to favourable photophysical properties, such studies have largely focussed on substituted toluenes and include substitution at the ortho, meta and para positions by a wide variety of substituents. We focus on these types of molecules in the present work and consider the changes in F in the three electronic states: S0, S1 and . The study encompasses 27 molecules in S0, 30 in S1 and 13 molecules in , with substantial overlap of the molecules for which data are available in these states. The ability to study the effect in three different electronic states presented by the data set enables any electronic influence of torsion–vibration interaction to be explored. Having the common toluene template will prove advantageous as we will show that the quantum chemistry calculations predict little difference in methyl group structures across the data set and little change among the three electronic states. This is shown to be at variance with the structural variation implied by the range of experimental F values if the relationship between F and methyl group structure is taken at face value.
Results
Background
The torsional state energies are given as the eigenvalues of the Hamiltonian in a basis of free rotor functions, with matrix elements2,4:
where V3 and V6 are terms defining the torsional potential:
α is the torsional angle, F is the torsional constant, discussed in detail in the following section, and m is the free rotor angular momentum quantum number, which takes values 0, ±1, ±2,… Generally, |V3| > |V6|, in which case V3 denotes the barrier height and the V6 term determines the shape of the potential. Since the torsional barrier terms link free rotor states differing in m by multiples of 3, the Hamiltonian factors into three non-interacting blocks, one for m = 3n states and two for m = 3n ± 1, where n = 0, ±1, ±2,… The two m = 3n ± 1 matrices are equivalent and lead to degenerate states of E symmetry in the G6 permutation–inversion group appropriate to the general case for a planar frame. The m = 3n matrix leads to A states. The eigenstates of the Hamiltonian, i.e. the hindered rotor states, are generally labelled m in the case of low barriers, where the states are little perturbed from the free rotor states and m = |m| or, in the case of high barriers, by a torsional quantum number υt and corresponding symmetry (e.g. υt(A) or υt(E)). For the degenerate m = ± 3n (n = 1, 2,…) pairs one obtains symmetric and anti-symmetric linear combinations of the m = −3n and +3n components: 3n(+) indicates the symmetric combination and 3n(−) the anti-symmetric one. The m and υt labels are related by υt (A) = 0 ≡ m = 0; υt (E) = 0 ≡ m = 1; υt (E) = 1 ≡ m = 2; υt (A) = 1 ≡ m = 3(−); υt (A) = 2 ≡ m = 3(+); υt (E) = 2 ≡ m = 4; etc.
Eqn 1a–b show that the parameters F, V3 and V6 define the energies of the torsional states. Thus, provided at least three torsional states are observed, unique values for these three constants can be determined from the torsional energies. Generally, torsional states are observed from m = 0 to |m| ≥ 4 (i.e. m = 0 to m ≥ 4; υt(A) = 0 to υt ≥ 2), leading to the number of observed energies exceeding the number of variables. This procedure for extracting F, V3 and V6 from the observed torsional energies has been used to determine most of the experimental torsional constants discussed here. In instances where such fits were not available, the data come from the analysis of rotational structure, either from rotational line spectra (microwave spectra) or high resolution electronic spectra where the rotational structure is observed. In several cases, both types of data are available, and the experimental F values discussed come from fits to the observed torsional band transition energies, since these are most susceptible to perturbations due to torsion–vibration interaction where it is present.
As discussed in the Introduction, when torsion–vibration interaction is present, the value for F determined in experimental analyses is smaller than the value associated with the molecular structure. In the present work, we examine experimentally determined F values for a series of substituted toluenes to see if there is evidence for the F values being systematically reduced, which is an indicator of torsion–vibration interaction routinely occurring in substituted toluenes.
Extracting FMethyl from experimental F values
F is the experimentally determined constant and incorporates aspects of both the methyl and frame structures since the angular momentum associated with methyl rotation is counterbalanced by rotation of the frame in the opposite direction. If the variation in F values among substituted toluenes (vide infra) is a consequence of changes in the methyl structure, this is best seen by comparing the experimental and calculated constants that depend only on the methyl group structure. This section discusses how this can be achieved.
F is given by:
where .5 Here the sum is over the three axes for the axis system chosen, IM denotes the moment of inertia for rotation of the methyl group about its (notionally) C3 axis, Ig is the moment of inertia for rotation of the molecule about the g axis and the λg are direction cosines between the methyl C3 axis and the molecular axis system used. Eqn 2 can be expressed in terms of rotational constants as:
where . FMethyl denotes the constant for rotation of the methyl group about its (notionally) C3 axis and Gg is the rotational constant for the molecule about the g axis. FMethyl is the constant we wish to extract from the experimental F constants for comparison with calculated methyl group structures. In the principal axis system, when the frame to which the methyl group is attached is planar, the c axis is perpendicular to the frame, with the a and b axes lying in the plane. Thus λc = 0 and the sum is over the a and b axes.
It can be seen from Eqn 3 that, since r < 1, F > FMethyl by an amount that varies depending on the frame. To extract FMethyl from F, we note that for the case of a planar frame, Eqn 3 can be written as:
where θ is the angle between the frame‒methyl bond and the principal a axis and A and B are the usual rotational constants for the molecule. Eqn 4 can then be rearranged to yield the expression for FMethyl:
For the molecules of interest, the positive solution is the correct one.
Although most of the substituted toluenes belong to the G6 permutation–inversion group, there is an important subset where the frame has C2v symmetry and these molecules belong to the G12 permutation–inversion group. In such cases, the methyl group lies parallel to either the a or b axis, and there is only a single non-zero term, leading to the simplified form:
where IF is the moment of inertia for the frame about the principal axis parallel to the methyl–frame bond and GFrame is the associated rotational constant. FMethyl is readily extracted if F and GFrame are known.
Eqn 5a shows that, in the general case of a planar frame, to convert from F into FMethyl requires values for the molecular in-plane rotational constants and the angle between the frame–methyl bond and the a principal axes, whereas Eqn 5b shows that when the frame has C2v symmetry this simplifies to requiring only the rotational constant for the frame about the axis parallel to the methyl–frame bond.
We have used Eqn 5a and 5b to determine FMethyl values from the reported F values for substituted toluenes. The results are given in Tables 1–3 for S0, S1 and respectively. Where experimental values for the rotational constants are available, they have been used. In their absence, values from optimised quantum chemistry structures have been used. In all cases, θ values are derived from optimised quantum chemistry structures. A detailed comparison between the experimental rotational constants and those determined from quantum chemistry optimised structures, and the effect that using experimental v. computational values has on the FMethyl values extracted, is given in the Supplementary material. Both Møller–Plesset perturbation theory (MP2) with Dunning correlation-consistent polarised valence-only triple zeta basis set (cc-pVTZ) and density functional theory (DFT) with the Becke, 3-parameter, Lee–Yang–Parr (B3LYP) functional and cc-pVTZ quantum chemistry calculations were performed for S0, these two quite different computational approaches being used in order to test the robustness of the computed FMethyl values. The S1 calculations used time dependent (TD) DFT B3LYP cc-pVTZ and used DFT B3LYP cc-pVTZ. The Computational methods section gives details of the calculations.
| Molecule | Exp. torsional constants | Ref. | MP2 cc-pVTZ | DFT B3LYP cc-pVTZ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F | V3 | V6 | |||||||||
| Toluene | 5.471 | −4.84 | 33 | 5.280 | 5.394 | 5.328 | 5.280 | 5.395 | 5.328 | ||
| o-Fluorotoluene | 5.306 | 228.1 | 6.6 | 27 | 5.204 | 5.386 | 5.319 | 5.204 | 5.388 | 5.321 | |
| m-Fluorotoluene | 5.28 | 20.2 | −7.7 | 15 | 5.170 | 5.393 | 5.327 | 5.170 | 5.393 | 5.326 | |
| p-Fluorotoluene | 5.46 | −4.6 | 14, A | 5.270 | 5.397 | 5.332 | 5.270 | 5.399 | 5.331 | ||
| m-Chlorotoluene | 5.32 | 1 | −8 | 34 | 5.239 | 5.392 | 5.326 | 5.239 | 5.393 | 5.326 | |
| p-Chlorotoluene | 5.40 | −17 | 34 | 5.210 | 5.395 | 5.329 | 5.210 | 5.396 | 5.329 | ||
| o-Tolunitrile | 5.49 | 178.1 | 31.3 | 28 | 5.422 | 5.386 | 5.318 | 5.423 | 5.391 | 5.324 | |
| m-Tolunitrile | 5.26 | 14 | −11 | 35 | 5.180 | 5.390 | 5.324 | 5.180 | 5.393 | 5.326 | |
| p-Tolunitrile | 5.40 | −10 | 35 | 5.209 | 5.392 | 5.326 | 5.208 | 5.392 | 5.325 | ||
| m-Ethynyltoluene | 5.332 | 19 | −6 | 36 | 5.253 | 5.392 | 5.326 | 5.253 | 5.395 | 5.328 | |
| trans-o-Cresol | 5.295 | 355 | −7 | 37 | 5.192 | 5.381 | 5.312 | 5.192 | 5.386 | 5.320 | |
| cis-o-Cresol | 5.20 | 600 | −30 | 37 | 5.098 | 5.400 | 5.335 | 5.098 | 5.404 | 5.337 | |
| trans-m-Cresol | 5.30 | 11 | −8 | 38 | 5.191 | 5.394 | 5.328 | 5.191 | 5.393 | 5.326 | |
| cis-m-Cresol | 5.31 | 26 | −9 | 38 | 5.200 | 5.395 | 5.329 | 5.200 | 5.394 | 5.327 | |
| p-Cresol | 5.224 | 18 | −13.8 | 39 | 5.034 | 5.398 | 5.333 | 5.034 | 5.400 | 5.333 | |
| o-Toluidine | 5.28 | 703 | 62 | 40 | 5.178 | 5.389 | 5.322 | 5.179 | 5.396 | 5.329 | |
| m-Toluidine | 5.37 | 9 | −10 | 40 | 5.264 | 5.394 | 5.328 | 5.264 | 5.393 | 5.326 | |
| p-Toluidine | 5.284 | 5.398 | 5.333 | 5.284 | 5.401 | 5.334 | |||||
| trans-o-Methylanisole | 5.32 | 427 | 27 | B | 5.264 | 5.379 | 5.310 | 5.264 | 5.385 | 5.319 | |
| trans-m-Methylanisole | 5.47 | 30.35 | 2 | C | 5.144 | 5.393 | 5.327 | 5.145 | 5.392 | 5.325 | |
| cis-m-Methylanisole | 5.46 | 57.07 | 2 | 29 | 5.538 | 5.394 | 5.328 | 5.538 | 5.393 | 5.326 | |
| p-Methylanisole | 5.30 | 52 | −20 | C | 5.137 | 5.398 | 5.333 | 5.137 | 5.400 | 5.333 | |
| trans-m-Methylthioanisole | 5.34 | 34 | −25.4 | 41 | 5.163 | 5.392 | 5.326 | 5.163 | 5.393 | 5.326 | |
| trans-m-Methylstyrene | 5.40 | 52 | 19 | 42 | 5.307 | 5.394 | 5.328 | 5.307 | 5.395 | 5.328 | |
| cis-m-Methylstyrene | 5.20 | 45 | 0 | 42 | 5.136 | 5.393 | 5.327 | 5.135 | 5.395 | 5.328 | |
| p-Methylstyrene | 5.253 | 23.22 | −14.3 | 43 | 5.083 | 5.394 | 5.328 | 5.083 | 5.395 | 5.328 | |
| p-Methylbenzaldehyde | 5.431 | 28.11 | −4.77 | 44 | 5.261 | 5.392 | 5.326 | 5.261 | 5.391 | 5.325 | |
Where available, the experimental F, V3 and V6 values come from fits to the observed torsional energies; in a few cases, the values come from fits to microwave spectra encompassing several torsional states. The results are shown for two sets of calculations, MP2/cc-pVTZ and DFT B3LYP/cc-pVTZ. values in roman were determined using the experimental F, A and B constants and the calculated methyl angle θ in Eqn 5a or, for G12 molecules, Eqn 5b; data in italic were determined using the experimental F and the calculated A, B and θ values (see Supplementary material for values). The calculated and scaled FMethyl values ( and ) are obtained from the optimised, minimum energy configuration structures. See text for a discussion of scaling.
| Molecule | Experimental torsional constants | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|
| F | V3 | V6 | ||||||
| Toluene | 5.298 | −26.376 | 46 | 5.116 | 5.371 | 5.306 | ||
| o-Fluorotoluene | 5.121 | 21.8 | −13.8 | 27 | 5.022 | 5.371 | 5.306 | |
| m-Fluorotoluene | 5.20 | 116.6 | −26.2 | 15 | 5.093 | 5.374 | 5.309 | |
| p-Fluorotoluene | 5.06 | −24.2 | 14, A | 4.879 | 5.363 | 5.299 | ||
| 2,6-Difluorotoluene | 5.08 | −10.6 | 19 | 5.022 | 5.386 | 5.320 | ||
| o-Chlorotoluene | 5.2 | 144.2 | −15 | 17 | 5.137 | 5.379 | 5.314 | |
| m-Chlorotoluene | 4.15 | 129 | −39 | 34 | 4.070 | 5.375 | 5.310 | |
| p-Chlorotoluene | 4.91 | −38 | 34 | 4.728 | 5.366 | 5.301 | ||
| 2-Chloro,6-fluorotoluene | 5.0 | 139.4 | −7 | 18 | 4.961 | 5.389 | 5.323 | |
| o-Tolunitrile | 5.16 | 188 | 51.8 | 28 | 5.094 | 5.359 | 5.295 | |
| m-Tolunitrile | 5.01 | 39 | −28 | 35 | 4.934 | 5.367 | 5.303 | |
| p-Tolunitrile | 5.60 | −6 | 35 | 5.414 | 5.384 | 5.317 | ||
| m-Ethynyltoluene | 5.121 | 101 | −22 | 36 | 5.044 | 5.370 | 5.305 | |
| p-Ethynyltoluene | 5.55 | −12 | 47 | 5.366 | 5.371 | 5.306 | ||
| trans-o-Cresol | 5.15 | 83 | −7 | 37 | 5.049 | 5.372 | 5.307 | |
| cis-o-Cresol | 5.10 | 90 | −5 | 37 | 5.001 | 5.427 | 5.357 | |
| trans-m-Cresol | 5.31 | 213 | −22 | 38 | 5.200 | 5.379 | 5.314 | |
| cis-m-Cresol | 5.21 | 211 | −39 | 38 | 5.101 | 5.377 | 5.312 | |
| p-Cresol | 5.108 | 7.99 | −24.7 | 39 | 4.930 | 5.361 | 5.297 | |
| o-Toluidine | 5.40 | 40 | −11 | 40 | 5.302 | 5.419 | 5.350 | |
| m-Toluidine | 5.24 | 317 | −19 | 40 | 5.132 | 5.380 | 5.314 | |
| p-Toluidine | 5.408 | 43.9 | 48 | 5.231 | 5.363 | 5.299 | ||
| trans-o-Methylanisole | 5.43 | 36.9 | −2.76 | B | 4.845 | 5.374 | 5.309 | |
| trans-m-Methylanisole | 5.51 | 225.7 | −24.45 | B | 5.347 | 5.378 | 5.312 | |
| cis-m-Methylanisole | 5.51 | 209.47 | −26 | 45 | 5.448 | 5.378 | 5.313 | |
| p-Methylanisole | 4.20 | 31 | −31 | B | 4.040 | 5.358 | 5.294 | |
| trans-m-Methylthioanisole | 5.33 | 304 | −10 | 41 | 5.254 | 5.378 | 5.313 | |
| trans-m-Methylstyrene | 5.40 | 79 | 5 | 42 | 5.300 | 5.369 | 5.304 | |
| cis-m-Methylstyrene | 6.10 | 165 | −13 | 42 | 6.038 | 5.367 | 5.302 | |
| p-Methylstyrene | 5.187 | 16.99 | −6.83 | 43 | 5.025 | 5.369 | 5.304 | |
Where available, the experimental F, V3 and V6 values come from fits to the observed torsional energies; in a few cases, the values come from fits to high resolution rotationally resolved spectra for two or more m/υt states. values in roman were determined using the experimental F, A and B constants and the calculated methyl angle θ in Eqn 5a or, for G12 molecules, Eqn 5b; data in italic were determined using the experimental F and the calculated A, B and θ values (see Supplementary material for values). The scaling factors used to convert from into are the same as those used for S0 (see text). The computed values were determined using time dependent density functional theory (TD DFT) calculations with the B3LYP functional and cc-pVTZ basis set.
| Molecule | Exp. torsional constants | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|
| F | V3 | V6 | ||||||
| Toluene | 5.3 | 16 | 49 | 5.117 | 5.353 | 5.289 | ||
| o-Fluorotoluene | 5.27 | 334 | −3 | 50 | 5.167 | 5.358 | 5.294 | |
| m-Fluorotoluene | 4.72 | 318 | −8 | 50 | 4.608 | 5.359 | 5.295 | |
| p-Fluorotoluene | 5.07 | −27 | 50 | 4.888 | 5.358 | 5.294 | ||
| 2,6-Difluorotoluene | 5.18 | 15 | 19 | 5.120 | 5.371 | 5.305 | ||
| o-Chlorotoluene | 5.1 | 456.5 | 17 | 17 | 5.033 | 5.373 | 5.308 | |
| 2-Chloro-6-fluorotoluene | 4.8 | 192.1 | 20 | 18 | 4.759 | 5.377 | 5.312 | |
| m-Tolunitrile | 5.03 | 137 | −2.37 | 51 | 4.947 | 5.355 | 5.292 | |
| p-Tolunitrile | 5.45 | −0.27 | 51 | 5.267 | 5.353 | 5.289 | ||
| trans-o-Cresol | 5.0 | 405 | −15 | 37 | 4.895 | 5.370 | 5.305 | |
| cis-o-Cresol | 4.8 | 540 | 135 | 37 | 4.695 | 5.389 | 5.322 | |
| trans-m-Cresol | 5.28 | 276 | −12 | 38 | 5.167 | 5.372 | 5.307 | |
| cis-m-Cresol | 5.11 | 328 | −20 | 38 | 4.996 | 5.371 | 5.306 | |
The outcome of the results discussed in the Supplementary material is that the computed optimised structures are sufficiently accurate that the uncertainty introduced into the FMethyl values is negligible when using computed v. experimental rotational constants and we can thus have confidence in the FMethyl values determined, irrespective of whether experimental or computational constants are used. For S0, the average difference between the two is 0.0005 ± 0.0008 cm−1 for MP2 cc-pVTZ and 0.0008 ± 0.0010 cm−1 for DFT B3LYP cc-pVTZ whereas for S1 the difference is 0.0005 ± 0.0016 cm−1, where the uncertainties correspond to ± one standard deviation. There are no data available to compare the cation structures, but the uncertainties are likely to be similar to those for the S0 and S1 cases. Since the experimental F values are typically specified to two decimal places (see Tables 1–3), the uncertainties associated with using calculated constants are an order of magnitude smaller than typical experimental uncertainties.
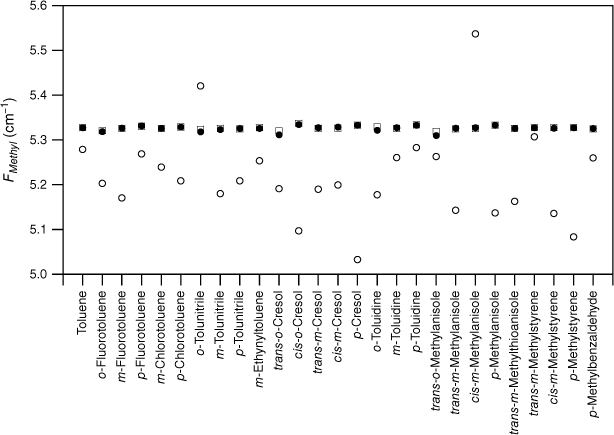
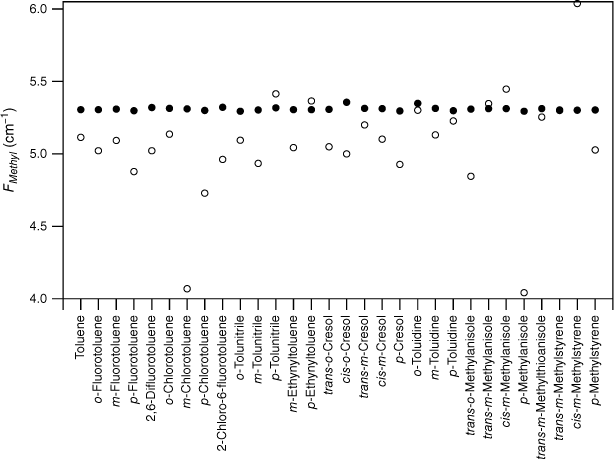
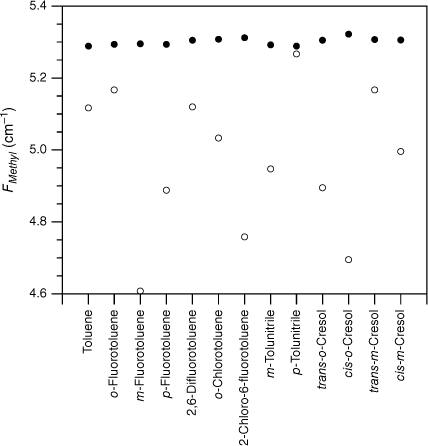
The experimental FMethyl values are plotted for the substituted toluenes in Fig. 1–3 for S0, S1 and respectively (see Tables 1–3). A feature of the data in all three electronic states is the significant scatter in FMethyl values, conventionally taken to imply that there are reasonably significant changes in the methyl structure among this set of molecules. The scatter is particularly pronounced for the S1 data.
values extracted from the experimental F values for various substituted toluenes in their S0 state (open circles; see Table 1). Shown for comparison are the scaled, calculated values, , for two sets of calculations, MP2 cc-pVTZ (closed circles) and DFT B3LYP cc-pVTZ (open squares). The scaled, calculated values are little different between the two computational methods, leading to the calculated points taking on the appearance of a closed square in many instances.
values for various substituted toluenes in their S1 state (open circles; see Table 2). The scaled, calculated values, , for TD DFT B3LYP cc-pVTZ calculations (closed circles) are shown for comparison.
values for various substituted toluene cations in the state (open circles; see Table 3) and the scaled, calculated values, , for DFT B3LYP cc-pVTZ calculations (closed circles).
Scaling factors for calculated FMethyl values
Before comparing calculated and experimental FMethyl values, there is a need to consider systematic inaccuracies in the calculations. The quantum chemistry optimised structures pertain to minimum energy, equilibrium structures, whereas the experimental values refer to the vibrationally averaged zero-point energy structures, which include anharmonic effects. These can be comparatively large for C–H stretch motions and affect calculations of FMethyl.
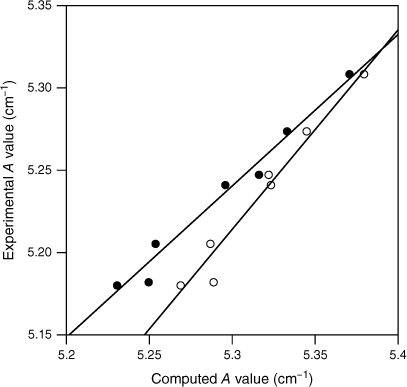
In the case of S0 values, we have previously considered the A constants for four substituted methanes in cases where the substituent is an atom or polyatomic that retains a linear structure with the methyl carbon atom.20 We found a linear relationship between the experimental and calculated A values for both MP2 cc-pVTZ and DFT B3LYP cc-pVTZ calculations. These calculations provide a measure of the accuracy of the calculated methyl structure since the A rotational constants for these molecules depend only on the methyl group structure. In the present work, we have extended this study to seven substituted methanes. The calculated and observed A constants, equivalent to FMethyl for the polyatomics, are given in Table 4 and shown in Fig. 4. The linear relationship between the calculated and observed constants is retained for this larger data set. These linear relationships provide a means to scale the calculated FMethyl values to yield the expected experimental values, akin to the long-established method of scaling quantum chemistry vibrational frequencies to match experiment.26 Linear fits give for the MP2 cc-pVTZ calculations and for DFT B3LYP cc-pVTZ. Given the variation in A values across the seven molecules, we expect the expressions to be useful for in the range 5.20–5.45 cm−1. In practice, the values for the substituted toluenes lie in a very limited range of ~5.39–5.40 cm−1 and the scaling factors for a given method are almost constant. Interestingly, Fig. 4 shows that the two calculations give much the same A value in this region. We thus anticipate that the MP2 cc-pVTZ and DFT B3LYP cc-pVTZ FMethyl values will be very similar. and values for S0 are shown in Table 1 and the values are plotted with the experimental values in Fig. 1. As anticipated, the S0 values are very similar for the MP2 cc-pVTZ and DFT B3LYP cc-pVTZ methods even before scaling. Scaling lowers the computed values and is an important aspect of the comparisons with experimental data, since the basis of the experimental v. calculated FMethyl comparison is that torsion–vibration interaction lowers the FMethyl values.
| Molecule | Ref. | Experiment | MP2 cc-pVTZ | B3LYP cc-pVTZ | |
|---|---|---|---|---|---|
| CH4 | 52 | 5.2410 | 5.3234 | 5.2958 | |
| CH3F | 53 | 5.1820 | 5.2887 | 5.2497 | |
| CH3Cl | 54 | 5.2053 | 5.2868 | 5.2537 | |
| CH3Br | 55 | 5.1800 | 5.2689 | 5.2305 | |
| CH3CN | 56 | 5.2736 | 5.3449 | 5.3331 | |
| CH3CCH | 57 | 5.3084 | 5.3795 | 5.3708 | |
| CH3NC | 58 | 5.2472 | 5.3220 | 5.3161 |
The molecules are a series of substituted methanes where the substituent retains a linear structure with the methyl carbon atom. The values are for the S0 state. The constants are in units of per centimetre. The A constants for these molecules are equivalent to FMethyl for molecules with a non-linear frame.
Plots of the observed vs computed A constants for a series of substituted methanes, where the substituent is either an atom or is linear (see Table 4). The A values for these molecules are equivalent to FMethyl. The MP2 cc-pVTZ values are shown as closed circles and the DFT B3LYP cc-pVTZ values are shown as open circles. The solid lines indicate the linear fits for the two computations (see text).
The scaling method used to adjust the S0 values to those expected experimentally is based on having experimental A constants for R–CH3 molecules, where R is an atom or linear frame. However, these are not available in the S1 or cases. Although this would seem to rule out this approach for these electronic states, examination of the values for S1 and (see Tables 2 and 3 respectively) compared with those for S0 (Table 1) suggests that the electronic state does not strongly influence the methyl group structure. We have noted this previously when analysing spectra perturbed by torsion–vibration interactions, where the F values for S1 and S0 are similar when the coupling is accounted for.12,14,15 For the 26 molecules common between the S0 and S1 sets, the average difference is 0.019 ± 0.015 cm−1 whereas for the 10 molecules common to S0 and , is 0.030 ± 0.010 cm−1. (As the B3LYP cc-pVTZ functional and basis set combination is common across the three electronic states, the S0 calculations for that combination have been used for these comparisons.) Thus, it is reasonable to expect that the scaling factors for the three electronic states will be sufficiently similar that the S1 and values can be well estimated using the scaling parameters developed for S0. We note that scaling reduces the value for FMethyl by a significantly larger amount than the computed differences between S0, S1 and .
The key feature of the quantum chemistry calculations is that the values show little variation across the series of substituted toluenes for the ground electronic state, S0, the excited electronic state, S1, and the cation ground electronic state, . For a given electronic state, quantum chemistry predicts that the methyl group structure is essentially unchanged with substituent and its position on the ring. Furthermore, the electronic state itself is predicted to have little influence on the methyl structure.
Discussion
Calculated v. experimental FMethyl values: evidence for widespread torsion–vibration interaction
Fig. 1–3 clearly demonstrate two significant differences between the quantum chemistry calculated FMethyl values and those derived from experimental F values. Firstly, there is significant scatter in the experimental values, whereas the computed values are almost uniform. Secondly, with few exceptions, the experimental values lie scattered below the scaled calculated values, in many cases significantly below. These differences are precisely what is expected should torsion–vibration interactions be largely ubiquitous for this set of molecules, as its omission in experimental analyses leads to the F values extracted being reduced by an amount that depends on the strength of the interaction, and thus varies. As ‘effective’ values, the experimental F constants no longer relate directly to the methyl structure as predicted by computational chemistry, which explains why there is a discrepancy between the two.
Although the experimental–computational comparison is consistent with torsion–vibration interaction being widespread among this set of substituted toluenes, it might be argued that the variability seen in comes from the experimental uncertainties of these fits rather than being an indicator for torsion–vibration interaction as we assert. The fits to extract F values from the experimental torsional state energies typically report this constant to two decimal places and rarely are uncertainties quoted. While it is certainly the case that there are reasonable uncertainties in individual F values, collectively, the random nature of such uncertainties would lead to the FMethyl values varying about the scaled calculated value (or a value close to it), with an average value equal to it (or close to it) assuming, of course, that the scaled calculated values accurately reflect the true FMethyl values (vide infra). By contrast, Fig. 1–3 show that, with very few exceptions, the FMethyl values from experiment lie below, and often well below, the scaled calculated values rather than being scattered about them. For S0, the average experimental FMethyl value is 0.11 cm−1 below the average scaled, calculated value for both sets of calculations, whereas for S1 and it is below by 0.24 and 0.33 cm−1 respectively. These differences show that, on average, the FMethyl values observed are lower than those calculated, even with the computed values scaled to account for the systematic differences observed between computed and observed methyl constants in related molecules. This occurs for all three electronic states and is particularly large for S1 and .
A conventional interpretation of the behaviour of for these substituted toluenes is that the experimental data reveal that significant changes occur within the methyl group structure according to the nature of the ring substituent, its position on the ring and the electronic state. This straightforward interpretation is based on the dependence of FMethyl on the methyl group structure as:
where mH is the mass of hydrogen, r is the C–H bond length and γ the H–C–H bond angle. Thus, differences in FMethyl imply changes in r, γ or both. FMethyl can also be expressed in terms of r and the X–C–H angle, ϕ, where X denotes the frame atom to which the methyl group is attached, as . Okuyama et al. have used this form to determine the combinations of r and ϕ that satisfy the FMethyl value in p-fluorotoluene,27 illustrating how the value of F is interpreted in terms of the methyl structure.
By contrast, the values show little variation across the series of substituted toluenes, predicting that the methyl group structure is essentially unchanged with substituent and its position on the ring. This consistency in the computed methyl structures is crucial and fundamentally different from the experimental FMethyl behaviour. The changes with electronic state are also modest, as has been discussed above. We have taken several steps to identify potential issues with the calculations and ensure that these trends are genuine. First, the S0 calculations were performed using two entirely different computational methodologies, MP2 and DFT B3LYP. The two sets of calculations give virtually identical values (see Table 1 and Fig. 1) and, crucially, both predict little variability in the methyl structures across the data set. Second, by scaling the calculated FMethyl values, we have sought to account for the expected differences between experimental and computed values. Even if the scaling based on linear CH3–X compounds is inaccurate, the consistency in the calculated methyl structures means that scaling would need to be both larger and vary significantly from molecule to molecule if one was to reconcile the calculated and experimental values on the basis of structure alone.
Our hypothesis was that FMethyl would be reduced in the substituted toluenes when torsion–vibration interaction is present, as this leads to the lower torsional states being reduced in energy and requiring a reduced value for F in fits of the torsional energies to the torsional parameters F, V3 and V6, which have become ‘effective’ constants. In addition to a reduction in FMethyl, one would expect a wider variation in F since the reduction in energy of the torsional states will depend on the coupling strength and vibrational frequencies of the interacting modes. Both behaviours are present in the data, providing evidence supporting the hypothesis that torsion–vibration interaction is widespread among these molecules.
For S0, only two of the 27 molecules, cis-m-methylanisole and o-tolunitrile, have experimental FMethyl values exceeding the scaled calculated values. In both cases, the values come from parameters extracted from the analysis of rotationally resolved electronic spectra for the υt = 0, A and E states.28,29 Clearly, it would be interesting to have experimental measurements of the torsional state energies in these cases to provide a check for these values. In the case of S1, 5 of the 30 molecules have experimental FMethyl values exceeding the scaled calculated values. In one case, cis-m-methylanisole, the values come from the same analysis of rotationally resolved electronic spectra that also puts the experimental S0 value higher than the calculated value.29 For the remainder, we suggest that future experimental studies of torsion–vibration interaction should focus on molecules from this subset to determine whether the large value for FMethyl is correct, particularly in view of the fact that the quantum chemistry calculations predict methyl group tilt in these molecules, an indicator for torsion–vibration interaction, as discussed below. We note that the presence of low vibrational frequency modes can lead to mis-assignment of the torsional states in the S1←S0 spectrum, and this can lead to incorrect values for the torsional parameters, as has been shown explicitly in the case of p-fluorotoluene, for example.14,30 In the case of , none of the 13 experimental FMethyl values exceed the scaled calculated values.
The torsional barriers have been included in Tables 1–3. The effects of torsion–vibration interaction, as revealed through a lowering of the FMethyl value, are not dependent on the barrier height. It appears to be present in molecules with barriers that are almost zero, and hence are essentially free rotors, through to those with barriers above 500 cm−1.
Methyl group tilt and the vibrational motions involved in torsion–vibration interaction
The results demonstrate that in virtually all cases FMethyl is reduced compared with the predictions of computational chemistry and, moreover, the amount by which it is reduced varies among the group of substituted toluenes. Although a reduced FMethyl, and F, indicates a torsion–vibration interaction, it does not indicate what vibrational modes are involved in the torsion–vibration interaction.
The link between methyl group tilt and torsion–vibration interaction involving the methyl group in- and out-of-plane wagging modes has been discussed in detail in Gascooke and Lawrance.20 Briefly, torsion–vibration interaction leads to a mixing between the υ = 0 and = 1 states of the vibrational mode involved (υ is the vibrational quantum number) and, consequently, the perturbed υ = 0 state contains some υ = 1 character. When the vibrations involved are in- or out-of-plane methyl group wagging modes, this manifests as a tilting of the methyl group in-plane at torsional angles of 0°, 60°, 120°, etc. (here one of the methyl CH bonds lies in the plane of the frame) and out-of-plane at torsional angles of 30, 90, 150°, etc. (here one of the methyl CH bonds is perpendicular to the plane of the frame). Previously, we have introduced the nomenclature α(x) to denote the torsional configuration, where x is the torsional angle, specified in radians.20 The torsional angle dependent methyl group tilting leads to precession of the methyl group accompanying the torsional motion. The corollary of this is that the presence of in-plane methyl tilt implies a torsion–vibration interaction involving an in-plane methyl group wag vibration and, similarly, the presence of an out-of-plane methyl tilt implies a torsion–vibration interaction involving an out-of-plane methyl group wag vibration. When the electronic structure of a molecule dictates that the methyl group is tilted in-plane at configurations where one of the methyl CH bonds lies in the plane of the frame and out-of-plane at configurations where one of the methyl CH bonds is perpendicular to the plane of the frame, this is manifest spectroscopically as a coupling between the torsion and those vibrations that involve motion along these methyl group tilt axes.
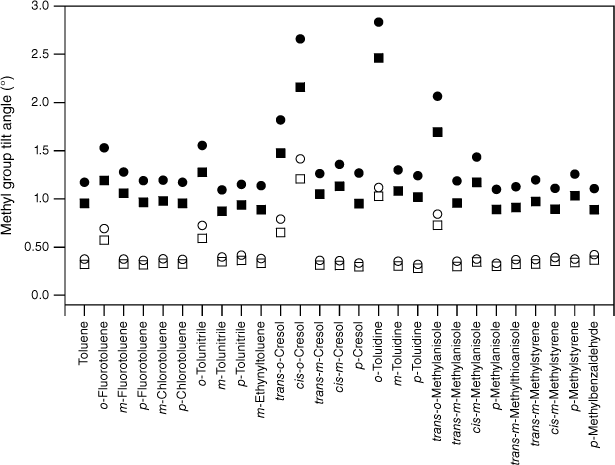
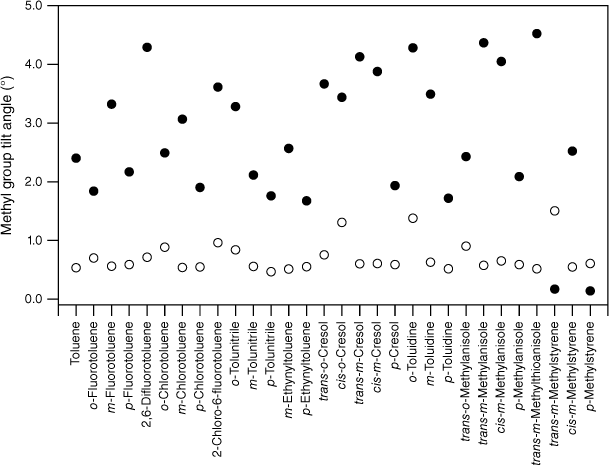
Given this correlation between methyl group tilt and torsion–vibration interaction involving the methyl group in- and out-of-plane wagging modes, the calculated optimised structures should demonstrate methyl group tilt if torsion–vibration interaction involving these types of modes is responsible for the reduction in FMethyl observed. Fig. 5–7 show the calculated in- and out-of-plane methyl group tilt angles for S0, S1 and respectively. The in-plane and out-of-plane tilt angles of the methyl group have been defined using a generalisation of the definitions proposed by Lu et al. in their study of substituted toluenes.31 If we denote the frame atom to which the methyl C is bonded as X and the two atoms directly bound to X by Y and Z, then the out-of-plane angle is defined at the α(π/2) configuration by the angle formed between the Cmethyl–X bond and the plane formed by Y–X–Z, whereas the in-plane angle is defined at the α(0) and α(π) configurations by the angle formed between the Cmethyl–X bond, and the bisector of the angle Y–X–Z (see fig. 4 of Lu et al.31). The torsional angles were defined in the quantum chemistry calculations by either fixing one of the dihedral angles or, where appropriate, using symmetry constraints.
Plots of the calculated in-plane and out-of-plane methyl group tilt angles (see text for definitions) for the substituted toluenes in the S0 state. The MP2 cc-pVTZ values are shown by squares and the DFT B3LYP cc-pVTZ values are shown by circles. The in-plane angles are shown as open symbols and the out-of-plane angles are shown as closed symbols.
Plots of the calculated (TD DFT B3LYP cc-pVTZ) in-plane and out-of-plane methyl group tilt angles (see text for definitions) for the substituted toluenes in the S1 state. The in-plane angles are shown as open circles and the out-of-plane angles are shown as closed circles.
Plots of the calculated (DFT B3LYP cc-pVTZ) in-plane and out-of-plane methyl group tilt angles (see text for definitions) for the substituted toluenes in the state. The in-plane angles are shown as open circles and the out-of-plane angles are shown as closed circles.
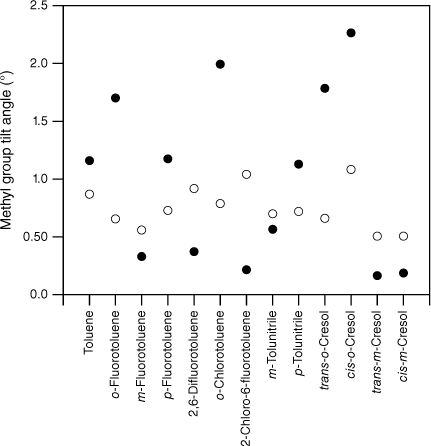
As expected, the molecules all show methyl group tilt in both planes. The predicted in- and out-of-plane methyl group tilt links the reduction in the F values to torsion–vibration interaction involving the in- and out-of-plane methyl group wagging modes. Indeed, viewed from the reverse perspective, given the relationship between methyl group tilt and torsion–vibration interaction for these motions established previously,20 the predicted methyl group tilt implies that torsion–vibration interaction is present in these molecules and that there should be evidence for it in the spectra: the reduced value for FMethyl is thus predicted from the computed methyl group tilt. For a given molecule, the tilt in S1 is generally larger than in S0 and this, combined with a lowering of frequencies in the excited electronic state, is most likely the reason for the larger average reduction in FMethyl in S1 compared with S0. The presence of methyl group tilt provides a key link that rationalises both the reduction in FMethyl and its variation observed experimentally, and why this is at odds with the uniformity of FMethyl values predicted by quantum chemistry calculations.
Conclusions
In this work we have tested the hypothesis that torsion–vibration interaction is widespread by comparing experimental FMethyl values with those based on quantum chemistry optimised structures. The computed FMethyl values were scaled to match experiment using the linear relationship found between the observed and calculated A constants for a series of substituted methanes. The study focused on substituted toluenes in their ground electronic state, first excited singlet electronic state and the ground electronic state of the corresponding cation. The quantum chemistry calculations show little variation in the methyl structure across a wide range of substituents, ring positions and electronic state. The twin observations of (i) the wide variation in FMethyl values extracted from the experimental F values and (ii) the fact that they overwhelmingly lie below the scaled calculated values, is attributed to the torsion–vibration interaction affecting the torsional band structure, supporting the postulate that this type of interaction is widespread. Calculations of the methyl group in- and out-of-plane tilt angles showed methyl tilt to be ubiquitous among the data set, which is a predictor for torsion–vibration interaction involving in- and out-of-plane methyl group wagging modes. The methyl group tilt calculations are thus consistent with the reduced FMethyl values observed experimentally compared with the scaled calculated value, showing that the experimental F values are effective constants that incorporate the effects of torsion–vibration interaction. Comparisons between calculated and experimental torsional constants need to be cognisant of this effect.
How ubiquitous is torsion–vibration interaction? Previously, we have discussed torsion–vibration interaction being present in a series of small molecules (typically with a carboxy group giving the planarity) due to the presence of precession terms in the fits to rotational line data.20 Here, we have considered larger molecules (substituted toluenes) where again we have found strong evidence for it. There is thus every indication that torsion–vibration interaction is the norm and quantum chemistry calculations can be useful in this regard to ascertain whether there is methyl group in- or out-of-plane tilt. If so, then we expect torsion–vibration interaction involving in- and out-of-plane methyl group wag vibrations, with F reduced from the structural value as it is now an effective constant. The presence of such torsion–vibration interaction also provides a mechanism for enhanced intramolecular vibrational energy redistribution.14
Interestingly, in searching the literature to compile the experimental F values considered here, it became apparent that the primary focus of discussions concerning the constants extracted from fits concerned the potential terms, V3 and V6, and the resulting torsional potential. It is not unusual for authors to report quantum chemistry calculations of the torsional potential for comparison with that extracted from experiment. However, rarely is the value of F and its relationship to the methyl group structure commented on in relation to these calculations. We hope that our study provides renewed focus on the meaning of F in such analyses.
Computational methods
Calculations were performed using Gaussian 09 (Revision B.01)32 on a desktop personal computer (PC). Ground electronic state calculations for the neutral (S0) electronic state were performed using both second order Møller–Plesset perturbation theory (MP2) with the Dunning correlation-consistent polarised valence-only triple zeta basis set (cc-pVTZ) and density functional theory (DFT) with the Becke, 3-parameter, Lee–Yang–Parr (B3LYP) functional and cc-pVTZ basis set. Calculations for the first excited singlet (S1) electronic state were performed using time dependent (TD) DFT with the cc-pVTZ basis set. Calculations for the ground electronic state of the cations () were performed using DFT B3LYP with the cc-pVTZ basis set. Structures were optimised using ‘tight’ or ‘very tight’ convergence criteria. Methyl torsional angles were fixed either by symmetry constraints or by freezing the appropriate dihedral angle in the optimisation. The angles between the methyl-frame bond and the molecular a axis were calculated from the optimised structure reported in cartesian coordinates. Methyl tilt angles were determined using the optimised structures in cartesian coordinates computed at torsional angles of 0, π/2 and π. The minimum energy methyl configuration, and hence structure appropriate to the calculation of FMethyl, was determined from the relative energies of these structures.
Supplementary material
Supplementary material is available giving the details and data required for extracting FMethyl constants from the experimental F values. Supplementary material is available online.
Acknowledgements
J. R. Gascooke acknowledges financial support from the ANFF. The authors thank Prof. Peter Gill for providing advice on computational methods at the outset of this project.
References
1 Nesbitt DJ, Suhm MA. Chemical dynamics of large amplitude motion. Phys Chem Chem Phys 2010; 12: 8151.
| Crossref | Google Scholar | PubMed |
3 Orellana W, Stephens SL, Pringle WC, Groner P, Novick SE, Cooke SA. Torsional splitting and the four-fold barrier to internal rotation: the rotational spectra of vinylsulfur pentafluoride. J Chem Phys 2018; 149: 144304.
| Crossref | Google Scholar | PubMed |
4 Lin CC, Swalen JD. Internal rotation and microwave spectroscopy. Rev Mod Phys 1959; 31: 841-892.
| Crossref | Google Scholar |
6 Kleiner I. Asymmetric-top molecules containing one methyl-like internal rotor: methods and codes for fitting and predicting spectra. J Mol Spectrosc 2010; 260: 1-18.
| Crossref | Google Scholar |
7 Ilyushin VV, Kisiel Z, Pszczólkowski L, Mäder H, Hougen JT. A new torsion-rotation fitting program for molecules with a sixfold barrier: application to the microwave spectrum of toluene. J Mol Spectrosc 2010; 259: 26-38.
| Crossref | Google Scholar |
8 Ito M. Spectroscopy and dynamics of aromatic molecules having large-amplitude motions. J Phys Chem 1987; 91: 517-526.
| Crossref | Google Scholar |
9 Breen PJ, Warren JA, Bernstein ER, Seeman JI. A study of nonrigid aromatic-molecules by supersonic molecular jet spectroscopy. I. Toluene and the xylenes. J Chem Phys 1987; 87: 1917-1926.
| Crossref | Google Scholar |
10 Gascooke JR, Lawrance WD. The effects of torsion–vibration coupling on rotational spectra: toluene reinterpreted and refitted. J Mol Spectrosc 2015; 318: 53-63.
| Crossref | Google Scholar |
11 Gascooke JR, Virgo EA, Lawrance WD. Direct observation of methyl rotor and vib-rotor states of S0 toluene: a revised torsional barrier due to torsion-vibration coupling. J Chem Phys 2015; 142: 024315.
| Crossref | Google Scholar | PubMed |
12 Gascooke JR, Virgo EA, Lawrance WD. Torsion-vibration coupling in S1 toluene: implications for IVR, the torsional barrier height, and rotational constants. J Chem Phys 2015; 143: 044313.
| Crossref | Google Scholar | PubMed |
13 Gascooke JR, Appadoo D, Lawrance WD. Torsion–vibration interactions determined from (far) infrared spectra. J Chem Phys 2021; 155: 124306.
| Crossref | Google Scholar | PubMed |
14 Gascooke JR, Stewart LD, Sibley PG, Lawrance WD. Pervasive interactions between methyl torsion and low frequency vibrations in S0 and S1 p-fluorotoluene. J Chem Phys 2018; 149: 074301.
| Crossref | Google Scholar | PubMed |
15 Stewart LD, Gascooke JR, Lawrance WD. A strong interaction between torsion and vibration in S0 and S1 m-fluorotoluene. J Chem Phys 2019; 150: 174303.
| Crossref | Google Scholar | PubMed |
16 Gascooke JR, Lawrance WD. Strong torsion–vibration interaction in N-methylpyrrole observed by far-infrared spectroscopy. J Phys Chem A 2022; 126: 2160-2169.
| Crossref | Google Scholar | PubMed |
17 Richard EC, Walker RA, Weisshaar JC. Hindered internal rotation and torsion–vibrational coupling in ortho‐chlorotoluene (S1) and ortho‐chlorotoluene+ (D0). J Chem Phys 1996; 104: 4451-4469.
| Crossref | Google Scholar |
18 Walker RA, Richard EC, Weisshaar JC. Barriers to methyl torsion in 2-fluoro-6-chlorotoluene: additivity of ortho-substituent effects in S0, S1, and D0. J Phys Chem 1996; 100: 7333-7344.
| Crossref | Google Scholar |
19 Walker RA, Richard EC, Lu K-T, Weisshaar JC. Methyl-group internal-rotation in 2,6-difluorotoluene (S1) and 2,6-difluorotoluene+ (D0). J Phys Chem 1995; 99: 12422-12433.
| Crossref | Google Scholar |
20 Gascooke JR, Lawrance WD. The case for methyl group precession accompanying torsional motion. Aust J Chem 2020; 73: 775-786.
| Crossref | Google Scholar |
21 Parmenter CS, Stone BM. The methyl rotor as an accelerating functional-group for IVR. J Chem Phys 1986; 84: 4710-4711.
| Crossref | Google Scholar |
22 Moss DB, Parmenter CS, Ewing GE. On the contributions of van der Waals interactions to vibrational level mixing. Torsion-vibration coupling in p-fluorotoluene. J Chem Phys 1987; 86: 51-61.
| Crossref | Google Scholar |
23 Kirtman B. Interactions between ordinary vibrations and hindered internal rotation. I. Rotational energies. J Chem Phys 1962; 37: 2516-2539.
| Crossref | Google Scholar |
24 Brodersen PM, Gordon RD. A precessing rotor model for structural flexing during torsional motion: is there evidence from the internal rotation kinetic energy coefficient F? J Mol Struct 2000; 522: 279-288.
| Crossref | Google Scholar |
25 Gascooke JR, Lawrance WD. Two dimensional laser induced fluorescence in the gas phase: a spectroscopic tool for studying molecular spectroscopy and dynamics. Eur Phys J D 2017; 71: 287.
| Crossref | Google Scholar |
26 Scott AP, Radom L. Harmonic vibrational frequencies: an evaluation of Hartree–Fock, Møller–Plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors. J Phys Chem 1996; 100: 16502-16513.
| Crossref | Google Scholar |
27 Okuyama K, Mikami N, Ito M. Internal rotation of the methyl group in the electronically excited state: o-, m-, and p-fluorotoluene. J Phys Chem 1985; 89: 5617-5625.
| Crossref | Google Scholar |
28 Ruiz-Santoyo JA, Wilke J, Wilke M, Yi JT, Pratt DW, Schmitt M, Álvarez-Valtierra L. Electronic spectra of 2- and 3-tolunitrile in the gas phase. I. A study of methyl group internal rotation via rovibronically resolved spectroscopy. J Chem Phys 2016; 144: 044303.
| Crossref | Google Scholar | PubMed |
29 Ichimura T, Suzuki T. Photophysics and photochemical dynamics of methylanisole molecules in a supersonic jet. J Photochem Photobiol C 2000; 1: 79-107.
| Crossref | Google Scholar |
30 Gardner AM, Tuttle WD, Whalley L, Claydon A, Carter JH, Wright TG. Torsion and vibration-torsion levels of the S1 and ground cation electronic states of para-fluorotoluene. J Chem Phys 2016; 145: 124307.
| Crossref | Google Scholar | PubMed |
31 Lu K-T, Weinhold F, Weisshaar JC. Understanding barriers to internal rotation in substituted toluenes and their cations. J Chem Phys 1995; 102: 6787-6805.
| Crossref | Google Scholar |
32 Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery Jr JA, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Keith T, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09, Revision B.01. Wallingford, CT, USA: Gaussian, Inc.; 2010.
33 Ilyushin VV, Alekseev EA, Kisiel Z, Pszczółkowski L. High-J rotational spectrum of toluene in |m|≤3 torsional states. J Mol Spectrosc 2017; 339: 31-39.
| Crossref | Google Scholar |
34 Kojima H, Sakeda K, Suzuki T, Ichimura T. Methyl internal rotation of photoexcited chlorotoluene molecules. J Phys Chem A 1998; 102: 8727-8733.
| Crossref | Google Scholar |
35 Fujii M, Yamauchi M, Takazawa K, Ito M. Electronic spectra of o-, m- and p-tolunitrile—substituent effect on internal rotation of the methyl group. Spectrochim Acta A 1994; 50: 1421-1433.
| Crossref | Google Scholar |
36 Tanaka S, Okuyama K. Internal rotation of methyl group in electronically excited o- and m-ethynyltoluene: new correlation between the Hammett substituent constant σm and rotational barrier change. J Chem Phys 2011; 134: 084311.
| Crossref | Google Scholar | PubMed |
37 Aota T, Ebata T, Ito M. Rotational isomers and internal rotation of the methyl group in S0, S1 and ion of o-cresol. J Phys Chem 1989; 93: 3519-3522.
| Crossref | Google Scholar |
38 Mizuno H, Okuyama K, Ebata T, Ito M. Rotational isomers of m-cresol and internal rotation of the methyl group in S0, S1, and the ion. J Phys Chem 1987; 91: 5589-5593.
| Crossref | Google Scholar |
39 Myszkiewicz G, Meerts WL, Ratzer C, Schmitt M. The structure of 4-methylphenol and its water cluster revealed by rotationally resolved UV spectroscopy using a genetic algorithm approach. J Chem Phys 2005; 123: 044304.
| Crossref | Google Scholar | PubMed |
40 Okuyama K, Mikami N, Ito M. Internal rotation of the methyl group in the electronically excited state: o- and m-toluidine. Laser Chem 1987; 7: 243965.
| Crossref | Google Scholar |
41 Lee H, Kim S-Y, Lim JS, Kim J, Kim SK. Conformer specific excited-state structure of 3-methylthioanisole. J Phys Chem A 2020; 124: 4666-4671.
| Crossref | Google Scholar | PubMed |
42 Hollas JM, Taday PF. Methyl and vinyl torsional potentials in cis- and trans-3-methylstyrene from supersonic jet fluorescence spectra. J Chem Soc Faraday Trans 1991; 87: 3585-3593.
| Crossref | Google Scholar |
43 Schmitt M, Ratzer C, Jacoby C, Leo Meerts W. Structure and barrier to internal rotation of 4-methylstyrene in the S0- and S1-state. J Mol Struct 2005; 742: 123-130.
| Crossref | Google Scholar |
44 Saal H, Grabow J-U, Hight Walker AR, Hougen JT, Kleiner I, Caminati W. Microwave study of internal rotation in para-tolualdehyde: local versus global symmetry effects at the methyl-rotor site. J Mol Spectrosc 2018; 351: 55-61.
| Crossref | Google Scholar |
45 Alvarez-Valtierra L, Yi JT, Pratt DW. Rotationally resolved electronic spectra of 2- and 3-methylanisole in the gas phase: a study of methyl group internal rotation. J Phys Chem B 2006; 110: 19914-19922.
| Crossref | Google Scholar | PubMed |
46 Borst DR, Pratt DW. Toluene: structure, dynamics, and barrier to methyl group rotation in its electronically excited state. A route to IVR. J Chem Phys 2000; 113: 3658-3669.
| Crossref | Google Scholar |
47 Philis JG, Melissas VS. An experimental and theoretical study of the S1 ← S0 transition of p-ethynyltoluene. J Chem Phys 2007; 127: 204310.
| Crossref | Google Scholar | PubMed |
48 Tan X-Q, Pratt DW. High-resolution electronic spectroscopy of p-toluidine. A precessing rotor model for G12 molecules. J Chem Phys 1994; 100: 7061-7067.
| Crossref | Google Scholar |
49 Lu KT, Eiden GC, Weisshaar JC. Toluene cation: nearly free rotation of the methyl group. J Phys Chem 1992; 96: 9742-9748.
| Crossref | Google Scholar |
50 Takazawa K, Fujii M, Ito M. Internal rotation of the methyl group in fluorotoluene cations as studied by pulsed field ionization‐zero kinetic energy spectroscopy. J Chem Phys 1993; 99: 3205-3217.
| Crossref | Google Scholar |
51 Suzuki K, Ishiuchi S-i, Sakai M, Fujii M. Pulsed field ionisation—ZEKE photoelectron spectrum of o-, m- and p-tolunitrile. J Electron Spectrosc Relat Phenom 2005; 142: 215-221.
| Crossref | Google Scholar |
52 Tarrago G, Dang-Nhu M, Poussigue G, Guelachvili G, Amiot C. The ground state of methane 12CH4 through the forbidden lines of the ν3 band. J Mol Spectrosc 1975; 57: 246-263.
| Crossref | Google Scholar |
53 Papousek D, Hsu YC, Chen HS, Pracna P, Klee S, Winnewisser M. Far infrared spectrum and ground state parameters of 12CH3F. J Mol Spectrosc 1993; 159: 33-41.
| Crossref | Google Scholar |
54 Nikitin A, Champion JP. New ground state constants of 12CH335Cl and 12CH337Cl from global polyad analysis. J Mol Spectrosc 2005; 230: 168-173.
| Crossref | Google Scholar |
55 Graner G. The methyl bromide molecule: a critical consideration of perturbations in spectra. J Mol Spectrosc 1981; 90: 394-438.
| Crossref | Google Scholar |
56 Šimečková M, Urban Š, Fuchs U, Lewen F, Winnewisser G, Morino I, Yamada KMT. Ground state spectrum of methylcyanide. J Mol Spectrosc 2004; 226: 123-136.
| Crossref | Google Scholar |
57 Graner G, Horneman VM, Blanquet G, Walrand J, Takami M, Jörissen L. A precise determination of the A0 rotational constant of propyne. J Mol Spectrosc 1989; 135: 32-44.
| Crossref | Google Scholar |
58 Pliva J, Le LD, Johns JWC, Lu Z, Bernheim RA. Methyl isocyanide: the low-frequency bands ν8 and ν7, and a determination of the rotational constant A0. J Mol Spectrosc 1995; 173: 423-430.
| Crossref | Google Scholar |


