The Dark Matter Crisis: Falsification of the Current Standard Model of Cosmology
P. KroupaArgelander Institute for Astronomy, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany. Email: pavel@astro.uni-bonn.de
Publications of the Astronomical Society of Australia 29(4) 395-433 https://doi.org/10.1071/AS12005
Submitted: 13 January 2012 Accepted: 21 March 2012 Published: 20 June 2012
Journal Compilation © Astronomical Society of Australia 2012
Abstract
The current standard model of cosmology (SMoC) requires The Dual Dwarf Galaxy Theorem to be true according to which two types of dwarf galaxies must exist: primordial dark-matter (DM) dominated (type A) dwarf galaxies, and tidal-dwarf and ram-pressure-dwarf (type B) galaxies void of DM. Type A dwarfs surround the host approximately spherically, while type B dwarfs are typically correlated in phase-space. Type B dwarfs must exist in any cosmological theory in which galaxies interact. Only one type of dwarf galaxy is observed to exist on the baryonic Tully-Fisher plot and in the radius-mass plane. The Milky Way satellite system forms a vast phase-space-correlated structure that includes globular clusters and stellar and gaseous streams. Other galaxies also have phase-space correlated satellite systems. Therefore, The Dual Dwarf Galaxy Theorem is falsified by observation and dynamically relevant cold or warm DM cannot exist. It is shown that the SMoC is incompatible with a large set of other extragalactic observations. Other theoretical solutions to cosmological observations exist. In particular, alone the empirical mass-discrepancy—acceleration correlation constitutes convincing evidence that galactic-scale dynamics must be Milgromian. Major problems with inflationary big bang cosmologies remain unresolved.
Keywords: cosmology: theory — dark energy — dark matter — Galaxy: evolution — galaxies: interactions — Local Group
1 Introduction
‘For if we are uncritical we shall always find what we want: we shall look for, and find, confirmations, and we shall look away from, and not see, whatever might be dangerous to our pet theories. In this way it is only too easy to obtain what appears to be overwhelming evidence in favor of a theory which, if approached critically, would have been refuted’ (Popper 1957, p. 124).
That Einstein’s general theory of relativity (GR, Einstein 1916) is an excellent description of gravitational physics has been established in the weak and strong (i.e. Solar System and Earth, respectively) and very strong (black hole and neutron star) field limits (e.g. Freire & Wex 2010). Albert Einstein had developed his field equation such that the Newtonian equations of motion be derivable from it, and thus that it be consistent with the then available celestial phenomena. 1 The currently popular understanding of cosmology is based on the null hypothesis (‘Hypothesis 0i’) that GR also be valid on galactic and cosmological scales. This is a vast extrapolation by many orders of magnitude from the well-tested scale of planetary dynamics to the galactic and cosmological ultra-weak-field scales, the dynamics of which were probed (Rubin & Ford 1970) only long after GR had been finalised by Einstein using Newtonian, i.e. essentially Solar System constraints. The nature of spiral nebulae and the dimensions of the universe were debated in 1920 by Harlow Shaply and Heber Curtis in The Great Debate, but galactic and extragalactic distance scales were proven later (Opik 1922; Hubble 1929). The other ‘Hypothesis 0ii’, so fundamental that it is usually not stated, is that all present-day matter is created as a relativistic fluid during the hot Big Bang (BB).
The observed state of the universe at the present-epoch is such that within the visible horizon physics appears to be identical. This implies that every part of the visible universe had to have been in causal contact at the BB, the geometry is extremely close to being flat as is deduced from the position of the cosmic microwave background (CMB) acoustic peaks, and the universe appears to be homogeneous and isotropic on large scales. Since there is observational evidence suggesting that the universe began in a very dense hot state, a disagreement with these observations emerged because GR plus the BB would predict a highly curved inhomogeneous universe. Thus inflation (Guth & Tye 1980; Sato 1981) was postulated as an auxiliary hypothesis (‘Hypothesis 1’) in order to solve the causality, flatness, homogeneity and isotropy problems implying a massive expansion of volume by at least a factor of 1078 driven by a scalar field called the ‘inflaton’.
Hypothesis 0i implies that dynamics on galaxy scales must be Newtonian. With the observation that galactic rotation curves remain nearly flat at large radii (Rubin & Ford 1970; Bosma 1981), and the rapidity with which structure emerges after the BB, new failures of the model emerged. These were solved by introducing a second auxiliary hypothesis (‘Hypothesis 2’), namely that exotic cold (C) or warm (W) dark matter (DM) particles be the dominant form of gravitating matter. The mass of the DM particle defines whether it is C or W: roughly 1–10 keV for WDM and above that for CDM although axions may be of smaller mass and still be CDM (Blumenthal et al. 1984). These postulated new particles have to interact through gravitation and perhaps weakly in order to decouple from the photon fluid and start to form structures before the baryons can.
The hypothesised existence of DM particles resonated with the contemporary extension of particle physics (see e.g. Aliu et al. 2012 for an account) by string theory (see Smolin 2006 for an overview as well as criticisms) and in particular by super-symmetry (e.g. Wess & Zumino 1974; Wess & Bagger 1992; Wess & Akulov 1998; Gao et al. 2012 and references therein). Super-symmetry is motivated by the ‘hierarchy problem’, because the constants of the standard model of particle physics (SMoPP) are highly fine-tuned. For example, the weak force being 1032 times stronger than gravity is claimed to be solved naturally by super-symmetry. These extensions contained new excited states that would appear in the form of additional particles beyond the SMoPP. This work was in turn driven by the previous successful prediction of atoms, electrons and the neutrino and anti-particles, and by the wish to understand the SMoPP in terms of a deeper physical description of matter in unification with GR.
The SMoPP is indeed a brilliant success in accounting for the known particles and their excited states, but has many parameters the origin of which remain unknown (Yao 2006). While no significant evidence for a failure of the SMoPP has emerged so far, it must be incomplete because it does not account for the oscillations of the neutrino. It accounts for the electromagnetic, weak and strong interactions, but fails to unify the latter with the two former and is also understood to be incomplete because it does not account for gravitation, dark energy, nor does it contain any viable DM particle. Leaving aside the issues with dark energy and DM, the tremendous success of the SMoPP can be seen in the recent break-through achieved in quantum-chromo-dynamical supercomputer calculations by accounting for the Hoyle state (Epelbaum et al. 2011).
Dark energy (DE, e.g. Bousso 2008; Amendola & Tsujikawa 2010; Bousso 2012; Afshordi 2012) had to be introduced into the cosmological model as a third auxiliary hypothesis (‘Hypothesis 3’) because the interpretation of flux and redshift data from type Ia supernovae, given Hypothesis 0–2, suggests that the universe expands increasingly rapidly (Riess et al. 1998; Schmidt et al. 1998; Perlmutter et al. 1999, and e.g. Kowalski et al. 2008). DE can be seen as the cosmological constant Λ inherent in Einstein’s GR formulation. DE is leading to a new era of inflation, and as BB inflation, the corresponding particle-physics formulation is unknown.
Currently, it can be stated that inflation and DE are mathematical ansatzes allowed by GR to solve failures of the straight-forward combination of GR plus particle physics (Brandenberger 2012). An unsolved issue is if these ansatzes contain physics.
The resulting ΛCDM or ΛWDM model can summarizingly be referred to as the currently popular standard model of cosmology (SMoC). Within the SMoC, structures first form through gravitational instabilities in the dissipationless cold or warm DM. The baryonic matter, once sufficiently cooled, accretes into the DM potential wells and begins to form stars. The emerging galaxies merge and interact, forming the present-day observed cosmological structures (filaments, galaxy clusters, galaxies and voids, Piontek & Steinmetz 2011 and references therein).
The SMoC is widely held to be an excellent description of cosmological reality. It is defined by a large number of parameters, the most important of which define a flat space time and the energy content of the universe to be about 4% by baryonic matter, about 23 per cent DM and about 73% DE (e.g. Kowalski et al. 2008; Famaey & McGaugh 2012). According to the SMoC the universe consists to more than 96% of unknown physics.
Among the often stated great successes of the SMoC are the excellent reproduction of the angular power spectrum of the galaxy distribution (e.g. Tegmark et al. 2002; Hayes, Brunner & Ross 2011), the success in accounting for the primordial Helium fraction through BB nucleosynthesis (e.g. Bludman 1998) and in accounting for the CMB power spectrum (e.g. Angus & Diaferio 2011), whereby the latter two are not sensitive to the validity of the SMoC as such (see Section 16.5).
While problems with the SMoC have been arising on galaxy scales, typically it is held that our incomplete knowledge of baryonic physics is responsible.
Is it possible to test the SMoC in such a way that the test is independent of the details of the baryonic processes? This contribution details just such tests. Since the pioneering cosmological N-body work by Aarseth, Turner & Gott (1979), 2 the cosmological N-body industry has matured to a vast and highly active world-wide research effort. The large volume of published output of this industry makes robust tests possible. This numerical work combined with observations is the basis for inferring or excluding the existence of dynamically relevant cold or warm DM without the need to resort to direct dark-matter particle searches. The nature of gravitation can therewith be probed in the ultra-weak field limit.
Can the SMoC be tested on the small scales of dwarf galaxies? Are the available simulations of high enough resolution? Yes and yes: The dynamics of dissipationless DM particles that orbit within the emerging potentials is well understood within the SMoC. The vast world-wide effort to address the sub-structure, or missing-satellite, problem has been producing consistent results on the distribution of the theoretical satellite population (see Section 14 for a dialogue and Footnote 14 for a list of many papers on this issue). Furthermore, the main part of the argument here rests on the phase-space distribution of sub-structures over scales of 10s to 100s of kpc, which is a scale well resolved.
Returning to the logics of scientific theories, it ought to be generally accepted that for a logical construction to be a scientific theory it has to be falsifiable. Otherwise predictions are not possible and the construction would not allow useful calculations. Following Popper (1935), a fundamental assumption underlying the approach taken here is that cosmological theory be falsifiable. The classical view of philosophy that hypothesis be proven by experiment is abandoned, because this approach would require deduction of general rules from a number of individual cases, which is not admissible in deductive logic. Thus, a single counter-example suffices to disprove a hypothesis, while no number of agreements with data can prove a hypothesis to be true.
In this contribution the SMoC is falsified using straightforward logical arguments as detailed below and summarised in Section 17.
2 The Definition of a Galaxy
The definition of a galaxy (Forbes & Kroupa 2011; Willman & Strader 2012) is an important question to consider because depending on it a whole class of objects may be excluded which may forestall further intellectual advance. For example, we may define a tidal dwarf galaxy (TDG) to be a self-bound system with stars and gas with baryonic mass >107 M⊙ formed within a tidal arm in a galaxy–galaxy encounter. With this definition, self-gravitating objects formed in a tidal arm but with lower masses would not constitute TDGs and we might then not be allowed to associate them with the dSph satellite galaxies of major galaxies. Given the evidence presented in this contribution this would be unphysical. Therefore, a more general definition of a galaxy needs to be used.
Throughout this text it is implicitly assumed that a self-gravitating object which consists of stars and perhaps gas is a galaxy if its Newtonian median two-body relaxation time is longer than the Hubble time, t rel > τ H ≈ 104 Myr. This definition of a galaxy (Kroupa 1998, 2008; Forbes & Kroupa 2011) naturally accounts for the dynamical process of energy equipartition not playing a role in galaxies over the age of the universe. In contrast, star clusters with t rel < τH, have an evolving morphology as a result of two-body-encounter driven evolution towards energy equipartition. Thus, ultra-compact dwarf galaxies and ultra-faint dwarf satellites are galaxies such that the collision-less Boltzmann equation and the Jeans equations may be used to study their properties. In other words, the phase-space density of stars remains constant in such a system and, put in yet other but synonymous words, the phase-space distribution function is incompressible in a galaxy over the age of the universe.
Thus, any object with a mass M in M⊙ and a half-mass radius R 0.5 in pc is here taken to be a galaxy if (combining equation 4, 5 and 7 in Kroupa 2008 for an average stellar mass of 0.5 M⊙)
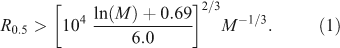
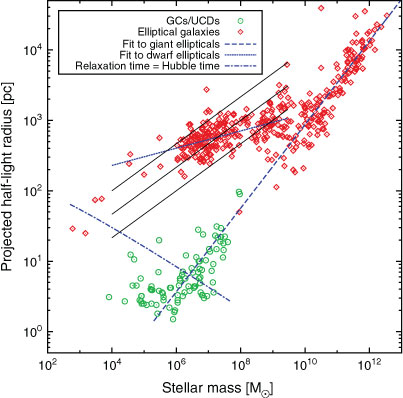
For example, for M = 104 M⊙, R 0.5 > 30 pc. Dwarf elliptical (dE), dwarf spheroidal (dSph) and ultra-faint dwarf (UFD) galaxies are then indeed galaxies according to this definition. Ultra-compact dwarfs (UCDs) would also be galaxies (in agreement with their classification as such by Drinkwater & Gregg 1998; Drinkwater et al. 2004, see Figure 1). Note that all objects traditionally referred to by astronomers as galaxies are galaxies according to Equation 1, while traditional star clusters are star clusters according to Equation 1.
|
Yoshida et al. (2008) discovered star formation in gas clouds stripped from a disk galaxy which is falling into a galaxy cluster (see also Yagi et al. 2010). These star-forming objects, which they call ‘fireballs’, have physical properties next to identical to dSph satellite galaxies (106 ![]() M/M
⊙
M/M
⊙ ![]() 107, 200
107, 200 ![]() R
0.5/pc
R
0.5/pc ![]() 300). Here these galaxies are referred to as ram-pressure dwarf galaxies (RPDGs).
300). Here these galaxies are referred to as ram-pressure dwarf galaxies (RPDGs).
According to Equation 1, a galaxy is a stellar-dynamically unevolved self-gravitating system (ignoring higher-order relaxational processes). At older times than the current age of the universe the boundary between star clusters and galaxies will shift to more massive objects, which would be consistent with for example the evaporation of stars having progressed to deplete what are present-day ‘galaxies’ such that they would necessarily have to be counted as massive star clusters then (cf. Chilingarian et al. 2011).
An alternative definition, according to which a galaxy is a self-bound stellar-dynamical object with characteristic radius ![]() 100 pc (Gilmore et al. 2007b), is based on the absence of observed objects in the radius range 30–100 pc (the ‘Gilmore gap’, e.g. Figure 1). According to this definition, TDGs would also be classified as galaxies. UCDs would be star-clusters (compare with Drinkwater et al. 2000; Mieske, Hilker & Infante 2002; Mieske, Hilker & Misgeld 2012, see also Hilker et al. 1999).
100 pc (Gilmore et al. 2007b), is based on the absence of observed objects in the radius range 30–100 pc (the ‘Gilmore gap’, e.g. Figure 1). According to this definition, TDGs would also be classified as galaxies. UCDs would be star-clusters (compare with Drinkwater et al. 2000; Mieske, Hilker & Infante 2002; Mieske, Hilker & Misgeld 2012, see also Hilker et al. 1999).
3 Rigorous Predictions of the SMoC
The following are robust predictions of the SMoC as discussed in the following sub-sections:
-
Each MW-sized galaxy contains hundreds of DM-dominated satellite galaxies (‘type A’ dwarfs) within the virial radius of its DM halo.
-
Due to their mostly individual in-fall histories type A dwarfs are distributed approximately spherically about the host, following the distribution of host-halo DM particles.
-
A significant fraction of MW-sized galaxies that had previous encounters with other galaxies are surrounded by TDGs (‘type B’ dwarf galaxies). Rich galaxy clusters should also contain RPDGs (Section 2) which are also of type B. Type B dwarfs do not contain significant amounts of DM.
-
Due to energy and angular momentum conservation type B dwarfs are typically distributed in phase-space correlated structures about their host galaxies.
-
The number of type B dwarfs is comparable to the number of dE galaxies.
Note that Predictions 1 and 2 follow from a conjecture made by Zwicky (1937): Interpreting his observational data in terms of Newtonian dynamics, he suggested that galaxies must be significantly more massive as their motions in the Coma cluster of galaxies are too rapid. This can be framed today as a conjecture (Kroupa et al. 2010):
| Conjecture 1: Galaxies contain DM, and by implication this DM must be cold or warm because hot DM would not condense to galaxy-sized structures. |
He also concluded from observation that new dwarf galaxies (i.e. TDGs) form from the matter expelled during galaxy encounters (Zwicky 1956, p 369). Again, this may be stated today as another conjecture (Kroupa et al. 2010):
| Conjecture 2: When galaxies interact TDGs form from the matter expelled during the encounter. These are largely DM free. |
Predictions 3–5 are related to this conjecture.
| Note 1: Type A dwarfs are speculative because they rely on the existence of C/WDM particles. The existence of type B dwarfs, on the other hand, is observationally established. |
3.1 Type A Dwarfs
One prediction of the SMoC which is valid for all galaxies and is independent of the details of baryonic physics is that each and every primordial galaxy is surrounded by a DM halo with a significant amount of sub-structure in the form of self-bound DM sub-haloes (Klypin et al. 1999; Moore et al. 1999).
As pointed out by Moore et al. (1999), ‘The model predicts that the virialized extent of the Milky Way’s halo should contain about 500 satellites with … bound masses about >108 M⊙ and tidally limited sizes larger than about 1 kpc.’ The sub-structure is in the form of individual dark-matter sub-haloes (self-bound sub-structures) which follow a power-law mass function (Maciejewski et al. 2011 and Kroupa et al. 2010, and references therein). The sub-structured halo of any galaxy is a necessary dynamical consequence of Hypothesis 2 (Section 1), through gravitationally self-bound structures developing on all scales from dissipationless cold or warm DM particles in an expanding universe.
The fraction of mass within self-bound sub-structures increases with radial distance, from 0.5% within a distance of 35 kpc to about 14% mass fraction within the whole MW-like host halo, while near the radius of the host halo about 30% of the mass is in self-bound sub-structures (Maciejewski et al. 2011). Kravtsov, Gnedin & Klypin (2004) find that about 10% of the sub-haloes with present-day masses ![]() 108–109 M⊙ had substantially larger masses and circular velocities when they formed at redshifts z
108–109 M⊙ had substantially larger masses and circular velocities when they formed at redshifts z ![]() 2. Tidal stripping of DM satellites is therefore not a process of significance for the whole population of self-bound sub-structures.
2. Tidal stripping of DM satellites is therefore not a process of significance for the whole population of self-bound sub-structures.
These sub-haloes are distributed in a spheroidal and nearly isotropic manner within the host halo (figure 12 in Metz et al. 2007), as is explicitly demonstrated by Pawlowski et al. (2012a). Within its virialised region, the spatial distribution of sub-structure in a present-day DM host halo closely follows that of its DM distribution (Diemand et al. 2008). Statistically, the anisotropy of DM haloes amounts to not more than about 15% (Aubert, Pichon & Colombi 2004). CDM models predict the host DM haloes to be oblate with flattening increasing with increasing mass and radius (Combes 2002; Merrifield 2002). The ratio of minor to major axis of the DM density distribution has the value q
d
= 0.7 ± 0.17 for MW sized haloes within the virial radius. The intermediate-to-major-axis ratio is q
d
′ ![]() 0.7 (Bullock 2002). When dissipative baryonic physics is taken into account the haloes become more axis-symmetric (larger q
d
′) and more flattened, q
d
= 0.5 ± 0.15 within the virial radius. The minor axis is co-linear with the angular momentum of the baryonic disk (Dubinski 1994).
0.7 (Bullock 2002). When dissipative baryonic physics is taken into account the haloes become more axis-symmetric (larger q
d
′) and more flattened, q
d
= 0.5 ± 0.15 within the virial radius. The minor axis is co-linear with the angular momentum of the baryonic disk (Dubinski 1994).
Concerning the MW, the empirical evidence is that its DM halo may be somewhat flattened (oblate) with q
d
![]() 0.8 within R
0.8 within R ![]() 60 kpc (Olling & Merrifield 2000, 2001; Ibata et al. 2001; Majewski et al. 2003; Martínez-Delgado et al. 2004). For example, Ruzicka, Palous & Theis (2007) find an oblate DM halo to fit the Magellanic Clouds and Stream. Koposov, Rix & Hogg (2010) discover, on analysing the GD-1 stellar stream, that within about 15 kpc from the MW center its halo is essentially spherical. Beyond this distance the shape is likely to be more oblate (Bullock 2002; Ruzicka et al. 2007), and invoking continuity shows that the axis ratio q
d
cannot change drastically (e.g. Vera-Ciro et al. 2011). The theoretical sub-structure distribution around MW-type hosts must therefore be quite isotropic (Ghigna et al. 1998; Zentner & Bullock 2003; Diemand, Moore & Stadel 2004).
60 kpc (Olling & Merrifield 2000, 2001; Ibata et al. 2001; Majewski et al. 2003; Martínez-Delgado et al. 2004). For example, Ruzicka, Palous & Theis (2007) find an oblate DM halo to fit the Magellanic Clouds and Stream. Koposov, Rix & Hogg (2010) discover, on analysing the GD-1 stellar stream, that within about 15 kpc from the MW center its halo is essentially spherical. Beyond this distance the shape is likely to be more oblate (Bullock 2002; Ruzicka et al. 2007), and invoking continuity shows that the axis ratio q
d
cannot change drastically (e.g. Vera-Ciro et al. 2011). The theoretical sub-structure distribution around MW-type hosts must therefore be quite isotropic (Ghigna et al. 1998; Zentner & Bullock 2003; Diemand, Moore & Stadel 2004).
Turning to the warm-dark matter SMoC, ΛWDM, it has been shown that the spatial and kinematical distribution of sub-haloes cannot be distinguished from those of the ΛCDM models (Bullock 2002; Knebe et al. 2008). In ΛWDM cosmologies, the sub-haloes are slightly more spherically distributed than in ΛCDM cosmologies (Bullock 2002). The number of WDM sub-structures is reduced in comparison with CDM haloes.
Therewith we can use ΛCDM and ΛWDM synonymously when discussing the spatial properties of satellite galaxy distributions. The robust prediction of the CDM or WDM SMoC is thus that the sub-haloes within each host halo are distributed nearly isotropically following the host halo density distribution.
A challenge facing the SMoC is to quantify how merely a small fraction of the sub-haloes become luminous to appear as primordial (type A) dwarfs, while the rest avoids forming stars. For example, the MW is supposed to have many hundred to thousands of DM sub-haloes while only 24 satellite galaxies have been discovered. This missing satellite problem (Klypin et al. 1999; Moore et al. 1999) is deemed to have been solved through the adjustment of various baryonic processes stopping star-formation in most sub-haloes (see Section 14 for a dialogue and a list of many contributions dealing with this problem in Footnote 14). According to this large body of work those dwarf galaxies that form in some of the many DM sub-haloes are DM dominated in their optical regions. Most of the research effort (e.g. de Lucia 2012 for a review) has dealt with the missing satellite problem by avoiding the disk of satellites problem (Kroupa, Theis & Boily 2005, and Failure 8 in Section 17.3.2).
3.2 Type B Dwarfs
Zwicky’s observation that new dwarf galaxies form from the material ejected as tidal tails when galaxies interact (Conjecture 2 in Section 3) has been confirmed many times since the seminal paper by Mirabel, Dottori & Lutz (1992) who reported such an event for the first time in detail.
Three implications follow from Conjecture 2.
3.2.1 Implication 1
TDGs and RPDGs cannot contain a dynamically significant amount of DM (Barnes & Hernquist 1992; Bournaud 2010) because the phase-space DM particles occupy is far larger than the cross section for capture by type B dwarfs. The phase space occupancy of gas and stars in the progenitors of the tidal debris from which TDGs are born or of the ram-pressure-stripped gas clouds from which the RPDGs form is that of a dynamically cold, thin disk which is very different from the dynamically hot, quasi-spherical halo of dark matter. The tidal and ram-pressure disruption process is very efficient at segregating the two components, because particles of similar phase-space occupancy retain this occupancy. So there should be basically no DM left attached specifically to tidal or ram-pressure stripped debris or any TDGs or RPDGs that form therefrom. The DM particles have virialised velocities too large to be trapped in the small forming baryonic potentials of TDGs and RPDGs (for a review of the formation of TDGs see Bournaud 2010).
Can a TDG or RPDG be accreted onto a pre-existing DM sub-halo? No. It would have to intercept the sub-halo in coordinate space and in velocity space. The latter is extremely unlikely because the relative velocity of the TDG or RPDG and the sub-halo is similar to the velocity dispersion of DM particles in the host halo such that a sub-halo with a circular velocity below 50 km s–1 will be unnoticed by the TDG or RPDG moving faster than 100 km s–1.
3.2.2 Implication 2
Type B dwarfs form as a population in individual galaxy-galaxy encounters. As a consequence, they are correlated in phase space because their orbital angular momenta retain a memory of their formation.
3.2.3 Implication 3
Assuming the SMoC to be correct within which larger galaxies form from the mergers of smaller objects, it follows that type B dwarfs may be a prominent contribution to the satellite dwarf galaxy population:
Okazaki & Taniguchi (2000) computed the expected population of TDGs within the SMoC. They adopted a structure formation merger tree and assumed each gas-rich encounter only produces 1–2 long lived TDGs that evolve from dwarf irregular (dIrr) gas-rich galaxies to dwarf elliptical (dE) galaxies in the tidal environment around a host galaxy or within the group or cluster. Okazaki & Taniguchi (2000) thereby discovered that so many TDGs would be generated over a Hubble time to account for all dE galaxies. The morphology–density relation of galaxies, according to which rich groups or clusters have more dwarfs, emerges naturally as well. That dIrr galaxies do evolve to dE and dwarf spheroidal (dSph) galaxies in a tidal environment has been demonstrated by Mayer et al. (2001). An impressive example of how a number of TDGs formed around Andromeda, which bears rather clear signatures of past interaction events, is shown in the simulations by Hammer et al. (2010).
The estimate by Okazaki & Taniguchi (2000) is, however, a lower-limit on the number of dwarf galaxies in galaxy clusters, because they did not take into account the formation of RPDGs (Section 2).
As demonstrated by simulations (Wetzstein, Naab & Burkert 2007, see also Bournaud 2010; Bournaud et al. 2011), the number of TDGs formed scales with the gas-fraction in the interacting galaxies. That TDGs form profusely at high redshift from interactions of gas-rich galaxies is implied by the high-resolution simulations by Bournaud et al. (2011). At early cosmological epochs, when the forming galaxies were very gas rich, closer together and interacting more often in small groups than today especially in the then emerging clusters of galaxies, the formation rate of TDGs is likely to have been significantly higher than today, perhaps by orders of magnitude per encounter. Indeed, it may even not be possible to discern the formation of primordial dwarf galaxies from TDG formation as they probably occurred simultaneously and not independently of each other. Clearly, there is much scope for further seminal research in this area.
3.2.4 Longevity of Type B Dwarfs
Once formed, can TDGs or RPDGs vanish? No: they have masses ![]() 109 M⊙ and dynamical friction on the DM halo of the host galaxy will therefore not significantly shrink their orbits over a Hubble time. Unless such a type B dwarf is on a radial orbit, it will remain close to its original orbit apart from precession. Kroupa (1997), Klessen & Kroupa (1998) and Casas et al. (2012) have demonstrated, using high-resolution computations, that DM-free TDGs with an initial stellar mass of 107 M⊙ readily survive for times comparable to a Hubble time on eccentric orbits in the tidal field of a host galaxy. Quite stable, dSph-like solutions with remnant masses of 104–105 M⊙ appear in such models (Metz & Kroupa 2007; Casas et al. 2012). And Recchi et al. (2007) have shown, using chemo-dynamical calculations, that DM-free gas-rich TDGs (or RPDGs for that matter) are not destroyed through the star-formation process and that they self-enrich chemically in agreement with observations of dwarf satellites. Type B dwarfs that retain their gas would appear as dIrr or low-mass disk galaxies (Hunter, Hunsberger & Roye 2000).
109 M⊙ and dynamical friction on the DM halo of the host galaxy will therefore not significantly shrink their orbits over a Hubble time. Unless such a type B dwarf is on a radial orbit, it will remain close to its original orbit apart from precession. Kroupa (1997), Klessen & Kroupa (1998) and Casas et al. (2012) have demonstrated, using high-resolution computations, that DM-free TDGs with an initial stellar mass of 107 M⊙ readily survive for times comparable to a Hubble time on eccentric orbits in the tidal field of a host galaxy. Quite stable, dSph-like solutions with remnant masses of 104–105 M⊙ appear in such models (Metz & Kroupa 2007; Casas et al. 2012). And Recchi et al. (2007) have shown, using chemo-dynamical calculations, that DM-free gas-rich TDGs (or RPDGs for that matter) are not destroyed through the star-formation process and that they self-enrich chemically in agreement with observations of dwarf satellites. Type B dwarfs that retain their gas would appear as dIrr or low-mass disk galaxies (Hunter, Hunsberger & Roye 2000).
There is much observational data on the formation of new and on the existence of older TDGs (Sections 13.6, 13.7 and e.g. Pawlowski et al. 2012b), and the formation of RPDGs has also been documented (Yoshida et al. 2008) and studied (Yagi et al. 2010, Section 2). Such observational work sometimes concludes that only a small fraction of satellite galaxies may typically be of type B (e.g. Kaviraj et al. 2012). However, the observational census of young type B dwarfs is currently flux-limited such that the detections are limited to the present-day universe and the low-mass (<107 M⊙) type B dwarfs are not detected. Examples of low-mass TDGs that have formed in tidal arms are the about 5-Myr-old star-cluster complexes in the Tadpole galaxy and the three about 1-to-2-Gyr-old dSph-like TDGs in NGC 5557 (Section 13.6).
4 The Dual Dwarf Galaxy Theorem
Within the SMoC there are thus exactly two competing hypotheses for the origin and nature of dwarf galaxies:
-
Hypothesis A: dSph/dE/dIrr ⇔ DM halo for type A dwarfs, and
-
Hypothesis B: dSph/dE/dIrr ⇔ TDG/RPDG for type B dwarfs.
Remember that by Implication 1 (Section 3.2) type B dwarfs do not contain much DM.
Within the SMoC it is proven that larger structures form hierarchically bottom-up from merging smaller sub-structures. Therefore, mergers and encounters between galaxies are logically implied events that shape all larger galaxies (e.g. Bournaud et al. 2011; Martig et al. 2012) such that, by Implication 3 (Section 3.2), type B dwarfs appear in significant numbers.
The Dual Dwarf Galaxy Theorem,
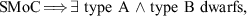
has thus been proven. It states that if the SMoC is true then type A and type B dwarf galaxies exist at the same time.
| Note 2: In any realistic cosmological theory a weak form of the Dual Dwarf Galaxy Theorem must be true because galaxies form directly from the cooling gas after the BB and TDGs also form when these primordial galaxies interact (there are thus two types of galaxy). RPDGs can only start forming once massive galaxy clusters have assembled. In a (non-Einsteinian) cosmological theory in which the laws of motion were to be such that the dynamical properties of all galaxies are identical without the existence of DM, no difference in the dynamical properties of isolated 3 primordial galaxies, TDGs and RPDGs would be evident. Type A dwarfs, as defined above, would not exist, but primordial galaxies would exist in addition to the type B dwarfs. Thus, dynamically, primordial and type B dwarfs would be identical, but type B dwarfs formed at a late cosmological epoch may be evident through unusual chemical and stellar population properties. |
In the SMoC, in which C/WDM plays a central role in structure formation, primordial dwarf galaxies are identical to the above type A galaxies and significant dynamical differences to type B dwarfs are expected:
If type A dwarfs exist (i.e. if the SMoC were valid), then they form within pre-collapsed DM haloes such that the accretion and feedback as well as environmental physics conditions are different from the formation of type B dwarfs without DM and within an expanding gas-rich tidal arm. In comparison to DM-free dwarf galaxies, galaxies that derive from DM haloes must show distinctly different morphological properties (rotation curves, masses, radii, density distributions) as well as different stellar-populations with distinct age and chemical-element distributions. Since the latter two are difficult to quantify we concentrate here on dynamical and morphological properties. 4
A robust prediction of the SMoC is therefore that there must exist DM-dominated and DM-free dwarf galaxies. And, by Section 3.1 type A (DM-dominated) dwarfs are distributed spheroidally around their host galaxy, tracing its DM halo. Type B dwarfs, on the other hand, show correlations in phase space (Section 3.2). Therefore, in addition to an expected dynamical and morphological difference between type A and type B dwarfs, the SMoC predicts them to have different distributions in phase-space.
It now becomes possible to test the SMoC at a fundamental level by studying which of the above two hypothesis may be falsifiable. Note that for a given dwarf galaxy both Hypothesis A and B cannot be valid simultaneously in the SMoC.
5 Falsification of the SMoC
Falsification of the Dual Dwarf Galaxy Theorem would invalidate the SMoC to be a model of the real universe. The procedure followed here is to test of which type (A or B) the observed dwarf galaxies are. Firstly, rotationally supported dwarf galaxies are considered to see if the two types of observed dwarfs (dIrr/dwarf-disk versus rotating gas-rich TDGs) do show the necessary dynamical differences. This is achieved by resorting to the baryonic Tully–Fisher (BTF) relation. Secondly, the pressure-supported dwarf galaxies are considered to see if dSph and dE galaxies differ from the known TDGs. Later (Sections 10 and 11) the phase-space occupancy and the physical properties of the known observed MW satellite galaxies are considered to ensure logical self-consistency of the deduction.
5.1 Rotationally Supported Dwarf Galaxies
Assuming the SMoC to be true it follows by the Dual Dwarf Galaxy Theorem that TDGs cannot lie on the BTF relation defined by DM-dominated galaxies. Thus,
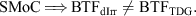
If, for rotationally supported gas-rich dwarf galaxies,
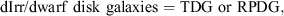
(Hypothesis B) were true, it would follow that the implication,  (not SMoC), would be true. The following first of two falsification theorems can now be stated:
(not SMoC), would be true. The following first of two falsification theorems can now be stated:
The First SMoC Falsification Theorem
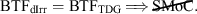
This states that if TDGs lie on the same BTF relation defined by primordial (DM-dominated) galaxies then the logically implied conclusion is that the SMoC is ruled out to be a representation of the real world.
5.2 Pressure-Supported Dwarf Galaxies
Turning now to dE/dSph satellite galaxies: Assuming the SMoC to be true it follows by the Dual Dwarf Galaxy Theorem that TDGs cannot have the same dynamical and morphological properties as primordial DM-dominated galaxies. Thus,
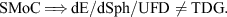
If, for pressure-supported dwarf galaxies,
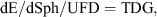
(Hypothesis B) were true, it would follow that the implication, 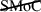 , would be true. Thus, the SMoC is proven wrong if the following second falsification theorem is true:
, would be true. Thus, the SMoC is proven wrong if the following second falsification theorem is true:
The Second SMoC Falsification Theorem
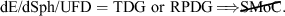
This states that if the dE/dSph/UFD satellite galaxies of the MW are ancient TDGs and are of the only kind then the logically implied conclusion is that the SMoC is ruled out to be a representation of the real world. This would be the case because if the MW were to have no dark matter dominated satellite galaxies then the model is falsified. 5
5.3 Procedure and Logical Consistency
It now remains to be shown that the First and Second SMoC Falsification Theorems hold.
In the real world there are only two logically possible outcomes of testing these theorems: Either they are both falsified (such that the SMoC is consistent with reality), or they are both true (such that the SMoC is falsified as a representation of reality). It is not permitted to have one Falsification Theorem being true and the other one false.
Once the Dual Dwarf Galaxy Theorem has been falsified such that both SMoC Falsification Theorems hold, logical consistency with this result should imply real data to show discord with the SMoC using other tests. Internal logical inconsistency in the present argument would emerge if such data would indicate excellent agreement with the SMoC predictions. The larger part of this contribution is devoted to studying how the observed universe, where excellent data do exist, matches to the SMoC.
The argument presented here must be logically sound. To ensure logical consistency we therefore cannot rely on measured high dynamical mass-to-light ratios, M/L, as a diagnostic for the presence of DM. Why is this?
It would be a circular argument: By adopting Hypothesis 0i (GR is valid) we are forced to introduce auxiliary Hypothesis 2 (DM exists) due to the mass-discrepancy observed in galaxies. When a mass-discrepancy is observed (as it is in the BTF data of normal galaxies and in dSph satellite galaxies of the MW) then taking this to be evidence for DM constitutes a circular argument. It is however permissible to compare normal/primordial galaxies and TDGs to test the Dual Dwarf Galaxy Theorem.
Here the foundations of gravitational theory in the ultra weak field limit are being tested. Rotation curves and large dynamical M/L ratia in MW satellites may also be explained by non-Newtonian theories (e.g. Brada & Milgrom 2000; Angus 2008; McGaugh & Wolf 2010; Hernandez et al. 2010; Famaey & McGaugh 2012) and tidal effects (Kroupa 1997), so large dynamical M/L values do not have a unique fundamental solution.
6 Extragalactic Evidence: How Many Types of Dwarf Galaxies are There in Reality?
It has been shown that the SMoC predicts there to be two fundamentally different types of dwarf galaxy. Which types are there in reality?
Observed dwarf galaxies with stellar masses M star < 1010 M⊙ come in two types: dIrr galaxies which are gas dominated and rotationally supported, and gas-poor dE and dSph galaxies which are largely pressure (i.e. random motion) supported (Ferguson & Binggeli 1994; Mateo 1998; Hunter et al. 2000; Dabringhausen, Hilker & Kroupa 2008; Forbes et al. 2008; Lisker 2009; Misgeld & Hilker 2011; Swaters et al. 2011). Satellite galaxies are, to a large extend, of the gas-poor type, which is naturally understood as a result of gas being stripped from initial gaseous dIrr-type satellite galaxies (Mayer et al. 2001).
6.1 Rotationally Supported dIrr/Dwarf-Disk Galaxies
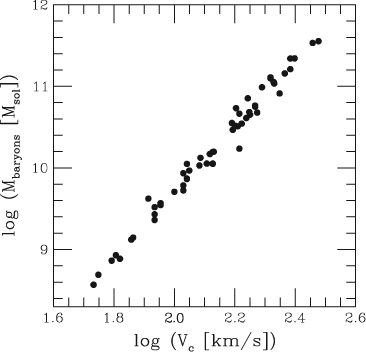
To differentiate DM-dominated type A dwarf galaxies from type B dwarfs that contain little or no DM can be achieved by comparing their internal kinematical state. Type B dwarfs of similar baryonic mass, M baryons, as type A dwarfs must have significantly slower motions of their stellar and gas components. A measure of the DM content is the asymptotically flat circular velocity, V c. Figure 2 shows M baryons versus V c data (McGaugh 2005) for primordial (i.e. DM-dominated) galaxies if the SMoC were true (Desmond 2012).
|
From the figure it is evident that the data form an excellent correlation over orders of magnitude in baryonic mass down to V c ≈ 15 km s–1 ≈ 5 × 106 M⊙ (see Section 17.4). 6
There is thus no evidence for the existence of multiple types of rotationally supported dwarf galaxies.
6.2 Pressure-Supported dE/dSph Galaxies
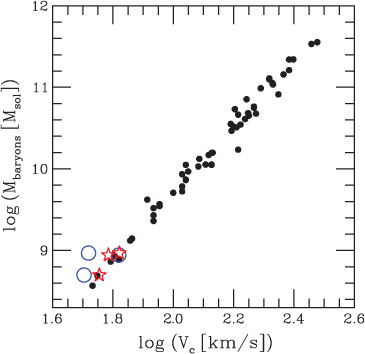
The next question to be addressed is if there are two types of pressure supported dwarf galaxies, namely those derived from DM sub-haloes and those derived from TDGs (Section 3). Figure 1 shows an overview of the distribution of pressure-supported stellar systems in the radius–stellar mass plot.
Taking R 0.5 to be the projected half-light radius and M star to be the stellar mass of the satellite galaxy and writing the radius–mass relation for pressure-supported stellar systems as
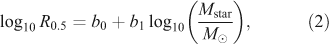
it follows for E galaxies (M star > 3×109 M⊙) that b 1 = 0.593 ± 0.027, b 0 = –2.99 ± 0.30, as already shown by Dabringhausen et al. (2008). That this relation extends into the ultra-compact dwarf (UCD) mass regime, which constitutes an extrapolation by at least three orders of magnitude in mass, is noteworthy. It may mean that the genesis of E galaxies and of UCDs may have followed the same physical principles, i.e. a rapid dissipational infrared-opacity-limited collapse (Murray 2009), possibly first into sub-clumps which then merge (Brüns et al. 2011). Note that the rare UCDs are deemed to be related to star clusters (Mieske et al. 2012). However, UCDs could be identified as the TDGs, while dE, dSph and UFD galaxies might be seen as the type A dwarfs. This being a false identification will become apparent in Section 9.
Concerning the dwarf galaxies (dE, dSph, UFD), it is evident that there is one single branch. Applying Equation 2 over the mass range 104 ≤ M
star/M
⊙ ≤ 3 × 109, the data yield b
1 = 0.122 ± 0.011 and b
0 = 1.87 ± 0.10 for dE and dSph galaxies. As is evident from Figure 1, dSph satellites (M
star ![]() 107 M⊙) are an extension of the dE galaxy population (M
star
107 M⊙) are an extension of the dE galaxy population (M
star ![]() 107 M⊙). This is particularly emphasised by Forbes et al. (2011). Ultra-faint dwarf (UFD) satellite galaxies with M
star
107 M⊙). This is particularly emphasised by Forbes et al. (2011). Ultra-faint dwarf (UFD) satellite galaxies with M
star ![]() 104 M⊙ form an extension of the dSph sequence to lower masses (Strigari et al. 2008).
7
Ferguson & Binggeli (1994) discuss dE and dSph galaxies as part of the same family.
104 M⊙ form an extension of the dSph sequence to lower masses (Strigari et al. 2008).
7
Ferguson & Binggeli (1994) discuss dE and dSph galaxies as part of the same family.
Thus, two fundamentally different types of satellite galaxies, as ought to exist if the Dual Dwarf Galaxy Theorem were true (Section 4), do not appear to be present.
7 Are the Known Dwarf Galaxies of Type A or Type B?
It has emerged that for M baryons < 1010 M⊙ there is no evidence for the existence of galaxy populations with two different dynamical or morphological properties. This constitutes a falsification of the Dual Dwarf Galaxy Theorem. But perhaps the observational data only contain dwarfs of the one type A? To achieve a rigorous falsification, TDGs and RPDGs (type B dwarfs) need to be directly compared with the putative type A dwarfs.
The question to be answered now is which type of dwarf galaxies do we have? Are dIrr/dwarf-disk, dE and dSph satellite galaxies DM dominated (i.e. of type A) or are they TDGs (i.e. of type B)? From past work (see Section 3.2) it is already established that type B dwarfs (TDGs), once formed, mostly do not dissolve but remain on orbits about their host for at least a Hubble time. Since they are observed to form and because galaxies are known to interact in the real universe they must be around. On the other hand, the existence of type A dwarfs depends solely on the truth of Hypothesis 2 which has until now not been verified. Type A dwarfs are therefore speculative objects, while type B dwarfs are known to form and to survive.
The following Sections 8 and 9 compare the hitherto known ‘normal’ dwarf galaxies, which have popularly but speculatively been assumed to be of type A, with observed TDGs (type B dwarfs).
8 Hypothesis A: dIrr and Dwarf Disk Galaxies are DM Dominated
If normal dwarf galaxies are DM dominated then the young TDGs of the same baryonic mass and dimension should have smaller rotational velocities. That is, in the BTF diagramme (Figure 2) the latter should lie significantly to the left of the former. But for three TDGs rotation curves have been measured, and all three coincide with the DM-dominated BTF relation (Figure 3).
|
The trivial solution that unobservable gas and/or not virialised young structures makes up the DM effect evident in the TDG galaxies is untenable because it would require a strong fine-tuning and chance configuration between the gas content, the gas flows and V c, to conspire in each of the three cases to move the TDG onto the BTF relation of DM dominated galaxies.
It is thus evident that type B dwarfs (the TDGs) lie on the same relation as the type A dwarfs. That is, only one dynamical type of rotating dwarf galaxy appears to exist. In other words, type B dwarfs are identical to type A dwarfs, BTFdIrr = BTFTDG, and observed rotationally supported dwarf galaxies falsify the Dual Dwarf Galaxy Theorem in logical consistency with Sections 6.1 and 6.2. By the First SMoC Falsification Theorem this implies the SMoC to be falsified.
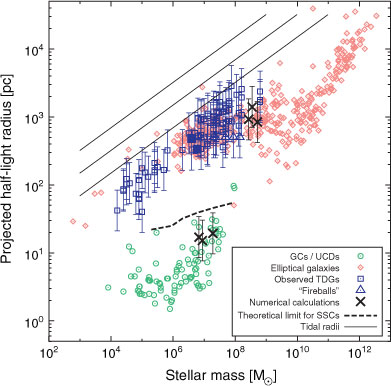
9 Hypothesis A: dE, dSph and UFD Galaxies are DM Dominated
Because the physics of the formation of type A (DM-dominated) galaxies differs significantly from the formation of type B dwarfs, they should show different radii at a given baryonic mass. That is, known TDGs should not follow the same radius–mass relation as dE, dSph and UFD galaxies. This is tested in Figure 4. It is evident that type B dwarfs (the TDGs) lie on the same relation as the type A dwarfs. That is, only one dynamical type of pressure-supported dwarf galaxy appears to exist. In other words, type B dwarfs are identical to type A dwarfs, dSph = TDG, and observed pressure supported dwarf galaxies falsify the Dual Dwarf Galaxy Theorem in logical consistency with Sections 6.1, 6.2 and 8. By the Second SMoC Falsification Theorem this implies the SMoC to be falsified. This deduction is logically consistent with the observed dynamical evidence that dE galaxies do not contain much if any DM.
|
For a further discussion on the origin of dE galaxies see Section 13.7.
10 Hypothesis A: MW dSph Satellites are DM Substructures
According to Sections 8 and 9 the SMoC is falsified through both the First and Second SMoC Falsification Theorems. If this is true, then other observational data concerning the properties and distribution of dwarf galaxies must be consistent with this deduction.
In the following Sections 11.1 to 11.6 further (auxilliary) tests of Hypothesis A (dSph are embedded in DM sub-haloes, Section 4) are provided. Before continuing with these tests, it is useful to first establish the observational facts on the phase-space distribution of satellite galaxies around the MW, because the MW is our primary auxilliary test case: if the SMoC is falsified (Sections 8 and 9) then the excellent MW data should be conform to this.
10.1 A Vast Polar Structure Around the Milky Way
An important test of the nature and origin of the MW satellite galaxies is provided by their distribution in phase-space. Detailed predictions have been made on this in the framework of the SMoC (Section 3). If they were to be dwarfs of type A then they would have independent formation and evolution histories since each would have formed within its own DM halo independently of the other DM haloes. The rare cases that two DM haloes interact can be neglected here given the vastness of the available phase-space (6-dimensional volume of roughly 2503 kpc3 × 4003 km3 s–3) in comparison with their small sizes. If, on the other hand, the satellites are of type B and stem from one encounter that involved the young MW then they would be highly correlated in phase-space (Section 3).
Here the following question is addresed: How are the satellite galaxies and the globular clusters and streams in the outer halo of the MW distributed in phase space?
10.1.1 Phase-Space Distribution
The highly anisotropic distribution of the known dSph satellites, of the two Magellanic Cloud satellite galaxies and of some globular clusters, as well as the association with the Magellanic Stream about the MW in a vast band on the Galactic sky, had been noted more than thirty years ago (Lynden-Bell 1976; Kunkel 1979). But the contradiction with the expectation from the later-adopted SMoC was emphasised for the first time by Kroupa, Theis & Boily (2005). The anisotropic distribution is a disk-like structure (the disk of satellites, DoS) with a root-mean-square height of 10-30 kpc which lies nearly perpendicularly to the plane of the MW. This distribution of the 9 ‘classical’ (i.e. brightest dSph satellites) has a likelihood of occurrence of 0.5% if the parent distribution were a spherical DM host halo.
A number of subsequent research papers continuously enhanced the discrepancy, and Metz et al. (2007) showed that even oblate and prolate DM host haloes of the MW do not match the observed satellite anisotropy. It was found that Andromeda also has a non-isotropic satellite distribution seen edge-on (Karachentsev 1996; Koch & Grebel 2006; Metz et al. 2007, see also figure 1 in Tollerud et al. 2012). The orbital planes of those satellites that have observational constraints on their orbital angular momenta suggest the MW satellite system to be a rotational disk-like structure (Metz, Kroupa & Libeskind 2008).
While already highly significant, the discrepancy with the expectations from the SMoC became more significant with the addition of the 13 new ultra-faint dSph satellite galaxies which independently define the same phase-space correlation (Metz, Kroupa & Jerjen 2009a; Kroupa et al. 2010), a result which is not affected by an incomplete survey sky coverage (Section 10.1.2).
Is the DoS a physical structure of the MW? If it is an unlikely chance occurrence among the 9 classical dSph satellites, or if the 13 UFD satellite galaxies are not physically related to the classical dwarfs, then the UFDs cannot be distributed in the same DoS. Furthermore, if the DoS is not physical, then the orbital angular momenta of the satellite galaxies would not align with the normal vector of the DoS. And, if the DoS is not physical then no other objects or structures (e.g. globular clusters, stellar and gaseous streams) ought to show a similar alignment.
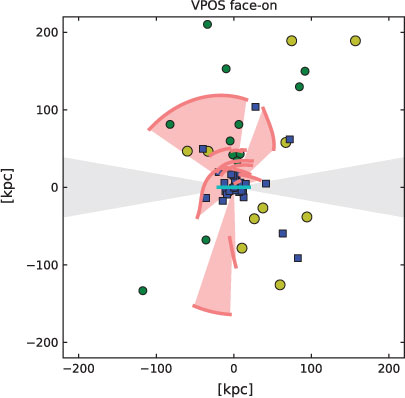
Instead, a vast polar structure (VPOS) surrounding the MW emerges which contains a highly significant overabundance of all mentioned components (Pawlowski et al. 2012b). The individual components of this VPOS are discussed next, and Figures 5–9 below visualise how these fit together and how a single model can account for this structure. The normal vector to the VPOS is referred to as NPOS. A detailed analysis and discussion of the VPOS data is provided by Pawlowski et al. (2012b).
10.1.2 UFD Satellites
The ultra-faint dwarfs — UFDs — have different discovery histories than the classical satellites. The latter were discovered mostly on photographic plates prior to about the year 2000 and their census is complete over most of the sky apart in the regions obscured by the MW disk. The UFDs on the other hand were discovered using the robotic Sloan Digital Sky Survey (SDSS) after 2000. The sky coverage is not complete, but the coverage extends over most part of the northern hemisphere therewith being a cone rather than a slab with small regions having also been surveyed in the southern Galactic hemisphere (see figure 1 in Metz et al. 2007). If there had been any observational bias that might have led to the discovery of those classical dSph satellites that, by an as yet unknown reason, lie in a DoS, then the UFDs clearly cannot be subject to the same bias.
Fitting a plane to the classical satellites yields the well-known DoS. The DoS is oriented such that when we look towards the Galactic centre from the Sun, the DoS is seen nearly face on. In Galactocentric angular coordinates the normal of the classical DoS points towards l = 157.6 ± 1.1°, b = –12.0 ± 0.5° with a RMS height of ΔdSph = 18.3 kpc. Fitting a plane only to the 13 UFDs yields a DoS which is next to identical to the classical DoS (l = 151.4 ± 2.0°, b = 9.1 ± 1.0° with ΔUFD = 28.6 kpc, Kroupa et al. 2010).
Thus, the parent phase-space distributions of the classical dwarfs and of the UFDs can be taken to be equal. Therefore they have a common origin, because if this were not to be the case an unnatural coincidence would need to be postulated without a known physical mechanism. The DoS normal vector of the combined population points towards l = 156.4 ± 1.8°, b = –2.2 ± 0.6° with Δ = 28.9 kpc.
10.1.3 Globular Clusters
Considering the GCs of the MW these can be differentiated into the bulge and disk (BD) GCs, into the old halo (OH) GCs and into the young halo (YH) GCs (Mackey & van den Bergh 2005 for the classification; Harris 1996, 2003 update, for positional data). The same disk-fitting algorithm used to quantify the DoS of the classical dSph satellites and of the UFDs can be applied to obtain the best-fitting planar description of the three GC populations (Pawlowski et al. 2012b).
The BDGCs lead to a planar fit with a normal oriented towards (l, b) = (175°, –85.7°), i.e. towards the Southern Galactic Pole. This is the exactly expected orientation for a component which is associated with the MW disk and bulge. For the OHGCs, on the other hand, no good plane solution is found. Again, this is exactly as expected because the OHGCs form a spheroidal distribution.
The YHGCs lead to a well defined disk of GCs (DoYHGCs) which is indistinguishable to the satellite DoS. Its normal points merely 13° away from the DoS normal. The probability of a randomly oriented vector being as close to the DoS normal direction as is the DoYHGC normal vector is about 2.5%.
Sub-dividing the YHGC population of 30 YHGCs into those 20 within 20 kpc and those 10 beyond 25 kpc leads to two independently obtained planar fits, each of which is well aligned with the DoS of the dSph and UFD satellites (Figure 9).
Thus, the inner and outer YHGCs, the classical dSph satellites and the UFD satellites independently of each other define the same vast polar disk-like structure about the MW. This is remarkable and cannot be due to observational bias.
10.1.4 Stellar and Gaseous Streams
Furthermore, the known stellar and gaseous streams within and around the MW can be analysed in terms of their orientations. Using a method introduced in Pawlowski et al. (2012b) to calculate the normal to the plane defined by two points on the stream and the MW centre, it is possible to study the directions of the normals to the 14 known stellar and gas streams. It turns out that half of the stream normals cluster around the above two DoS and the two DoYHGCs, an alignment which has a likelihood of 0.34% if the streams were randomly oriented. The actual chance of finding the degree of orientation evident in the MW streams is smaller, because it would be expected that the streams predominantly map the continuous addition of material into the MW disk. That is, the stream normals ought to be preferentially oriented towards the poles of the MW.
10.1.5 Combined Likelihood
The chance that the normals of the disks fitted to the classical dSph satellites, the UFD satellites, the inner and outer YHGCs as well as to the stellar and gaseous streams all cluster around the same region on the Galactic sky is smaller than 2.5% × 0.34% = 8.5×10–5 if they were physically unrelated. It is significantly smaller still because this number only considers the YHGCs and streams.
10.1.6 Orbital Angular Momenta of Satellite Galaxies
A consistency check on the physical reality of the VPOS is provided by the motions of its constituents. These need to be confined within the VPOS for it to be a physical structure. At present only the motions of the nearest satellite galaxies are known.
Proper-motion measurements of the innermost 6 classical dSph and of the LMC and SMC satellites have shown that the majority have orbital angular momenta about the MW that point into a direction towards the normal to the VPOS, i.e. towards the NPOS (e.g. Pawlowski et al. 2012b; Figure 9). The Sculptor dSph has an orbital angular momentum direction which places it within the DoS but on a retrograde orbit relative to the average direction of the other orbits.
It follows that of the eight satellite galaxies with proper motion measurements, seven appear to orbit within the DoS with one being within the DoS but on a retrograde orbit compared to the six others. One satellite, namely Sagittarius, orbits approximately perpendicularly both to the DoS and to the MW disk. Sagittarius may have been deflected onto its present highly bound orbit. Such a scenario has been studied for the first time by Zhao (1998) and will need to be re-investigated in view of the most recent data on the Sagittarius stream (e.g. Carlin et al. 2012) and the orbits of the other satellite galaxies, and in view of the question whether Sagittarius may have originally been orbiting within the DoS.
10.1.7 Conclusions: The VPOS is a Physical Structure
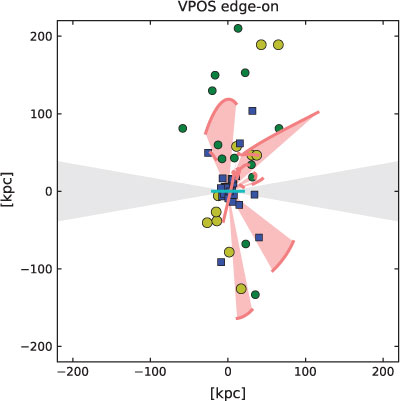
Pawlowski et al. (2012b) have thus discovered a vast polar structure surrounding the MW. It is identified by a region on the Galactic sky towards which the normals of the DoS, DoYHGC and half of all known stellar and gaseous streams point. Figures 5 and 6 show the VPOS face-on and edge-on, respectively. 8
|
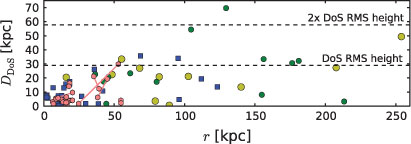
It is useful to study how the various components are arranged in the VPOS. As is suggested by Figure 7, the UFD satellites which are fainter and thus have a smaller baryonic mass have a somewhat larger dispersion in D DoS values than the classical dSph satellites, which have larger baryonic masses. This is also evident in ΔUFD > ΔdSph (Section 10.1.2). Is this mass segregation towards the mid-plane of the VPOS?
|
|
Counting the number of objects out of all that have a distance, D DoS, within one and within two times the RMS height of the DoS, Δ: In total there are, at Galactocentric distances larger than r = 10 kpc, 2 Magellanic satellites and 9 classical dSph satellites, 13 UFD satellites, 22 young halo GCs and 28 stream anchor points (74 objects, Pawlowski et al. 2012b). For D DoS < Δ are found 17 of 24 satellites, 20 of 22 YHGCs, 25 of 28 anchor points. For D DoS < 2Δ we have 23 of 24 satellites, 22 of 22 YHGCs, 26 of 28 anchor points. That is, within Δ can be found 84%, and within 2Δ are 96% of all objects.
The VPOS therefore contains a variety of components and extends from about 10 kpc out to at least 250 kpc. It has a height-to-radius ratio of about 1 : 10 and therefore it constitutes a thin disk-like polar structure. The existence of this VPOS, or disk-like polar arrangement of baryonic matter on a vast scale about the MW, stands beyond any reasonable amount of doubt. It is incompatible with being derived from accreted dark-matter sub-structures, taking the likelihoods from Section 11.1 below into account (0.056%) as well as the likelihood that the streams are also associated with the YHGC and satellite galaxy distribution (less than 8.5×10–3%, Section 10.1.5). 9
11 Testing Hypothesis A on the Local Group
11.1 The Phase-Space Distribution and Properties of the Local Group
From Section 10.1 it has thus become apparent that the MW is surrounded by a vast phase-space-correlated structure, the VPOS, which is made up of dSph and UFD satellite galaxies, inner and outer YHGCs as well as stellar and gaseous streams.
The observed phase-space distribution of the MW satellites can be compared to the allowed phase-space region assuming they are of type A. To obtain significant anisotropies in the luminous sub-halo distribution the following problem needs to be overcome: a physical process needs to be found which allows star formation only in sub-haloes that are highly correlated in phase-space, while all the others remain dark. However, no such physical mechanism is available within the SMoC despite many attempts (Metz et al. 2009b; Pawlowski et al. 2012a; Pawlowski et al. 2012b).
High-resolution computations of the formation of MW-mass DM host haloes within the SMoC have been performed by Libeskind et al. (2009) using semi-analytic modelling trimmed to account for the observed galaxy population in order to study the formation of MW-type galaxies and their satellite systems. These calculations provide the following data which have been published by the seminal work of Libeskind et al.:
These supercomputer simulations with 109 particles yield 31 000 DM haloes of mass comparable to the DM halo of the MW (2 × 1011 < M DM/M ⊙ < 2 × 1012). These host 3201 main galaxies of similar luminosity as the MW (a galaxy more luminous in the V-band than M V = –20). The remaining types of galaxies which are in similar DM host haloes are not specified by the authors. The relevant sample of 3201 ‘MW-type galaxies’ host 436 galaxies with at least 11 luminous satellites. About 35% of these have a satellite system in which at least 3 satellites have orbital angular momenta pointing within 30 degrees of the normal to the plane defined by the 11 brightest satellites.
A DM halo of MW mass thus has a likelihood less than 3201/31 000 ≈ 10% of hosting a MW-type galaxy (defined to be a galaxy with an absolute V-band magnitude M V < –20, without considering whether it is a major disk galaxy or a spheroid). The majority of other galaxies also hosted by similar DM haloes are not described further by the authors, but are galaxies fainter than M V = –20. This appears to be in disagreement with the real population of galaxies, since Disney et al. (2008) have shown that the galaxy population is remarkably invariant at any luminosity. The observed uniformity is a significant failure of the cosmological model, because of the large variation expected within the SMoC: Each DM host halo has a different merger history (this is the invariant baryonic galaxy problem, Kroupa et al. 2010). Further, of the 31 000 host haloes 436/31 000 = 1.4% have a host galaxy of MW luminosity and at least 11 luminous satellites. Of the original sample of 31000 host haloes, about 0.4% have these properties and at least 3 satellites orbit within 30 degrees of the normal to the plane defined by the 11 brightest satellites. According to these numbers, and if the SMoC were valid, then the MW and its phase-space correlated bright satellites would be a highly significant exception of likelihood 0.4%. This likelihood is lower still because neither the thinness of the model DoS nor the orientation of the DoS, being polar relative to the disk of the host galaxy, are taken into account.
The Local Group however contains the MW and Andromeda. Andromeda is a galaxy similar to the MW (but somewhat more complex, Hammer et al. 2010) and it also hosts >11 luminous satellites, in full conformity with the invariant baryonic galaxy property of the real universe. Thus, given a DM halo of MW/Andromeda mass, the chance of obtaining an Andromeda-type galaxy within it is 1.4%, by the above reasoning. The combined likelihood of having, within the Local Group, two independent MW-type DM haloes hosting a MW and Andromeda galaxy with their satellite systems is thus <1.4 × 0.4 = 0.056%.
The SMoC can thus be discarded with better than 99.9% confidence, by this one test alone.
But are we not merely making ever more precise demands to the point that yes, the MW is a unique case just as each and every galaxy is (e.g. Hammer et al. 2007)? The above argument rests on generic properties of the Local Group in how likely it is for a group of two major galaxies to contain, in the SMoC, two similar MW-type galaxies which have similar satellite systems whereby at least one of them has an anisotropic satellite distribution. Nevertheless, this one test alone would not suffice to discard the SMoC, because it can always be argued that the Local Group happens to be an exception given the unique properties we are interested in.
Ignoring the falsification of the SMoC through the Dual Dwarf Galaxy Theorem (Sections 8 and 9), a relevant question that may be answered by considering the catalogues of numerical SMoC simulations is how often groups of galaxies occur in the model which have properties similar to those of the Local Group by consisting of two major and similar disk galaxies. Such Local-Group-type systems are common in the real universe with the majority of galaxies being disk galaxies in such groups (Karachentsev 1996; Marino et al. 2010). The invariant baryonic galaxy problem discussed above would indicate that in the SMoC such groups would be rare. Indeed, Forero-Romero et al. (2011) also arrive at small likelihoods of finding a Local-Group equivalent if the SMoC were true (their Sections 5.3 and 6).
In the present context, the following statement by Libeskind et al. (2011) is interesting: ‘While the planarity of MW satellites is no longer deemed a threat to the standard model, its origin has eroded a definitive understanding.’ Lovell et al. (2011), who also address the anisotropy problem using the numerical data from the Aquarius SMoC simulation, write: ‘All six Aquarius haloes contain statistically significant populations of sub-halo orbits that are aligned with the main halo spin. All haloes possess a population of sub-haloes that rotates in the same direction as the main halo and three of them possess, in addition, a population that rotates in the opposite direction. These configurations arise from the filamentary accretion of sub-haloes. Quasi-planar distributions of coherently rotating satellites, such as those inferred in the Milky Way and other galaxies, arise naturally in simulations of a CDM universe.’ This statement is clearly in contradiction with the above Libeskind et al. (2009) numbers, which is odd given that both papers are published by the same SMoC research team. Indeed, Pawlowski et al. (2012a) demonstrate that the Lovell et al. contribution needs to be viewed critically, as in essence the authors mark a sub-set of DM sub-haloes which have orbital angular momenta aligned with the spin of the host halo. Considering this sub-set the authors conclude that the disk-like distribution of MW satellites arises naturally in the SMoC. They do not state however, why the vast number of sub-haloes on other orbits should not play a role in establishing the satellite population. That is, which physics would be active to select no other than those sub-haloes to make stars which happen to be in the disk-like sub-sample is not specified. Given that the host halo spin tends to roughly align with the spin of the host disk galaxy, the Lovell et al. (2011) claim would suggest the MW satellite system in the SMoC to be more in equatorial orientation in contradiction to the observed VPOS (Section 10.1). 10
Can the sub-grid parametrisation of baryonic physics be responsible for the disagreement between model and observation? This cannot be the case because the phase-space occupied by dark matter sub-haloes and the star-formation processes within them are uncorrelated. Indeed, the large volume of published galaxy formation models up until 2011 (not counting the contribution by Lovell et al. 2011) have all been in mutual agreement with each other in reproducing the luminous properties and spheroidal distribution of model satellite galaxies in DM sub-haloes. The vast number of galaxy-formation simulations are thus quite consistent with each other, which is an important consistency check on the physics used in the simulations: the reported research (see Footnote 14) shows an internal consistency within the framework of the SMoC.
In summary: it has thus emerged that the satellite phase-space distribution of the MW in a VPOS extending from about 10 kpc to at least about 250 kpc is not compatible with Hypothesis A. This conclusion is based on one auxiliary test, as discussed here. If one type of test falsifies Hypothesis A, and if it is a robust test, then other independent tests ought to yield the same conclusion.
In the following five additional and independent tests of Hypotheses A are performed for MW satellites. These can be viewed as stand-alone tests, or as further consistency/auxiliary tests.
11.2 Mass–Luminosity Data
Assume that Hypothesis A (Section 4) is true. Then by energy conservation the dSph satellite galaxies must show a correlation between their luminosity, L, and hypothesised dark-matter halo mass, M DM, which is deduced from observations of the density and velocity dispersion profiles of the dSph satellites by solving the Newtonian Jeans equation (e.g. Klimentowski et al. 2007; Lokas 2011). Note that the statistical correlation between L and M DM does not rely on the details of baryonic physical processes, since the binding energy of the structure dictates what can form within it by whatever process, as long as the processes are generically the same in all satellites (i.e. gas physics and stellar feedback, ionisation from outside; tides do not play a major role for the population of satellites as shown in Section 3). That such a correlation exists among galaxies (interpreting their matter content within the SMoC) is very well established (e.g. Leauthaud et al. 2012).
However, it has already been shown that the dSph satellite galaxies of the MW violate the expected correlation (Mateo et al. 1993; Strigari et al. 2008; Wolf et al. 2010). By solving the Newtonian Jeans equation the DM mass, M 0.3, within the central 300 pc radius of each satellite can be calculated; M 0.3 is a measure of M DM by virtue of the properties of the SMoC. Kroupa et al. (2010) test all available SMoC models of satellite galaxies for the existence of a positive correlation between model luminosity and model DM mass. 11 This correlation is quantified by the slope, κ, of the log(DM mass)–log(luminosity) relation. The eight tested SMoC models include the physics of feedback, inhomogeneous re-ionisation, in-fall, CDM and WDM and semi-analytical models as well as stellar population synthesis models, and each one has κ > 0.12. The observational data, on the other hand, have κ < 0.11 at the 99.7% (3-sigma) confidence level. In other words, as Wolf et al. (2010) state: ‘… all of the Milky Way dwarf spheroidal galaxies (MW dSph) are consistent with having formed within a halo of a mass of approximately 3 × 109 M⊙, assuming a Λ cold dark matter cosmology. The faintest MW dSph seem to have formed in dark matter haloes that are at least as massive as those of the brightest MW dSph, despite the almost five orders of magnitude spread in luminosity between them.’
Both, the observational data and the models thus agree at a confidence level of 0.5%.
Tollerud et al. (2012) perform a resolved-star spectroscopic survey of 15 dSph satellites of Andromeda and find that the luminosities of these satellites are independent of their DM mass, as is the case for the MW satellites. Thus, for Andromeda, κ ≈ 0 as well.
In summary: The hypothesis that the SMoC models of dSph satellite galaxies represent the real dSph satellite galaxies can thus be discarded with a confidence of 99.5%. In other words, the hypothesis that the satellites reside in DM haloes made of C/WDM particles appears to be unphysical, in full consistency with the conclusion of Section 11.1 above.
11.3 Mass Function of dSph DM Haloes
There are various aspects of this test:
Firstly, the missing satellite problem is well known: 24 dSph satellites (counting both, the 11 bright, ‘classical’, satellites discovered mostly on photographic plates, and the 13 UFD satellites discovered with the SDSS) have been found while hundreds are expected. It is popularly (there exists a vast number of research papers on this problem) claimed to be solved within the SMoC (Kroupa et al. 2010 and references therein, see also e.g. Font et al. 2011) as the parametrisation of sub-grid baryonic physics is tuned to reproduce the small number of observed dSph satellite galaxies. If the SMoC were true then even within the solar neighbourhood there ought to be hundreds of concentrated dark matter clumps (Diemand et al. 2008). According to these state-of-the-art SMoC computations there ought to be about 150 additional faint satellite galaxies within the MW DM halo which must be discovered (e.g. Bovill & Ricotti 2011). According to Boylan-Kolchin et al. (2011a) up to a ‘factor of 5 to 20 times as many faint galaxies could remain undetected at present owing to incomplete sky coverage, luminosity bias, and surface brightness limits.’
Secondly, assuming the SMoC to be true and each dSph satellite galaxy to be embedded in a DM halo, the form of the mass function (MF) of these observed luminous DM haloes is not in agreement with the theoretically expected MF of luminous sub-haloes. Including the Large and Small Magellanic Clouds (LMC, SMC, respectively) leads to the following result: the hypothesis that the MW satellites stem from the SMoC can be discarded with more than 96% confidence, but a more realistic assessment implies exclusion at the 99% level (Kroupa et al. 2010). In particular, the observed sample of satellites has a significant overabundance of M 0.3 ≈ 1.5 × 107 M⊙ DM haloes.
Thirdly, as documented in figure 2 in Kroupa et al. (2010), all DM sub-haloes containing dSph satellites have a mass M 300 < 2.5 × 107 M⊙, while 15% of the sub-haloes in the MW DM halo ought to be more massive within 300 pc according to the ΛCDM model. The MW halo is thus missing a substantial fraction (15%) of its massive sub-haloes. Bovill & Ricotti (2011) emphasise this failure of the SMoC for the first time. Boylan-Kolchin et al. (2011a) continue to point out that the MW should host at least six sub-haloes that had maximum circular velocities in excess of 30 km s–1 but are incompatible with any known MW satellite (including the Magellanic Clouds) having a V-band luminosity L V > 105 L⊙.
To solve this problem, Boylan-Kolchin et al. (2011a) suggest that galaxy formation in DM haloes with a mass ![]() 1010 M⊙ may become stochastic, or that the MW is an exception. However, this is not conform to known physical laws. The suggestion that the MW (and by implication) Andromeda (which has the same problem) are exceptions is ruled out by Strigari & Wechsler (2012) who study a large ensemble of MW-type galaxies from the SDSS confirming the significant deficit of bright satellites around the hosts if the SMoC were true.
1010 M⊙ may become stochastic, or that the MW is an exception. However, this is not conform to known physical laws. The suggestion that the MW (and by implication) Andromeda (which has the same problem) are exceptions is ruled out by Strigari & Wechsler (2012) who study a large ensemble of MW-type galaxies from the SDSS confirming the significant deficit of bright satellites around the hosts if the SMoC were true.
Fourthly, in modelling galaxy formation within the SMoC it has to be assumed that the galaxy formation efficiency decreases sharply with decreasing DM halo mass because the DM halo mass function rises steeply with decreasing mass. Effectively below a threshold mass ≈1010 M⊙ galaxies do not form (Ferrero et al. 2011). These authors demonstrate that almost one half of dwarf galaxies with stellar mass in the range 106 < M star/M ⊙ < 107 are in haloes with masses substantially below that threshold. They emphasise that this is not easily accommodated within the SMoC. In their abstract they state ‘Extending galaxy formation to haloes well below 1010 M⊙ would lead to severe disagreement with the low mass end of the galaxy stellar mass function; at the same time, the extremely low stellar mass of the systems involved make it unlikely that baryonic effects may be responsible for reducing their dark matter content.’
In summary, the number and DM halo mass distribution of MW satellite galaxies is in highly significant disagreement with the expectations from the SMoC and there is no physically known process that may be able to solve the disagreements. In brief, the concept that the satellites reside in DM haloes made of C/WDM particles breaks down, in full consistency with the conclusions of Sections 11.1–11.2 above.
11.4 Morphological Appearance of dSph Satellite Galaxies
Globular star clusters (GCs) have a stellar velocity dispersion σ ≈ 10 km s–1. For a typical diameter of 2r ≈ 8 pc, this implies that the crossing time scale is about 1 Myr. Any internal sub-structure is thus phase-mixed away on a time scale of a few Myr, which is why GCs appear as perfectly smooth, symmetric and spheroidal stellar systems despite being immersed in the tidal field of the MW.
The dSph satellite galaxies also have σ ≈ 10 km s–1 but radii of about 300 pc. If this velocity dispersion is related to their DM halo mass, which it must be if the SMoC were correct, then any internal sub-structure would phase-mix away within 100 Myr. Given their ages of about 10 Gyr, it follows that the satellites ought to appear as smooth and symmetric as GCs.
Tidal forces from the MW cannot be effective in distorting the satellites, as most of them are at Galactocentric distances D > 50 kpc, if each is surrounded by an extensive (radii > few kpc) DM halo weighing about 109 M⊙. Computational work has shown about 10% of the DM sub-haloes to be affected by tidal forces (Section 3). A smaller fraction will be affected so severely that the innermost 1 kpc regions that contain the stars would be distorted by tides.
In this context, Hayashi et al. (2003) write ‘We apply these results to substructure in the Milky Way and conclude that the dark matter haloes surrounding its dwarf spheroidal (dSph) satellites have circular velocity curves that peak well beyond the luminous radius at velocities significantly higher than expected from the stellar line-of-sight velocity dispersion. Our modeling suggests that the true tidal radii of dSph lie well beyond the putative tidal cutoff observed in the surface brightness profile, suggesting that the latter are not really tidal in origin but rather features in the light profile of limited dynamical relevance.’ Following on from this, Walcher et al. (2003) emphasise a statement by Stoehr, White & Springel (2002): ‘Although there is no problem accommodating a single disrupting object like Sagittarius, it would become uncomfortable if tidal stripping were detected unambiguously in other systems.’ Note that the inner region of a satellite is affected by tides after significant tidal destruction of its outer parts (Kazantzidis et al. 2004).
Thus, a small fraction, far less than 10%, of the satellites may show morphological evidence for tidal affects such as being flattened or somewhat distorted. Indeed, the Sagittarius satellite galaxy, at D ≈ 16 kpc, is the best known example of a satellite galaxy being strongly affected by the MW tidal field.
From the sample of 24 dSph satellite galaxies, too many show non-spherical and in many cases also asymmetric morphologies. Ursa Minor (D ≈ 65 kpc) is a well known case with internal sub-structure and a highly flattened and asymmetric appearance (Kleyna et al. 1998). It counts as one of the most DM dominated galaxy with a mass-to-light ratio, M/L ≈ 70, but its internal structure is incompatible with the existence of a CDM halo (Kleyna et al. 2003). The Fornax dSph satellite (D ≈ 140 kpc) also shows significant distortions by appearing flattened, asymmetric and with twisted isophotes (Demers, Irwin & Kunkel 1994; Walcher et al. 2003). The Carina dSph satellite (D ≈ 93 kpc) similarly shows a flattening with one side appearing to be more compact than the other, and it has isophotes that are not ellipsoidal (Walcher et al. 2003). Among the faintest satellites, Hercules is highly elliptical and somewhat amorphous (Coleman et al. 2007). Sand et al. (2011) find that a large fraction of the faint satellites, which are supposedly the most DM dominated dwarf galaxies, show tidal signatures. Noteworthy is that this problem appears to persist for Andromeda satellites too: Andromeda X is found to be highly elongated at a distance of 170 kpc from its host galaxy (Brasseur et al. 2011).
McGaugh & Wolf (2010) study the internal dynamics and the elongation of most of the MW and Andromeda satellites finding very strong evidence for the majority being affected by tidal forces. From their figure 5 it is seen that of the 24 satellites plotted, 75% have an ellipticity larger than 0.3, whereby the ellipticity correlates strongly with the distance from the host galaxy. That even the classical (bright) dSph satellites of the MW have substantial ellipticities is evident from table 1 in Lokas (2011).
In summary, while a homogeneous statistical study of the morphological appearance of each dSph satellite is wanted, the above examples and reasults already demonstrate that the notion that the satellites are immersed in DM haloes appears to be unphysical because there are too many satellites with distorted morphologies. This is in full consistency with the conclusions of Sections 11.1–11.3 above.
11.5 Orbital Decay of MW Satellites
The conventional Newtonian interpretation of the MW dSph satellite galaxies is that they are hosted within DM-sub-haloes. With this assumption, Jeans modelling implies them to have similar DM halo masses of 109 M⊙ (Mateo et al. 1993; Strigari et al. 2008; Wolf et al. 2010). This appears to be the case for the Andromeda satellites as well (Tollerud et al. 2012).
To account for the existence of the DoS, and if the satellites were of type A (i.e. hosted in DM sub-haloes), then they would have been accreted onto the growing DM halo of the MW from a DM filament that would need to connect to the MW DM halo. They would thus have fallen in from large distances, and dynamical friction would have decayed and circularised their initial orbits to the present-day orbits about the MW. Angus, Diaferio & Kroupa (2011) demonstrate that for this to be viable, the satellites with measured proper motions must have been significantly more massive than 109 M⊙. This is in contradiction to the Jeans modelling.
In summary, there is therefore no consistent combined solution of the existence of the DoS, the orbital angular momenta and masses of the dSph satellites within the framework of the SMoC. dSph satellites cannot be DM sub-haloes in full consistency with the conclusions of Sections 11.1–11.4 above.
11.6 Further Logical Inconsistencies
All independent tests concerning dSph satellite galaxies (Sections 11.1–11.5) yield the same result: Hypothesis A is incompatible with the data.
While Hypothesis A can by now be taken to have been disproven, it is nevertheless of use to point out the following mutually excluding results based on excellent high resolution simulations of the formation of MW-type galaxies and their satellites within the SMoC framework:
In a detailed discussion of the problem at hand, Deason et al. (2011) write ‘The satellite galaxies have been accreted relatively recently’ (at a redshift of z < 1) in order to account for their disk-like distribution in the VPOS.
Nichols & Bland-Hawthorn (2011) model the evolution of initially gas rich satellite galaxies. Since these are today essentially free of gas, even out to about 250 kpc, the authors conclude ‘This model of evolution is able to explain the observed radial distribution of gas-deficient and gas-rich dwarfs around the Galaxy and M31 if the dwarfs fell in at high redshift (z ≈ 3–10).’
The observed MW satellite system is arranged in a large polar disk-like structure and the satellites are void of gas. Both, recent and long-past accretion into the MW halo of the same satellites is not physically possible.
Apart from this inconsistency arrived at in the SMoC, infall of a group of dwarf galaxies as the origin of the phase-space correlation is ruled out by the following reasons (Metz et al. 2009b):
Firstly, the putative group would have had to have been compact with a diameter of less than about 30 kpc to account for the thinness of the VPOS (Figure 7). But all known groups of dwarf galaxies have diameters of a few hundred kpc. It would thus be necessary to postulate that the MW accreted a group of a type which does not exist any longer. This however would be an inferior hypothesis because in order to ‘solve’ the DoS problem the existence of an unobserved ad-hock type of dwarf group would need to be postulated.
Secondly, there would then be no endemic luminous DM sub-haloes of the MW. The missing satellite problem would then become a catastrophic failure, since all simulations of major galaxy formation require them to have hundreds of luminous satellites that have individual in-fall histories.
12 Conclusions on Testing Hypothesis A
While there is a strong notion and peer-pressure 12 that Hypothesis 0i must be valid on galactic and cosmological scales, it is quite remarkable that all tests (Sections 8, 9, 10 and 11.1–11.6) fail Hypothesis A consistently and without exception.
It could well have been different: We could have had the situation that one of the tests fails, but that others show consistency of the models with the data. For example, the dSph satellites could have had κ > 0, about the correct mass distribution and morphological appearance. In this case the challenge would have to have been to understand the remaining failure given the otherwise agreement. However, the consistent failure, always in the same sense that the observational data are in conflict with Hypothesis A, i.e. the existence of dwarf-galaxy-hosting DM haloes, is so grave that a remedy cannot be found within the SMoC.
In summary:
-
Young gas-rich rotationally supported TDGs lie on the BTF relation defined by DM-dominated dwarf and normal galaxies. This cannot be the case if DM defines the rotation velocities of the dIrr galaxies. Thus BTFdIrr = BTFTDG which implies
 .
. -
Intermediate-age TDGs lie on the radius–mass relation of dE and dSph galaxies. This cannot be the case if dE and dSph galaxies formed in a mass-dominating DM halo. Thus dE, dSph = TDG (or RPDG) which implies
 .
. -
The dSph satellites of the MW (and to a certain degree also of Andromeda) have a highly significant phase-space correlation which, for the MW, is a vast polar structure. This VPOS is inconsistent with the satellites being accreted individually or with them being endemic DM sub-haloes.
-
The dSph satellites of the MW and Andromeda have constant DM sub-halo masses over many orders of magnitude of luminosity in violation of the necessary correlation between the two quantities if the satellites were in their own DM sub-haloes.
-
The DM-mass function of the observed MW satellite galaxies does not agree with the theoretical one of luminous sub-haloes derived from the SMoC. The suggestion that star formation in DM haloes less massive than 1010 M⊙ becomes stochastic has no physical basis.
-
Too many dSph satellites show morphological distortions which ought not to be the case if they were embedded in their own mass-dominating DM sub-haloes.
-
Within the same framework of the SMoC the gas-free dSph satellites loose their gas if they were accreted at a redshift z > 3 while they may appear in a disk-like VPOS distribution if they accreted at z < 1. The MW satellites are both, gas poor and in a disk-like VPOS.
-
Finally, the emergence in the SMoC of a group of galaxies with the generic properties of the Local Group (two similar spirals, each with at least 11 luminous satellites) is negligibly small.
Therefore, Hypothesis A needs to be discarded. That is, dwarf galaxies cannot be of type A and therefore they cannot be embedded in DM sub-haloes. By Section 4, the allowed alternative is then for dwarf satellite galaxies to be TDGs, as is indeed already suggested by points 1. and 2. above.
13 Hypothesis B: The dE Galaxies and dSph Satellites are Ancient TDGs and RPDs
In the above Section 10.1 it has been shown that the MW is surrounded by a VPOS which is a physical structural part of the MW made up of all known satellite galaxies, the young halo globular clusters and half of all known stellar and gaseous streams. The existence of this structure is perfectly consistent with the falsification of the Dual Dwarf Galaxy Theorem in Sections 8–11. As suggested in Section 4, the only available alternative would be for the VPOS to be a remnant tidal structure that formed when the young MW had encountered another galaxy about 10–11 Gyr ago.
How does the theoretical and observational evidence on dE galaxies in general, and dSph satellites in particular stand up to this interpretation? Are there other extragalactic satellite galaxy systems which also show phase-space correlations? If the MW were unique and thus an exception confidence in the interpretation of dE galaxies and of dSph and UFD satellite galaxies as TDGs would be compromised.
13.1 Formation of TDGs and Associated GCs
It is well known that star clusters and TDGs form in one and the same galaxy–galaxy encounter. This is observed in many cases, but TDGs with masses lower than about 107 M⊙ can usually not be detected. 13 An example of a young TDG with a mass near 106 M⊙ is the complex of star clusters in the tidal arm of the Tadpole galaxy which has a half-light radius near 160 pc (Tran et al. 2003), while other cluster complexes in the arm are of lower mass still. Such objects may evolve through the merging of the clusters to spheroidal dwarf galaxies (Kroupa 1998) such that the progenitors of the faint MW satellites may have looked similar to these Tadpole objects.
The highest-ever-resolution particle-mesh computation by Bournaud et al. (2008) of a wet galaxy–galaxy encounter has a gas fraction of 17% and a resolution (or cell-length) which is cl = 32 pc within Galactocentric distances of D = 25 kpc, cl = 64 pc within D = 50 kpc and cl = 128 pc for D > 50 kpc. This pioneering work demonstrates that star-cluster sized bound objects with masses in the range 105–106 M⊙ form readily. Also, a few TDGs with masses 108–109 M⊙ are formed. These are rotating dIrr gas-rich galaxies with diameters of a few kpc (Figure 4).
It is important to note that less-massive TDGs cannot form in these simulations because the resolution is still too poor at D > 50 kpc, while the tidal stresses at smaller D only allow compact star clusters to emerge in the simulations. These have resolution-given radii of tens of pc and form due to the pressured colliding inter stellar media of the two galaxies. At D > 50 kpc gas accretes from the expanding tidal arms into gravitationally unstable regions forming rotation-supported gas-rich dwarf-galaxies.
The phase-space density of matter in the tidal arm is comparable to that of the pre-collision galactic disk from where it stems because the flow in phase-space is incompressible for two-body relaxation-free, i.e. collision-less, stellar-dynamical systems. Therefore, regions which become self-gravitating within the tidal arm due to density variations along it should have, approximately, the matter density of galactic disks. Within these gravitationally decoupled dIrr galaxies star-formation proceeds as in any other dwarf galaxy in a distribution of star-formation events which can, for all practical purposes, be described as embedded star clusters (Lada & Lada 2003) with a maximum mass which correlates with the star-formation rate of the TDG (Weidner, Kroupa & Larsen 2004; Kroupa 2011).
The average density of young TDGs must therefore be comparable to roughly 0.01–1 M⊙ pc–3, which is the baryonic matter density in disk galaxies. It is noteworthy that the dE and dSph satellite galaxies have such densities: Returning to the observable properties of dwarf galaxies, a constant density relation, ρ ∝ M star/R 0.5 3, implies b 1 = 1/3. As is evident from Figure 1, dE galaxies with M star ≈ 109 M⊙ have densities around 1 M⊙ pc–3, while less-massive dE and the dSph satellites have densities of 0.01 M⊙ pc–3. This is similar to the typical density of baryonic matter within a disk galaxy. For example, the present-day density of baryonic matter nearby to the Sun is about 1 M⊙ pc–3, with an exponential decrease to larger Galactocentric distances. Star-formation activity is observed to be taking place at Galactocentric distances out to about 25 kpc. For a radial exponential disk scale-length of 3.5 kpc (e.g. Sale et al. 2010) the average density at 25 kpc becomes 0.01 M⊙ pc–3.
A lower density cutoff for TDGs is given by the necessity for self-gravitation to be sufficiently strong to overcome tidal shear. That is,
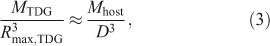
is required, where M TDG and R max,TDG are the mass and maximal radius of the TDG, while M host is the mass of the host galaxy and D the distance of the TDG to the host. For typical birth distances of D = 105 pc and M host ≈ 1010 M⊙ it follows that
Such objects are not likely to form since regions of the extend implied are not likely to be filled with matter, the tidal tails usually being more confined. But if they would form, then they would not readily be found by observation because they have low projected densities. For example, a TDG with a mass of 109 M⊙ would have R max,TDG ≈ 46 kpc. Such an object would not likely survive its first perigalactic passage, but sub-regions of sufficient self-binding energy may. It is remarkable though that a low-density stellar population of such a dimension has recently been discovered nearby the host galaxy NGC 7531 with a high-sensitivity survey using small telescopes (panel E in figure 1 of Martínez-Delgado et al. 2010). The stellar structure nearby the dwarf galaxy NGC 4449 may also be of this category (figure 1 in Martinez-Delgado et al. 2012).
Taking the Newtonian tidal radius estimate from Binney & Tremaine (1987),

it can be seen from Figure 4 that the upper envelope of dE data corresponds to M host ≈ 1012 M⊙ which is consistent with the majority of dE galaxies having been formed in galaxy clusters, taking the red-shift evolution of their mass into account.
13.2 The Physical Nature of the MW VPOS
The VPOS is composed of satellite galaxies, globular clusters and stellar and gaseous streams (Section 10.1). Can the VPOS be an ancient remnant of a major tidal arm created about 10–11 Gyr ago around the MW?
The pioneering work of Bournaud et al. (2008) demonstrates the simultaneous formation of star clusters and TDGs during galaxy-galaxy encounters while it cannot yet reach the resolution relevant to the MW dSph satellite galaxies. The number of satellite galaxies formed also scales with the gas fraction, and it is expected to have been higher about 10 Gyr ago when the gas fractions where higher (Wetzstein et al. 2007).
Streams then arise from these DM-free TDGs and star clusters as they dissolve over time through energy-equipartition driven evaporation of stars in the collisional systems (i.e. the star clusters) that have median two-body relaxation times shorter than a Hubble time and/or through time-variable tidal fields (Kroupa 1997; Küpper et al. 2010).
The gaseous streams in the VPOS may be either ancient remnants from the original tidal material from the encounter or gas that has been ram-pressure stripped or otherwise from the satellite galaxies. Indeed, the Magellanic Stream, being well aligned with the VPOS, is such a young structure.
That the UFD satellites have a larger spread away from the DoS than the classical satellites (Section 10.1.7) would be consistent with UFDs having formed in lower-density tidal material which was spatially more extended than the denser material. Theoretical results on this suggestion do not exist yet.
Can a structure such as the VPOS be obtained naturally in galaxy–galaxy encounters? A large number of galaxy–galaxy encounters have been calculated by Pawlowski et al. (2011) to study the phase-space distribution of tidal material expelled during the encounter or merger. This work has demonstrated that the VPOS can be naturally understood as the remnant of tidal material expelled during a flyby-encounter of the young scaled-down MW and another similar young galaxy about 10 Gyr ago. An encounter with a smaller young galaxy is also possible. Interesting in this context is that about 10 Gyr ago the scaled-down young MW would have appeared similar to M33 today. A bulge forms in such a major encounter and a disk can regrow (e.g. Hammer et al. 2005; Bournaud, Jog & Combes 2005; Hammer et al. 2007, 2009, Wei et al. 2010, Bournaud et al. 2011; Martig et al. 2012).
Thus, as argued below, consistency with the observed properties of the MW is achieved, since the Galactic thin disk is younger than about 10 Gyr while a significant fraction of the bulge is old, as are the constituents of the VPOS (e.g. Tsujimoto & Bekki 2012 for constraints on the formation of the MW bulge).
In some of the galaxy–galaxy encounters by Pawlowski et al. (2011) the tidal material populates phase-space next-to identically to the currently available information on the MW VPOS. Documented for the first time by Pawlowski et al. (2011) is the natural emergence of counter-rotating tidal material in excellent agreement with the counter-orbiting Sculptor dSph satellite. These models show how the ratio of pro- and counter-rotating tidal debris about the MW significantly constrains the allowed encounter.
The phase-space constraints provided by the VPOS allow a re-construction of the events that played a role in forming the young MW. The encounter had to have been near-polar relative to the young MW and the incoming galaxy must have been close to edge-on. Figure 8 shows a sequence of images of such interacting pairs in the present universe. In Figure 8 is also shown a time-sequence of a model fly-by encounter involving the young MW and a young galaxy of similar mass as the young MW. The material pulled out from the incoming galaxy spreads about the MW in a model VPOS similar to the real VPOS (Figure 6). The distribution of orbital poles of tidal debris on the Galactic sky that this model produces is shown in Figure 9.

|

|
Striking is that the directions of orbital angular momenta of the tidal debris in the model populate the same diagonal region (from the upper left to below centre in Figure 9) on the Galactic sky as the actual real VPOS does. The existence of counter-rotating tidal debris is also evident, coinciding well with the orbital-angular-momentum direction of Sculptor. The model shown has not been created to match the data particularly well, and other models computed by Pawlowski et al. (2011, 2012b) also match, demonstrating that the generic properties of the VPOS can be readily accounted for by a wide class of encounter models. Its detailed properties can however allow a reconstruction of the events that shaped the MW about 10 Gyr ago.
13.3 VPOS, Mergers, Bulges and Disk Regrowth
If the young MW would have had a major encounter that lead to the present-day VPOS, would such an encounter not have destroyed the MW disk? Would it leave visible morphological evidence? This is an important question, and it turns out that the MW bulge may hold clues.
Within the Local Group there exists a near-to-perfectly linear correlation between bulge mass and the number of satellite galaxies (Figure 10): M33 has no bulge and no known satellite galaxies, while Andromeda has a more massive bulge and more satellites than the MW and is in general more complex with a probably more recent merger event than the MW (Hammer et al. 2010).
|
Evidently, the validity of such a correlation needs to be tested with galaxies beyond the Local Group. On the basis of extragalactic observational data, Karachentsev, Karachentseva & Sharina (2005) note, but do not quantify, the existence of a correlation between the bulge luminosity and the number of associated satellite galaxies such that galaxies without a bulge have no known dSph companions, such as M101. Karachentsev et al. (2005) also point out that the number of known dSph satellites increases with the tidal environment. In effect, Figure 10 shows a correlation between the colour or bulge-to-disk ratio of the host galaxy and the number of its satellites. That redder host galaxies do have more satellite galaxies than bluer hosts has indeed been discovered using the SDSS of isolated bright host galaxies (Wang & White 2012).
A correlation as evident in Figure 10 ought to arise naturally if the majority of satellite galaxies are ancient TDGs, because bulges form in major galaxy–galaxy encounters (Hammer et al. 2005): Due to time-variable changes in the potentials of each galaxy its gaseous component is channeled onto radial orbits where it dissipates and forms stars rapidly forming a central spheroidal component on a dynamical time-scale (a few 108 yr). When the encounter or merger is over, the bulges may regrow disks from accreting gas (Hammer et al. 2005, 2007, 2009; Bournaud et al. 2011). The combination of chemical and age constraints available on the growth of the MW bulge (e.g. Tsujimoto & Bekki 2012) with corresponding constraints available for the thick disk and the VPOS constituents should allow a detailed re-construction of the early encounter event which would have occurred after the MW old halo spheroid formed (Marks & Kroupa 2010).
It is known that present-day disk galaxies are sustaining their SFRs through on-going gas accretion. That disk galaxies regrow their disks after significant encounters which may produce thickened older disk components has been demonstrated in models (e.g. Bournaud et al. 2005, 2011, see also Reshetnikov & Combes 1997).
The existence of the VPOS with counter-rotating constituents, and the MW having a bulge and a thickened disk are thus understandable as structures created in an early encounter between the young MW and another galaxy.
13.4 Recreating the Event
It will be interesting to investigate if this entire MW structure of VPOS, bulge and thick disk can be created using one self-consistent simulation. This work is likely to re-construct quite precisely the events that occurred about 10 Gyr ago (compare with Hammer et al. 2007), and it may also identify which the other galaxy involved may have been. Indeed, currently there are two galaxies that may have been involved: the LMC is on about the right orbit already (Pawlowski et al. 2011). And alternatively, Andromeda is also close to the DoS in projection (figure 1 in Metz et al. 2007) and is currently approaching the MW again. If Andromeda was the early fly-by candidate, then the LMC may be a massive TDG (compare with a similar suggestion by Yang & Hammer 2010).
Galaxy interactions, bulge formation and the associated emergence of TDGs would have been most common in the early universe when the young galaxies were spaced closer to each other and when they were presumably more gas rich than today. This is consistent with the bulges and satellite galaxies being typically old.
It is thus proven that VPOSs emerge naturally from galaxy–galaxy encounters, and that they allow a reconstruction of the encounter. It needs to be studied how unique such a reconstruction is. That is, which range of initial conditions (galaxy mass ratios, relative inclinations and orbital angular momenta) are allowed given the properties and constituents of the real VPOS.
13.5 Was the Young MW a Polar-Ring Galaxy?
According to the evidence uncovered in the course of this work (Pawlowski et al. 2012b), the MW has a VPOS which is naturally explained as the remnant of an ancient encounter that must have occurred about 10–11 Gyr ago between the young MW and another perhaps similar gas-rich galaxy. The correlation between bulges and the number of satellites evident in the Local Group is consistent with bulges being produced during galaxy encounters. That galaxy encounters readily produce polar rings has been demonstrated by Bournaud & Combes (2003). While the likelihood of creating polar ring galaxies from mergers is small, according to Bournaud & Combes (2003) fly-by encounters readily produce polar rings through the accretion of gas from the passing donor to the host galaxy (Figure 8). The fly-by event would have pulled a tidal arm out of the passing galaxy which fell onto the young MW thereby forming the polar ring. At the same time, star-formation throughout the tidal arm would have produced the young halo globular clusters (YHGCs), and the TDG precursors of the present-day ancient dSph and UDF galaxies out to distances of 100s of kpc. As the tidal arm swept across, MW satellites and possibly YHGCs on counter-rotating orbits would have been generated (Section 13.1). The tidal perturbation would have lead to bar formation in the young MW which would have formed a bulge-component as well as a thickened disk. Other observational evidence for the MW possibly being a polar ring galaxy was presented by Haud (1988).
13.6 Other Extragalactic Satellite–Stream Alignments
If the MW VPOS is the remnant of an ancient tidal structure that was created in a galaxy–galaxy encounter about 10–11 Gyr ago, is there evidence for other galaxies also having alignments in their satellite systems? If the MW were unique, confidence in this scenario would be eroded.
In the local universe there are a number of known host galaxies with stream–TDG satellite alignments: (1) The NGC 1097 ‘dog leg’ stellar stream with two typical dSph satellite galaxies (Galianni et al. 2010). (2) The about 300 kpc long tidal stream with at least three dSph satellite galaxies in the 1–2 Gyr old post-interaction NGC 5557 (Duc et al. 2011).
Furthermore, NGC 5291 (Bournaud et al. 2007) is surrounded by a vast gaseous tidal ring with many embedded young and gas-rich TDGs, altogether amounting to a vast phase-space correlated structure containing gaseous streams and young dIrr galaxies.
Notwithstanding these examples, the Tadpole galaxy is an ongoing merger with a tidal tail with many star clusters within it. Many of the clusters are clustered in young (4–5 Myr old) cluster complexes (CCs). The most prominent one of mass 1.3 × 106 M⊙ and half-light radius of 160 pc (Tran et al. 2003) may evolve into a low-mass UCD (Brüns et al. 2011), or even a typical dSph satellite if the gas and clusters surrounding the CC were to be taken into account as a larger structure.
Finally, the Dentist Chair is an example of an interacting galaxy with tidal tails which contain many TDG candidates in a highly phase-space correlated overall structure (Weilbacher et al. 2002).
The above examples are extragalactic systems in the local universe which are surrounded by prominent young to intermediate-age correlated phase-space structures which include gaseous streams, star clusters and TDGs. Such vast structures evolve over many orbital times but remain evident for longer than a Hubble time in phase space due to the conservation of orbital angular momentum and energy.
Thus, phase-space correlated assemblages of stellar and gaseous streams, young TDGs as well as old dSph satellite galaxies exist in the Local Universe. These are probably not rare, given that such systems are hard to find because of their low surface densities and the faintness of the satellite galaxies. Due to the observational flux limits, an observational bias towards discovering fairly massive (>108 M⊙) satellite galaxies exists implying that fainter structures are likely to be even more common. An important task will be to survey as many nearby galaxies as possible for the faintest streams and possibly associated faint satellite galaxies to quantify the frequency of occurrence of such correlated systems.
That the MW has a VPOS, while Andromeda also shows an anisotropic satellite distribution with strong evidence for a chain-like arrangement of a substantial number of its satellites (Karachentsev 1996; Koch & Grebel 2006; Metz et al. 2007, notably figure 1 in Tollerud et al. 2012) already suggest that phase-space correlated satellite populations may be quite common around disk galaxies with bulges. This is consistent with dSph satellite galaxies being mostly old TDGs (Casas et al. 2012).
13.7 On the Origin of dE Galaxies
In Section 9 the coincidence of dE galaxies with observed and model TDGs in the radius–baryonic-mass diagramme has already emerged, suggesting that the majority if not all dwarf satellite galaxies may be TDGs, whereby RPDGs may also play a role in the dwarf population of galaxy clusters. This is consistent with some of the observed extragalactic dSph satellites being in phase-space correlated structures (Section 13.6).
Okazaki & Taniguchi (2000) have demonstrated with conservative assumptions that the number of long-lived TDGs produced over cosmological times due to galaxy–galaxy encounters within the SMoC amounts to the number of observed dE galaxies. They have also demonstrated that the morphology–density relation is reproduced: poor groups of galaxies end up having fewer dwarf galaxy members than rich groups and clusters of galaxies.
Also, the stellar mass-to-light ratios of dE galaxies are fully consistent with them not having DM (e.g. Lisker 2009 and references therein), which is expected for this class of object since TDGs cannot capture significant amounts of DM even if it were to exist (Section 3.2). Concerning the putative DM content of dE galaxies, the clash with the SMoC is so significant that some authors speculate baryonic processes to be responsible for pushing out the DM to radii where it is dynamically unimportant (Forbes et al. 2011, see also Footnote 12). However, none of the realistic galaxy evolution or formation simulations has ever resulted in the DM being pushed out to the degree required.
The majority of TDGs would have been produced in the young universe and are thus metal poor. The presently born TDGs are a minority since galaxy–galaxy encounters are today rarer and the galaxies are not as gas rich as in the cosmological past. Therefore the metallicity criterion for distinguishing TDGs from normal dwarf galaxies cannot be applied as a robust test for TDG status. TDGs, once they decouple, begin their own chemo-dynamical evolution and thus follow the mass–metallicity relation (Recchi et al. 2007). That even low-mass TDGs survive for a Hubble time despite being on eccentric orbits about their host galaxy has been shown by Kroupa (1997) and Casas et al. (2012).
From the above it would thus appear that the existing data and theoretical work are consistent with dE galaxies being old TDGs.
14 A Dialogue: The Discovery of Ultra-Thin Dark-Matter Filaments and Dark Force
The SMoC is highly regarded and for many as established as the SMoPP (Section 1). Given that is seems unlikely for the vast majority of contemporary astronomers to be interpreting the data so wrongly, it may therefore be that we are here missing some essential aspect of the SMoC. Perhaps the SMoC is valid after all, and there are unknown baryonic processes which would account for, among the other issues, (i) TDGs lying on the DM-defined BTF relation, (ii) TDGs coinciding with dE galaxies in the radius–baryonic-mass diagramme, (iii) dE galaxies not having evidence for DM, (iv) the existence of the VPOS around the MW, (v) correlated phase-space structures composed of satellite galaxies about other host galaxies, and (vi) the existence of a host-galaxy-bulge-mass—number-of-satellite correlation. Here is a dialogue which is based on true conversations that occurred in November 2011 in Bonn and January 2012 in Vienna:
-
SMoC Enthusiast 1: ‘OK, I can agree that the MW satellite dwarf galaxies are TDGs.’
-
Dynamicist: ‘But then there are no DM-dominated satellite galaxies in DM haloes, and this would invalidate the SMoC since it requires each larger galaxy to be accompanied by hundreds of DM satellites.’
-
SMoC Enthusiast 1: ‘No, this does not invalidate the SMoC because I can just turn up re-ionisation and other effects such that all satellite dark matter sub-haloes with mass about
 1010 M⊙ remain dark.’
1010 M⊙ remain dark.’ -
Dynamicist: ‘But would you not be going into extremes of fine tuning? And, no existing galaxy-formation and evolution simulation has ever shown that re-ionisation can be made so destructive that all DM sub-haloes with about <1010 M⊙ remain dark. Also, what about the more isolated dwarf-galaxy groups (Tully et al. 2006)?’
-
SMoC Enthusiast 2: ‘Well, we have the freedom to recompute the models and the lack of such satellites constrains the physical processes that played an important role during early galaxy assembly. We can in actuality constrain the relevant sub-grids physics in order to match the observations.’
-
Dynamicist: ‘But here is the final nail into the coffin: You agree that the satellite galaxies are TDGs. But TDGs cannot have DM, as has been emphasised many times. Now, the satellites of the MW have large dynamical M/L ratia (>10 up to a few hundred in some cases). So this clearly disproves the SMoC because in it TDGs cannot contain DM. The solution is to move away from DM on galaxy scales and to accept that gravity in non-Newtonian. Then we can understand the satellites as being TDGs. And they appear to be dominated by DM if we interpret the motions of their stars in Newtonian dynamics, but in actuality what we are seeing is non-Newtonian dynamics. That Milgromian dynamics plus tidal effects is a good solution to the satellites has already been shown by Brada & Milgrom (2000); Angus (2008); Kroupa et al. (2010) and McGaugh & Wolf (2010), so this appears to be the right research path to be taken.’
-
SMoC Enthusiast 1: ‘No, I still disagree. The high dynamical mass-luminosity ratios suggest that TDGs, once formed, connect to thin dark-matter filaments from which they accrete kinematically cold DM.’
-
Dynamicist: ‘Now I have you cornered: There are at least two problems with your postulated thin DM filaments: (1) 100 Myr old TDGs show convincing evidence for having DM (Bournaud et al. 2007; Gentile et al. 2007). At this age, there is not enough time for them to connect to the postulated thin DM filaments which must originate from outside the virial radius of the host DM halo (if it were to exist).’
-
SMoC Enthusiast 2: ‘Yes but these young TDGs you are talking about are different, they are coming from only one galaxy progenitor, and this galaxy happens to probably have a lot of cold molecular gas which makes up the missing mass in these young TDGs. The dynamical M/L ratia are much smaller than those of some of the old satellites of the Milky Way you are referring to. So actually two different dominant types of DM (exotic and gas) would be involved in these two age groups. Nothing is wrong with that.’
-
Dynamicist: ‘But what about problem (2): the fact that these young TDGs fall onto the baryonic Tully–Fisher relation (Gentile et al. 2007)? This clearly cannot be the case if they are a fundamentally different type of galaxies than the normal DM-dominated ones.’
-
SMoC Enthusiast 3: ‘Look, it is generally known that the SMoC cannot be tested on the small scales of dwarf galaxies because the baryonic physics is uncertain and the simulated models lack the resolution.’
-
Dynamicist: ‘I would not agree with this. After all, the DM structures that form at a mass scale of
 108 M⊙ due to the dissipationless gravitating DM particles are rather well understood. See e.g. the work of Diemand et al. (2008). Are you then implying that the large body of research output from the SMoC community over the past 5 to 10 years claiming to solve the missing satellite problem is essentially unbelievable? It seems that this statement would suggest that these many published results
14
cannot be resorted to in order to test the SMoC? If this were the case, then the whole model becomes untestable.’
108 M⊙ due to the dissipationless gravitating DM particles are rather well understood. See e.g. the work of Diemand et al. (2008). Are you then implying that the large body of research output from the SMoC community over the past 5 to 10 years claiming to solve the missing satellite problem is essentially unbelievable? It seems that this statement would suggest that these many published results
14
cannot be resorted to in order to test the SMoC? If this were the case, then the whole model becomes untestable.’ -
SMoC Enthusiast 3: ‘You are resting your tests on the MW, but this is not permissible. One cannot test the whole SMoC just on one single galaxy. We are within the MW and the data are poor. The surveys suffer from serious obscuration and there are whole regions of the sky where we cannot even look at properly, like in the disk of the MW. You need to use other galaxies.’
-
Dynamicist: ‘We are testing also Andromeda, but it is true that as we are acquiring ever better data on the MW we are finding that the discrepancies with the SMoC expectations are increasing. The surveys are sufficiently complete to allow robust tests. For example, the SDSS is a cone such that the disk-like distribution of ultra-faint satellites cannot be due to selective surveying. The surveys for the brighter satellites and the young halo globular clusters have a quite complete sky coverage. The tests do not rely on a single property of the MW but on generic features that together signal a failure. Obviously the MW must be part of the SMoC, as it is within this universe.’
-
SMoC Enthusiast 4: ‘Listening to this conversation I think you are wrong: the MW satellites are not TDGs. Instead, the SMoC is mostly valid but needs to be slightly modified. Similarly to the argument by Peebles & Nusser (2010), who also emphasise the SMoC to be an overall successful description of cosmology, I would argue that the problems of the SMoC on galactic scales shows that DM particles must couple to the baryons or to each other differently than only through gravitation.
-
‘There may well be a dark force (e.g. Nusser, Gubser & Peebles 2005) which allows DM particles and baryons to couple in such a way as to enhance structure formation, as demanded by Peebles & Nusser (2010), and at the same time to reduce the missing satellite problem and enforce the satellites forming a DoS. We could postulate that this dark force becomes active when the thermal temperature of the baryons has decayed sufficiently, so that structure formation in the early universe is not affected. The dark force may have a number of components that couple differently to the different constituents, and all of these may be time variable (e.g. van den Aarssen, Bringmann & Pfrommer 2012). So I see absolutely no reason to discard the SMoC in favour of a purely speculative and ad-hock modification of Newtonian dynamics in the ultra-weak field limit, such as what Milgromian dynamics, i.e. MOND, is.’
15 Conclusion on Testing Hypothesis A and B
Hypothesis A (the MW satellite galaxies are DM sub-structures) has been ruled out, while Hypothesis B (the satellites are ancient TDGs) stands up to all available constraints and tests. According to the First and Second SMoC Falsification Theorems (Section 5) the SMoC must be discarded and C/WDM cannot exist.
15.1 Why Is the Existence of Cold or Warm DM Ruled Out?
By having shown that only one type of dwarf galaxy exists, and that this type has all the required properties associated with the known type B dwarfs, the Dual Dwarf Galaxy Theorem has been falsified, and C/WDM particles cannot exist leading to the SMoC being falsified. But why does the falsification of the ‘Dual Theorem’ imply that C/WDM particles cannot exist?
The reason is as follows: With the falsification of the Dual Theorem the existence of C/WDM is immediately ruled out because by the satellite galaxies being TDGs (i.e. type B dwarfs) none of the C/WDM sub-haloes would have been able to have formed stars in stark contradiction to the calculations. Amending the physics of the C/WDM particles to allow this to have occurred would already be a non-SMoC model. However, such an approach would also be violated because the dSph satellite galaxies are observed to show large dynamical M/L ratia, i.e. they appear to be dominated by DM. Thus, if, by virtue of their phase-space correlation they are TDGs, then the only logically allowed solution is to discard the SMoC entirely and to consider modified gravity models. This conclusion is fully consistent with the known young rotating TDGs lying on the BTF relation (see Section 17.4), and by the existence of the MDA correlation (Figure 11), both of which cannot be understood as a result of the physics of DM particles.
|
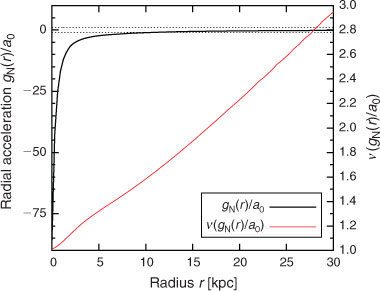
|
Finally, the extensive effort world-wide to detect DM particles in terrestrial experiments has so far not been successful (e.g. Baudis 2012). For example, the CRESST-II DM search has reported a possible detection of a CDM particle signal (Angloher et al. 2012), but their figure 13 also shows this putative signal to be in the parameter region excluded by the CDMS-II (CDMS II Collaboration et al. 2010) and XENON100 (Aprile et al. 2011) DM-particle experiments. The search for a DM-particle-annihilation or DM-particle-decay signature from regions where high DM densities are measured assuming Newtonian dynamics to be valid has also been unsuccessful (e.g. the MW satellite galaxy Segue 1 has the highest DM density known but no DM signal has been detected, Aliu et al. 2012).
|
Increasing loss of confidence is suffered by the experiments having to postulate ever decreasing interaction cross sections for the putative DM particles, significantly below and away from the originally favoured ones. This is at the same time a fallacy of the adopted procedure: The existence of DM particles can never be disproven by direct experiment because ever lighter particles and/or ever smaller interaction cross sections just below the current detection threshold may be postulated for every non-detection. There exists no falsifiable prediction concerning the DM particles.
15.2 Can a Modified SMoC be Constructed?
That the SMoC needs to be discarded as a model of the real universe is true even if cold DM filaments or dark forces (Section 14) were to exist because structure formation simulations would have to be repeated with these ingredients. That is, the currently available cosmological models would need to be revised substantially. But the revisions would be many, since many new degrees of freedom appear with the notion of a multi-component dark force (Section 14). Predictability of this model would not be given any longer, since any new discordant observation would be accounted for, at least in principle, by new parameters in the dark sector.
A simpler and more elegant option may be obtained by considering non-Newtonian alternatives and therewith the foundations of the SMoC.
16 The SMoC is Falsified, Long Live . . . ?
As detailed in Section 1 the foundation of the SMoC is Hypothesis 0i. Since Albert Einstein constrained his ansatz on gravitation by solar system (i.e. Newtonian) dynamics, it is useful to reconsider this assumption.
16.1 The MDA Correlation and Solar System Constraints
The need to introduce dynamically relevant DM on galactic scales arose because the assumption that Einstein’s field equation (Einstein 1916) be valid on galactic and cosmological scales led to a failure of it as soon as kinematical measurements in galaxies and of galaxies in galaxy clusters became available long after 1916 if it is assumed that only baryonic matter exists (Zwicky 1937; Rubin & Ford 1970; Faber & Gallagher 1979; Blumenthal et al. 1984). But the speculation that exotic DM particles exist that are to be dynamically relevant in galaxies cannot be understood within the SMoPP, have not been discovered by direct experiment despite a highly significant effort world-wide over the past decades to detect them, and lead to the contradictions with astronomical observations that constitute the falsification of the SMoC above. With the failure of the SMoC it has now become evident that Einstein’s ansatz may need additions in the dark-physics sector (Section 14).
The discrepancy between Newtonian dynamics and the dynamics observed in galaxies is concisely documented as the mass-discrepancy introduced by McGaugh (2004). The mass-discrepancy (MD) in a disk galaxy is the ratio between the observed circular velocity squared, V 2(= V c 2), and the circular velocity squared, V b 2, expected from the observed amount of baryonic matter assuming Newtonian dynamics is applicable. The observational data are plotted in Figure 11.
The observed mass-discrepancy data follow a well defined correlation with acceleration. This is the McGaugh mass-discrepancy–acceleration (MDA) correlation. The MDA data show that the discrepancy and thus evidence for DM only appears when the observed (true) acceleration, a, is smaller than a critical acceleration a 0,
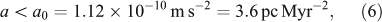
which cannot be accounted for by the SMoC because the physics of DM particles does not depend on a . The critical acceleration a 0 constitutes a constant of nature. It is constrained by e.g. only one single rotation curve of one galaxy. McGaugh & de Blok (1998) had already pointed out that understanding the MDA correlation within the SMoC ‘leads to troublesome fine-tuning problems’.
Figure 11 demonstrates the excellent agreement between the prediction 15 of Milgromian dynamics and the data. According to Milgrom’s suggestion, the gravitational force acting on a mass m which experiences the acceleration a is
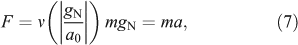
where g N is the Newtonian acceleration and the function which describes the transition from classical Einsteinian/Newtonian dynamics to Milgromian dynamics can be written (Famaey & McGaugh 2012)
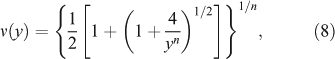
where y = g N/a 0 and ν(y) → 1 for y ≫ 1 and ν(y) → y –1/2 for y ≪ 1. When n = 1 we have the ‘simple ν function’.
For a circular Newtonian orbit the velocity squared is V b 2(r) = g N r. With V c 2 = a r being the actual observed circular velocity and a = ν(y)g N, the MD becomes

Concerning the MW, it is useful to graph the Milgromian radial acceleration as a function of r (Figure 12). The MW model has a baryonic Plummer bulge of mass M
bulge = 3.4 × 1010 M⊙ and Plummer radius r
pl = 0.7 kpc, and a Miyamoto–Nagai disc with baryonic mass M
disk = 1011 M⊙, radius r
0 = 6.5 kpc and scale height of 0.26 kpc. Figure 12 shows that Milgromian dynamics is expected to become evident at r ![]() 8 kpc where ν
8 kpc where ν ![]() 1.4.
1.4.
What is Milgromian dynamics (i.e. MOND = Modified Newtonian Dynamics)? The existence of transition functions is well know in physics, notable examples being the transitions from quantum mechanics to classical mechanics and from relativistic to classical speeds. The Milgromian ν function can be interpreted to be such a transition function. Milgrom (1999) showed that ν may be derived by considering quantum mechanical effects in space-time for very small a. This allows Milgromian dynamics to be seen as a modification of inertial mass m, as is also evident from Equation 7 through the terms {ν(y)m} g N = m a (see also Appendix A in Kroupa et al. 2010 for a description of this ansatz). Alternatively, Einstein’s assumption may have been invalid, and gravitation does not follow the field equation in the ultra-weak field limit. In both cases, effective gravity would be non-Newtonian and is described by Mordehai Milgrom’s formulation (Milgrom 1983a).
Thus, the MDA correlation constitutes a consistency with the general failure of the SMoC discovered above (see also Section 17). Indeed, the postulate by Milgrom (1983a) that below the acceleration scale a 0 ≈ 3.6 pc Myr–2 dynamics becomes non-Newtonian is fully verified by the latest high-quality kinematical data in galaxies, as demonstrated in Figure 11 and in much depth in Famaey & McGaugh (2012).
16.2 Non-Einsteinian Effective Gravity
That effective gravitation may be non-Einsteinian/non-Newtonian thus appears to be the simpler if not the sole option (Section 15.2): by relaxing Einstein’s assumption that gravity should conform to Newtonian dynamics in the ultra-weak field limit and thus allowing new effective field equations to be suggested, it becomes possible to keep particle physics entirely within the SMoPP (Section 1). This is a highly attractive option because the SMoPP is the most successful physical theory at hand, and because gravitation remains poorly understood as we still do not know how matter couples to space-time and which of the two is an emergent property.
An example of new interpretations of gravity is given by the recent suggestion that ‘Newton’s law of gravitation naturally arises in a theory in which space emerges through a holographic scenario’ (Verlinde 2011). And, a scalar tensor vector gravity theory (leading to modified gravity, or MOG) is suggested by Moffat (2006) according to which, effectively, far from a source gravity is stronger than the Newtonian prediction, while at shorter distances it is compensated by a vector-field-generated repulsive fifth force. This can also be viewed as a Yukawa-type modification of the gravitational force due to a point source. And, it is well known that a successful theory of quantum gravity has not been discovered yet (Abdo et al. 2009).
Whatever the true solution to gravitation may be, Milgrom’s suggestion of how to modify the effective gravitational force law at ultra-low accelerations a ![]() 3.6 pc Myr–2 (Section 16.1) has stood the test of time. That Milgrom’s dynamics can be embedded in a generalised relativistic tensor vector scalar (TeVeS) gravity theory (not to be confused with the above ‘scalar tensor vector gravity theory’) has been proven by Bekenstein (2004). TeVeS is derived from the action principle and therewith respects conservation laws. The impact of this break-through is evident in the increase in citations to the original research paper (Milgrom 1983a), which has by now accumulated about 1000 citations. Furthermore, Modesto & Randono (2010) have studied the approach of Verlinde (2011) and suggest that Milgromian-like dynamics ensue once well-motivated corrections are applied.
3.6 pc Myr–2 (Section 16.1) has stood the test of time. That Milgrom’s dynamics can be embedded in a generalised relativistic tensor vector scalar (TeVeS) gravity theory (not to be confused with the above ‘scalar tensor vector gravity theory’) has been proven by Bekenstein (2004). TeVeS is derived from the action principle and therewith respects conservation laws. The impact of this break-through is evident in the increase in citations to the original research paper (Milgrom 1983a), which has by now accumulated about 1000 citations. Furthermore, Modesto & Randono (2010) have studied the approach of Verlinde (2011) and suggest that Milgromian-like dynamics ensue once well-motivated corrections are applied.
Given that Milgromian dynamics is the correct description of galactic dynamics (just as Newtonian dynamics correctly accounts for Solar system dynamics), an increased effort to embed Milgromian dynamics within a Lorentz-covariant framework has ensued (e.g. Bekenstein 2004; Sanders 2005; Zlosnik et al. 2007; Bruneton & Esposito-Farèse 2007; Zhao 2008; Blanchet & Le Tiec 2009; Skordis 2009; Milgrom 2009). A quasi-linear formulation of Milgromian dynamics has been discovered only recently (Milgrom 2010; Zhao & Famaey 2010) which appears to allow easier access to N-body calculations. An interesting suggestion has been followed by Bruneton et al. (2009) who study theories in which DM is the source of the Milgromian phenomenology by introducing an interaction term between baryonic matter, DM and gravity. Additional approaches to an environmentally dependent dark sector, where the merits of CDM on large scales are unified with the merits of Milgromian dynamics on galactic scales, have also been suggested and studied (Zhao 2007; Li & Zhao 2009; Zhao & Li 2010) (but see the ‘dark force’ issues in Section 15.2).
It is expected that the coming years will be providing many new exciting insights into gravitation and the dynamics and evolution of galaxies as well as of larger cosmological structures. An excellent comprehensive treatment of this entire ansatz and an overview of the most recent progress and research activity is available in the major review by Famaey & McGaugh (2012) and in the book by Sanders (2010a).
16.3 Galactic-Scale Problems Vanish
It is rather noteworthy that virtually all problems on galactic scales disappear naturally within Milgrom’s framework (Famaey & McGaugh 2012 for a thorough review). For example, the MW satellite galaxies and the VPOS would naturally be TDGs since the early encounter of the MW with another galaxy would have occurred also in this framework. The existence of phase-space correlated structures such as the MW VPOS would then be a natural consequence of satellite galaxies forming as TDGs (Failure 8 in Section 17). Because there would be no DM halo around the MW and the other galaxy, dynamical friction would not decay their relative orbits such that the fly-by scenario between the young MW and the young LMC or even the young Andromeda would be feasible. Multiple encounters between two gas rich galaxies become readily possible, each time spawning new TDG and GC populations in correlated phase-space structures. Also, the invariant baryonic galaxy problem (Failure 10 in Section 17) in the SMoC (Kroupa et al. 2010) disappears entirely. And, the structure growth problem in the SMoC (Peebles & Nusser 2010) is alleviated in a Milgromian cosmology whereby the Bullet Cluster problem (Failure 17 in Section 17) of obtaining the high relative-cluster velocity is also avoided (Angus & Diaferio 2011). With baryonic matter as the sole source of gravitation on galactic scales, the TDG mass-deficit problem (Failure 9 in Section 17) disappears in Milgromian dynamics (Gentile et al. 2007; Milgrom 2007), while it is unsolvable in the SMoC: In Milgromian dynamics TDGs and all rotating stellar systems lie on the Tully–Fisher relation, and the Faber-Jackson relation for pressure-supported stellar systems also emerges naturally (Sanders 2010b).
16.4 The Bullet and Train-Wreck Clusters
The Bullet Cluster is often perceived to be a disproof of Milgromian dynamics because even in Milgromian dynamics DM is required to explain the observed separation of the weak lensing signal and the baryonic matter. In actuality, the Bullet Cluster is, if anything, a major problem for the SMoC because the large relative cluster–cluster velocity at the mass scale of the two observed clusters required to provide the observed gas shock front cannot be attained in the SMoC (Lee & Komatsu 2010; Thompson & Nagamine 2012). But such velocities arise naturally and abundantly in a Milgromian cosmology.
Assuming the Milgromian framework to be the correct description of effective gravitational dynamics, it has been shown that the Bullet Cluster lensing signal can be accounted for in it (Angus, Famaey & Zhao 2006). If a Milgromian cosmology is allowed to have a hot DM component then the Bullet Cluster is well explainable (Angus & McGaugh 2008; Angus et al. 2011). We know that neutrinos oscillate, therefore they must have a mass. That mass is small. This makes them a form of hot DM that we most definitely know to exist. In order to explain the oscillations, particle physics suggests the possible existence of more massive, sterile neutrinos, which interact by gravity. If they exist they might be massive enough to account for the missing mass in galaxy clusters in Milgromian dynamics (and they can fit the first three acoustic peaks in the CMB). Taking this ansatz, Angus, Famaey & Diaferio (2010) demonstrate that consistency in solving the mass-deficit in galaxy clusters and accounting for the CMB radiation power spectrum is achieved if sterile neutrinos (SN) have a mass near 11 eV. They write ‘we conclude that it is intriguing that the minimum mass of SN particle that can match the CMB is the same as the minimum mass found here to be consistent with equilibrium configurations of Milgromian clusters of galaxies.’ 16
The Train-Wreck Cluster (Abell 520) has been shown to be incompatible with the SMoC because the putative C/WDM particles have separated from the galaxies such that a core of DM is left (Mahdavi et al. 2007; Jee et al. 2012). While these authors speculate on a possible solution such as DM possibly having a self-interaction property (but see Section 15.2), in a Milgromian cosmological model with HDM it is conceivable for the self-bound galaxy-cluster-sized HDM core to dissociate itself from the baryonic matter in galaxies, which individually would remain on the BTF relation. However, different groups analysing the same lensing data obtain different mass maps (see Okabe & Umetsu 2008). The monopole degeneracy, which can lead to false peaks in the mass map (Liesenborgs et al. 2008), also affects the weak lensing mass reconstruction. Thus the issue remains inconclusive.
Within the MOG framework, Moffat & Toth (2009a) argue to be able to account for both the Bullet and the Train Wreck Cluster.
16.5 Milgromian Cosmology
A cosmological model based on Milgromian dynamics is presented by the pioneering work of Llinares, Knebe & Zhao (2008); Angus (2009) and Angus & Diaferio (2011). It has the same expansion history as the SMoC and therefore shares the same BB physics, but it differs from the SMoC at the galactic scale where it outperforms the SMoC comprehensively. Structures form more rapidly (Nusser 2002; Llinares et al. 2008; Angus & Diaferio 2011) as demanded by Peebles & Nusser (2010) on studying data in the Local Volume of galaxies. The structure-formation computations are more demanding due to the gravitational theory being non-linear which limits the currently attainable numerical resolution. Merely ‘dust’ simulations have been achieved so far in which the baryonic matter is approximated by particles that interact only via gravitation. A realistic structure formation simulation would however have to account for galaxies being purely baryonic objects such that dissipationless physics, as dominates structure formation in the SMoC, is not applicable. Currently such computations within the Milgromian framework are out of reach. Figure 13 demonstrates that this Milgromian-based ‘Angus-cosmological model’ accounts for the CMB power spectrum as well as the SMoC does.
The above thus disproves any claims to the effect that the SMoC be the only cosmological model accounting for the CMB and data on structure formation. The pioneering work done by Garry Angus and others has demonstrated that the SMoC is not unique in explaining the CMB. Therewith the final obstacle against discarding the SMoC has been surmounted. There is no logically consistent argument for adopting the SMoC over other models.
As a challenge for the future, any alternative to the SMoC needs to be shown to agree with the measured galaxy correlation function, as well as with all the other observational data that have been accumulating over time.
17 Conclusions
17.1 Summary of SMoC Falsification
The falsification of the SMoC can be summarised with the following steps:
-
It is an observed as well as theoretical fact that new (type B) dwarf galaxies can from in galaxy–galaxy encounters as TDGs and as RPDGs in galaxy clusters. If the SMoC were true then type B dwarfs still could not contain much DM and many TDGs would have been born during the early cosmological epoch. It is emphasised that the dwarf galaxies discussed here have baryonic masses
 104 M⊙ and include dwarfs significantly lower in surface luminosity than can be observed currently near interacting galaxies.
104 M⊙ and include dwarfs significantly lower in surface luminosity than can be observed currently near interacting galaxies. -
If the SMoC were valid then this implies the existence of two types of dwarf galaxies: those with DM (type A dwarfs) and type B dwarfs without DM (the Dual Dwarf Galaxy Theorem, Section 4). Note that the existence of type A dwarfs rests on the speculation that there is cold or warm DM. Type B dwarfs on the other hand are observed to exist and are known to survive.
-
But the observed type B dwarfs lie on the BTF relation, which is supposedly defined by DM dominated galaxies (both dwarf and major). This proves the First SMoC Falsification Theorem. And, type B dwarfs are observed to coincide morphologically with dE/dSph galaxies. dE galaxies are observed to not contain DM. This proves the Second SMoC Falsification Theorem.
-
Type A (DM) dwarfs are expected to be distributed approximately isotropically about their host galaxy. Type B dwarfs ought to typically form phase-space correlated populations surrounding their host galaxy. The MW satellites are found to be in a phase-space-correlated structure. That this anisotropic distribution of MW satellites may be due to an anisotropic search is ruled out by the dSph satellites, the UFDs, the inner YHGCs, the outer YHGCs and stellar and gaseous streams all independently showing the same distribution despite completely unrelated and different discovery and search strategies and methods. Seven of eight measured satellite motions confine these to be within the VPOS. The satellites of other galaxies are found to be in phase-space-correlated structures as well.
-
The observed properties of dE galaxies and the distribution of dwarf galaxies about the MW within the VPOS and in phase-space correlated structures about other galaxies requires these to be ancient type B dwarfs.
-
Observations thus only ever show evidence for the existence of one type B of dwarf galaxy, therewith falsifying the Dual Dwarf Galaxy Theorem.
-
Therewith there are no type A dwarf galaxies and there are no type A satellites near the MW. Cold or warm DM therefore cannot exist.
-
Consistency checks show that the SMoC is in disagreement with other observational properties of galaxies.
-
It has been established that the SMoC is not unique in accounting for the CMB and BB nucleosynthesis.
-
The SMoC appears to suffer under generic failures (Section 17.3.1 below).
It is important to seek consistency of this deduction with other arguments: if the SMoC Falsification Theorems are true, then the SMoC must fail on other tests as well:
17.2 The VPOS
Concerning only the MW, the vast polar structure — VPOS — is a physical property of the MW galaxy.
By itself, the VPOS is not fundamentally incompatible with the SMoC since such structures are expected to arise in any cosmological theory which allows galaxy–galaxy interactions to occur. The logical reason for why the existence of the VPOS alone already does exclude the SMoC is because the VPOS does not allow any luminous DM sub-structures to exist around the MW. The vast output from the world-wide cosmological simulation community has, however, shown beyond any doubt that the MW must contain hundreds of shining DM sub-structures.
If the existence of these shining DM sub-structures around the MW is excluded by observation, then there is no logical nor physical basis for arguing that dark DM sub-structures exist. This is because there is no known physical process that can avoid star formation in all DM haloes of mass ![]() 1010 M⊙.
1010 M⊙.
If the MW has no DM sub-structures, then no other galaxy can have them. This is the case because the MW is expected to have many thousands of DM sub-structures. The chance occurrence of a major galaxy such as the MW having no DM sub-structures is ruled out at an extraordinarily high confidence level, as even simple Poisson statistics demonstrate.
17.3 Logical Consistency of the SMoC Falsification
As stated above, if the SMoC is truly a false representation of reality, then there must be many failures of it when confronted with observational data. This is indeed the case, as summarised in the following two subsections.
17.3.1 Generic Failures of Inflationary BB Models?
Starkman et al. (2012) have shown the CMB fluctuations to be incompatible with the SMoC causing major tension with standard inflationary cosmologies. Liu & Li (2012) find that the WMAP data completely miss the quadrupole CMB signal posing a serious challenge to the SMoC, but this also constrains any cosmological model.
BB nucleosynthesis, which is usually reported to successfully account for the emergence of elements, has not been able to explain the observed low Li abundance (Coc et al. 2012; Famaey & McGaugh 2012).
An important problem related to Hypothesis 0ii which plagues all known BB-based cosmological models are the two missing baryon problems (e.g. Anderson & Bregman 2010; McGaugh et al. 2010): (i) From BB-nucleosynthesis and CMB observations the cosmic average baryon-to-DM mass-density fraction is f b, DM = 0.171 ± 0.006 but less than half of the baryon density has been found. (ii) Galaxies are observed to have a significantly smaller baryon fraction relative to the cosmic average. Both problems remain unresolved, as it is not known in which form the missing baryons reside nor why galaxies are so depleted in baryons. The above are generic failures of inflationary BB cosmologies.
That the distribution and properties of galaxies in the whole Local Volume is incompatible with the expectations from the SMoC has been emphasised by Peebles & Nusser (2010).
17.3.2 A Long List of Failures
1. Curvature and Homogeneity (1980) The BB would imply the universe to be highly inhomogeneous and curved in disagreement with observations. This is solved by introducing inflation (Guth & Tye 1980).
2. The Super-Keplerian Galactic Rotation Curve (1981) Rotation curves of disk galaxies are observed to remain quite flat (Rubin & Ford 1970; Bosma 1981). This is solved by introducing cold or warm DM (Blumenthal et al. 1984).
3. Angular-Momentum (1991) Disk galaxies forming in the C/WDM cosmological model dissipate too much angular momentum by virtue of the baryons falling into the DM potential wells, ending up being too compact with too little angular momentum in comparison with observed disk galaxies (Navarro & Benz 1991, see also Piontek & Steinmetz 2011; Martig et al. 2012; Dutton & van den Bosch 2012; Scannapieco et al. 2012).
4. The Cusp/Core (1991) CDM haloes have cusps whereas the observationally deduced DM halo profiles have substantial core radii similar to the dimension of the luminous galaxy (Dubinski & Carlberg 1991, see also Gilmore et al. 2007a, b; de Blok 2010; Chen & McGaugh 2010; Jardel & Gebhardt 2012). A possible solution has been suggested by the simulations of Governato et al. (2012) but relies among other assumptions on a bursty star-formation rate (SFR) required to repeatedly blow out gas and a steep Kennicutt-Schmidt exponent (n = 1.5) in SFR ∝ ρgas n , where SFR is the star formation rate and ρgas is the local gas density. However, in reality it is not clear if the dSph and UFD satellites experienced bursty SFRs, n = 1 (Pflamm-Altenburg & Kroupa 2008, 2009), the IMF would have had a lack of massive stars at the low SFRs of the MW satellites, as is inferred by Tsujimoto (2011), and the threshold for SF is lower in reality than assumed in the simulations (see further below). Repeated gas blow-out which is required to evolve the cusps to cores is thus not likely to be possible. WDM models tuned to account for the observed large cores in dwarf galaxies have such long DM particle streaming lengths that the dwarf galaxies cannot form in the first place (Macciò et al. 2012).
5. Dark-Energy (1998) The fluxes and redshifts of observed type Ia supernovae (SNIa) do not match the cosmological model (Riess et al. 1998; Schmidt et al. 1998; Perlmutter et al. 1999) unless the universe is assumed to expand at a larger rate. To account for the implied accelerated expansion dark energy (DE) is introduced. As with inflation, while mathematically allowed, it remains unclear if DE constitutes physics (see e.g. the discussion in Afshordi 2012). The SNIa flux–redshift data may at least partially be explained with an inhomogeneous universe (Wiltshire 2009; Smale & Wiltshire 2011; Marra, Pääkkönen & Valkenburg 2012) rather than with DE, whereby systematics in SNIa light curve fitting remain an issue (Smale & Wiltshire 2011). Bull & Clifton (2012) find that the ‘appearance of acceleration in observations made over large scales does not necessarily imply or require the expansion of space to be accelerating, nor does it require local observables to indicate acceleration’. It might perhaps be surprising that a homogeneous SMoC should lead to a perfect agreement with the observed SNIa data. In other words, the SNIa data that stem from the real inhomogeneous universe (Karachentsev 2012) should show some deviations from a homogeneous SMoC. If none are seen then this may imply an over-constrained model. 17
6. Missing Satellites (1999) Computations with more powerful computers showed that many more DM sub-structures form than observed galaxies have satellites (Klypin et al. 1999; Moore et al. 1999; the problem is somewhat reduced with WDM: Menci et al. 2012).
7. Hierachical Structure Formation (2002) As more-massive galaxies are build-up hierarchically from smaller building blocks in the SMoC, their [α/Fe] ratios ought to reflect the sub-solar [α/Fe] ratios of the building blocks (e.g., dE galaxies have low [α/Fe] ratios). In conflict with this expectation, observed massive E galaxies show high near-solar [α/Fe] values (Thomas, Maraston & Bender 2002). This may be partially alleviated by a prescription for AGN quenching of star formation in massive haloes but not so in the intermediate-galaxy-mass regime (Pipino et al. 2009, see also Nagashima et al. 2005; Recchi, Calura & Kroupa 2009).
8. The Disk of Satellites (DoS/VPOS, 2005) The observed satellite galaxies of the MW are arranged in a vast polar structure (Kroupa, Theis & Boily 2005; Metz et al. 2007, 2008, 2009a; Kroupa et al. 2010; Pawlowski et al. 2012b). Of all objects at Galactocentric distances larger than 10 kpc, only 4% are not associated with the VPOS (Section 10.1.7). Extragalactic anisotropic satellite systems are common, and Andromeda appears to have a flattened satellite system seen edge-on (Section 13.6).
9. The TDG Mass-Deficit (2007) Unexpectedly, observed young TDGs show evidence for DM which however is not possible if the SMoC were true (Barnes & Hernquist 1992) unless they contain undetectable gas (Bournaud et al. 2007, see also Gentile et al. 2007).
10. Invariant Disk Galaxies (2008) Observed disk galaxies are too similar following a simple one-parameter scaling law over many orders of magnitude in mass in conflict with the expected variation in the SMoC due to the chaotic formation history of each DM host halo (Disney et al. 2008, see also Hammer et al. 2007; Kroupa et al. 2010).
11. The Common Mass-Scale (2008) In the SMoC, DM sub-haloes are distributed according to a power-law mass function. But observed satellite galaxies have too similar DM masses (Strigari et al. 2008, see also Kroupa et al. 2010 and for Andromeda Tollerud et al. 2012).
12. Constant Surface-Density (2009) Considering the matter distribution in observed galaxies within one DM-halo scale radius, Gentile et al. (2009) find ‘This means that the gravitational acceleration generated by the luminous component in galaxies is always the same at this radius. Although the total luminous-to-dark matter ratio is not constant, within one halo scale-length it is constant’. In the SMoC there is no physical principle according to which the DM and baryonic densities ought to be invariant within this radius.
13. The Luminous Sub-Halo Mass Function (2010) The mass function of observed satellite galaxies disagrees with the predicted mass function of luminous sub-haloes (Kroupa et al. 2010).
14. Bulgeless Disk Galaxies (2010) That the bulge-to-disc flux ratios are smaller than those produced by LCDM simulations is pointed out by Graham & Worley (2008). 58–74 per cent of all observed disk galaxies are claimed to not have a classical bulge (Kormendy et al. 2010). This is in conflict with the heavy merging history expected for bright galaxies if the SMoC were true (Hammer et al. 2007). For attempts to produce bulgeless disk galaxies see text below.
15. Isolated Massive Galaxies (2010) In the observed Local Volume of galaxies there are three massive disk galaxies that are too far off the matter filament (Peebles & Nusser 2010).
16. The Void (2010) The Local Void is observed to be too empty in comparison to the SMoC expectation (Tikhonov et al. 2009; Peebles & Nusser 2010).
17. The Bullet Cluster (2010) The observed large relative velocity of the two interacting galaxy clusters is not accountable for in the SMoC (Lee & Komatsu 2010; Thompson & Nagamine 2012).
18. The Missing Bright Satellites (2011) The predicted mass function of DM sub-haloes implies that a significant number of bright satellite galaxies is missing (Bovill & Ricotti 2011; Boylan-Kolchin et al. 2011a). Vera-Ciro et al. (2012) suggest this problem does not occur if the DM sub-haloes have Einasto rather than NFW density profiles. Wang et al. (2012) suggest this problem does not occur if the MW DM halo is less massive than about 2 × 1012 M⊙. But this is unlikely as the large proper motion of the LMC implies the MW to be more massive than about 2 × 1012 M⊙ and the LMC to be a recent acquisition and on its first passage (Boylan-Kolchin et al. 2011b). Furthermore, if this were the case then the question would need to be posed as to how likely the LMC happens to pass the MW within the VPOS.
19. The Thin Old Disk (2011) The MW has a thin disk which has stars as old as 10 Gyr. Such old thin disks have still not been produced in the SMoC (House et al. 2011).
20. The Train-Wreck Cluster (2012) The galaxy cluster A 520 has been shown to contain what appears to be a DM core with too few galaxies as well as evidence for a cluster–cluster encounter. The C/WDM paradigm cannot account for this separation of DM from the luminous matter, which is the opposite behaviour to the Bullet Cluster (Failure 17 above, Jee et al. 2012, see also Mahdavi et al. 2007).
21. Missing Dark Matter (2012) Over spatial scales of 100 Mpc the density of matter fluctuates by 10% if the SMoC were valid. By counting up all matter within the local sphere with a radius of 50 Mpc, Karachentsev (2012) demonstrates the actual density to be too low by a factor of 3–4. Most of the missing mass is DM.
22. Massive Galaxy Clusters (2012) The most massive most distant galaxy clusters are important constraints on cosmological theory because the rapidity with which mass assembles to galaxy clusters depends on dark matter and/or on modified gravitation (Section 16.5). Gonzalez et al. (2012) discover a giant lensed arc near the cluster IDCS J1426.5+3508 and deduce ‘For standard LCDM structure formation and observed background field galaxy counts this lens system should not exist.’
The Theory-Confidence Graph, Figure 14, visualises the development of confidence in the SMoC as a function of time. 18 While some of the failures have been taken as major discoveries of new physics (inflation, DM, DE) because they can be solved by mathematical formulations in principle allowed by Einstein’s field equation, while other failures are typically discussed away as minor problems, the consistent appearance of ever new failures suggests rather that the whole construction based on Hypothesis 0i and 0ii needs to be revised. Since their discovery, each of the problems has received attention. Nevertheless, despite important seminal work no convincing and importantly, no mutually consistent solutions have emerged for these problems.
|
For example, the angular momentum, cusp/core, invariant baryonic galaxy, the constant surface density and bulge problems (Failures 3, 4, 10, 12 and 14, respectively) are related and it is thought that a better understanding of the complex baryonic processes may solve these. The seminal work by Brook et al. (2011) has shown that it is possible, at least in principle, to grow galactic disks in DM haloes such that they resemble the real galaxies. But the proposed solution is for host DM haloes that have a mild history of mergers, therewith applying to a minority of DM host haloes, while bulgless disk galaxies are the dominant galactic population (Kormendy et al. 2010). And, the feedback energy required to blow out the baryons such that they cool and slowly re-accrete is extreme. The density threshold for star-forming gas is far higher in the models over a resolution limited spatial region of extend of about 200 pc in comparison to real molecular clouds where the density is high in only pc-sized regions. In the models, the full stellar initial mass function (IMF) hits the gas once star-formation ensues, while in reality the dependency of feedback on the star-formation rate (SFR) is smaller at low SFRs through the dependency of the IMF on the SFR (Weidner, Kroupa & Pflamm-Altenburg 2011; Kroupa et al. 2012).
Also, the presence of the many sub-haloes with satellites in the SMoC models leads to problems understanding how major disk galaxies such as our MW can have old thin disks that can extend beyond 20 kpc. After studying resolution issues in different numerical schemes, House et al. (2011) write in their conclusion about the CDM MW models studied ‘None has a thin disc older than ~6 Gyr, indicating that it would be difficult to gain a thin disc as old as some estimates for the Milky Way thin disc within the current cold dark matter paradigm.’ Similarly, Kormendy et al. (2010) state ‘It is hard to understand how bulge-less galaxies could form as the quiescent tail of a distribution of merger histories.’ And, ‘Our Galaxy provides an additional important conclusion. Its disk stars are as old as 9–10 Gyr…. Unless our Galaxy is unusual, this suggests: The solution to the problem of forming giant, pure-disk galaxies is not to use some physical process like energy feedback to delay star formation until recently and thereby to give the halo time to grow without forming a classical bulge’. The existence of massive, pure disk galaxies in the most massive DM host haloes (e.g. M101), which must have had a significant growth/merger history, are a problem if not a falsification of the SMoC.
That thin self-supporting disk galaxies can form readily if the DM sub-structures and their merging does not occur has been shown by Samland (2004). These models still require a slowly growing DM host halo, but by the absence of the DM sub-structures they are not consistent with the SMoC, for which the work by Samland had been critisised.
17.4 No Dark Matter but Modified Gravity
If the SMoC is falsified and cold or warm DM does not exist, then how can the dynamics of galaxies be accounted for?
Without C/WDM an approach to understanding the physics of galaxies is to include non-Einsteinian/non-Newtonian dynamics. All known observational features of galaxies do demonstrate that the currently best available dynamics for this purpose is Milgrom’s such that below an accelaration of about a 0 = 3.6 pc Myr–2 gravitation is effectively larger, as originally proposed by Milgrom (1983a, b, c); Bekenstein & Milgrom (1984). The MDA correlation (Figure 11) is one such example, and another independent falsification of the SMoC because the physics of the putative DM particles is independent of the local acceleration. The MDA correlation is a successful prediction of Milgromian dynamics, since the data shown in Figure 11 have been obtained long after the original formulation of Milgromian dynamics. The observationally well-defined BTF relation and the observed super-Keplerian rotation curves (Sanders 2009; Famaey & McGaugh 2012) are other such examples (Figure 15). That dwarf galaxies with circular velocities V c = V f ≈ 15 km s–1 and that the TDGs all lie on the BTF relation defined by the more massive galaxies constitutes a brilliantly successful prediction by Milgromian dynamics, given that such data were not available in the early 1980s. The rotation curve of the gas-rich Local Group dwarf galaxy DDO 210 is perfectly reproduced with Milgromian dynamics without adjustment of parameters (figure 25 in Famaey & McGaugh 2012). It is the lowest point (V f ≈ 15 km s–1) in Figure 15.
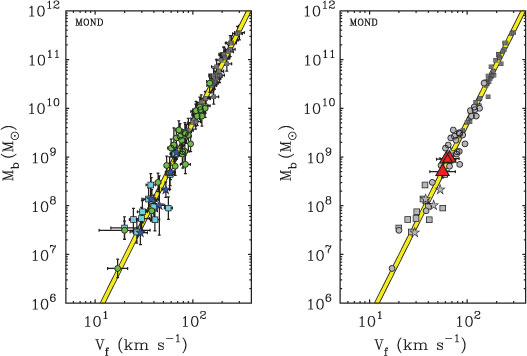
|
In Milgromian dynamics, galaxy evolution and interactions have been shown, with the first available simulations, to naturallly reproduce observational properties of galaxies (Combes & Tiret 2010; Tiret & Combes 2007), and TDGs form readily (Tiret & Combes 2008).
Returning to the work by Samland (2004), his slowly growing DM halo model leads to an excellent reproduction of the MW galaxy. The physical interpretation of the Samland model is that it is essentially a model for the emergence of the MW in modified gravity, because a slowly growing DM halo without sub-structure is a first order approximation of the phantom DM halo associated with a Milgromian baryonic galaxy viewed as a Newtonian object (Bienaymé et al. 2009; Famaey & McGaugh 2012 ). If anything, the work by Samland (2004) and collaborators had captured a reality that had eluded the main-stream research community.
How, then, does a Milgromian cosmological model fare?
Figure 16 shows the confidence in a Milgromian Angus-cosmological model universe in an equivalent plot as Figure 14 for the confidence in the Einstein-based model. The situation is definitely better for the Angus-cosmological model, and if sterile neutrinos with a mass of about 11 eV were to be discovered then this would massively boost confidence in Milgromian-based cosmologies. Also, Milgromian cosmological models do require DE. But, as emphasised in e.g. Famaey & McGaugh (2012), an interesting correspondence emerges in this model (but not in the SMoC) for the acceleration scale a 0 (Figure 11): a 0 2/c 2 ≈ Λ, where c is the speed of light. Why should this be the case? Remember that a 0 is derived from galactic-scale problems (e.g. using one single rotation curve). This correspondence may hint at deeper physics of space-time we are yet to discover. Thus, Milgromian models do not show as massive a drop in confidence as the SMoC. The situation remains tense since the distant and extended MW globular cluster data have until now failed to show the expected Milgromian behaviour, although Scarpa et al. (2011) consistently report to have observed super-Keplerian stellar motions in the outskirts of GCs for which such data are available (see also Hernandez & Jimenez 2012).
|
While the SMoC has been demonstrated to reproduce the large-scale distribution of matter well, agreement with data is never a proof of a model, and we do not yet know if a Milgromian cosmology will not also be able to achieve the same level of agreement. The reason is that baryonic physics is far more dominant in a Milgromian cosmology but the available computer power is not available to achieve numerical resolution high enough to compute the distribution of galaxies, for example. At the present we do know that structures form more rapidly in a Milgromian universe than in SMoC, in consistency with the observations (Section 16.5), but it is not known what the smallest structures that emerge in a Milgromian cosmology may be (dIrr galaxies?). But any galaxy which forms in a Milgromian universe falls on the Tully–Fisher relation, independently of whether it forms as a TDG or as a primordial dwarf (Figure 15). Indeed, both will later appear indistinguishable to an observer, given that the dominant fraction of TDGs would have been born soon after the BB when the forming gas-rich galaxies were assembling and encountering each other. A TDG forming at a late cosmological epoch may, however, be identified by it being metal rich and lying above the metallicity–luminosity relation of most dwarf galaxies.
How does the Dual Dwarf Galaxy Theorem fare in a Milgromian cosmology? Only a weak form of the theorem would be valid (Section 4): In a Milgromian universe gas-rich, rotationally supported TDGs would lie on the BTF relation together with gas-dominated primordial dwarf disk galaxies and primordial star-dominated major galaxies, as is observed. And old, pressure-supported TDGs would be identical dynamically to dE and dSph galaxies, as is observed. Thus, in a Milgromian universe, TDGs and primordial galaxies would only differ by TDGs that formed at later cosmological epochs having relatively young stellar populations and perhaps being relatively metal-rich, if they formed from pre-enriched material.
Another alternative, Modified Gravity (MOG) (e.g. Moffat 2006; Moffat & Toth 2009b) has been suggested and eliminates all need for DM and DE. But, MOG must effectively become Milgromian on galaxy scales. In addition, it has been shown that flat rotation curves of galaxies can be accounted for without DM by brane-world models (Gergely et al. 2011) as well as by f(R)-gravity models (Capozziello et al. 2009) whereby lensing constraints are also being studied in these and other theories.
17.5 Summarising
Taking all the evidence together, it emerges that all arguments converge consistently to the result that the SMoC is falsified and that dark-matter sub-structures do not exist. If they do not exist, then DM particles that are dynamically relevant on galactic scales cannot exist. This is consistent with such particles not appearing within the SMoPP, which is at present the most successful existing theory of physics, and the simple empirical fact that they have not been found despite a massive world-wide search for their existence (Section 15.1).
Noteworthy is that the SMoPP cannot, however, account for mass. Since mass is the one property of particles that couples to space-time it is perhaps not surprising that our lack of understanding of this coupling becomes evident on the astronomical arena as a failure of our popular formulation of gravitation when confronted with post-Einsteinian observational data. Perhaps interesting in this context is the complimentary principle (a material object is both a particle and a wave): this suggests that matter has also space-time properties and may hint at a not yet achieved unification of matter, space and time in the sense that space-time is an emergent property of matter. Put another way: that the currently popular SMoC needs to be based to more than 96% on unknown physics is nothing more than an expression of our present-day ignorance of how mass, space and time unify, i.e. of cosmological physics. Some proposed quantum-gravity theories have already been disfavoured through measurements of the constancy of the speed of light with photon energy (Abdo et al. 2009).
17.6 Future Tests
Independently of the beauty and general acceptance of a model, it must stand up to observational scrutiny. 19 This is true also for the conclusions of this contribution, namely that dynamics is Milgromian and dwarf satellite galaxies are mostly of type B (TDGs and RPDs).
If these conclusions reached here are correct then the following ought to hold up to future observational tests:
-
BTFTDG = BTFdIrr must continue to hold. That is, it would be important to measure rotation curves of other gas-rich TDGs to test if they conform to the BTF relation and thus to Milgromian dynamics (Figure 15).
-
TDGs that are older than about one Gyr should lie on the radius–mass relation of dE, dSph and UFD galaxies subject to tidal deformation. It would be important to determine the density profiles of TDGs in order to place them into the radius–mass or radius–luminosity diagram (Figure 4). Expansion through gas loss from the observed gas-rich TDGs needs to be accounted for in the comparison. TDGs forming today are likely to be subject to stronger tidal fields than in the cosmological past (Figure 4).
-
If satellite galaxies are mostly TDGs then their number should scale with the mass of the bulge of the host galaxy. It would be important to survey nearby early-type disk galaxies with prominent bulges and nearby late-type disk galaxies with similar rotational velocities but no bulges to test the correlation of bulge-mass to the number-of-satellites (Figure 10).
-
Can the number of observed satellite galaxies be accounted for in a realistic cosmological model if they are typically TDGs and perhaps RPDGs? To study this issue it would be important to perform high-resolution very gas-rich galaxy–galaxy encounter simulations as well as computations of gas-stripping from disk galaxies in galaxy clusters to study the formation rate of TDGs and RPDGs, respectively, and their survival in Milgromian dynamics.
-
Is it possible to re-create realistic events that created the MW VPOS from a tidal arm about 10–11 Gyr ago?
-
Hickson compact groups would not merge efficiently in Milgromian dynamics because the dynamical friction on DM halos would not exist. If the SMoC were true after all, then such groups would merge within about a dynamical time (≈ 1 Gyr). How quickly do observed Hickson compact groups merge (Kroupa et al. 2010)?
-
Does Milgromian dynamics hold on all scales? Observe globular clusters and galaxy clusters.
Acknowledgments
An anonymous referee must be thanked for a rigorous but constructive report. I am especially grateful to Sambaran Banerjee, Benoit Famaey, Stacy McGaugh and Simone Recchi for valuable comments. I also thank Klaas de Boer, Joerg Dabringhausen, Gerhardt Hensler, Marcel Pawlowski, Jan Pflamm-Altenburg and Günther Wuchterl for useful discussions. Figures were kindly provided by Joerg Dabringhausen, Gianfranco Gentile, Fabian Lüghausen, Stacy McGaugh and Marcel Pawlowski. This work was partially suported by the German Research Foundation (DFG) through grants KR1635/18-1 and HE1487/36-2 within the priority programme 1177 ‘Witnesses of Cosmic History: Formation and Evolution of Black Holes, Galaxies and Their Environment’.
I would like to express my sincere admiration for those young researchers who dare follow their curiosity and who publish their non-conforming findings even though this may put their careers at risk.
References
Aarseth, S. J., Turner, E. L. and Gott, J. R., 1979, ApJ, 228, 664| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE1MXhvFersbY%3D&md5=4c29b75a5b58615c426cadd57608b955CAS |
Abdo, A. A. et al., 2009, Natur, 462, 331
| 1:CAS:528:DC%2BD1MXhtlaksrvK&md5=0313d57905e651e6d6ad7e7c23d2fc84CAS |
Afshordi, N., 2012, arXiv:astro-ph/1203.3827
Aliu, E. et al., 2012, PhRvD, 85, 062001
Amendola, L. & Tsujikawa, S., 2010, Dark Energy: Theory and Observations (Cambridge: Cambridge University Press)
Anderson, M. E. and Bregman, J. N., 2010, ApJ, 714, 320
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXmsleqtbg%3D&md5=e08d0116847d5521e4d01e26bf741eebCAS |
Angloher, G. et al., 2012, EPJC, 72, 1971
Angus, G. W., 2008, MNRAS, 387, 1481
| Crossref | GoogleScholarGoogle Scholar |
Angus, G. W., 2009, MNRAS, 394, 527
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXkvVWls7Y%3D&md5=538a27b1d195c0ec98f4c5bdf301d2a6CAS |
Angus, G. W. and Diaferio, A., 2011, MNRAS, 417, 941
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhsVOjs7%2FF&md5=2f40499d3014c5d44b3cdb2bad308f1fCAS |
Angus, G. W. and McGaugh, S. S., 2008, MNRAS, 383, 417
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhslSnu7w%3D&md5=6b1cb3fd310372d8fea99ef0208e7582CAS |
Angus, G. W., Famaey, B. and Zhao, H. S., 2006, MNRAS, 371, 138
| Crossref | GoogleScholarGoogle Scholar |
Angus, G. W., Famaey, B. and Diaferio, A., 2010, MNRAS, 402, 395
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXjtVWjsb8%3D&md5=e39aa0bdbcc42720279aff1382d6883eCAS |
Angus, G. W., Diaferio, A. and Kroupa, P., 2011, MNRAS, 416, 1401
| Crossref | GoogleScholarGoogle Scholar |
Aprile, E. et al., 2011, PhRvL, 107, 131302
| 1:STN:280:DC%2BC38vnsFGmsA%3D%3D&md5=0744f4d3f4692fc0289303a94aaab37fCAS |
Aubert, D., Pichon, C. and Colombi, S., 2004, MNRAS, 352, 376
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXnt1Giur4%3D&md5=439ce7d65896f3d0db29441a4082154bCAS |
Barnes, J. E. and Hernquist, L., 1992, Natur, 360, 715
| Crossref | GoogleScholarGoogle Scholar |
Baudis, L., 2012, arXiv:astro-ph/1203.1589
Baumgardt, H., Grebel, E. K. and Kroupa, P., 2005, MNRAS, 359, L1
| Crossref | GoogleScholarGoogle Scholar |
Bekenstein, J. D., 2004, PhRvD, 70, 083509
Bekenstein, J. and Milgrom, M., 1984, ApJ, 286, 7
| Crossref | GoogleScholarGoogle Scholar |
Bienaymé, O., Famaey, B., Wu, X., Zhao, H. S. and Aubert, D., 2009, A&A, 500, 801
Binney, J. & Tremaine, S., 1987, Galactic Dynamics (Princeton: Princeton University Press), 747
Blanchet, L. and Le Tiec, A., 2009, PhRvD, 80, 023524
Bludman, S. A., 1998, ApJ, 508, 535
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXmvFCh&md5=34576d4aa9a9528318c9eecdad3b1e99CAS |
Blumenthal, G. R., Faber, S. M., Primack, J. R. and Rees, M. J., 1984, Natur, 311, 517
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2cXlvF2mt7Y%3D&md5=722d7dfbbb8792bc413b5dd5f9b0a0b9CAS |
Bosma, A., 1981, AJ, 86, 1791
| 1:CAS:528:DyaL38XnslWmug%3D%3D&md5=77fbb656e521b3bce5adc5d07b0a0e39CAS |
Bournaud, F., 2010, AdAst, , 735284
Bournaud, F. and Combes, F., 2003, A&A, 401, 817
Bournaud, F., Jog, C. J. and Combes, F., 2005, A&A, 437, 69
Bournaud, F. et al., 2007, Sci, 316, 1166
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXls1KisL8%3D&md5=4b49806430c8d9c2a0f1dde7696baaf0CAS |
Bournaud, F., Duc, P.-A. and Emsellem, E., 2008, MNRAS, 389, L8
Bournaud, F. et al., 2011, ApJ, 730, 4
| Crossref | GoogleScholarGoogle Scholar |
Bousso, R., 2008, GReGr, 40, 607
Bousso, R., 2012, in Proc. Subnuclear Physics: Past, Present and Future, Pontificial Academy of Sciences, Vatican (October 2011), arXiv:astro-ph/1203.0307v1
Bovill, M. S. and Ricotti, M., 2011, ApJ, 741, 18
| Crossref | GoogleScholarGoogle Scholar |
Boylan-Kolchin, M., Bullock, J. S. and Kaplinghat, M., 2011a, MNRAS, 415, L40
Boylan-Kolchin, M., Besla, G. and Hernquist, L., 2011b, MNRAS, 414, 1560
| Crossref | GoogleScholarGoogle Scholar |
Brada, R. and Milgrom, M., 2000, ApJ, 541, 556
| Crossref | GoogleScholarGoogle Scholar |
Brandenberger, R. H., 2012, Proceedings of the 6th Aegean Summer School, Quantum Gravity and Quantum Cosmology, Chora, Naxos, Greece, 12–17 September 2012, arXiv:1203.6698B (see also arXiv:1204.6108)
Brasseur, C. M. et al., 2011, ApJ, 729, 23
| Crossref | GoogleScholarGoogle Scholar |
Brook, C. B. et al., 2011, MNRAS, 415, 1051
| Crossref | GoogleScholarGoogle Scholar |
Bruneton, J.-P. and Esposito-Farèse, G., 2007, PhRvD, 76, 124012
Bruneton, J.-P., Liberati, S., Sindoni, L. and Famaey, B., 2009, JCAP, 3, 21
Brüns, R. C., Kroupa, P., Fellhauer, M., Metz, M. and Assmann, P., 2011, A&A, 529, 138
Bull, P. & Clifton, T., 2012, arXiv1203.4479B
Bullock, J. S., 2002, in Proc. Yale Cosmology Workshop, ed. P. Natarajan (Singapore: World Scientific Publishing), 109
Busha, M. T., Alvarez, M. A., Wechsler, R. H., Abel, T. and Strigari, L. E., 2010, ApJ, 710, 408
| Crossref | GoogleScholarGoogle Scholar |
Capozziello, S., Piedipalumbo, E., Rubano, C. and Scudellaro, P., 2009, A&A, 505, 21
Carlin, J. L. et al., 2012, ApJ, 744, 25
| Crossref | GoogleScholarGoogle Scholar |
Casas, R. A., Arias, V., Pena Ramirez, K. and Kroupa, K., 2012, MNRAS, ,
CDMS II Collaboration, 2010, Sci, 327, 1619
Chen, D.-M. and McGaugh, S., 2010, RAA, 10, 1215
| 1:CAS:528:DC%2BC3MXhs1yrur0%3D&md5=68a5baa4681049592f0bebeb239779b9CAS |
Chilingarian, I. V., Mieske, S., Hilker, M. and Infante, L., 2011, MNRAS, 412, 1627
| Crossref | GoogleScholarGoogle Scholar |
Coc, A., Goriely, S., Xu, Y., Saimpert, M. and Vangioni, E., 2012, ApJ, 744, 158
| Crossref | GoogleScholarGoogle Scholar |
Coleman, M. G. et al., 2007, ApJL, 668, 43
| Crossref | GoogleScholarGoogle Scholar |
Combes, F., 2002, NewAR, 46, 755
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XosFCjsr8%3D&md5=aa24dc083291aaff802c8a17e6db86e2CAS |
Combes, F. and Tiret, O., 2010, AIPC, 1241, 154
| 1:CAS:528:DC%2BC3cXotVKhsL8%3D&md5=284733a16eb1897f5d248feb99a546c0CAS |
Cooper, A. P. et al., 2010, MNRAS, 406, 744
| Crossref | GoogleScholarGoogle Scholar |
D′Onghia, E. and Lake, G., 2008, ApJL, 686, 61
| Crossref | GoogleScholarGoogle Scholar |
Dabringhausen, J., Hilker, M. and Kroupa, P., 2008, MNRAS, 386, 864
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXntFyku7o%3D&md5=85690c49e95fae6aa0df8715323168c1CAS |
de Blok, W. J. G., 2010, AdAst, 2010, article id 789293
de Lucia, G., 2012, RvMA, 24, in press, arXiv1203.5208D
Deason, A. J. et al., 2011, MNRAS, 415, 2607
| Crossref | GoogleScholarGoogle Scholar |
Dekel, A. and Woo, J., 2003, MNRAS, 344, 1131
| Crossref | GoogleScholarGoogle Scholar |
Dekel, A. and Silk, J., 1986, ApJ, 303, 39
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28XhvFKgsLg%3D&md5=2d052de5b846ae3a1e3dc057aa9c0284CAS |
Demers, S., Irwin, M. J. and Kunkel, W. E., 1994, AJ, 108, 1648
Desmond, H., 2012, MNRAS, submitted, arXiv:astro-ph/1204.1497
Diemand, J., Moore, B. and Stadel, J., 2004, MNRAS, 352, 535
| Crossref | GoogleScholarGoogle Scholar |
Diemand, J. et al., 2008, Natur, 454, 735
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXps1Snsbg%3D&md5=8fe77f3de698961da5f97de245d5781fCAS |
Disney, M. J. et al., 2008, Natur, 455, 1082
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXht1yju7%2FP&md5=a6d15b4e60cd76f5149e65bd099cb14aCAS |
Drinkwater, M. J. and Gregg, M. D., 1998, MNRAS, 296, L15
| Crossref | GoogleScholarGoogle Scholar |
Drinkwater, M. J., Jones, J. B., Gregg, M. D. and Phillipps, S., 2000, PASA, 17, 227
| Crossref | GoogleScholarGoogle Scholar |
Drinkwater, M. J. et al., 2004, PASA, 21, 375
| Crossref | GoogleScholarGoogle Scholar |
Dubinski, J., 1994, ApJ, 431, 617
| Crossref | GoogleScholarGoogle Scholar |
Dubinski, J. and Carlberg, R. G., 1991, ApJ, 378, 496
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXmtFKmtbo%3D&md5=3ef63cd52a3b8b67d1414f5fa56e1e3aCAS |
Duc, P.-A. and Mirabel, I. F., 1998, A&A, 333, 813
Duc, P.-A., Braine, J., Lisenfeld, U., Brinks, E. and Boquien, M., 2007, A&A, 475, 187
| 1:CAS:528:DC%2BD1cXnt1Kntw%3D%3D&md5=4f61f225fb460db92762c8b8d775a8e8CAS |
Duc, P.-A. et al., 2011, MNRAS, 417, 863
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhsVOjs7%2FO&md5=d19a4eadf866d28363fe489b2502481cCAS |
Dutton, A. A. and van den Bosch, F. C., 2012, MNRAS, 421, 608
Einstein, A., 1916, AP, 354, 769
Epelbaum, E., Krebs, H., Lee, D. and Meisner, U.-G., 2011, PhRvL, 106, 192501
Esposito-Farese, G., 2009, arXiv:astro-ph/0905.2575
Faber, S. M. and Gallagher, J. S., 1979, ARA&A, 17, 135
| Crossref | GoogleScholarGoogle Scholar |
Famaey, B. & McGaugh, S., 2012, LRR, arXiv:astroph/1112.3960
Fanelli, D., 2010, PLoS ONE, 5, e10271
| Crossref | GoogleScholarGoogle Scholar |
Ferguson, H. C. and Binggeli, B., 1994, A&AR, 6, 67
Ferrero, I., Abadi, M. G., Navarro, J. F., Sales, L. V. & Gurovich, S., 2011, arXiv:astro-ph/1111.6609v1
Font, A. S. et al., 2011, MNRAS, 417, 1260
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhsVOjs73J&md5=12a1cb307489cadd05495a40181e3186CAS |
Forbes, D. A. and Kroupa, P., 2011, PASA, 28, 77
| Crossref | GoogleScholarGoogle Scholar |
Forbes, D. A., Lasky, P., Graham, A. W. and Spitler, L., 2008, MNRAS, 389, 1924
| Crossref | GoogleScholarGoogle Scholar |
Forbes, D. A. et al., 2011, MNRAS, 413, 2665
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvFeqsb4%3D&md5=b84869c7735b5c1dcd99f91d7423d961CAS |
Forero-Romero, J. E. et al., 2011, MNRAS, 417, 1434
| Crossref | GoogleScholarGoogle Scholar |
Freire, P. C. C. and Wex, N., 2010, MNRAS, 409, 199
| Crossref | GoogleScholarGoogle Scholar |
Galianni, P., Patat, F., Higdon, J. L., Mieske, S. and Kroupa, P., 2010, A&A, 521, 20
Gao, L., Frenk, C. S., Jenkins, A., Springel, V. and White, S. D. M., 2012, MNRAS, 419, 1721
| 1:CAS:528:DC%2BC38Xhslegsb4%3D&md5=ab344e47215268fb516ee849917d490eCAS |
Gentile, G. et al., 2007, A&A, 472, L25
Gentile, G., Famaey, B., Zhao, H. and Salucci, P., 2009, Natur, 461, 627
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXht1Sqtr%2FM&md5=e1eceb17240e19d05f82a508856401ecCAS |
Gergely, L. Á., Harko, T., Dwornik, M., Kupi, G. and Keresztes, Z., 2011, MNRAS, 415, 3275
Ghigna, S. et al., 1998, MNRAS, 300, 146
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXntlSrs74%3D&md5=6b7a70010ac168e4c0d8a04284236563CAS |
Gilmore, G. et al., 2007a, NuPhS, 173, 15
| 1:CAS:528:DC%2BD2sXhtlClt7bP&md5=afe22fba4e99f99d121f14fd8b8172f1CAS |
Gilmore, G. et al., 2007b, ApJ, 663, 948
| Crossref | GoogleScholarGoogle Scholar |
Gonzalez, A. H., et al., 2012, ApJ, in press, arXiv:astro-ph/1205.3788
Governato, F. et al., 2012, MNRAS, 422, 1231
Graham, A. W. and Worley, C. C., 2008, MNRAS, 388, 1708
| 1:CAS:528:DC%2BD1cXhtVKmtLnP&md5=6d116241631ad52528dfc5a305dcb1b0CAS |
Guth, A. H. and Tye, S.-H. H., 1980, PhRvL, 44, 631
Hammer, F. et al., 2005, A&A, 430, 115
| 1:CAS:528:DC%2BD2MXhvFCqtLY%3D&md5=91e04b6e5e64129ca56531c52f883f3cCAS |
Hammer, F., Puech, M., Chemin, L., Flores, H. and Lehnert, M. D., 2007, ApJ, 662, 322
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXnsV2lsr4%3D&md5=3d179172a2ba15823bbc668cb553ec77CAS |
Hammer, F. et al., 2009, A&A, 496, 381
| 1:CAS:528:DC%2BD1MXlsFWru7w%3D&md5=34c604febfbe1ef93d6b874f9177dec3CAS |
Hammer, F. et al., 2010, ApJ, 725, 542
| Crossref | GoogleScholarGoogle Scholar |
Harris, W. E., 1996, AJ, 112, 1487
Haud, U., 1988, A&A, 198, 125
| 1:CAS:528:DyaL1cXkvValu7c%3D&md5=a9b0b39688cd4ee033161d75e6c07e6eCAS |
Hayashi, E., Navarro, J. F., Taylor, J. E., Stadel, J. and Quinn, T., 2003, ApJ, 584, 541
| Crossref | GoogleScholarGoogle Scholar |
Hayes, B., Brunner, R., & Ross, A., 2012, arXiv:astroph/1112.5723
Hernandez, X. and Jimenez, M. A., 2012, ApJ, 750, 9
Hernandez, X., Mendoza, S., Suarez, T. and Bernal, T., 2010, A&A, 514, A101
Hilker, M., Infante, L., Vieira, G., Kissler-Patig, M. and Richtler, T., 1999, A&AS, 134, 75
House, E. L. et al., 2011, MNRAS, 415, 2652
| Crossref | GoogleScholarGoogle Scholar |
Hubble, E. P., 1929, ApJ, 69, 103
| Crossref | GoogleScholarGoogle Scholar |
Hunter, D. A., Hunsberger, S. D. and Roye, E. W., 2000, ApJ, 542, 137
| Crossref | GoogleScholarGoogle Scholar |
Ibata, R., Lewis, G. F., Irwin, M., Totten, E. and Quinn, T., 2001, ApJ, 551, 294
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXjvVals7w%3D&md5=8beb815c3d4764b939e3d9cc869ef7c2CAS |
Jardel, J. R. and Gebhardt, K., 2012, ApJ, 746, 89
| Crossref | GoogleScholarGoogle Scholar |
Jee, M. J. et al., 2012, ApJ, 747, 96
Karachentsev, I., 1996, A&A, 305, 33
Karachentsev, I. D., 2012, AstBu, 67, 123
Karachentsev, I. D., Karachentseva, V. E. & Sharina, M. E., 2005, in IAUC 198: Near-Fields Cosmology with Dwarf Elliptical Galaxies, ed. H. Jerjen & B. Binggeli, (Cambridge: Cambridge University Press), 295
Kaviraj, S., Darg, D., Lintott, C., Schawinski, K. and Silk, J., 2012, MNRAS, 419, 70
| Crossref | GoogleScholarGoogle Scholar |
Kazantzidis, S. et al., 2004, ApJ, 608, 663
| Crossref | GoogleScholarGoogle Scholar |
Kirby, E. N., et al., 2009, Astro2010: The Astronomy and Astrophysics Decadal Survey, Science White Papers, 156
Klessen, R. S. and Kroupa, P., 1998, ApJ, 498, 143
| Crossref | GoogleScholarGoogle Scholar |
Kleyna, J. T., Geller, M. J., Kenyon, S. J., Kurtz, M. J. and Thorstensen, J. R., 1998, AJ, 115, 2359
Kleyna, J. T., Wilkinson, M. I., Gilmore, G. and Evans, N. W., 2003, ApJL, 588, 21
| Crossref | GoogleScholarGoogle Scholar |
Klimentowski, J. et al., 2007, MNRAS, 378, 353
| Crossref | GoogleScholarGoogle Scholar |
Klypin, A., Kravtsov, A. V., Valenzuela, O. and Prada, F., 1999, ApJ, 522, 82
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXlvFalsLY%3D&md5=23414bd8a4ea23bff16b9b2d30a7edd1CAS |
Knebe, A., Arnold, B., Power, C. and Gibson, B. K., 2008, MNRAS, 386, 1029
| Crossref | GoogleScholarGoogle Scholar |
Koch, A. and Grebel, E. K., 2006, AJ, 131, 1405
Koposov, S. E. et al., 2009, ApJ, 696, 2179
| Crossref | GoogleScholarGoogle Scholar |
Koposov, S. E., Rix, H.-W. and Hogg, D. W., 2010, ApJ, 712, 260
| Crossref | GoogleScholarGoogle Scholar |
Kormendy, J., Drory, N., Bender, R. and Cornell, M. E., 2010, ApJ, 723, 54
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhsFGksr%2FK&md5=b3f6b5e041963c5c27278c89edcd4e7fCAS |
Kowalski, M. et al., 2008, ApJ, 686, 749
| Crossref | GoogleScholarGoogle Scholar |
Kravtsov, A. V., Gnedin, O. Y. and Klypin, A. A., 2004, ApJ, 609, 482
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXms1aisL8%3D&md5=028020222c72037ab3ce76eeb1cd8515CAS |
Kroupa, P., 1997, NewA, 2, 139
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXmsVersb0%3D&md5=0399b3858d4425633edac751673ccb9eCAS |
Kroupa, P., 1998, MNRAS, 300, 200
| Crossref | GoogleScholarGoogle Scholar |
Kroupa, P., 2008, LNP, 760, 181
Kroupa, P., 2011, Stellar Clusters & Associations: ARIA Workshop on Gaia, 17, arXiv:astroph/1111.5613
Kroupa, P., Theis, C. and Boily, C. M., 2005, A&A, 431, 517
Kroupa, P. et al., 2010, A&A, 523, A32
Kroupa, P., et al., 2012, arXiv:astro-ph/1112.3340
Kunkel, W. E., 1979, ApJ, 228, 718
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaE1MXhslOqtLo%3D&md5=be99208ad159a556cdbc3e76ecc8c291CAS |
Küpper, A. H. W., Kroupa, P., Baumgardt, H. and Heggie, D. C., 2010, MNRAS, 401, 105
| Crossref | GoogleScholarGoogle Scholar |
Lada, C. J. and Lada, E. A., 2003, ARA&A, 41, 57
| Crossref | GoogleScholarGoogle Scholar |
Leauthaud, A. et al., 2012, ApJ, 744, 159
| Crossref | GoogleScholarGoogle Scholar |
Lee, J. and Komatsu, E., 2010, ApJ, 718, 60
| Crossref | GoogleScholarGoogle Scholar |
Li, Y.-S. and Helmi, A., 2008, MNRAS, 385, 1365
| Crossref | GoogleScholarGoogle Scholar |
Li, B. and Zhao, H., 2009, PhRvD, 80, 064007
Libeskind, N. I., Frenk, C. S., Cole, S., Jenkins, A. and Helly, J. C., 2009, MNRAS, 399, 550
| Crossref | GoogleScholarGoogle Scholar |
Libeskind, N. I., Knebe, A., Hoffman, Y., Gottlöber, S., Yepes, G. and Steinmetz, M., 2011, MNRAS, 411, 1525
Liesenborgs, J., de Rijcke, S., Dejonghe, H. and Bekaert, P., 2008, MNRAS, 389, 415
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtFCit77N&md5=cfd801b2507539d57892562aaf6f323aCAS |
Lisker, T., 2009, AN, 330, 1043
Liu, H. & Li, T.-P., 2012, arXiv:astro-ph/1203.5720
Llinares, C., Knebe, A. and Zhao, H., 2008, MNRAS, 391, 1778
| Crossref | GoogleScholarGoogle Scholar |
Lokas, E. L., 2011, AcPPB, 42, 2185
| 1:CAS:528:DC%2BC38XnvFGhsw%3D%3D&md5=ebff36b4b324ec8b4a78cc6cda053185CAS |
Lovell, M. R., Eke, V. R., Frenk, C. S. and Jenkins, A., 2011, MNRAS, 413, 3013
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvFeqtrg%3D&md5=a24d3f98b836bc0287fde914154ca1f9CAS |
Lynden-Bell, D., 1976, MNRAS, 174, 695
| 1:CAS:528:DyaE28XhsFOrurs%3D&md5=7c89cb79f3db151b5009353ad6c35bd1CAS |
Macciò, A. V. and Fontanot, F., 2010, MNRAS, 404, L16
Macciò, A. V., Kang, X. and Moore, B., 2009, ApJL, 692, 109
| Crossref | GoogleScholarGoogle Scholar |
Macciò, A. V., Kang, X., Fontanot, F., Somerville, R. S., Koposov, S. and Monaco, P., 2010, MNRAS, 402, 1995
| Crossref | GoogleScholarGoogle Scholar |
Macciò, A. V., Paduroiu, S., Anderhalden, D., Schneider, A. & Moore, B., 2012, MNRAS, in press, arXiv:astro-ph/1202.1282
Maciejewski, M., Vogelsberger, M., White, S. D. M. and Springel, V., 2011, MNRAS, 415, 2475
| Crossref | GoogleScholarGoogle Scholar |
Mackey, A. D. and van den Bergh, S., 2005, MNRAS, 360, 631
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXmtl2ns7s%3D&md5=af83b881527a1ba7811f297aea7fd1a3CAS |
Mahdavi, A., Hoekstra, H., Babul, A., Balam, D. D. and Capak, P. L., 2007, ApJ, 668, 806
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtlaksrvM&md5=a3e4d3f81305153ad8066cfdbf0fef6fCAS |
Majewski, S. R., Skrutskie, M. F., Weinberg, M. D. and Ostheimer, J. C., 2003, ApJ, 599, 1082
| Crossref | GoogleScholarGoogle Scholar |
Marino, A., Bianchi, L., Rampazzo, R., Buson, L. M. and Bettoni, D., 2010, A&A, 511, 29
Marks, M. and Kroupa, P., 2010, MNRAS, 406, 2000
| 1:CAS:528:DC%2BC3cXhtFGnurrF&md5=b945cdacfae03f1a217fde16278be464CAS |
Marra, V., Pääkkänen, M. & Valkenburg, W., 2012, arXiv:astro-ph/1203.2180
Martig, M., Bournaud, F., Croton, D. J., Dekel, A. & Teyssier, R., 2012, arXiv:astro-ph/1201.1079
Martínez-Delgado, D., Gòmez-Flechoso, M. Á., Aparicio, A. and Carrera, R., 2004, ApJ, 601, 242
| Crossref | GoogleScholarGoogle Scholar |
Martínez-Delgado, D. et al., 2010, AJ, 140, 962
Martinez-Delgado, D. et al., 2012, ApJ, 748, 24
Mateo, M. L., 1998, ARA&A, 36, 435
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXmsFGqsr8%3D&md5=c1b10c9b0d18c5375e4bc6dc5bf398c9CAS |
Mateo, M., Olszewski, E. W., Pryor, C., Welch, D. L. and Fischer, P., 1993, AJ, 105, 510
Mayer, L. et al., 2001, ApJ, 559, 754
| Crossref | GoogleScholarGoogle Scholar |
McGaugh, S. S., 2004, ApJ, 609, 652
| Crossref | GoogleScholarGoogle Scholar |
McGaugh, S. S., 2005, ApJ, 632, 859
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtlSjs7jN&md5=da336fcd1845a345102c696ce78bcb8fCAS |
McGaugh, S. S., 2011, PhRvL, 106, 121303
McGaugh, S. S., 2012, AJ, 143, 40
McGaugh, S. S. and de Blok, W. J. G., 1998, ApJ, 499, 41
| Crossref | GoogleScholarGoogle Scholar |
McGaugh, S. S. and Wolf, J., 2010, ApJ, 722, 248
| Crossref | GoogleScholarGoogle Scholar |
McGaugh, S. S., Schombert, J. M., de Blok, W. J. G. and Zagursky, M. J., 2010, ApJL, 708, 14
| Crossref | GoogleScholarGoogle Scholar |
Menci, N., Fiore, F. and Lamastra, A., 2012, MNRAS, 421, 2384
Merrifield, M. R., 2002, in The Shapes of Galaxies and Their Dark Haloes, Proc. of the Yale Cosmology Workshop, ed. P. Natarajan (Singapore: World Scientific Publishing), 170
Metz, M. and Kroupa, P., 2007, MNRAS, 376, 387
| Crossref | GoogleScholarGoogle Scholar |
Metz, M., Kroupa, P. and Jerjen, H., 2007, MNRAS, 374, 1125
| Crossref | GoogleScholarGoogle Scholar |
Metz, M., Kroupa, P. and Libeskind, N. I., 2008, ApJ, 680, 287
| Crossref | GoogleScholarGoogle Scholar |
Metz, M., Kroupa, P. and Jerjen, H., 2009a, MNRAS, 394, 2223
| Crossref | GoogleScholarGoogle Scholar |
Metz, M., Kroupa, P., Theis, C., Hensler, G. and Jerjen, H., 2009b, ApJ, 697, 269
| Crossref | GoogleScholarGoogle Scholar |
Mieske, S., Hilker, M. and Infante, L., 2002, A&A, 383, 823
Mieske, S., Hilker, M. and Misgeld, I., 2012, A&A, 537, A3
Milgrom, M., 1983a, ApJ, 270, 365
| Crossref | GoogleScholarGoogle Scholar |
Milgrom, M., 1983b, ApJ, 270, 371
| Crossref | GoogleScholarGoogle Scholar |
Milgrom, M., 1983c, ApJ, 270, 384
| Crossref | GoogleScholarGoogle Scholar |
Milgrom, M., 1999, PhLA, 253, 273
| 1:CAS:528:DyaK1MXitV2hurw%3D&md5=dc634d1cce0dbaff19703516c8e409dbCAS |
Milgrom, M., 2007, ApJL, 667, 45
| Crossref | GoogleScholarGoogle Scholar |
Milgrom, M., 2009, PhRvD, 80, 123536
Milgrom, M., 2010, MNRAS, 403, 886
| Crossref | GoogleScholarGoogle Scholar |
Mirabel, I. F., Dottori, H. and Lutz, D., 1992, A&A, 256, 19
Miralles-Caballero, D., Colina, L. and Arribas, S., 2012, A&A, 538, 61
Misgeld, I. and Hilker, M., 2011, MNRAS, 414, 3699
| Crossref | GoogleScholarGoogle Scholar |
Modesto, L. & Randono, A., 2010, arXiv:hep-th/1003.1998
Moffat, J. W., 2006, JCAP, 3, 4
Moffat, J. W. and Toth, V. T., 2009a, MNRAS, 397, 1885
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtFGmurvL&md5=76e04189d933fd3a03037e0187f7380cCAS |
Moffat, J. W. and Toth, V. T., 2009b, CQGra, 26, 085002
| Crossref | GoogleScholarGoogle Scholar |
Moore, B. et al., 1999, ApJL, 524, 19
| Crossref | GoogleScholarGoogle Scholar |
Murray, N., 2009, ApJ, 691, 946
| Crossref | GoogleScholarGoogle Scholar |
Nagashima, M. et al., 2005, MNRAS, 363, L31
Navarro, J. F. and Benz, W., 1991, ApJ, 380, 320
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXmvVyqt7Y%3D&md5=c42a8c619d05044168d9701bf3bfa240CAS |
Nichols, M. and Bland-Hawthorn, J., 2011, ApJ, 732, 17
| Crossref | GoogleScholarGoogle Scholar |
Nusser, A., 2002, MNRAS, 331, 909
| Crossref | GoogleScholarGoogle Scholar |
Nusser, A., Gubser, S. S. and Peebles, P. J., 2005, PhRvD, 71, 083505
Okabe, N. and Umetsu, K., 2008, PASJ, 60, 345
| 1:CAS:528:DC%2BD1cXnvFCju70%3D&md5=eeb1bde6bde2b14929aec629e96bf4f2CAS |
Okamoto, T. and Frenk, C. S., 2009, MNRAS, 399, L174
Okazaki, T. and Taniguchi, Y., 2000, ApJ, 543, 149
| Crossref | GoogleScholarGoogle Scholar |
Olling, R. P. and Merrifield, M. R., 2000, MNRAS, 311, 361
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXpvVequw%3D%3D&md5=392ebcc3e59d55fc04a2e8e3e6065685CAS |
Olling, R. P. and Merrifield, M. R., 2001, MNRAS, 326, 164
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXntFGru7Y%3D&md5=76a1fa64c0ae8cb6628b505629634ef5CAS |
Opik, E., 1922, ApJ, 55, 406
| Crossref | GoogleScholarGoogle Scholar |
Pawlowski, M. S., Kroupa, P. and de Boer, K. S., 2011, A&A, 532, A118
Pawlowski, M., Kroupa, P., Angus, G., de Boer, K. S., Famaey, B. & Hensler, G., 2012a, MNRAS, in press, arXiv:astro-ph/1204.6039
Pawlowski, M., Pamm-Altenburg, J. & Kroupa, P., 2012b, MNRAS, in press, arXiv:astro-ph/1204.5176
Peebles, P. J. E. and Nusser, A., 2010, Natur, 465, 565
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXmvFWksLw%3D&md5=bf0404506af2348a49a517538d61156cCAS |
Perlmutter, S. et al., 1999, ApJ, 517, 565
| Crossref | GoogleScholarGoogle Scholar |
Pflamm-Altenburg, J. and Kroupa, P., 2008, Natur, 455, 641
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtF2hsb3L&md5=719b51a9eb7f124744cc5f49834993f1CAS |
Pflamm-Altenburg, J. and Kroupa, P., 2009, ApJ, 706, 516
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhsFOmtbzE&md5=56dfcaece6d6e76777237fb6c19faad3CAS |
Piontek, F. and Steinmetz, M., 2011, MNRAS, 410, 2625
| Crossref | GoogleScholarGoogle Scholar |
Pipino, A., Devriendt, J. E. G., Thomas, D., Silk, J. and Kaviraj, S., 2009, A&A, 505, 1075
| 1:CAS:528:DC%2BD1MXhsFaqu7nM&md5=985313ed0d96caf83f1b366474245efcCAS |
Popper, K., 1935, Logik der Forschung (Vienna: Julius Springer)
Popper, K., 1957, The Poverty of Historicism (London: Routledge)
Primack, J. R., 2009, AIPCS, 1166, 3
| 1:CAS:528:DC%2BD1MXhtFaks7vF&md5=4c3573d1d7525cae8538ec88f178acccCAS |
Recchi, S., Theis, C., Kroupa, P. and Hensler, G., 2007, A&A, 470, L5
| 1:CAS:528:DC%2BD2sXhtVSrurbF&md5=f1fe41f962ba3582d8e00aa76ce3b659CAS |
Recchi, S., Calura, F. and Kroupa, P., 2009, A&A, 499, 711
| 1:CAS:528:DC%2BD1MXpsVekur4%3D&md5=d890c2b31447d586a095a2f7997f297fCAS |
Reshetnikov, V. and Combes, F., 1997, A&A, 324, 80
Reverte, D., Vílchez, J. M., Hernández-Fernández, J. D. and Iglesias-Páramo, J., 2007, AJ, 133, 705
| 1:CAS:528:DC%2BD2sXislWlu7w%3D&md5=704323efc0983509114499003080ede4CAS |
Riess, A. G. et al., 1998, AJ, 116, 1009
Rubin, V. C. and Ford, W. K., 1970, ApJ, 159, 379
| Crossref | GoogleScholarGoogle Scholar |
Ruzicka, A., Palous, J. and Theis, C., 2007, A&A, 461, 155
| 1:CAS:528:DC%2BD2sXivVOnsr8%3D&md5=70fd45f1bb4c861588320f834d3ef12dCAS |
Sale, S. E. et al., 2010, MNRAS, 402, 713
| Crossref | GoogleScholarGoogle Scholar |
Samland, M., 2004, PASA, 21, 175
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXntFOhsrs%3D&md5=63fe160ee8088a75ac1deeaaa816fca4CAS |
Sand, D. J., et al., 2011, arXiv:astro-ph/1111.6608
Sanders, R. H., 2005, MNRAS, 363, 459
Sanders, R. H., 2009, AdAst, 2009, 752439
Sanders, R. H., 2010a, The Dark Matter Problem: A Historical Perspective (Cambridge: Cambridge University Press)
Sanders, R. H., 2010b, MNRAS, 407, 1128
| Crossref | GoogleScholarGoogle Scholar |
Sanders, R. H., 2012, MNRAS, 422, 21
Sato, K., 1981, MNRAS, 195, 467
Scannapieco, C., et al., 2012, MNRAS, in press, arXiv:astro-ph/1112.0315
Scarpa, R., Marconi, G., Carraro, G., Falomo, R. and Villanova, S., 2011, A&A, 525, A148
Schmidt, B. P. et al., 1998, ApJ, 507, 46
| Crossref | GoogleScholarGoogle Scholar |
Shaya, E., et al., 2009, Astro2010: The Astronomy and Astrophysics Decadal Survey, Science White Papers, no. 274
Skordis, C., 2009, CQGra, 26, 143001
| Crossref | GoogleScholarGoogle Scholar |
Skordis, C., Mota, D. F., Ferreira, P. G. and Boehm, C., 2006, PhRvL, 96, 011301
| 1:STN:280:DC%2BD287gslGgtw%3D%3D&md5=1c77c309163789d039ce9bce10656bc9CAS |
Slosar, A., Melchiorri, A. and Silk, J. I., 2005, PhRvD, 72, 101301
Smale, P. R. and Wiltshire, D. L., 2011, MNRAS, 413, 367
| Crossref | GoogleScholarGoogle Scholar |
Smolin, L., 2006, The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next (Boston: Houghton Mifflin)
Starkman, G. D., Copi, C. J., Huterer, D. & Schwarz, D., 2012, arXiv:astro-ph/1201.2459
Stoehr, F., White, S. D. M., Tormen, G. and Springel, V., 2002, MNRAS, 335, L84
| Crossref | GoogleScholarGoogle Scholar |
Strigari, L. E. and Wechsler, R. H., 2012, ApJ, 749, 75
Strigari, L. E. et al., 2008, Natur, 454, 1096
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVGgtr%2FK&md5=ba73390cc1a15eb643241ef59a18f181CAS |
Swaters, R. A., Sancisi, R., van Albada, T. S. and van der Hulst, J. M., 2011, ApJ, 729, 118
| Crossref | GoogleScholarGoogle Scholar |
Tegmark, M. et al., 2002, ApJ, 571, 191
| Crossref | GoogleScholarGoogle Scholar |
Thomas, D., Maraston, C. and Bender, R., 2002, RvMA, 15, 219
| 1:CAS:528:DC%2BD2cXjvVKit7k%3D&md5=6e7040e5a18424035cae885cc9e888caCAS |
Thompson, R. and Nagamine, K., 2012, MNRAS, 419, 3560
| Crossref | GoogleScholarGoogle Scholar |
Tikhonov, A. V., Gottlöber, S., Yepes, G. and Hoffman, Y., 2009, MNRAS, 399, 1611
| Crossref | GoogleScholarGoogle Scholar |
Tiret, O. and Combes, F., 2007, A&A, 464, 517
| 1:CAS:528:DC%2BD2sXkslersrk%3D&md5=1a94271401501cf5bc7137e5f34a1e69CAS |
Tiret, O. and Combes, F., 2008, ASPC, 396, 259
Tollerud, E. J., Bullock, J. S., Strigari, L. E. and Willman, B., 2008, ApJ, 688, 277
| Crossref | GoogleScholarGoogle Scholar |
Tollerud, E. J et al., 2012, ApJ, 752, 45
Trachternach, C., de Blok, W. J. G., McGaugh, S. S., van der Hulst, J. M. and Dettmar, R.-J., 2009, A&A, 505, 577
| 1:CAS:528:DC%2BD1MXhsFahs7vM&md5=295d3164fcd990d81ef563da41e646bcCAS |
Tran, H. D. et al., 2003, ApJ, 585, 750
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXislWjs7Y%3D&md5=d1891c88a51e469cf1f48e99a04d2e99CAS |
Tsujimoto, T., 2011, ApJ, 736, 113
| Crossref | GoogleScholarGoogle Scholar |
Tsujimoto, T. and Bekki, K., 2012, ApJ, 747, 125
| Crossref | GoogleScholarGoogle Scholar |
Tully, R. B. et al., 2006, AJ, 132, 729
| 1:CAS:528:DC%2BD28XptVejtbk%3D&md5=0d739de4873465204b1327fc87943aefCAS |
van den Aarssen, L. G., Bringmann, T. & Pfrommer, C., 2012, arXiv:astro-ph/1205.5809
Vera-Ciro, C. A. et al., 2011, MNRAS, 416, 1377
| Crossref | GoogleScholarGoogle Scholar |
Vera-Ciro, C. A., Helmi, A., Starkenburg, E. & Breddels, M. A., 2012, MNRAS, submitted, arXiv:astro-ph/1202.6061
Verlinde, E., 2011, JHEP, 4, 29
| Crossref | GoogleScholarGoogle Scholar |
Walcher, C. J., Fried, J. W., Burkert, A. and Klessen, R. S., 2003, A&A, 406, 847
Wang, W. & White, S. D. M., 2012, MNRAS, arXiv:astro-ph/1203.0009v1
Wang, J., Frenk, C. S., Navarro, J. F. & Gao, L., 2012, arXiv:astro-ph/1203.4097v1
Wei, L. H., Kannappan, S. J., Vogel, S. N. and Baker, A. J., 2010, ApJ, 708, 841
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhs1agsLs%3D&md5=d87ea2c1a2ca61e86fa269dc23a33974CAS |
Weidner, C., Kroupa, P. and Larsen, S. S., 2004, MNRAS, 350, 1503
| Crossref | GoogleScholarGoogle Scholar |
Weidner, C., Kroupa, P. and Pflamm-Altenburg, J., 2011, MNRAS, 412, 979
Weilbacher, P. M., Fritze-v. Alvensleben, U., Duc, P.-A. and Fricke, K. J., 2002, ApJL, 579, 79
| Crossref | GoogleScholarGoogle Scholar |
Wess, J. & Akulov, V. P., 1998, Supersymmetry and Quantum Field Theory (New York: Springer)
Wess, J. & Bagger, J., 1992, Supersymmetry and Supergravity (Princeton: Princeton University Press)
Wess, J. and Zumino, B., 1974, NuPhB, 70, 39
Wetzstein, M., Naab, T. and Burkert, A., 2007, MNRAS, 375, 805
| Crossref | GoogleScholarGoogle Scholar |
Whitmore, B. C. et al., 1990, AJ, 100, 1489
Willman, B. & Strader, J., 2012, AJ, submitted, arXiv:astro-ph/1203.2608
Wiltshire, D. L., 2009, PhRvD, 80, 123512
Wolf, J. et al., 2010, MNRAS, 406, 1220
Yagi, M. et al., 2010, AJ, 140, 1814
Yang, Y. and Hammer, F., 2010, ApJL, 725, 24
| Crossref | GoogleScholarGoogle Scholar |
Yao, W.-M. et al., 2006, JPhG, 33, 1
| 1:CAS:528:DC%2BD28XptVGgtro%3D&md5=1b0fbb6ade85c886a48ff6e4e49d97dfCAS |
Yoshida, M. et al., 2008, ApJ, 688, 918
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsFWitbjO&md5=ce41c655507cfea39ec6d22c987b6e65CAS |
Zentner, A. R. and Bullock, J. S., 2003, ApJ, 598, 49
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhs1GktQ%3D%3D&md5=5ac2e760a2453ac5684cf39423c52196CAS |
Zhao, H., 1998, ApJL, 500, 149
| Crossref | GoogleScholarGoogle Scholar |
Zhao, H., 2007, ApJL, 671, 1
| Crossref | GoogleScholarGoogle Scholar |
Zhao, H. S., 2008, JPhCS, 140, 012002
Zhao, H. and Famaey, B., 2010, PhRvD, 81, 087304
Zhao, H. and Li, B., 2010, ApJ, 712, 130
| Crossref | GoogleScholarGoogle Scholar |
Zlosnik, T. G., Ferreira, P. G. and Starkman, G. D., 2007, PhRvD, 75, 044017
Zwicky, F., 1937, ApJ, 86, 217
| Crossref | GoogleScholarGoogle Scholar |
Zwicky, F., 1956, ErNW, 29, 344
1 But the new theory implied a perihelion shift of Mercury, as was observed but not understood with Newton’s theory.
2 At the Aarseth-Nbody meeting in Bonn in December 2011 Sverre Aarseth explained over a Glühwein at the Christmas market why he did not continue his pioneering cosmology work: he left the field because the necessity of introducing dynamically relevant dark matter particles became too speculative in his view. Thereafter Sverre concentrated on developing the Aarseth N-body codes for collisional dynamics research.
3 In some non-Newtonian theories a satellite galaxy may show dynamical differences to the same but isolated dwarf due to the external field effect (see Famaey & McGaugh 2012 for details).
4 TDGs may form from pre-enriched material and during their formation they may capture stars from the interacting galaxies because stars and gas occupy a similar phase-space in disk galaxies. It is therefore expected that TDGs forming today will be metal enriched compared to primordial (type A) dwarfs. Such cases have indeed been observed (Duc & Mirabel 1998; Miralles-Caballero, Colina & Arribas 2012). However, TDGs may also form from the outer metal-poor material of gas-rich disk galaxies and they will then commence to self-enrich therewith following the usual metallicity–luminosity relation of galaxies. Since the majority of TDGs is expected to have formed early in the universe before major enrichment of the gas through star formation, such TDGs will today appear as normal self-enriched dwarf galaxies. Such TDGs, which do follow the metallicity–luminosity relation, may have been observed by Reverte et al. (2007). Thus, the metal-rich criterion is sufficient to identify dwarf galaxies as being TDGs, but if a dwarf galaxy lies on the metallicity–luminosity relation of galaxies it cannot be discarded as being a TDG.
5 We are not considering the trivial ad hock solution that all DM sub-haloes with mass M DM < 1010 M⊙ did not form stars and thus remain dark, because there is no known physical process that could arrange for this to be the case (see Ferrero et al. 2011).
6 Galaxies having such a well defined BTF relation is a major challenge for the SMoC (e.g. McGaugh 2011; Piontek & Steinmetz 2011; McGaugh 2012; Desmond 2012): For each individual DM halo of a given DM mass (i.e. for a given V c), the assembly history is different, and a wide range of baryonic content would be expected and thus a significant variation of M baryons (Disney et al. 2008).
7 On the issue of what constitutes a galaxy in view of the faintest satellites recently discovered, as opposed to being classified as star clusters, see Section 2.
8 A movie visualising the vast polar structure around the Milky Way, by Marcel Pawlowski, is available on YouTube.
9 An accretion origin of the satellite galaxies from dark matter filaments is negated by Angus, Diaferio & Kroupa (2011) and explicitly by Pawlowski et al. (2012a).
10 The contributions by Lovell et al. (2011) and Libeskind et al. (2011) constitute examples of an overly optimistic interpretation of numerical SMoC data in view of the necessity to solve a major problem. See also Footnote 12.
11 The tests were conducted using models that had been computed before the tests were conducted. At the present time this is not possible any longer, because new satellite-galaxy models within the SMoC may be influenced by the posterior need to solve the κ = 0 problem.
12 Perhaps of relevance in this context is the research on the sociology of science by Fanelli (2010) whose abstract reads ‘The growing competition and publish or perish culture in academia might conflict with the objectivity and integrity of research, because it forces scientists to produce ‘publishable’ results at all costs. Papers are less likely to be published and to be cited if they report ‘negative’ results (results that fail to support the tested hypothesis). Therefore, if publication pressures increase scientific bias, the frequency of positive results in the literature should be higher in the more competitive and productive academic environments.’ The study of Fanelli (2010) finds that ‘…these results support the hypothesis that competitive academic environments increase not only scientists’ productivity but also their bias.’ This may be the reason why the academic system of la Grande Nation has allowed France to take leadership on issues pertaining to TDG formation and non-Newtonian/non-Einsteinian gravitational research. In France intellectual freedom is highly cherished and fostered in an academic system without major hierarchies. Germany, being a heavily hierarchical academic environment in which the majority of resources are controlled long-term by merely a few, and the USA, being an extremely competitive and research-grant-driven environment, do not leave much room for such research at the present. In these environments, often the mere opinion of a few is crucial for the success in obtaining research money. A good example of the Fanelli effect can be seen in figure 44 of Famaey & McGaugh (2012) where the constraints on the measured cosmological baryon density are plotted in dependence of time: Prior to the CMB data (around the year 2000) the independent measurements yielded a low density. After the CMB acoustic peak data became available and after it emerged that the previously measured cosmological baryon density was consistently too low to be consistent with the SMoC and the acoustic peak data, the new independent constraints typically and magically began yielding density measurements consistent with the measured acoustic peaks for the SMoC to be correct.
13 This can lead to the erroneous conclusion that TDGs contribute only a small fraction to the dwarf galaxy population. While this is true for the TDGs being formed in the present-day universe, the number of low-mass TDGs formed during the early cosmological era would have been sufficient to account for the observed population of dSph and dE galaxies (Section 3.2.3, Section 13.6).
14 E.g. listing mostly more recent papers: Dekel & Silk (1986); Dekel & Woo (2003); Tollerud et al. (2008); D’Onghia & Lake (2008); Li & Helmi (2008); Macciò, Kang & Moore (2009); Koposov et al. (2009); Okamoto & Frenk (2009); Kirby et al. (2009); Shaya et al. (2009); Busha et al. (2010); Primack (2009); Macciò & Fontanot (2010); Macciò et al. (2010); Cooper et al. (2010); Deason et al. (2011); Nichols & Bland-Hawthorn (2011); Font et al. (2011).
15 This is a true prediction because the data did not exist when Milgrom formulated a non-Newtonian approach in 1983. Alas, modern cosmological jargon often uses the word ‘prediction’ to mean a value calculated within the SMoC in order to account for existing data.
16 As Angus (2009) emphasises, a mass of 11 eV for sterile neutrinos is excluded by cosmological data only if it is assumed that Newton’s laws are correct.
17 That the SMoC with DE does not conserve energy is well known (e.g. Kroupa et al. 2010).
18 For example, if there are two tests of a model, each yielding a confidence of 10–4 that the model represents two different aspects of the data, then the combined confidence is 10–8 if the two tests are independent. Therefore a logarithmic confidence scale is indicated in Figure 14.
19 The most famous example of this is Galileo Galilei’s telescopic observations of heavenly bodies that instantly shattered the since many generations cherished ‘truth’ about the origin, structure and functioning of the universe. Today it is often amusingly questioned how it was possible for educated people to have ignored the evidence shown to them by Galilei through his telescope, or even how it was possible for people of high rank to deny looking through the telescope in the first place. Then, two major intellectual steps had to be taken simultaneously if Galilei's observations were to be grasped by an individual, considering the excellent success of the geocentric model to account for the observed phenomena and the precise predictions it allowed: it had to be accepted that the Sun, and not the Earth, was the centre of the then known universe and it had to be accepted that orbits were Keplerian rather than perfectly circular.

