The Structure of Galaxies I: Surface Photometry Techniques
J. Schombert A B and A. K. Smith AA Department of Physics, University of Oregon, Eugene, OR 97403, USA
B Corresponding author. Email: jschombe@uoregon.edu
Publications of the Astronomical Society of Australia 29(2) 174-192 https://doi.org/10.1071/AS11059
Submitted: 12 October 2011 Accepted: 12 March 2012 Published: 24 April 2012
Journal Compilation © Astronomical Society of Australia 2012
Abstract
This project uses the 2MASS all-sky image database to study the structure of galaxies over a range of luminosities, sizes and morphological types. This first paper in this series will outline the techniques, reliability and data products to our surface photometry program. Our program will analyze all acceptable galaxies (meeting our criteria for isolation from companions and bright stars) from the Revised Shapley–Ames and Uppsala galaxy catalogs. Resulting photometry and surface brightness profiles are released using a transparent scheme of data storage which includes not only all the processed data but knowledge of the processing steps and calibrating parameters.
Keywords: galaxies: photometry — galaxies: structure — methods: data analysis — techniques: image processing — techniques: photometric
1 Introduction
The photometry and structure of galaxies are key testing predictions from galaxy formation scenarios and in understanding the later evolution of galaxies. Photometry reveals the amount and distribution of stellar mass (with proper SED modeling to determine M/L), where the stars are the primary baryonic component for most galaxy types. Multi-color photometry explores the properties of the underlying stellar population (chemical and star formation history). The distribution of light, as given by galaxy structure, is used to deduce the size and shape of the gravitational potential, a primary variable to the fundamental plane (Kormendy 1977). However, where recent semi-analytic formation models have successfully been applied to galaxy morphology, chemical histories, luminosity function, gas fractions and galaxy sizes (Cole et al. 2000), the theoretical world has been strangely quiet on predictions for the structure of galaxies themselves.
The use of structural information varies with galaxy type. For example, structure of early-type galaxies is critical in distinguishing between cold dissipationless collapse versus hierarchical merging scenarios (Conselice 2008). These same models predict the ratio of spheroid to disk galaxies, as well as the distribution of bulge-to-disk ratios (Almeida, Baugh & Lacey 2007), so the structure of early-type galaxies is relevant to these predictions and their structural parameters are of importance to dark matter studies
Both photometric and structural analysis are the domain of galaxy surface photometry (de Vaucouleurs 1948; Fish 1964; Freeman 1970). Surface photometry, the study of extended objects in the sky, has the primary goal of quantifying the 2D light distribution of galaxies (Milvang-Jensen & Jorgensen 1999) and ultimately reducing the isophotes to a 1D set of parameters. Reduction of galaxy images to surface photometry is aided by the fact that, for most morphological types, galaxy isophotes are closely approximated by ellipses. Elliptical isophotes, of course, simply reflect the condition that underlying stellar orbits in galaxies are Keplerian and, even for irregular galaxies, an ellipse is a fair description for isophotes lacking the distorting effects of ongoing star formation or dust extinction.
The reduction of galaxy images to surface brightness profiles was, in the past, a time consuming process due to the amount of user interaction required by the nature of imaging processing. However, advances in computer languages and processing power has simplified many of the initial stages of image analysis to the point where it is currently possible to reduce extremely large numbers of galaxies in less time than that needed to actually construct and test the algorithms. However, galaxies are not uniform in their appearance, and forcing the reduction of their light distributions (either at the 2D or 1D levels) often leads to a loss of potentially valuable information (this is particularly true of late-type galaxies).
The goal of this project is the map the structure of galaxies over a large range of luminosities, sizes and morphological types. To this end, we have extracted a sample of large angular-sized (D > 1 arcmin) galaxies from the 2MASS near-IR all-sky survey. The 2MASS survey is ideal as near-IR wavelengths are dominated by stellar light, the primary baryonic component in galaxies, and minimizes distorting effects due to gas and dust extinction. While 2MASS images are short in exposure time (effectively 7.8 s), there is sufficient S/N to achieve faint surface brightness levels for axial symmetric objects. In addition, 2MASS images provide simultaneous coverage in JHK (i.e. multi-color photometry) in order to study the color gradients, important to population studies.
There is no attempt to obtain a complete sample of galaxies in this project, and galaxies with companions or nearby bright stars are rejected due to complications from overlapping isophotes. Our goal is to analyze as many galaxies in the Revised-Shapley–Ames catalog (RSA, a catalog selected by luminosity) and Uppsala Galaxy Catalog (UGC, an angular limit catalog) which satisfy our criteria of isolation from foreground or background objects. Thus, this series of papers will explore the surface photometry of galaxies in the 2MASS image database over a full range of galaxy morphological types, starting with the early-type systems and proceeding through the Hubble sequence. Our first papers will outline our techniques and statistical methods, focusing in particular on the limits and errors to 2MASS galaxy photometry. Later papers will address each morphological class and the discoveries we make in each category.
We also introduce, in this series of papers, a new avenue for published data access and transparency. We will present all the data contained in our study with the full set of calibrated data along with the scripts used to transform raw image numbers into astronomically meaningful values. This allows any researcher access to the parameters for any galaxy we have reduced and, most importantly, to cross check our results. In addition, we provide all the reduced numbers in XML format, which allows a user to ask for specific parameters seamlessly across the dataset (i.e. make your own tables). Full access to the data can be found at http://abyss.uoregon.edu/~js/sfb.
2 2MASS Imaging Database
The 2MASS project was a NASA ground-based, all-sky, near-IR sky survey (Skrutskie et al. 2006). 2MASS uniformly scanned the entire sky using two 1.3-m telescopes (north KPNO and south CTIO). Each telescope was equipped with a three-channel camera, where each channel consisting of a 256 × 256 HgCdTe detector. Each camera was capable of observing the sky simultaneously at J (1.25 microns), H (1.65 microns), and K (2.17 microns). The 2MASS arrays imaged the sky in a drift-scan mode. Each final pixel consisted of six pointings on the sky for a total integration time of 7.8 s per pixel. The final image frames have a plate scale of one arcsec per pixel.
Any region of the sky is available from 2MASS’s Atlas Image server. However, these images are in the form of sky strips, which rarely conform to the centroids of bright galaxies. Lacking a tool at the 2MASS website to merge sky frames, a short image construction script was developed that introduces a novel combination of network and image processing tools. The script takes a galaxy’s name from a user supplied list. It then parses that name through the NED (NASA’s Extragalactic Database) server to extract correct RA and Dec information. With these coordinates, the script then accesses the 2MASS Atlas Image server extracting the four sky strips to the north, east, west and south of the galaxy center. These four images are than stitched together, using the geometric information found in each frame’s header, to produce a 512 × 512 or 1024 × 1024 sized raw image (image size is irrelevant to the software, these numbers were simply a historically pleasing choice with sufficient sky around each galaxy). Galaxies greater than 5 arcmins in diameter were excluded from the study since the night sky would vary between sky strips for objects larger than a few scans. These image sizes allowed for a sufficient number of pixels to determine sky values, and to exclude any galaxies with companions.
Calibration was provided by the 2MASS project, although we confirmed these values by comparison with galaxy aperture photometry values in the literature. The supplied calibrations were never in difference with aperture values by more than 2% and do not contribute a notable fraction of the error budget. Other relevant information in the scan headers provided information of the original counts and sky conditions. This information was passed to the processing pipeline to be incorporated into our error analysis.
3 Data Reduction
Our surface photometry pipeline used the galaxy photometry package ARCHANGEL (Schombert 2007). ARCHANGEL is a long running software project by one of us (JS) that has its origins in photographic imaging data of the Second Palomar Sky Survey. Its history has extended over four computer languages and five different operating systems. While numerous tools and GUI’s have been developed to provide increasingly sophisticated image analysis capability, the core elements of galaxy surface photometry are 1) global frame cleaning, flattening and sky determination; 2) isophotal fitting (typically with ellipses); and 3) reduction of the 2D information to 1D surface brightness profiles, aperture magnitudes and structural parameter (compactness, asymmetry, etc.). Interpretation of the surface brightness profiles deserves a separate enterprise that involves the specifics of fitting functions and kinematic models and will be addressed in a separate paper.
Image preparation is the first step in an galaxy photometry project. Initial work can range from correcting for instrumental distortions (flattening, dark current, cosmic rays, dead pixels, etc.) to characterizing the properties of a frame (readout noise, geometric distortion, etc.). For this project, the 2MASS project provides calibrated, flattened, kernel smoothed, sky-subtracted images. There are artifacts due to instrument irregularities (e.g. latent images), however, these are treated in the same manner as stellar and other non-galaxian objects.
3.1 Sky Determination
Good galaxy photometry is critically dependent on accurate knowledge of the sky value. For, in the outer regions of galaxies, the galaxy luminosity per pixel is a small percentage of the sky flux. Thus, errors in the sky value will dominate Poisson noise or calibration errors. Errors in the sky value are limited by 1) quality of the flatness to an image and 2) its proper assessment using regions that are free of artifacts, foreground stars and galaxy or background light.
With regard to image quality, the 2MASS observing scheme (co-added drift scans) produced extremely flat, uniform images. Our estimates, during the initial stages of this project, was that the sky values had a mean variation on small scales (estimated from hundreds of images) of only 0.1%. No coarse gradients or other large scale features were detected.
This means that the greatest source of uncertainty in determining a global sky value is careful selection of the proper pixels free of any contaminating objects. For this reason, based on experience working with low surface brightness galaxies data from optical CCD’s, the use of sky boxes is recommended. Sky determination by sky boxes involves an interaction with the data frame where the user selects areas, clear of obvious stellar or galaxy sources, which are then summed and averaged. The pixels in each sky box are also clipped at the 3σ level to eliminate ‘hot’ pixels and cosmic rays.
This procedure has the advantage in that if ten or more sky boxes are measured, then the user not only determines the mean and standard deviation for every box but also extracts the mean of the mean values for all the boxes, and the standard deviation for that total average. It is the variation between the mean box values that is the true measure of the correct sky value and is the primary estimate of error at low galaxy light levels.
The 2MASS image frames are sky subtracted, i.e. the sky value is zero. The typical standard deviation on the sky was 0.11 DN (which corresponds to 23.2 J-mag arcsec–2) and only varied by 0.05 between the frames examined for this project. Our own estimates of the sky value using our sky box method only deviated from zero by 0.04 DN, less than 30% the variance on the 2MASS project’s sky value. While we adopted our sky values, there was no significant difference than the value of zero provided by 2MASS. The actual sky brightness was between 15.5 and 16.3 J-mag arcsec–2 for the frames we examined, remarkably consistent considering the variability of the near-IR sky.
3.2 Isophotal Analysis
Once sky has been determined, and gross contaminating features have been removed, the next step towards surface photometry is the extraction of isophotal values as a function of radius. As mentioned above, isophotes in galaxies are typically elliptical in shape. This is a convenient description for isophotes as an ellipse only has its center, position angle and eccentricity as variables.
Fitting a best ellipse to a set of intensity values in a 2D image is a relatively straight forward technique that has been pioneered by Cawson et al. (1987) and refined by Jedrzejewski (1987) (see also an excellent review by Milvang-Jensen & Jorgensen 1999). The core routine from these techniques (PROF) was eventually adopted by STSDAS IRAF (i.e. ELLIPSE). The primary fitting routine for this project follows the same techniques (in fact, uses much of the identical FORTRAN code from the original GASP package of Cawson with some notable additions).
These codes start at some intermediate distance from the galaxy core with an estimated x–y center, position angle and eccentricity then begin sampling the pixel data around the given ellipse. The variation in intensity values around the ellipse can be expressed as a Fourier series with small second order terms. Next, an iterative least-squares procedure adjusts the ellipse parameters searching for a best fit, i.e. minimized coefficients. There are several halting conditions, such as maximum number of iterations or minimal/extreme change in the coefficients, which then moves the ellipse outward for another round of iterations. Once a stopping condition is met (edge of the frame or sufficiently small change in the isophote intensity), the routine returns to the start radius and completes the inner portion of the galaxy. A side benefit to above procedure is that the cos(4θ) components to each isophote fit are easily extracted, which provides a direct measure of the geometry of the isophote (i.e. boxy versus disk-like, Jedrzejewski 1987).
One addition, from the original routines, is the ability to clean (i.e. mask) pixels along an isophote. Basically, this routine first allows a few iterations to determine a mean intensity and RMS around the ellipse. Any pixels above (or below) a multiple of the RMS (i.e. 3σ) are set to not-a-number (NaN) and ignored by further processing. Due to the fact that all objects, stars and galaxies, have faint wings, a growth factor is applied to the masked regions. While this process is efficient in early-type galaxies with well defined isophotes, it may be incorrect in late-type galaxies with bumpy spiral arms and Hii regions. The fitting will be smoother, but the resulting isophotometry will be underestimated.
An example of the above procedure is shown in Figure 1, the J image of the late-type galaxy NGC 157. Converging ellipses are shown in blue, best fits (but exceeding a maximum iteration value) are shown in green. Even though this galaxy has axial symmetric, there are several regions of star formation which could distort the ellipse fitting. However, the subtraction algorithm works through the irregular light distribution to find reasonable fits (masked pixels are later restored to the mean isophotal value for aperture luminosities determination). For early-type galaxies this is not an issue, but we will revisit this problem during our analysis of late-type systems.

|
3.3 Aperture Photometry
Historically, determining isophotal or aperture magnitudes has required the use of curves of growth (de Vaucouleurs 1977), and assumptions to the overall structure of galaxies, in order to capture the luminosity in the outer regions. The movement from photographic materials to digital imaging results in a more accurate measure of the outer luminosity of galaxies and curves of growth are no longer required to obtain total magnitudes.
This is not to say that galaxy photometry is not without its challenges. For example, an obvious problem to measuring galaxy magnitudes is separating galaxy light from foreground stars or background galaxies. Fortunately, a byproduct of the ellipse fitting routine is the elimination of non-galaxy sources by the cleaning algorithms. The ellipse fitting routine replaces bad pixels with a non-value (NaN). It is a simple procedure to replace those masked pixels with intensity values interpolated from the nearest ellipse values. This results in a more accurate measurement of the galaxy light through any aperture.
An example of the output from the cleaning procedures is shown in Figure 2 for the early-type galaxy NGC 3087. The visual difference is impressive, although the difference in the total flux measurements with versus without star subtraction is only 3% since the stars only obscure a very small portion of the typical galaxy. While the difference is small, there is still merit in using star subtracted frames for a clearer view of the morphological appearance of galaxies and, for late-type galaxies, a clearer view of the color distribution.

|
The greatest challenge in galaxy photometry is correctly determining the total luminosity since this is equivalent to the total stellar mass for a galaxy (using an assumed M/L and ignoring internal extinction effects). The difficulty is that a significant portion of a galaxy’s total light is in the outer regions, where the S/N per pixel is the lowest. This is demonstrated in Figure 3, a plot of elliptical aperture magnitude for the galaxy NGC 3087 as a function of radius (arcsec). The luminosity is plotted as the ratio of the aperture luminosity to the total luminosity. One can see that over 50% of the total luminosity of a galaxy is contained in the outer 95% of a galaxy’s area.

|
Since a majority of the luminosity of galaxy is in the region of its light distribution with the lowest S/N per pixel, this places a high burden on the algorithms that are attempted to measure this luminosity. In particular, the pixel-to-pixel noise will quickly dominate the error budget. Traditional methods of plotting luminosity as a function of radius, and mapping the total magnitude to a convergence point, will frequently fail when small errors in the sky value produce a divergence for the aperture luminosities.
The procedure adopted by this project is to allow the surface photometry to guide the aperture pixels, where the apertures are defined by the best-fit ellipses (a visual example is found in figure 9 of Schombert 2007). In other words, in the outer regions, where the S/N per pixel is low, rather than summing the pixels, our algorithms use the mean isophotal value at that radius for the pixel’s intensity. This procedure assumes strong symmetry to the galaxy’s light distribution and will be more effective for early-type galaxies than late-type galaxies.

|

|

|

|

|

|
As discussed in our photometry package paper (Schombert 2007), it was rare to fail to find convergence of the luminosity-radius plot using this technique. The final value is calculated by fitting an asymptotic function to the data points at large radius, with the calculated magnitude stored in our XML files as tot_sfb_mag. An example of this procedure, for clarity, is found in Appendix B.
Extracted during the same processing for total magnitude is the total size of the galaxy, defined as the radius where the total luminosity is reached. However, this value is extremely uncertain as even small errors in the total magnitude reflect into large changes in the radius where the total magnitude is reached. However, total radius is correlated with other characteristic scalelengths (such as half-light radius, isophotal radius and effective radius) which will be discussed in a later paper.
3.4 Surface Photometry
The last step in characterizing the structure of galaxies is conversion of the 2D isophotes into a 1D surface brightness profile. The elliptical isophotes are converted to luminosity density (magnitudes arcsec–2) by subtracting sky, dividing by the plate scale (squared) and adding the appropriate photometric constant. For this study, all structural parameters are determined in the uncorrected units (i.e. surface brightness without corrections for galactic extinction or cosmological dimming, radii in arcsec rather than kpc).
As with all reduction techniques, the goal is to summarize complex data (e.g. an image) into some set of parameters which are representative of the original data, but which allows for comparison to other data. It is also assumed that there is no critical loss of information in the reduction process or that the loss is not relevant to the science questions being addressed. With respect to surface photometry, this tension between the images and reduced data is reflected in the loss of morphological information with the conversion of a galaxy’s light distribution to a surface brightness profile. However, even in this circumstance, some morphological information is preserved, e.g. a bulge+disk versus a power-law profile.
A second concern for data reduction techniques is repeatability. In our current era of fast digital imaging, repeatability for the original images is high, varying only as given by the observing conditions (this differs from the photographic era where the ‘art’ of astrophotography produced a wide range in image quality). The many steps between image and surface brightness profile raises the concern that different methods would produce wildly different results.
Repeatability usually depends on comparison of the same galaxy from different projects. Comparison to 2MASS profiles is not meaningful as it has already been demonstrated (Schombert 2007) that their reduction pipeline improperly reduced their galaxy images by distorting the ellipse fitting and underestimating the sky value (see Appendix A and Schombert 2011).
In order to demonstrate repeatability we have compared our current data with a set of ellipticals reduced by one us (JS) for a study of cluster galaxies (Schombert 1986). One such comparison is shown in Figure 4 where we overlay the V and J surface brightness profiles for the Coma elliptical NGC 4881 (the V data has been corrected for V – J = 2.57, taken from NED). NGC 4881 is a popular surface brightness target as its elliptical shape is close to a perfect circle and its profile is r1/4 over a large range of surface brightness. The close correspondence between the two profiles is remarkable since the V data is taken from PDS scans of Palomar Schmidt photographic material over 20 years ago. There is a slight difference in slope for the two profiles, however, due to the blue nature of this slope, this is more than likely the result of a small metallicity gradient (i.e. negative V – J slope).
Of the 15 galaxies in common with the Schombert (1986) sample, 80% were in good agreement with the new J data, meaning the slope of the profiles agree within the errors and the photometric offset corresponds to within 20% of the V – J color (see a later paper for more detailed discussion of color profiles). Disagreements were typically due to strong color gradients or poor calibration in the V data (based on recent V aperture measurements). While this does not prove absolute repeatability of our current dataset, it does give us some confidence in the reliability of the profiles. In addition, it will be argued in a later paper, that the largest source of uncertainty in determining the structure of galaxies is not the errors in the photometry, but rather the interpretation of the profiles.
3.5 PSF Effects
The inner regions of any galaxy surface brightness profile will be distorted by the inherent limitations of atmospheric and detector resolution. This distortion is represented by the point source function (PSF), and the effects of the PSF on the surface brightness profiles of galaxies is well studied by Saglia et al. (1993). The 2MASS PSF is also well documented for 2MASS images (Jarrett et al. 2000), and is gaussian in shape with typical FWHM’s ranging from 2.5 to 3 arcsec.
The PSF of an image is produced when atmospheric and detector distortion moves core photons to larger radii. The resulting surface brightness profile is slightly dimmer at the core, and slightly brighter at the wings of the PSF. For the 2MASS images, the PSF is primarily driven by the large detector pixels used (2 arcsec), but some resolution is recovered by a dithering observing strategy. For a majority of the 2MASS images, the mean 2MASS PSF is determined to have a FWHM of 2.5 arcsec, although when atmospheric seeing degrades below this level, the FWHM increases (although 2MASS restricted data acquisition during poor seeing conditions). For our experiments we have assumed a FWHM of 2.5 arcsec.
To generate a 2MASS PSF, we have taken the gaussian description from Saglia et al. (1993, see their figure 6) where the FWHM/2re ratio is the model variable (re is the effective scalelength for an assumed r1/4 profile shape, see Appendix C for how these simulations are generated). As a test simulation, we have adopted a pure r1/4 shape using mean parameter values from our elliptical sample (re = 8.5 arcsec μe = 16.7 K-mag arcsec–2). Note that this is a poor description of the outer regions of galaxies, but an adequate one for the core regions (Schombert 1987). For a FWHM of 2.5, this corresponds to a Saglia PSF of 0.15. The resulting profile is shown in Figure 5. Note that the 2MASS PSF distorts a galaxy’s surface brightness profile out to at least a radius of 5 arcsec.
As an additional test of the effects of the PSF, we compare the 2MASS profile for NGC 7097 with a deep K image from Kent (2012) shown in Figure 6. The profiles agree fainter than 16 K-mag arcsec–2, but the effects of the PSF distortion are visible in the 2MASS data at brighter surface brightnesses (the Kent data was taking under sub-arcsec seeing with 0.2 arcsec pixels). We correct the 2MASS profile with two FWHM’s of 2.5 (blue curve) and 3.5 (green curve) arcsec. While a FWHM of 2.5 arcsec is typical for 2MASS images, the 3.5 arcsec PSF is a better fit producing agreement with pointed observations down to a radius of 1.5 arcsec. Information below that radius point is difficult to recover without some assumptions to the shape of the core region of a galaxy, a problematic approach given the core/cusp dilemma for ellipticals.
The shape of the PSF from Figure 6 is salient to fitting surface brightness profiles. One could attempt to correct a galaxy’s surface brightness profile, thus, gaining a few arcsec of resolution at the core. However, this makes the assumption of an underlying r1/4 profile which, while a reasonable assumption for early-type galaxies, defeats the purpose of actually measuring the structure of galaxies. The more honest evaluation of the profiles would be to only fit 2MASS galaxy profiles outside the 5 arcsec radius and this study will apply this 5 arcsec inner limit, even when correction to an r1/4 profile seems appropriate.
3.6 Error Analysis
The source of error in surface brightness profiles is threefold: 1) error in the detector and photometric calibrations, 2) RMS noise around the best fit ellipse (this includes error due to deviations from an elliptical shape for a particular isophote) and 3) error in the value of sky. Numerical experiments with ellipse fitting on both symmetric and irregular galaxies has shown that the surface photometric values are very robust to variations in the ellipse parameters, contributing less than 2% to the photometric noise (Schombert 1986). Cleaning too many pixels can have a negative effect on the inner regions of a galaxy, but is negligible in the outer regions where the S/N is the lowest.
Addressing each of these sources in order, the detector and photometric calibration for pointed observations can be problematic. However, the 2MASS sky survey calibrates many times a night and the characteristics of the detectors are extremely well known. The observing strategy eliminates most pixel-to-pixel errors. Given the project reports on the photometric calibration (Skrutskie et al. 2006), we assume the calibration error is negligible.
The RMS noise around each ellipse is calculable and stored in the raw data files. For most regular shaped galaxies, the S/N does not decrease below five until the surface brightness reaches one magnitude below sky. Until this point, the RMS errors are strictly photon count limited and decrease in importance as the number of pixels in the ellipse increases. For the outer isophotes, where the number of pixels is large, the calculated RMS on the mean intensity produces an artificially low estimate of the error. For, while the value of the mean intensity is more accurate because of increases in N, its absolute value is more uncertain due to sky error.
Of greater concern is the exact knowledge of the sky value. Figure 7 displays the error budget for a typical elliptical comparing the error due to RMS noise and the error associated with the knowledge of the correct sky value. Typically, at the point where the effective radius is reached, the sky error dominates the surface brightness error budget. Since a majority of a galaxy’s light is beyond this radius, then any parameter that involves the total luminosity of the galaxy is limited by the correct knowledge of the sky value.
With respect to the total error values for the surface brightness profiles, Figure 8 displays all the error values assigned to each surface brightness point in our elliptical sample. These values are the quadrature sum of the RMS noise and the error on the sky value. Given the narrow range of sky variation and common detector, the errors are remarkable consistent with surface brightness. Basically, the errors grow larger than the meaning of the observations below 25 J-mag arcsec–2 (which corresponds to roughly 27 V-mag arcsec–2). Thus, the data presented here is similar to deep optical samples in the past (Schombert 1986).
3.7 Fitting Functions
The last stage in the data reduction pipeline is the fitting of the uncorrected surface brightness profiles to various fitting functions. The choice to fit to the uncorrected magnitudes and radii in arcsec merely allows other researchers to apply their own corrections. As extinction and distance corrections are in the data files, this becomes a stylistic point rather than a critical part of the reduction process. All the fitting variables can be corrected for extinction and distance without changing the quality of the fits themselves.
The profiles in this study are fit to the three most popular fitting functions 1) de Vaucouleurs r1/4 (de Vaucouleurs 1959), 2) Sérsic (Graham & Driver 2005) and 3) r1/4 bulge plus exponential disk (bulge+disk, Freeman 1970; Kent 1985). While there are other fitting functions in the literature (Oemler 1976), these three are mathematically equivalent to any other function. The r1/4 law has two parameters (effective surface brightness, μe, and effective radius, re). The Sérsic function has three parameters (μe, re and the power law index, n). The bulge+disk function has four parameters (bulge μe, re, central disk surface brightness, μo, and disk scalelength, α, sometimes called h in the literature). Note that a pure disk profile is simply a bulge+disk fit with a zero sized bulge.
This project’s procedures for applying each function deviated from accepted practices in the literature. The r1/4 law is fit by plotting the data in surface brightness versus r1/4 space and isolating the region of the galaxy that displays a straight line for fitting, ignoring other data. Typically, the r1/4 region of a galaxy’s surface brightness profile is the middle portion of a galaxy’s profile (between 14 and 17 J-mag arcsec–2), where the inner regions display the core/cusp dilemma and the outer regions develop curvature in a luminosity dependent fashion (Schombert 1986). While this is a subjective fitting procedure (visual inspection determines the region to fit), fits made to the entire profile leads to erroneous parameters since galaxies are simply not r1/4 in their shape over all regions and luminosities.
The Sérsic function is fit over the region of a galaxy profile outside the seeing effected core and stopping where the error in the surface brightness exceeds one mag arcsec–2. This procedure is automatic and, of the three fitting functions, is the most objective. In general, a Sérsic fit is superior to an r1/4 fit simply because the n index adds an additional free parameter that primarily branches the non-r1/4 portion of the outer envelope of a galaxy. We will explore this in greater detail in a later paper.
The bulge+disk fitting follows the prescription given by Schombert & Bothun (1987). First, a linear portion of a galaxy’s outer region (i.e. the disk) is visually located and fit to an exponential (a straight line in mag arcsec–2 versus radius space). Holding the slope of the disk fit constant (but allowing the central surface brightness to vary) a r–1/4 fit is applied to the inner regions (the bulge). The three parameter bulge+disk fit is recorded, than the constraint on the disk slope is released and a four parameter fit is made. Strong changes in the disk slope between the first and second fits signals a galaxy which did not have a strong disk component at the start, but rather is dominated by a power-law bulge.
A technical note, fits made with the bulge+disk function assume rotation generated circular symmetry to the galaxy, so the major axis of each ellipse is used on the assumption that the minor axis length is due to orientation on the sky. Fits using the r1/4 or Sérsic functions do not assume circular symmetry and, thus, the generalized radius (ab1/2) is used. Ellipticals are not typically oblate, thus the bulge+disk fit simply becomes an open four parameter polynomial.
An example of all three fitting functions is shown in Figure 9, a plot of the J surface brightness profile for NGC 3379. The quality of each fit is evaluated using a simplified χ2 estimator where all the datapoints are equally weighted and the χ2 simply becomes the sum of the square of the differences. Weighting the data by its photometric error is the normal procedure, but this gives too much weight to the inner isophote datapoints since their RMS errors are very small and their larger number (due to the smaller ellipse annuli) overwhelms the data in the outer regions. This produces erroneous fits, particular since the outer regions are often the most interesting for determining global structure parameters (such as half-light radii). This is particularly problematic for galaxies with bulge and disk components, where the brighter and more compact bulge component dominates the fit over a few outer disk points. The χ2 values shown in the figures are unweighted for comparison between profiles. A later paper will detail the different fitting strategies adopted for different morphological types.
Of the three fitting functions, the bulge+disk function provides the lowest formal χ2 value, despite the fact there is no obvious evidence of a disk. This is simple due to the fact that four parameters provides more flexibility to the fitting, resulting in a technically better fit. The Sérsic has the lowest formal χ2, using three free parameters. The r1/4 law is only fit to the middle portion of the profile and fails in the outer envelope. The green circle in Figure 9 marks a common inflection point for bright ellipticals. Typically where this inflection point occurs is the point where a bulge+disk fit separates the disk component.
A better method to display this information is shown in Figure 10 where the residuals to the various fitting functions are shown. While the formal fit is best for the Sérsic function, we will show in Paper II that each function has specific deviations from a best fit that are correlated with luminosity. Our conclusion is that all fitting functions are simply computational French curves that only contain information on structure as constrained by the procedure for applying them. We will discuss the usefulness of fitting functions in greater detail for each morphological type in later papers.

|
3.8 Data Storage/Access
Data storage and presentation for a image reduction project of this type entails many complications. In the past, researchers would simply publish the resulting surface brightness profiles as luminosity versus radius. However, this habit of only presenting the finished product has two disadvantages. First, while reduced data is the goal of any imaging project, in fact, there is a great deal of information contained in the processing files. For example, the Fourier quotients on the ellipses contains information on the shape of the isophotes as they deviate from a perfect ellipse (i.e. disk versus boxy). Interpretation of the surface brightness profiles is critically dependent on that information. Luminosity by apertures, color gradients, spatial anomalies are also contained in the processing files.
Second, there is a level of transparency to the reduction process by presenting all the data including the raw and processed data. Repeatability is a key component to the scientific process. Presenting all the processed data, and the actual software used to process the frames, is more than just a statement of the honesty of a dataset, but also key to understanding the meaning of the final numbers.
To this end, this project maintains all the final and processed data in XML files linked to the raw image frames. In these files are all the parameters used during the processing and calibration of the images. For example, if a user selected region of the surface brightness profile is used for fitting, the fit and the user selected limits are recorded. Cosmological corrections, such as galactic extinction and distance (obtained from NED) are also stored in these files.
In addition, the scripts used to process the data are presented with the data. Rather than publishing appendices describing the algorithmic procedures to each reduction step, these scripts, loaded with comments, guide the user in both the computational and astrophysical data analysis steps. These scripts are Python code, which often call c++ or iraf subroutines. python is ideal for this type of pipeline processing as it can handle numerical and text decision processing as well as file and directory instructions. With the addition of the PyFITS module from the PyRAF project, these scripts can now also access information with the images themselves (e.g. headers and pixel values). A cookbook example of the processing is available at the data website (http://abyss.uoregon.edu/~js/sfb) although with descriptions of the data values and the raw and reduced images.
4 Summary
This paper presents the techniques and philosophy for a large scale, galaxy surface photometry project using 2MASS imaging data. Our ultimate goal is to investigate the surface brightness profiles across all morphological types providing a comprehensive view of the structure of galaxies. We summarized the key points of this first paper of our series as the following:
-
The 2MASS all-sky survey presents an ideal database in which to study galaxy structure. For imaging in the near-IR emphasizes the primary baryonic component of galaxies, stars. The observing technique used by the 2MASS project produces extremely flat and well calibrated images, the two primary sources of error in pointed observations.
-
We have developed unique network tools to automatically extract and assemble regions from the 2MASS image server based on input catalogs. For our goals, we have selected the Revised Shapley–Ames (a luminosity limited) and the Uppsala (a diameter limited) galaxy catalogs from which to extract our galaxies.
-
We have made no attempt to be complete in our sample in terms of galaxy luminosity or size nor galactic latitude, although we have attempted to reduce every large galaxy in the sky in order to maximize our samples range of galaxy characteristics. We have eliminated all galaxies in our initial catalog selection that had companions, or nearby bright stars, which would complicate our analysis. Our goal was to obtain as many isolated galaxies for study per morphological bin as was possible with the limited depth of the 2MASS survey.
-
Data reduction used the ARCHANGEL galaxy photometry package (Schombert 2007). Particular attention was given to star removal and sky determination (as these are the two main contributors to error in the resulting surface brightness profiles).
-
Repeatability is supported by comparison with surface brightness profiles in the literature. The error budget is completely dominated by errors in the sky value.
-
Fitting functions, and our procedures for using them, are outlined. We use only three of the more common fitting functions (r1/4, Sérsic and r1/4 bulge plus exponential disk).
-
We present our method of data storage in an attempt to open the access to all levels of the data product as a great deal of structural information is found beyond simple fits to the final surface brightness profiles.
Four appendices are attached to this paper that A) outlines the problems in the 2MASS Extended Source Catalog (XSC) with respect to total magnitudes and surface brightness, B) provides an example of our asymptotic total magnitude procedure, C) outline the PSF results and procedures, and D) list the variables found in the XML data files for each galaxy.
Acknowledgments
Most of the comparative values were extracted from NED (NASA’s Extragalactic Database) using new network tools. The quick access to difference galaxy catalogs on one site made this project doable in reasonable timescales. The model for future science is not faster cycles, but faster and clearer access. The software for this project was supported by NASA’s AISR and ADP programs.
References
Almeida, C., Baugh, C. M. and Lacey, C. G., 2007, MNRAS, 376, 1711| Crossref | GoogleScholarGoogle Scholar |
Burstein, D. et al., 1987, ApJS, 64, 601
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXkvVKlsbc%3D&md5=8c0914c52ec87b3d8782d4bc82cb9a5fCAS |
Cawson, M. G. M., Kibblewhite, E. J., Disney, M. J. and Phillipps, S., 1987, MNRAS, 224, 557
| 1:CAS:528:DyaL2sXht1ymtbY%3D&md5=191407ba95ec47167b4711c58788529fCAS |
Cole, S., Lacey, C. G., Baugh, C. M. and Frenk, C. S., 2000, MNRAS, 319, 168
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3MXitVek&md5=b1f89cfea055279ae727fc30d94eed77CAS |
Conselice, C. J., 2008, in ASP Conf. Ser., Pathways Through an Eclectic Universe, ed. J. H. Knapen, T. J. Mahoney & A. Vazdekis (San Francisco: ASP), 390, 403
de Vaucouleurs, G., 1948, AnAp, 11, 247
de Vaucouleurs, G., 1959, HDP, 53, 311
de Vaucouleurs, G., 1977, ApJS, 33, 211
| Crossref | GoogleScholarGoogle Scholar |
Fish, R. A., 1964, ApJ, 139, 284
| Crossref | GoogleScholarGoogle Scholar |
Freeman, K. C., 1970, ApJ, 160, 811
| Crossref | GoogleScholarGoogle Scholar |
Graham, A. W. and Driver, S. P., 2005, PASA, 22, 118
| Crossref | GoogleScholarGoogle Scholar |
Jarrett, T. H., Chester, T., Cutri, R., Schneider, S., Skrutskie, M. and Huchra, J. P., 2000, AJ, 119, 2498
Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E. and Huchra, J. P., 2003, AJ, 125, 525
Jedrzejewski, R. I., 1987, MNRAS, 226, 747
Kent, S. M., 1985, ApJS, 59, 115
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXlvVKntLw%3D&md5=659bb13b6955279451b01d7de45382b6CAS |
Kent, A., 2012, PhD Thesis, University of Southampton
Kormendy, J., 1977, ApJ, 218, 333
| Crossref | GoogleScholarGoogle Scholar |
Milvang-Jensen, B. and Jorgensen, I., 1999, BaltA, 8, 535
Oemler, A., 1976, ApJ, 209, 693
| Crossref | GoogleScholarGoogle Scholar |
Saglia, R. P. et al., 1993, MNRAS, 264, 961
Schombert, J. M., 1986, ApJS, 60, 603
| Crossref | GoogleScholarGoogle Scholar |
Schombert, J. M., 1987, ApJS, 64, 643
| Crossref | GoogleScholarGoogle Scholar |
Schombert, J., 2007, arXiv:astro-ph/0703646
Schombert, J., 2011, arXiv:1107.1728
Schombert, J. M. and Bothun, G. D., 1987, AJ, 93, 60
Skrutskie, M. F. et al., 2006, AJ, 131, 1163
Appendices
A Comparison to 2MASS Total Magnitudes
During the initial stages of this project a comparison between total magnitudes determined for the elliptical sample of this project and the values provided by 2MASS XSC revealed a large discrepancy. This appendix describes the analysis that lead to the conclusion that the 2MASS XSC was consistently underestimating the total magnitude values due to a systematic error in their sky measurements. Note: this appendix was released to arXiv as Schombert (2011), ‘Systematic Bias in 2MASS Galaxy Photometry’.
A comparison sample of elliptical galaxies was selected from the Revised Shapley–Ames (RSA) and Uppsala Galaxy Catalogs (UGC) in order to cover a magnitude and angular limited sample with sufficient S/N in the 2MASS image library. The only other criteria was that the galaxies to be studied be free of nearby companions or bright stars which might disturb the analysis of the isophotes to faint luminosity levels. The comparison sample contained 421 galaxies all classed ‘E’ by both catalogs.
Images from 2MASS for regions around all the galaxies in the sample were downloaded from 2MASS’s Interactive Image Service. These sky images were flattened and cleaned by the 2MASS project and contained all the information needed to produce calibrated photometry. The images were analyzed as described in §3, thus, the only difference in the final results is the analysis method, not the data themselves.
A.1 2MASS Repeatability
The first step, once surface photometry reduction was completed, was to compare our photometric and structural values with those extracted by 2MASS. Metric magnitudes are the simplest for comparison, and the 2MASS project provides magnitudes through various aperture sizes (e.g. 14 arcsec apertures are found in NED). The 2MASS project also provides Kron magnitudes, where Kron magnitudes are isophotal magnitudes measuring a galaxy’s light through an elliptical aperture whose size is defined by the 20 K-mag arcsec–2 surface brightness level. These magnitudes contain less intrinsic error than metric magnitudes as the Kron apertures follow the shape of the galaxy and maximizes the galaxy flux to sky ratio. NED provides those magnitudes and the aperture sizes for all the galaxies in our sample. A comparison between our Kron magnitudes (using 2MASS’s aperture sizes) with their Kron magnitudes is shown in Figure 11.

|
As can be seen from Figure 11, the agreement between our Kron magnitudes and 2MASS values is excellent, meaning that we can reproduce the same fluxes as the 2MASS project using the same apertures off of 2MASS provided images and calibration. There is a slight offset (0.01 mag) such that our magnitudes are slightly fainter than 2MASS (see inset histogram). This is probably due to the fact that our reduction procedure subtracts stars and replaces the masked pixels with interpolated galaxy flux which, on average, would lower the aperture flux. We note that our values for the Kron ellipses were significantly larger than 2MASS’s estimates.
A.2 Problems with 2MASS Total Magnitudes
The next comparison is with our total magnitudes and 2MASS’s total magnitudes. This comparison can be found in Figure 12 and, as is visible in the figure, a significant difference is found between our calculated total magnitudes and the values presented for the same galaxies by the 2MASS project. In general, our total magnitudes are 10 to 40% brighter than the 2MASS total luminosities.

|
This discrepancy in total luminosities is especially puzzling since our reduction methods can reproduce 2MASS aperture and Kron magnitudes (see Figure 11). This would indicate that the images provided by the 2MASS project are reliable and the calibration is correct. The difference must lie in the reduction procedures to determine total magnitudes.
Total magnitudes determined by the 2MASS project use an aperture magnitude that is four scalelengths in radius, where the scalelength is determined Sérsic fits to their surface brightness profiles. Our project determines total magnitudes through asymptotic fits to the curve of growth, where we increase the accuracy of the outer isophotes by using the mean intensities give by the surface brightness profiles (see Appendix B).
The key difference in our photometric methodology lies in the determination and use of the galaxy’s surface brightness profile to determine the aperture. Therefore, an error between the surface brightness profiles deduced by our procedures and the ones extracted by the 2MASS project must be the source the magnitude offset. To explore this hypothesis, we compare the procedures used by 2MASS and our procedures in the next section.
A.3 Surface Photometry Comparison
The 2MASS project also published surface brightness profiles for 100 large galaxies (Jarrett et al. 2003), 31 of them in common with our elliptical sample. Agreement between our surface brightness profiles and the 2MASS project’s profiles is less than adequate. An example is found in Figure 13, the surface brightness profiles of NGC 3379 from Jarrett et al. and our study. The difference between the profiles is extreme at large radii, well beyond expectations from the RMS errors in the data.

|
And the discrepant surface brightness profiles for NGC 3379 is not unique. The profile differences for all 31 galaxies is shown in Figure 14, presented as a density distribution of Δμ versus radius. As can be seen in that figure, all the comparison galaxies have varying degrees of surface brightness differences, mostly concentrated in the outer regions and can reach 1 to 2 mag arcsec–2 in error.

|
A.4 Data Reduction Differences
One obvious conclusion is that some difference exists in the reduction process that reflects in the final profiles, the data frames themselves are not in question since we can reproduce 2MASS’s aperture luminosities. There are several procedural differences between the isophotal techniques used by the 2MASS project and our photometry package (ARCHANGEL).
For example, the 2MASS project determines an elliptical shape based on a first moment analysis of some intermediate, but high S/N region in a galaxy’s envelope. The calculated eccentricity and position angle are used for the entire galaxy, determining isophote intensity levels based on pixels around those ellipses. Our project, on the other hand, fits each radii for eccentricity and position angle (as well as x and y center) allowing these ellipse parameters to vary with radius.
This difference in ellipse shape was noted in Schombert (2007), but these different ellipses parameters are not sufficient explain the large surface brightness differences found in the galaxy sample (numerical experiments with ellipses in 2MASS data displays only a 1 to 2% difference in intensities). There are a few extreme cases (e.g. LSB galaxy, NGC 3109), but in general ellipticals have fairly constant eccentricities.
In one-to-one comparisons to the raw intensity files provide by the 2MASS project, one can see there are large differences in the quoted intensity values per radius between the 2MASS project and our study. These differences range from small to up to 60%, largest at the lowest intensity values. An example is outlined in the next section.
A.5 NGC 1407: A Test Case
To resolve the differences in the surface brightness profiles, elliptical NGC 1407 was selected for more detailed inspection. NGC 1407 is an excellent test galaxy for its isophotes are nearly circular (axial ratio of 0.93 from 2MASS, 0.95 from our study), it is isolated with no large companions and its envelope is free of any foreground stars or distortions.
At 100 arcsec from the center of NGC 1407, the 2MASS project quotes an isophotal intensity of 0.97 DN (20.82 J-mag arcsec–2). Our project finds a value of 1.42 DN (20.41 J-mag arcsec–2). To determine which value more closely represents the isophote at that radius, we have plotted a histogram of intensity values for all pixels between 99.5 and 100.5 arcsec from the galaxy center. This histogram is shown in Figure 15 (both regular and normalized).

|
From this figure, it is obvious that the intensity values deduced by the 2MASS project are not in agreement with the mean value of the pixels in the image, whereas our calculated intensity value is in good agreement with the mean and median value. Since the isophotes of NGC 1407 are nearly a perfect circle, this is not an effect of the ellipse fitting procedure. This is also not due to calibration errors, as these are raw data numbers.
Comparison to other isophotes reveals the same difference, always at a constant value in intensity at all radii and suggests a additive error in the deduced sky value. Communication with the 2MASS project (T. Jarrett, private communication) confirms that the difference to the 2MASS surface brightness profiles is due to an error in the sky subtraction scheme. Simply adding a constant value to the raw intensities (e.g. 0.22 DN for NGC 3379) results in a good agreement between our current profiles and 2MASS LGA (see Figure 16).

|
The effect these underestimated surface brightness values have on 2MASS photometry is subtle. Both 2MASS Kron and total magnitudes use the surface brightness profiles to deduce isophotal levels (Kron) and scalelengths (total). For Kron magnitudes, the 20 K-mag arcsec–2 level is used to define an elliptical aperture. However, since the 2MASS surface brightness profiles underestimate the intensity values per radius, this, in turn, leads to smaller estimates of the isophotal size of the aperture and, therefore, fainter magnitudes.
Total magnitudes for 2MASS are calculated using an outer aperture set to be four times the scalelength determined by Sérsic function fits. Decreased intensities in the outer regions produce smaller scalelengths, on average, which produce smaller apertures and fainter total magnitudes. This is exactly what we observe in Figure 12.
A.6 Summary
First, we note that this discrepancy has no impact on projects which use 2MASS aperture colors. For galaxy colors are calculated using 2MASS total magnitudes still use the same sized apertures for J, H and K, and the colors will remain consistent (although for a smaller portion of the total galaxy light). However, comparison between other total magnitudes (e.g. RC3 magnitudes) and 2MASS total magnitudes will be biased towards the blue.
An example of this effect is shown in Figure 17, a histogram of V – J colors for the 421 ellipticals in our sample. As can be seen, the 2MASS colors are 0.25 mag bluer than colors calculated from our total magnitudes since the RC3 V-mag nitude is determined from an asymptotic fit and, therefore, contains more flux that 2MASS’s total magnitude. There appears to be no standard correction from 2MASS colors to the correct colors, this would require information on how deviant the 2MASS surface brightness profiles (from which the aperture sizes are extracted) are from reality.

|
A priority science goal for 2MASS was large baseline color comparison. An example of relevance of large wavelength comparisons is the color-magnitude relation (CMR). The CMR is a long known correlation between galaxy color and luminosity. The best explanation is that galaxies with higher mass have higher metallicities. Global metallicity reflects in the mean temperature of the RGB such that low metallicities produce bluer colors. The CMR for this data sample is shown in Figure 18. Again, we see that the 2MASS colors predict the opposite expectation from earlier optical work in that they find roughly bluer colors with higher luminosity. Using our total magnitudes (combined with RC3 colors) restores the correct CMR, redder colors with higher galaxy luminosity.

|
B Asymptotic Total Magnitude Fitting
Often the scientific goal of a galaxy project is to extract a total luminosity for the system (and colors for multiple filters). For small galaxies, a metric aperture or isophotal magnitude is suitable for comparison to other samples (certainly the dominate source of error will not be the aperture size). However, for galaxies with large angular size (i.e. many pixels), their very size makes total luminosity determination problematic.
Naively, one would think that a glut of pixels would make the problem of determining a galaxies luminosity easier, not more difficult. However, the problem here arises with the question of assigning a point where the galaxy luminosity ends. Or, even if one estimates or calculates an outer radius, does the luminosity estimate contain all the galaxy’s light. The solution proposed by de Vaucouleurs decades ago is to use a curve of growth (de Vaucouleurs 1977). A majority of galaxies follow either an exponential or r1/4 curve of growth such that the total light of a galaxy can be calculated (Burstein et al. 1987). However, for modern large scale CCD imaging, the entire galaxy can easily fit onto a single frame and there is no need for a curve of growth as all the data exists in the frame.
With adequate S/N, it would seem to be a simple task to place a large aperture around the galaxy and sum the total amount of light (minus the sky contribution). However, in practice, a galaxy’s luminosity distribution decreases as one goes to larger radii, when means the sky contribution (and, thus, error) increases. In most cases, larger and larger apertures simply introduce more sky noise (plus faint stars and other galaxies). And, to further complicate matters, the breakover point in the optical and near-IR, where the galaxy light is stronger than the sky contribution will not contain a majority of the galaxy’s light (see Figure 7). So the choice of a higher accuracy inner radius will underestimate the total light.
The procedure selected in this study, after some numerical experimentation, is to plot the aperture luminosity as a function of radius and attempt to determine a solution to an asymptotic limit of the galaxy’s light. This procedure begins by summing the pixel intensities inside the various ellipses determined by the ellipse fitting routines. For small radii, a partial pixel algorithm is used to determine aperture luminosity (using the surveyors technique to determine each pixel’s contribution to the aperture). At larger radii, a simple sum of the pixels, and the number used, is used. In addition, the intensity of the annulus based on the ellipse isophote and one based on the fit to the surface photometric profile are also outputted at each radii.
Note that a correct aperture luminosity calculation requires that both an ellipse fit and a 1D fit to the resulting surface photometry has to have been made. The ellipse fit information is required as these ellipses will define the apertures, and masked pixels are filled with intensities given by interpolation of the nearest ellipse. A surface photometric fit allows the aperture routine to use a simple fit to the outer regions as a quick method to converge the curve of growth. The end result is three possible values for aperture luminosity as a function of radius, 1) raw pixel counts, 2) pixel counts determined by the mean isophote and 3) pixel counts determined by the mean surface brightness from fits to the galaxy surface brightness profile.
Once the aperture luminosities are calculated, there are two additional challenges to this procedure. The first is that an asymptotic fit is an unstable calculation to make as the smallest errors at large radii reflect into large errors for the fit. Two possible solutions are used to solve this dilemma. The first solution is to fit a 2nd or 3rd order polynomial to the outer radii in a luminosity versus radius plot. Most importantly for this fit, the error assigned to the outer data points is the error on the knowledge of the sky, i.e. the RMS of the mean of the sky boxes. This is the dominant source of error in large apertures and the use of this error value results in a fast convergence for the asymptotic fit. The resulting values from the fit will be the total magnitude and total isophotal size, determined from the point where the fit has a slope of zero.
A second solution is to use an obscure technique involving rational functions. A rational function is the ratio of two polynomial functions of the form
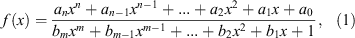
where n and m are the degree of the function. Rational functions have a wide range in shape and have better interpolating properties than polynomial functions, particularly suited for fits to data where an asymptotic behavior is expected. A disadvantage is that rational functions is their non-linear behavior which, when unconstrained, will produce vertical asymptotes due to roots in the denominator polynomial. A small amount of experimentation found that the best rational function for aperture luminosities is the quadratic/quadratic form, meaning a degree of two in the numerator and denominator. This is the simplest rational function and has the advantage that the asymptotic magnitude is simply a2/b2, although is best evaluated at some radii in the halo of the galaxy under study.
Usually aperture luminosity values do not converge at the outer edges of a galaxy. This is the second challenge to aperture photometry, correct determination of the total luminosity due to the faint galaxy halo component. In this instance, the surface photometry profile is critical in determining the total flux. Contained in the surface brightness profile of a galaxy is the relationship between isophotal luminosity and radius, using all the pixels around the galaxy. The isophotal intensity times the area of an annulus is often a more accurate number than attempting to determine the integrated luminosity in an annulus by summing pixels.
The isophotal information can be used to constrain the curve of growth in two ways. One, we can use the actual surface brightness intensities and convert them to a luminosity for each annulus by multiplying the mean intensity times the area of the annulus. Then, this value can be compared to the aperture value and flagged where the two begin to radically deviate. Sometimes, for particularly low surface brightness halos, even the isophotal intensities will vary at large radii and, thus, a second, more stable method is to make a linear fit of an exponential, r1/4 or combined function to the outer radii and interpolate/extrapolate that fit to correct the aperture numbers.
Figure 19 displays the results for all three techniques for the galaxy NGC 3379. The black symbols are the raw intensities summed from the image file. The blue symbols are the intensities determined from the surface photometry. The green symbols are the intensities determined from the fits to the surface photometric profile. Since the surface brightness profile of NGC 3379 is well fit by a Sérsic function, the curve of growth using the actual surface brightness data and the fit are nearly identical. Typically the raw intensities profile falls below the surface brightness intensities due to losses from masked pixels. This is the case for NGC 3379, the aperture values fall below the surface brightness intensities to produce a fainter total magnitude.

|
C 2MASS PSF Fitting
While the 2MASS PSF is well known, removing the effects of PSF distortion involves a assumption to the underlying galaxy profile. For a majority of galaxies (ellipticals and spirals with significant bulges), an r1/4 profile is a good approximation for PSF correction. However, the effective radius must be included in the PSF fit and can only be estimated by r1/4 fits to the region outside the PSF. Therefore, PSF correction, using an FWHM measured from nearby stars and an re value measured from the middle portions of a galaxy profile, simply converts the inner profile into an r1/4 shape that is an extension to the middle regions (where the value of re is determined).
Whether this technique is appropriate can be tested by comparing 2MASS profiles with surface brightness profiles extracted from pointed observations with higher spatial resolution. During a project to study the luminosity function of galaxies in the near-IR, Kent (2012) imaged several of our the galaxies from our elliptical sample in sub-arcsec seeing with 0.2 arcsec pixels. The profile for NGC 7097 was shown in Figure 6.
As a test of the observed PSF, we can subtract the Kent profile from the 2MASS profile for NGC 7097, shown in Figure 20 as the blue symbols. Note that the resulting data curve matches the gaussian shape from Saglia et al. To find a best match, one only needs the effective radius and the seeing FWHM. For this exercise, we have fit the profiles outside the seeing region and determined that both profiles have re values of 8.6 arcsec.

|
Two curves for FWHM of 2.5 and 3.3 arcsec are shown. The value of 2.5 is extracted from the FITS header for the central frames header (taken from the output of the 2MASS project’s SEEMAN routine). The fit for the 2.5 arcsec seeing does not fit the data. A good fit is found for a FWHM of 3.3 arcsec (which matches our estimate of the 2MASS seeing from examining stars in the same data frame), which supports the hypothesis that 2MASS PSF is a gaussian, although the seeing FWHM estimate from 2MASS appears to underestimate the true seeing. The true value can be extracted from stars in the same image frame, and supports our conservative policy of only using data outside 5 arcsec for profile fitting.
D ARCHANGEL XML Parameter List
The information for the reduction pipeline, and the resulting structural and photometric parameters, are contained in each galaxy’s XML file. The following is a short description of each of those values.

|

