Galactic Anisotropy of Cosmic Ray Intensity Observed by an Air Shower Experiment

Keywords: cosmic rays

Cosmic rays have a remarkably uniform distribution over the sky, yet small anisotropies do exist. The deviation from isotropy is typically below 1% and can be as low as 0.03% (Smith & Clay 1997). The galactic anisotropy of the cosmic-ray intensity is expected to carry information about the origin and the propagation mechanism of galactic cosmic rays, as it reflects the galactic magnetic field through which they have passed and their energy spectrum at source. It is presumed that the anisotropy at multi-TeV energies is almost free from heliosphere disturbance, while in the lower energy events the additional diurnal anisotropy is probably due to solar modulation. Cosmic rays in the lower energy range have gyro radii of about 1 pc or less in typical galactic magnetic fields (a proton with an energy of 10¹⁵ eV would have a gyro radius of 1 pc in a 1 μG field). Because of low anisotropy, it is assumed that cosmic ray propagation is diffusive in some way (Allan 1972). This diffusion may be broadly along the magnetic field lines which are in tubes of dimensions greater than the gyro radii. If so, then the direction of the peak of the anisotropy would indicate the direction back towards the cosmic ray source, and the amplitude of the anisotropy would give information on the scattering process involved in the diffusion. Specifically, an estimate of the mean free path might be obtained. A well known asymmetry effect is the Compton–Getting Effect (CGE). The earth’s rapid motion in space due to the rotation of our galaxy, results in variations in cosmic ray intensity fore and aft of the earth’s motion. Following Compton & Getting (1935), the magnitude of the anisotropy is expressed as

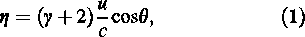
where γ denotes the power law index of the energy spectrum of cosmic rays, u the velocity of the detector relative to the production frame of the cosmic rays (where they are presumed to be isotropic), c the speed of light, and θ the cosmic ray direction relative to u, i.e. cos θ is the projection of the cosmic ray along the forward direction of u. In fact the value of (γ + 2)(u / c) is (f_max – f_min)/(f_max + f_min) with f_max being the counting rate along the direction of the velocity and f_min the rate along the contrary direction. The magnitude of the anisotropy is extremely small and independent of the cosmic ray energy. Our data will be analyzed in a sun-centered frame, and so if data accumulation is done over an integer number of solar years, it is only necessary that the orbital speed of the Earth around the sun (~30 km s^–1) be considered; the large effect due to the Galactic rotational speed (220 km s^–1) will cancel out as the data are averaged over this time (Poirier, D'Andrea & Dunford 2001). Many experiments have been carried out for detection of the former effect (Poirier et al. 2001; Lin 1999).

Doppler effect studies of globular clusters and extra-galactic nebulae have revealed a motion of the earth of about 220 km s^–1 towards right ascension α ∼ 21 h and declination δ ∼ 47° N, due chiefly to the rotation of the Galaxy. This motion, with a speed of about 0.1% c, will affect the intensity of the incoming cosmic rays by changing both the energy of the cosmic ray particles and the number received per second. Using a value of 220 km s^–1 for u, and 2.7 for the spectral index, Eqn (1) gives a CGE amplitude of 0.345 × 10^–2 for the fractional forward–backward asymmetry caused by the motion of the earth in the Galaxy. Because of the small anisotropy, large data sets are required to make useful measurements which overcome the statistical uncertainties of counting experiments. A simple way of recording many cosmic rays is to record coincidences between a number of scintillation detectors. Few statistically significant anisotropics have been reported from extensive air shower experiments in the two last decades. Aglietta et al. (1996, EAS-TOP) published an amplitude of (3.7 ± 0.6) × 10^–4 at E_° ≈ 200 TeV. Analyzing the Akeno experiment, Kifune et al. (1986) reported a result of about 2 × 10^–3 at about 5–10 PeV. An overview of experimental results can be found in Clay et al. (1997). We have operated a small air shower array on the roof of the Physics Department at Sharif University of Technology in Tehran (35°43′ N, 51°20′ E, at 1200 m = 890 g cm^–2) as a prototype for constructing an Extensive Air Shower (EAS) array on Alborz mountain range ataltitude of over 2500 m near Tehran. At the time of writing, more than 1.1 × 10⁶ showers have been recorded. In the present paper we discuss the design of this scintillator array and describe its operation. The main purpose of the experiment is to study the anisotropy due to the Compton–Getting effect and a unidirectional anisotropy of cosmic ray flow along the Galactic arms which was observed in the sidereal time at energies in the decade below 1 PeV.

Figure 1 shows an array including four slab plastic scintillators (100 × 100 × 2 cm³) arranged in a square with an edge size of about 10 m (Bahmanabadi et al. 2003). All scintillators are on a flat level surface. Each scintillator is housed in a pyramidal steel box with a height of 15 cm. The interior surface of each box is coated with white paint (Bahmanabadi et al. 1998) and a 5 cm diameter photo multiplier tube (PMT, EMI 9813 KB) is placed at the vertex of the pyramidal box. Figure 1 shows a schematic diagram of the array and its electronic circuit which logs each EAS event. If at least one particle hits a detector, the PMT creates a signal with a pulse height which is related to the direction, the number of particles, and the location of the particle track in the scintillator. The output signals from the PMTs are amplified in a one-stage amplification (×10) with an 8-fold fast amplifier (CAEN N412), and then transferred one by one to an 8-fold fast discriminator (CAEN N413A) used in leading edge mode which is operated at a fixed level of 20 mV. The threshold of each discriminator is set at the separation point between the signal and background noise levels. Each discriminator has two outputs, one of them connected to a coincidence logic unit (CAEN N455) which acts as a trigger condition. The trigger condition is satisfied when at least one charged particle passes through each of the four detectors within a time window of 150 ns. The other discriminator output is connected to one of three Time to Amplitude Converters (TAC, EG&G ORTEC 566) which are set to a full scale of 200 ns (maximum acceptable time difference between two scintillators). The output of scintillator #4 is connected to the start input of TAC1, whereas the output of scintillator #2 is connected to the start inputs of TAC2 and TAC3. The output of scintillator #3 is connected to the stop input of TAC2, and that of #1 to the stop inputs of TAC1 and TAC3. Finally the outputs of these three TACs are fed into a multi-parameter Multi Channel Analyzer (MCA, KIAN AFROUZ Inc.,) via an Analogue to Digital Converter (ADC, KIAN AFROUZ Inc.,) unit. When all of the scintillators have coincidence pulses, the TACs are trigged by the logic unit and the three time lags between the output signals of three pairs of the PMTs (4,1), (2,3), and (2,1), where the numbers in parentheses are the start and stop of the two TACs respectively, are read out by a computer and an EAS event is logged. All events with zenith angles ≤60° are used in the present analysis. About 1.1 × 10⁶ events remained after these selections.

Over a period of about 132 days (2002 Aug 01–Dec 10) we logged more than 1.1 × 10⁶ events. The mean event rate of the experiment was 0.107 events per second. The distribution of the time between successive events is in good agreement with an exponential function, indicating that the event sampling was completely random (Bahmanabadi et al. 2003). We refined the data by selecting out acceptable events, i.e. those with good coincidence between the four scintillator pulses. To ensure reconstruction quality, only showers well inside the detector field with zenith angles smaller than 60° have been used. After the selection, about 1.1 × 10⁶ events remained for analysis. Further, only sidereal days with continuous data taking were used.

Since we cannot determine the energy of the showers on an event-by-event basis, we estimate the lower energy threshold by comparing our event rate to the well-known Hillas spectrum (Gaisser 1990), which can be represented as

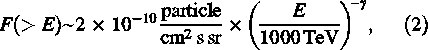
with γ = 1.7 for E < 1000 TeV.

We used corsika (Heck et al. 1998), using the hadronic interaction models qgsjet and gheisha, to determine the surface such that, if a primary particle passes through it, our array could detect its EAS event. The energy range for primary particles was selected to be from 1 TeV to 5 PeV, with differential flux given by dN/dE ∝ E^–2.7. These simulations are in different directions, with zenith angles in bins 0°–10°, 10°–20°,..., and 50°–60°, with all azimuth angles in each 10° zenith angle interval. Since our scintillation detectors are 1 m × 1 m in size, and if at least one particle passes through a detector it is sufficient to record a pulse, we used the condition of particle density greater than 1 m^–2 (ρ ≥ 1 m^–2) is used. Based on the NKG formula (Gaisser 1990), the mean effective surface of EAS events at Tehran level is about 2000 m². With this result we estimate the mean effective surface area of our array in the upper level of the atmosphere (the surface such that if a primary particle passes through it, the array could detect its EAS event) to be about 1500 m². The field of view of our array to zenith angle 60° is π steradian. Therefore, based on Eqn (2), the energy threshold is about 250 TeV. The mean energy of cosmic rays, calculated by the differential spectrum obtained by Eqn (2), is about 420 TeV.

If either temperature or pressure variations have Fourier components in sidereal time, spurious components may be introduced into the shower detection rate (Farley & Storey 1954). Various methods are used in order to study the dependence of event rate on atmospheric ground pressure, P, and temperature, T (Antoni et al. 2004). In a previous paper (Bahmanabadi et al. 2003), we took only the influence of the pressure into account. In the present analysis, the influence of the atmospheric ground pressure, P, and temperature, T, on the rate of extensive air showers at ground level is taken into account by a second order polynomial (Antoni et al. 2004),

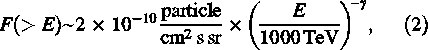
The values of R₀ = 0.107 s^–1, P₀ = 880 mbar, and T₀ = 18.5° C are the long-term mean values of rate, pressure, and temperature, respectively, obtained from the data. The parameters α₁, α₂, α₃, α₄, and α₅ were determined by a fit to the time-dependent rates for the whole observed time, the results being:

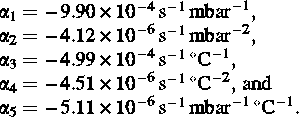
The correction is done for time intervals of half an hour (in sidereal time ~1795 SI seconds) by subtracting or adding the necessary number of events calculated by Eqn (3). The quality of the correction can be estimated from Figure 2 which shows the event rate distributions with and without correction for atmospheric ground pressure and temperature. The distribution of uncorrected rates is asymmetric. The distribution of corrected rates is compatible with a Gaussian distribution, as expected for the remaining statistical fluctuation of the event rate.

Table 1. Parameters of the best fit coefficients found for Eqn. (4)

After the atmospheric correction is made, sidereal time (ST) is calculated using the formula ST = ST₀ + α(ZT – ZT₀), where ST₀ can be found in an almanac¹ for the time ZT₀, ZT is the solar time, and α = 1.00273790935.

Figure 3 shows percentage variation in intensity of the cosmic rays with sidereal time. The data have been fit to Eqn (4) which describes a curve with first and second harmonics (i.e. with a once-per-day and a twice-per-day variation),

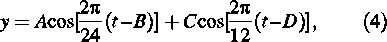
where t is in hours. The results of fitting the data are summarized in Table 1. This analysis shows that the anisotropy has a peak close to the sidereal time 21 h, when the zenith is toward the direction of the earth’s motion. The amplitude of the anisotropy is of the order of 0.43%. A definite sidereal time variation is seen, whose phase and amplitude are close to those predicted. In order to calculate the magnitude of the anisotropy due to CGE, i.e. the value η in Eqn (1), a mean value for cos θ is needed (Figure 4). Figure 4 shows the celestial sphere of an observer at latitude λ. If δ is the declination of the direction of earth’s motion, λ the latitude of the observer, and H the hour angle between the observer’s meridian and the direction of motion, then the angle φ between the observer’s zenith and the direction of earth’s motion is given by

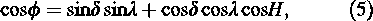
On the other hand, cos θ is calculated by

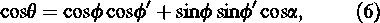
where φ′ is the zenith angle of the cosmic ray and α the difference between the azimuth angle of the direction of motion and of the cosmic ray that is, α = A₁ – A₂, where A₁ and A₂ are obtained from the equations

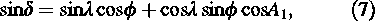
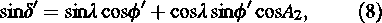
where δ′ is the declination of the cosmic ray. Following Eqns (5)–(8), the 24-hour mean of the component of cosmic rays in the direction of motion (cos θ) may be obtained. The differential zenith angle distribution of cosmic rays can be represented by dN = constant (cosφ′)ⁿ sinφ′ dφ′ with n = 6; (Khakian et al. 2005). By this distribution, we calculated the mean cosφ′ value which is 0.93. Also the mean values of A₁ and A₂ were obtained by using λ = 35° 43′, δ′ = 47°, and the mean value of δ′ ≈ 30° (Bahmanabadi et al. 2003). A value of 0.39 is obtained for cos θ and this is multiplied by the expected CGE amplitude of 0.345% to yield a predicted effect of expected value of 0.135% and the value obtained from experimental data, 0.43%, is about 0.30%. This remaining asymmetry of 0.30% should have a different origin than CGE.

Since the data were recorded in Tehran at latitude 35°43′ N, the majority of cosmic rays are from the Galactic spiral arm inwards direction, which is at about 20 h in right ascension and 35° in declination (Jacklyn 1986). Therefore the remaining asymmetry is probably due to a unidirectional anisotropy of cosmic ray flow along the Galactic arms. A simple diffusion model (Allan 1972) suggests that the value of this asymmetry, 0.30%, would be roughly equal to the ratio of the scattering mean free path to a characteristic dimension of the containment region (i.e. the central Galactic region, with a scale of 10 kpc). With the amplitude of the anisotropy found in this work being 0.30%, we obtain a mean free path of about 30 pc which is perhaps about 30 gyro radii.

Since the anisotropies are low, it is necessary to consider the effect on the measured counting statistics for a finite data set. If there are N events, then the probability of getting a fractional amplitude greater than r is given by (Linsley 1975),

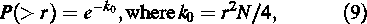
with k₀ being a convenient parameter for characterizing the anisotropy amplitude probability distribution. We can take (√2)r_rms, which corresponds to k₀ = 1, as the noise amplitude.

For the number of events that we have accumulated, 1.1 × 10⁶, the total amplitude of 0.43% calculated in this work could have arisen by chance with a probability of ∼6.2 × 10^–3, corresponding to k₀ = 5.08 and indicative of an apparently significant anisotropy (k₀ > 1) at the sidereal period. We conclude therefore that this data set provides evidence of anisotropy of the cosmic ray intensity additional to the CGE.

Cosmic ray data obtained at the Alborz observatory clearly shows an anisotropy in sidereal time at energies in the decade below 1 PeV, with the energy threshold of ∼250 TeV and the mean energy of ∼420 TeV. One part of this anisotropy is due to Earth’s motion around the Galaxy (the CGE), but our measured asymmetry suggests the possible existence of some other additional effects, probably a unidirectional anisotropy of cosmic ray flow along the Galactic arms. The amplitude of our total measured anisotropy is about 0.43%. The CGE contribution to this anisotropy is about 0.135% and the rest, 0.30%, is predicted to be due to the flow along the Galactic arm. The latter anisotropy suggests a mean free path of about 30 pc for these high-energy cosmic rays. The evidence for these anisotropies is based on the value of the parameter k₀, as suggested by Linsley (1975) and found in this work to be 5.08, that is, more than k₀ = 1, the value for the noise amplitude.

The EAS-TOP experiment reported somewhat lower limits in the energy range below 1200 TeV (Aglietta et al. 2003). The relatively large amplitudes published by the Akeno experiment (Kifune et al. 1986) and our experiment are difficult to reconcile with the results of the EAS-TOP experiment.