Science at Very High Angular Resolution with the Square Kilometre Array
L. E. H. Godfrey A H , H. Bignall A , S. Tingay A , L. Harvey-Smith B , M. Kramer C D , S. Burke-Spolaor B E , J. C. A. Miller-Jones A , M. Johnston-Hollitt F , R. Ekers A B and S. Gulyaev GA International Centre for Radio Astronomy Research, Curtin University, GPO Box U1987, Perth, WA 6845, Australia
B CSIRO Astronomy and Space Science, Australia Telescope National Facility, PO Box 76, Epping, NSW 2121, Australia
C Max-Planck-Institut fur Radioastronomie, Auf dem Hugel 69, D-53121 Bonn, Germany
D Jodrell Bank Centre for Astrophysics, University of Manchester, Manchester M13 9PL, UK
E Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
F School of Chemical and Physical Sciences, Victoria University of Wellington, PO Box 600, Wellington, 6140, New Zealand
G Institute for Radio Astronomy and Space Research, Auckland University of Technology, Auckland, New Zealand
H Corresponding author. Email: L.Godfrey@curtin.edu.au
Publications of the Astronomical Society of Australia 29(1) 42-53 https://doi.org/10.1071/AS11050
Submitted: 14 September 2011 Accepted: 24 November 2011 Published: 16 December 2011
Journal Compilation © Astronomical Society of Australia JYEAR
Abstract
Preliminary specifications for the Square Kilometre Array (SKA) call for 25% of the total collecting area of the dish array to be located at distances greater than 180 km from the core, with a maximum baseline of at least 3000 km. The array will provide angular resolution θ ⪅ 40–2 mas at 0.5–10 GHz with image sensitivity reaching ⪅50 nJy beam–1 in an 8-hour integration with 500-MHz bandwidth. Given these specifications, the high-angular-resolution component of the SKA will be capable of detecting brightness temperatures ⪅200 K with milliarcsecond-scale angular resolution. The aim of this article is to bring together in one place a discussion of the broad range of new and important high-angular-resolution science that will be enabled by the SKA, and in doing so, address the merits of long baselines as part of the SKA. We highlight the fact that high angular resolution requiring baselines greater than 1000 km provides a rich science case with projects from many areas of astrophysics, including important contributions to key SKA science.
Keyword: telescopes
1 Introduction
The future of radio astronomy at centimetre wavelengths lies with the Square Kilometre Array (SKA): a radio interferometer currently in the design stages, that will have a total collecting area in the order of one square kilometre (see e.g. Schilizzi 2007). The current design stipulates that 25% of the total collecting area will reside in a number of remote array stations at distances of between 180 km and 3000 km from the centre of the array. It is envisaged that each of these remote stations will comprise several dishes with single-pixel receivers operating in the approximate frequency range 0.5–10 GHz (e.g. Schilizzi 2007). Such an instrument will provide very high sensitivity at angular resolutions ranging from several arcseconds to one milliarcsecond.
In the following sections, we highlight the fact that high angular resolution requiring baselines greater than 1000 km provides a rich science case with projects from many areas of astrophysics, including important contributions to key SKA science. This was presented in SKA Memo 135 (Godfrey et al. 2011), and the following represents a subset of the science discussed in that work.
We note that the SKA remote stations will not include the sparse or dense aperture array technologies proposed for the SKA core, nor will they involve phased array feeds on the dishes. For the remote stations, only the standard technologies — dishes with single-pixel feeds — will be involved. Much of the proposed high-angular-resolution science does not require access to very wide fields of view or very low frequencies (<500 MHz). Therefore, dishes with single-pixel receivers operating in the approximate frequency range 0.5–10 GHz are adequate for the vast majority of proposed high-angular-resolution science.
The science case will continue to develop as the SKA design proceeds over the coming years, as part of the Pre-Construction Phase Project Execution Plan or PEP (Schilizzi 2011).
In Section 2 we compile a list of science drivers for the high-angular-resolution component of the SKA. The science cases are extracted largely from the book ‘Science with the Square Kilometre Array’ (Carilli & Rawlings 2004), and the Design Reference Mission for SKA-mid and SKA-lo (SKA Science Working Group 2010), and we include more recent advances and additional science cases. In Section 3 we present the conclusions and closing remarks resulting from this work.
2 The Science Case for High Angular Resolution
2.1 Strong Field Tests of Gravity
One of the major science goals of the SKA is to test relativistic theories of gravity in the strong field regime via precision timing of pulsars. This will be achieved by (1) timing relativistic binary systems, e.g. pulsar–neutron star binaries and any pulsar–black hole binaries discovered in the future, including pulsars in orbit around the Galactic Centre; and (2) monitoring an array of millisecond pulsars (a pulsar timing array) to detect gravitational waves with nanoHertz frequencies (Kramer et al. 2004; Cordes et al. 2004). This science goal is discussed in the Design Reference Mission (SKA Science Working Group 2010), Chapters 16 and 17. So far the discussions of the strong field gravity tests using pulsars have concentrated on the critical precision timing information, but the importance of high angular resolution has not been emphasised. Here, we highlight the importance of high angular resolution to achieve the aims of this important science goal.
Approximately 100 compact relativistic binaries are expected in the SKA Galactic pulsar census (Smits et al. 2009), of which some fraction (⪆5–25) are expected to be in stellar-mass black hole binary systems (Lipunov, Bogomazov & Abubekerov 2005). The likelihood of dynamic interactions in globular clusters means that the chances of finding exotic binaries such as millisecond pulsar–black hole systems is enhanced in these environments (e. g. Sigurdsson 2003). However, the most common black hole–pulsar binary system are likely to be normal rather than recycled (millisecond) pulsars (see Pfahl et al. 2005; Lipunov et al. 2005).
In this section dealing with strong field tests of gravity, we focus on relativistic binaries in which the pulsar companion is a stellar-mass black hole, neutron star, or white dwarf. The discovery of a pulsar in a sufficiently compact orbit around the supermassive black hole (SMBH) at the Galactic Centre (GC) would also enable tests of relativistic gravity that are complementary to those enabled by pulsars in compact orbits around stellar-mass black holes. The prospects of probing the space-time of the supermassive black hole at the Galactic Centre with pulsar timing measurements are discussed in detail by Liu et al. (2011). For GC pulsars, an orbital period ⪅0.3 yrs would be required to ensure that perturbations caused by the mass distribution around Sgr A* are negligible (Liu et al. 2011). Furthermore, frequencies ⪆15 GHz would be required to optimise the timing precision (Liu et al. 2011) which is strongly affected by pulse-broadening caused by the extreme interstellar scattering at the Galactic Centre.
2.1.1 Accurate Pulsar Distances Are Essential
Precise measurements of the proper motion and distance to each of the relativistic binaries detected in the pulsar census are essential for these systems to be used as laboratories for testing theories of gravity. Accurate distance and proper motion measurements are required in order to correct for the acceleration terms that affect the spin and orbital-period derivatives. The latter parameter is of particular relevance for testing alternative theories of gravity (Cordes et al. 2004; Stairs 2010; Kramer 2010) and potentially detecting, or at least constraining, extra spatial dimensions (Simonetti et al. 2011).
Let P
b be the binary period, 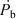 the corresponding time derivative, c the speed of light, d the distance and μ the proper motion of the system. The so-called Shklovskii Effect (Shklovskii 1970) contributes to the observed period derivative an amount
the corresponding time derivative, c the speed of light, d the distance and μ the proper motion of the system. The so-called Shklovskii Effect (Shklovskii 1970) contributes to the observed period derivative an amount

This effect, if not precisely accounted for, limits the precision with which theories of gravity may be tested in relativistic binary pulsars. In some cases, the magnitude of the Shklovskii Effect can be comparable to, or greater than the intrinsic orbital period derivative due to gravitational radiation (see e.g. Bell & Bailes 1996). A similar effect arises due to the differential acceleration of the Solar System and the pulsar in the gravitational potential of the Galaxy (Damour & Taylor 1991). The determination of this Galactic acceleration term requires precise knowledge of the pulsar's spatial position, as well as the Galactocentric radius (R 0) and speed of the solar system (v 0). To underline the importance of precise distance measurements, it is worth noting that the tests of relativistic gravity in the Hulse–Taylor binary system B1913+16, which currently provides one of the most precise constraints of this kind, are limited by the uncertainty in the distance, which has been determined using the pulsar's dispersion measure to a precision of ~30% (Weisberg et al. 2008).
As noted above, the Galactic constants R 0 and v 0 are of fundamental importance in correcting for the acceleration terms that impact the observed binary period derivative. The high-angular-resolution component of the SKA could provide a measurement of R 0 with 1% precision from parallax measurements of Sgr A* (Fomalont & Reid 2004).
2.1.2 Trigonometric Parallax Measurements Are Required to Maximise the Science Return
Pulsar distances, in some cases, may be determined by timing measurements alone via the method of timing parallax. The orbital motion of the Earth causes a 6-monthly variation in the pulse arrival times due to the curvature of the wavefront, and consequent periodic change in the path length from the pulsar to Earth. The amplitude of this timing parallax signature is very small: 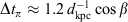 [μs], where β is the ecliptic latitude, and d
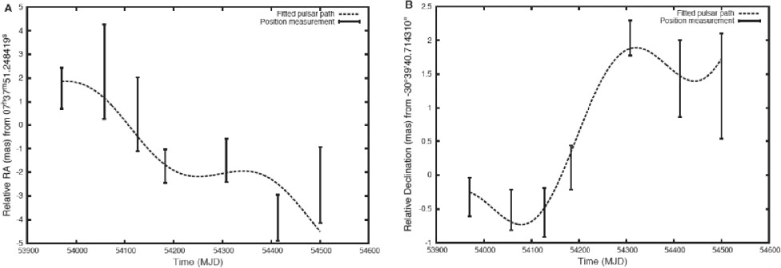
kpc is the pulsar distance in kpc (Ryba & Taylor 1991). Therefore, accurate timing parallax measurements are limited to a subset of pulsars with very high timing precision; that is, millisecond pulsars with stable timing characteristics, and preferably low ecliptic latitude (Smits et al. 2011). In contrast, the ability to determine trigonometric (imaging) parallax (Figure 1) depends only on the flux density and distance of the source, and is therefore applicable to a much wider range of systems.
[μs], where β is the ecliptic latitude, and d
kpc is the pulsar distance in kpc (Ryba & Taylor 1991). Therefore, accurate timing parallax measurements are limited to a subset of pulsars with very high timing precision; that is, millisecond pulsars with stable timing characteristics, and preferably low ecliptic latitude (Smits et al. 2011). In contrast, the ability to determine trigonometric (imaging) parallax (Figure 1) depends only on the flux density and distance of the source, and is therefore applicable to a much wider range of systems.
|
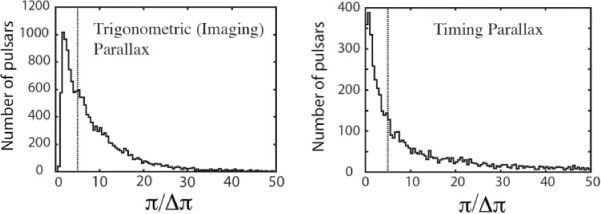
Smits et al. (2011) simulated and compared the accuracy of trigonometric parallax measurements with various methods of timing parallax distance determination, and concluded that both timing parallax and trigonometric parallax capabilities will be required to enable precision tests of gravity in the strong field regime. The results of the simulations (Figure 2) suggest that the SKA can potentially measure the trigonometric parallax distances for ~9000 pulsars up to a distance of 13 kpc with an error of 20% or better, and timing parallax distances for only about 3600 millisecond pulsars out to 9 kpc, with an error of 20% or better.
|
It is highly likely that some of the most interesting relativistic binary systems will not provide sufficient timing precision to allow accurate timing parallax distance determination, but could still provide excellent tests for relativistic theories of gravity. This is possible because, despite the limited timing precision, accurate measurement of long term secular trends such as the orbital period derivative, 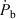 , can still be achieved, given a long enough enough time. For example, the measured uncertainty in
, can still be achieved, given a long enough enough time. For example, the measured uncertainty in 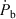 decreases approximately as T
–2.5, where T is the total time span of data for the system (Damour & Taylor 1992).
decreases approximately as T
–2.5, where T is the total time span of data for the system (Damour & Taylor 1992).
A good example of this is the pulsar–white dwarf relativistic binary system, J1141–6545. Owing to the asymmetry in self-gravitation between the pulsar and white dwarf companion, this system provides a unique laboratory for testing alternative theories of gravity (Bhat, Bailes & Verbiest 2008). However, the young pulsar in this system exhibits significant ‘timing noise’ which limits the timing precision (Bailes 2005). Despite the timing noise, J1141–6545 is likely to provide some of the most stringent tests of alternative theories of gravity: already four post-Keplerian parameters have been measured, and the orbital period derivative for this system is expected to be determined to better than 2% by 2012, at which point uncertainty in the kinematic Doppler term, or Shklovskii Effect (the term involving the pulsar distance and proper motion) will dominate the errors (Bhat et al. 2008).
With this example in mind, it should be noted that many of the pulsar–black hole binaries are likely to be normal pulsars (and probably young pulsars like J1141–6545, due to evolution of the systems), rather than recycled (millisecond) pulsars (see Pfahl et al. 2005; Lipunov et al. 2005). This suggests that trigonometric (imaging) parallax measurements will be required to determine accurate distances for a large fraction of pulsar–black hole binaries.
2.1.3 Why Is the SKA Required?
The high sensitivity of the long-baseline SKA is required not only to detect weak and distant pulsars, but also to provide a high density of calibrator sources surrounding the pulsars that will enable multi-view, in-beam calibration, and therefore high-precision astrometry (Rioja et al. 2009; Fomalont & Reid 2004). Owing to its high sensitivity, the long-baseline component of the SKA will be able to perform multi-view in-beam calibration using several compact, closely spaced calibrator sources, the closest of which will be in the order of several arcminutes from the target (see Godfrey et al. 2011). This technique will provide extremely accurate phase calibration at the position of the target, and provide astrometric precision of order 15μarcsec at 1.4 GHz (Fomalont & Reid 2004). Observations at frequencies below ~5 GHz are affected by ionospheric refraction, but the ionospheric effects may be calibrated out using a wide bandwidth (Brisken et al. 2000). Only with the substantial improvement in sensitivity provided by the SKA will high-precision astrometry on weak pulsars (and other weak sources) be possible.
2.1.4 Benefits of High Angular Resolution to the Pulsar Timing Array
High angular resolution could also be important in establishing the pulsar timing array (PTA) (Smits et al. 2011). Accurate astrometric information reduces the amount of observing time required to obtain a coherent timing solution by breaking the degeneracies between position uncertainty and pulsar spin-down (Smits et al. 2011). In the absence of accurate positional information, this can take 12 months or more. Therefore, the high-angular-resolution component of the SKA will assist the selection of stable millisecond pulsars to be included in the pulsar timing array.
Further, the PTA may detect the gravitational wave signal from individual nearby binary black holes. In that case, precise distances to the pulsars in the PTA are required to enable a precise measurement for the gravitational wave source location (Lee et al. 2011).
Lastly, the high-angular-resolution component of the SKA will compile a significant sample of SMBH binaries (see Section 2.7). The identification of a large sample of SMBH binaries would enable statistical studies of the inspiral rates in various phases of the binary evolution. The inspiral rates, and the possible existence of a ‘stalling radius’ are important factors in the interpretation of the gravitational wave background that will be investigated with the pulsar timing array (Jaffe & Backer 2003).
2.2 Modelling the Large-Scale Galactic Magnetic Field Using Pulsars
Wavelet tomography using a grid of thousands of pulsars with known rotation measures (RMs), dispersion measures (DMs) and distances will provide the best possible map of the Galactic magnetic field and electron density on large (⪆100 pc) scales (Stepanov et al. 2002; Noutsos 2009; Gaensler et al. 2004; Beck & Gaensler 2004; Gaensler 2006). So far discussions about mapping the Milky Way magnetic field using pulsars have concentrated on the ability to search for and identify many thousands of pulsars, but the importance of high angular resolution has not been emphasised. Here we highlight the importance of high angular resolution to achieve the aims of this important science goal.
The DM and RM for a grid of thousands of pulsars will be obtained via the SKA Galactic Pulsar Census. The final ingredient to enable accurate tomographic models of the large-scale Galactic magnetic field — accurate distance estimates to each of the pulsars — will require trigonometric parallax measurements to thousands of pulsars. Currently, distance estimates to pulsars are most commonly obtained via the pulsar's dispersion measure combined with the galactic electron-density model. Distance estimates using this method are typically uncertain by tens of percent, and can be in error relative to accurate parallax measurements by more than a factor of 2, due to the large uncertainty in the electron-density model (Deller et al. 2009b). Precise pulsar distances will require either parallax distance measurements, or an improved electron-density model, which itself will require parallax distance measurements to a large sample of pulsars (Cordes et al. 2004). Therefore, precision astrometry is a requirement for the SKA to enable the best possible model of the large-scale Galactic magnetic field. Mapping the magnetic field of the Milky Way provides an excellent opportunity to address the issues surrounding the generation and preservation of galactic magnetic fields. The importance of understanding the large-scale Galactic magnetic field configuration in the context of fundamental questions of astrophysics is discussed at length in e. g. Gaensler et al. (2004); Beck & Gaensler (2004, and references therein).
2.3 Imaging Protoplanetary Disks at Centimetre Wavelengths
The scientific motivation for obtaining high-angular-resolution radio images of protoplanetary disks (Figure 3) is three-fold. Firstly, it will enable imaging of various structures in the disk such as density waves and radial gaps formed by the interaction of the disk with a planetesimal (Wilner 2004). Secondly, it will enable studies of the spatial dependence of spectral signatures relating to different grain properties in the disk (Greaves et al. 2009). Thirdly, imaging the Hi 21-cm line emission will probe the kinematics and effects of photoevaporation in the disk surface layers (Kamp et al. 2007).

|
Grains in protoplanetary disks grow from sub-micron sizes up to millimetre sizes by sticking together in low-velocity collisions. Larger grains tend to shatter in collisions rather than sticking together. How, and under what conditions, do the millimetre-sized grains overcome this barrier to become pebble-sized grains? This question is the subject of ongoing debate, and is a question that may be addressed with the high-angular-resolution component of the SKA. Dust particles emit inefficiently at wavelengths larger than their size, and therefore emission at centimetre wavelengths provides evidence for pebble-sized grains, which in turn provides evidence for significant progress towards planet formation. The high-angular-resolution component of the SKA will address the following questions: Where does the growth of decimetresized grains occur within the disk? Are the grains clumping into protoplanets? In what environments do these large grains occur (stellar age, spectral type, etc.)?
Such information will benefit our understanding of planet formation and improve models of protoplanetary disks (Wilner 2004; Wilner et al. 2005; Greaves et al. 2009; Natta et al. 2007). The reader is referred to Greaves et al. (2009) for a more detailed discussion of the science case for imaging protoplanetary disks at centimetre wavelengths.
Imaging protoplanetary disks with the SKA was initially proposed for frequencies in the range 20–35 GHz (Wilner 2004). However, studies of protoplanetary disks can be carried out in the frequency range ⪅10 GHz (Hoare 2009; Greaves 2010; Greaves et al. 2009). It is expected that the SKA will be able to image in detail the distribution of large dust particles in the disks around hundreds of nearby young stars at ν ⪅10 GHz (Wilner et al. 2005). Initial estimates of the technical requirements indicate the need for very high sensitivity (~100 nJy beam–1) on long (~1000 km) baselines (Greaves 2010). This would enable observations at ~5–10 GHz of Earth analogues forming in southern star clusters at ~20–60 pc (the β Pic, TW Hya, AB~Dor, Tuc/Hor groups). The e-MERLIN Legacy Project ‘PEBBLES’ is aimed at studying the centimetre emission from pebble-sized dust grains to show where and when planet-core growth is proceeding, and to identify accreting protoplanets. The initial results of the PEBBLES e-MERLIN Survey will help to inform the scientific and technical requirements for this project with the SKA.
Kamp et al. (2007) propose that mapping the Hi line in nearby systems will also be an important tool for studying circumstellar disks with the high-angular-resolution component of the SKA. Neutral Hydrogen 21-cm line emission traces a layer near the disk surface that is directly exposed to soft UV irradiation from the parent star, but shielded from the ionising UV and X-ray (h ν > 13.6 eV) radiation by the outer layer of the disk. High angular resolution SKA observations of 21-cm line emission will probe the kinematics of protoplanetary disks, as well as the effects of irradiation and photoevaporation at the surface layer.
In addition to these primary scientific motivations, high angular resolution could potentially be used to pin-point the location of any extra-terrestrial intelligence (ETI) signals detected from planets orbiting relatively nearby stars (Morganti et al. 2006), by direct imaging and measuring the orbit of the planet.
2.4 Resolving AGN and Star Formation in Galaxies
At sub-mJy flux densities, the radio-source counts at GHz frequencies are thought to be dominated by star-forming galaxies, as opposed to AGN which dominate source counts at higher flux densities (e. g. Seymour et al. 2008). Without morphological information or a measurement of brightness temperature, it is generally not possible to determine, for a given galaxy, whether the observed radio flux is dominated by emission from a compact, nuclear starburst or an active galactic nucleus (Norris et al. 1990). The brightness temperature of a radio source indicates which process, AGN or star formation, dominates the radio emission: starbursts are typically limited to brightness temperatures of 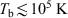 , and this clearly distinguishes them from the compact cores of AGN, which exhibit brightness temperatures
, and this clearly distinguishes them from the compact cores of AGN, which exhibit brightness temperatures 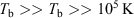 Norris et al. 1990; Condon 1992). Baselines longer than 3000 km are required to unambiguously distinguish AGN and star-formation in sources up to redshift z = 7 with flux densities down to at least 30 μJy (SKA Science Working Group 2010, ch. 2). Discriminating between AGN and starburst galaxies will be possible in most cases based on the morphological information provided by high-angular-resolution images (e.g. Garrett 2000).
Norris et al. 1990; Condon 1992). Baselines longer than 3000 km are required to unambiguously distinguish AGN and star-formation in sources up to redshift z = 7 with flux densities down to at least 30 μJy (SKA Science Working Group 2010, ch. 2). Discriminating between AGN and starburst galaxies will be possible in most cases based on the morphological information provided by high-angular-resolution images (e.g. Garrett 2000).
It is widely believed that AGN play an important role in the growth and evolution of galaxies. The interaction between the AGN and the surrounding medium may promote star formation at high redshift (e.g. Klamer et al. 2004; Elbaz et al. 2009) and/or suppress star formation at lower redshifts (e.g. Croton et al. 2006). A powerful approach to addressing questions on the relationship between AGN activity, black hole growth, and galaxy evolution, will be deep, high-resolution imaging with the SKA to detect and distinguish between the first starburst galaxies and the first AGN jets, and to determine the frequency of occurrence of low luminosity AGN in different galaxy types (SKA Science Working Group 2010, Chapter 2). This will enable a determination of the full range of SMBH masses and accretion rates and how these relate to galaxy histories.
This aspect of high-angular-resolution SKA science is discussed in detail in the SKA Design Reference Mission (SKA Science Working Group 2010, Chapter 2). The goal will be to conduct a high-angular-resolution SKA survey to obtain a statistically significant sample of galaxies through which to explore the contribution and role of AGNs versus star formation in galaxy evolution. The high-angular-resolution SKA survey will be coordinated with other multi-wavelength surveys to maximise the scientific return, and an additional benefit will be in studying the cosmic evolution of AGN activity, which will address important questions relating to radio AGN, such as the lifetimes, duty-cycles, fuelling and triggering mechanisms.
2.5 The First Generation of AGN Jets
The discovery of powerful distant quasars at z ⪆ 6 indicates that supermassive black holes >109 M⊙ existed at that time. This suggests that the first supermassive black holes formed before, or during, the epoch of reionisation. Indeed, it has been suggested that AGN jets may have played a key role in the formation of some of the first stars and galaxies in the universe, through jet-induced star formation (Klamer et al. 2004; Silk 2005; Elbaz et al. 2009; Elbaz 2010).
Falcke, Kording & Nagar (2004) suggest that the first generation of AGN jets produced by accreting supermassive black holes will be strongly confined by their dense environment and appear as distant Gigahertz Peak Spectrum (GPS)-like sources, that is faint, compact sources with unusually low turn-over frequencies. The turn-over frequency, νpeak and linear size, L, of GPS and Compact Steep Spectrum (CSS) sources are found to follow an expression of the form
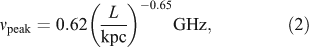
which results from the basic properties of synchrotron self-absorption (Falcke et al. 2004). Since the source size and turn-over frequency of GPS sources are correlated but angular size and frequency scale differently with redshift, the first AGN jets should stand out from their low redshift counterparts in the parameter space defined by angular size, turn-over frequency, and flux density (see Figure 4).
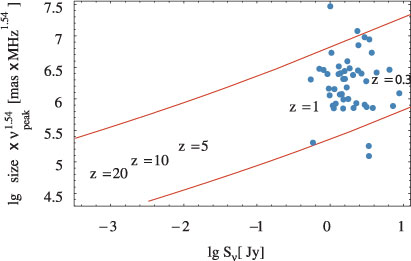
|
Falcke et al. (2004) suggest the following strategy for finding the first generation of AGN jets in the universe:
-
a shallow all-sky multi-frequency survey in the range 100–600 MHz down to 0.1 mJy at arcsecond resolution;
-
identification of compact, highly peaked spectrum sources in that frequency range;
-
identification of empty fields in the optical;
-
re-observation to exclude variable sources;
-
observations with long baselines and resolutions of ~10 mas to determine sizes and to pick out the ultra-compact low-frequency peaked (ULP) sources;
-
spectroscopic confirmation of remaining candidates with Hi observations or by other means.
The stated goal of 10-mas resolution, at a frequency of 1.4 GHz, would require baseline lengths up to ~4000 km.
2.5.1 Radio and CO Studies of High-Redshift AGN Jets
Klamer et al. (2004) reviewed molecular gas observations for a sample of z > 3 galaxies, and found that the gas and dust are often aligned with the radio emission. Based on these results, they proposed a scenario in which CO is formed at the sites of star formation that are triggered by relativistic jets, as is seen in some nearby sources (e.g. Cen A, 3C40). High-sensitivity, high-angular-resolution imaging of high-redshift radio galaxies will be required to complement high-redshift CO imaging with ALMA, in order to study the relationship between radio jets and early star formation. Resolution of order tens of milliarcseconds will likely be required at low frequency (⪅1.4 GHz) to map the radio structures in detail.
2.6 Exploration of the Unknown
The Exploration of the Unknown has been identified as an important guiding principle for the design of the SKA (Carilli & Rawlings 2004; Wilkinson et al. 2004). This recognises the discovery potential provided by instruments that are capable of probing unexplored regions of parameter space. Whilst high angular resolutions are reached with existing radio telescopes, this domain has not been explored at the sensitivity of the SKA. The combination of high sensitivity and high angular resolution with the SKA will increase the observational phase space being searched, by opening up a large, unexplored region of the flux-density–angular-size plane. Observations at milliarcsec-scale resolution will, for the first time, be possible for thermal and non-thermal emission regions with brightness temperatures as low as hundreds of Kelvin. Current VLBI networks are, in general, limited to non-thermal sources with brightness temperatures ⪆106 K. The combination of high sensitivity with a broad range of angular resolution up to milliarcsecond scales will provide greater discovery potential for the SKA. Furthermore, the ability to perform high angular resolution follow-up of transient radio sources will maximise the science return of transient searches, as discussed below.
2.6.1 Transients
High angular resolution will play an important role in localising, identifying and understanding transient radio sources. Arcsecond resolution may be sufficient to identify the host galaxies of extragalactic fast transients, and follow-up spectroscopy of the host galaxies would provide the redshifts. However, milliarcsecond-scale resolution could potentially localise transient sources on a much finer scale and help to determine their nature. High angular resolution follow-up observations of newly discovered classes of radio source would be of great benefit to understanding the source physics. Resolving the source morphology and its evolution could provide information on the energetics of the event and environment of the source. For the slower transient sources (with time-scales of weeks or longer), high angular resolution would enable measurement of the source proper motion which could discriminate between Galactic and extragalactic events. This would be particularly important if sources were found to be unresolved with no optical counterparts.
Long baselines are also an excellent discriminant between RFI and genuine astronomical events (Wayth et al. 2011; Thompson et al. 2011). A triggered buffer (e.g. Macquart et al. 2010) would allow for off-line analysis of the transient sources, and would function as follows.
Data from antennas on long baselines would be stored for a couple of minutes in a rolling buffer. A transient source detected within the long-baseline field-of-view (effectively the 15-m antenna primary beam) would trigger the download of this buffer for post-processing. The station beams could then be formed in the direction of the transient source whose location would be determined by the SKA core to within a few arcseconds. A rolling buffer is not required for the antennas of the SKA core, since these antennas will have access to the whole field of view, and the standard output would enable the transient source position to be determined to within a few arcseconds.
A pilot survey (V-FASTR) for VLBI detection of fast transients using a triggered buffer is currently being implemented on the VLBA (Wayth et al. 2011). The results of the V-FASTR survey will inform the technical requirements for this experiment with the SKA.
2.7 Binary Supermassive Black Holes
Binary supermassive black holes play an important role in a number of areas of astrophysics, including the formation and evolution of galaxies, galactic dynamics, and gravitational wave science. Hierarchical structure formation models predict that a significant fraction of supermassive black holes reside in binary systems (Volonteri, Haardt & Madau 2003), and these systems will have a strong impact on the central galactic environment (e. g. Merritt 2006). Simulations of binary black hole evolution in a galactic environment suggest that the inspiral efficiency (that is, the rate of decay of the binary orbital radius) may decrease at an orbital radius of 0.001 ⪅r ⪅10 pc (Yu 2002), potentially leaving a fraction of SMBH binaries ‘stalled’ for extended periods of time at these orbital radii.
The identification of a large sample of SMBH binaries would enable statistical studies of the inspiral rates in various phases of the binary evolution. This will be an important step in studies of galaxy merger rates and understanding the dynamical processes responsible for removing angular momentum from these systems, and delivering them to the gravitational wave dominated phase of evolution. The inspiral rates, and the possible existence of a ‘stalling radius’ are important factors in the interpretation of the gravitational wave background that will be observed by the pulsar timing array (Jaffe & Backer 2003). Statistical studies would also allow measurements of the influence of accretion versus mergers in SMBH growth, and lead to a more precise estimate of binary-merger rates (Burke-Spolaor 2011a).
Nearby binary systems that are sufficiently massive may generate gravitational radiation strong enough to enable the object to be resolved above the stochastic background (e.g. Sesana, Vecchio & Volonteri 2009). Whilst it may not carry a high probability (Burke-Spolaor 2011b; Sesana et al. 2009), the detection of both electromagnetic and gravitational wave emission from a nearby SMBH binary system would have a great scientific impact. Identification of the sky position and rough orbital solution for a nearby binary would not only raise the sensitivity of the pulsar timing array to the object manyfold (Jenet et al. 2004), but allow a study of the impact of the binary system on the dynamics of the host galaxy.
High angular resolution imaging is an effective method of searching for SMBH binaries over a wide range of orbital radii, at both high and low redshift. Binary BH candidates may be identified by surveying a large number of radio-emitting AGN (which could be initially identified in existing, lower resolution surveys) to look for dual, compact, weakly polarised, flat-spectrum radio cores (Burke-Spolaor 2011a). Particular classes of AGN thought to harbour binary black holes may be targeted (Tingay & Wayth 2011). Some SMBH binary-merger models predict ejected AGN, which could be revealed by astrometric measurements of AGN showing an offset from the optical host's kinetic centre.
Source statistics are rather uncertain, since the inspiral time-scale of binary black holes, and the probability that both black holes in the binary system will be radio loud, are unknown factors. At present, only one paired SMBH system at a separation much less than 1 kpc is known (and supported by multi-wavelength evidence). This system, 0402+379 (Rodriguez et al. 2006), was first identified via VLBI imaging as a candidate binary supermassive black hole (see Figure 5). In a search of archival VLBA data aimed at SMBH binary detection, this was the only binary detected from a sample of more than 3000 radio-loud AGN (Burke-Spolaor 2011a). The results indicate that the VLBA is limited by (u, v) coverage, sensitivity and dynamic range, rendering a large statistical study unfeasible. However, these crucial capabilities are realised by the SKA. The great improvement in sensitivity and dynamic range will increase the detection efficiency by allowing weaker binary companions to be identified, and weaker AGN to be searched. Improved sample selection may also significantly improve the binary detection efficiency.

|
It is likely that tens of thousands of AGN must be surveyed in order to compile a significant sample of SMBH binaries, and the sensitivity of the SKA will be crucial in this regard, reducing the required integration time per source, and enabling a much larger sample of objects to be searched. Such a survey could be done in combination with a survey of strong gravitational lenses and a survey of Hi absorption against AGN. Angular resolution of ~1 mas could resolve projected separations of 8.5 pc at all redshifts, and sub-parsec separations for the nearest galaxies. This survey could feasibly be carried out at frequencies ν ~ 5–10 GHz.
2.8 X-Ray Binary Systems and Relativistic Jets
2.8.1 Jet Formation and Evolution
Understanding the connection between accretion and jet production has implications for the understanding of AGN and γ-ray bursts as well as X-ray binaries. X-ray binary systems (XRBs) provide a unique tool to study the coupling between jet production and accretion flow, due to the rapid evolution of the systems through a wide range of characteristic accretion states (on the time-scale of weeks to months), and the associated rapid changes in jet characteristics (Fender 2004).
There exist two different classes of X-ray binary jet that show dramatically different spectral and morphological characteristics. These are the compact, steady ‘hard-state’ jets, and transient ‘flaring-state’ jets (see e.g. Fender 2006, 2010). The two different jet classes are associated with different characteristic X-ray states, and a typical XRB will transition between the two jet classes on varying timescales, in unison with transitions between X-ray spectral states.
Transient jets in flaring XRBs are produced during outbursts in which bright, optically thin jet components are seen moving at relativistic speeds away from the core. This type of radio jet is associated with a transition from a hard power-law X-ray spectrum to a softer power-law X-ray spectrum, and later, a thermal disk, blackbody dominated X-ray spectrum. Unlike the compact, steady ‘hard-state’ jets, transient jets are typically resolved at VLBI scale resolution, and the optically thin, relativistic jet components are often observed to move away from the core on a timescale of hours.
Relativistic ejections in X-ray binary systems can exhibit significant amplitude and structural changes over the course of a typical observation of several hours. Thus, high sensitivity, high-angular-resolution radio observations with good snapshot (u, v)-coverage are required to enable high time resolution ‘movies’ of these relativistic outflows and avoid the problems that arise from rapid evolution of the jet morphology and brightness within a single observation Tingay et al. 1995; Mioduszewski et al. 2001). Such observations are crucial in order to tie jet-ejection events to X-ray timing and spectral changes in the accretion flow. The high-angular-resolution component of the SKA will be of fundamental importance in this regard, particularly in the case of transient jets from neutron star XRBs, and even accreting white dwarf systems, about which very little is currently known, and which may be fainter than transient jets from black hole XRBs. It is certainly the case that the compact hard-state jets from neutron star XRBs are inherently fainter than black hole XRBs at the same X-ray luminosity (Migliari & Fender 2006). By comparing the jets produced by accreting black hole, neutron star and white dwarf systems, the relationship between jet formation and system parameters (e.g. depth of the potential well, stellar surface, stellar magnetic field, black hole spin etc.) can be determined. Understanding the similarities and differences between disk-jet coupling in black hole, neutron star and white dwarf systems is a crucial step in understanding the jet production mechanisms and the role played by various physical parameters.
High angular resolution will also be required to resolve X-ray binary systems in nearby galaxies from the background emission (Fender 2004).
2.8.2 Precise Distances and Luminosities
Determining the physical characteristics of an object depends critically on knowing its distance. At present, X-ray binary distances, and therefore luminosities, have significant fractional uncertainties. Distances are typically only known to within a factor of two (Jonker & Nelemans 2004). Due to the limited sensitivity of existing VLBI arrays only three X-ray binary parallax distances have been measured to date (Bradshaw, Formalont & Geldzahler 1999; Miller-Jones et al. 2009b; Reid et al. 2011). The high sensitivity and astrometric precision of the SKA will enable precise parallax distances to be measured for a large number of X-ray binary systems, and thereby enable a number of fundamental questions to be addressed, for example, by what factor can Galactic X-ray binary systems exceed their Eddington luminosities.
This issue is relevant to the interpretation of ultra-luminous X-ray sources (ULXs), from which the existence of intermediate-mass black holes has been inferred. Furthermore, it is claimed that a discrepancy between the quiescent luminosities of black hole and neutron star X-ray binaries provides evidence for the existence of event horizons in black holes (Garcia et al. 2001). Accurate luminosity measurements are required to test this claim. Accurate distances will also enable more precise estimates of the basic physical parameters such as component masses, orbital orientation, and black hole spins, as recently demonstrated by Reid et al. (2011) and Gou et al. (2011).
2.8.3 The Formation of Stellar-Mass Black Holes
Compiling the full 3-dimensional space velocities for a large sample of X-ray binaries will provide constraints on theoretical models of stellar mass black hole formation. It is generally accepted that neutron stars receive a ‘kick’ during their formation, due to intrinsic asymmetries in the supernova explosion or the recoil due to the associated mass ejection (see e.g. Nordhaus et al. 2010, and references therein). Supernova kicks are invoked to explain the anomalously high space velocities that are common among pulsars. It is currently not known whether all stellar mass black holes receive kicks during formation. Theoretical models predict that the highest mass black holes are formed by direct collapse of the progenitor star, with little mass ejection. These systems are not expected to show anomalously high space velocities. The less-massive systems are thought to form in two stages: initially a neutron star is created in a supernova explosion, followed by fallback of ejected material which pushes the compact object over the stable mass limit, resulting in the formation of a stellar mass black hole (Fryer 1999; Fryer & Kalogera 2001). These lower mass black holes are expected to exhibit high velocities, similar to neutron stars.
Do the most massive black holes form via direct collapse, rather than a two stage process involving an initial supernova explosion? What is the mass threshold between these two black hole formation mechanisms? How does binarity and compact object mass affect the supernova explosion? Accurate distances and proper motions for a large sample of accreting black holes, when combined with data in other wavebands, can address these important questions (Miller-Jones et al. 2009a).
Very few X-ray binaries have accurate distance (Bradshaw et al. 1999; Miller-Jones et al. 2009b; Reid et al. 2011) or proper-motion measurements (e.g. Mirabel et al. 2001; Dhawan et al. 2007). Astrometry on X-ray binaries is only possible during the so-called ‘low-hard’ or quiescent states. During these states, in which X-ray binaries spend the majority of their time, there exists a faint, steady, often unresolved radio jet, and there is no contribution from the bright milliarcsec-scale jet that exists during the flaring states. The closest black hole X-ray binary in quiescence, A0620–00, at a distance of 1.06 kpc (Cantrell et al. 2010), has a flux density of 51 μJy beam–1 at 8.5 GHz and lies on the fundamental plane of black hole activity (Gallo et al. 2006) that defines the relationship between black hole mass, X-ray luminosity and radio luminosity (Merloni, Heinz & di Matteo 2003). Scaling from the flux density of A0620–00 using 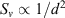 with the best current distance estimates (Jonker & Nelemans 2004) for the known population of X-ray binaries (Remillard & McClintock 2006), we expect that the SKA will be capable of compiling accurate proper motions and parallaxes for several tens of black hole X-ray binaries. This would enable statistical studies of the velocities of stellar mass black holes. These conclusions are based on an assumed SKA image sensitivity of ⪅100 nJy beam–1. More robust estimates of the expected outcomes will be considered in an upcoming paper (Miller-Jones et al., in preparation).
with the best current distance estimates (Jonker & Nelemans 2004) for the known population of X-ray binaries (Remillard & McClintock 2006), we expect that the SKA will be capable of compiling accurate proper motions and parallaxes for several tens of black hole X-ray binaries. This would enable statistical studies of the velocities of stellar mass black holes. These conclusions are based on an assumed SKA image sensitivity of ⪅100 nJy beam–1. More robust estimates of the expected outcomes will be considered in an upcoming paper (Miller-Jones et al., in preparation).
2.9 Mapping High-Mass Star Formation in Nearby Galaxies
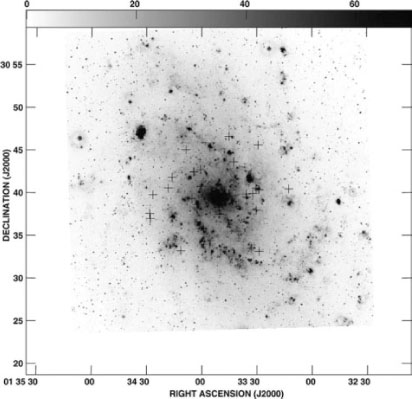
The combined sensitivity and high angular resolution of the SKA will permit detailed studies of extragalactic Hii regions for the first time. Global aspects of massive star formation, as traced by the Hii region population, are best studied in nearby, face-on spirals such as M33 M33 (Hoare 2004). Figure 6 shows the location of some Hii regions in M33 discovered with the VLA overlaid on an Hα image of the spiral galaxy. Only the top end of the initial mass function is accessible with the EVLA due to the limited sensitivity. The increased sensitivity of the SKA will be of fundamental importance in this regard. The high-angular-resolution component of the SKA will be able to distinguish ultra-compact Hii regions, which are young and therefore most relevant to identifying conditions at the star's birth-place. Ultra Compact Hii (UCHii) regions are typically deeply embedded in their parent molecular cloud and so cannot be studied at optical or near-IR wavelengths. The SKA will be capable of detecting individual UCHii regions out to a distance of nearly 50 Mpc, and will be able to resolve UCHii regions from their surrounding environment out to a distance of 1 Mpc (Johnson 2004). Questions such as what triggers high mass star formation, are much easier to answer in nearby spirals than in the Milky Way because a wider range of conditions can be investigated and there are no line-of-sight issues with everything lying in the Galactic plane (Hoare 2004; Johnson 2004).
|
The SKA will determine the exact location of massive star formation relative to other protostars, density enhancements in the molecular gas, shock fronts and other features of the ISM, and will enable an investigation into the relationship between properties of star formation and environmental parameters such as metallicity, pressure, turbulence, stellar density, triggering scenarios, and how star formation differs in ‘burst’ and quiescent modes (Johnson 2004; Hoare 2004).
2.10 Other Science
The preceding sections represent just a selection of the science case, and demonstrate that the high-angular-resolution component of the SKA provides a rich science case covering many areas of astrophysics, including important contributions to key SKA science. Due to length constraints, we do not consider every possible scientific application. Further science enabled by the high-angular-resolution component of the SKA includes (see Godfrey et al. 2011):
-
strong gravitational lensing;
-
small-scale structure and evolution in AGN jets;
-
Hi absorption against AGN;
-
absolute astrometry and geodesy;
-
relative astrometry, parallax and proper Motions;
-
stellar winds/outflows;
-
star-formation from studies of astrophysical masers;
-
stellar atmospheres:
-
-
imaging stellar atmospheres;
-
resolving stellar radio flares;
-
parallax and proper motions of radio-detected normal stars.
-
-
spatial and temporal changes in the fundamental constants;
-
ultra-high-energy particle astronomy at ⪆2-degree angular resolution using the Lunar Cherenkov Technique;
-
scattering:
-
-
probing the intergalactic medium using angular broadening;
-
resolving AU-scale structure in the ISM using diffractive scintillation;
-
extreme scattering events.
-
-
spacecraft tracking.
This is by no means meant as an exhaustive list of science enabled by the high-angular-resolution component of the SKA, and the science case will continue to develop over the coming years, as part of the pre-construction-phase Project Execution Plan (PEP Schilizzi 2011).
3 Conclusions
High angular resolution requiring baselines greater than 1000 km provides a rich science case with projects from many areas of astrophysics, including important contributions to key SKA science. Much of the high-angular-resolution science can be achieved within the approximate frequency range 0.5–10 GHz, or can be recast for this frequency range, and the vast majority of high-angular-resolution science does not require access to wide fields of view.
Acknowledgments
We wish to thank the following people for helpful discussions: Joe Lazio, Clancy James, Jane Greaves, Richard Dodson, Maria Rioja and Tim Colegate.
References
Bailes, M., 2005, ASPC, 328, 33Beck, R. and Gaensler, B. M., 2004, NewAR, 48, 1289
| Crossref | GoogleScholarGoogle Scholar |
Bell, J. F. and Bailes, M., 1996, ApJL, 456, 33
| Crossref | GoogleScholarGoogle Scholar |
Bhat, N. D. R., Bailes, M. and Verbiest, J. P.W., 2008, PhRvD, 77, 124017
Bradshaw, C. F., Fomalont, E. B. and Geldzahler, B. J., 1999, ApJL, 512, 121
| Crossref | GoogleScholarGoogle Scholar |
Brisken, W. F., Benson, J. M., Beasley, A. J., Fomalont, E. B., Goss, W. M. and Thorsett, S. E., 2000, ApJ, 541, 959
| Crossref | GoogleScholarGoogle Scholar |
Burke-Spolaor, S., 2011a, MNRAS, 410, 2113
| Crossref | GoogleScholarGoogle Scholar |
Burke-Spolaor, S., 2011b, PhD Thesis, Supermassive Blackhole Binaries and Transient Radio Events: Studies in Pulsar Astronomy, http://hdl.handle.net/1959.3/196878
Cantrell, A. G. et al., 2010, ApJ, 710, 1127
| Crossref | GoogleScholarGoogle Scholar |
Carilli, C. and Rawlings, S., 2004, NewAR, 48, 979
Condon, J. J., 1992, ARA&A, 30, 575
| Crossref | GoogleScholarGoogle Scholar |
Cordes, J. M., Kramer, M., Lazio, T. J. W., Stappers, B. W., Backer, D. C. and Johnston, S., 2004, NewAR, 48, 1413
| Crossref | GoogleScholarGoogle Scholar |
Croton, D. J. et al., 2006, MNRAS, 365, 11
| Crossref | GoogleScholarGoogle Scholar |
Damour, T. and Taylor, J. H., 1991, ApJ, 366, 501
| Crossref | GoogleScholarGoogle Scholar |
Damour, T. and Taylor, J. H., 1992, PhRvD, 45, 1840
Deller, A. T., Bailes, M. and Tingay, S. J., 2009a, Science, 323, 1327
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXisFemtrg%3D&md5=161dbf6f6cdba2e7c4def7e66f7a22f6CAS |
Deller, A. T., Tingay, S. J., Bailes, M. and Reynolds, J. E., 2009b, ApJ, 701, 1243
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtFWqsrzO&md5=baf5a485a65885cd0a3880d4631bc616CAS |
Dhawan, V., Mirabel, I. F., Rib'o, M. and Rodrigues, I., 2007, ApJ, 668, 430
| Crossref | GoogleScholarGoogle Scholar |
Elbaz, D., 2010, IAUS, 267, 17
Elbaz, D., Jahnke, K., Pantin, E., Le Borgne, D. and Letawe, G., 2009, A&A, 507, 1359
| 1:CAS:528:DC%2BC3cXhslSisr4%3D&md5=4c1e051764ad321e248e0d482e506b68CAS |
Falcke, H, Kording, E. and Nagar, N. M., 2004, NewAR, 48, 1157
| Crossref | GoogleScholarGoogle Scholar |
Fender, R., 2004, NewAR, 48, 1399
| Crossref | GoogleScholarGoogle Scholar |
Fender, R., 2006, in Compact Stellar X-Ray Sources, ed. W. Lewin & M. van der Klis, Cambridge Astrophysics Series (Cambridge, UK: Cambridge University Press), 39, 381
Fender, R., 2010, Lecture Notes in Physics, Vol. 794 (Berlin: Springer Verlag), 115
Fomalont, E and Reid, M., 2004, NewAR, 48, 1473
| Crossref | GoogleScholarGoogle Scholar |
Fryer, C. L., 1999, ApJ, 522, 413
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXlvFaltrY%3D&md5=c649cffa654e007913fcc19c25d52585CAS |
Fryer, C. L. and Kalogera, V., 2001, ApJ, 554, 548
| Crossref | GoogleScholarGoogle Scholar |
Gaensler, B. M., 2006, AN, 327, 387
Gaensler, B. M., Beck, R. and Feretti, L., 2004, NewAR, 48, 1003
| Crossref | GoogleScholarGoogle Scholar |
Gallo, E. et al., 2006, MNRAS, 370, 1351
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XpvFens74%3D&md5=ccccfe0bf065c05a08f71f0e2db522b6CAS |
Garcia, M. R., McClintock, J. E., Narayan, R., Callanan, P., Barret, D. and Murray, S. S., 2001, ApJL, 553, 47
| Crossref | GoogleScholarGoogle Scholar |
Garrett, M. A., 2000, in Perspectives on Radio Astronomy: Science with Large Arrays, ed. M. P. van Haarlem (Dwingeloo: ASTRON), 139
Godfrey, L., Bignall, H., Tingay, S., 2011, SKA Memo 135, http://www.skatelescope.org/uploaded/16339_135_Memo_Godfrey.pdf
Gou, L. et al., 2011, BAAS, ,
Greaves, J., 2010, ‘PEBBLES: Protoplanetary Disks with eMERLIN and SKA’, presented at the SKA 2010 Science and Engineering Meeting, Manchester
Greaves, J. S., Richards, A. M. S., Rice, W. K. M. and Muxlow, T. W. B., 2008, MNRAS, 391, L74
Greaves, J. et al., 2009, ‘PEBBLES’ e-MERLIN Legacy Project Proposal, http://www.e-merlin.ac.uk/legacy/proposals/e-MERLIN_Legacy_PEBBLES.pdf
Hoare, M. G., 2004, NewAR, 48, 1327
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhtVGitL7K&md5=eec5ae0ec4807a817733e5000e6a0655CAS |
Hoare, M. G., 2009, ‘Protoplanetary Disks with SKA-mid’, presented at the prepSKA work package 2 Annual Meeting, Manchester
Jaffe, A. H. and Backer, D. C., 2003, ApJ, 583, 616
| Crossref | GoogleScholarGoogle Scholar |
Jenet, F. A., Lommen, A., Larson, S. L. and Wen, L., 2004, ApJ, 606, 799
| Crossref | GoogleScholarGoogle Scholar |
Johnson, K. E., 2004, NewAR, 48, 1337
| Crossref | GoogleScholarGoogle Scholar |
Jonker, P. G. and Nelemans, G., 2004, MNRAS, 354, 355
| Crossref | GoogleScholarGoogle Scholar |
Kamp, I., Freudling, W. and Chengalur, J. N., 2007, ApJ, 660, 469
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXmtVGjsr0%3D&md5=5e0dcbc256f0b19558d4df35f3ecc594CAS |
Klamer, I. J., Ekers, R. D., Sadler, E. M. and Hunstead, R. W., 2004, ApJL, 612, 97
| Crossref | GoogleScholarGoogle Scholar |
Kramer, M., 2010, IAUS, 261, 366
Kramer, M., Backer, D. C., Cordes, J. M., Lazio, T. J. W., Stappers, B. W. and Johnston, S., 2004, NewAR, 48, 993
| Crossref | GoogleScholarGoogle Scholar |
Lee, K. J., Wex, N., Kramer, M., Stappers, B. W., Bassa, C. G., Janssen, G. H., Karuppusamy, R. and Smits, R., 2011, MNRAS, 414, 3251
| Crossref | GoogleScholarGoogle Scholar |
Lipunov, V. M., Bogomazov, A. I. and Abubekerov, M. K., 2005, MNRAS, 359, 1517
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXlslemtb8%3D&md5=d6516a9e68cbdc0563c516e79186d660CAS |
Liu, K., Wex, N., Kramer, M., Cordes, J. M. and Lazio, T. J. W., 2011, ApJ, ,
Macquart, J.-P. et al., 2010, PASA, 27, 272
| Crossref | GoogleScholarGoogle Scholar |
Merloni, A., Heinz, S. and di Matteo, T., 2003, MNRAS, 345, 1057
| Crossref | GoogleScholarGoogle Scholar |
Merritt, D., 2006, ApJ, 648, 976
| Crossref | GoogleScholarGoogle Scholar |
Migliari, S. and Fender, R. P., 2006, MNRAS, 366, 79
Miller-Jones, J. C. A., Jonker, P. G., Nelemans, G., Portegies Zwart, S., Dhawan, V., Brisken, W., Gallo, E. and Rupen, M. P., 2009a, MNRAS, 394, 1440
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXls1Snsr0%3D&md5=42b08035e3f4af182e98982ecf63e682CAS |
Miller-Jones, J. C. A., Jonker, P. G., Dhawan, V., Brisken, W., Rupen, M. P., Nelemans, G. and Gallo, E., 2009b, ApJL, 706, 230
| Crossref | GoogleScholarGoogle Scholar |
Mioduszewski, A. J., Rupen, M. P., Hjellming, R. M., Pooley, G. G. and Waltman, E. B., 2001, ApJ, 553, 766
| Crossref | GoogleScholarGoogle Scholar |
Mirabel, I. F., Dhawan, V., Mignani, R. P., Rodrigues, I. and Guglielmetti, F., 2001, Nature, 413, 139
| Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD3MrhtVamug%3D%3D&md5=50853b0c3c5117a60b0082250836f403CAS |
Morganti, R., Hoare, M., Garrett, M., 2006, ‘The Magnificent Memo Series: Trade-Offs between Science and Engineering for the Square Kilometre Array’, SKA Memo No. 82, August
Natta, A., Testi, L., Calvet, N., Henning, T., Waters, R. and Wilner, D., 2007, Protostars and Planets V, , 767
Nordhaus, J., Brandt, T. D., Burrows, A., Livne, E. and Ott, C. D., 2010, PhRvD, 82, 103016
Norris, R. P., Kesteven, M. J., Troup, E. R., Allen, D. A. and Sramek, R. A., 1990, ApJ, 359, 291
| Crossref | GoogleScholarGoogle Scholar |
Noutsos, A., 2009, IAU Symposium, 259, 15
Pfahl, E., Podsiadlowski, P. and Rappaport, S., 2005, ApJ, 628, 343
| Crossref | GoogleScholarGoogle Scholar |
Reid, M. J., McClintock, J. E., Narayan, R., Gou, L., Remillard, R. A. and Orosz, J. A., 2011Bulletin of the American Astronomical Society, 43, #223.01, , ,
Remillard, R. A. and McClintock, J. E., 2006, ARA&A, 44, 49
| Crossref | GoogleScholarGoogle Scholar |
Rioja, M., Dodson, R., Porcas, R. W., Ferris, D., Reynolds, J., Sasao, T., Schilizzi, R., 2009, in Proceedings of the 8th International e-VLBI Workshop, 14, http://pos.sissa.it/archive/conferences/082/014/EXPReS09_014.pdf
Rodriguez, C., Taylor, G. B., Zavala, R. T., Peck, A. B., Pollack, L. K. and Romani, R. W., 2006, ApJ, 646, 49
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XptFWnu7g%3D&md5=79eda2bc248515c473cede2126aedbdfCAS |
Ryba, M. F. and Taylor, J. H., 1991, ApJ, 371, 739
| Crossref | GoogleScholarGoogle Scholar |
Schilizzi, R. T., et al., 2007, ‘Preliminary Specifications for the SKA’, SKA Memo, 100
Schilizzi, R. T., et al., 2011, ‘Project Execution Plan Pre-Construction Phase for the Square Kilometre Array’, SKA Memo, 130
Sesana, A., Vecchio, A. and Volonteri, M., 2009, MNRAS, 394, 2255
| Crossref | GoogleScholarGoogle Scholar |
Seymour, N. et al., 2008, MNRAS, 386, 1695
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXnvVCru7g%3D&md5=768954a623dbacc9397e4e4a97762952CAS |
Shklovskii, I. S., 1970, Soviet Astron., 13, 562
Sigurdsson, S., 2003, Radio Pulsars, 302, 391
| 1:CAS:528:DC%2BD3sXnsV2jsrk%3D&md5=6a94d1620b9041ab71b41a37d37711a3CAS |
Silk, J., 2005, MNRAS, 364, 1337
| Crossref | GoogleScholarGoogle Scholar |
Simonetti, J. H., Kavic, M., Minic, D., Surani, U. and Vejayan, V., , ApJL, 737, 28
SKA Science Working Group, 2010, ‘The Square Kilometre Array Design Reference Mission: SKA-mid and SKA-lo v. 1.0’
Smits, R., Tingay, S. J., Wex, N, Kramer, M and Stappers, B, 2011, A&A, 528, A108
Smits, R., Kramer, M., Stappers, B., Lorimer, D. R., Cordes, J. and Faulkner, A., 2009, AAP, 493, 1161
Stairs, I. H., 2010, IAUS, 261, 218
Stepanov, R., Frick, P., Shukurov, A. and Sokoloff, D., 2002, A&A, 391, 361
Thompson, D. R., Wagstaff, K. L., Brisken, W. F., Deller, A. T., Majid, W. A., Tingay, S. J. and Wayth, R. B., 2011, ApJ, 735, 98
| Crossref | GoogleScholarGoogle Scholar |
Tingay, S. J. and Wayth, R. B., 2011, AJ, 141, 174
Tingay, S. J. et al., 1995, Nature, 374, 141
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXkt1yju7k%3D&md5=5dd38a6a5768abbda59517e4de26054fCAS |
Volonteri, M., Haardt, F. and Madau, P., 2003, ApJ, 582, 559
| Crossref | GoogleScholarGoogle Scholar |
Wayth, R. B., Brisken, W. F., Deller, A. T., Majid, W. A., Thompson, D. R., Tingay, S. J. and Wagstaff, K. L., 2011, ApJ, 735, 97
| Crossref | GoogleScholarGoogle Scholar |
Weisberg, J. M., Stanimirović, S., Xilouris, K., Hedden, A., de la Fuente, A., Anderson, S. B. and Jenet, F. A., 2008, ApJ, 674, 286
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXivFagt7Y%3D&md5=3e8eb9600c15ab563b1e72fe3435174bCAS |
Wilkinson, P. N., Kellermann, K. I., Ekers, R. D., Cordes, J. M. and Lazio, T. J. W., 2004, NewAR, 48, 1551
| Crossref | GoogleScholarGoogle Scholar |
Wilner, D. J., 2004, NewAR, 48, 1363
| Crossref | GoogleScholarGoogle Scholar |
Wilner, D. J., D'Alessio, P., Calvet, N., Claussen, M. J. and Hartmann, L., 2005, ApJL, 626, 109
| Crossref | GoogleScholarGoogle Scholar |
Yu, Q., 2002, MNRAS, 331, 935
| Crossref | GoogleScholarGoogle Scholar |


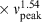 ) versus the peak flux density for a sample of GPS sources. Size, turn-over frequency, and flux density roughly form a fundamental plane for GPS radio galaxies. Standard GPS sources found at z ~ 1 occupy the upper right of the plot. High redshift ‘GPS-like’ sources are expected to stand out from their low redshift counterparts, and occupy the lower left portion of the plot. See
) versus the peak flux density for a sample of GPS sources. Size, turn-over frequency, and flux density roughly form a fundamental plane for GPS radio galaxies. Standard GPS sources found at z ~ 1 occupy the upper right of the plot. High redshift ‘GPS-like’ sources are expected to stand out from their low redshift counterparts, and occupy the lower left portion of the plot. See