Updating the Australian digital soil texture mapping (Part 2*): spatial modelling of merged field and lab measurements
Brendan Malone A C and Ross Searle B
A C and Ross Searle B
A CSIRO Agriculture and Food, Clunies Ross Street, Black Mountain, ACT 2601, Australia.
B CSIRO Agriculture and Food, 306 Carmody Road, St Lucia, Qld 4067, Australia.
C Corresponding author. Email: brendan.malone@csiro.au
Soil Research 59(5) 435-451 https://doi.org/10.1071/SR20284
Submitted: 30 September 2020 Accepted: 11 February 2021 Published: 27 April 2021
Journal Compilation © CSIRO 2021 Open Access CC BY
Abstract
Malone and Searle (2021) described a new approach to convert field measured soil texture categories into quantitative estimates of the proportion of clay, silt and sand fractions. Converted data can seamlessly integrate with laboratory measured data into digital soil mapping workflow. Here, we describe updating the Australian national coverages of clay, sand and silt content. The approach, based on machine learning, predicts each soil texture fraction at 90 m grid cell resolution, at depths 0–5 cm, 5–15 cm, 15–30 cm, 30–60 cm, 60–100 cm and 100–200 cm. The approach accommodates uncertainty in converting field measurements to quantitative estimates of texture fractions. Existing methods of bootstrap resampling were exploited to predict uncertainties, which are expressed as 90% prediction intervals about the mean prediction at each grid cell. The models and the prediction uncertainties were assessed by an external validation dataset. Results were compared with Version 1 Soil and Landscape Grid of Australia (v1.SLGA) (Viscarra Rossel et al. 2015). All predictive and functional accuracy diagnostics demonstrate improvements compared with v1.SLGA. Improvements were noted for the sand and clay fraction mapping with average improvement of 3% and 2%, respectively, in the RMSE estimates. Marginal improvements were made for the silt fraction mapping, which was relatively difficult to predict. We also made comparisons with recently released World Soil Grid products (v2.WSG) and made similar conclusions. This work demonstrates the need to continually revisit and if necessary, update existing versions of digital soils maps when new methods and efficiencies evolve. This agility is a key feature of digital soil mapping. However, without a companion program of new data acquisition through strategic field campaigns, continued re-modelling of existing data does have its limits and an eventual model skill ceiling will be reached which may not meet expectations for delivery of accurate national scale digital soils information.
Keywords: soil texture, digital soil mapping, spatial resolution, compositional data analysis, isometric log-ratio, uncertainty analysis, functional accuracy, pedometric
Introduction
Australia first delivered national scale GlobalSoilMap (GSM; Arrouays et al. 2014) compliant products in late 2014 as the Soil and Landscape Grid of Australia (v1.SLGA; Grundy et al. 2015). The development of this first version of soil attribute surfaces was a collaborative effort between Federal, State and Territory governments and key contributors including universities. The initial project developed and fostered a vibrant community of digital soil mapping (DSM) practitioners that now forms the core of operational DSM activities throughout Australia. In 2018, the Australian DSM community secured a new funding commitment through the Terrestrial Ecosystem Research Network (TERN), which through collaboration with the remote sensing community, will further evolve and improve the nationally consistent DSM products, hereafter referred to as v2.SLGA.
Besides the imperative to create consistent, reliable, functional and comprehensive digital soil maps at the national scale, Searle et al. (2019) also stipulated the need to make the workflow for doing DSM repeatable and updatable. Now that much of the work these days is done via computer coded workflows, these key features are relatively easy to manage by way of releasing not only the mapping, but the code that went into creating these products. This is done through popular version control systems such as Git and SVN and delivers to end-users and other soil mapping practitioners, the transparency needed to properly assess and scrutinise the products that are created.
In Australia, a website resource has been set up (https://aussoilsdsm.esoil.io/home) and an associated git repository (https://github.com/AusSoilsDSM) to facilitate this transparency, and to provide a platform for the multiple actors across the Australian DSM community to contribute knowledge, provide feedback and even upskill. Moreover, being public facing, these tools and the materials and workflows are not exclusive and are available to all.
In this present study, the digital soil mapping of soil texture fractions is a case-in-point about the need to re-visit and where feasible, to update and improve upon the existing products. The existing product is v1.SLGA where the technical details of the general work method for all products is described in Viscarra Rossel et al. (2015). Focusing specifically on soil texture fractions, in that study, ~15 000 site observations were used to fit models and produce the maps. The maps were created in compliance with the specifications of the GSM in terms of depth support and quantification of uncertainties. The v1.SLGA products showed demonstrable improvement over historically created ones, including those derived from attribution of the polygons in the Atlas of Australian Soils (Northcote et al. 1960–1968; McKenzie et al. 2000), and from area-weighted averages of a compilation of survey data in the Australian Soil Resource Information System (ASRIS; Johnston et al. 2003).
Five years since the creation of v1.SLGA, end-users have provided helpful feedback and critique about each of the products, and in the case of the soil texture mapping, issues identified included spatial artefacts due to use of categorial predictive covariates or otherwise. This has made using these base products, for example, to develop derived products such as plant available water capacity, somewhat challenging (Stockmann et al. 2020). Another issue has been the identification of data or simplex closure issues (i.e. the components of clay, sand and silt fractions do not sum to 1 exactly) because the v1.SLGA modelling was implemented without consideration of the compositional properties of the data. These issues are relatively easy to address in later updating and improvement efforts. In addition to these, there has been some new soil survey activity around the country, together with discovery of historical data from existing sources, leading to an incremental increase in the total numbers of available data.
The ability to access these data now and into the foreseeable future is facilitated though the newly created soil data federator (Searle et al. 2021b). As the name suggests, this is a federation approach to data unification, where data is managed by individual custodians, but is federated on the fly into a consistent form that is readily analysed for DSM work. An application programming interface (API) is built into the federator making it relatively simple and efficient to develop programmatic workflows to interrogate and retrieve data from disparate data sources as needed.
The other development since v1.SLGA is rethinking around incorporating field observed data into spatial modelling. These largely underutilised data across Australia can potentially contribute more than 150 000 additional sites into a spatial modelling framework (Searle 2014). The efforts previously undertaken to incorporate these types of data into a DSM exercise have been largely constructed around defining or utilising existing texture class centroids and then adopting a spatialisation technique to generate maps of the soil texture fractions.
For example, once the centroids were defined, they were used to estimate via weighted averaging (guided by information recorded in soil mapping unit metadata) the spatial patterns of the soil texture fractions across Australia (Carlile et al. 2001). In another example, Taylor and Minasny (2006) used soil texture class centroids derived by Minasny and McBratney (2001) and attributed the soil texture class allocations of numerous soil profile descriptions in order to apply ordinary kriging across two different vineyards and two depths (0–30 cm and 30–90 cm).
As illustrated by Malone and Searle (2021), there exists a substantial amount of within texture class variation when comparing field classifications and corresponding laboratory measured values. With this knowledge, it would seem focusing just on the centroid value is potentially inappropriate in order to yield maps of soil texture fractions from field texture class data. Consequently, we developed an algorithm that could produce plausible values of soil texture fractions given information about the centroids, the within class variation and covariance between texture fractions.
Plausibility here has two meanings. The first is that the simulated simplex (compositional data term to describe the vector of the proportions of clay, sand and silt) is known to exist in the empirical data space of the given soil texture class. The second is the accommodation of soil contextual information to ensure there is some coherence between field observation and simulated data. The contextual information here is other soil texture information recorded at different depths of a soil profile, an awareness of gradational and other pedological texture changes within a soil profile and incorporation of pedological functions to cater for features like soil texture class modifiers and sub-plastic texture consistencies.
The useful outcome of the soil texture algorithm (STA) from Malone and Searle (2021) is that one can derive a numerical (and sensible) characterisation of soil texture fractions for multi-layered or horizonal soil profiles where soil texture classes have been recorded only. This permits the opportunity to incorporate laboratory measured data with converted field texture data into a spatial modelling workflow. More importantly, repeating the simulations many times over for a single profile or for a collection of profiles realises a second benefit, which is the ability to accommodate in any subsequent spatial statistical modelling workflows, the subjectivity that is inherent when allocating a field observation to a given soil texture class. For clarity, this subjectivity henceforth will be described as measurement error in the same sense that even laboratory measured data has a quantifiable, albeit rarely reported amount of measurement error.
If it is known that different types of data are on hand and each have varying levels of quality, then it is appropriate, if not expected, to use statistical models and methods that accommodate these differences. However, one could surmise that by utilising a very large amount of data with not insignificant measurement errors, correspondingly poor digital soil maps (based on prediction accuracy, and the extent of the prediction uncertainties) would be produced. This summation warrants testing in the case of soil texture mapping across Australia. We propose that despite the higher uncertainty of using field characterisations (converted to numerical form), the collective weight of these data is invaluable in terms of expected modelling benefits brought about by improved spatial coverage and density both geographically and within the environmental covariate data space. The question that remains to be tested via comparative analysis against v1.SLGA and other publicly available products is what improvements there are in terms of producing useful and potentially improved digital soil maps.
Measurement uncertainty is generally accommodated through inclusion of measurement error variance in the variogram or covariance structure of the spatial model (Cressie 1991). This is also known as kriging with uncertain data, where in the simplest terms, while acknowledging the diversity of contexts and approaches, the error variance is added to the diagonal of the spatial covariance matrix (Delhomme, 1978; Christensen 2011). This filters the measurement error variance from the nugget component of the experimental variogram, which leads to smoother mapped representations of the data, albeit with a lower amount of prediction uncertainty of spatial predictions. Somarathna et al. (2018), using this geostatistical tool together with multi-variate calibration, regressed upon a suite of predictive covariates. They demonstrated this approach for integrating laboratory measured and spectral inferred soil carbon data for DSM with good results. These sorts of geostatistical tools are suited to relatively small datasets and medium levels of granularity (for interpolation) where performing the required matrix inversions to do the kriging is not too much of a computational burden.
Most DSM outputs in recent times have been largely derived using machine learning algorithms (Wadoux et al. 2020), which have been found to be a powerful tool for discerning complex relationships between target variables and predictor variables compared to what the relatively simpler regression and kriging tools can provide separately. However, estimating prediction uncertainties with these models is not done analytically as is done with linear regression and kriging, but via some form of repeated cross-validation or bootstrapping process in order to derive empirical probability density functions for each prediction case (Viscarra Rossel et al. 2015).
There appears to be less literature describing how the measurement errors of the target variables can be incorporated into these models. In general, the methods are based around iterative resampling of the sample space that exists for each uncertain case in the model calibration data (Czarnecki and Podolak, 2013). For example, when mapping soil thickness across Australia, Malone and Searle (2020) treated censored data (observed soil thickness does not correspond to the actual soil thickness) as uncertain cases. Here, a repeated-cross validation (using sampling with replacement) was used, whereupon each iteration, a new calibration set was derived by simulating an estimated soil thickness (underpinned by a β distribution function) for all the censored data cases. This procedure was largely used because the size of the dataset was very large, making other candidate models such as survival models (e.g. Chen et al. 2019) computationally unfeasible. The benefit of the described approach is the simplicity of implementation and scalability, and the assurance, provided enough iterations are performed, that the full data and sample space is characterised in the modelling.
The modelling framework used in Malone and Searle (2020) seems an appropriate approach to integrate both laboratory measured and transformed field measurements. Here, the measurement error of the field description data would be akin to the sample space from which to draw plausible outcomes. As has been established already, the STA described in Malone and Searle (2021) is quite capable in establishing these plausible outcomes that can subsequently be used in the above-described iterative machine learning framework.
In summary, this study will investigate the digital soil mapping of soil texture clay, sand and silt fractions across Australia via a machine learning approach that is cognisant of the measurement uncertainties of the data pertaining to field observations. This approach utilises the STA described in Malone and Searle (2021) for generating plausible outcomes of soil texture fractions within a whole soil profile. In the following sections, we first describe the available data and predictive covariates, their acquisition and pre-processing. We then describe the machine learning modelling framework inclusive of uncertainty quantification used to derive the digital soil maps of clay, sand and silt fraction across Australia. These derived products are compared to corresponding v1.SLGA products, and recently released Version 2 World Soil Grid (v2.WSG) products. Further work and future considerations for ongoing programs to update and improve digital soil maps are also discussed.
Materials and methods
This study encompasses the continent of Australia including Tasmania and near-shore small islands. As in Viscarra Rossel et al. (2015), the specific motivation in this study is the creation of GSM compliant digital soil maps of soil texture fractions: clay, silt and sand. The rationale for doing this is to update and potentially improve upon the existing mapping. We used publicly available datasets and applied integrated modelling and bespoke computational workflows to generate the final outputs.
Datasets
Observational data
The Australian soil data federator (Searle et al. 2021b) publishes API endpoints that allows one to retrieve and integrate soils data from around Australia. The federator is supported by numerous data custodians that currently include the CSIRO, which manages the Australian National Soil Archive and associated NATSOIL database, and the various State and Territory government soil survey agencies. Programmatic workflows developed in R (R Core Team, 2018) were written to compile all available data regarding measured soil texture fractions. Soil texture fractions are represented as percentage mass of coarse sand (200–2000 µm), fine sand (20–200 µm), silt (2–20 µm) and clay (<2 µm) particles. Two main search queries were developed. The first was the extraction of laboratory measured data, and the second was the extraction of morphological descriptions of soil texture classes. For the laboratory measured data, additional information regarding site IDs, locational information and depth increments and laboratory method were also retrieved.
Across Australia, particle size analyses have primarily been done by either the hydrometer method (Gee and Bauder 1986) or pipette methods from either Coventry and Fett (1979) or Bowman and Hutka (2002). Relatively fewer samples were measured with the Plummet Balance method (Marshall 1956). We noted virtually no cases where multiple methods were used for the same sample, so all data were compiled as is, irrespective of laboratory method.
For the morphological data, in addition to retrieving the soil texture class information, we also extracted the locational and identifying metadata, depth increments, and where available, the observed soil class and texture class modifiers. These latter two extractions were for the purposes of running the STA as described in Malone and Searle (2021).
After the initial data compilation, pre-processing steps were undertaken to remove entries such as missing or clearly erroneous locational data, clearly spurious data entries and repeated observations. As noted in Malone and Searle (2021), several sites have both laboratory measured and field measured soil texture estimates. In these instances, we removed the repeated site that had the morphological data in order to preference the laboratory data as it is comparatively more certain.
Where applicable for the laboratory data, we summed the coarse sand and fine sand fractions to generate a complete dataset of samples with clay, silt, and sand fractions. Some screening of the data entailed removing samples where the sum of the texture fractions was less than 90%. For samples where the sum of fractions was between 90% and 100% (non-inclusive), each fraction was normalised to sum to 100%.
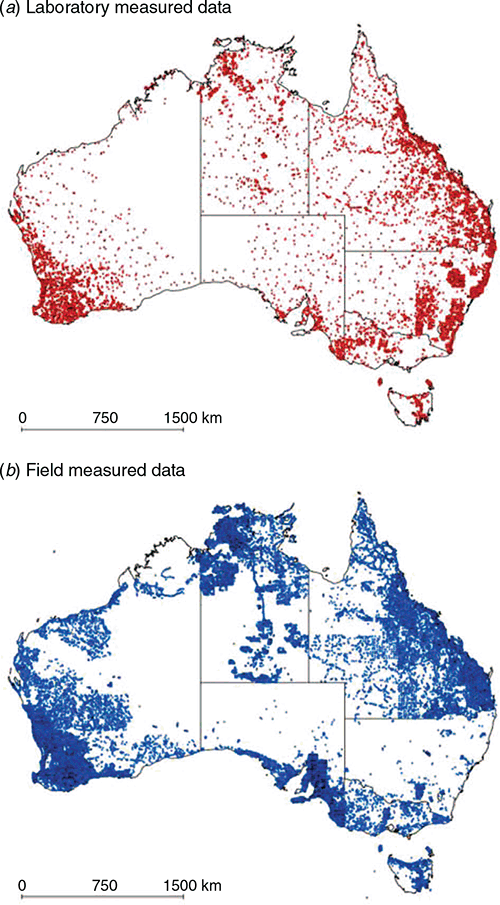
For the morphological data, the soil texture classes were cross-checked with the 46 texture classes that were studied in Malone and Searle (2021). Spurious data entries or classes not part of the 46 classes were removed from the dataset. After pre-processing, there were 17 367 sites with laboratory measurements and 180 498 sites with soil texture class descriptions to work with in this study. Fig. 1 shows the spatial distribution of these data across Australia distinguished in terms of measurement approach.
|
Environmental covariates
This study used the same suite of covariates that were described in Malone and Searle (2020). The 35 covariates, each had the same extent (112.99958°E–153.99958°E; 10.0004°S–44.00042°S) coordinate reference system (WGS84 (EPSG:4326) projection) and resolution (three arc second grid cell). As described in Malone and Searle (2020), these raster layers are grouped into scorpan-themed principal component analysis (PCA) stacks (McBratney et al. 2003). Specifically, there were 12, 4, 9 and 10 PCA layers for the climate, organism, relief and parent material + soil scorpan variables. As mentioned, this was to aid in balancing the number of covariates for each scorpan factor, and to reduce the burden of handling more than 100 continental coverages of spatial data.
The data sources included those from processed SRTM elevation data (Gallant et al. 2012), long-term climatic data summaries (Harwood et al. 2014), gamma radiometric and related data (Viscarra Rossel 2011; Wilford 2012) and some remote sensing derived products and spatial contextual derived products (Viscarra Rossel et al. 2015). For more complete summaries of the source covariate data, see supplementary table provided in Malone and Searle (2020).
Spatial modelling framework
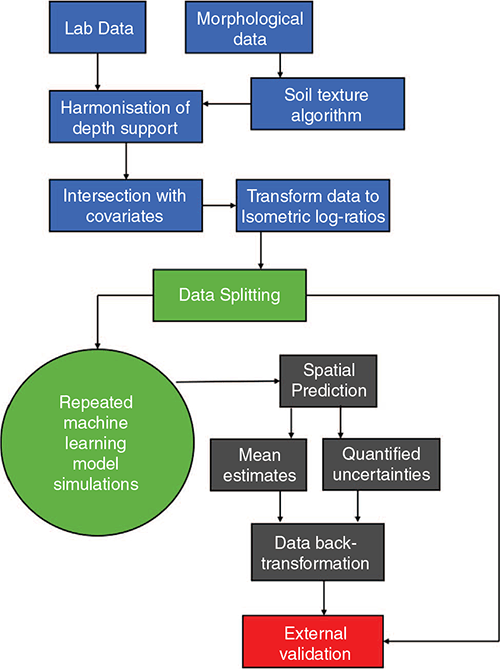
A schematic of the general workflow is illustrated in Fig. 2. There are four main stages involved. The first is the suite of approaches to prepare the data for spatial modelling. Then methods for model fitting and uncertainty quantification are implemented. These models are then used to generate maps of clay, silt and sand percentages at specified depth intervals, together with associated prediction intervals. The models and maps are then validated with an external dataset. The following describes in more detail the individual components of this spatial modelling framework.
|
Preparation of data for digital soil mapping
Focussing first on the morphological data, each soil profile was processed with the STA described in Malone and Searle (2021) to generate whole profile soil characterisations of clay, silt and sand fractions. A total of 50 realisations were derived for each site profile for the purposes of uncertainty propagation in the modelling step. Fifty seemed a plausible number given the substantial computation required to derive the final outputs, which is discussed further on, and this is the same number of iterations used to create v1.SLGA products.
The combination of laboratory and morphological data (197 865 sites) was then processed with a mass-preserving spline soil depth function (Bishop et al. 1999) to harmonise the depth support across all sites. The harmonised depths are those detailed in the GSM specification: 0–5 cm, 5–15 cm, 15–30 cm, 30–60 cm, 60–100 cm, and 100–200 cm. The mass-preserving or pycnophylactic properties of the spline make this an ideal tool to process soil profile data because the harmonised data ultimately become parameters of the spline, which can be used to reproduce the original data. The mechanism that controls the fidelity of spline fit to the original data is determined by a lambda parameter, which in this study was set to 0.01 based on optimisation using numerous candidate values. Here, the intention was not to find an optimal lambda for each soil profile but to find the optimum for the collection of all soil profiles. This was done by averaging of the fitting error across all soil profiles for a specified lambda value and selecting the value where the averaged error criteria were minimised. The underlying math of the spline function is described in Bishop et al. (1999) with further description in Malone et al. (2009).
For the purposes of model fitting, all the soil profile data were then intersected with each of the 35 raster PCA covariates to extract the corresponding vector of data covariate at each site. A nearest neighbour extraction was used for this process.
In Malone and Searle (2021), some discussion was made about compositional data analysis given that the tools for this sort of analysis are embedded into the STA. Because soil texture fractions are an example of compositional (the fractions sum to 1 or 100 depending on whether they are expressed as a proportion or percentage), it should naturally follow that compositional data analysis be performed on these data. Aitchison (1986) introduced tools for appropriate treatment of compositional variables namely in the form of additive-log-ratio (alr) and centred-log-ratio (clr) transformations. Paraphrasing from Malone and Searle (2021), these transformations from the simplex to an n-dimensional Euclidean vector exhibit important properties that enable the data to be analysed in the same way as standard data. A soil texture composition (clay, silt and sand fractions) would be considered as a three-part Aitchison-simplex and the alr-transform would map the composition non-isometrically to a 2-dimensional Euclidean vector, treating the last part as common denominator of the others. The isometry (or lack thereof with respect to alr-transformation) is a geometric concept about the association of angles and distances in the simplex (following the Aitchison geometry) to angles and distances in the Euclidean space. Because the mapping is done non-isometrically, this precludes using alr-transforms in the distance-based data analytics which are commonly used in pedometric applications such as soil entity allocations (Odgers et al. 2011). The other drawback of using alr-transforms is that by changing the part in the denominator, we obtain different alr transformations, which is likely to result in different analysis outcomes. The clr-transform maps a composition in the D-part Aitchison-simplex isometrically to a D-dimensional Euclidean vector subspace. This imparts an advantage over alr-transformation; however, the transformation is not injective, resulting in the covariance matrices of the Euclidean variables to be always singular. Egozcue et al. (2003) identified the few shortcomings of both alr and clr transformations and proposed the isometric log-ratio transformation (ilr) to address these. The data in the D-1-dimensional Euclidean vector generated by ilr-transformation can be analysed in this space by classical multivariate analysis tools. However, the interpretation of the results may be difficult since there is no one-to-one relation between the original parts and the transformed variables.
In this study, all the spline processed soil profile data were ilr-transformed. We note prior DSM investigations of soil texture mapping including Odeh et al. (2003), Lark and Bishop (2007) and Muzzamal et al. (2018) among others. Beside Muzzamal et al. (2018), who explored irl-transforms of compositional soil texture data, most research has been done with alr-transformed data. Noting some of the caveats of using ilr-transforms mentioned above, besides the method integration reasons (with the STA described in Malone and Searle 2021), this data transformation is merely used as an instrument for data analysis and not interpretation. Subsequently, any interpretation of the results and efficacy of the modelling is done based on the back-transformed data. As mentioned above, the result of doing an ilr-transform on a three-part Aitchison-simplex is a 2-dimensional Euclidean, which we will refer to hereafter as components of the ilr-transformation 1 and 2, respectively.
Model calibration and quantification of uncertainties
Spatial modelling in this work utilised individual machine learning models for components of the ilr-transformation at each of the six harmonised depth intervals. Effectively, 12 main model systems were created. Before constructing these model systems, 10% of the available data from each depth interval was removed for the purposes of ensuring an external validation set. These were selected at random and a summary of the data configurations are given in Table 1. Note that the number of sites and mix of laboratory and morphological data remain fixed for the external data, while for the model calibrations and cross-validation, the exact numbers and mix of data types will change from iteration to iteration due to the random sampling (with replacement) that underpins the modelling approach.

|
This study uses the random forest (RF) data modelling algorithm (Breiman 2001), specifically the ‘Ranger’ implementation (Wright and Ziegler 2017), which is computationally more efficient and particularly suited to high dimensional data. For each model system, we optimised the RF hyperparameter ‘mtry’ (number of variables to possibly split at in each node of the random forest model) using a purpose built cross-validation scheme that is facilitated in the caret R package (Kuhn et al. 2019). The number of trees to grow was not optimised and set to 500 as this was computationally efficient for our computer system. After the model hyperparameter optimisation, 50 iterations of model fitting were performed whereupon each iteration the target variable included the laboratory data plus a simulation instance from the STA that was performed in the sample data preparation step described above. Data used for model calibration on each iteration was selected using random sampling with replacement, with sample size equal to the number of cases in the available dataset. For example, in the case of modelling ilr-transformation 1 as a function of the 35 predictive covariates for the 0–5 cm depth interval, the total number of data available was 178 079. For implementation of sampling with replacement, this is the size of the sample selected. But when looking at the unique cases in the selected data, this on average will equate to 63% of the data for model calibration leaving the remaining 37% for cross validation (Efron and Tibshirani 1997). A typical data splitting configuration is shown in Table 1. While we are aware that a similar bootstrap routine is central to the random forest algorithm, it is unable to account for the target variable uncertainty explicitly, thus necessitating a customised approach.
Ultimately, 50 models for each of the 12 model systems were developed and saved for later use in the spatial prediction step. Other information captured included modelled predictions for the out-of-bag data points from each iteration, as these were to be used to assist in deriving the uncertainty quantifications.
The resampling approach described above lends itself to quantification of the prediction uncertainties at each prediction location. Whether it be a data point or pixel, there are 50 contributing predictions, which collectively constitute an empirical probability distribution (EPD).
The variance of the EPD is the quantity we use to express uncertainties; however, the EPD variance contributes only one part of the overall variance, VARtot (Eqn 1). The additional source of prediction variance in the modelling framework is what Viscarra Rossel et al. (2015) describe as the discrepancies brought about through systematic (bias) and random (imprecision) errors in the modelling. This is expressed as MSEcv and in this study it is calculated as the average of the mean squared error values from each model iteration on out-of-bag data. The variance of the EPD (right-hand side of Eqn 1) accounts for errors in the deterministic component of the models. The other terms in Eqn 1 include n, the number of iterations which is equal to 50; xi, the prediction at a data point or pixel with a given model i; and µ, the mean prediction at a data point or pixel over all 50 iterations.
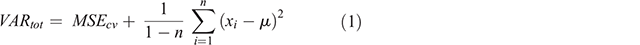
Note that the EPD and associated variance of the EPD, in addition to the MSEcv, were defined based on back-transformed data from ilr components using the inverse equations (Malone and Searle 2021). For clarity, each back-transformed variable; i.e. clay, silt and sand for each standard depth had an estimate of the MSEcv. Similarly, every data point and pixel had an individually defined EPD and ultimately an estimated VARtot for each variable and standard depth.
With VARtot defined, it is then a relatively straightforward approach to define prediction intervals for any defined confidence level. This is done by taking the square root of VARtot then multiplying it by 1 – α, where α is the quantile function of a normal distribution (upper tail) for a defined confidence level. For example, for a 90% prediction interval, the quantile function is ~1.64 (α = 0.95). The multiplication of the square root of VARtot and the specified quantile function equates to a standard error, which is added to and subtracted from the mean estimate of the EPD to derive the upper and lower prediction intervals respectively. In this study, for the purposes of DSM, we derive prediction intervals with 90% level of confidence about the mean estimates of the EPD.
From a validation perspective (of the uncertainties), we also derive prediction intervals at a series of confidence levels in order to assess the sensitivity and quality of the quantified uncertainties, for example, via the prediction interval coverage probability (PICP; Shrestha and Solomatine 2006) criterion as described below.
External validation
The model predictions and their derived uncertainty estimates were validated using the dataset that was removed from the overall dataset before any calibrations and cross-validations were performed. We report the root mean square error (RMSE) and Lin’s concordance coefficient (CCC) to quantify the prediction accuracy and fidelity about the 1:1 line when comparing predictions with associated observations, respectively. The predictions here are the averaged value of the EPD at each data point. For laboratory measured data, the comparison was a simple observed data vs measured data comparison. However, for the morphological data, we took the observed data as the mean value of the 50 simulations derived from the soil texture algorithm.
For assessment of the prediction uncertainties, we used the PICP criterion, which entails estimation of the proportion of observations in the total dataset that are encapsulated between the estimated prediction interval at a given confidence level for that data point. The confidence levels used in this study included: 99%, 97.5%, 95%, 90%, 80%, 60%, 40%, 20%, 10% and 5%. One should expect the PICP value or proportion to be close to the corresponding confidence level in order to determine whether the quantified uncertainties have been satisfactorily estimated (Solomatine and Shrestha 2009).
A measure of functional accuracy (Ruddell et al. 2019) is defined in this study in terms of soil texture class allocation discrepancies. This measure was included because of the vast amount of morphological data used in this study. It is based on the comparison (Euclidean Distance) of an observed texture class (centroids) and the associated texture class derived through allocation to the nearest texture class centroid based on the predicted clay, sand and silt fractions (note these distance comparisons were done with the ilr-transformed data).
For each data point, the predicted texture class was compared to its 1st, 2nd, 3rd and right up to 10th nearest texture class neighbour groupings in order to determine at what grouping size the observed soil texture class is found. For perfect correspondence, the prediction and associated observed class would match when just the prediction its nearest neighbour are compared. Conversely, if the predicted soil texture class did not make a match of its nearest 10 texture classes, the quality of the prediction would be deemed very poor. In our analysis, we estimated the proportion of cases where there was a positive match between prediction and observation for a given nearest neighbour grouping size. For large groupings it is expected to have a high to perfect proportion of matches, and this will almost always decrease with smaller and smaller groupings.
The reason for determining these proportions is an attempt to replicate the natural variation experienced when more than one person is in the field, with each independently analysing the same soil sample by hand bolus method and then allocating this sample to a soil texture class. We would expect there to be some discrepancy between each person’s allocation, but one would expect the allocation to cluster across a given number of classes. The smaller the number of classes of coverage means a good agreement and presumably a good allocation. Allocations spread across a high number of classes means poor agreement and allocation.
The discrepancy measure we have defined attempts to mirror this idea where a high proportion of matches in small groupings is an indication of good allocation, which is potentially a useful measure of the functional utility of the map in terms of how the predictions of clay, sand and silt fraction translate to what might be observed from a field survey context.
Spatial predictions
The scorpan variable themed raster PCA covariate stacks were used to inform the predictions across all grid cells and at each depth. The prediction process was the same as that described for external validation, except the predictions were made at grid cells. Specifically, this entailed at each standard soil depth for each model iteration, predicting both ilr-transformation components and then using the inverse of the ilr transform to derive individual maps of clay, silt and sand %. The outputs from each iteration were then combined and the EPD was estimated at each pixel, followed by the estimation of the VARtot as defined in Eqn 1 using the specific MSEcv for the selected target variable and depth interval. From this, the spatial prediction of uncertainty was expressed as 90% prediction intervals using the method described earlier.
Comparison between v1.SLGA and v2.WSG
The final maps for each soil texture fraction at each depth interval were benchmarked against two publicly available products. The first were those derived for v1.SLGA (Viscarra Rossel et al. 2015). The second set of products were v2.WSG (https://maps.isric.org/) where we used OGC web-services to pull soil data directly from ISRIC servers. The R programmatic workflow for doing this is available at https://git.wur.nl/isric/soilgrids/soilgrids.notebooks/-/blob/master/markdown/wcs_from_R.md.
The v2.WSG is a 250 m resolution product with a depth support the same as used in this current study. In order to harmonise products, the v2.WSG products were re-projected to the same resolution and extent as both the v1.SLGA and v2.SLGA products. Here, a bilinear interpolation was used. Once all the raster datasets were organised, the same external validation dataset was used to check their quality in terms of the RMSE and CCC metrics. To give a visual comparison of similarities and difference amongst the three products, we subtracted both v1.SLGA or v2.WSC from v2.SLGA. In the context of uncertainty assessment, v1.SLGA uncertainty products (the 90% prediction intervals) were compared with those from v2.SLGA in a simple way that entailed comparison of the prediction interval widths. This was to visually determine whether v2.SLGA uncertainty estimates are larger, smaller or equivalent to those derived for v1.SLGA.
Implementation of methods
To carry out the work in this study, numerous bespoke R code scripts were developed, which are available at from Github (https://github.com/AusSoilsDSM/SLGA/tree/master/SLGA/Development/soiltexture). Some of the main R packages used in this work include ‘ranger’ (Wright and Ziegler 2017) for model fitting and both ‘raster’ (Hijmans 2019) and ‘sp’ (Bivand et al. 2013) for specific spatial data analysis tasks. The ‘compositions’ R package (van den Boogaart et al. 2018) was used by data transformations and inversions of the compositional soil texture data. Many of the computations were optimised to run in parallel compute mode, particularly the spatialisation of the predictions step. CSIRO supercomputer systems (https://www.csiro.au/en/Research/Technology/Scientific-computing/Pearcey-cluster) were used for all computational tasks in this study.
Results and discussion
Fitted models and external validation
Table 2 summarises the external validation outcomes for each soil texture fraction and at each depth for v2.SLGA, v1.SLGA and v2.WSG. While we know that the validation dataset for v2.SLGA is completely external, it is possible, even likely, that some of these data were used in the modelling to develop the v1.SLGA and v2.WSG products. Consequently, there may be some inflation and ultimately bias in the reporting of their reliability. Nonetheless, the RMSE and concordance outcomes for v2.SLGA are more skilful for each variable and depth in comparison to the other products. The phenomenon of relatively higher prediction skill on the upper soil layers compared with the lower soil layers is apparent for all products. Examining the clay RMSE results, the average error is improved by ~3% (based on the simple difference between estimated RMSE values) across all depths when comparing v2.SLGA with v1.SLGA. The v2.WSG predictions of clay are marginally better than v1.SLGA. Taken together, these outcomes may not appear to be much, but given the amount of data used for the external validation, this represents a significant overall shift in predictive skill. This improvement is more distinguishable for the sand fraction predictions where the difference between v2.SLGA and v1.SLGA is ~3% on average in terms of RMSE. The v2.WSG sand predictions are less accurate compared with v1.SLGA and are on average 5% different in terms of the error attributed to v2.SLGA. The predictions of silt content represent the poorest outcomes in comparison to the other texture fractions for v2.SLGA, and this is true for the other two products as well. In general, however, there is about a 2% improvement in in RMSE for v2.SLGA silt predictions compared with the other two products.

|
The concordance measures, which tell a similar story to the RMSE, are more easily compared through visualisation of observed vs predicted plots. In Fig. 3, we show these plots for the 0–5 cm depth interval for clay, sand and silt of each of the three products. Supplementary material (Figs S1, S2, S3) shows the same plots for the other five depth intervals. Dispersion about the 1:1 line is to be expected, and this is probably made more apparent when looking at the plots pertaining to v2.WSG predictions. Clay prediction, for example for v1.SLGA, appears to over-predict at relatively lower clay contents and under-predicts at relatively higher clay contents. Products from v2.WSG do not have these differing biases. For clay content, v2.SLGA largely corrects these biases. For sand content, the predictive skill of sandier textures is clearly apparent. However, there does not appear to be much greater improvement in predicting in the less sandy soils. The plots for silt content for each of the three products just emphasises the relative indifference between the predictive outcomes and lower predictive skill in general.

|
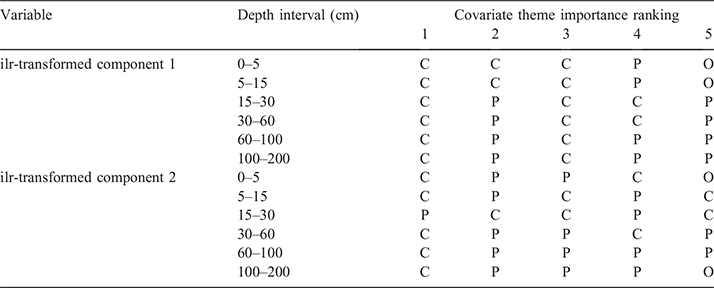
Regarding which types of predictive covariates were favourably selected in the fitted models, Table 3 provides a summary for each of the ilr-transformed components used for the modelling at each depth interval. Using the variable importance measure provided as output from the ranger models, we summarised these outputs across all 50 model realisations and provide a top five ranking of the scorpancovariate themes used for each model system. Perhaps a little surprisingly, predictive covariates related to long-term climate data summaries and topo-climatic information feature strongly for each model system. This is followed by variables pertaining to parent material information, which are mainly made up of variables derived from gamma radiometric data, magnetics and soil secondary clay mineral data. The variables pertaining to the organism scorpan-theme feature minimally but do occur a few times in the top five rankings. Relief variables did not feature in any of the model system top five rankings. This is an interesting finding overall but at the continental spatial extent, it would generally be expected that climate and parent materials are the dominating factors determining soil variability. This is also an interrelatedness between climate and relief to consider where there are broad relief/spatial position contributions to climate variables (higher altitudes are cooler, orographic rainfall etc.), which may explain why relief is not as strong a driver of soil texture variability. Nevertheless, at smaller spatial extents, the relief and organism variables may feature more strongly as differences in hillslopes and vegetation patterns manifest. This type of hierarchical determinism on soil variability has been studied and identified for soil variables like soil carbon (Wiesmeier et al. 2019; Adhikari et al. 2020;) and it is not without question that these relationships also hold for other variables too, particularly those that are coupled with soil carbon variability including soil texture.
The importance of climatic variables in spatial modelling at the continental scale has also been identified by Malone et al. (2020) in Australia where they proved critical to understanding to variability of soil thickness. In that study, it became clearly apparent that the direct and indirect effects of climate on biota and weathering of parental materials were important to understanding soil thickness variation across the country. We expect a similar biophysical relationship to be apparent in the present study, but also coupled with parent material variation and types, and the differential weathering products each one of these produces; e.g. fine grain, coarse grained and intermediate parent material types etc.
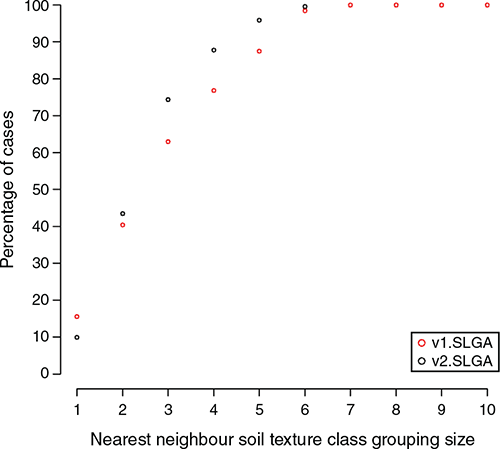
The results in Table 2 do not provide a clear indication of whether the prediction outcomes are potentially useful from a field surveying perspective. Therefore, we introduced the assessment of functional accuracy that looks at the dissimilarity between observed texture classes, and their neighbours, with corresponding predictions allocated to their nearest texture classes. The plot on Fig. 4 shows the maximum class discrepancies and the associated number of cases (expressed as a percentage) where the observed soil texture class matched the predicted soil texture class. The example here is for the 0–5 cm depth interval, with the plots for the other depth intervals provided in the online supplementary material (Fig S4).
|
In general, the interpretation for the 0–5 cm depth interval extends also to the other soil layers. The black dots are the data outputs for v2.SLGA while the red ones are for v1.SLGA. As expected, increasing the class grouping size results in a higher proportion of matches. What can be noted here though is that when the grouping size is 1, v1.SLGA predictions are better, which we surmise is the result of using field measured data for v2.SLGA, which will to some degree increase the amount of uncertainty associated with the prediction. The other possibility is that some of the data used in the external validation were used in the model calibrations for v1.SLGA, resulting in a possibly inflated estimate of precision. Whatever the case, it is natural to expect that when using uncertain data in a modelling framework, some precision penalty is to be expected, and it just so happens that it manifests when assessing the match between predictions and associated observed soil texture class without consideration of nearby texture classes (single class grouping).
More will be said later about the prediction uncertainties. What is interesting to note however, is that with increasing grouping size, v2.SLGA prediction converge towards 100% faster than v1.SLGA, which is a manifestation of the overall prediction skill differences between both products. A possible benchmark set at a three-class discrepancy allocation indicates that for v2.SLGA, over 75% of external validation data were correctly matched to the observed soil texture class, while for v1.SLGA, this was just over 60% of cases. Taken together, what these outcomes mean is that despite a greater uncertainty attributed to using field measured data (appearing as a relatively smaller single class grouping match), these data collectively confer an improved precision for prediction of soil texture. We attribute this result basically to the size differential of the datasets used in the modelling of the v1.SLGA and v2.SLGA.
External validation of quantified uncertainties
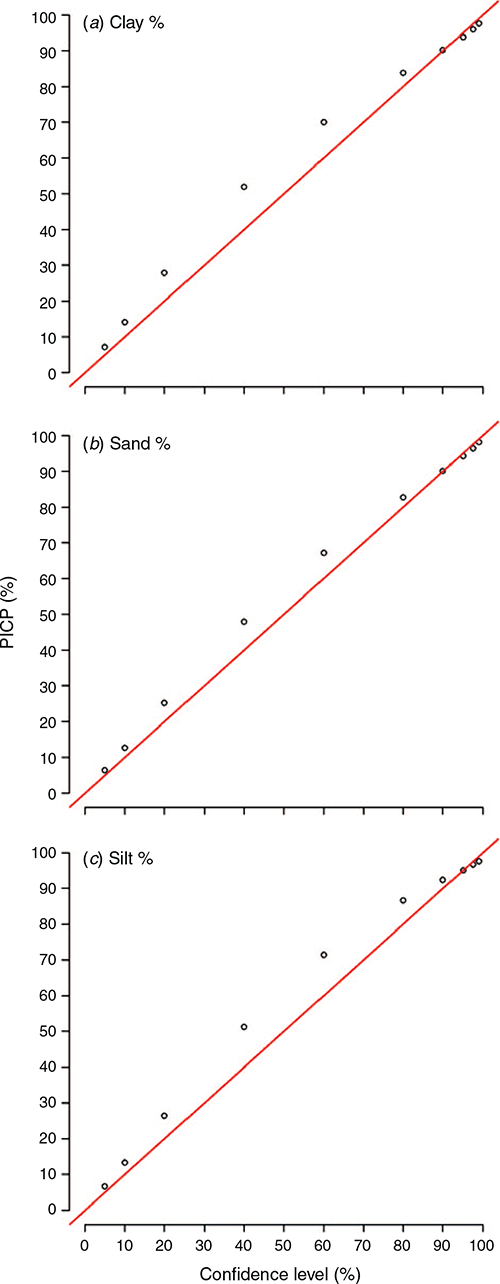
The PICP approach was our selected tool to assess how well the estimated uncertainties perform under testing. This is simply done by assessing the coverage of the prediction intervals at different levels of confidence around an observed value. Plots shown in Fig. 5 provide a good indication of what to expect when there is a relatively close tracking of the coverage probability with confidence level along the 1:1 line. These plots are for the 0–5 cm depth interval and the results are similar for the other depths, which are provided in the online supplementary material (Figs S5, S6, S7). Probabilities above the red line in the plots of Fig. 5 indicate a mild overprediction of the uncertainty range. This warrants some further investigation, but it is probably an outcome of the uncertainty method itself whereby a single value of the systematic model errors is assigned to all uncertainty estimates. On average, this will perform as intended but does not take into consideration locally varying estimates of the errors in a way that other methods, such as that described in Shrestha and Solomatine (2006), where model errors are weighted based on membership to fuzzy classes each of which has an underlying distribution of the model errors.
|
Some comparative work has been done in Malone et al. (2017, p. 150), which does show some merit to this locally varying error approach compared to the approach used in the present study, where a similar pattern in the coverage probabilities was observed. Possibly the hurdle to overcome in advancing the approach made by Shrestha and Solomatine (2006) is the implementation, in that it requires a more detailed architecture and marginally more effort to compute.
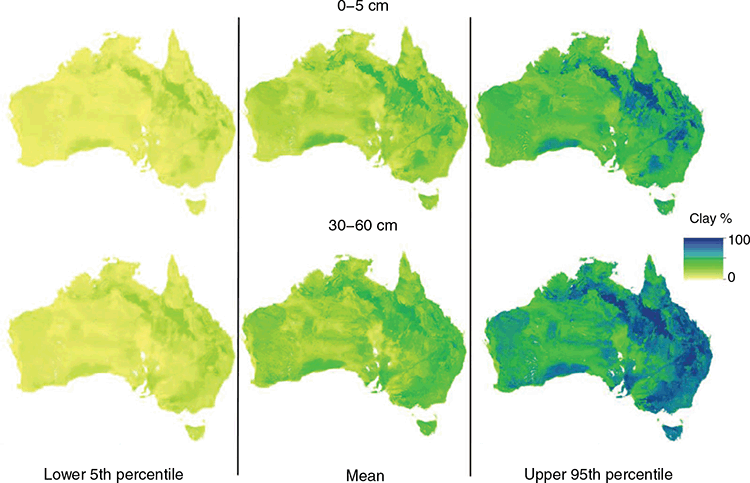
Spatial predictions
The main objective of this work was the updating of the soil texture mapping for Australia. Examples of some of the outputs are provided in Fig. 6, which shows the spatial distribution of the clay fraction for the 0–5 cm and 30–60 cm depth intervals and their quantified uncertainties, which are expressed as upper and lower prediction limits. The maps for the other depth intervals can be found in the supplementary material (Figs S8, S9, S10). We will not go into a deep discussion interpreting the spatial pattern of the maps as at a very general level, the overall patterns are about the same compared with the equivalent products from v1.SLGA and v2.WSG (maps are also provided in supplementary material Figs S11, S12, S13), and even those derived from the work by McKenzie et al. (2000) and Johnston et al. (2003), which largely drew upon conversion of polygon maps to thematic soil information maps of soil texture. However, there are numerous subtle differences between the products when they are compared in a quantitative manner as has been done in this study.
The maps shown in Fig. 7 depict the v2.SLGA soil texture fraction maps for the 0–5 cm depth interval and the associated differences to products from both v1.SLGA and v2.WSG. The side-by-side comparisons for the other depths and texture fractions are provided in the supplementary material (Fig S14). For clay and sand content maps shown in Fig. 7, there appears a re-adjustment of the predictions where in both v1.SLGA and v2.WSG, there are widespread areas estimated as relatively higher clay content and lower sand content to what is estimated for v2.SLGA. Note that these comparisons have been done based on the mean estimates and do not presently assess the relative uncertainties; these are discussed later in terms of comparisons between v1.SLGA and v2.SLGA only. The differences appear to be most dominant for v1.SLGA over eastern Australia, in the Murray–Darling Basin region, and across the top of end of Australia. For comparisons with the v2.WSG, the differences are more widespread. In comparing the silt content maps, while there are some notable corrections, these are relatively small compared with the other two texture fractions. For the other five depths, there are similarities and differences compared with what is shown in Fig. 7, but ultimately, these are attributed to the differences in model types and data used to create the different mapping products.
We would expect both the v1.SLGA and v2.WSG product to be based mostly on the same data (with some exceptions) since the data is freely and publicly available. Therefore, the differences will be mainly attributed to the model implementation and different sets of environmental covariates given that the v2.WSG products have a resolution of 250 m. The differences associated with the comparisons with v2.SLGA products would be mainly attributed to the additional data used in the modelling that has mostly been sourced from field measurements. As will be discussed shortly, the use of such data brings expected consequences of increasing the range of the uncertainty estimates. However, what we have been able to show in this study are that the predictions are demonstrably more accurate in terms of the mean estimates than either v1.SLGA or v2.WSG. The logical next step is to consider ensemble approaches such as model averaging (Chen et al. 2020) in order to leverage the good parts from each output to derive a better or equally good output than the current best estimate.
While variance weighted approaches have been recommended as the best and perhaps the easiest approach to do a model averaging workflow, one would also need to propagate the associated uncertainties, which to date has not been investigated with much fervour. Essentially, to do this would involve the combination of empirical probability density functions. Some methods to do this are discussed in Malone et al. (2014) and perhaps they should be investigated further as ongoing updating and improvements to digital soil mapping products becomes more of a normal procedure.
The uncertainties of the model outputs have been determined and the PICP (Fig. 5) indicates that they have been well quantified. Now we focus on whether there are any differences in the uncertainties of v1.SLGA and v2.SLGA. Side-by-side comparisons of the estimates of uncertainty are done in a simple manner in this study to examine the location and extent of similarities and differences in terms of the 90% prediction interval ranges. Fig. 8 shows some of these comparisons for each soil texture fraction for the 0–5 cm and 30–60 cm depth interval. As with other outputs, the difference maps for each of the other depth intervals is provided in the supplementary material.
Maps in Fig. 8 use colour to show no change between prediction interval ranges (we allowed a 5% margin of difference to evaluate a difference), v2.SLGA prediction ranges are wider than v1.SLGA prediction ranges, or v1.SLGA prediction ranges are wider than v2.SLGA prediction ranges. The maps clearly show that the prediction intervals for clay content are measurably wider for v2.SLGA. There are a few areas of exception, but this result is to be expected given that much of the data used in the modelling had a measurable amount of uncertainty given they were field derived estimates. It is encouraging from a modelling perspective that these uncertainties are propagated through to the mapped predictions, but the relatively wider prediction intervals should not detract from the fact that on average, the mean predictions associated with v2.SLGA are more accurate than v1.SLGA.
The concept of the prediction interval should not be interpreted as a uniform distribution of plausible values within the ranges of the uncertainty bounds. Rather, uncertainty is commonly expressed either as a normal distribution (the case in this study) or some other empirical distribution function where most of the prediction mass is centred about the mean or median of the interval. What the efforts in v2.SLGA have demonstrated is that there has been an improvement in estimating the prediction average, but because of the use of relatively less certain input data, the associated prediction intervals are wider in a lot of cases. Encouragingly, this is not always true because the corresponding comparisons between sand and silt show quite distinct areas where v1.SLGA prediction intervals are wider.
Regarding the predictions of sand, at least for the 0–5 cm depth interval, the prediction intervals either show wider prediction intervals for v1.SLGA or no change. For the deeper soil layers, a distinct east–west pattern is evident whereby the prediction intervals for sand are wider in the east for v2.SLGA but are relatively narrower in WA. For silt content, much larger areas of no change are apparent, as well as relatively large areas of wider prediction intervals for v1.SLGA. Our interpretation of why prediction intervals for v2.SLGA for clay are seemingly wider compared with sand or silt content is due to the nature of the data and how the soil texture values are drawn from the empirical distribution in the soil texture algorithm described in Malone and Searle (2021).
Looking at the supplementary material of Malone and Searle (2021), there are plots of the observed data for each soil texture class displayed on a soil texture triangle. What is notable about those plots is the nature of the variation of each of the texture fractions. The variation of clay content is much higher relative to sand and silt contents, which ultimately manifests in the phenomenon clearly observed in Fig. 8 and associated plots in the supplementary material regarding the uncertainty mapping for clay content.
Ultimately, there is a trade-off that happens when uncertain data gets used in a model. While it is encouraging and clearly demonstrated in our case that such data improves the prediction accuracy, a penalty is imposed by way of inflated prediction ranges. One positive outcome from this is that the additional input data uncertainty did not always manifest as wider prediction intervals compared with v1.SLGA but were in fact narrower in some areas, which points towards some clear benefits for using this type of data on an ongoing basis. Given that there is value in using the field data in a DSM context, there is perhaps a need to investigate in detail the veracity of data, which have corresponding field and laboratory values to determine first, if any clear errors or biases can be detected (and subsequently removed or corrected), and second, whether there are some nuances in the data that have been overlooked but could be exploited in further studies.
General discussion
The operationalisation of DSM around the world is clearly apparent (Arrouays et al. 2014) and across Australia, numerous examples exist and continue to grow (Kidd et al. 2020). Now that there are many examples of national digital soil mapping coverages, it is natural to begin thinking about and performing updates when opportunity presents. DSM by design, is largely a data driven framework, and therefore dynamic in its implementations. Leveraging new and additional data sources and the refinement and improvement of model approaches, collectively permit a greater level of efficiency in terms of the creation of maps compared with traditional soil mapping approaches.
Our arguments for updating Australia’s soil texture mapping included addressing some shortcomings in terms of data quality that have been found since the release of v1.SLGA and exploiting additional data resources in the form of field measured data. The latter instigated an exploration of methods to deal with uncertain data. This effort has been rewarded with demonstrable improvements in the overall prediction accuracy compared with existing products.
Next steps for further refinement include those options described earlier on model averaging, or a geostatistical analysis of model residuals. Experience has demonstrated that only incremental improvements are gained by doing this, but nonetheless, it is important work.
A more pressing work plan to instigate would be a detailed look at the soil data that goes into the modelling, because as our method clearly shows, the uncertain data contributes towards an increase in prediction uncertainty. This would require a significant investment of expertise to check the consistency of the data and refine accordingly. The advancement and continual refinement of DSM products is not solely the task of data modellers but extends also to other more traditional areas of soil science and those experts who can provide the necessary oversight as updated soil maps are produced.
We expect that in the future the computational and modelling efficiencies experienced currently will continue to improve DSM performance. However, an important consideration going forward is the sustainability of data and model refinements as a mechanism to improve soil mapping quality without implementing strategic and perhaps concurrent programs to collect new field data to augment that work.
Operationally, new projects will begin and end, and in the process, new data will be collected. Then through mechanisms such as soil data federation systems, these new data will be easily captured for use in future soil mapping projects despite not being considered in the design of those projects. This project-to-project patchwork of soil surveys is ultimately how most countries have amassed their collections of legacy soil data. Clearly, these have been valuable exercises, and DSM has proven to be a useful tool to leverage these data and inform our understanding of soil variability across vast landscapes. However, the current research has provided another reason to consider whether we survey and sample soils in the right places.
Obviously, a substantially larger amount of data was used in the updating of soil texture maps in this study compared to what was used in v1.SLGA, but the improvements in terms of accuracy perhaps might have been expected to be higher. This may just be the perception of authors who have completed a very large amount of work; however, it is worth considering that perhaps a model skill ceiling has been reached or is near to being reached without a considerable new investment in collecting soil data where there are clear data gaps, or where prediction uncertainties persist. Searle et al. (2021a) provides some practical options and examples of gap-filling that centre upon efforts to examine the current suite of soil legacy data with respect to environmental data coverage, in order to identify which parts of the landscape have adequate coverage of soil information and which parts do not.
In Australia, the logistics of implementing a strategic soil surveying program need some deep thought given each Sate and Territory has their own soil survey agency with their own priorities, but clearly, an over-arching national plan is needed. To date, DSM has been all about showcasing the very latest and greatest in cutting edge models and data informatics but could have reached their limits if a similar fervour is not extended towards strategic and widespread data acquisition and survey.
Conclusions
The intention of this study was to update v1.SLGA soil texture maps for Australia, and in doing do, produce v2.SLGA products. These updated maps are of the same spatial resolution, support and extent as v1.SLGA products, but the underlying data used to produce them are significantly different. Most data used in the modelling of v2.SLGA soil texture maps are sourced from field measured data, as opposed to laboratory measured data. In work by Malone and Searle (2021), an algorithm, Soil Texture Algorithm (STA), which transforms field measured soil texture class data into continuous vectors of clay, sand and silt fractions was developed and subsequently used in this study. There is uncertainty built into this transformation which is carried over to the spatial modelling and ultimately propagated through the final produced maps. Our models underpinned by machine learning ultimately yielded:
-
Measurable improvement relative to v1.SLGA and v2.WSG products in the mean prediction for all texture fractions and soil depth intervals
-
There was a spatial component to whether the 90% prediction intervals were wider for v1.SLGA or v2.SLGA, and this varied for the different textures
-
With some exceptions, the clay content uncertainties, expressed as 90% prediction intervals, were measurably wider than those derived for v1.SLGA.
Ultimately, despite using a significant amount of relatively less precise data, v2.SLGA soil texture products are more accurate and in a lot of cases, more certain than v1.SLGA products. In future, we expect to perform and observe more research instances in DSM that investigate the utility of incorporating field measured data into the workflows. As in our case, these data are often plentiful relative to laboratory data, but under-utilised. This study has demonstrated their potential value for successfully updating and improving digital soil maps.
Conflict of interest
The authors declare no competing interests.
Declaration of funding
The authors acknowledge the Terrestrial Ecosystem Research Network (TERN), an Australian Government NCRIS-enabled research infrastructure project, for facilitating and supporting this research.
Acknowledgments
The authors acknowledge CSIRO colleagues Jenet Austin and Uta Stockmann for their expert analysis and review of earlier drafts of this manuscript.
References
Adhikari K, Mishra U, Owens PR, Libohova Z, Wills SA, Riley WJ, Hoffman FM, Smith DR (2020) Importance and strength of environmental controllers of soil organic carbon changes with scale. Geoderma 375, 114472| Importance and strength of environmental controllers of soil organic carbon changes with scale.Crossref | GoogleScholarGoogle Scholar |
Aitchison J (1986) 'The Statistical Analysis of Compositional Data.' (Chapman & Hall: London)
Arrouays D, McBratney A, Minasny B, Hempel J, Heuvelink G, Macmillan RA, Hartemink A, Lagacherie P, McKenzie N (2014) The GlobalSoilMap project specifications. In 'GlobalSoilMap: Basis of the Global Spatial Soil Information System. Proceedings of the 1st GlobalSoilMap Conference'. Eds D Arrouays, N McKenzie, J Hempel, A Richer-de-Forges, A McBratney.) pp. 9–12. (CRS Press/Balkema: The Netherlands)
Bishop TFA, McBratney AB, Laslett GM (1999) Modelling soil attribute depth functions with equal-area quadratic smoothing splines. Geoderma 91, 27–45.
| Modelling soil attribute depth functions with equal-area quadratic smoothing splines.Crossref | GoogleScholarGoogle Scholar |
Bivand RS, Pebesma E, Gomez-Rubio V (2013) ‘Applied spatial data analysis with R.’ (Springer: New York)
Bowman G, Hutka J (2002) Particle size analysis. In ‘Soil physical measurement and interpretation for land evaluation’. (Eds NJ McKenzie, K Coughlan, HP Cresswell.) pp 224–239. (CSIRO Publishing: Melbourne, Vic)
Breiman L (2001) Random Forests. Machine Learning 45, 5–32.
| Random Forests.Crossref | GoogleScholarGoogle Scholar |
Carlile P, Bui E, Moran C, Minasny B, McBratney AB (2001) ‘Estimating soil particle size distributions and percent sand, silt and clay for six texture classes using the Australian Soil Resource Information System point database.’ (CSIRO Land and Water Technical Report 29/01: Canberra)
Chen S, Mulder VL, Martin MP, Walter C, Lacoste M, Richer-de-Forges AC, Saby NPA, Loiseau T, Hu B, Arrouays D (2019) Probability mapping of soil thickness by random survival forest at a national scale. Geoderma 344, 184–194.
| Probability mapping of soil thickness by random survival forest at a national scale.Crossref | GoogleScholarGoogle Scholar |
Chen S, Mulder VL, Heuvelink GBM, Poggio L, Caubet M, Román Dobarco M, Walter C, Arrouays D (2020) Model averaging for mapping topsoil organic carbon in France. Geoderma 366, 114237
| Model averaging for mapping topsoil organic carbon in France.Crossref | GoogleScholarGoogle Scholar |
Christensen WF (2011) Filtered Kriging for Spatial Data with Heterogeneous Measurement Error Variances. Biometrics 67, 947–957.
| Filtered Kriging for Spatial Data with Heterogeneous Measurement Error Variances.Crossref | GoogleScholarGoogle Scholar | 21361891PubMed |
Coventry RJ, Fett DER (1979) A pipette and sieve method of particle‐size analysis and some observations on its efficacy. CSIRO Australia, Division of Soils, Divisional Report No. 38: Australia.
Cressie NAC (1991) ‘Statistics for Spatial Data.’ (Wiley: New York)
Czarnecki WM, Podolak ITK (2013) Machine Learning with Known Input Data Uncertainty Measure. In: Computer Information Systems and Industrial Management. CISIM 2013. Lecture Notes in Computer Science, vol 8104. (Eds K Saeed, R Chaki, A Cortesi, S Wierzchoń) pp 379–388. (Springer, Berlin, Heidelberg)
Delhomme JP (1978) Kriging in the hydrosciences. Advances in Water Resources 1, 251–266.
| Kriging in the hydrosciences.Crossref | GoogleScholarGoogle Scholar |
Efron B, Tibshirani R (1997) Improvements on Cross-Validation: The. 632+ Bootstrap Method. Journal of the American Statistical Association 92, 548–560.
| Improvements on Cross-Validation: The. 632+ Bootstrap Method.Crossref | GoogleScholarGoogle Scholar |
Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barceló-Vidal C (2003) Isometric Logratio Transformations for Compositional Data Analysis. Mathematical Geology 35, 279–300.
| Isometric Logratio Transformations for Compositional Data Analysis.Crossref | GoogleScholarGoogle Scholar |
Gallant J, Read A, Dowling T (2012) Building the national one-second digital elevation model for Australia. In ‘Water Information Research and Development Alliance: Science Symposium Proceedings’, Melbourne, 1–5 August 2011. (Eds J Sims, L Merrin, R Ackland, N Herron) pp. 250–245. (CSIROL Melbourne)
Gee GW, Bauder JW (1986) Particle-size analysis. In ‘Methods of soil analysis. Part 1. 2nd ed’. (Ed. A Klute.) pp. 382–411. (ASA and SSSA: Madison, WI)
Grundy MJ, Rossel RAV, Searle RD, Wilson PL, Chen C, Gregory LJ (2015) Soil and Landscape Grid of Australia. Soil Research 53, 835–844.
| Soil and Landscape Grid of Australia.Crossref | GoogleScholarGoogle Scholar |
Harwood T, Ferrier S, Harman I, Ota N, Perry J, Williams K (2014) ‘Gridded continental climate variables for Australia.’ (CSIRO Land and Water: Canberra)
Hijmans RJ (2019) ‘raster: Geographic Data Analysis and Modeling.’ (R package version 2.9–5: https://CRAN.R-project.org/package=raster)
Johnston RM, Barry SJ, Bleys E, Bui EN, Moran CJ, Simon DAP, Carlile P, McKenzie NJ, Henderson BL, Chapman G, Imhoff M, Maschmedt D, Howe D, Grose C, Schoknecht N, Powell B, Grundy M (2003) ASRIS: the database. Soil Research 41, 1021–1036.
| ASRIS: the database.Crossref | GoogleScholarGoogle Scholar |
Kidd D, Searle R, Grundy M, McBratney A, Robinson N, O’Brien L, Zund P, Arrouays D, Thomas M, Padarian J, Jones E, Bennett JM, Minasny B, Holmes K, Malone BP, Liddicoat C, Meier E, Stockmann U, Wilson P, Wilford J, Payne J, Ringrose-Voase A, Slater B, Odgers N, Gray J, van Gool D, Andrews K, Harms B, Stower L, Triantafilis J (2020) Operationalising digital soil mapping – Lessons from Australia. Geoderma Regional 23, e00335
| Operationalising digital soil mapping – Lessons from Australia.Crossref | GoogleScholarGoogle Scholar |
Kuhn M, Wing J, Weston S, Williams A, Keefer C, Engelhardt A, Cooper T, Mayer Z, Kenkel B, Benesty M, Lescarbeau R, Ziem A, Scrucca L, Tang Y, Candan C, Hunt T (2019) ‘caret: Classification and Regression Training. R package version 6.0–84.’ https://CRAN.R-project.org/package=caret
Lark RM, Bishop TFA (2007) Cokriging particle size fractions of the soil. European Journal of Soil Science 58, 763–774.
| Cokriging particle size fractions of the soil.Crossref | GoogleScholarGoogle Scholar |
Malone BP, Searle R (2020) Improvements to the Australian national soil thickness map using an integrated data mining approach. Geoderma 377, 114579
| Improvements to the Australian national soil thickness map using an integrated data mining approach.Crossref | GoogleScholarGoogle Scholar |
Malone BP, Searle R (2021) Updating the Australian digital soil texture mapping: Part 1. Re-calibration of field soil texture class centroids. Soil Research
| Updating the Australian digital soil texture mapping: Part 1. Re-calibration of field soil texture class centroids.Crossref | GoogleScholarGoogle Scholar |
Malone BP, McBratney AB, Minasny B, Laslett GM (2009) Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 154, 138–152.
| Mapping continuous depth functions of soil carbon storage and available water capacity.Crossref | GoogleScholarGoogle Scholar |
Malone BP, Minasny B, Odgers NP, McBratney AB (2014) Using model averaging to combine soil property rasters from legacy soil maps and from point data. Geoderma 232–234, 34–44.
| Using model averaging to combine soil property rasters from legacy soil maps and from point data.Crossref | GoogleScholarGoogle Scholar |
Malone BP, Minasny B, McBratney A (2017) ‘Using R for Digital Soil Mapping.’ (Springer: The Netherlands)
Malone B, Luo Z, He D, Viscarra Rossel R, Wang E (2020) Bioclimatic variables as important spatial predictors of soil hydraulic properties across Australia’s agricultural region. Geoderma Regional 23, e00344
| Bioclimatic variables as important spatial predictors of soil hydraulic properties across Australia’s agricultural region.Crossref | GoogleScholarGoogle Scholar |
Marshall TJ (1956) A plummet balance for measuring the size distribution of soil particles. The Journal of Applied Science 7, 142–147.
McBratney AB, Mendonça Santos ML, Minasny B (2003) On digital soil mapping. Geoderma 117, 3–52.
| On digital soil mapping.Crossref | GoogleScholarGoogle Scholar |
McKenzie N, Jacquier D, Ashton L, Cresswell H (2000) ‘Estimation of soil properties using the atlas of Australian soils. Technical Report 11/00.’ (CSIRO Land and Water: Canberra, ACT)
Minasny B, McBratney AB (2001) The Australian soil texture boomerang: a comparison of the Australian and USDA/FAO soil particle-size classification systems. Soil Research 39, 1443–1451.
| The Australian soil texture boomerang: a comparison of the Australian and USDA/FAO soil particle-size classification systems.Crossref | GoogleScholarGoogle Scholar |
Muzzamal M, Huang J, Nielson R, Sefton M, Triantafilis J (2018) Mapping Soil Particle-Size Fractions Using Additive Log-Ratio (ALR) and Isometric Log-Ratio (ILR) Transformations and Proximally Sensed Ancillary Data. Clays and Clay Minerals 66, 9–27.
| Mapping Soil Particle-Size Fractions Using Additive Log-Ratio (ALR) and Isometric Log-Ratio (ILR) Transformations and Proximally Sensed Ancillary Data.Crossref | GoogleScholarGoogle Scholar |
Northcote, K, Beckmann, G, Bettenay, E, Churchward, H, Van Dijk, D, Dimmock, G, Hubble, G, Isbell, R, McArthur, W, Murtha, G, Nicolls, K, Paton, T, Thompson, C, Webb, A, Wright, M (1960–1968) ‘Atlas of Australian soils, sheets 1 to 10.’ (Melbourne University Press: Melbourne)
Odeh I, Todd A, Triantafilis J (2003) Spatial Prediction of Soil Particle-Size Fractions As Compositional Data. Soil Science 168, 501–515.
| Spatial Prediction of Soil Particle-Size Fractions As Compositional Data.Crossref | GoogleScholarGoogle Scholar |
Odgers NP, McBratney AB, Minasny B (2011) Bottom-up digital soil mapping. I. Soil layer classes. Geoderma 163, 38–44.
| Bottom-up digital soil mapping. I. Soil layer classes.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2018) 'R: A Language and Environment for Statistical Computing.' (R Foundation for Statistical Computing: Vienna, Austria)
Ruddell BL, Drewry DT, Nearing GS (2019) Information Theory for Model Diagnostics: Structural Error is Indicated by Trade-Off Between Functional and Predictive Performance. Water Resources Research 55, 6534–6554.
| Information Theory for Model Diagnostics: Structural Error is Indicated by Trade-Off Between Functional and Predictive Performance.Crossref | GoogleScholarGoogle Scholar |
Searle R (2014) The Australian site data collation to support the GlobalSoilMap. In ‘GlobalSoilMap: Basis of the global spatial soil information system. CRC Press’. Eds D Arrouays, AB McBratney, J Hempel, AC Richer-de-Forges.) pp. 127–133. (CRC Press: London, UK)
Searle R, Grundy MJ, McBratney AB, Gregory LJ, Wilson PL, Malone BP, Stenson M (2019) ‘Phased development of digital soil infrastructure for Australia and its contribution to global initiatives, 2019 Joint workshop for Digital Soil Mapping and GlobalSoilMap IUSS Working groups’. Santiago, Chile.
Searle R, Kidd D, Grundy M, McBratney A, Robinson N, O’Brien L, Zund P, Arrouays D, Thomas M, Padarian J, Jones E, Bennett JM, Minasny B, Holmes K, Malone BP, Liddicoat C, Meier E, Stockmann U, Wilson P, Wilford J, Payne J, Ringrose-Voase A, Slater B, Odgers N, Gray J, van Gool D, Andrews K, Harms B, Stower L, Triantafilis J (2021) Digital Soil Mapping and Assessment for Australia and Beyond: A Propitious Future. Geoderma Regional 24, e00359
| Digital Soil Mapping and Assessment for Australia and Beyond: A Propitious Future.Crossref | GoogleScholarGoogle Scholar |
Searle R, Stenson M, Wilson PL, Gregory LJ, Singh R, Malone BP (2021b) ‘Soil data, united, will never be defeated – The SoilDataFederator, Joint Australian and New Zealand Soil Science Societies Conference’. Cairns, QLD.
Shrestha DL, Solomatine DP (2006) Machine learning approaches for estimation of prediction interval for the model output. Neural Networks 19, 225–235.
| Machine learning approaches for estimation of prediction interval for the model output.Crossref | GoogleScholarGoogle Scholar | 16530384PubMed |
Solomatine DP, Shrestha DL (2009) A novel method to estimate model uncertainty using machine learning techniques. Water Resources Research 45,
| A novel method to estimate model uncertainty using machine learning techniques.Crossref | GoogleScholarGoogle Scholar |
Somarathna PDSN, Minasny B, Malone BP, Stockmann U, McBratney AB (2018) Accounting for the measurement error of spectroscopically inferred soil carbon data for improved precision of spatial predictions. The Science of the Total Environment 631–632, 377–389.
| Accounting for the measurement error of spectroscopically inferred soil carbon data for improved precision of spatial predictions.Crossref | GoogleScholarGoogle Scholar | 29525716PubMed |
Stockmann U, Austin J, Gallant J, Cocks B, Glover M, Thomas M, Verburg K (2020) ‘Macquarie-Bogan floodplain Plant Available Water Capacity prediction case study.’ (CSIRO Technical Report: Canberra, Australia)
Taylor J, Minasny B (2006) A protocol for converting qualitative point soil pit survey data into continuous soil property maps. Australian Journal of Soil Research 44, 543–550.
| A protocol for converting qualitative point soil pit survey data into continuous soil property maps.Crossref | GoogleScholarGoogle Scholar |
van den Boogaart KG, Tolosana-Delgado R, Bren M (2018) ‘compositions: Compositional Data Analysis.’ (R package version 1.40–2: https://CRAN.R-project.org/package=compositions)
Viscarra Rossel RA (2011) Fine-resolution multiscale mapping of clay minerals in Australian soils measured with near infrared spectra. Journal of Geophysical Research. Earth Surface 116,
| Fine-resolution multiscale mapping of clay minerals in Australian soils measured with near infrared spectra.Crossref | GoogleScholarGoogle Scholar |
Viscarra Rossel RA, Chen C, Grundy MJ, Searle R, Clifford D, Campbell PH (2015) The Australian three-dimensional soil grid: Australia’s contribution to the GlobalSoilMap project. Soil Research 53, 845–864.
| The Australian three-dimensional soil grid: Australia’s contribution to the GlobalSoilMap project.Crossref | GoogleScholarGoogle Scholar |
Wadoux AMJC, Samuel-Rosa A, Poggio L, Mulder VL (2020) A note on knowledge discovery and machine learning in digital soil mapping. European Journal of Soil Science 71, 133–136.
| A note on knowledge discovery and machine learning in digital soil mapping.Crossref | GoogleScholarGoogle Scholar |
Wiesmeier M, Urbanski L, Hobley E, Lang B, von Lützow M, Marin-Spiotta E, van Wesemael B, Rabot E, Ließ M, Garcia-Franco N, Wollschläger U, Vogel H-J, Kögel-Knabner I (2019) Soil organic carbon storage as a key function of soils - A review of drivers and indicators at various scales. Geoderma 333, 149–162.
| Soil organic carbon storage as a key function of soils - A review of drivers and indicators at various scales.Crossref | GoogleScholarGoogle Scholar |
Wilford J (2012) A weathering intensity index for the Australian continent using airborne gamma-ray spectrometry and digital terrain analysis. Geoderma 183–184, 124–142.
| A weathering intensity index for the Australian continent using airborne gamma-ray spectrometry and digital terrain analysis.Crossref | GoogleScholarGoogle Scholar |
Wright MN, Ziegler A (2017) ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. Journal of Statistical Software 77, 17
| ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R.Crossref | GoogleScholarGoogle Scholar |
* Part 1, Soil Research 2021, https://doi.org/10.1071/SR20283