Sulfate sorption measured by a buffering index over a range of properties of soils from south Western Australia
G. C. Anderson
Department of Primary Industries and Regional Development, PO Box 483, Northam, WA 6401, Australia. Email: geoff.anderson@dpird.wa.gov.au
Soil Research 58(7) 651-661 https://doi.org/10.1071/SR20005
Submitted: 6 January 2020 Accepted: 1 July 2020 Published: 30 July 2020
Journal Compilation © CSIRO 2020 Open Access CC BY
Abstract
Sulfate sorption by the soil affects the rate of sulfate leaching, which impacts on the availability of soil sulfate for plant uptake. In Australia, plant-available sulfur is measured using 0.25 M KCl heated for 3 h at 40°C to extract soil sulfur (SKCl40). This paper describes a technique referred to as a sulfate buffering index (SBI), which provides a measurement of sulfate sorption. SBI when combined with the estimates of the q and b parameters of the Freundlich equation, can be used to define a sorption curve. The equation is S = acb – q; where S is the amount of sulfate adsorbed (mg S kg–1), c is the equilibrium concentration of sulfate measured in solution (mg S L–1) and a, b and q are coefficients that describe the soil sulfate sorption curve. Coefficients S and c were measured using six sulfate solution concentrations ranging from 0 to 250 mg S kg–1. The adsorption curve was fitted using the modified Freundlich equation including setting of b = 0.41 and q = SKCl40 using recently collected soil samples. The modified Freundlich a coefficient or SBI was calculated as SBI = (S + SKCl40)/c0.41; where S and c were determined using 50 mg S kg–1 of added sulfate. The SBI ranged within 1–40. The SKCl40 was related to SBI below a depth of 10 cm (r2 = 0.71) but not for the 0–10 cm soil layer where S sorption was minimal.
Additional keywords: crop management, leaching.
Introduction
Sulfur deficiency in wheat (Triticum aestivum L.) and canola (Brassica napus L.) occurs when sulfate fertilisers are not applied to soils low in natural sulfur reserves (Anderson et al. 2006; Brennan and Bolland 2006). Sulfate is readily soluble in soil solution and subject to loss by leaching (Till 2010) in soils with low sorption capacities. This is less of a problem in soils with high anion exchange capacities, which occurs in acidic subsoils. These soils are expected to have lower rates of nitrate and sulfate leaching (Wong and Wittwer 2009). In many soils, sulfate leaching during the growing season reduces the ability of soil test methods to accurately predict wheat and canola grain yield response to applied sulfate fertiliser (Anderson et al. 2013).
Water movement through the soil profile in south Western Australia (SWA) is highest near the coast and lowest inland, in line with the decreasing gradient of annual rainfall (Asseng et al. 2001). Similarly, the low sulfate sorption capacity combined with intense rainfall after sowing of crops can result in the rapid displacement of sulfate from the 0–20 cm soil layer, leading to a sulfur deficiency in wheat (Anderson et al. 2006). Sulfate sorption reduces the rate of sulfate leaching and is dependent on the shape of the sulfate adsorption curve (Bolan et al. 1986). Subsoils typically have higher sulfate sorption capacities and thus can retain surface-applied sulfate (Chen et al. 1999; Anderson et al. 2006). Subsoil sulfate can be an important source for lupin (Lupinus angustifolius) growth (Anderson et al. 2006).
Measurement of sulfate sorption capacity of soils is described by Blair et al. (1997, hereafter ‘Blair method’). However, the Blair method requires the use of two extracting solutions, a long extraction time of 48 h, the use of chloroform and the monitoring of the solution pH. Sulfate sorption capacity is not measured routinely in SWA because the Blair method is impractical for use by commercial soil testing laboratories. In contrast, phosphorus (P) sorption has been widely studied for the 0–10 cm soil layer in SWA (Barrow 1983, 2000, 2008; Bolland and Allen 2003). Several simple single-point measurements of P sorption are available at commercial soil testing laboratories (Barrow 2000; Allen et al. 2001; Burkitt et al. 2002). Both P and sulfate sorption can be described by the Freundlich equation (Bolan et al. 1986; Barrow 2000). Therefore, it is reasonable to suggest that a single-point sulfate sorption method could be developed for the soil profile, using similar approaches to that used for P sorption.
A single-point estimate of the phosphate buffering index (PBI) can be obtained using the modified Freundlich equation (Barrow 2000). The Freundlich equation is written as

where S is measured sorption, c is the equilibrium solution concentration, a is the amount adsorbed when c = 1, b is the affinity of the soil for P sorption and q is the amount of P in the soil before additions. Coefficient a is calculated as follows: a = (S + q)/cb. When the Freundlich equation is applied in P sorption studies, coefficients b and q are correlated (Barrow 1978). Thus, changes in the value of one coefficient result in changes in the value of the other. Coefficient b is accurately defined for values of 0.2–0.5 (Barrow 2000; Peltovuori 2007). Fixing b to 0.41 and q to Colwell extractable P (Colwell P; Colwell 1963), results in the calculated a (termed the PBI) that is well correlated with the P buffer capacity measured by the procedure of Ozanne and Shaw (1968) (Burkitt et al. 2002). The PBI is calculated as follows: PBI = (PS + Colwell P)/c0.41 where PS is measured P sorption and c is the equilibrium solution P concentration (Burkitt et al. 2002).
In the case of P, Colwell P is used as the q coefficient (Barrow 2000; Burkitt et al. 2002). If this approach is applicable to sulfate, an equivalent estimate of q is required using a sulfate extraction technique. In Australia, the SKCl40 soil test is commonly used, which estimates plant-available sulfur from the soil by defining a soil test–pasture or crop response relationship (Blair et al. 1991; Anderson et al. 2013). Alternative sulfur soil test extractants include 0.01 M calcium chloride (SCaCl2) and 0.01 M calcium monophosphate (SMCP) with sulfur concentration measured using inductively coupled plasma atomic emission spectroscopy (ICP-AES) (Santoso et al. 1995). The extractants SCaCl2 and SKCl40 only extract soil solution sulfate and sulfate adsorbed in the diffuse double layer (Blair et al. 1991; Watkinson and Kear 1996; Till 2010). In contrast, P solutions such as SMCP extract soil solution sulfate, sulfate adsorbed in the diffuse double layer and sulfate adsorbed on specific sorption sites (Probert 1976; Watkinson and Kear 1996). The difference between soil sulfur pools extraction methods could affect the ability of the soil test method to define q.
Historically, sulfate was a problematic nutrient to measure in laboratories because the presence of dissolved organic matter in the extracting solution interfered when using the turbidimetric method (Anderson et al. 1992). With the development of new laboratory equipment, specifically ICP-AES and high performance liquid chromatography (HPLC), significantly improved the ability of laboratories to measure sulfur in soil extractant (Blair et al. 1991; Watkinson and Kear 1994). The advantage of ICP-AES over HPLC is that it measures the amount of dissolved organic sulfur in the soil extractant, which is essential when assessing the ability of the extractant to measure plant-available sulfur (Blair et al. 1991). Also, ICP-AES can measure sulfur concentration much more quickly than HPLC, making it much more suitable for commercial soil testing laboratories. Finally, the cost and reliability of ICP-AES have greatly improved over time. Hence, in Australia, ICP-AES is more commonly used to measure sulfur concentration in soil extracts than HPLC (Blair et al. 1991; Anderson et al. 2013).
This paper aims to appraise the use of a modified Freundlich equation to estimate sulfate sorption and develop a single-point index (SBI) for estimating sulfate adsorption for soils of SWA.
Materials and methods
Sulfate sorption measurements
Sulfate sorption was determined using two methods. Method 1 uses two sulfate extracting solutions of 0.01 M CaCl2 (Blair et al. 1997): one with 50 mg S kg–1 added and the other with no added sulfur. Sulfate sorption is calculated as added sulfate (50 mg S kg–1) minus SCaCl2 from the soil with added 50 mg S kg–1 (S50) plus pre-existing sulfate extracted with SCaCl2 or S = (50 – S50) + SCaCl2. Hence, the method takes into account the pre-existing sulfate extracted by the 0.01 M CaCl2 solution.
Method 2 determines the sulfate sorption curve using six incremental amounts of added sulfate: 0–250 mg S kg–1 (Lisle et al. 1991). Because Lisle et al. (1991) is not a readily available publication, the method is described as the following steps.
-
Measurement of soil pHCaCl2.
-
Addition of 3 g of air-dried soil to a 50-mL centrifuge tube.
-
Addition of 0, 3, 6, 9, 12 or 15 mL of 50 mg S L–1 K2SO4 solution (equivalent to 0, 50, 100, 150, 200 and 250 mg S kg–1) to the centrifuge tubes.
-
Addition of 15, 12, 9, 6, 3 or 0 mL of 0.003 M KCl to the centrifuge tubes to ensure the potassium concentration is balanced among sulfate concentrations.
-
Addition of 15 mL of 0.02 M CaCl2 to the centrifuge tubes followed by adding two drops of chloroform. The final concentration of the extracting solution is 0.01 M CaCl2.
-
The solution soil mixture is tumbled for 48 h at 25°C; pH is measured at 6, 24 and 30 h and, if necessary, adjusted to the original soil pHCaCl2 using varying amounts of 0.01 M HCl or NaOH depending on the soil’s pH buffering capacity, which is related to the carbon content (Wong et al. 2013).
-
Tubes are centrifuged at 2670 g for 5 min and then filtered using Whatman no. 42 filter paper.
-
Sulfate concentration in the supernatant is measured using HPLC (Watkinson and Kear 1994).
-
Calculated sulfate adsorption (Sc mg S kg–1) is the amount of sulfate added minus sulfate extracted by SCaCl2. The subscript c represents the amount of added sulfate which is 0, 50, 100, 150, 200 or 250 mg S kg–1. The data are plotted with the sulfate concentration in the final extract solution on the x-axis (mg S L–1) vs adsorbed sulfate on the y-axis (mg S kg–1).
Soil samples for method development
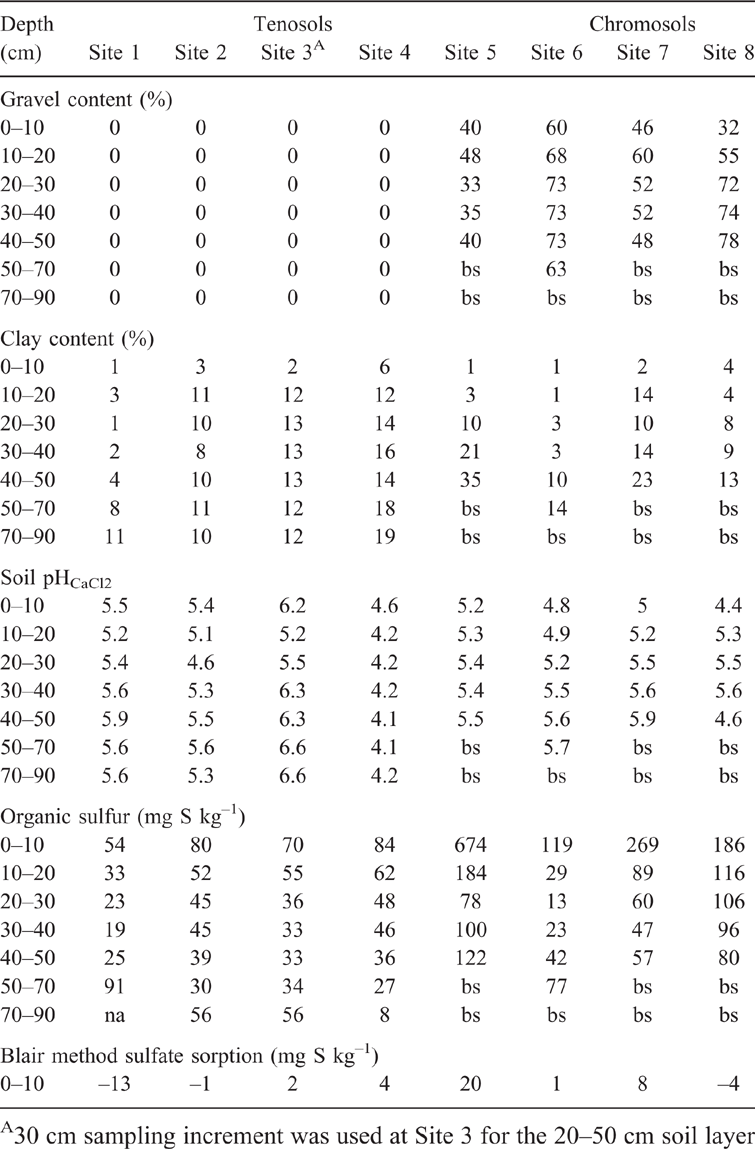
Sulfate sorption was measured by methods 1 and 2 using soil profile samples from eight sites in SWA (Table 1). The sites were from the low rainfall zone, 325–450 mm (Mullewa – Site 1, 450 km north of Perth; Latham – Site 2, 310 km north-east of Perth; Ballidu – Site 3, 220 km north-east of Perth; and Kalannie – Site 4, 250 km north-east of Perth), and in the high rainfall zone, 450–800 mm (Williams – Site 5, 160 km south-east of Perth; Arthur River – Site 6, 200 km south-east of Perth; Narrogin – Site 7, 200 km south-east of Perth; and Moora – Site 8, 170 km north of Perth). The soils at sites 1–4 were described as Tenosols and at sites 5–8 as Chromosols (Isbell and National Committee on Soil and Terrain 2016).
Soil samples were collected to a depth of 90 cm for the Tenosol sites and to a depth of 50 cm for the Chromosol sites in June. Samples were from four random locations of the edge or border plots of sulfate fertiliser experiments after seeding. The border plots were chosen to avoid sampling areas which had received sulfate fertiliser. After collection, soil samples were placed in a glasshouse and allowed to air dry and then sieved through a 2-mm sieve. Stone material greater than 2 mm was classified as gravel. The sieved soil samples were then stored in a cold room until the completion of the measurements.
The soil samples were grouped into samples collected from depth 0–10 cm, and samples collected below 10 cm. The 0–10 cm soil samples were not used as it was not possible to define a sulfate sorption curve and calculate SBI for these samples. In the rest of the paper, I refer to the samples used in the development of the SBI as the development samples >10 cm.
Soil properties measured on the deep soil profile samples were particle size (Day 1965), Colwell P (Colwell 1963), organic carbon (Walkley and Black 1934), pH (0.01 M CaCl2, pHCaCl2) and ammonium oxalate extractable iron (Rayment and Higginson 2010). Soil sulfate was extracted using four methods to evaluate which one best estimated the Freundlich coefficient q:
-
0.01 M CaCl2 as the extracting solution (SCaCl2; Lisle et al. 1991);
-
0.25 M KCl heated for 3 h at 40°C as the extracting solution (SKCl40; Blair et al. 1991);
-
0.01 M Ca(H2PO4)2 as the extracting solution (SMCP; Watkinson and Kear 1994); and
-
An acid digest to measure total extractable sulfur (total S; Till et al. 1984).
Sulfate concentrations in the SCaCl2 and the SMCP extraction methods were measured using HPLC (Watkinson and Kear 1994); sulfur concentration in the SKCl40 and total sulfur methods were measured using ICP-AES (Blair et al. 1991) due to changing availability of laboratory equipment.
Soil samples for method evaluation
Sulfate sorption was measured using method 2 (Lisle et al. 1991) but using a single addition of sulfate (50 mg kg–1) rather than a range of sulfate additions used in method 2 to derive S and c coefficients.
For the evaluation of soil samples, ICP-AES was used (Blair et al. 1991) instead of HPLC (Watkinson and Kear 1994). This is in line with the original method used by Lisle et al. (1991), where solution sulfate concentration was measured using an ICP-AES. A small experiment I conducted showed that chloroform and shaking time did not affect the SBI when ICP-AES is used to measure the sulfate concentration. Hence, I modified the method used on the development soil samples to decrease the extracting time to 16 h without the addition of chloroform, with solution concentration measured using an ICP-AES. The modified method is more practical for commercial soil testing laboratories. The advantage of this approach is that it overcomes the problem of measuring sulfate sorption on 0–10 cm samples observed when measuring 0–10 cm samples treated with chloroform using HPLC. Chloroform is added to solutions which have a long extraction time to prevent immobilisation of nutrients by microbial activity. However, addition of chloroform to soil extracting solutions can result in the breakdown of microbial biomass and so release microbial P (Burkitt et al. 2002).
The ability of the SBI approach in assessing sulfate sorption was then examined by conducting SBI measurements on two sets of soils. One set consisted of samples from the 0–10 cm soil layer, referred to as the ‘evaluation 0–10 cm’. The other set were soil profile layers samples collected in 10 cm increments to a depth of 50 cm, referred to as the ‘evaluation 0–50 cm’. These soils were independent of the samples used to develop the SBI method.
Set 1 of the evaluation soil samples consisted of 82 samples collected from the 0–10 cm soil layer, selected from among the 173 stored samples used by Walton and Allen (2004). These samples were chosen because there was sufficient soil to undertake SBI measurements. After collection, the samples were air-dried and sieved through a 2-mm sieve and stored at room temperature. The long-term storage at room temperature, at least 15 years, may have an impact on the measured soil property. Hence, SKCl40 and soil pHCaCl2 were re-measured. These results were then compared to the values measured by Walton and Allen (2004) to determine the impact of storage time on the measured values. Long-term storage of the samples did not affect soil pHCaCl2; however, it did increase SKCl40, especially for soils with higher SKCl40 content. Hence, the new SKCl40 measurement was used in the calculation of SBI because it was considered to be important to use the SKCl40 measured at the same time as measuring S and c.
Set 2 of the evaluation soil samples consisted of soil profile samples collected in increments of 10 cm to a depth of 50 cm from two experimental sites located in the eastern wheatbelt of SWA located near South Burracoppin and Bonnie Rock. These samples are referred to as the ‘evaluation 0–50 cm samples’. The experiments examine the effectiveness of lime and gypsum to treat subsoil aluminium toxicity. Hence, measurements of the sulfate sorption properties of the soil profile are important in understanding the rate of sulfate leaching.
Statistical analysis
Correlations between the various soil sulfate measurements were determined using regression analysis in GenStat® version 19.
The Freundlich equation was used to define the sulfate sorption curve (Eqn 1). The Freundlich equation coefficients and adjusted r2 values were obtained using the regression function of SigmaPlot® version 12.5. Initially, I fitted a single curve to each soil layer. I then pooled the data for near soil layers when the same curve was defined. I then fitted a single curve to the combined data. The advantage of combining the soil layers is that it increases the number of data points, resulting in a reduction in r2 values required to obtain a 5% significance level (Neave 1978).
Results and discussion
Soil properties
The Tenosol profiles contained no gravel, while gravel accounted for up to 73% of some soil layers in the Chromosol profiles (Table 1). The pHCaCl2 of the top 10 cm of soil ranged within 4.4–6.2. Soil pHCaCl2 below 10 cm was in the range of 4.6–5.9 in the Chromosols, 4.6–6.6 in the Tenosols at Sites 1–3 and 4.1–4.2 in Tenosol at Site 4. The clay content of the top 10 cm of soil was less than 7% in all samples. Below 10 cm, clay content increased with soil depth and ranged within 1–11% at Sites 1–3 and 12–19% at Site 4. The subsoils of Chromosols contained up to 35% clay. Total organic sulfur content in the 0–10 cm soil layer ranged within 54–84 mg S kg–1 for the Tenosols and 119–674 mg S kg–1 for the Chromosols. Below 10 cm, organic sulfur content for both soil types ranged within 13–122 mg S kg–1, except for the 0.1–0.2 m soil layer at Site 5, where it was 184 mg S kg–1. Colwell P in the 0–10 cm soil layer ranged within 12–39 mg P kg–1 soil in the Tenosols compared to 31–80 mg P kg–1 for the Chromosols (data not presented). Ammonium oxalate extractable iron ranged within 135–828 mg Fe kg–1. Organic carbon content in the top 10 cm was within 0.4–0.7% in the Tenosols. Chromosols (Sites 6–8) had a higher organic carbon content of 1.5–1.7%, while Site 5 had the highest organic carbon of 5.7%.
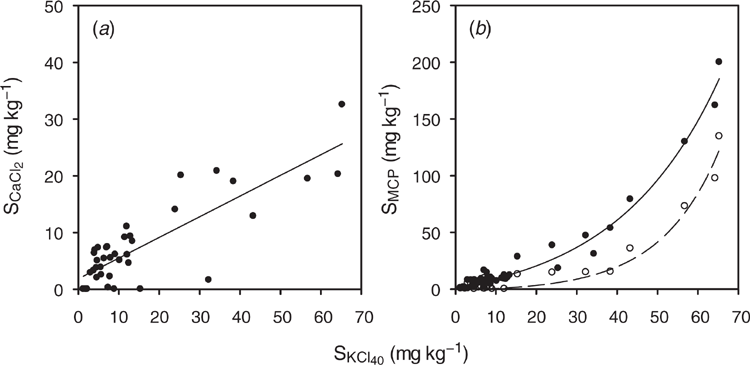
For the development soil samples from greater than 10 cm depth, SKCl40 was correlated with SCaCl2 (Fig. 1a). In contrast, SKCl40 was correlated with SMCP for all soil layers (Fig. 1b). The fitted equation indicates that SKCl40 was less than SMCP when SKCl40 was greater than 15 mg S kg–1, which occurred in the soil profile from Site 2 (50–90 cm), Site 4 (10–90 cm) and Site 5 (10–50 cm).
The soil test methods SCaCl2, SKCl40 and SMCP extract different soil sulfur pools (Till 2010). All methods extract some organic sulfur, with the SKCl40 method extracting more organic sulfur than SCaCl2 and SMCP due to the heat treatment (Blair et al. 1991). The higher pH of the CaCl2 and KCl40 solution means that these methods extract organic sulfur than the MCP solution, which has pH 4.0 (Barrow 1967). The higher amount of sulfur extracted by SMCP compared to SKCl40 is due to SMCP extracting sulfate adsorbed in the diffuse double layer and sulfate adsorbed on specific sorption sites compared to SKCl40, which extracts sulfur from only the diffuse double layer (Probert 1976; Watkinson and Kear 1996).
Soil properties measured on the 0–10 cm soil samples of the evaluation dataset had a pHCaCl2 range of 4.2–6.9, soil carbon of 0.3–6.1%, clay content of 0.5–43.0%, phosphorus retention index (PRI) of –0.5 to 880, SKCl40 of 3.5–38.0 mg S kg–1 and Colwell P of 5.0–77.0 mg P kg–1. Soil properties measured on the soil profile soil samples of the evaluation dataset were as follows. At South Burracoppin, pHCaCl2 was 5.5 in the 0–10 cm soil layer decreasing to 4.2–4.4 in the 20–50 cm layer. Soil SKCl40 increased with increasing soil depth from 22.1 mg S kg–1 in the 0–10 cm to 61.1 mg S kg–1 in the 40–50 cm soil layer. At Bonnie Rock, soil pHCaCl2 was 4.5–4.7 in the 0–50 cm soil layer. Soil SKCl40 increased from 13.6 mg S kg–1 in the 0–10 cm soil layer to 30.0 mg S kg–1 in the 40–50 cm layer.
Soil samples with clay < 6% (Table 1) had low sulfate sorption measured using the Blair method (Table 2). These soil samples included the 0–10 cm soil layer for all sites, with sulfate sorption ranging between –20 and 8 mg S kg–1. Also, for the Tenosol profile at Site 1 and the Chromosols at Sites 6 and 8, for soil layers 10–50, 10–40 and 10–20 cm respectively, the Blair method sulfate sorption ranged within 0–7 mg S g–1 (data not presented).
There was a trend of soil samples with clay > 6% (Table 1) having sulfate sorption measured using the Blair method of >7 mg S g–1 (Table 2). This was illustrated for the Tenosol at Site 1 and Chromosols at Sites 5, 6 and 8, with the highest sulfate sorption (18–22 mg S kg–1) for the deepest sampling layer or the soil layers with the highest clay content (10–35%). However, sulfate sorption was variable between the soil layers at Site 3 of 7–24 mg S kg–1. These differences in sulfate sorption could not be explained by the variation in clay content or pHCaCl2. Hence, although there were some trends of higher sulfate sorption measured by the Blair method with higher clay content, the relationship between these two measurements was poor (i.e. sulfate sorption = 1.00 × clay (%), r2 = 0.32).
SBI development
The development of the SBI required selection of a soil extraction technique to define q, the definition of b and selection of the amount of sulfate required to be added to the solution to measure S and c.
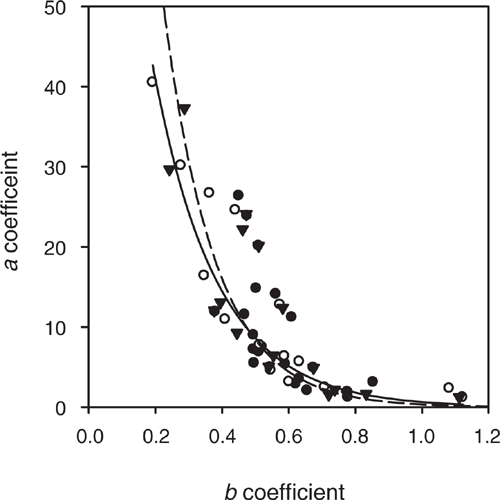
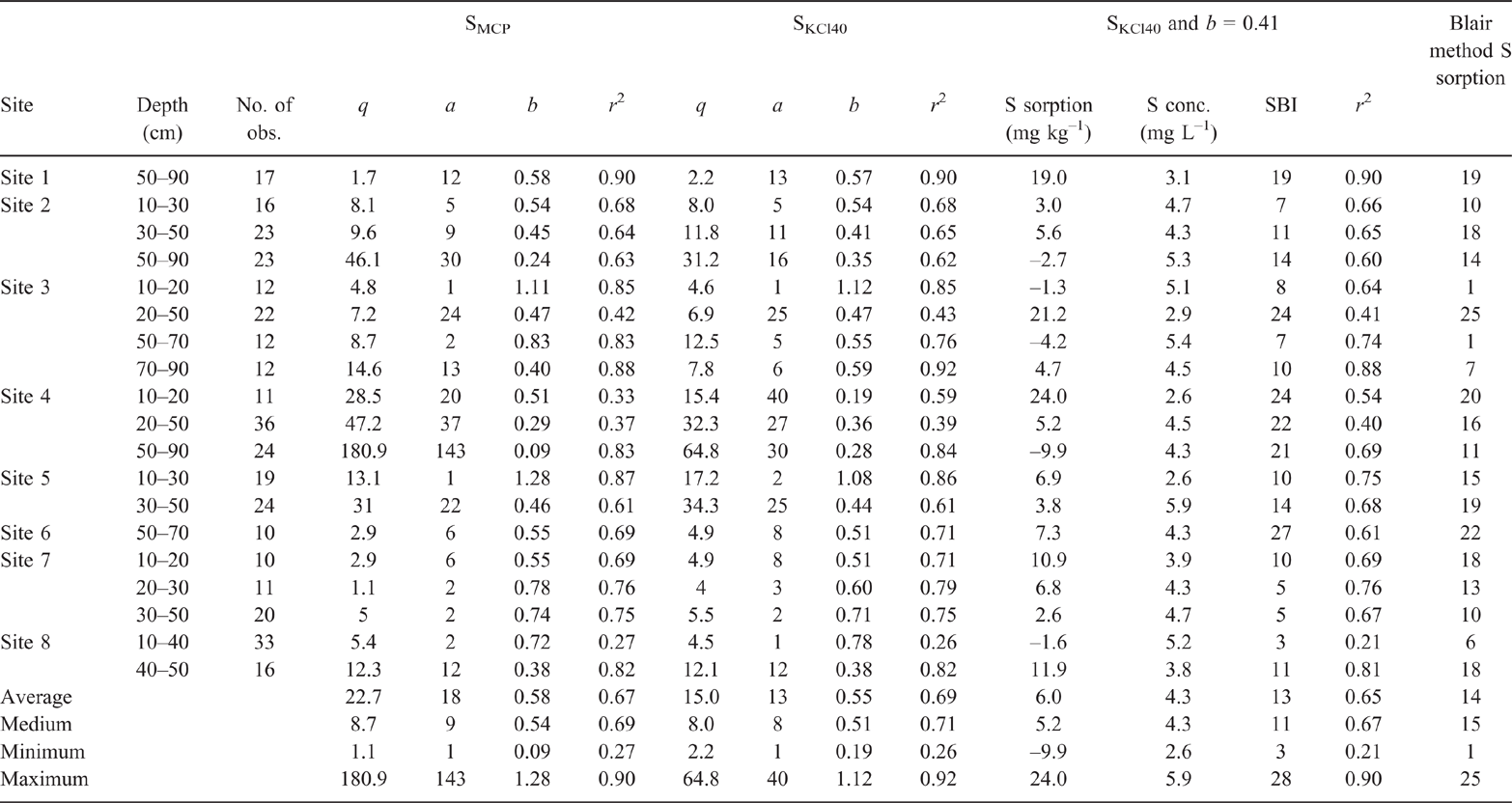
Fixing q to be equal to a sulfur extraction technique changed the a and b coefficients (Fig. 2). The calculated a and b when q was fixed to be equal to SKCl40 and SMCP, and the associated regression coefficients, are presented in Table 2. Setting q = SKCl40 resulted in a ranging within 1–40 and b within 0.19–1.12, with an average of 0.55 and a median of 0.51 (Table 2). Setting q = SMCP resulted in a broader range of a with 1–143, and b with 0.09–1.28, an average of 0.58 and a median of 0.54. Hence, the SKCl40 method resulted in a narrow range of the modified Freundlich a and b coefficients compared to the SMCP method. Also, when q was set equal to SKCl40, this resulted in a higher regression coefficient for the relationship between the modified Freundlich a and b coefficients compared to the SMCP method (Fig. 2; r2 = 0.79 for SKCl40 compared to 0.68 for SMCP). The SKCl40 method thus provided a better estimate of q than the SMCP. This is because SKCl40 measures a fraction of the soil’s inorganic sulfate from the solution and absorbed in the diffuse double layer (Watkinson and Kear 1996; Till 2010); in contrast, SMCP extracts all of the soil’s inorganic sulfate, including sulfate, adsorbed on the specific sorption sites (Watkinson and Kear 1996; Till 2010). The higher SMCP compared to SKCl40 measured at Site 4 for the soil layer 50–90 cm was shown by fixing q to SMCP resulting in a higher a and lower b than when SKCl40 was used to define q (Table 2). Hence, SKCl40 was used to determine q in subsequent analyses.
|
In P sorption studies, the reliable definition of b occurs for values of 0.20–0.50 (Barrow 2000). Subsequently, in the development of the PBI, b was fixed to a value of 0.41 (Burkitt et al. 2002). In a sulfate sorption study, b ranged within 0.11–0.24 for a small group of five soils (Gustafsson et al. 2015). Soils have a measured anion exchange capacity (Wong and Wittwer 2009). Sulfate and P sorption by soils is intimately linked (Barrow and Debnath 2015). Hence, I tested if setting b in the Freundlich equation to 0.41 could define the sulfate sorption curve (Figs 3 and 4). Using this approach, SBI described a similar range (3–28) in sulfate sorption to the range (1–25) measured by the Blair method of sulfate sorption (Table 2).
|
The modified Freundlich equation is then given by Eqn 2, and a or SBI is calculated using Eqn 3:


where SBIc, subscript c represents the amount of added sulfate (i.e. 0, 50, 100, 150, 200 or 250 mg S kg–1), can be calculated using different combinations of S and c obtained from the five added amounts of sulfate.
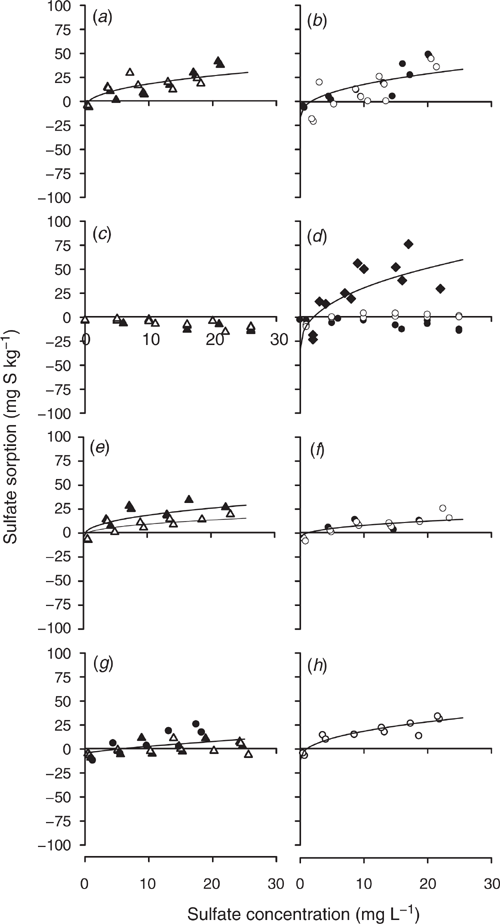
The sulfate sorption curves defined using the modified Freundlich equations that used SKCl40 to determine q and b set to equal 0.41 are shown for Tenosols (Fig. 3) and Chromosols (Fig. 4). Duplicate measurements are presented for each soil depth and sulfate concentration, with little variability between the duplicate measurements for most site and layer combinations. However, there were notable exceptions, with high variability at Site 2 for the 20–30 cm soil layer (Fig. 3d) and at Site 3 for 20–30 and 30–50 cm (Fig. 3h). High variability reduced the capacity to fit the modified Freundlich equations accurately.
Negligible sulfate sorption occurred at Site 1 to a depth of 50 cm (Fig. 3a) and Site 6 to 30 cm (Fig. 4c). No attempt was made to fit modified Freundlich equations for these non-adsorbing soil layers. It is also notable that sulfate desorption occurred at low concentrations of added sulfate in the Site 4 soil below 50 cm, and large amounts of added sulfate were needed to induce sulfate sorption (Fig. 3l).
The following sites and soil layers resulted in the fitting of a single curve. At Site 1, for 50–70 and 70–90 cm soil layers (Fig. 3c). At Site 2, for 10–20 and 20–30 (Fig. 3d), 30–40 and 40–50 (Fig. 3e), and 50–70 and 70–90 cm soil layers (Fig. 3f). At Site 3, for 20–30 and 30–40 cm soil layers (Fig. 3h). At Site 4 for 20–30, 30–40 and 40–50 (Fig. 3k) and 50–70 and 50–90 cm soil layers (Fig. 3l). At Site 5, for 10–20 and 20–30 (Fig. 4a) and 30–40 and 30–50 cm soil layers (Fig. 4b). At Site 7, for 30–40 and 30–50 cm soil layers (Fig. 4f). At Site 8, for 10–20, 20–30 and 30–40 cm soil layers (Fig. 4h).
The fitted modified Freundlich equations regression coefficients values typically exceeded the 5% significance level defined by Neave (1978). Exceptions to this rule occurred at Site 2 for the 50–90 cm soil layer, r2 = 0.41, n = 23 (Fig. 3f); Site 3 for 20–50 cm, r2 = 0.42, n = 22 (Fig. 3h); and Site 4 for 10–20 cm, r2 = 0.35, n = 11 (Fig. 3j, Table 2).
Calibration of SBI was done at the individual and grouped depths because some layers of a soil profile resulted in different calculated SBI. For example, at Site 1 for the 50–90 cm soil layer, Site 3 for 20–50 cm and Site 6 for 50–70 cm had higher SBI values than the other soil layers, indicating that these soil layers had a higher capacity to adsorb sulfate than other soil layers within the soil profile (Table 2). In other cases, the calculated SBI values were similar, but the shapes of the curves differed due to differences in SKCl40 or the defined q; for example, for Site 4 for sample depths 10–20, 20–30 and 50–90 cm (Fig. 3j–l).
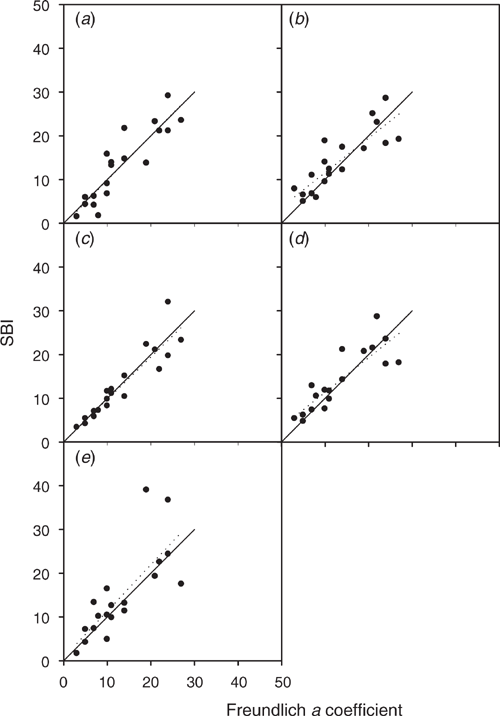
For the single-point measurement, the S and c of the modified Freundlich equations can be measured using 50, 100, 150, 200 or 250 (mg S kg–1) of added sulfate. Figure 5 compares the a derived from the fitted curve using the modified Freundlich equation with b = 0.41 and q = SKCl40 (x-axis) vs the SBI calculated using each single concentration of added sulfate (y-axis). Adding 250 mg S kg–1 was a poor predictor of SBI compared with a fitted from the sorption curve, as indicated by the low r2 value of 0.60 (Fig. 5e). In contrast, using 50, 100, 150 or 200 mg S kg–1 of added sulfate, all produced higher r2 ranging within 0.72–0.85. Both 100 and 200 mg S kg–1 of added sulfate resulted in a lower r2 (0.70–0.73) than using 50 mg S kg–1 (0.80). Hence, I selected 50 mg S kg–1 of added sulfate for measuring S and c to calculate SBI (Eqn 4), with Eqn 5 used to calculate the sulfate sorption curve.


|
SBI evaluation
The previous sections illustrated that SKCl40 was the best extract to estimate q, and addition of 50 mg S kg–1 provided the best concentration by single-point sulfur adsorption method to calculate SBI. Because shaking time and addition of chloroform did not affect SBI when sulfur concentration in the 0.01 M CaCl2 solution was measured using ICP-AES, SBI was measured using a shaking time of 16 h without adding chloroform and with 50 mg S kg–1 of sulfate added to derive S and c. The SBI was then calculated using Eqn 4.
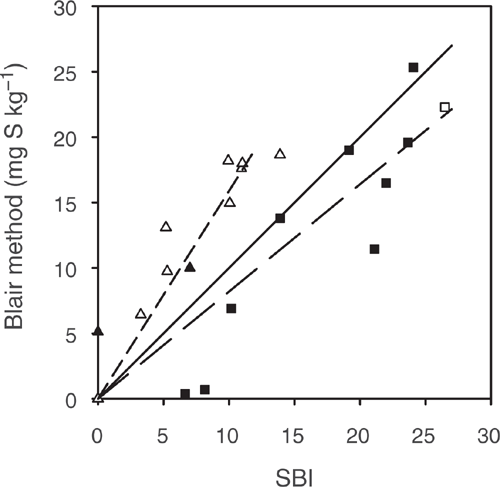
Plotting SBI vs sulfate sorption measured by Blair method illustrates that the data is divided into two groups (Fig. 6). Group 1 included measures where SBI ≥ sulfate sorption measured by Blair method, consisting of Tenosols Site 1 and 2 for soil layer 50–90 cm, Site 3 for soil layer 20–50 cm and Site 4 for all soil layers and one Chromosol (Site 6, layer 50–70 cm). In contrast, group 2 included measurements where SBI < sulfate sorption measured by Blair method, consisting of the other Chromosols plus the Tenosol Site 2 for depths 20–30 and 30–50 cm. Separating the soils into these two groups resulted in SBI being correlated with the Blair method results (Fig. 6). The SBI method takes into account the effect of the concentration of the extracting solution to define a sulfate sorption curve. In contrast, the Blair method measures sulfate sorption at a single sulfate concentration. Higher SBI values than that obtained with the Blair method occurred when the soil had a relatively high sulfate sorption capacity (group 1). This was observed for Tenosols with SKCl40 > 15 mg S kg–1 and the soil could adsorb more sulfate (Fig. 3f and j–l), and for a Chromosol soil layer 50–70 cm with a high capacity to adsorb sulfate (Fig. 4d). In contrast, SBI values lower than obtained with the Blair method occurred when the soil had low SKCl40 content and a low capacity to adsorb more sulfate (group 2) as presented in Fig. 3d and e and Fig. 4a–c and e–h. Hence, the Blair method appears to underestimate sulfate sorption on soils with a high capacity to adsorb sulfate and overestimate it for soils with a low ability to adsorb sulfate. This indicates that the SBI method, which defines the sulfate sorption curve, provides a more accurate measurement of sulfate sorption than the Blair method, which measures a single point on the sorption curve.
|
The measurements SKCl40 and SBI are measures of sulfate sorption: SKCl40 being the amount adsorbed before addition and SBI the amount adsorbed when c = 1 and b = 0.41. Hence, SKCl40 was correlated with SBI for the development samples >10 cm and the evaluation 0–50 cm samples (Fig. 7). However, there were some outliers for the development samples >10 cm. These include data points with low SKCl40 and relatively high SBI for the Tenosols at Site 1 with sampling depth of 50–90 cm (Fig. 3c), Site 3 for 20–50 cm (Fig. 3h) and Site 4 for 10–20 cm (Fig. 3i). The data point with high SKCl40 and relatively low SBI (Fig. 7) occurred for the Tenosol at Site 4 for 50–90 cm (Fig. 3l).
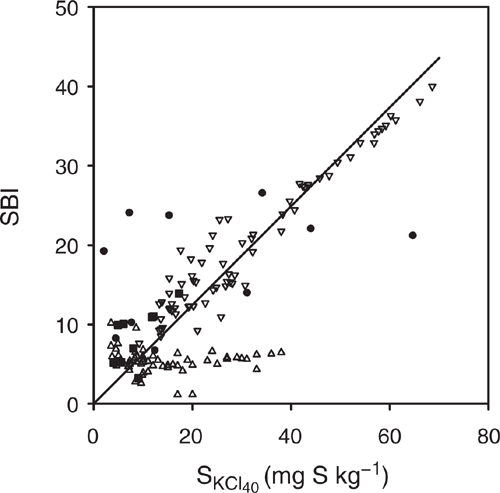
|
The SKCl40 was not correlated with SBI for the evaluation surface (0–10 cm) soil samples. These samples had relatively low SBI, consistent with the soil having high pH, soil P and carbon content, which result in the soil having a low ability to adsorb sulfate (Johnson and Todd 1983; Barrow and Debnath 2015). However, the increase in soil SKCl40 due to long-term storage of the samples could have affected the relationship between SKCl40 and SBI for this set of samples. Furthermore, for these soil samples, SBI was not correlated with soil properties including clay, silt, sand, Colwell P, PRI, pHCaCl2 and carbon content (data not presented).
Sulfate sorption curves
The SBI and Blair methods both use a single-point measurement of sulfate sorption using an added amount of sulfate of 50 mg S kg–1. The SBI approach differs from that of the Blair method in that it can be used to define a sulfate sorption curve using the modified Freundlich equation. Hence, the SBI method accounts for the impact of sulfate concentration on sulfate sorption (Figs 3 and 4). Defining sulfate sorption over a range of sulfate concentrations is important because, under conditions that result in sulfate leaching, the amount of sulfate retained is concentration-dependent (Selim et al. 2004). Also, the response of sulfate adsorption to increased sulfate concentrations varies across soil types as indicated by the large variation in the shape of the sorption curves (Figs 3 and 4). The shape of the sulfate sorption curves is critical because the reduction in sulfate leaching due to sulfate sorption is dependent on the shape of the adsorption curve (Bolan et al. 1986).
The clay mineralogy influences the shape of the sulfate sorption curve (Bolan et al. 1986). Soil which contains allophane-type clays has a higher ability to adsorb sulfate compared to soils that contain vermiculite-type clays. The clay mineralogy of soils from SWA is dominated by the occurrence of kaolinite and iron (haematite, goethite and magnetite) and aluminium oxides (Wong and Wittwer 2009). However, the anion exchange capacity of the soil is not correlated with iron and aluminium oxide content but is correlated with SKCl40 and SMCP (Wong and Wittwer 2009).
The most significant impact of solution concentration on the shape of the sulfate sorption curve occurred when the soil contained adsorbed sulfate or when SMCP was higher than SKCl40, which occurred at Site 4 for soil layers below 30 cm (Fig. 3k, l). For these soil layers, the SBI was higher (21–24) than the sulfate sorption values measured using the Blair method (11–20 mg S kg–1) (Table 2, Fig. 5). The anion exchange capacity for 10–30 cm soil layer of this soil ranged within 0.13–0.44 mmolc kg–1 (Kalannie geographical origin in Table 1, Wong and Wittwer 2009). Higher anion exchange capacity up to 2.47 mmolc kg–1 was observed for other acidic subsoils and was correlated with the SKCl40 and SMCP content of the soil. The effect of soils with higher anion exchange capacity was to delay nitrate leaching. Similarly, delayed leaching of sulfate should occur in these soils.
Application of the SBI technique
The SKCl40 soil test procedure is correlated with pasture response to sulfur fertiliser application in low sulfate leaching environments, i.e. Northern Tablelands and North West Slope and Plains of New South Wales (Blair et al. 1991). The SKCl40 method extracts mainly sulfate from the soil solution and a pool of labile organic sulfur which is mineralised over the growing season. In contrast, in environments where there is a higher potential for sulfate leaching, i.e. SWA, the soil solution sulfate can be leached early in the growing season (Anderson et al. 2006). Hence, the SKCl40 method tends to have a lower correlation with crop and pasture response to applied sulfate fertilisers (Anderson et al. 2013; Gourley et al. 2019). Using a deeper sampling depth, i.e. 0–30 cm, improved the definition of the SKCl40 crop response relationship (Anderson et al. 2013). Nevertheless, r2 is still less than 0.48. Hence, there is a need to improve the ability of the SKCl40 method to predict sulfur fertiliser requirements for SWA. It is argued the SKCl40 method of assessing sulfur availability to plants can be improved by measuring the sulfate sorption capacity of the soil using the SBI. The SKCl40 and SBI measurements could then be used to develop modelling routines to make predictions of sulfate leaching in relation to sulfate leaching rainfall events. For example, the low SBI values of –4.0 to 2.7, helps explain that the large grain yield response to applied sulfate fertiliser was due to the high rates of sulfate leaching observed by Anderson et al. (2006).
Further experimental work should examine the link between soil solution sulfate concentration, SKCl40 content and SBI, enabling the development of modelling routines for sulfate uptake by plants and sulfate leaching. Also, SBI measurements should be done on a broader range of soil types to identify soil that has low SBI values, which could be associated with low sulfate efficiency of utilisation due to sulfate fertiliser leaching.
Conclusion
A single-point measurement of SBI can be used to define the sulfate sorption curves of agricultural soils by setting b = 0.41 and q = SKCl40. The c and S coefficients are then determined using 50 mg S kg–1 of added sulfate. The SBI is then calculated as SBI = (S + SKCl40 )/c0.41. The modified Freundlich equation, S = (SBI × c0.41) – SKCl40 S is then used to calculate the sulfate sorption curve. The defined sulfate sorption curve can then be used to model sulfate leaching to improve sulfate fertiliser advice for growing crops and pastures.
Conflicts of interest
The author declares no conflicts of interest.
Acknowledgements
The Department of Primary Industries and Regional Development, Grains Research and Development Corporation, Commonwealth Scientific and Industrial Research Organisation and CSBP Limited provided the funding for this work.
References
Allen DG, Barrow NJ, Bolland MDA (2001) Comparing simple methods for measuring phosphate sorption by soils. Australian Journal of Soil Research 39, 1433–1442.| Comparing simple methods for measuring phosphate sorption by soils.Crossref | GoogleScholarGoogle Scholar |
Anderson GC, Lefroy RDB, Chinoim N, Blair GJ (1992) Soil sulfur testing. Sulfur in Agriculture 16, 6–14.
Anderson GC, Fillery IRP, Ripper FH, Leach BJ (2006) Sulfur mineralisation in a coarse-textured soil after different sulfate fertilisation histories and yield responses of wheat and lupin. Australian Journal of Soil Research 44, 165–174.
| Sulfur mineralisation in a coarse-textured soil after different sulfate fertilisation histories and yield responses of wheat and lupin.Crossref | GoogleScholarGoogle Scholar |
Anderson GC, Peverill K, Brennan R (2013) Soil sulfur – crop response calibration relationships and criteria for field crops grown in Australia. Crop and Pasture Science 64, 523–530.
| Soil sulfur – crop response calibration relationships and criteria for field crops grown in Australia.Crossref | GoogleScholarGoogle Scholar |
Asseng S, Fillery IRP, Dunin FX, Keating BA, Meinke H (2001) Potential deep drainage under wheat crops in a Mediterranean climate. 1. Temporal and spatial variability. Australian Journal of Agricultural Research 52, 45–56.
| Potential deep drainage under wheat crops in a Mediterranean climate. 1. Temporal and spatial variability.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ (1967) Studies on extraction and on availability to plants of adsorded plus soluble sulfate. Soil Science 104, 242–249.
| Studies on extraction and on availability to plants of adsorded plus soluble sulfate.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ (1978) The description of phosphate adsorption curves. Journal of Soil Science 29, 447–462.
| The description of phosphate adsorption curves.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ (1983) A mechanistic model for describing the sorption and desorption of phosphate by soil. Journal of Soil Science 34, 733–750.
| A mechanistic model for describing the sorption and desorption of phosphate by soil.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ (2000) Towards a single-point method for measuring phosphate sorption by soils. Australian Journal of Soil Research 38, 1099–1113.
| Towards a single-point method for measuring phosphate sorption by soils.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ (2008) The description of sorption curves. European Journal of Soil Science 59, 900–910.
| The description of sorption curves.Crossref | GoogleScholarGoogle Scholar |
Barrow NJ, Debnath A (2015) Effect of phosphate status and pH on sulphate sorption and desorption. European Journal of Soil Science 66, 286–297.
| Effect of phosphate status and pH on sulphate sorption and desorption.Crossref | GoogleScholarGoogle Scholar |
Blair GJ, Chinoim N, Lefroy RDB, Anderson GC, Crocker GJ (1991) A soil sulfur test for pasture and crops. Australian Journal of Soil Research 29, 619–629.
| A soil sulfur test for pasture and crops.Crossref | GoogleScholarGoogle Scholar |
Blair GJ, Anderson GC, Crestani M, Lewis D (1997) Soil sulfur status, sulfur fertiliser responses and rainfall sulfur accession at trial sites in the National Reactive Phosphate Rock Project. Australian Journal of Experimental Agriculture 37, 995–1001.
| Soil sulfur status, sulfur fertiliser responses and rainfall sulfur accession at trial sites in the National Reactive Phosphate Rock Project.Crossref | GoogleScholarGoogle Scholar |
Bolan NS, Scotter DR, Syers JK, Tillman RW (1986) The effect of adsorption on sulfate leaching. Soil Science Society of America Journal 50, 1419–1424.
| The effect of adsorption on sulfate leaching.Crossref | GoogleScholarGoogle Scholar |
Bolland MDA, Allen DG (2003) Phosphorus sorption by sandy soils from Western Australia: effect of previously sorbed phosphorus on PBC and single–point phosphorus sorption indices. Australian Journal of Soil Research 41, 1369–1388.
| Phosphorus sorption by sandy soils from Western Australia: effect of previously sorbed phosphorus on PBC and single–point phosphorus sorption indices.Crossref | GoogleScholarGoogle Scholar |
Brennan RF, Bolland MDA (2006) Soil and tissue tests to predict the sulphur requirements of canola in south-western Australia. Australian Journal of Experimental Agriculture 46, 1061–1068.
| Soil and tissue tests to predict the sulphur requirements of canola in south-western Australia.Crossref | GoogleScholarGoogle Scholar |
Burkitt LL, Moody PW, Gourley CJP, Hannah MC (2002) A simple phosphorus buffering index of Australian soils. Australian Journal of Soil Research 40, 497–513.
| A simple phosphorus buffering index of Australian soils.Crossref | GoogleScholarGoogle Scholar |
Chen W, Blair G, Scott J, Lefroy R (1999) Nitrogen and sulfur dynamic of contrasting grazed pastures. Australian Journal of Agricultural Research 50, 1381–1392.
| Nitrogen and sulfur dynamic of contrasting grazed pastures.Crossref | GoogleScholarGoogle Scholar |
Colwell JD (1963) The estimation of the phosphorus fertiliser requirements of wheat in southern New South Wales by soil analysis. Australian Journal of Experimental Agriculture and Animal Husbandry 3, 190–198.
| The estimation of the phosphorus fertiliser requirements of wheat in southern New South Wales by soil analysis.Crossref | GoogleScholarGoogle Scholar |
Day PR (1965) Particle fractionation and particle-size analysis. In ‘Methods of soil analysis Part 1’. (Eds CA Black, DD Evans, JL White, LE Ensminger, FE Clark) pp. 545–66. (Madison, WI, USA).
Gourley CJP, Weaver DM, Simpson RJ, Aarons SR, Hannah MM, Peverill KI (2019) The development and application of functions describing pasture yield responses to phosphorus, potassium and sulfur in Australia using meta-data analysis and derived soil-test calibration relationships. Crop and Pasture Science
| The development and application of functions describing pasture yield responses to phosphorus, potassium and sulfur in Australia using meta-data analysis and derived soil-test calibration relationships.Crossref | GoogleScholarGoogle Scholar |
Gustafsson JP, Akram M, Tiberg C (2015) Predicting sulphate adsorption/desorption in forest soils: evaluation of an extended Freundlich equation. Chemosphere 119, 83–89.
| Predicting sulphate adsorption/desorption in forest soils: evaluation of an extended Freundlich equation.Crossref | GoogleScholarGoogle Scholar | 24972174PubMed |
Isbell RF, National Committee on Soil and Terrain (2016) ‘The Australian soil classification.’ (CSIRO Publishing: Melbourne)
Johnson DW, Todd DE (1983) Relationships among iron, aluminium, carbon, and sulfate in a variety of forest soils. Soil Science Society of America Journal 47, 792–800.
| Relationships among iron, aluminium, carbon, and sulfate in a variety of forest soils.Crossref | GoogleScholarGoogle Scholar |
Lisle L, Gaudron J, Lefory R (1991) ‘Laboratory techniques for plant and soil analysis.’ (University of New England, Department of Agronomy and Soil Science: Armidale, NSW)
Neave HR (1978) ‘Statistics tables for mathematicians, engineers, economists and the behavioural and management sciences.’ (Allen & Unwin: London)
Ozanne PG, Shaw TC (1968) Advantages of the recently developed phosphate sorption test over older extractant methods for soil phosphate. In ‘Transactions of the 9th International Congress in Soil Science’. Adelaide. vol. 2. pp. 273–280. (International Society of Soil Science)
Peltovuori T (2007) Sorption of phosphate in field–moist and air-dry samples from four weakly developed cultivated soil profiles. European Journal of Soil Science 58, 8–17.
| Sorption of phosphate in field–moist and air-dry samples from four weakly developed cultivated soil profiles.Crossref | GoogleScholarGoogle Scholar |
Probert ME (1976) Studies on ‘available’ and isotopically exchangeable sulfur in some North Queensland soils. Plant and Soil 45, 461–475.
| Studies on ‘available’ and isotopically exchangeable sulfur in some North Queensland soils.Crossref | GoogleScholarGoogle Scholar |
Rayment GE, Higginson FR (2010) ‘Soil chemical methods – Australasia.’ (CSIRO Publishing: Melbourne)
Santoso D, Lefroy RDB, Blair GJ (1995) A Comparison of sulfur extractants for weathered acid soils. Australian Journal of Soil Research 33, 125–133.
| A Comparison of sulfur extractants for weathered acid soils.Crossref | GoogleScholarGoogle Scholar |
Selim HM, Gobrun GR, Guan X, Clake N (2004) Mobility of sulfate in forest soils: kinetic modelling. Journal of Environmental Quality 33, 488–495.
| Mobility of sulfate in forest soils: kinetic modelling.Crossref | GoogleScholarGoogle Scholar | 15074799PubMed |
Till AR (2010) ‘Sulphur and sustainable agriculture.’ 1st edn. (International Fertilizer Industry Association: Paris, France)
Till AR, McArthur GS, Rocks RL (1984). An automated procedure for the simultaneous determination of sulfur and phosphorus and radioactivity in biological samples. In ‘Proceedings of International Conference, Sulphur-84’, Calgary, Alberta, Canada, 3–6 June 1984. pp. 649–660. (Sulphur Development Institute of Canada (SUDIC): Calgary, Canada)
Walkley A, Black IA (1934) An examination of Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Science 37, 29–38.
| An examination of Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method.Crossref | GoogleScholarGoogle Scholar |
Walton K, Allen D (2004) Mehlich No. 3 soil test - the Western Australian experience. In ‘SuperSoil 2004: 3rd Australian New Zealand Soils Conference’, 5–9 December 2004, University of Sydney, Australia. (Ed B Singh). Available at www.regional.org.au/au/asssi/ [verified 15 July 2020].
Watkinson JH, Kear MJ (1994) High-performance ion chromatography measurement of sulfate in 20 mM phosphate extracts of soil. Communications in Soil Science and Plant Analysis 25, 1015–1033.
| High-performance ion chromatography measurement of sulfate in 20 mM phosphate extracts of soil.Crossref | GoogleScholarGoogle Scholar |
Watkinson JH, Kear MJ (1996) Sulfate and mineralisable organic sulfur in pastoral soils of New Zealand. I. A quasi-equilibrium between sulfate and mineralisable organic sulfur. Australian Journal of Soil Research 34, 385–403.
| Sulfate and mineralisable organic sulfur in pastoral soils of New Zealand. I. A quasi-equilibrium between sulfate and mineralisable organic sulfur.Crossref | GoogleScholarGoogle Scholar |
Wong MTF, Wittwer K (2009) Positive charge discovered across Western Australian wheatbelt soils challenges key soil and nitrogen management assumptions. Australian Journal of Soil Research 47, 127–135.
| Positive charge discovered across Western Australian wheatbelt soils challenges key soil and nitrogen management assumptions.Crossref | GoogleScholarGoogle Scholar |
Wong MTF, Webb MJ, Wittwer K (2013) Development of buffer methods and evaluation of pedotransfer functions to estimate pH buffer capacity of highly weathered soils. Soil Use and Management 29, 30–38.
| Development of buffer methods and evaluation of pedotransfer functions to estimate pH buffer capacity of highly weathered soils.Crossref | GoogleScholarGoogle Scholar |


 ), 30–40 (•), 40–50 (○) and 30–50 m (▪) for Site 3, 50–70 (⧫) and 70–90 cm (◊) with the fitted lines through the data points.
), 30–40 (•), 40–50 (○) and 30–50 m (▪) for Site 3, 50–70 (⧫) and 70–90 cm (◊) with the fitted lines through the data points.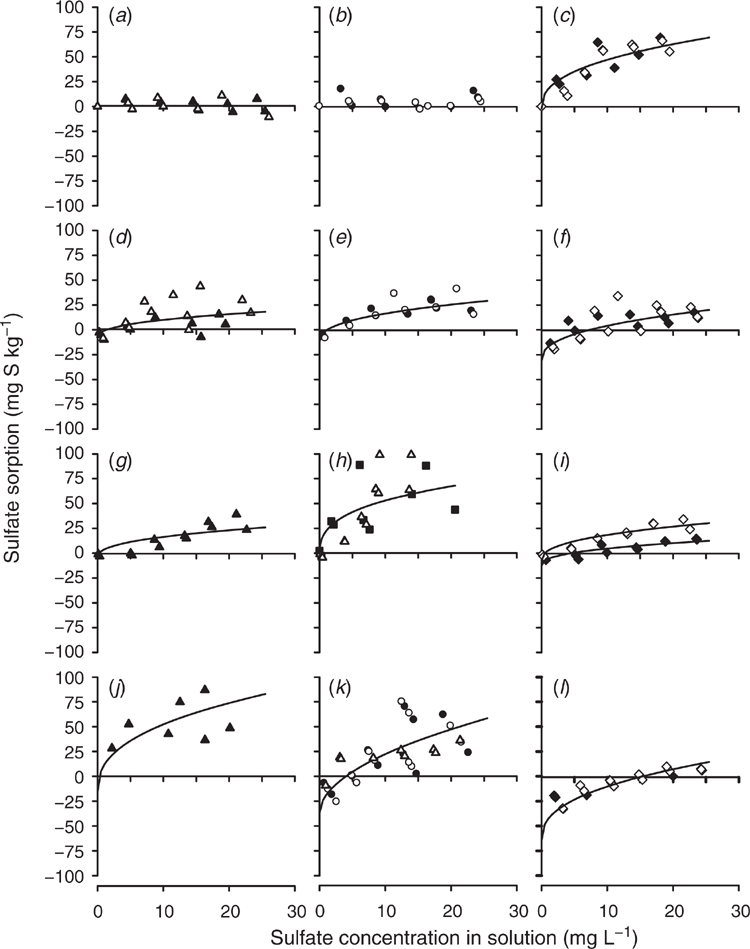
 ) and 0–10 cm (
) and 0–10 cm (