New parameterisation method for three-dimensional otolith surface images

Additional keywords: fast Fourier transforms, feature extraction, shape analysis, three-dimensional contour descriptors, three-dimensional shape parameterisation.

Fish otolith morphology has been widely used in the identification of stocks (Bird et al. 1986) and species (Schmidt 1969), phylogenetic reconstructions (Gaemers 1983), paleontological studies (Nolf 1985), food web analyses (Fitch and Brownell 1968), ecomorphological work (Lombarte and Fortuño 1992) and even sex identification and age estimation (Cardinale et al. 2004; Doering-Arjes et al. 2008). In all cases, adequate and complete information about otolith morphology is required. The Anàlisi de FORmes d’Otòlits (AFORO) website (http://aforo.cmima.csic.es, accessed 22 August 2015) is an open online catalogue of otolith images. It offers image analysis for automatic identification of fish species and populations using two-dimensional (2-D) closed contours representing otolith shape (Lombarte et al. 2006).

At present, the AFORO database contains more than 4600 images from 1440 Teleostean species, and its software tools have been used to generate an otolith atlas (Tuset et al. 2008; Sadighzadeh et al. 2012), morphological indices (Tuset et al. 2006), stock identifications (Capoccioni et al. 2011; Tuset et al. 2013; Sadighzadeh et al. 2014a), automatic species identifications (Parisi-Baradad et al. 2005, 2010; Tuset et al. 2012), ecomorphological comparisons (Cruz and Lombarte 2004; Lombarte and Cruz 2007; Sadighzadeh et al. 2014b), archaeological studies (Harrison 2009) and, most especially, prey identifications (Veiga et al. 2011; Neves et al. 2012; Otálora-Ardila et al. 2013; Rosas-Luis et al. 2014).

Attempts to develop three-dimensional (3-D) morphological studies of otoliths started with the use of X-ray microtomographies (Hamrin et al. 1999) for ageing fish and were followed by anatomical studies of the inner ear (Ramcharitar et al. 2004; Schulz-Mirbach et al. 2011, 2013; Kéver et al. 2014). We are engaged in a Spanish National Research Program project titled AFORO3-D, the main objective of which is to create 3-D morphological descriptors for whole otoliths and to provide more effective analysis and classification tools. The possibility of obtaining 3-D pictures will offer more reliability for the identification of otoliths by including external side and internal side (sulcus acusticus) curvature descriptions with high taxonomic value (Smale et al. 1995; Torres et al. 2000; Campana 2004; Tuset et al. 2008; Sadighzadeh et al. 2012). Most importantly, the software we develop will allow production and study of virtual 3-D models without having the otoliths actually in hand (Gauldie 1988; Popper and Fay 1993; Schulz-Mirbach et al. 2013). To that end, the University of Girona (Girona, Spain; Computer Vision and Robotics Research Group, ViCOROB) and AQSENSE Co. (see http://www.aqsense.com/, accessed 27 August 2015) have developed a purpose-built, single-camera, 3-D scanner prototype based on projected light-emitting diode (LED) light capable of digitising the shapes of otoliths ranging in size from 1 mm to a few centimetres. The objective of the present study was to create 3-D morphological descriptors of whole otoliths for analysis, automatic classification and automatic retrieval from an image database. Introducing a shape into a computer system in order to find the most similar shape already in the database or to fit a new 3-D natural object into a classification by comparing it with all the shapes in the database is very time consuming because of the huge amount of information involved for each object; it becomes progressively more difficult as the size of the database increases.

Our study of 3-D methods has focussed on otoliths of the family Scienidae (Percifomes). The sciaenids (drums or croakers) are characterised by their specialised acoustic communication. Their ability to produce sounds has long been known, as their English common names suggest, and it is part of their reproductive behaviour (Luczkovich et al. 1999; Ramcharitar et al. 2001). Their sagittae are characterised by their relatively large size (Cruz and Lombarte 2004), compared to the average size of fish otoliths, with strong development of the external side (Nolf 2013; Ramcharitar et al. 2004) and a specialised sulcus acusticus (Volpedo and Echevarría 2000; Monteiro et al. 2005; Ramcharitar et al. 2006; Tuset et al. 2008; Lin and Chang 2012).

In order to obtain 3-D otolith surface images, samples from three species of Scienidae (Argyrosomus regius, Sciaena umbra and Umbrina cirrosa) were digitised, following a protocol similar to that used to capture the images in AFORO (Lombarte et al. 2006; Tuset et al. 2008) and also used by palaeontologists (Gaemers 1983; Nolf 1985; Schwarzhans 1996; Reichenbacher et al. 2007). Thus, all specimens share the same positions and orientations in the Cartesian coordinates after being digitised. In biological terms, the x-axis corresponds to the rostrum–postrostrum axis of the otolith. The y-axis corresponds to the otolith’s dorso–ventral axis. The z-axis is placed midway between the internal and external side extremes of the otolith and represents the width of the sagitta. Application of that protocol makes it unnecessary to determine descriptors invariant to rotations. The only invariance we need to consider with regard to scale, and that normalisation requires a scale factor. The otolith shape is scaled so that its length along the y-axis is 2 units (Fig. 1); therefore, for all the 3-D otolith shapes, this axis in our coordinate system extends from the point (0,–1,0) to (0,1,0).

Fig. 1.  Representation of the left sagittal otolith position of Argyrosomus regius according to the Cartesian coordinates of the scanning protocol.

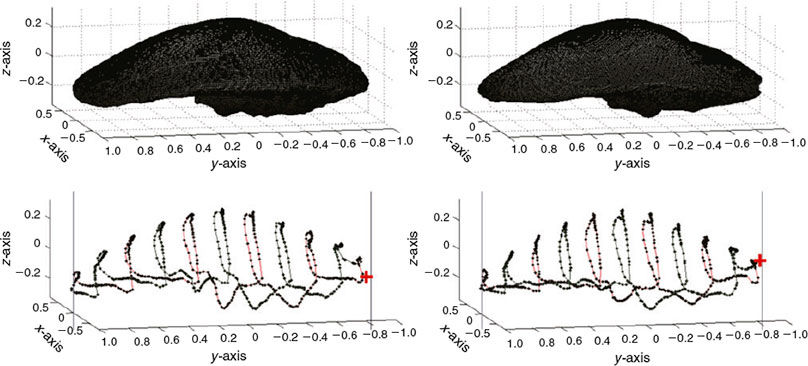
The otolith digitisation process involves scanning all otolith sides and the partial scans are joined to represent the entire 3-D object. The final result is a file containing a cloud of points representing the otolith’s shape. Specialised software and a technical expert are necessary for these tasks, so they are expensive and time consuming. Furthermore, the scanner system is limited by otolith size and only big sagittae, like those of the sciaenids, provide optimal results. The cloud of points representing an otolith surface can be seen in Fig. 2.

Fig. 2.  Cloud-of-points on an otolith surface represented in Cartesian coordinates after its digitisation according to the scanning protocol. The otolith represented belongs to Umbrina cirrosa.

The proposed method can be broken down into two parts. The first consists of a subsampling process that generates a set of points that can always be interpreted as on a closed curve in the 3-D space. This process preserves important morphological information, but the number of points is markedly reduced. The second part consists of computing the discrete Fourier transform (DFT) on each of the 3-D coordinates. Periodic functions, such as those obtained from closed curves, can be expanded into a Fourier decomposition. This step achieves greater information compression by selecting a reduced set of the Fourier coefficients to represent the shape.

The subsampling process is driven by an auxiliary curve composed of two paths (forward and backward) that depend on two main parameters, P and L, selected for a particular application: P is the even number of points retained in the subsample and L is the number of loops that each of the two paths takes. The forward and backward paths of the auxiliary curve that guide the subsampling process are shown on the left side of Fig. 3. Each point on the auxiliary curve corresponds to a point on the otolith surface. The forward path is described by half the points (cx_n,cy_n,cz_n) and is shown in green on the left in Fig. 3. Those points are obtained using the following equations:

The points of the backward path are represented in red on the right in Fig. 3 and are obtained using the following equations:

The constant A can be taken as 1 (in practice, a larger number is used). Note that by construction the coordinate y goes from –1 to 1 and comes back from 1 to –1 in regular steps. So, the proposed subsampling process occurs by increments and decrements (forward and backward paths) along the y-axis, following the cy_n points. On the right side of Fig. 3, there is a partial representation of the lines that go from the centre of the otolith mass to the points on the auxiliary curves.

Fig. 3.  The left-hand panel shows the auxiliary curves forward (from 1 to –1 on the y-axis, 1 on the z-axis) and backward (from 1 to –1 on the y-axis, –1 on the z-axis) used to guide the subsampling process. In this example, the number of loops L = 3. The right-hand panel shows a representation of the first 38 auxiliary straight lines.

For each of the auxiliary curve points, a set of points is selected on the surface that belongs to the interval cy_n – 2/P < cy_n ≤ cy_n + 2/P. Those points correspond to a slice orthogonal to the y-axis of width 4/P. If coordinates x and z of those selected points are represented on the x–z plane, a figure similar to a section of the shape is drawn. This idea is illustrated for a synthetic shape in Fig. 4. Next, the coordinates mx_n and mz_n of the centre of mass of each slice of points are computed to obtain the centre of the section at the point cy_n (mx_n,cy_n,mz_n). For every cy_n point, the straight line from the centre of mass to the point on the auxiliary curve and orthogonal to the y-axis is computed using the coordinates of those points. That line guides the selection-of-point process. This idea is also represented in the illustration in Fig. 4 in which, for a given cy_n, a representation of a set of points of a section appears together with the auxiliary line. In the x–z planes, the straight line equations are expressed in continuous form by the following:

The last step consists of selecting the point on the otolith surface that intersects with that line. In practice, because we have a discretised surface, there is no point on that surface that matches perfectly with the line, so different approaches could be considered. One is to select the discrete point on the surface closest to the line; another is to obtain an interpolation given a set of candidates. Both approaches begin with selecting a reduced set of points by narrowing the area around the line and analysing the points of the otolith included inside. In the first case, the region is tapered until it contains only a single point. In the second case, the process of narrowing the space around the line is stopped with several points inside and the point of interest is computed from them. With the original 3-D high-resolution otolith shapes used in our work, all these approaches perform very similarly. Fig. 5 is a representation of the normalised otolith cloud of points together with the auxiliary curve that guides the subsampling.

Fig. 4.  Illustration of the subsampling process. For a given y_n, the set of points is shown belonging to a slice, together with the auxiliary line. The selected point comes from the intersection of the line with the section boundary. This section was obtained from a synthetic shape.

Fig. 5.  Representation of the normalised cloud of points together with the auxiliary curve.

The subsampling process finishes once all the P points of the auxiliary curve have been processed, obtaining P points on the otolith surface representative of otolith shape. Fig. 6 shows the partial result of processing the forward (upper) and backward (bottom) paths when P = 1600 and L = 20; and the complete result for the same otolith is shown in Fig. 7.

Fig. 6.  Partial results of processing the forward (top) and backward (bottom) paths of an otolith surface when the parameters of the auxiliary curve are P = 1600 (number of points retained) and L = 20 (number of loops). The consecutive points are joined by continuous lines.

Fig. 7.  Result of performing subsampling on the cloud of points from the Umbrina cirrosa otolith represented in Fig. 2 when the number of points retained P = 1600 and the number of loops L = 20. The picture was completed by joining the forward and backward paths of Figs 5 and 6.

Fig. 8 shows plots of the coordinates x, y and z for the set of P = 1600 points that are represented in 3-D in Fig. 7. The x, y and z plots can be interpreted as the fundamental period of a periodic function. Note that the graph in the middle, once the number of P points is chosen, is, by construction, always the same. Because we know a priori that it contains no information, the y coordinate can be discarded in the next parameterisation step. Furthermore, notice that the y coordinate is always the same for all shapes. To provide an idea of the information reduction achieved by the down-sampling process, the shape represented with 150 000 real numbers in the present example could be represented with only 3200 real numbers: those required to represent x and z coordinates of the closed curve. Comparing the information provided by the original shape in Fig. 2 with the selection of points shown in Fig. 7, the reduction of points can be appreciated. However, Fig. 7 retains the most important morphological information from the otolith shape.

Fig. 8.  Representation of the coordinates of the three-dimensional closed curve given in Fig. 7. The graphs represent a periodical function derived from ‘wrapping’ an otolith. In the representation the function has been subsampled using P = 1600 points. The x coordinate appears at the top, the y coordinate is in the centre and the z coordinate is shown at the bottom.

The subsampling method just presented has some particular characteristics. Samples of the otolith surface are taken at regular increments along the y-axis, thus the velocity of the closed curve sampling is constant. This approach differs from that described by Kuhl and Giardina (1982), which imposes constant sampling velocities around the closed curve for all of its x, y and z components, not just for one (y) as described herein. The advantage of our approach compared with that of Kuhl and Giardina (1982) is that our approach always uses the same number of points to obtain a closed curve from a scale-normalised shape. In our approach, the samples are taken at regular angular increments around the auxiliary curve; however, the otolith sections are not regular and can differ considerably in size, meaning that parts of the otolith are represented with different densities of points, with more points in the small sections, usually located at the otolith extremes. The considerable advantage of our approach is that all the closed curves obtained are described with the same number of points (P) regardless of the shape they describe. The user can choose the parameter P depending on the quality of the digital data or according to a given application.

With our subsampling process, a set of P representative points is selected from the original surface. Their spatial relationships are described with those points. They can also be described by the coefficients of a Fourier expansion derived by a DFT. The fast Fourier transform (FFT) algorithm applied to the P representative points provides a reduced set of parameters with which to reconstruct the closed contour of the objects. This will be illustrated for a single coordinate x and can be extended in a similar way to the coordinate z.

Consider the P points (x_n,y_n,z_n) of the 3-D closed curve and take without loss of generality only the coordinate x_n, where n = 0, 1,…, P – 1. By applying the DFT on x_n, the DFT coefficient X_k is computed by:

and, therefore, the original x_n can be written as X_k using the inverse DFT (IDFT) as follows:

Of course, with all the DFT coefficients X_k, the reconstruction x_n where n = 0, 1,…, P – 1 is perfect. Now, let us take advantage of some DFT properties. Because we always deal with x_n samples that are real, from Eqn 4 it is easy to see the well-known property of DFT coefficients (Proakis and Manolakis 1996):

where the superindex asterisk (*) in Eqn 6 stands for the complex conjugate operation. This result means that only the first half of complex coefficients bring information and the other half are redundant, because they can be obtained from the first half. Now, let us split Eqn 5 into four parts:

Then, analysing the last term of Eqn 7, rearranging the index of its summation from the last element to the first and using Eqn 6, from simple algebra of complex numbers, we have:

Then, considering this term together with the second term in Eqn 7 and taking into account that one is the complex conjugate of the other, we can rewrite Eqn 8 as follows:

Eqn 9 uses the result that the addition of a complex number with its complex conjugate gives twice its real part. Therefore, Eqn 5 becomes:

Note than (–1)ⁿ comes from cos when k = P/2. Then, if we consider the discrete Fourier expansion of the coordinate x_n, (n = 0, 1, ..., P – 1) provided by the coefficients a_k and b_k in the form:

we can establish from Eqn 10 the relationship between real coefficients a_k and b_k with the complex DFT coefficients X_k as follows:

The coefficients X_k can be computed very quickly from the P samples of x_n using the FFT algorithm, and similarly the x_n samples can be recovered very quickly from X_k using the inverse fast Fourier transform (IFFT) algorithm. From only a reduced set of coefficients of X_k we can reconstruct the P samples of x_n, , where Q + 1 is the number of DFT coefficients employed in the reconstruction, and easily evaluate the appropriate number of those coefficients required to properly approximate the closed curve. So, to obtain the P samples of the reconstruction from the first Q+1 DFT coefficients of X_k, (X_0,…_, X_Q) and keeping Q < P/2, we must construct the following vector of length P and take its IFFT in the following way:

The same applies for the z coordinate:

Here, Z_k is the DFT coefficient of z_n. Then, the points of the 3-D closed curve reconstruction will take the form () when n = 0, 1,…, P – 1. Note that two real numbers are required for a pair of coefficients a_k and b_k, the same as required for X_k coefficients that are complex, so the use of both forms is equivalent, as was shown in Eqn 12. If reconstruction of shapes from a subset of coefficients is needed, then the use of DFT coefficients in Eqns 13 or 14 is preferable because the P selected points of 3-D closed curves can be recovered by performing only two one-dimensional (1-D) IFFT algorithms, which is achieved at computational cost of order of P × log2(P), P being the number of points (Van Loan 1992; Proakis and Manolakis 1996).

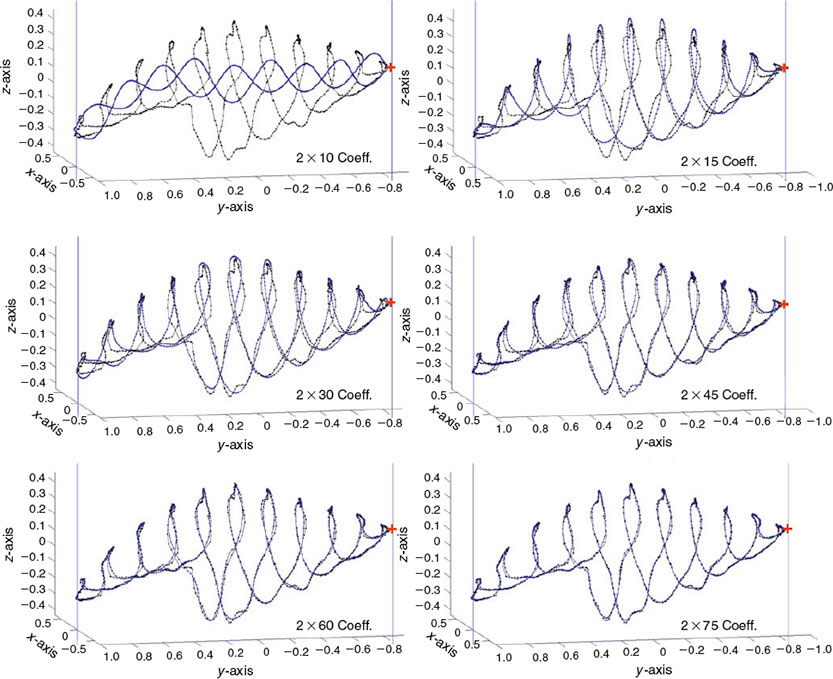
In order to show some reconstruction results, let us consider the shape shown in Fig. 2, now subsampled using P = 800 and L = 5. The set of the closed curve points requires 3 × 800 = 2400 real numbers to be represented in a 3-D space (the original cloud of points is defined by 150 000 real numbers). Reconstructions (the most smoothed curves) are shown in Fig. 9, together with the true points (which are repeated in all graphics) using 10 × 2, 15 × 2, 30 × 2, 45 × 2, 60 × 2 and 75 × 2 complex DFT coefficients, which represent 40, 60, 120, 180, 240 and 300 real numbers respectively.

Fig. 9.  Reconstructions of the closed curve of points on the Umbrina cirrosa otolith when the number of points retained P = 800 and the number of loops L = 5. In all figures, the true points are shown in black and the reconstructions have been done with 10 × 2, 15 × 2, 30 × 2, 45 × 2, 60 × 2 and 75 × 2 complex discrete Fourier transform (DFT) coefficients.

It can be appreciated (Fig. 9) that reconstructions using more than 100 coefficients start to become very close to the original information. Those numbers could also be taken as a reference of the power compression achieved by this parameterisation. For instance, in the case shown, when 120 real numbers (30 × 2) are used, the information compression factor is greater than 1000.

To validate the present 3-D parameterisation method by solving an automatic classification problem in a practical context, we have performed a set of experiments. The first task was the training of different classification models based on those parameters. The first point to deal with was the limitations of working with a small dataset of only fourteen 3-D otolith images. To manage the data for training and testing the models, we used a cross-validation strategy because, for small datasets, it gives a good estimate of the predictive accuracy of the final trained model. Cross-validation requires multiple fits but makes efficient use of all the data. So, in all experiments, we partitioned the data into five divisions or ‘folds.’ Each fold is taken in turn for testing. A model is trained for each fold using all the data outside the fold and then the performance of each model is tested using the data inside the fold. Finally, we calculated the average test error over all the folds. As in AFORO project (Parisi-Baradad et al. 2010), we obtained good results with k-Nearest Neighbour (k-NN) classifications, so we decided to use those as basis of comparison. All the comparitor classifications were done using the algorithms provided by the Statistics and Machine Learning App of Matlab (MathWorks, see http://es.mathworks.com/products/statistics/?s_tid=hp_fp_list, accessed 27 August 2015).

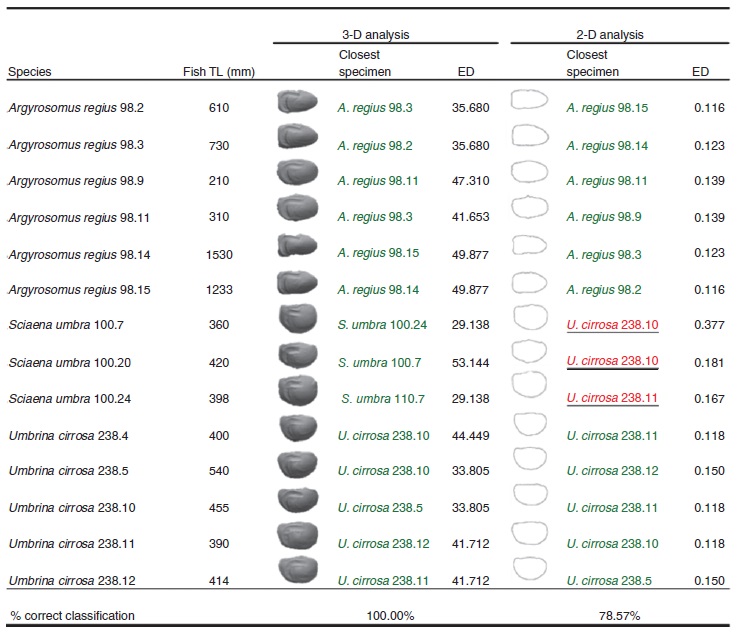
Comparisons of the newly paramaterised 3-D contour analyses calculated in the present study with those from the 2-D AFORO system (Parisi-Baradad et al. 2010) were performed in terms of correct classification rate. Both parameterisations were obtained from a set of 14 otoliths belonging to the AFORO collection.

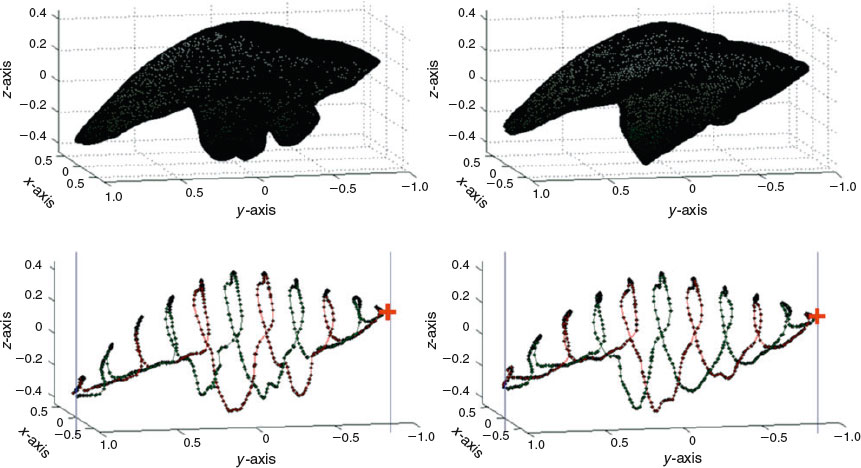
In order to provide some descriptive information first, in this section we show a comparison between pairs of otoliths of the same species together with their closed curves obtained with L = 5 and P = 800. This information is represented graphically for A. regius (Fig. 10), S. umbra (Fig. 11) and U. cirrosa (Fig. 12). For all three species, the closed curve captures important morphological information about the original shape, and the information is more similar between otoliths from the same species than between those from different species (Figs 13, 14). In addition, the selection of a reduced set of coefficients produces a smoothing of the high-frequency information, which mostly derives from individual variability, so that consequently there is an increase of the similarity statistics between conspecific individuals.

Fig. 10.  Sagittal otolith of Argyrosomus regius from 110- and 140-cm specimens when the number of points retained P = 800 and the number of loops L = 5.

Fig. 11.  Sagittal otolith of Sciaena umbra from 36- and 40-cm specimens when the number of points retained P = 800 and the number of loops L = 5.

Fig. 12.  Sagitta otolith of Umbrina cirrosa from 39- and 41-cm specimens when the number of points retained P = 800 and the number of loops L = 5.

Fig. 13.  Scatterplot of a parameterisation composed of only two real coefficients or features (the parts of the first and the fifth fast Fourier transformation (FFT) of the x closed curve coordinate obtained with the number of loops L = 3). From that parameterisation, a system able to correctly classify the whole dataset was developed.

Fig. 14.  Scatterplot of a parameterisation composed of only three real coefficients or features obtained by applying the fast Fourier transformation (FFT) on the x closed curve coordinate obtained with the number of loops L = 1. From that parameterisation, a system able to correctly classify the whole dataset was also developed.

To explore the effect that the parameter L, half the number of loops in the closed curve, has on the automatic classification success rate, we developed the following experiment. For each value of L going from 1 to 6 and for all 3-D shapes in the database, we computed a particular parameterisation by taking the first 10 Fourier coefficients of both x and z closed contour coordinates to have 40 real coefficients per shape (formed by their real and imaginary parts). For every value of L, a parameterisation was obtained and a classification model was computed and tested. Very robust classification results of more than 92% correct were obtained in all cases. The next experiment was to do a feature selection process for each L in order to get the smallest selection of coefficients (among those 40) required to achieve, or even improve, the classification results. The feature selection process yielded very promising results. For some values of L, only two real coefficients (of our 3-D parameterisation) were required to achieve an estimated classification rate of 100%. Those results were obtained using the same cross-validation protocol and applying k-NN classifiers. Fig. 13 shows a scatterplot of the parameterisation composed only by two features, the real parts of the first and the fifth Fourier coefficients (computed, in that case, by applying the FFT on the x closed curve coordinate originated with L = 3). The parameterisation identified as Parameterisation 1, shows that the first and fifth FFT coefficients for each species cluster together when plotted as variables. A more general and powerful result shows that, for each value of L in the explored range 1–6, there are many different combinations of only three real coefficients that allow us to train and test a perfect classification model able to achieve a correct classification rate of 100%. Fig. 14 shows one of these three-parameter combinations, in this case also obtained from the FFT of the x coordinate given by L = 1.

Comparing both analytical methods (the 2-D AFORO v. the proposed 3-D methods; Fig. 15), the results of 3-D analysis give a greater percentage, reaching 100% correctly classified specimens compared with 78% with the previous 2-D analysis. The better results of 3-D analyses are related to including 3-D structures such as the sulcus acusticus and the external dome. In the case of S. umbra, the species that showed very poor results in 2-D analyses (0% of correct classifications), the 3-D analysis detects a squared and shorter cauda of the sulcus acusticus and less-developed external dome than of the other two sciaenid species compared in the analyses. For a wide range of parameter L, a very small set of FFT parameters is able to capture 3-D information relevant to classification of fish species from their otoliths.

Fig. 15.  Comparison of classifications from three-dimensional (3-D; new) and two-dimensional (2-D; Anàlisi de FORmes d’Otòlits (AFORO)) parameterisations from three species of Mediterranean Sciaenidae. Underlined, misidentified specimens; ED, Euclidean distance; TL, fish total body length (mm).

We have presented herein a new parameterisation method to represent 3-D otolith shapes that exhibits very good information compaction properties. The method deals with 3-D objects using 1-D transformations, so that operations required for the parameterisation and reconstruction are performed very fast, especially compared with methods that use higher-dimensional transformations (Van Loan 1992) or more complex and time-consuming decompositions, including spherical harmonics (Tanaka et al. 1993; Ertürk and Dennis 1997), two-variable Fourier descriptors (Wu and Sheu 1998), harmonic maps (Brett and Taylor 2000), spherical wavelets (Greenshields 2001), local geometric properties (Caunce and Taylor 2001), modelling from curves (Tubić et al. 2004) or geodesic analysis (Dam et al. 2008).

The proposed parameterisation method, in addition to its ability to compact information, deals with objects of different sizes with different numbers and heterogeneous densities of shape-defining points in different regions. The interesting property of this parameterisation is that, from a small selection of the coefficients, it is always possible to reconstruct the x,y,z coordinates. Thus, the users can maintain intuition about the object’s shape, providing a qualitative way to evaluate the information preserved and discarded when a selection of coefficients is considered. The best aspect of our approach is that the parameterisation and reconstruction of 3-D objects only requires two 1-D, fast transformations: the FFT in the parameterisation step and the IFFT in the reconstruction. Comparing this with previous 3-D otolith descriptions (Hamrin et al. 1999; Ramcharitar et al. 2004; Schulz-Mirbach et al. 2011, 2013), the process of otolith digitalisation developed under the AFORO3-D framework obtained very good 3-D representations.

There is an important drawback to this method. The imaging scanner and post-production image require a lot of human supervision, making the process slow and expensive. However, fast developments in 3-D technology are likely to produce faster and lower cost imaging in the very near future (Zitek et al. 2014). The new outputs can be analysed using our 3-D methods. Despite the present limitation of having very few images in the 3-D database, our parameterisation approach seems promising for automatic retrieval and classification. For the small sets of images available, it works perfectly when the available 2-D methods fail.

The parameterisation method must be proven with a bigger database in order to identify the best values of P (number of points per curve) and L (number of loops). The results obtained to date show that values of L from 1 to 6 are appropriate to parameterise the shapes. Those values of L seem to provide a balance between otolith shape preservation and robustness against small rotations that can appear in the digitisation protocol. It is known that the sulcus acusticus provides important information to identify species. The combined matching of 2-D outlines, curvatures and sulcus features (Torres et al. 2000; Monteiro et al. 2005; Sadighzadeh et al. 2012; Nolf 2013) seems to be a way to improve automatic classification results in large datasets (Parisi-Baradad et al. 2010). The proposed method provides an elegant and efficient way to do this in a simple 3-D parameterisation.