Computational Investigation of Adsorptive Removal of Pb2+ from Water by the UiO-66 Metal–Organic Framework: Comparison of Adsorption Sites on Defects and Functionalised Linkers
Claudia S. Cox A , Valeria Cossich Galicia B and Martina Lessio A C
A C
A School of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia.
B Columbia College, Columbia University, New York, NY 10027, USA.
C Corresponding author. Email: martina.lessio@unsw.edu.au

Dr Martina Lessio obtained her undergraduate degree in chemistry from the University of Torino (Italy). She was awarded a Ph.D. in chemistry in 2017 from Princeton University (USA), working under the mentorship of Professor Emily Carter on computational modelling of catalysts for CO2 conversion. After her Ph.D., Martina became a Columbia Science Fellow at Columbia University (USA), where she was a Lecturer and Research Fellow collaborating with the group of Professor David Reichman. In 2019, Martina was awarded a University of Sydney Fellowship by the University of Sydney (Australia) to investigate metal-organic frameworks for water purification applications. In 2020, Martina established her own research group in the School of Chemistry at UNSW (Australia) as a Scientia Lecturer. Her group uses computational methods to investigate molecules and materials for sustainability applications. |
Australian Journal of Chemistry 75(2) 142-154 https://doi.org/10.1071/CH21139
Submitted: 10 June 2021 Accepted: 5 August 2021 Published: 3 September 2021
Journal Compilation © CSIRO 2022 Open Access CC BY
Abstract
Adsorption using metal–organic frameworks (MOFs) such as UiO-66 has shown great promise in remediating water sources contaminated with toxic heavy metals such as Pb2+, but detailed information about the adsorption process remains limited. In this article, we gained mechanistic insights into Pb2+ adsorption using both functionalised and defective UiO-66 by performing density functional theory calculations using cluster models. Our benchmarked approach led to a computational model of solvated Pb2+ (a hemidirected Pb(H2O)62+ complex) fully consistent with experimental reports. The analysis of Pb2+ adsorption using functionalised UiO-66 determined that factors such as electrostatic attraction, chelation, and limited constraints on the Pb2+ coordination geometry lead to enhanced binding affinity. For these reasons, UiO-66-COO– was identified as the most promising functionalised MOF, consistent with experimental literature. We additionally explored a novel aspect of Pb2+ adsorption by UiO-66: the role of missing linker defects that often characterise this MOF. We found that the defects expected to form in an aqueous environment can act as excellent adsorption sites for Pb2+ and the preferred adsorption geometry is again determined by electrostatic attraction, chelation, and constraints on the Pb2+ coordination geometry. Overall, we conclude that functional groups and defect sites can both contribute to Pb2+ adsorption and our study provides crucial design principles for improving the UiO-66 MOF performance in toxic Pb2+ removal from water.
Keywords: lead, adsorption, water purification, UiO-66, metal–organic frameworks, computational chemistry, heavy metals, defects.
Introduction
As a bivalent cation, lead has diverse and extremely detrimental impacts on the body in all quantities.[1,2] The high toxicity of Pb2+ is attributed to this metal’s mimicry of calcium in the body and subsequent ability to disrupt enzymes, resulting in protein malfunction that interferes significantly with the processes of the central nervous system. Water poisoning with lead remains a modern and global issue.[3] Dangerous elevated blood lead levels that lead to developmental delays in children are found across the world, including countries such as Australia, Canada, and the US.[4–7] Identifying an efficient way to remove this toxic heavy metal from water is imperative. This urgent need is heightened by the fact that water pollution is rising with increasing wastewater discharge from the agriculture industry, urbanisation, and other practices.[8] Water purification techniques include chemical, physical, and biological means such as filtration, electrodialysis, ion exchange, adsorption, and membrane bioreactors.[8] Adsorption techniques represent a particularly promising option as they are easy to operate, typically inexpensive, and do not produce as much sludge or other toxic pollutants as other methods.[9] As a consequence, adsorption today is an effective, simple process that has become one of the most common ways to purify water sources.[8] The efficacy and selectivity of the absorbent materials can be manipulated by changing pore size, surface area, and functional groups.[10] As an example, adsorption of Pb2+ ions from aqueous solutions has been successfully achieved using carbon nanotubes as well as other carbonaceous materials functionalised with oxygen and nitrogen.[11,12]
Metal–organic frameworks (MOFs) are one class of materials that has proven success in water purification applications, often demonstrating adsorption capacities for toxic heavy metals greater than those of conventional adsorbents[13,14] such as modified clays (78.74 mg g−1 reported Pb2+ adsorption capacity for tripolyphosphate-modified kaolinite clay[15]) and activated carbon (Pb2+ adsorption capacity of 17.5 mg g−1[16]). MOFs are characterised by unprecedented porosity and surface area, explaining their excellent performance in separations and water purification applications. Significant research effort has been dedicated to a subclass of MOFs – UiO-66 and its functionalised derivatives – for the removal of a variety of heavy metals from water; we direct the interested reader to a recent review on this topic.[17] UiO-66 is a highly porous and water-stable MOF composed of Zr6(OH)4(O)4 nodes connected by 1,4-benzenedicarboxylic acid (BDC) linkers.[18,19] In addition to the pristine form of UiO-66, stable structures with functionalised BDC linkers as well as defects consisting of missing linkers and nodes have been synthesised. UiO-66 with defects produced by missing linkers requires other groups to saturate the undercoordinated Zr sites and balance charge; these capping ligands can be monocarboxylic acids used in some synthesis procedures[20] or hydroxide anions and water molecules ubiquitously present in aqueous solution.[21] Interestingly, these functionalised and defective MOFs often have adsorption capacities, catalytic performance, and gas separation capabilities superior to that of pristine UiO-66.[20]
UiO-66 with functionalised linkers has shown significant aptitude for the adsorption of Pb2+ from water sources and recent studies suggest that functional groups, pore size, and defects may play a significant role in influencing its adsorption capacity. Wang et al. obtained UiO-66–NH2 using a microwave-promoted synthesis technique and found a maximum Pb2+ adsorption capacity of 116.74 mg g−1.[22] Saleem et al. conducted post-synthetic modification in order to replace the amine functional group on UiO-66–NH2 with a range of sulfur- and nitrogen-containing groups such as NCO, NCS, and NHCSNHCH3.[23] The latter bulky functional group led to a maximum adsorption capacity of 232 mg g−1. A significant adsorption capacity of 420 mg g−1 by UiO-66–(COOH)2 (i.e. two –COOH groups present on each BDC linker) at pH 6 was reported by Zhao et al.[24] The authors propose that this outstanding adsorption capacity is due to electrostatic attraction between Pb2+ and the deprotonated –COO– groups, which are likely to dominate at pH 6. Using the more functionalised UiO-66–(COOH)4 led to less Pb2+ adsorption,[24] potentially owing to steric effects and reduced pore size, which then limits the diffusion of ions through the material. This indicates that there is a balance that needs to be reached for maximum Pb2+ adsorption: increasing the number of functional groups increases the number of binding sites but decreases the pore size, thus limiting access to more binding sites. A separate study by Morcos et al. found UiO-67 (an analogue of UiO-66 with larger apertures and pores) to have increased adsorption capacity relative to UiO-66, highlighting the importance of pore size as a factor for Pb2+ adsorption.[25]
A relatively unexplored factor affecting adsorption performance is the presence of defects. A recent study using UiO-66–NH2 found that an increased concentration of defects due to missing linkers connecting the metal oxide nodes led to enhanced Pb2+ adsorption.[26] Defects might enhance adsorption performance simply by facilitating diffusion through the MOF but it is also possible that they might play an active role in adsorption. For instance, in another recent study, the defect sites created at the metal oxide nodes by absent linkers were directly functionalised to be capped by thiourea and amidinothiourea groups; these functional groups adsorbed Pb2+ with a maximum adsorption capacity of 245.8 mg g−1.[25] Defects spontaneously formed under experimental conditions may also act as adsorption sites. Previous reports suggest that in aqueous conditions, the most common type of defect likely to form consists of a hydroxide and water group capping the undercoordinated Zr atoms.[21,27] These capping groups could potentially coordinate Pb2+. However, it remains difficult to establish the effect of defects conclusively simply based on experimental adsorption capacities of samples reported in the literature owing to the many confounding factors that influence defect concentration. For example, many synthesis steps that are not directly targeted towards defect engineering can lead to increased defect concentration, such as washing the MOF with solvent[28] or synthesising UiO-66 with functionalised and bulky linkers[29,30] (e.g. the precursors to UiO-66–(COOH)2 and UiO-66–(COOH)4 MOFs previously mentioned[24]), consequently influencing adsorption capacity.
Overall, the recent experimental work in the field indicates that both defective metal oxide nodes with unsaturated metal sites capped by nucleophilic groups as well as functionalised linkers could play a complementary role in Pb2+ adsorption. This emphasises the need for more research efforts directed at untangling the multitude of factors that influence Pb2+ adsorption. This article seeks to address this gap by comparing the viability of linker functional groups and node defect sites as Pb2+ adsorption sites on UiO-66 using a robust computational model centred on density functional theory (DFT) simulations with cluster models. We first examine the coordination geometry of solvated Pb2+ generated by a range of computational methods and benchmark our computational method against relevant experimental results. Additionally, we explore the preferred coordination number of solvated Pb2+ by considering the energetics of sequential water addition, solvation energies, and Pb–O bond lengths; we compare our findings with previous literature on Pb2+ hydration. This is a crucial step to ensure the accuracy of our computational model. We then employ our model of solvated Pb2+ to determine the energetics of adsorption onto a range of functionalised linkers and compare the results with non-functionalised UiO-66. To complement this study, we also investigate how the adsorption thermodynamics is affected by partial desolvation, which may be required for solvated Pb2+ to pass through the UiO-66 apertures and diffuse through the MOF. Finally, we examine adsorption onto UiO-66 defective nodes and compare the reaction free energies (ΔGs) of adsorption with those obtained for the adsorption sites on the functionalised linkers. Out of a wide range of potential defect sites present in UiO-66 depending on synthesis conditions,[19,31] we chose to focus our analysis on the defect site with a hydroxide and water molecule bound to the open Zr metal sites created by the missing BDC linker (i.e. UiO-66–[OH–/H2O] adsorption site). We selected this site for several reasons, including its ubiquity in aqueous conditions[21] and superior stability compared with other hydroxide and water containing defect sites,[27] as well as the presence of several oxygen atoms available to coordinate the Pb2+ cation. We conclude by discussing the key aspects that lead to more favourable adsorption energies based on our analysis to help disentangle the complex interplay of factors that could lead to enhanced Pb2+ adsorption. From this, we determine general design principles for the fine-tuning of UiO-66 and other MOFs for Pb2+ removal.
Results and Discussion
In order to accurately model Pb2+ interactions with UiO-66, it is important to first determine how the cation prefers to be solvated in aqueous solution. The solvation shell of Pb2+ has been studied extensively both experimentally and computationally in previous literature with the main aims of determining the coordination number of Pb2+ and determining the orientation of the solvating water molecules around the cation. In the following, we first give an overview of these results from the literature and then compare them with our own computational findings to benchmark our model.
There are two relevant solvation geometries for Pb2+ (Fig. 1). Holodirected geometries involve a symmetric organisation of ligands around the central Pb2+ atom (Fig. 1a), due to the stereochemically inactive 6s lone pair. However, it is possible for there to be a visible void in the structure, leading to a hemidirected geometry (Fig. 1b).[32] It has been suggested in the literature that this is due to the hybridisation of the inert 6s orbital with the 6p orbitals to form a stereochemically active lone pair.[33] Alternatively, it has been proposed that the structural distortions visible in the hemidirected geometries are due to the Pb2+ complex attempting to minimise energetically unfavourable antibonding interactions between Pb2+and the coordinating ligands.[34] There are several factors that influence whether a given Pb2+ complex exhibits a hemidirected or holodirected geometry. One factor is the coordination number; it is often reported in the literature that Pb2+ complexes with coordination numbers less than six exhibit hemidirected geometries while coordination numbers greater than nine always produce holodirected geometries.[32,33,35] A hemidirected geometry is also more likely if there is higher charge transfer between the ligands and Pb2+, there are attractive interactions between the ligands, or if the Pb–ligand bond is more ionic in nature.[32,36] It is possible for more unusual geometries such as bisdirectional structures to form where the lone pair of Pb2+ is split over the equatorial plane[37] but these structures are formed owing to bulky ligands such as protein fragments and hence are not relevant to the present study. A study by Persson et al. used extended X-ray absorption fine structure (EXAFS) spectroscopy to determine the Pb–O bond lengths of Pb2+ in aqueous solution. The authors found a large distribution of Pb–O bond lengths and this result along with the absence of multiple scattering contributions in the spectra indicated asymmetry in the structure, suggesting a hemidirected arrangement.[34] Furthermore, the derived ionic radii and average Pb–O bond lengths compared with the spectral data led the authors to conclude the most likely coordination geometry involves six water molecules in the Pb2+ first solvation shell.[34]
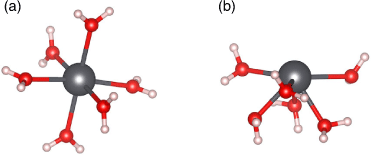
|
A flurry of computational work has also aimed to conclusively establish the structure of the first solvation shell of Pb2+,[35,36,38–40] but the final geometries obtained are heavily dependent on the computational method. Molecular dynamics simulations indicate that Pb2+ has a coordination number of nine and a holodirected geometry.[38,40,41] On the other hand, static quantum mechanical calculations find that coordination numbers between six and nine are all isoenergetic and thermodynamically accessible at room temperature.[35,36,39] The chosen DFT functional, basis set, and dispersion correction scheme greatly affect whether the solvated Pb2+ ion optimises to a holodirected or hemidirected geometry. Wander and Clark found holodirected geometries for Pb(H2O)n2+ (n = 6–8) structures using B3LYP/aug-cc-pvdz-PP geometry optimisations conducted in the gas phase.[36] Kuznetsov et al. attempted to replicate their geometries using a range of model chemistries and found that incorporating implicit solvation in the geometry optimisation transformed initial holodirected structures into hemidirected structures;[39] they additionally found that the ωB97X-D/6–311++G(d,p) and ωB97X-D/aug-cc-pVDZ model chemistries led to an average Pb–O bond length of 2.56 Å, extremely close to the experimental value of 2.54 Å found by Persson et al.[34]
In order to disentangle the effect of model chemistry on coordination geometry, we optimised the Pb(H2O)62+ structure using a range of functionals and basis sets as well as testing the effect of including the D3BJ dispersion correction[42,43] (Table 1). The four functionals chosen were ωB97X[44] and ωB97X-D3BJ[45,46] (as both of these functionals have been used successfully to model heavy metals[39,47]), B3LYP[48] (a common functional used in the literature for Pb2+ hydration studies[36,39]), and PBE0[49] (a functional recommended specifically for optimising geometries of late transition metal structures[50]). We studied a range of basis sets and effective core potentials (ECPs) chosen because they have been used in the literature for modelling either Pb2+ hydration (aug-cc-pVDZ on H and O, aug-cc-pVDZ-PP with the Stuttgart–Koeln small-core multiconfiguration Dirac–Hartree–Fock-adjusted (SK MCDHF RSC) ECP on Pb[51–54] as well as 6-31G(d,p) on H and O, LANL2DZ with the HayWadt ECP on Pb[55–58]) or other heavy metals (def2-SVP on H and O, def2-TZVPP with the def2-ECP on Pb[53,59,60]). We also tested removing the larger basis set on Pb and using def2-SVP on all atoms with either the def2-ECP or the HayWadt ECP for Pb. The initial geometry for each calculation was an octahedral holodirected configuration. The geometries generated by PBE0 are dependent on basis set choice: the Ahlrichs basis sets lead to hemidirected geometries while the Dunning basis sets lead to holodirected ones. B3LYP produces holodirected geometries with all tested basis sets and also leads to bond Pb–O lengths significantly smaller than the experimental ones (2.44 Å average with B3LYP/def2-SVP (def2-TZVPP with def2-ECP on Pb) v. 2.54 Å experimental value[34]). Adding dispersion corrections (D3BJ) to B3LYP significantly improves the model, creating a hemidirected geometry with an average Pb–O bond length of 2.57 Å (with the def2-SVP basis set (def2-TZVPP with def2-ECP on Pb)). This finding is consistent with a previous benchmarking paper on transition metal geometries that stressed the importance of dispersion corrections.[50] We found that ωB97X-D3BJ always produced hemidirected geometries with all tested basis sets, as did the ωB97X functional with the def2-SVP (def2-TZVPP with the def2-ECP on Pb) basis set. These hemidirected geometries have average Pb–O bond lengths (2.55 Å with ωB97X-D3BJ/def2-SVP (def2-TZVPP with the def2-ECP on Pb)) in excellent agreement with experimental findings.[34] Using the ωB97X-D3BJ/aug-cc-pVDZ (aug-cc-pVDZ-PP with the SK MCDHF RSC ECP on Pb) model chemistry slightly worsens the average Pb–O bond length (2.58 Å), indicating that the Ahlrichs basis sets are the most suitable for these calculations. Overall, we concluded that our chosen model chemistry (ωB97X-D3BJ/def2-SVP (def2-TZVPP with def2- ECP on Pb)), which is further discussed in the Computational Details section, provides the best description of the coordination geometry of hydrated Pb2+. Additionally, as illustrated in the following, this approach led to optimised hemidirected coordination geometries also for Pb2+ coordinated by ligands other than water.
In addition to the coordination geometry of hydrated Pb2+, we also investigated the preferred coordination number. We found that all coordination numbers ranging from six to nine are thermodynamically accessible at room temperature, owing to the small energy cost or gain for transitioning between these coordination numbers (maximum of 3.8 kcal mol−1 (1 kcal mol−1 = 4.186 kJ mol−1); Fig. 2). A negative ΔG value indicates exergonicity. This finding is fully consistent with previous literature[35,36,39] and reflects the extremely dynamic nature of the solvation shell. Additionally, we also found that all of these coordination numbers lead to similar computed solvation energies for Pb2+ within a 4 kcal mol−1 range and that they are all in good agreement with the experimental value (see Table S1 and related discussion in the Supplementary Material). Among the coordination numbers investigated, we found that the Pb–O bond lengths in Pb(H2O)62+ (2.55 Å average) are significantly closer to experimental values (2.54 Å average[34]) than those associated with Pb(H2O)72+ (2.62 Å), Pb(H2O)82+ (2.66 Å), and Pb(H2O)92+ (2.70 Å). This result is consistent with a previous computational study on Pb2+ hydration.[39] Additionally, we found that coordination numbers below seven led to hemidirected geometries consistent with experimental findings,[34] while coordination numbers eight and nine had holodirected geometries due to the steric crowding of water molecules forcing a symmetric arrangement (see Fig. S1 and accompanying discussion in the Supplementary Material). Overall, based on these findings and the comparison with the literature, we identified hemidirected Pb(H2O)62+ as the best model of solvated Pb2+, and therefore chose to use it to model solvated Pb2+ interaction with UiO-66 in the following.
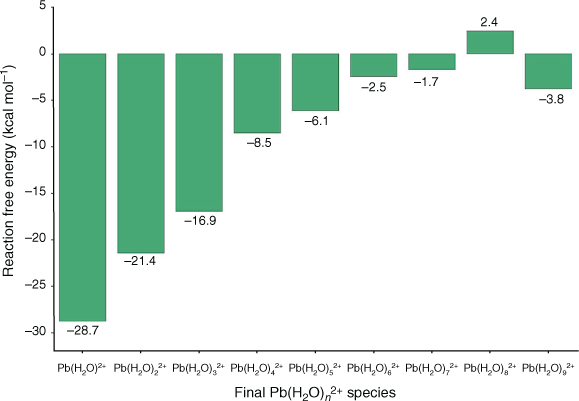
|
We started our investigation of Pb2+ adsorption by UiO-66 by focusing on the functionalised linkers as the adsorption sites, as the bulk of experimental work has been devoted to these systems.[22–24,26] We selected a variety of functionalised linkers that have either demonstrated success for adsorption of Pb2+ (UiO-66–COOH/COO–[24], UiO-66–NHCSNHCH3,[23] UiO-66–NCS,[23] UiO-66–NCO,[23] and UiO-66–NH2[22,23,26]) or possess attributes that could improve Pb2+ adsorption (UiO-66–SO3H/SO3–, UiO-66–CONH2, UiO-66–SH). For conciseness, throughout the manuscript we refer to the functionalised linkers by their functional groups (e.g. UiO-66–SH is referred to as –SH). While –NHCSNHC6H6 was also tested by Saleem et al.,[23] we excluded it from our study owing to its significant steric bulk and relatively poor experimental adsorption performance. As discussed in the Computational Details section, the functionalised linkers adsorption sites were modelled using small cluster models consisting of benzene rings with the functional group attached (see Fig. 3); this approach is well documented in the literature.[61,62] This model captures the bonding interaction between Pb2+ and the functional group at the adsorption site, thus allowing us to determine the relative favourability of each functionalised linker for Pb2+ absorption. The optimised geometries of the functionalised linkers coordinating solvated Pb2+ are illustrated in Fig. 3 and the ΔGs for Pb(H2O)62+ adsorption by these linkers are compared in Fig. 4. A coordination number of six for Pb2+ is maintained across reactant and product to avoid biasing the ΔGs; the adsorption reactions are hence modelled as a ligand exchange where solvating water molecules are replaced by functionalised linkers.
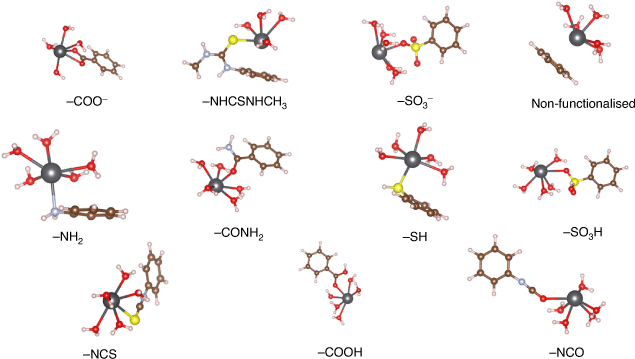
|
|
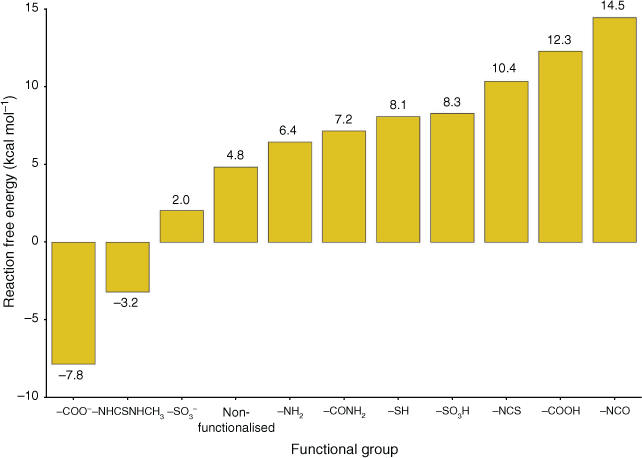
Out of all studied functionalised linkers, –COO– (–7.8 kcal mol−1, Fig. 4), –NHCSNHCH3 (–3.2 kcal mol−1, Fig. 4), and –SO3– (+2.0 kcal mol−1, Fig. 4) display the largest thermodynamic driving force for binding to Pb(H2O)62+ and displacing solvating water molecules. Factors that lead to enhanced Pb2+ affinity for these functional groups are negative charge (–COO–, –SO3–) and the ability to chelate the Pb atom (–COO– and –NHCSNHCH3, with the latter coordinating Pb2+ with both the S site and the benzene as shown in Fig. 3); the combination of these two factors for –COO– leads it to be the most favourable functionalised linker for Pb2+ adsorption, consistent with experimental reports showing a high Pb2+ adsorption capacity by UiO-66–(COOH)2.[24] We attempted to stabilise a multidentate binding geometry also for –SO3–, but the significant steric strain imposed by this planar tridentate binding mode caused this binding configuration to be less favourable than a monodentate binding mode by 2 kcal mol−1. Similarly, the only feasible adsorption geometry for –CONH2 involves the Pb2+ atom bound to the carbonyl group, as we found that geometries with Pb2+ bound to the amine group were not stable upon geometry optimisation. While binding solely to the sulfur atom is unfavourable (–SH, 8.1 kcal mol−1, Fig. 4), the additional interaction with the benzene ring in –NHCSNHCH3 stabilises the complex significantly; this interaction is possible due to the size and flexibility of the latter functional group. Owing to these steric considerations, there is no other functionalised linker that allows this interaction with the benzene ring. Several linkers such as –NH2 (+6.4 kcal mol−1), –NCO (+14.5 kcal mol−1), and –NCS (+12.3 kcal mol−1) perform worse than pristine UiO-66 but have been experimentally demonstrated to be more successful for Pb2+ removal from water,[22,23] thus suggesting that factors other than the thermodynamic binding strength influence Pb2+ adsorption. This aspect is further discussed later in the manuscript.
The overall trend in Fig. 4 is mostly consistent with hard–soft acid–base (HSAB) theory,[63] with three exceptions (–COO–, –NHCSNHCH3, –SO3–). HSAB theory classifies electron acceptors (acids) and electron donors (bases) as ‘hard’ or ‘soft’ based on criteria such as atomic radius, effective nuclear charge, and polarisability. Soft acids and bases typically possess large atomic radii and high polarisability, while hard acid and bases have the opposite characteristics. Acids form strong bonds with bases of the same class. Pb2+ is a borderline acid. Our trend shows Pb2+ base preference in the order N (borderline when bound to benzene) > benzene (soft) > S (soft) > O (hard), hence mostly as expected from HSAB theory except for the three linkers noted earlier. The preference for the –COO–, –NHCSNHCH3, and –SO3– groups due to electrostatic and chelating effects has already been thoroughly explained earlier. The overall trend is also fully consistent with previous work that found that Pb2+ prefers to bind to soft groups such as benzene over hard groups such as ammonia and water.[64]
Overall, while the absolute ΔGs are generally unfavourable (Fig. 4), this does not mean it is impossible for Pb2+ to interact with these functionalised linkers. It is important to note that the relative ordering of functionalised linkers is a more significant result than the absolute thermodynamic binding strength. While extensive effort has been made on our part to accurately model the coordination geometry and energetics of solvated Pb2+, it is impossible to thoroughly account for the full chemical environment. This could include a second solvation shell, counterions, or solvents such as water or dimethylformamide (DMF) captured in the pores of the MOF during synthesis, which could all hamper adsorption either by direct competition with Pb2+ or by limiting diffusion. Another aspect not considered by our model thus far is the fact that Pb2+ may need to partially desolvate in order to pass through the small triangular apertures of pristine UiO-66 (6 Å side length)[18,65,66] despite the dynamic rotation of the BDC linkers.[67] The need for desolvation may also be exacerbated in the presence of functional groups on the BDC linkers that would lead to even smaller or more crowded apertures. The partial desolvation hypothesis is consistent with the fact that experimental studies indicate using UiO-67[25] and the presence of defects[26] can lead to increased Pb2+ adsorption, likely owing to easier diffusion of Pb2+ through the MOF. Furthermore, partial desolvation in order to pass through apertures in porous materials is a well-documented process,[68,69] and moderate dehydration only has a minor energy cost (see Fig. 2). Given the plausibility of the partial desolvation hypothesis both in terms of sterics and energetics, it is important to analyse the possible fate of partially desolvated Pb2+ once it has passed through the narrow UiO-66 apertures. We therefore decided to investigate the energetics of direct adsorption when the solvation shell was partially removed.
Pb(H2O)42+ was selected to model partially desolvated Pb2+ and study the effect of partial desolvation on the energetics of adsorbing onto the full range of studied functionalised linkers with no loss of water molecules (Fig. 5). We chose this initial species as the energetic cost of desolvation relative to fully solvated Pb2+ is not excessively high (–8.6 kcal mol−1 to remove two water molecules from Pb(H2O)62+, Fig. 2). The trends of favourability across linkers are maintained from Fig. 4, with some minor changes in ordering for nearly isoenergetic species (non-functionalised UiO-66, –NH2, –CONH2). Not surprisingly, ΔGs for Pb(H2O)42+ adsorbing without losing water molecules are overall ~10 kcal mol−1 more favourable than the ΔGs obtained for fully solvated Pb(H2O)62+ undergoing linker/water exchange (Fig. 4). We additionally examined the extreme case of adsorption of fully desolvated Pb2+ and found that removing all water molecules predictably leads to significantly more favourable adsorption ΔGs (e.g. ΔG = –64.8 kcal mol−1 for adsorption on –COO– as shown in Fig. S2 and accompanying discussion in the Supplementary Material). The latter study also showed that desolvation may lead to increased accessibility of additional binding sites on the functionalised linkers with multiple adsorption sites once the steric bulk caused by the solvation shell of Pb2+ is removed (see Section 4 of the Supplementary Material). In particular, we were able to stabilise adsorption geometries where the bare Pb2+ ion is bound to the nitrogen atom for the –NCO and –NCS functionalised linkers in addition to the adsorption geometries on the terminal oxygen and sulfur atoms.
We further explored the adsorption thermodynamics by studying the different extent of desolvation that may be induced by the small apertures as well as different degrees of rehydration that may occur once Pb2+ enters the pore. In Fig. 6, we report the energetics of adsorption of partially desolvated and fully solvated Pb2+ onto –COO– with varying final coordination number. The –COO– adsorption site was chosen for this case study as it led to the most thermodynamically favourable adsorption (Fig. 4). As already noted in Fig. 5, the ΔGs become significantly more favourable for species with a lower initial coordination number. A final coordination number of six is preferred (–16.4 kcal mol−1 for a Pb(H2O)42+ initial species) compared with lower coordination numbers such as four (–10.8 kcal mol−1) and five (–15.3 kcal mol−1) or a higher final coordination number of seven (–13.6 kcal mol−1); this trend is consistent across all initial coordination numbers investigated. The reason for a final coordination number of six being preferred over seven for –COO– is the steric strain generated by attempting to maintain a hemidirected geometry at higher coordination numbers, as indicated by the elongation of the Pb–O bond to the fifth water in –COO––Pb(H2O)52+ (2.88 Å compared with the maximum Pb–O bond length of 2.76 Å in –COO––Pb(H2O)42+). A significant result is that it is more favourable for the destabilised Pb(H2O)42+ species to adsorb onto –COO– to a final coordination number of six (–16.4 kcal mol−1, Fig. 6) relative to rehydrating to form Pb(H2O)62+ (–8.6 kcal mol−1 in total, Fig. 2). This suggests that the desolvation of Pb2+ possibly occurring under experimental conditions could truly enhance the affinity of Pb2+ to functional groups, making adsorption competitive, if not more favourable, than rehydration. Overall, our results suggest that desolvation induced by small apertures may favour adsorption and removal of Pb2+, but there is clearly a fine balance between driving desolvation and impeding diffusion. Molecular dynamics simulations may be used to further explore this aspect in future work.
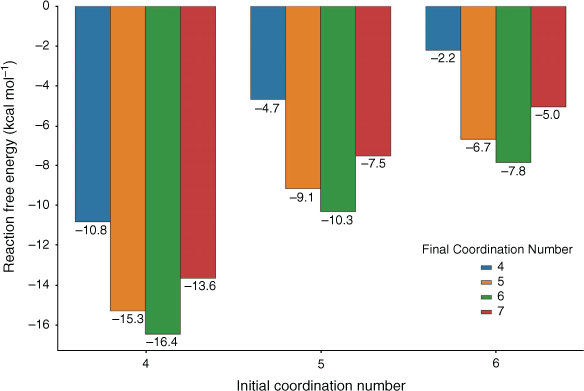
|
To summarise, our analysis of the Pb2+ cation interacting with different functionalised linkers of UiO-66 shows that changing the functional group may lead to significantly different adsorption outcomes in agreement with the literature on UiO-66[22–24] as well as other materials.[11,12] However, our observations do not fully account for all reported experimental results in terms of which functional groups lead to the greatest adsorption,[23,24,26] even when the effects of potential Pb2+ desolvation are taken into account. This indicates other factors such as the presence of defects should also be critically analysed. This aspect is investigated next.
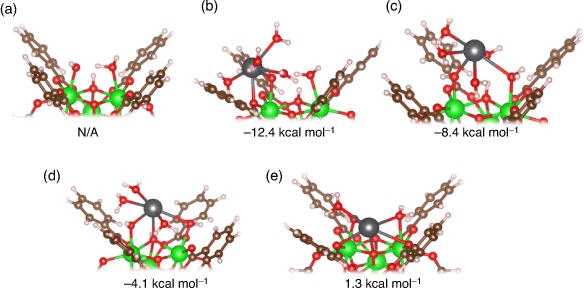
Defects in UiO-66 are ubiquitous,[21] but their impact on Pb2+ adsorption has yet to be thoroughly determined. Our results indicate that defects could play a significant role in the adsorption of Pb2+ in aqueous solutions by forming thermodynamically favourable Zr–O–Pb bonds. Shown in Fig. 7a is the original hydroxide–water capped defect site (UiO-66–[OH–/H2O]), and Fig. 7b–e depicts the adsorption geometries of Pb2+ on this defect site investigated in this study with the coordination sites indicated in the caption. These four unique geometries were identified after a thorough search of stable adsorption geometries, using several different initial guesses in which the Pb2+ cation was placed close to different potential adsorption sites on UiO-66–[OH–/H2O]. To improve the accuracy of our geometry search, we used both the solvated and the fully desolvated cation when building initial guesses. Working with the fully desolvated ion allowed us to easily probe all the possible adsorption sites, as Pb2+ would not be restricted in making new bonds by its hydration shell. On the other hand, the use of the solvated cation allowed us to determine how much of its first solvation shell Pb2+ preferred to retain when interacting with the defective UiO-66 nodes. In all of the identified adsorption geometries (Fig. 7b–e), Pb2+ has a coordination number of six.
|
In the most energetically favourable structure (Fig. 7b), Pb2+ forms two bonds with the MOF: one to the –OH– group in the defect site and another bond to the carboxylic oxygen belonging to a BDC linker. The structure in Fig. 7c is also characterised by two bonds – one to the –OH– group and one to the –H2O group on the defect site – but is less stable by 4 kcal mol−1. We suggest the latter structure is less stable because of bond constraints on Pb2+; more specifically, when Pb2+ binds to the –OH– group on the defect site (which is extremely favourable, given that this group is negatively charged), it is much easier for Pb2+ to bind to the carboxylic oxygen on the BDC linker rather than the oxygen on the –H2O group. In fact, the bond between Pb2+ and the carboxylic oxygen in Fig. 7b (2.44 Å) is much closer in length to the bonds in Pb(H2O)62+ (see Fig. S1 in the Supplementary Material) than the bond between Pb2+ and the –H2O group on the defect site in Fig. 7c (2.89 Å).
In the structure in Fig. 7d, Pb2+ makes three bonds: one to the –OH– group and another to the –H2O group on the defect site, and a third bond to μ3-OH group in the MOF. This structure is 8.3 kcal mol−1 less stable than the most stable structure (Fig. 7b). The structure in Fig. 7e is the least stable structure (ΔG 13.7 kcal mol−1 less favourable than the most stable structure) and is characterised by five bonds between Pb2+ and the MOF: one to the –OH–group and one to the –H2O group on the defect site, two bonds to different carboxylic oxygens from BDC linkers, and a fifth bond to μ3-O in the MOF. From this, a clear negative trend between stability and the number of bonds between Pb2+ and UiO-66 emerges. We believe that this trend is explained by the increased steric constraints on Pb2+ coordination geometry, since making bonds to UiO-66 would prevent Pb2+ from freely orientating the coordination shell as if it was an ideal solvation shell. This is especially evident for the structure in Fig. 7e, where the Pb2+ ion sits deep within the node. This results in one out of the six Pb–O bonds (the bond to the carboxylic O; 2.93 Å) being significantly elongated relative to others (2.49 Å average). Additionally, this structure is characterised by the greatest distortion of the UiO-66 node as the Zr–μ3-O bonds in the MOF are lengthened upon Pb2+ adsorption, with ~0.05 Å average distortion (Fig. 7a).
Overall, we observe that Pb2+ chose to bind to the –OH– group on the defect site in all cases. This is easily explained by the electrostatic attraction between Pb2+ and the negative charge on the –OH– group and is consistent with our results showing that Pb2+ prefers to bind to negatively charged functional groups. While it is possible for monocarboxylic acids such as formate, acetate or trifluoroacetate to act as capping ligands for defects, the only available adsorption site for Pb2+ is the carboxylic oxygens (i.e. the same adsorption site as pristine UiO-66). However, as demonstrated by the fact that all the identified adsorption configurations involve Pb2+ bound to the negatively charged hydroxide group on the UiO-66–[OH–/H2O] site, the hydroxide group belonging to the defect site is a preferred coordination site relative to the carboxylic oxygens of BDC and monocarboxylic acids. This result offers further justification for our analysis being focussed solely on the UiO-66–[OH–/H2O] defect rather than other defects generated by monocarboxylic acid modulators and solvents acting as capping ligands. While binding to the OH–group on the UiO-66 defect site is always preferred, it is also favourable to adsorb onto the H2O site (Fig. 7c) as well as to an arm of the UiO-66 (i.e. carboxylic O of the BDC linkers, Fig. 7b). Binding to deeper parts of UiO-66 (i.e. μ3-O or μ3-OH, Fig. 7d, e) is less favourable, likely owing to increased bond strain as previously discussed. We conclude that there is a significant thermodynamic driving force (up to ~12 kcal mol−1) for Pb2+ to bind to the MOF defect site, as long as a large portion of its hydration shell is retained and Pb–O bond strain is limited.
A comparison of all the energetics of adsorption reported in this work suggests that both defective nodes and functionalised linkers could cooperatively contribute to Pb2+ adsorption, with the defective UiO-66–[OH–/H2O] node showing the greatest thermodynamic affinity for Pb2+. The inclusion of negatively charged sites was found to enhance the adsorption strength at both defective nodes and adsorption sites owing to electrostatic attraction between the MOF and Pb2+, as indicated by the thermodynamic preference of Pb2+ for the –COO– and –SO3– linkers and the –OH– group at the defect site. Based on these results, we propose that the deprotonated μ3-OH group may also act as an adsorption site. In fact, in the acidic conditions typically utilised for Pb2+ adsorption,[24,25] some of μ3-OH groups are likely to be deprotonated according to the pKas determined in previous work (3.15, 4.43, 6.9, and 11).[70] Furthermore, adsorption modes involving coordination by both the OH– group at the defect site and the μ3-O– group may lead to even stronger adsorption. This aspect will be the subject of future investigations. Chelation of Pb2+ (i.e. the formation of multiple bonds between Pb2+ and the adsorption site) also plays a significant role, as demonstrated by our results for the –COO– and –NHCSNHCH3 adsorption sites as well as the UiO-66–[OH–/H2O] site. Given these results, we hypothesise that multiple functionalised linkers may coordinate Pb2+ at once, leading to an increase of Pb2+ binding affinity to the MOF. On the other hand, coordination by multiple linkers may lead to significant constraints on the coordination geometry of Pb2+and result in less favourable adsorption thermodynamics. This is demonstrated by our results showing that too many bonds to the UiO-66 defective node leads to distortion of either the MOF itself or the Pb2+ coordination shell.
The comparable ΔGs between functionalised linkers and nodes hint at the complex interconnectedness of factors that contribute to a measured adsorption capacity. Functionalised linkers could have many subtle effects on the chemistry and structure of the MOF beyond acting as direct adsorption sites. As an example, a study by Wei et al. found that using functionalised linkers during synthesis led to more linker vacancies (i.e. defect sites).[30] This suggests that the extremely high adsorption capacity reported by Zhao et al. with UiO-66–(COOH)2 of 420 mg g−1 [24] may be due to a synergistic effect with Pb2+ adsorption occurring both at –COO– functionalised linkers (as proposed by the authors of the study) and at defective nodes created by the synthesis conditions. The functional groups on linkers could also influence the nucleophilicity of the defect sites, in addition to the quantity. Wei et al. also found that functionalised linkers alter the electron density, and hence the chemical behaviour, of Zr atoms on the nodes; it is hence possible that some functionalised linkers could subtly affect the chemical behaviour of capping hydroxide and water molecules on nearby defect sites.[30] These effects could be investigated in future work by using either larger cluster models that incorporate both functionalised linkers and defective nodes in one structure or periodic calculations. Another indirect effect of functionalised linkers previously discussed is the reduction of the UiO-66 aperture size. This could have a complex effect on Pb2+ adsorption, as we demonstrated that desolvation potentially induced by these functional groups leads to more thermodynamic driving force for adsorption. At the same time, numerous and bulky functional groups may hamper Pb2+ diffusion through the MOF,[24] thus limiting adsorption. Overall, our investigation and analysis of all the factors discussed in this work provide critical design principles for the synthesis of UiO-66 MOFs to be employed in water purification from toxic Pb2+.
Conclusions
In this work, we present a DFT analysis of Pb2+ adsorption using functionalised and defective UiO-66. We began our study by thoroughly exploring the effect of the model chemistry on the coordination geometry and coordination number of solvated Pb2+ and validate our computational model by comparing our results with the literature. We found that B3LYP, while a popular functional in the literature, could not replicate the hemidirected coordination geometry of Pb2+ found in experimental reports. The functional ωB97X-D3BJ produced a hemidirected geometry for Pb2+ solvated by six water molecules; additionally, the average Pb–O bond length of 2.55 Å in this optimised complex is almost identical to the experimental value of 2.54 Å.[34] Overall, our chosen model chemistry (ωB97X-D3BJ/def2-SVP (def2-TZVPP with def2-ECP on Pb)) led to results in agreement with previous computational as well as experimental work. All coordination numbers between six and nine were found to be thermodynamically accessible at room temperature, with the six-coordinated Pb2+ species giving a solvation energy in best agreement with experiments. Our study on functionalised UiO-66 for Pb2+ capture identified several functional groups that may lead to more favourable adsorption energetics relative to non-functionalised UiO-66, in which the main adsorption site on the BDC linker is the benzene ring. We determined that the factors that lead to linkers with greater Pb2+ affinity are electrostatic attraction and the ability to chelate Pb2+, and identified UiO-66–COO– and UiO-66–NHCSNHCH3 as the most favourable absorption sites for Pb2+ removal, in agreement with experimental reports.[23,24] We further explored the possibility that solvated Pb2+ may not be able to pass through the small UiO-66 triangular window while maintaining its full solvation shell; this effect may be worsened by the further narrowing of the aperture by bulky functional groups, hindering diffusion. The solvated Pb2+ ion may thus have to partially or fully desolvate in order to diffuse through the MOF and reach adsorption sites. We therefore modelled adsorption of partially desolvated Pb2+ onto the functionalised linkers without loss of water molecules and found that, not surprisingly, desolvation led to energetics of adsorption that are significantly more exergonic. Our case study on partially desolvated Pb2+ adsorption using UiO-66–COO– determined that there is a strong preference for adsorption onto a linker compared with rehydration within the pore. The thorough screening of the functionalised linkers carried out in this work also revealed that some adsorption sites on the functionalised linkers such as UiO-66–NCO were less thermodynamically favourable than non-functionalised UiO-66. However, these functional groups have demonstrated moderate experimental efficacy for Pb2+ adsorption, indicating that factors other than the thermodynamic binding strength may be at play. There is likely a complex interplay of factors that leads to enhanced adsorption, and one that has not yet been fully explored by the literature is the presence of defects, which are ubiquitous in UiO-66. Defects can likely play a significant role in adsorption by creating larger apertures and allowing Pb2+ to diffuse more easily through the MOF pores. A novel finding presented in this work is that defect sites created by missing linkers could boost adsorption capacity by directly acting as an adsorption site. The UiO-66–[OH–/H2O] site, formed by hydroxide and water molecules capping the undercoordinated Zr atoms created by the missing BDC linker, is able to coordinate Pb2+ using the many oxygen atoms available at this site. The capacity of the UiO-66–[OH–/H2O] defect site to directly adsorb Pb2+ could contribute to explaining high adsorption capacities reported in some experimental reports. Future work could be aimed at modelling the process of Pb2+ desolvating, rehydrating, and diffusing through the UiO-66 pores in the presence of defects and functionalised linkers using molecular dynamics simulations. Overall, our work provides several new insights into the removal of toxic Pb2+ from water using functionalised UiO-66 and suggests that defects may be playing a critical role, although this area of research is still mostly unexplored. We also determined that electrostatic attraction and the ability to chelate Pb2+ without unduly constraining its hydration shell are key factors that must be considered when designing MOFs for water purification from toxic cations.
Computational Details
All of the calculations in this study were conducted using Kohn–Sham DFT[71,72] as implemented in Orca 4.2.1.[73–75] The protocol for these calculations is based on previous work in our group where we successfully modelled AsV adsorption using UiO-66.[47] The ωB97X-D3BJ range-separated hybrid functional was used as it produced geometries consistent with experimental findings as discussed in the Results and Discussion section; a previous computational study on the hydration shell of the Pb2+ ion found a similar result using the ωB97X functional.[39] The included parameterised D3BJ dispersion correction[42,43] is recommended in the literature for optimising geometries of transition metal complexes.[50] The RIJCOSX approximation[76] was also applied in order to reduce computational cost. Final Gibbs free energies in solution were calculated using a multi-step approach. Geometry optimisations and vibrational frequency calculations were conducted using the def2-SVP basis set on all atoms except for Pb and Zr, which were described with the def2-TZVPP basis set[59,60] in conjunction with the def2-ECP effective core potential.[53,77] The def2-ECP describes the core 60 electrons in the Pb atom and the core 28 electrons for Zr. Single-point refinements were conducted on the optimised geometries using the ma-def2-TZVPP basis set for Pb and Zr and the ma-def2-TZVP for all other atoms.[59,78] The use of def2-TZVPP for transition metals is recommended in the literature;[50] the polarisation and diffuse functions present in these basis sets are ideal for modelling transition metals as well as non-covalent interactions such as the weak interactions between the solvating water molecules.
We incorporated the effect of solvation using a mixed implicit/explicit solvation model. Implicit solvation was included using the Conductor-like Polarizable Continuum Model (CPCM) with a scaled van der Waals surface and Gaussian charge scheme.[79,80] The first solvation shell of the Pb2+ cation was accurately modelled by including explicit water molecules as thoroughly discussed in the Results and Discussion section. Similarly to our previous study,[47] we described water molecules in solution using a nonamer; the reasoning behind this choice is thoroughly discussed in Fig. S3 as well as Table S2 and associated discussion in the Supplementary Material.
Two types of cluster models were used to model UiO-66 depending on the adsorption site of interest. This approach has been used commonly and successfully in the literature to model UiO-66 nodes and linkers, and we direct the interested reader to some recent reviews on this topic.[81,82] The cluster model used to simulate adsorption on the functionalised linker is constructed using a benzene ring with the relevant functional group attached (see Fig. 3 and accompanying discussion) to model functionalised UiO-66. This is a valid approach for modelling interactions with the adsorption site on the functionalised linkers as demonstrated by previous studies in the literature.[61,62,83] The cluster model used to study adsorption on the UiO-66 defective node (Fig. 7 and accompanying discussion) has been used widely in the literature in the past,[27,30,84–87] including in recent work by our group where we report the details of how the cluster model was obtained.[47] For reasons thoroughly discussed in the Introduction section, we chose to model our defective node as UiO-66–[OH–/H2O] (i.e. a UiO-66 node with a missing linker defect and the undercoordinated Zr atoms saturated by a OH– group and H2O). This cluster model was then used to calculate the energetics of Pb2+ adsorption onto the defect site (see Fig. 7 and accompanying discussion).
The lack of imaginary frequencies in the vibrational frequency analysis was used to verify whether the optimised structure was at a local minimum on the potential energy surface. The frequency calculations also provided thermal corrections to the final electronic energy. For all species involving the MOF cluster models, only the vibrational corrections were considered in order to account for the constraints exerted by the ordered crystal structure that prevent translational and rotational degrees of freedom. The translational, rotational, and vibrational corrections were all included for the species free in solution, such as the water cluster or solvated Pb2+.
ΔGs were calculated according to the equation
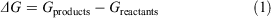
where Gproducts is the sum of the free energies of all the products and Greactants is the sum of the free energies of all the reactants. Favourable reaction free energies are associated with a negative ΔG value. Gproducts and Greactants were calculated using the standard thermodynamic cycle approach in order to incorporate thermal and solvation effects.[88,89] Using this cycle, the Gibbs free energy for each solvated species is given by:
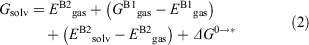
where the superscripts B1 and B2 indicate that the energy is determined using the basis set choice for optimisations and frequencies (B1) or the basis set choice for refined single-point energy calculations (B2) respectively; the subscripts gas and solv signify whether the calculation was performed in gas phase or with implicit solvation; E denotes electronic energies while G denotes free energies at room temperature; ΔG0→* is the correction for the change in standard states from gas phase to liquid phase as detailed in ref. [89].
Supplementary Material
More benchmark results, calculations details, and Cartesian coordinates of all the geometries used to obtain the data in this work are available on the Journal’s website.
Data Availability Statement
The data that support this study are available in the article and accompanying online supplementary material.
Conflicts of Interest
The authors declare no conflicts of interest.
Declaration of Funding
This research was supported by an Australian Government Research Training Program (RTP) Scholarship awarded to C. S. C.
Acknowledgements
The authors acknowledge and are grateful for computational resources and services from the National Computational Infrastructure (NCI), provided by the Australian Government under the National Computational Merit Allocation Scheme, and the computational cluster Katana supported by Research Technology Services at UNSW Sydney.
References
[1] T. Dudev, C. Grauffel, C. Lim, Inorg. Chem. 2018, 57, 14798.| Crossref | GoogleScholarGoogle Scholar | 30411871PubMed |
[2] H. Needleman, Annu. Rev. Med. 2004, 55, 209.
| Crossref | GoogleScholarGoogle Scholar | 14746518PubMed |
[3] M. Valcke, M. H. Bourgault, M. Gagné, P. Levallois, Sci. Total Environ. 2021, 775, 145866..
[4] M. P. Taylor, C. Winder, B. P. Lanphear, Environ. Int. 2014, 70, 113.
| Crossref | GoogleScholarGoogle Scholar | 24927499PubMed |
[5] W. Wheeler, MMWR Morb. Mortal. Wkly. Rep. 2013, 62, 245.
[6] M. Edwards, S. Triantafyllidou, D. Best, Environ. Sci. Technol. 2009, 43, 1618.
| Crossref | GoogleScholarGoogle Scholar | 19350944PubMed |
[7] G. Ngueta, M. Prévost, E. Deshommes, B. Abdous, D. Gauvin, P. Levallois, Environ. Int. 2014, 73, 57.
| Crossref | GoogleScholarGoogle Scholar | 25087106PubMed |
[8] C. F. Carolin, P. S. Kumar, A. Saravanan, G. J. Joshiba, M. Naushad, J. Environ. Chem. Eng. 2017, 5, 2782.
| Crossref | GoogleScholarGoogle Scholar |
[9] L. Ruihua, Z. Lin, T. Tao, L. Bo, J. Hazard. Mater. 2011, 190, 669.
| Crossref | GoogleScholarGoogle Scholar | 21514994PubMed |
[10] A. Ewecharoen, P. Thiravetyan, E. Wendel, H. Bertagnolli, J. Hazard. Mater. 2009, 171, 335.
| Crossref | GoogleScholarGoogle Scholar | 19576692PubMed |
[11] M. Vesali-Naseh, M. R. Vesali Naseh, P. Ameri, J. Clean. Prod. 2021, 291, 125917.
| Crossref | GoogleScholarGoogle Scholar |
[12] E. Deliyanni, A. Arabatzidou, N. Tzoupanos, K. Matis, Adsorpt. Sci. Technol. 2012, 30, 627.
| Crossref | GoogleScholarGoogle Scholar |
[13] L. Rani, J. Kaushal, A. L. Srivastav, P. Mahajan, Environ. Sci. Pollut. Res. Int. 2020, 27, 44771.
| Crossref | GoogleScholarGoogle Scholar | 32975757PubMed |
[14] J. Li, X. Wang, G. Zhao, C. Chen, Z. Chai, A. Alsaedi, et al. Chem. Soc. Rev. 2018, 47, 2322.
| Crossref | GoogleScholarGoogle Scholar | 29498381PubMed |
[15] K. O. Adebowale, E. I. Unuabonah, B. I. Olu-Owolabi, Chem. Eng. J. 2008, 136, 99.
| Crossref | GoogleScholarGoogle Scholar |
[16] L. Giraldo, J. C. Moreno-Piraján, Braz. J. Chem. Eng. 2008, 25, 143.
| Crossref | GoogleScholarGoogle Scholar |
[17] J. Ru, X. Wang, F. Wang, X. Cui, X. Du, X. Lu, Ecotoxicol. Environ. Saf. 2021, 208, 111577.
| Crossref | GoogleScholarGoogle Scholar | 33160184PubMed |
[18] J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga, et al. J. Am. Chem. Soc. 2008, 130, 13850.
| Crossref | GoogleScholarGoogle Scholar | 18817383PubMed |
[19] J. Winarta, B. Shan, S. M. McIntyre, L. Ye, C. Wang, J. Liu, et al. Cryst. Growth Des. 2020, 20, 1347.
| Crossref | GoogleScholarGoogle Scholar |
[20] Y. Feng, Q. Chen, M. Jiang, J. Yao, Ind. Eng. Chem. Res. 2019, 58, 17646.
| Crossref | GoogleScholarGoogle Scholar |
[21] C. A. Trickett, K. J. Gagnon, S. Lee, F. Gándara, H. B. Bürgi, O. M. Yaghi, Angew. Chem. Int. Ed. 2015, 54, 11162.
| Crossref | GoogleScholarGoogle Scholar |
[22] K. Wang, J. Gu, N. Yin, Ind. Eng. Chem. Res. 2017, 56, 1880.
| Crossref | GoogleScholarGoogle Scholar |
[23] H. Saleem, U. Ra, R. P. Davies, Microporous Mesoporous Mater. 2016, 221, 238.
| Crossref | GoogleScholarGoogle Scholar |
[24] X. Zhao, Y. Wang, Y. Li, W. Xue, J. Li, H. Wu, et al. J. Chem. Eng. Data 2019, 64, 2728.
| Crossref | GoogleScholarGoogle Scholar |
[25] G. S. Morcos, A. A. Ibrahim, M. M. H. El-Sayed, M. S. El-Shall, J. Environ. Chem. Eng. 2021, 9, 105191.
| Crossref | GoogleScholarGoogle Scholar |
[26] N. Yin, K. Wang, Z. Li, Chem. Lett. 2016, 45, 625.
| Crossref | GoogleScholarGoogle Scholar |
[27] M. Vandichel, J. Hajek, A. Ghysels, A. De Vos, M. Waroquier, V. Van Speybroeck, CrystEngComm 2016, 18, 7056.
| Crossref | GoogleScholarGoogle Scholar |
[28] G. C. Shearer, S. Chavan, J. Ethiraj, J. G. Vitillo, S. Svelle, U. Olsbye, et al. Chem. Mater. 2014, 26, 4068.
| Crossref | GoogleScholarGoogle Scholar |
[29] J. M. Taylor, T. Komatsu, S. Dekura, K. Otsubo, M. Takata, H. Kitagawa, J. Am. Chem. Soc. 2015, 137, 11498.
| Crossref | GoogleScholarGoogle Scholar | 26302312PubMed |
[30] R. Wei, C. A. Gaggioli, G. Li, T. Islamoglu, Z. Zhang, P. Yu, et al. Chem. Mater. 2019, 31, 1655.
| Crossref | GoogleScholarGoogle Scholar |
[31] G. C. Shearer, S. Chavan, S. Bordiga, S. Svelle, U. Olsbye, K. P. Lillerud, Chem. Mater. 2016, 28, 3749.
| Crossref | GoogleScholarGoogle Scholar |
[32] L. Shimoni-Livny, J. P. Glusker, C. W. Bock, Inorg. Chem. 1998, 37, 1853.
| Crossref | GoogleScholarGoogle Scholar |
[33] A. Moncomble, J. P. Cornard, M. Meyer, J. Mol. Model. 2017, 23, 24.
| 28064375PubMed |
[34] I. Persson, K. Lyczko, D. Lundberg, L. Eriksson, A. Pjaczek, Inorg. Chem. 2011, 50, 1058.
| Crossref | GoogleScholarGoogle Scholar | 21226482PubMed |
[35] C. Gourlaouen, H. Gérard, O. Parisel, Chem. – Eur. J. 2006, 12, 5024.
| Crossref | GoogleScholarGoogle Scholar | 16642524PubMed |
[36] M. C. F. Wander, A. E. Clark, Inorg. Chem. 2008, 47, 8233.
| Crossref | GoogleScholarGoogle Scholar |
[37] M.-C. Van Severen, U. Ryde, O. Parisel, J.-P. Piquemal, J. Chem. Theory Comput. 2013, 9, 2416.
| Crossref | GoogleScholarGoogle Scholar | 26583732PubMed |
[38] T. S. Hofer, B. M. Rode, J. Chem. Phys. 2004, 121, 6406.
| Crossref | GoogleScholarGoogle Scholar | 15446939PubMed |
[39] A. M. Kuznetsov, A. N. Masliy, G. V. Korshin, J. Mol. Model. 2018, 24, 193.
| Crossref | GoogleScholarGoogle Scholar | 29974247PubMed |
[40] A. Bhattacharjee, T. S. Hofer, A. B. Pribil, B. R. Randolf, L. H. V. Lim, A. F. Lichtenberger, B. M. Rode, J. Phys. Chem. B 2009, 113, 13007.
| Crossref | GoogleScholarGoogle Scholar | 19728688PubMed |
[41] C. S. Babu, C. Lim, J. Phys. Chem. A 2006, 110, 691.
| Crossref | GoogleScholarGoogle Scholar | 16405342PubMed |
[42] S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 2010, 132, 154104.
| Crossref | GoogleScholarGoogle Scholar | 20423165PubMed |
[43] S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 2011, 32, 1456.
| Crossref | GoogleScholarGoogle Scholar | 21370243PubMed |
[44] J. Da Chai, M. Head-Gordon, J. Chem. Phys. 2008, 128, 084106..
[45] N. Mardirossian, M. Head-Gordon, Phys. Chem. Chem. Phys. 2014, 16, 9904.
| Crossref | GoogleScholarGoogle Scholar | 24430168PubMed |
[46] A. Najibi, L. Goerigk, J. Chem. Theory Comput. 2018, 14, 5725.
| Crossref | GoogleScholarGoogle Scholar | 30299953PubMed |
[47] C. S. Cox, V. Cossich Galicia, M. Lessio, J. Phys. Chem. C 2021, 125, 3157.
| Crossref | GoogleScholarGoogle Scholar |
[48] A. D. Becke, J. Chem. Phys. 1993, 98, 5648.
| Crossref | GoogleScholarGoogle Scholar |
[49] C. Adamo, V. Barone, J. Chem. Phys. 1999, 110, 6158.
| Crossref | GoogleScholarGoogle Scholar |
[50] M. K. Kesharwani, J. M. L. Martin, Theor. Chem. Acc. 2014, 133, 1452.
| Crossref | GoogleScholarGoogle Scholar |
[51] R. A. Kendall, T. H. Dunning, R. J. Harrison, J. Chem. Phys. 1992, 96, 6796.
| Crossref | GoogleScholarGoogle Scholar |
[52] K. A. Peterson, J. Chem. Phys. 2003, 119, 11099.
| Crossref | GoogleScholarGoogle Scholar |
[53] B. Metz, H. Stoll, M. Dolg, J. Chem. Phys. 2000, 113, 2563.
| Crossref | GoogleScholarGoogle Scholar |
[54] T. H. Dunning, J. Chem. Phys. 1989, 90, 1007.
| Crossref | GoogleScholarGoogle Scholar |
[55] R. Ditchfield, W. J. Hehre, J. A. Pople, J. Chem. Phys. 1971, 54, 724.
| Crossref | GoogleScholarGoogle Scholar |
[56] W. J. Hehre, K. Ditchfield, J. A. Pople, J. Chem. Phys. 1972, 56, 2257.
| Crossref | GoogleScholarGoogle Scholar |
[57] P. C. Hariharan, J. A. Pople, Theor. Chim. Acta 1973, 28, 213.
| Crossref | GoogleScholarGoogle Scholar |
[58] W. R. Wadt, P. J. Hay, J. Chem. Phys. 1985, 82, 284.
| Crossref | GoogleScholarGoogle Scholar |
[59] F. Weigend, R. Ahlrichs, Phys. Chem. Chem. Phys. 2005, 7, 3297.
| Crossref | GoogleScholarGoogle Scholar | 16240044PubMed |
[60] F. Weigend, Phys. Chem. Chem. Phys. 2006, 8, 1057.
| Crossref | GoogleScholarGoogle Scholar | 16633586PubMed |
[61] J. Ye, J. K. Johnson, ACS Catal. 2015, 5, 2921.
| Crossref | GoogleScholarGoogle Scholar |
[62] K. C. Kim, D. Yu, R. Q. Snurr, Langmuir 2013, 29, 1446.
| Crossref | GoogleScholarGoogle Scholar | 23305323PubMed |
[63] T. L. Ho, Chem. Rev. 1975, 75, 1.
| Crossref | GoogleScholarGoogle Scholar |
[64] B. Sharma, Y. I. Neela, G. Narahari Sastry, J. Comput. Chem. 2016, 37, 992.
| Crossref | GoogleScholarGoogle Scholar | 26833683PubMed |
[65] S. Biswas, J. Zhang, Z. Li, Y. Y. Liu, M. Grzywa, L. Sun, et al. Dalton Trans. 2013, 4730.
| Crossref | GoogleScholarGoogle Scholar | 23361454PubMed |
[66] S. Chavan, J. G. Vitillo, D. Gianolio, O. Zavorotynska, B. Civalleri, S. Jakobsen, et al. Phys. Chem. Chem. Phys. 2012, 14, 1614.
| Crossref | GoogleScholarGoogle Scholar | 22187720PubMed |
[67] M. Wehbe, B. J. Abu Tarboush, M. Shehadeh, M. Ahmad, Chem. Eng. Sci. 2020, 214, 115396.
| Crossref | GoogleScholarGoogle Scholar |
[68] L. A. Richards, A. I. Schäfer, B. S. Richards, B. Corry, Small 2012, 8, 1701.
| Crossref | GoogleScholarGoogle Scholar | 22434668PubMed |
[69] G. Feng, R. Qiao, J. Huang, B. G. Sumpter, V. Meunier, J. Phys. Chem. C 2010, 114, 18012.
| Crossref | GoogleScholarGoogle Scholar |
[70] A. H. Ibrahim, W. A. El-Mehalmey, R. R. Haikal, M. E. A. Safy, M. Amin, H. R. Shatla, et al. Inorg. Chem. 2019, 58, 15078.
| Crossref | GoogleScholarGoogle Scholar | 31661254PubMed |
[71] P. Hohenberg, W. Kohn, Phys. Rev. 1964, 136, B864.
| Crossref | GoogleScholarGoogle Scholar |
[72] W. Kohn, L. J. Sham, Phys. Rev. 1965, 140, A1133.
| Crossref | GoogleScholarGoogle Scholar |
[73] F. Neese, F. Wennmohs, U. Becker, C. Riplinger, J. Chem. Phys. 2020, 152, 224108.
| Crossref | GoogleScholarGoogle Scholar | 32534543PubMed |
[74] F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73.
| Crossref | GoogleScholarGoogle Scholar |
[75] F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327.
| Crossref | GoogleScholarGoogle Scholar |
[76] F. Neese, F. Wennmohs, A. Hansen, U. Becker, Chem. Phys. 2009, 356, 98.
| Crossref | GoogleScholarGoogle Scholar |
[77] D. Andrae, U. Häußermann, M. Dolg, H. Stoll, H. Preuß, Theor. Chim. Acta 1990, 77, 123.
| Crossref | GoogleScholarGoogle Scholar |
[78] J. Zheng, X. Xu, D. G. Truhlar, Theor. Chem. Acc. 2011, 128, 295.
| Crossref | GoogleScholarGoogle Scholar |
[79] V. Barone, M. Cossi, J. Phys. Chem. A 1998, 102, 1995.
| Crossref | GoogleScholarGoogle Scholar |
[80] D. M. York, M. Karplus, J. Phys. Chem. A 1999, 103, 11060.
| Crossref | GoogleScholarGoogle Scholar |
[81] J. L. Mancuso, A. M. Mroz, K. N. Le, C. H. Hendon, Chem. Rev. 2020, 120, 8641.
| Crossref | GoogleScholarGoogle Scholar | 32672939PubMed |
[82] V. Bernales, M. A. Ortuño, D. G. Truhlar, C. J. Cramer, L. Gagliardi, ACS Cent. Sci. 2018, 4, 5.
| Crossref | GoogleScholarGoogle Scholar | 29392172PubMed |
[83] H. Demir, S. J. Stoneburner, W. Jeong, D. Ray, X. Zhang, O. K. Farha, et al. J. Phys. Chem. C 2019, 123, 12935.
| Crossref | GoogleScholarGoogle Scholar |
[84] D. Yang, S. O. Odoh, J. Borycz, T. C. Wang, O. K. Farha, J. T. Hupp, et al. ACS Catal. 2016, 6, 235.
| Crossref | GoogleScholarGoogle Scholar |
[85] D. Yang, S. O. Odoh, T. C. Wang, O. K. Farha, J. T. Hupp, C. J. Cramer, et al. J. Am. Chem. Soc. 2015, 137, 7391.
| Crossref | GoogleScholarGoogle Scholar | 25990021PubMed |
[86] D. Yang, M. A. Ortuño, V. Bernales, C. J. Cramer, L. Gagliardi, B. C. Gates, J. Am. Chem. Soc. 2018, 140, 3751.
| 29458253PubMed |
[87] C. Caratelli, J. Hajek, F. G. Cirujano, M. Waroquier, F. X. Llabrés i Xamena, V. Van Speybroeck, J. Catal. 2017, 352, 401.
| Crossref | GoogleScholarGoogle Scholar |
[88] J. Ho, Phys. Chem. Chem. Phys. 2015, 17, 2859.
| Crossref | GoogleScholarGoogle Scholar | 25503399PubMed |
[89] J. A. Keith, E. A. Carter, J. Chem. Theory Comput. 2012, 8, 3187.
| Crossref | GoogleScholarGoogle Scholar | 26605730PubMed |




