The Completeness and Reliability of Threshold and False-discovery Rate Source Extraction Algorithms for Compact Continuum Sources
M. T. Huynh A G , A. Hopkins B F , R. Norris C , P. Hancock D F , T. Murphy D E F , R. Jurek C and M. Whiting CA International Centre for Radio Astronomy Research, M468, University of Western Australia, Crawley, WA 6009, Australia
B Australian Astronomical Observatory, P.O. Box 296, Epping NSW 1710, Australia
C CSIRO Astronomy & Space Sciences, Australia Telescope National Facility, PO Box 76, Epping NSW 1710, Australia
D Sydney Institute for Astronomy, School of Physics, The University of Sydney, NSW 2006, Australia
E School of Information Technologies, The University of Sydney, NSW 2006, Australia
F ARC Centre of Excellence for All-sky Astrophysics (CAASTRO)
G Corresponding author. Email: minh.huynh@uwa.edu.au
Publications of the Astronomical Society of Australia 29(3) 229-243 https://doi.org/10.1071/AS11026
Submitted: 12 June 2011 Accepted: 19 October 2011 Published: 14 December 2011
Journal Compilation © Astronomical Society of Australia 2012
Abstract
The process of determining the number and characteristics of sources in astronomical images is so fundamental to a large range of astronomical problems that it is perhaps surprising that no standard procedure has ever been defined that has well-understood properties with a high degree of statistical rigour on completeness and reliability. The Evolutionary Map of the Universe (EMU) survey with the Australian Square Kilometre Array Pathfinder (ASKAP), a continuum survey of the Southern Hemisphere up to declination +30°, aims to utilise an automated source identification and measurement approach that is demonstrably optimal, to maximise the reliability, utility and robustness of the resulting radio source catalogues. A key stage in source extraction methods is the background estimation (background level and noise level) and the choice of a threshold high enough to reject false sources, yet not so high that the catalogues are significantly incomplete. In this analysis, we present results from testing the SExtractor, Selavy (Duchamp), and sfind source extraction tools on simulated data. In particular, the effects of background estimation, threshold and false-discovery rate settings are explored. For parameters that give similar completeness, we find the false-discovery rate method employed by sfind results in a more reliable catalogue compared to the peak threshold methods of SExtractor and Selavy.
Keywords: methods: data analysis — radio continuum: general — techniques: image processing
1 Introduction
The Australian Square Kilometre Array Pathfinder (ASKAP) (Johnston et al. 2008; DeBoer et al. 2009) is a new radio telescope being built on the Australian candidate Square Kilometre Array (SKA) site in Western Australia. ASKAP will consist of 36 12-m antennas spread over a region 6 km in diameter. Although the array of antennas is no larger than many existing radio telescopes, each antenna will be equipped with a phased-array feed of 96 dual-polarisation pixels, giving it a 30 deg2 field of view and a very fast survey speed. The Evolutionary Map of the Universe (EMU) project (Norris et al. 2011) is a wide-field radio continuum survey planned for ASKAP. The primary goal of EMU is to make a deep (rms ~ 10 μJy/bm) radio continuum survey of the entire southern sky at 1.3 GHz, extending as far north as +30° declination, with a 10-arcsec resolution. EMU is expected to detect and catalogue about 70 million galaxies, including typical star-forming galaxies up to z = 1, powerful starbursts to even greater redshifts, and active galactive nuclei (AGNs) to the edge of the visible universe. The amount of data involved with ASKAP (~2.5 GB/s, or 100 PB/year) requires that the source detection and measurement is fast, robust and highly automated.
Source detection and measurement is a problem common to all astronomical imaging surveys and projects, and numerous software tools have been developed to perform this initial step in the analysis of imaging data. With the advent of large-area surveys the automation of this process is clearly crucial. This has led to a variety of survey-specific source-finders being developed, each optimised to address the specific issues associated with the imaging technology of each survey and its corresponding image properties and artefacts. What has not developed in parallel is an analysis of the common steps in source identification and measurement in order to assess the optimal approaches or algorithms that should be used to maximise the robustness and scientific utility of the resulting source catalogues. This is partially a consequence of images obtained using different telescope or imaging technologies (UV/optical/near infrared/far infrared, compared to radio, or X ray, or gamma ray) having very different characteristics. Consequently, the assumptions used in source-finders developed for images at one wavelength or technology are not typically applicable for others.
The analysis presented here looks at the first steps taken in the source-finding process, those of background estimation and thresholding. This is done explicitly in the context of radio interferometric imaging, although the expectation is that the conclusions should be more broadly applicable. Furthermore, our investigation has a focus on identifying an optimal approach for the source identification and measurement to be implemented in the ASKAP image-analysis software pipeline. This analysis complements that of Hancock et al. 2011 (in prep.), which presents a detailed exploration of existing source-finding tools, their underlying algorithms, and how they perform on simulated radio interferometer images. Together, these analyses comprise the first part of a thorough investigation of each stage of the source-identification and measurement process that is being pursued as part of the design study for EMU.
Several radio source identification and measurement tools are in common use. These include the miriad/aips Gaussian fitting routines imsad, sad and vsad, sfind (Hopkins et al. 2002), and Duchamp (Whiting 2008) as well as SExtractor (Bertin & Arnouts 1996). There are also a variety of survey-specific tools, such as happy (a modified version of sad used in the FIRST survey, White et al. 1997), a machine-learning back-end to vsad used to construct the SUMSS catalogue (Mauch et al. 2003), bdsm (used for the LOFAR source-finding, N. Mohan, in prep.), and the floodfill algorithm being used in the Australia Telescope Large Area Survey (ATLAS) Data Release 2 (Murphy et al. 2007; Hales et al. 2011 in prep.).
As stand-alone tools, none of these are adequate for EMU, due to limitations evident in the treatment of background estimation, approaches to treating a varying noise level across an image, and importantly in the numbers of artefacts incorrectly identified as sources. Here we aim to test the approaches to both background estimation and thresholding, in order to identify an optimal approach for the EMU survey. All existing tools have implemented the complete sequence of steps, from background and noise-level estimation, through threshold-setting and ‘source-pixel’ identification, to source measurement. It is thus challenging to extract robust information about each independent step in the source-identification process. We do this here for a selection of tools through a judicious choice of parameters in the tasks we investigate, and interpret our results cautiously as a consequence. We emphasise that we are focussing here on two-dimensional data (radio continuum images), with our results expected to be applicable generically to two-dimensional image source identification.
We present details of the simulated data used in our analysis in Section 2, and the algorithms being tested in Section 3. The background estimation and local rms noise estimates are discussed in Section 4, with the reliability and completeness statistics being used as a metric to compare the different approaches in Section 5. Our results are summarised in Section 6.
2 Simulated Data
2.1 ASKAP Simulation
We used the December 2010 set of simulations by the ASKAP team, hereafter referred to as the ASKAP simulation, to test the source extraction methods. This simulation is of a full continuum observation with critically sampled beams and full 6-km ASKAP configuration, using an input catalogue of ~7.7 million sources down to 1 μJy from the SKADS S3-SEX simulation (Wilman et al. 2008, 2010). The effect of the phased-array feed was simulated by using 16 idealised beams, spaced in a rectangular grid one degree apart. This results in 30–40% peak-to-peak sensitivity variation in the simulation. The pixel scale of this simulation is 2.75 arcsec. For these tests we removed the outer 500 pixels of the simulated continuum to reduce potential edge effects. The simulated continuum image used in these tests is shown in Figure 1. The noise in the simulated image is approximately 35 μJy rms, although it varies across the field.
2.2 Hancock et al. Simulation
The ASKAP simulation is made up of millions of sources and includes instrumental artefacts. The SKADS S3-SEX input source list contains many multiple sources (FRI and FRII galaxies) as well as extended sources. We wish to test the source extraction algorithms where deblending and extended sources are not an issue. We also wish to test the algorithms for an idealised case of Gaussian noise. For this we use the simulation of Hancock et al. 2011 (in prep.). In this simulation a catalogue of sources was created with the flux of the sources drawn from the source count distribution N(S) ~ S–2.3 (Hopkins et al. 1998). The sources are all compact (1–2 FWHM) when convolved with the synthesised beam (30 arcsec). A map with 25 μJy Gaussian noise was then created and convolved with a 30 arcsec beam, before the sources were injected into the image. The image has a pixel scale of 6 arcsec so that the synthesised beam of the telescope is sampled 5 times in each direction. There are 15,000 sources in the simulated image with fluxes >1 σ.
3 Source Extraction Algorithms
A review of existing source-finding tools, their underlying algorithms, and how they perform on simulated radio interferometer images, is presented by Hancock et al. 2011 (in prep.), which compares the performance of the source-finders imsad, sfind, SExtractor, Selavy, Floodfill and a newly developed tool, Tesla, in the identification and characterisation of artificial sources. Their analysis emphasises some common failure modes in existing tools, and identifies a potential solution, implemented and tested using the new tool, Tesla, to rectify these shortcomings.
To complement the analysis of Hancock et al. (2011, in prep.), we focus here on the background estimation and thresholding approaches as implemented in the SExtractor, Duchamp and sfind algorithms for source extraction. SExtractor and Duchamp implement a fixed signal-to-noise (S/N) thresholding technique while sfind uses a statistical method called false-discovery rate (FDR) that sets a threshold based on a user-specified limit to the fraction of falsely detected sources (Miller et al. 2001; Hopkins et al. 2002). The thresholds set by these algorithms are based on peak flux densities, not integrated flux densities.
SExtractor (Bertin & Arnouts 1996) is a source extraction tool that detects sources through thresholding. A group of connected pixels brighter than some threshold above the background is identified as a detection. SExtractor uses several steps to detect sources. These are background subtraction, image filtering, thresholding, deblending, and source parameterization (including isophotal analysis, photometry and astrometry).
Duchamp (Whiting 2011, in prep.) is a source-finding tool designed for use with spectral-line cubes, particularly those dominated by noise with relatively small sources present (for example extragalactic HI surveys or maser surveys). Sources are identified by applying a threshold (a uniform one for the entire image/cube) and grouping sets of adjacent (or suitably close) voxels together. It is possible to do various types of pre-processing to enhance the detectability of sources (e.g. smoothing, spectral baseline subtraction, wavelet reconstruction). Duchamp forms the basis for the prototype source finder for the ASKAP science processing pipeline. This implementation, known as Selavy to distinguish it from the standalone Duchamp, is still under development. It has several features that do not appear in Duchamp. These are described in the paper by Whiting (2011) in this volume. The key feature of these, relevant to this work, is the ability to vary the threshold according to the local noise properties. This uses a similar procedure to SExtractor: defining a set box size, and, for each pixel, finding the noise properties within a box centred on that pixel. In this way, a different flux threshold can be defined for each pixel, given a signal-to-noise ratio threshold. This work makes use of the Selavy implementation, to take advantage of this and other new features, and we refer to this algorithm as Selavy hereafter.
FDR is a statistical procedure which is an alternative to the simple threshold definition used in the identification of sources. In SExtractor or Selavy (and many traditional approaches to source identification) a source is initially identified by pixels with an intensity above a threshold defined as some multiple of the local rms noise level, xσ. In the FDR approach, the threshold is defined through a robust statistical procedure that takes into account the intensity distribution of all pixels in an image (both source and noise), compared to an image of equal size containing only noise, in setting a threshold. The resulting threshold places a limit on the fraction of sources identified that may be false based simply on the statistics of the noise distribution (Miller et al. 2001). This procedure has been implemented for source measurement in radio images in the Miriad task sfind (Hopkins et al. 2002) but while it is also an option for defining the threshold in the stand-alone version of Duchamp, it is not yet implemented in Selavy. The key parameters for sfind in implementing the FDR algorithm are the rmsbox size (similar to the mesh-size for SExtractor) and α, which is the desired fractional limit to the number of false detections in the final source list.
4 Background and Noise Maps
The first stage of source extraction in general is background estimation. In most astronomical images the background is non-zero and varies over the frame. Radio images from interferometeric synthesis techniques may in general have a non-zero background, although in many cases it is small (e.g. Rich et al. 2008). It is not expected that the EMU images will have a significant non-zero background, but the background estimation step is nevertheless important. In the first place, a significant non-zero background may be an indicator of problems with the data or the observation, and can be used as a step in quality control of the imaging data. Moreover, there will be low-level diffuse emission close to the galactic plane, and extended structures such as supernova remnants at latitudes up to tens of degrees. For the identification and measurement of point sources, these extended diffuse structures and emission can be treated as a background and removed in the same fashion. The Planck Early Release Compact Source Catalogue (PERCSC; Planck Collaboration 2011) demonstrated that extragalactic radio sources can still be extracted successfully in the galactic plane with careful background estimation. Regions away from the plane of the Milky Way are expected to have a zero background.
It is also a common technique to apply some filtering or weighting of images before the background and noise estimation is performed. SExtractor allows both filtering and weighting, and Selavy allows filtering, but sfind does not perform either filtering or weighting. These aspects of background estimation are not explored in the current analysis, in order to enable more direct comparison of the actual background estimation algorithms being applied.
4.1 SExtractor
The value measured at each pixel of a radio image is a sum of the background signal and the emission from the radio sources of interest. To construct a background map SExtractor computes an estimator for the local background in a rectangular region, or ‘mesh’, of a grid that covers the whole image. The estimator is a combination of κσ clipping and mode estimation (similar to DAOPHOT; see e.g. Da Costa 1992). In brief, the local background is clipped iteratively until convergence at ±3σ around its median and then the mode is estimated. The background map is generated from a bicubic spline interpolation between the meshes of the grid.
The choice of mesh size is very important. If it is too large then small-scale variations in the background and noise will be lost, but if it is too small then the background and noise estimations will be affected by object emission. Published surveys have found mesh sizes with widths of 8 to 12 times the point-spread function (PSF), or synthesised beam size, produced good results for noise estimation in deep radio continuum surveys (Huynh et al. 2005; Schinnerer et al. 2007, 2010). In the Galactic plane, PERCSC (Planck Collaboration 2011) found empirically that a background mesh size of 4 to 24 beamwidths yields a background image that successfully combines substructure in the background and the instrumental noise in the image.
In this study we explore mesh sizes of 3, 10, 20 and 100 times the beamwidth. SExtractor also has a smoothing parameter which allows the background map to be smoothed to suppress any local overestimations due to bright sources, hence a mesh size of 10 beamwidths with a smoothing filter of 3 mesh sizes (30 beamwidths) is also investigated. The difference between choosing a large mesh size and smoothing on the same scale is subtle. Choosing a mesh size of 30 beamwidths splits the image into a grid of 30 × 30 beamwidth squares, the background level and rms is calculated in those regions, and then the background and noise images are made from a bicubic spline fit to this grid of statistics. Smoothing, on the other hand, is a median filter (here 30 beamwidths) applied after the background and noise image is made from the smaller mesh size (here 10 beamwidths). Smoothing is therefore useful where the bicubic spline interpolation breaks down, such as in crowded fields. Initial investigation showed that mesh sizes of 10 and 20 beamwidths produce satisfactory background and noise images, and subsequent investigation of reliability and completeness will focus on those, as well as that with the smoothing filter applied.
The background and rms noise images for mesh sizes of 10, 20 and 30 (10 smoothed by 3) beamwidths are shown in Figures 2 to 5. All background maps show large-scale ripples in the image from sidelobes near the brightest sources in the ASKAP simulations. The rms noise maps show high-noise regions around these brightest sources, as desired for spurious source rejection. The rms noise map, however, is affected by fainter (~1 to 10 mJy) point sources when the mesh size is only 10 beamwidths (Figures 3 and 5). These sources are well-cleaned and do not have significant sidelobes, so they should not be contributing to the noise in the image. We therefore find that using a mesh size of 10 beamwidths but smoothing to 30 beamwidths seems to result in the highest quality background and rms maps. The effect of the phased array feed on the ASKAP simulations can be seen in the grid pattern of low- and high-noise regions in the background images (Figure 3).
4.2 sfind
sfind determines the fraction of expected false sources by first estimating the background and rms for the whole image using uniformly distributed regions of a user-specified ‘rmsbox’ size in pixels. A normalised image is made from the input image by subtracting the mean and then dividing by the rms. If the image noise properties are Gaussian, then the normalised image would ideally show a Gaussian distribution with a mean of 0 and σ = 1. The false-discovery rate method is implemented on this normalised image. Each pixel is assigned a p-value, a probability that it is drawn from the noise distribution, from this image. Therefore the quality of this normalised image is important and the ‘rmsbox’ parameter needs to be carefully considered.
The output-normalised and rms images for rmsbox sizes corresponding to 10 and 20 beamwidths are shown in Figures 6 and 7. For both rmsbox sizes, the ASKAP normalised images have a mean of 0.03 and standard deviation of 1.04, when pixels with an absolute value greater than 5 are excluded from the statistics. Similarly, for the Hancock et al. simulations an rmsbox size of 10 beamwidths results in a mean of 0.10 and standard deviation of 1.10, while 20 beamwidths results in a mean of 0.10 and standard deviation of 1.08. So the normalised images are close to the ideal Gaussian distribution of 0 mean and σ = 1.

|
The rms image from an rmsbox size of 10 beamwidths appears to be more affected by bright sources than rms image using the larger rmsbox of 20 beamwidths. As with the SExtractor rms maps, high noise estimates are expected around the brightest sources with significant sidelobes, and this is necessary to accurately reject false detections. Sources as faint as a few mJy affect the noise image for an rmsbox size of 10 beamwidths (Figures 6 and 7), but this is not desirable as these sources do not have significant sidelobes.
4.3 Selavy
As with the other source-extraction algorithms, Selavy requires the background and noise levels to determine a threshold level. It does this by calculating the mean or median for the background, and rms or the median absolute deviation from the median (MADFM) for the noise level. The median and MADFM are robust statistics which are not biased by the presence of only a few bright pixels, and are used by Selavy by default. The ASKAP software pipeline implementation of Selavy used in this work does not yet allow the output of the background and noise images, so no direct comparison of these images can be made.
4.4 Results of Background and Noise Estimation
To examine the background and noise images quantitatively we examined the distribution of pixel values of these images. A mesh size of 10 beamwidths results in a larger spread in background values than either 20 beamwidths or 10 beamwidths plus smoothing (Figure 8). All mesh sizes give a similar median pixel value in the background image, i.e. similar average background across the whole image. For comparison we also show the pixel distribution for a mesh size of 3 beamwidths (grey dotted line in Figure 8). This also has a similar median pixel value, but a much greater variation in background levels, indicating that the background determination is probably affected by local structure (e.g. radio sources, local noise peaks and troughs) for this small mesh size.
The pixel distributions of the rms noise images constructed by SExtractor and sfind are shown in Figure 9. In the case of the ASKAP simulations there is no significant difference between using a 10 beamwidth mesh size and 20 beamwidth mesh size, with only minor differences appearing in the distributions seen at the lowest rms noise levels, below about 30 μJy. The rms noise level of the ASKAP simulation is approximately 35 μJy, although with 30–40% variations over the field. Both SExtractor and sfind appear to be recovering noise estimates that peak around 35 μJy, for both mesh sizes tested.
In the case of the Hancock et al. simulation, however, there is a significant difference in noise image pixel values for mesh sizes of 10 versus 20 beamwidths. The input rms noise level for this image was 25 μJy, but is effectively a few percent higher due to the convolution with a Gaussian beam leading to correlated noise between pixels. All estimates seem to be slightly higher than 25 μJy, as expected, but with those from sfind being marginally (but systematically) lower than those from SExtractor. We also see a bimodal distribution in the noise image pixel values for some cases (20 beamwidths and smoothing to 30 beamwidths). This is because the convolution with a Gaussian was only applied to a circular region of interest (as seen in Figure 1). The empty (noise-only) areas in the full Hancock et al. image which lie outside this region remain included in these statistics, however, leading to the secondary ‘peak’ near 25 μJy. The 20 beamwidth mesh sizes in both cases show more narrowly peaked distributions than those of 10 beamwidths, and with the peak value at higher flux densities. This is likely to lead, for the 20 beamwidth mesh sizes, to fewer spurious detections (a higher reliability) for a given threshold level, but possibly at the expense of completeness.
The pixel distribution for an SExtractor mesh size of 3 beamwidths peaks at a substantially lower value for both simulations, indicating underestimated rms noise values. The reliability estimates in § 5 below imply that such a small mesh size and the correspondingly lower rms noise values inferred leads to an increased number of spurious sources being detected.
Overall, the background estimation behaviours of both SExtractor and sfind, for common mesh sizes in each simulation, were similar. It is clear, though, that the choice of mesh size can lead to substantially different background estimates, and the fact that this is typically a user-defined step in existing source-finding tools suggests that it is perhaps a challenging parameter to estimate in an automated fashion.
5 Reliability and Completeness
The efficacy of different approaches to background estimation and threshold setting is assessed in our analysis by reference to the completeness and reliability statistics for the resulting source catalogues, compared to the known input catalogues. Here we present the details of these metrics for different combinations of the approach to the background estimation and the threshold level, for each of the algorithms being explored, as implemented in the three software tools.
Completeness is a measure of the fraction of real sources detected. For our analysis we define completeness as the fraction of input sources which have a detected output source counterpart. Input sources were deemed to be detected if they had at least one measured source within 0.5 synthesised beam FWHM.
Reliability is a measure of the fraction of detected sources that are real. For our analysis we define reliability as the fraction of output sources which have an input catalogue counterpart. The input source list was limited to those artificial sources having a flux density greater than 1 σ, in order to keep the number of ‘truth’ sources to a manageable quantity. Sources fainter than 1 σ, (which exist in the input SKADS S3-SEX simulated source list for the ASKAP image), are much fainter than the lowest tested threshold (3 σ) for our analysis. We do not expect that the omission of these from our analysis will have any effect on our results.
The measured sources were deemed to have a counterpart based only on positional coincidence, specifically if there is at least one ‘truth’ source within 0.5 synthesised beam FWHM. We place no constraint on how the output flux density compares to the ‘truth’ value, although this is another criterion that has been applied by other teams in determining whether a source has been recovered successfully (e.g. Planck ERCSC team). Here we are not exploring the properties of the source fitting routines, limiting ourselves only to the statistics of detections as a metric for assessing the background and noise-estimation algorithms. Consequently we do not include the output flux density estimates in assessing the recovery of input artificial sources.
5.1 SExtractor
SExtractor detects, and performs source-measurement on, pixel islands that lie above the user given threshold, which we set as a multiple of the noise image calculated in Section 3.1. This is in effect applying a local S/N threshold, provided the rms noise image is accurate. Our goal is to estimate the reliability and completeness of the source extraction for various thresholds.
The reliability for SExtractor on the ASKAP simulation, for thresholds of 3 σ to 20 σ, is summarised in Table 1. The reliability rises sharply between 3 σ and 5 σ from 54% to 88%. There is little difference in results from noise maps made from a 10 beamwidth mesh size compared to that made with a 20 beamwidth mesh size or with a 3 mesh-size smoothing. The 15 σ and 20 σ threshold SExtractor catalogues have surprisingly low reliabilities of only 92% and to 94%, and it turns out that this is due to a deblending issue. Multiple bright sources may be extracted as a single source with a position halfway between the input sources, hence they have no ‘truth’ counterpart. This effect is exacerbated when the threshold level is set so high, and a relatively large fraction of the input sources fall into this scenario.

|
The reliability for SExtractor on the Hancock et al. simulation is summarised in Table 2. The reliability rises sharply between 3 σ and 4 σ, from 88% to 98% in the case of a 10 beamwidth mesh size. Again, there is no significant difference to the reliability from applying the larger mesh size or smoothing in the noise calculation. The reliability is almost 100% by a threshold of 5 σ, which is expected in this simulation where the noise is completely Gaussian and the ‘truth’ catalogue is known.

|
The completeness as a function of input source flux density is shown in Figure 10, for SExtractor thresholds of 3, 4, 5, and 10 σ. A known bug in sfind limits results to an rmsbox size of 10 beamwidths (see 5.2), so we show results from a mesh size of 10 beamwidths to allow a comparison across all three algorithms. The completeness increases significantly at the faint flux density levels going from 10 σ to 3 σ, as expected. The completeness does not reach unity, however, even for low thresholds of 3 σ and 4 σ, for the ASKAP simulation. Since the noise is ~ 40 μJy in the ASKAP simulation we expected completeness to be about 100% by ~400 μJy for these detection thresholds. In comparison, SExtractor performs as expected with the Hancock et al. simulations and in this ‘perfect’ image the completeness reaches 100% for 3 σ and 4 σ thresholds at about 300 μJy.
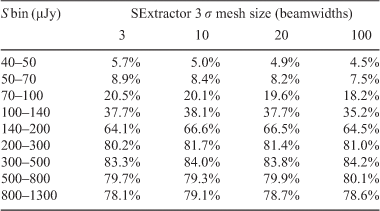
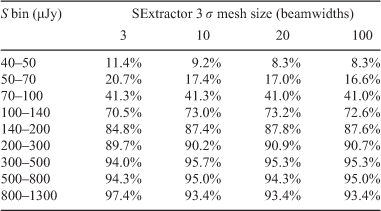
Tables 3 and 4 summarise the completeness for various flux density bins and SExtractor mesh sizes for a threshold of 3 σ. For both simulations the completeness increases in the lowest flux density bins as the mesh size is decreased to 3 beamwidths. This is consistent with the lower reliability of sources for this small mesh size. In this case more sources are extracted, hence the greater completeness, but at the cost of reduced reliability. At high flux densities the completeness does not appear to have a significant trend with mesh size, but this is as expected as small differences in the local noise value are only a tiny fraction of the source total flux density and therefore unlikely to affect whether a source is detected.
|
|
To further explore why the completeness does not reach unity for the ASKAP simulations, we examined bright (S > 1 mJy) input sources which were not extracted. The SKADS input list results in many multiple-component, or extended, sources which the extraction algorithms extract as one source at the midpoint between the two input sources (Figure 11). These input sources are extracted as a single source with a position further than 0.5 synthesised beam FWHM from the input sources, and hence the input sources are not identified as having been detected. In addition to the deblending issue, which accounts for some of the incompleteness, there are also extended sources with large total flux densities but low peak flux densities (Figure 11). This results in sources being missed by SExtractor as it searches only for pixels above the detection threshold.

|
5.2 sfind
The reliability and completeness are again estimated for sfind. The reliability estimates for the ASKAP simulation are presented for α values of 0.1, 1, 2, 5 and 10 percent in Table 5, for an rmsbox size of 10 beamwidths only. Due to a known bug, apparently triggered by particular configurations of pixels in a complex source, sfind failed to return a source list on this simulation for the larger rmsbox size (although the background estimation and associated images were correctly produced). The reliability for all tested values of α ranges from 91.9% to 92.5% for the ASKAP simulation. The reliability is quite flat for this simulation, over typical choices for α. We expect the reliability to be better than 99% for α = 0.1. The values here, as for SExtractor, are affected by the bright sources in the image which aren't in the original input catalogue. For the Hancock et al. simulation, and an rmsbox size of 10 beamwidths, the reliability increases from 91% to 97% for α = 10 to 0.1 (Table 6). The result is very similar for a rmsbox size of 20 beamwidths with the Hancock et al. simulation.

|

|
The completeness as a function of input source flux density is plotted in Figure 10, for sfind α values of 0.1, 1, 2, and 5 percent. For the ASKAP simulation, we find the completeness increases significantly between 100 and 300 μJy for all α values, but as for SExtractor the completeness does not reach unity at high flux density levels. Here sfind with α values of 1 to 5 gives completeness results that span similar values to those of SExtractor run with thresholds of 4 to 5 σ. The reliability of the sfind sources at these levels of completeness, however, is ~92% compared to 80 to 88% for the SExtractor sources.
In the case of the Hancock et al. simulation, an sfind α value of 5 results in completeness similar to SExtractor with a threshold of 4 σ (Figure 10), but with slightly worse reliability (93% compared to 98%). An sfind α value of 0.1, though, gives a completeness similar to an SExtractor threshold of 5 σ as well as similar reliability (virtually 100%), but 7% more sources were extracted by sfind with these parameters.
5.3 Selavy
We estimated the reliability and completeness of the Selavy source extraction on both sets of simulations. The reliability results are shown in Tables 7 and 8, for the ASKAP and Hancock et al. simulations, respectively. The reliability of Selavy increases sharply between 3 and 10 σ, but the reliability does not reach 100% for either simulation. The reliability is 88% and 85% for Selavy 20 σ runs on the ASKAP and Hancock et al. simulations, respectively. It is surprising that the reliability is greater for the ASKAP simulation, as the Hancock et al. image has only Gaussian noise and threshold techniques are expected to perform better in the case of pure white noise with no introduced instrumental artefacts. Although Selavy is more reliable than SExtractor at 3 σ for the ASKAP simulation, it is 5 to 10% less reliable than SExtractor overall. It also does not reach a reliability of 100% at the brightest thresholds for the Hancock et al. simulations, whereas this performance is reached by SExtractor. This is likely to be a deblending issue as we found that Selavy split a large proportion of bright sources into separate components, which would then not be matched to an input source. Limiting Selavy to fit only one or two Gaussians per detected ‘island’ of bright pixels may improve results and this needs to be tested in future work.
|
|
The completeness of the Selavy algorithm on both sets of simulations is shown in Figure 12. The completeness of SExtractor and Selavy are very similar for the Hancock et al. simulation. However, for the ASKAP simulation we find that Selavy is 5 to 10% more complete than SExtractor for the same nominal threshold limit. For the ASKAP simulations, Selavy reaches a maximum of ~90% completeness at high flux densities at low thresholds, compared to a maximum completeness of ~80% with SExtractor. So Selavy appears to be more complete than SExtractor, for the same nominal threshold limit, but this greater completeness comes at the cost of lower reliability.
Comparing Selavy to sfind, we find a similar outcome in that Selavy reaches relatively higher completeness but has much lower reliability. In the case of the ASKAP simulations, Selavy with a threshold of 5 σ has a completeness better than sfind with α = 0.1 to 5, however reliability is ~10% worse. For the Hancock et al. simulations the Selavy comparison to sfind is much like that with SExtractor, except that Selavy has ~15% lower reliability than SExtractor. For example, a Selavy threshold of 4 σ gives a completeness level comparable to sfind with α = 2, but with ~30% less reliability (68% compared to 95%).
5.4 Bright Source Region in ASKAP Simulation
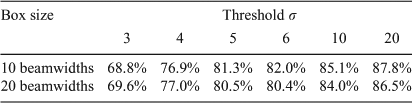
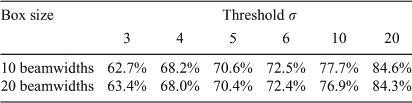
The ASKAP simulation has several regions near bright sources which contain significant sidelobes. The performance of source extraction algorithms may be degraded in regions with imaging artefacts, so we examine the reliability and completeness of the three source extraction algorithms in one such region (shown in Figure 13). This region, in the center of the top-right quadrant of the ASKAP image, has the most significant sidelobes in the ASKAP simulation. The reliability and completeness for two radial distances was investigated: distances less than 10 beams from the bright (3.6 Jy) source, and distances 10 to 20 beams from the bright source. The results are summarised in Tables 9 to 11.

|
SExtractor is only 2 to 25% reliable for the region closest to the bright source (<10 beams), for the thresholds explored, and different mesh sizes do not affect the reliability or completeness significantly. sfind and Selavy perform better in this region, with reliability reaching 100% for the most stringent parameters. However, the reliability of Selavy close to the sidelobe-producing source is significantly degraded using a mesh size of 20 beamwidths.
SExtractor reaches 100% reliability for high thresholds in the region 10 to 20 beams from the sidelobe producing source, but is only ~10% reliable at 5 σ and ~6% reliable at 3 σ. mesh sizes of 20 beamwidths or 10 beamwidths with smoothing give marginally better results than a mesh size of 10 beamwidths at these low thresholds. sfind is 100% reliable, and Selavy is 75% reliable or better, in this region for all the thresholds explored. So while Selavy is less reliable than SExtractor overall (see Section 5.3), it seems to perform better in this high noise region. The sfind generated noise map has values marginally lower than the SExtractor ones in this region, so this confirms the FDR routine is more effective in rejecting false sources compared to a simple peak thresholding technique.
The greater noise in this region of the image results in low completeness for all three algorithms. The high reliability of sfind and Selavy comes at the cost of lower completeness compared to SExtractor. However, even with a threshold of 3 σ, SExtractor has a maximum completeness of only 26%. A mesh size of 10 beamwidths instead of 20 beamwidths results in approximately 5% worse completeness, at the lowest thresholds, for SExtractor.
Finally we note that there are only 7 input sources within 10 beams of the bright source, and 23 input sources between a distance of 10 and 20 beams. More analysis on other regions is needed to derive better statistics, but from this work we can conclude that sfind and Selavy perform better than SExtractor in regions affected by significant sidelobes from a bright source.
6 Summary and Conclusions
We have tested SExtractor, Selavy and sfind to explore the effects of background and noise estimation, along with two approaches to thresholding, a simple nσ level compared to the false-discovery rate method, on source extraction. The tests were performed on two sets of simulations, the ASKAP simulations which are based on SKADS input source catalogue and include instrumental artefacts, and the Hancock et al. simulation which has only Gaussian noise. The Hancock et al. simulation is an idealised case that is useful for testing the algorithms in ‘perfect’ conditions.
The first step in source extraction is background subtraction and noise estimation. We have confirmed the results from the Planck team (Planck Collaboration 2011) and previous deep continuum radio surveys (Huynh et al. 2005; Schinnerer et al. 2007, 2010) that mesh sizes of 10 to 20 PSFs or beamwidths produce satisfactory background and noise images. We find that SExtractor background mesh sizes of 10 and 20 beamwidths produce similar results in terms of reliability. A visual inspection shows the background and noise images are still affected by local bright sources for a mesh size of 10 beamwidths, but combining a mesh size of 10 beamwidths with smoothing of 3 meshes produces the highest quality background and noise images. The reliability of the catalogues resulting from 10 and 20 beamwidth mesh sizes, however, does not differ significantly.
The fact that the background estimation step, so crucial in all the subsequent stages of source-identification and measurement, still needs to be manually tuned in most existing source-detection software, is a major concern. The optimum mesh size for background subtraction and noise estimation is likely to be image specific, and to vary perhaps substantially depending on the distribution of sources within the image. Developing an automated process for setting the mesh size when implementing the background and noise properties is clearly a priority, and will need to be developed as part of an automated pipeline for radio telescopes of the future such as ASKAP and the SKA. One possible method could be to use a tree-based approach, identifying rms noise levels for the whole image and for progressively smaller regions, so that each pixel can be associated with a ‘tree’ of rms noise values on each scale. Identifying the scale for which the rms noise plateaus for each pixel could be a suitable approach, and will be tested as part of the EMU design study.
The thresholding comparison was limited for the ASKAP simulation due to a ceiling in the completeness values, resulting from bright input sources with small separations that were not deblended well by any of the algorithms, and by the low peak flux density values for extended sources. Nevertheless, in this simulation we find that sfind with α values of 1 to 5 results in similar completeness to SExtractor run with thresholds of 4 to 5 σ. The reliability of the sfind sources is higher however, ~92% for sfind compared to 80–88% for the SExtractor. Selavy results in higher completeness than SExtractor or sfind for the ASKAP simulations, but at the cost of lower reliability. In regions with significant artefacts such as sidelobes from bright sources sfind and Selavy perform much better than SExtractor in rejecting spurious detections.
In the case of the Hancock et al. simulation, where noise is Gaussian and the sources more well-separated, SExtractor is 98% reliable with thresholds of 4 σ or greater. For the Hancock et al. simulation we find that nσ threshold approach of SExtractor and the FDR approach of sfind perform similarly, although the FDR thresholding of sfind seems to give somewhat better reliability at thresholds that produce comparable levels of completeness. In this idealised simulation SExtractor and Selavy gives similar completeness but the Selavy sources are 15% to 30% less reliable.
There is a trade-off between completeness and reliability in source extraction algorithms: parameters which give high completeness result in lower reliability. Overall, the false-discovery rate method, as tested with sfind, results in more reliable sources than SExtractor or Selavy, for parameters that give similar completeness levels. While more fine-tuning of Selavy, the prototype source finder for EMU, is required, our analysis suggests that the FDR approach is worthwhile pursuing and we recommend this be implemented in Selavy.
This analysis demonstrates that existing approaches to background and noise estimation seem to be limited not by the specific algorithms but rather the requirement to select appropriate mesh sizes over which to calculate a ‘local’ background and noise estimate. Future work will require development of an automated background mesh size estimation process for the ASKAP software pipeline, in particular for the EMU images. In addition, a complementary analysis of the source-fitting and parameter measurement approaches is also underway (Hancock et al. in prep.) which will establish the optimum approaches to these latter stages of source extraction.
Acknowledgments
We thank the anonymous referee for useful comments that have helped to improve this paper.
References
Bertin, E. and Arnouts, S., 1996, A&AS, 117, 393Da Costa, G. S., 1992, in Astronomical CCD Observing and Reduction Techniques, ed. S. B. Howell, ASP, 23, 90
DeBoer, D. R., 2009, IEEE Proceedings, 97, 1507
| Crossref | GoogleScholarGoogle Scholar |
Hopkins, A. M., Mobasher, B., Cram, L. and Rowan-Robinson, M., 1998, MNRAS, 296, 839
| Crossref | GoogleScholarGoogle Scholar |
Hopkins, A. M., Miller, C. J., Connolly, A. J., Genovese, C., Nichol, R. C. and Wasserman, L., 2002, AJ, 123, 1086
Huynh, M. T., Jackson, C. A., Norris, R. P. and Prandoni, I., 2005, AJ, 130, 1373
Johnston, S. et al., 2008, ExA, 22, 151
| Crossref | GoogleScholarGoogle Scholar |
Mauch, T., Murphy, T., Buttery, H. J., Curran, J., Hunstead, R. W., Piestrzynski, B., Robertson, J. G. and Sadler, E. M., 2003, MNRAS, 342, 1117
| Crossref | GoogleScholarGoogle Scholar |
Miller, C. J. et al., 2001, AJ, 122, 3492
Murphy, T., Mauch, T., Green, A., Hunstead, R. W., Piestrzynska, B., Kels, A. P. and Sztajer, P., 2007, MNRAS, 382, 382
| Crossref | GoogleScholarGoogle Scholar |
Norris, R. P., et al., 2011, submitted to PASA
Planck Collaboration, 2011, submitted to A&A, arXiv:1101.2041
Rich, J. W., de Blok, W. J. G., Cornwell, T. J., Brinks, E., Walter, F., Bagetakos, I. and Kennicutt, R. C., 2008, AJ, 136, 2897
| 1:CAS:528:DC%2BD1MXnsVKntw%3D%3D&md5=6d57067f1469ca5bb850302aade05abcCAS |
Schinnerer, E. et al., 2007, ApJS, 172, 46
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtFahtbrM&md5=f399119ee12980a25b8c4e6c108402f0CAS |
Schinnerer, E. et al., 2010, ApJS, 188, 384
| Crossref | GoogleScholarGoogle Scholar |
White, R. L., Becker, R. H., Helfand, D. J. and Gregg, M. D., 1997, ApJ, 475, 479
| Crossref | GoogleScholarGoogle Scholar |
Whiting, M. T., 2008, in Galaxies in the Local Volume, ed. B. S. Koribalski & H. Jerjen, Astrophysics and Space Science Reviews (Springer), 343.
Wilman, R. J., 2008, MNRAS, 388, 1335
Wilman, R. J., Jarvis, M. J., Mauch, T., Rawlings, S. and Hickey, S., 2010, MNRAS, 405, 447














